Employment of multivariate curve resolution to liquid chromatography coupled with NMR
Mohsen
Kompany-Zareh
*,
Somayeh
Gholami
and
Babak
Kaboudin
Department of Chemistry, Institute for Advanced Studies in Basic Sciences (IASBS), Zanjan, 45137-66731, Iran. E-mail: kompanym@iasbs.ac.ir; Fax: +98-241-415-3232; Tel: +98-241-415-3123
First published on 29th November 2011
Abstract
NMR spectral data from aliquots at different retention times of an ordinary liquid chromatographic column were resolved into individual concentration and spectral profiles using multivariate curve resolution based on alternative least squares (MCR-ALS) and canonical correlation analysis (CCA). Samples were a number of the reaction product mixtures obtained at different experimental conditions, based on a simple experimental design, and for synthesis of α-amido phosphonate. NMR data from different experiments were augmented and aligned using correlation optimized warping (COW) procedure. Orthogonal projection approach (OPA) was applied to make initial estimates for MCR-ALS. CCA was implemented in three steps; the first step was determining the regions of NMR peak clusters, the second was the rank analysis of each peak cluster, and the third was assignment of peak clusters to different compounds using CCA. Employing both resolution methods, the NMR data from liquid chromatographic column was successfully resolved to spectral and concentration profiles of pure components. From the resolved concentration profiles the optimum experimental conditions with maximum yield of reaction were obtained as air atmosphere and at 25 °C. Due to the fact that there is rotational ambiguity in the obtained results of MCR-ALS, the resolved concentration profiles from the two methods were different. However, both methods resulted in the same optimal experimental conditions.
1. Introduction
There are two fundamental approaches for the resolution of complex mixtures. The first is to improve physical separations, e.g. by optimizing chromatographic conditions, and the second is to use chemometrics methods for resolution, as discussed in this paper. There are numerous methods of coupled chromatography all with different characteristics both in terms of spectroscopy (e.g. sensitivity, selectivity) and chromatography (e.g. as a consequence of the detection method there may be limitations). Each coupled technique has its own advantages and limitations. For example, LC-NMR is less sensitive and has a higher limit of detection compared to LC-MS and LC-DAD. Consequently, it requires higher concentrations and usually chromatographic columns are overloaded, which often causes severe overlap and sometimes tailing to the chromatographic peaks. Most chemometric methods for resolution have been applied to liquid chromatography diode array detection (LC-DAD), liquid chromatography mass spectrometry (LC-MS) and gas chromatography mass spectrometry (GC-MS). Liquid chromatography nuclear magnetic resonance (LC-NMR) poses specific challenges especially in the limits of resolution, that many existing methods, are unable to cope well with. On-flow LC-NMR has an important role in various fields1–8 especially in the confirmation of the chemical composition of mixtures. In this report after complementation of reaction (t = tfinal), off-line NMR measurments of different aliquots (departed mixture from chromatographic column at different polarities of mobile phase) at different retention times from a simple chromatographic column were measured and considered. The application of this work is in cases when on-flow LC-NMR is not available and only a simple liquid chromatographic column (available in most organic chemistry labs) is accessible.NMR is a powerful technique for elucidating the structure of organic compounds. Before undertaking NMR analysis of a complex mixture, separation of the individual components by chromatography is ideal. During the last decade, the combination of the separation efficiency of LC with the specificity of NMR lead to a extremely powerful technique in carrying out qualitative and quantitative analysis of unknown compounds in complex matrices. The first paper on LC-NMR was published in 1978 using stop-flow to analyze a mixture of two or three known compounds.9 There are several publications using on-flow LC-NMR in various fields such as the confirmation and characterization of the chemical compositions of mixtures of aromatics,5 identification of plant constituents, food, biomolecules, metabolomics and metabonomics.10–14
Chemometrics or computational methods have been used for retention time measurement,15 rank determination16,17 and curve resolution18–20 of LC-NMR data in recent publications. The most common procedures for curve resolution such as HELP, WFA and ALS do not have a good resolution in LC-NMR data.21,22 In recent publications, canonical correlation analysis (CCA) with good performance for resolving these type of data has been reported.23
Multivariate curve resolution (MCR) methods are suitable for multidimensional data and their purpose is the correct determination of concentration profiles of individual components in time as well as in the spectral dimension, when mixtures cannot be resolved simply by chromatography. The methods have been classified in different ways21,22,24 including both modeling and self-modeling curve resolution (SMCR) methods.16 Modeling methods force a specific mathematical model, for example the shape of an elution profile25 or the shape of a curve in kinetics.26 Self-modeling methods do not demand a priori information about the spectral or concentration profiles but apply natural constraints27 such as unimodality and non-negativity. SMCR can further be categorized as iterative, non-iterative and hybrid according to the algorithm used. Commonly used iterative methods include iterative target transformation factor analysis (ITTFA),28,29 alternating least squares (ALS),30,31 positive matrix factorization32 and simplex-based methods.33 Methods which take advantage of local rank information and are non-iterative in nature include evolving factor analysis (EFA),34,35 window factor analysis (WFA),36,37 heuristic evolving latent projections (HELP),38,39 subwindow factor analysis (SFA)40,41 and parallel vector analysis (PVA).42 A third category consists of hybrid methods like automatic window factor analysis (AUTOWFA),43 and Gentle.44 Two new methods have specifically been reported recently for LC-NMR, belonging to the last category, including canonical correlation analysis (CCA)23 and constrained key variable regression (CKVR).45,46 Most multivariate methods for regression were first reported in the context of LC-DAD and infrared spectroscopy (IR) where noise level and chromatographic resolution are not such serious problems; in those datasets these methods have usually yielded excellent results.
In this paper, we use chemometric methods to resolve LC-NMR spectral and concentration profiles for the reaction synthesis of α-amido phosphonate by making use of well-defined NMR clusters. The main objective of this paper is determining the optimum conditions for this reaction and identification of the 1H-NMR spectrum of the main product using two chemometric methods and comparing the ability of MCR-ALS and CCA to resolve the complex mixtures.
2. Theory
2.1. Canonical correlation analysis (CCA)
“Resonance cluster” denotes a region of resonance in NMR spectra which appears with noise on both sides. Each peak cluster contains the same number of rows as in the original data matrix but a reduced number of columns. An NMR spectrum consists of several peak clusters and the relationships between each peak cluster provides valuable information. Canonical correlation analysis (CCA) as a mathematical tool can be used to consider these relationships. The theory of CCA will be explained briefly here and the reader is referred to the literature for more details.23 Suppose that the ranks of resonance clustersA and B are m and n (m ≤ n), respectively. Using PCA one can find orthonormal basis sets H and Q in the direction of samples which span the chromatographic direction of the peak cluster A and B, respectively. Any vector in clustersA and B can be written in terms of linear combination of the basis sets H and Q, for example:| k = Qb | (1) |
| p = Ha | (2) |
The cosine of the angle between p and k vectors is:
| pTk = aTHTQb | (3) |
It can be proved that a and b are the left and right singular vectors of HTQ40 by singular value decomposition (SVD),47e.g., the first singular vectors (left and right) are the first canonical weights. So, the canonical weight is spectrum of the first common component between two clusters. If there are n common components between two resonance clusters, there are n pairs of canonical weights for which the n singular value of HTQ is 1.
2.2. Shift correction
In NMR spectra the chemical shifts of peaks can vary as result of variations in physicochemical factors e.g. temperature, concentration, pH, and ion strength of the surrounding matrix that affect the sample.48 To have a bilinear resolvable data matrix of different samples, it is necessary to correct for shifts to ensure that all spectra are aligned in frequency throughout the data matrix. In this study, the correlation optimized warping49 (COW) approach has been applied for this purpose. COW operates on discrete signals by aligning a sample spectrums (length Ls) to a reference spectrumr (length Lr) by stretching or compression of sample segments using linear interpolation. The steps involved in the COW are presented below:501) Both reference and sample spectra are split into a user-defined number of segments N (length Ln).
2) The outer boundaries in either the reference or the sample have fixed positions. In the basic COW algorithm, the first and last point of the reference and sample are forced to match and the remaining N−1 boundary in the sample are the subject of the optimisation as in the following steps.
3) In Step 1 the left boundary of the first segment to align in the sample spectrum is then moved one data point to the left, not moved, and then moved one point to the right. Thus, three new segments of length Ln−1, Ln and Ln+1 data points, respectively, are created.
4) New sample segments of length Ln−1 and Ln+1 data points are interpolated or stretched to a length of Ln data points.
5) The correlation coefficient between the new three sample segments and the reference segment is calculated and stored.
6) Step 2 includes the second segment of the sample spectrum. The best position of the second boundary is achieved by calculating the three correlation coefficients (step 2) between the second segment (interpolated to Ln data points) and the segment of the reference spectrum.
7) The performance of the total warping so far is then the sum of the two correlation coefficients available in each of all the step 2 combinations.
8) This is continued until all boundaries have been moved.
9) From this, the optimal warping path can be found as the combination holding the maximum sum of correlation coefficients—stated differently to score a warping solution, an objective function, P, is constructed as the cumulative sum of the correlation coefficient of the previous sections.
10) Having done this gives the best possible aligned sample spectrum using the specific segment length and slack size (and reference spectrum).
2.3. Multivariate curve resolution–alternating least squares (MCR-ALS)
Multivariate curve resolution-alternating least squares is an iterative resolution method where at each iterative cycle, matrices C and S are calculated under constraints so that they minimize as much as possible the error in the reproduction of the original data set, D. The resolution of the profiles of species is accomplished by means of iterative alternating least squares consisting of the following steps.1) Least-squares calculation of concentration profiles C, (or spectral profiles, S), using the preliminary spectral (or concentration) estimations of species as an initial input of S (or C).
2) Given D and C, least-squares calculation of S under the suitable constraints.
These steps are repeated until reaching the optimal C and S contributions according to various optimization criteria.
2.4. Orthogonal projection approach (OPA)
The orthogonal projection approach (OPA) is a stepwise method for finding the pure variables in the data sequentially. OPA produces dissimilarity plots, which can be utilized in different ways to identify the number of components. The principle of OPA is as follows:In the first step a dispersion matrix Yi (Yi = [dmeandi]) is defined as a matrix consisting of the mean spectrum (dmean) and ithspectrum (di) of data matrix, D, dissimilarity of each spectrum with respect to the mean spectrum is calculated by the determinant of the dispersion matrix of Yi. The spectrum that is most dissimilar with respect to the mean spectrum (the highest determinant) is selected as ds1.
In the second step, the mean spectrum (dmean) is substituted by ds1 as a reference in Yi (Yi = [ds1di]) and the dissimilarity of each individual spectrum of D is calculated with respect to ds1. If a second reference spectrum, corresponding to maximum dissimilarity, is present, then a second reference vector, ds2, is added to the Yi matrix and dissimilarity is calculated again. This procedure is repeated until there is only random noise left in the dissimilarity plot. The rank of the data becomes equal to the number of reference spectra found in the whole process.
3. Experimental
Aniline (>99%), acyl chloride (99%), dichloromethane (>99%), n-hexane (95%), ethyl acetate (>99.5%) and sodium sulfate (>98%) were from Merck and were used without further purification. Diethyl phosphite (98%) was from Sigma-Aldrich and benzaldehyde (99%) was purchased from Fluka and used as received. In this reaction water was an effective parameter on the reaction and the presence of it could destroy the reaction, so all the solvents should be dry.3.1. Procedure
In the first step, by reaction of benzaldehyde with aniline in presence of sodium sulfate, imine as an initial material was sensitized. 0.55 g of prepared imine was dissolved in dry dichloromethane and then 0.12 ml acyl chloride was added to the reaction vessel and after 30 to 60 s 0.4 ml diethyl phosphite was added. The reaction proceeded at different temperatures (the reaction was done at room temperature, 25 °C, or under ice bath, 0 °C) and applied atmosphere (Ar or air) smoothly to afford the corresponding α-amido phosphonate after 13 h. After completion of the reaction (t = final), the final mixture of reaction that contained several products was introduced an ordinary column chromatography.3.2. Chromatography
Liquid chromatography was performed on a silica gel stationary phase and combined mobile phase. Ethyl acetate and n-hexane were used as the mobile phase in different concentrations of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 (v/v) to 0
0 (v/v) to 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 (v/v). TLC was applied regularly during the elution of the compounds on silica gel Polygram SIL/UV 245, to check the number of eluting compounds. Different ratios of ethyl acetate to n-hexane (1
30 (v/v). TLC was applied regularly during the elution of the compounds on silica gel Polygram SIL/UV 245, to check the number of eluting compounds. Different ratios of ethyl acetate to n-hexane (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 to 4
4 to 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) were used for TLC to arrange the elution of components with different polarities. After each step elution of the liquid chromatography column, solvents were rotary evaporated and then 1H-NMR spectra were obtained. Spectra were acquired on a Bruker JCAMP-DX-250 spectrometer using a 5 mm broad-band probe tuned to detect 1H resonances at 500.13 MHz. Data were collected at 300 K, without sample rotation, as 32,768 complex points, and with pre-saturation to remove the residual water signal. Scans were acquired with a spectral width of 7042.25 Hz. The data were processed using XWIN-NMR software.
1) were used for TLC to arrange the elution of components with different polarities. After each step elution of the liquid chromatography column, solvents were rotary evaporated and then 1H-NMR spectra were obtained. Spectra were acquired on a Bruker JCAMP-DX-250 spectrometer using a 5 mm broad-band probe tuned to detect 1H resonances at 500.13 MHz. Data were collected at 300 K, without sample rotation, as 32,768 complex points, and with pre-saturation to remove the residual water signal. Scans were acquired with a spectral width of 7042.25 Hz. The data were processed using XWIN-NMR software.
3.3. Software
All of the programs were used under Matlab 7.2. The data analysis was performed by computer programs written by the authors of this paper except the following: cow from the website maintained by Skov and his coworkers,50lsqnonneg from Optimization Toolbox of Matlab software.4. Results and discussion
The following approaches were employed to estimate spectral and chromatographic elution profiles in off-line LC-NMR data. The synthesis reaction of α-amido phosphonate was considered in this study. For the synthesis of this industrially valuable compound, initially an imine was synthesized (Scheme 1). The imine was then reacted with acyl chloride in a two step reaction. The two step imine reaction was performed in the presence of diethyl phosphite, with controlled temperature and controlled atmosphere. The first step was the formation of an unstable intermediate (Scheme 2). Nucleophilic attack of diethyl phosphite to the intermediate and formation of α-amido phosphonate was the second step of the expected mechanism (Scheme 3). Finally, a mixture of products, reagents and side products was obtained. Usually, separation methods are essential in identification and quantification of the considered products from the mixtures. In some conditions the similar polarity of products and side products prevents a complete separation of the components in the mixture by column chromatography. Similarly, this problem was observed in this system and it was not possible to separate the chromatogram of α-amido phosphonate from other compounds (as shown in Fig. 1 it is clear that the chromatogram of α-amido phosphonate was not resolved from that of other compounds). As a result, using a new dimension to measure the data and applying chemometrics methods for analysing the data appeared helpful. The added dimension to the data in this study was from the combination of chromatography with NMR spectroscopy, as an informative method.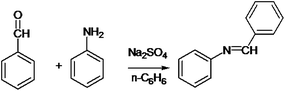 | ||
| Scheme 1 Formation of an imine with reaction of benzaldehyde and aniline in presence of sodium sulfate and n-hexane. | ||
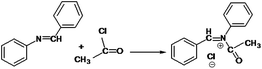 | ||
| Scheme 2 The first step of the imine reaction with acyl chloride in the presence of diethyl phosphite and the formation of an unstable intermediate. | ||
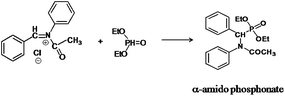 | ||
| Scheme 3 The second step of the expected mechanism, nucleophilic attack of diethyl phosphite to the intermediate and formation of α-amido phosphonate. | ||
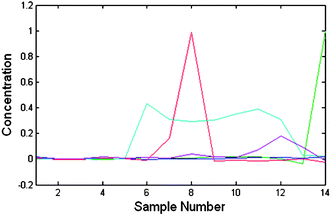 | ||
| Fig. 1 The obtained chromatograms of the 1st experiment using CCA shows that the α-amido phosphonate chromatogram (in green) has close polarity to other compounds and in all samples it has a co-eluent. | ||
For this purpose, the final mixture of reaction products was introduced into an ordinary liquid chromatographic column and was eluted with different mixtures of solvents. The polarity of the mobile phase (binary mixture of n-hexane and ethyl acetate) was changed during elution of the components in the column, by increasing the percentage of ethyl acetate. Departed aliquots from the chromatographic column at different polarities of mobile phase (different ratios of n-hexane to ethyl acetate) were measured by NMR spectroscopy and two way data were obtained.
Temperature and applied atmosphere were the two affecting parameters on the reaction. For optimization of these parameters, a simple two level experimental design was applied and at four different conditions of temperature and atmosphere the reactions were performed. Table 1 demonstrates the temperature and applied atmospheric conditions of all four experiments. 1H-NMR spectra of different eluted samples from four different experiments are shown in Fig. 2. Spectra for 14 eluted samples of experiment 1 (25 °C with air as applied atmosphere), 9 eluted samples of experiment 2 (25 °C with argon (Ar) as applied atmosphere), 14 eluted samples of experiment 3 (0 °C with air as applied atmosphere) and 10 eluted samples of experiment 4 (0 °C with argon (Ar) as applied atmosphere) are shown in Fig. 2(a) to 2(d). The obtained four data sets from these experiments were column wise augmented (in the direction of chemical shifts) and were analyzed together. Fig. 2(e) demonstrates the augmented data and Fig. 3(a) represents a part of the augmented data at the chemical shift 0.4 to 0.6 ppm. It evidently illustrates the unwanted local peak shifts in the data.
| T/°C | Argon | Air | |
|---|---|---|---|
| MCR-ALS | 25.0 | 0.81 | 4.86 |
| 0.0 | 0.00 | 0.86 | |
| CCA | 25.0 | 0.36 | 2.40 |
| 0.0 | 0.38 | 0.75 |
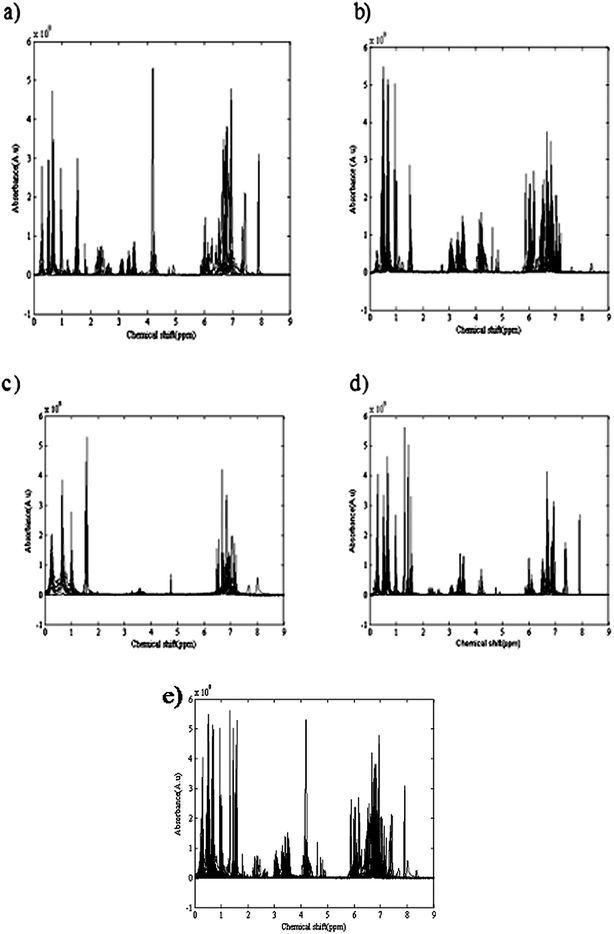 | ||
| Fig. 2 1H-NMR spectra of different eluted samples from four different experiments: (a) 14 eluted samples of experiment 1 (25 °C and air as applied atmosphere); (b) 9 eluted samples of experiment 2 (25 °C and argon (Ar) as applied atmosphere); (c) 14 eluted samples of experiment 3 (0 °C and air as applied atmosphere; (d) 10 eluted samples of experiment 4 (0 °C and argon (Ar) as applied atmosphere); (e) The column wise augmented four data sets (in direction of chemical shifts). | ||
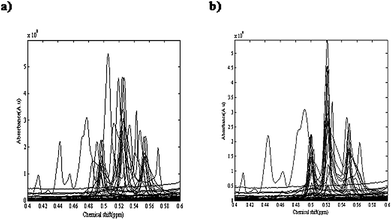 | ||
| Fig. 3 A part of the augmented four NMR data sets in chemical shifts ranging from 0.4 to 0.6 ppm, (a) before alignment and (b) after alignment. | ||
4.1. Alignment of NMR data signals using COW
In the manually performed simple liquid chromatographic system, the position and shape of peaks were found to be varied from one experiment to another. Therefore, it was necessary to correct these shifts to ensure that all spectra are aligned in frequency throughout the data matrix. A three-step procedure was proposed to correct and realign the spectra.Step 1: Because of the large number of variables (i.e. chemical shifts) in NMR data, before application of the COW procedure the data were divided into a number of regions and each region was aligned as follows.
Step 2: Reference spectrum selection was based on the product of the correlation coefficients between different spectra. The spectrum most similar to all others showed the largest correlation coefficient product and was selected to be the most suitable reference spectrum to use within the given data set.
Step 3: The COW algorithm required two user input parameters of segment length and slack size (flexibility). These two parameters were optimized using an automated method that has been introduced by Skov.50 Alignment of the NMR spectra was performed and the peaks were shifted according to the optimum parameter values (for example, about frequency region 29231 to 29485, slack size and segment length were optimized on 7 and 14, respectively). Fig. 3(a) demonstrates the augmented data before alignment. Fig. 3(b) shows the aligned spectra in the chemical shift ranging from 0.4 to 0.6 ppm that shows a considerable improvement.
4.2. MCR-ALS
The orthogonal projection approach (OPA) is a stepwise method for selection of key variables51 which was applied for rank analysis of 1H-NMR data and determination of the number of components. The rank of the data would be equal to the number of found pure spectra in the whole process of OPA, in the samples direction. The method could be applied in the chemical shift direction, as well, and concentration profiles of the components be estimated from the pure chemical shift regions. The rank of the data is the number of meaningful concentration profiles. Using orthogonal projection in either direction the number of components was obtained as six. Fig. 4(a) shows the obtained concentration profiles of OPA in the chemical shifts direction. The shapes of the sixth and seventh profiles were similar. It means that there is no additional information in the 7th profile (in green), compared to the 6th profile (in red). It suggests that there are a total of six components in the mixture. The initial estimate for the ALS algorithm was constructed using OPA. The MCR-ALS optimization was carried out under the constraints of non-negativity for both the spectral and the concentration profiles and unimodality for the concentration profiles. Fig. 4(b) presents the obtained concentration profiles from MCR-ALS that show concentration variations of each component as a function of sample number. Sample numbers 1 to 14 are due to experiment one, sample numbers 15 to 23 are nine samples of experiment two, sample numbers 24 to 37 are fourteen samples of experiment three and sample numbers 38 to 47 contain the obtained ten samples of experiment four. The conditions of each experiment have been mentioned in Table 1. The corresponding spectra were optimized during alternative least squares. Fig. 4(c) shows the obtained spectra of six compounds after convergence of MCR-ALS. The obtained spectrum for the considered product and the corresponding concentration profile of this compound also has been shown in Fig. 4(d).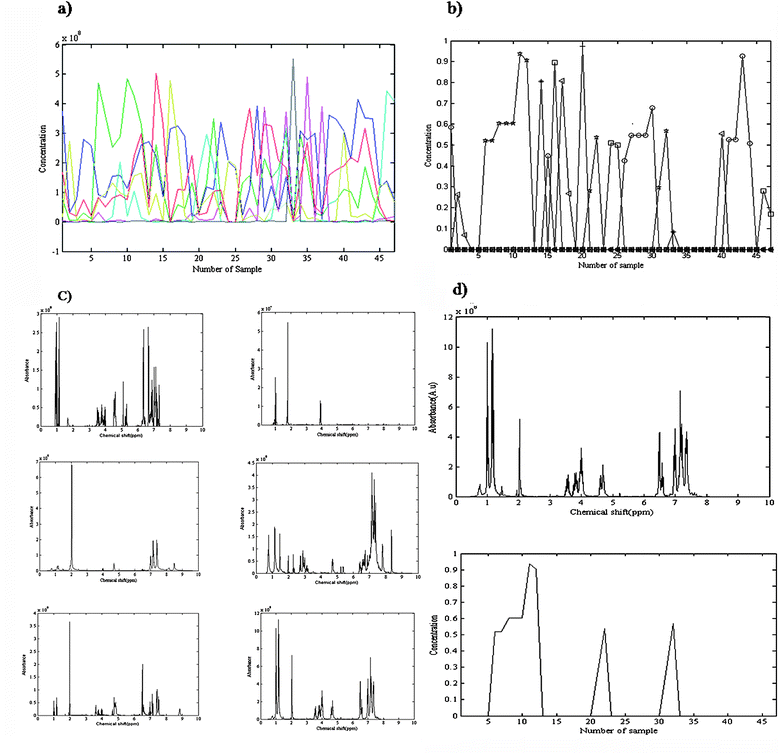 | ||
| Fig. 4 (a) Obtained concentration profiles of OPA in chemical shifts direction. There is no additional information in 7th profile (in green), compared to the 6th profile (in red). (b) Concentration variations of each of six components (squares, circles, triangles, plus signs, minus signs, stars) as a function of sample number. Samples numbers 1 to 14 relate to experiment one, samples number 15 to 23 are nine samples of experiment two, samples number 24 to 37 are fourteen samples of experiment three and samples number 38 to 47 contain the obtained ten samples of experiment four. (c) The obtained 1H-NMR spectra for all compounds in the final mixture of reaction after convergence of MCR-ALS, (d) the obtained 1H-NMR spectrum and corresponding concentration profile for α-amido phosphonate using MCR-ALS. | ||
4.3. CCA
In this study, some components showed very similar structures that resulted in high overlap in the measured spectral data. NMR spectra were characterized by several distinct clusters of resonances. Considering the relation between different clusters in the NMR spectral data from a number of mixtures, it can be determined which peaks belonged to which compounds. Canonical correlation analysis (CCA) is a mathematical tool for analyzing the relation and correlation between these regions.The first step was the determination of regions of NMR peak clusters. Determination of these regions can be implemented automatically by calculating the standard deviation52 along the column at each variable (frequency) using eqn (4).
 | (4) |
Here σn is the standard deviation, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) n is the mean intensity of nth column and M is the total number of rows in data matrix X. If a frequency does not include a significant NMR signal, its standard deviation is low that is related to noise. So, the peak cluster regions can be determined by plotting the standard deviation against frequency. The variation of standard deviation as a function of frequency is presented in Fig. 5(a). It shows nine clusters, from A to I.
n is the mean intensity of nth column and M is the total number of rows in data matrix X. If a frequency does not include a significant NMR signal, its standard deviation is low that is related to noise. So, the peak cluster regions can be determined by plotting the standard deviation against frequency. The variation of standard deviation as a function of frequency is presented in Fig. 5(a). It shows nine clusters, from A to I.
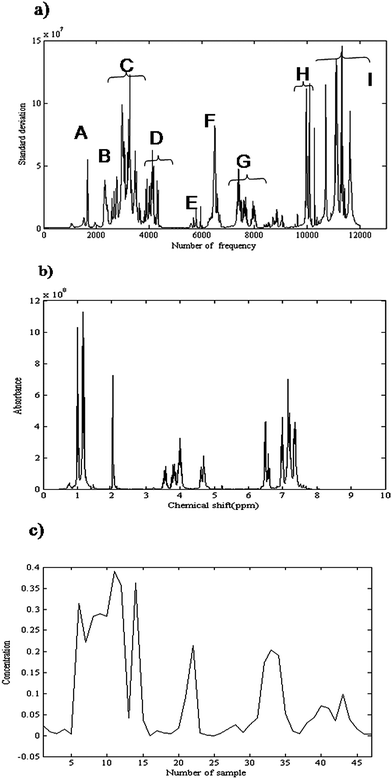 | ||
| Fig. 5 (a) Variation of standard deviation as a function of frequency. It shows nine peak cluster regions, from A to I. (b) Obtained 1H-NMR spectrum for considered product (α-amido phosphonate) using CCA. (c) Obtained concentration profile of α-amido phosphonate as a function of sample number using CCA. | ||
The second step was determining the rank of each peak cluster. Several rank analysis methods related to signal to noise ratio were applicable for rank determination.53 OPA was used for determining rank of each cluster. The rank of peak clusters A to I, which was obtained by OPA, was 4, 4, 2, 4, 4, 4, 2, 4, 3, respectively. The first k singular vectors from SVD on each peak cluster were kept for CCA. Indeed k was the rank of the considered peak cluster.
The third step in CCA was considering the relationship between clusters. Concentration profiles of common species between clusters were determined by considering the relationship between clusters. As explained in section 2.1, following SVD of HTQ in eqn (3) the singular values were considered as the angle between two peak clusters. For example 1st and 2nd singular values for combination of clusters G and F are 0.99 and 0.14, respectively. So, there is one common component between these clusters. Pure concentration profiles could be estimated by identifying peak clusters that represent only one common component. The corresponding spectra were obtained by nonnegative least square (NNLS). Fig. 5(b) shows the obtained 1H-NMR spectrum for the considered product (α-amido phosphonate). The obtained spectrum is similar to that obtained from MCR-ALS and both results show a good accordance with the measured spectrum of this compound. The corresponding concentration profile is shown in Fig. 5(c). The concentration profiles are due to four performed experiments. The profile obviously shows that the amount of product in the first experiment (first fourteen points) is higher than the other experiments.
4.4. Effective parameters on the reaction
In the considered system the reaction efficiency (yield) depended on factors such as temperature (T) and applied atmosphere (A). It was valuable to know the effect of each factor and determine their interactions. For a particular application it would be important to adjust the levels of these factors to ensure that the reaction efficiency is as high as possible. The peak area of the concentration profile of α-amido phosphonate was considered as a criterion of determination. According to a two levels two factor experimental design, argon and air were the two types of applied reaction atmospheres, and reaction temperatures were adjusted at 0.0 and 25.0 °C. Therefore, the effect of the parameters was investigated using the peak areas of the main product obtained from four experiments (Table 1). The estimated peak areas are by using MCR-ALS and CCA.The effect of changing the level of T was found as the average difference in response when T changes from high (25 °C) to low level (0 °C), keeping the level of A fixed. The average effect of altering the level of A was found similarly as shown in Table 2. If there was no interaction between factors then the change in response between the two levels of T should be independent of the level of A. The change in response when A changes from air to argon with T at a high level (25 °C) was calculated. Then the effect of changing A when T is at a low level (0 °C) also was calculated. If there was no interaction, these estimates of the effect of changing the level of A would be equal. The calculated effects of TA interaction for the result of MCR-ALS and CCA were 1.50 and 1.67, respectively. The effect was comparable to the main factors effect and was significant. It illustrated the necessity of employing a multivariate optimization method. It was concluded that response was at a maximum at T = 25 °C and A = air comparing the peak area values in four experiments. So, although they resulted in different profiles, the results from both methods predict that these conditions provide the optimum response. Both resolution results showed the significant interaction between the temperature and atmosphere as the two considered factors, and that the two factors cannot be optimized separately.
| Method | Effect of Temperature (T) | Effect of Atmosphere (A) | Interaction effect (TA) |
|---|---|---|---|
| MCR-ALS | 2.31 | 2.36 | 1.50 |
| CCA | 0.81 | 1.20 | 1.67 |
The results from both methods were acceptable. However, the obtained results from CCA, in comparison with MCR-ALS, showed a better agreement with the obtained results of thin layer chromatography (TLC) that shows the absence of a selective region in the concentration profiles. On the other hand, the rotational ambiguity in the MCR-ALS results is a problem that resulted in the estimated profiles not being the actual profiles, however, the obtained profiles are acceptable and useful because they fulfill all of the applied constraints such as non-negativity and unimodality.
5. Conclusion
The goal in this study was the identification of the 1H-NMR spectrum of product components (particularly the main product), determining the elution profiles of each component in the reaction at different experimental conditions, and determining the optimum conditions for the reaction. Aliquots from different retention times were manually transferred for measurement of the NMR spectra. In this way, low precision and poor chromatographic resolution were the main challenges in the analysis of this type of data. The results from both the MCR-ALS and CCA methods were acceptable and in good agreement. However, the obtained concentration profiles (elution of components in column chromatography) from CCA, in comparison with MCR-ALS, showed a better agreement with the obtained results of thin layer chromatography (TLC). In almost all the eluting samples of column chromatography at least two compounds were expected by TLC, which was not surprising as result of the close polarity of the materials. But the results of MCR-ALS reveal the one compound in all samples. The optimum conditions for this reaction were T = 25 °C and A = air by experimental designing at four levels. The results reveal that both parameters were affecting factors in the reaction and there was an interaction between these factors. The results show that using a simple low cost off-line liquid chromatographic column, before recording the NMR spectra could be helpful in the resolution of pure spectral data and yield of components in a reaction product mixture.Appendix
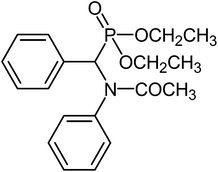
Characterizations of NMR spectrum of α-amido phosphonate-[(Acetyl-phenyl-amino)-phenyl-methyl]-phosphonic acid diethyl ester (α-amido phosphonate): White solid;
1H-NMR (CDCl3/TMS-250 MHz): 1–1.35 (t, OCH2–CH3), 2–2.1 (s, CO–CH3), 3-4-4.1 (m, O–CH2CH3), 4.78 (d, –CHP), 6.48–7.9 (m, Aromatic)
Acknowledgements
The authors wish to thank the Institute for Advanced Studies in Basic Sciences (IASBS) for supporting this study. We also thank Ms. Elahe Jafari for her valuable comments about reaction procedure.References
- J. L. Wolfender, S. Rodriguez and K. Hostettmann, J. Chromatogr., A, 1998, 794, 299–316 CrossRef CAS.
- J. L. Wolfender, K. Ndjoko and K. Hostettmann, J. Chromatogr., A, 2003, 1000, 437–455 CrossRef CAS.
- F. C. Stintzing, J. Conrad, I. Klaiber, U. Beifuss and R. Carle, Phytochemistry, 2004, 65, 415–422 CrossRef CAS.
- K. Iwasa, A. Kuribayashi, M. Sugiura, M. Moriyasu, D. U. Lee and W. Wiegrebe, Phytochemistry, 2003, 64, 1229–1238 CrossRef CAS.
- A. M. Gil, I. F. Duarte, M. Godejohann, U. Braumann, M. Maraschin and M. Spraul, Anal. Chim. Acta, 2003, 488, 35–51 CrossRef CAS.
- M. V. S. Elipe, Anal. Chim. Acta, 2003, 497, 1–25 CrossRef.
- E. Bezemer and S. Rutan, Anal. Chim. Acta, 2002, 459, 277–289 CrossRef CAS.
- K. Albert (Ed.), On-line HPLC-NMR and Related Techniques, Wiley, Chichester, 2002 Search PubMed.
- N. Watanabe and E. Niki, Proc. Jpn. Acad. Ser. B, 1978, 54, 194 CrossRef CAS.
- D. A. Laude, R. W. K. Lee and C. L. Wilkins, Anal. Chem., 1985, 57, 1464–1469 CrossRef CAS.
- D. G. Robertson, M. D. Reily and J. D. Baker, Expert Opin. Drug Metab. Toxicol., 2005, 1, 363–376 CrossRef CAS.
- J. T. Brindle, H. Antti, E. Holmes, G. Tranter, J. K. Nicholson, H. W. L. Bethel, P. M. Clarke, E. Scofield, D. E. McKillikghan, D. Mosedale and D. Grainger, Nat. Med., 2002, 8, 1439–1444 CrossRef CAS.
- H. C. Keun, Pharmacol. Ther., 2006, 109, 92–106 CrossRef CAS.
- J. C. Lindon, E. Holmes and J. K. Nicholson, Pharm. Res., 2006, 23, 1075–1088 CrossRef CAS.
- M. Wasim, M. S. Hassan and R. G. Brereton, Analyst, 2003, 128, 1082 RSC.
- E. R. Malinowski, Factor Analysis in Chemistry, Wiley, NewYork, 2002 Search PubMed.
- R. B. Cattell, Multivar. Behav. Res., 1966, 1, 145–276 CrossRef.
- E. Pere-Trepat, A. Hildebrandt, D. Barcelo, S. Lacorte and R. Tauler, Chemom. Intell. Lab. Syst., 2004, 74, 293–303 CrossRef CAS.
- W. H. Lawton and E. A. Sylvestre, Technometrics, 1971, 13, 617–633 CrossRef.
- P. Geladi, Spectrochim. Acta, Part B, 2003, 58, 767–782 CrossRef.
- H. Shen, C. Y. Airiau and R. G. Brereton, J. Chemom., 2002, 16, 165–175 CrossRef CAS.
- H. Shen, C. Y. Airiau and R. G. Brereton, J. Chemom., 2002, 16, 469–481 CrossRef CAS.
- H. Shen, C. Y. Airiau and R. G. Brereton, Chemom. Intell. Lab. Syst., 2002, 62, 61–78 CrossRef CAS.
- J. H. Jiang, Y. Liang and Y. Ozaki, Chemom. Intell. Lab. Syst., 2004, 71, 1 CrossRef CAS.
- S. D. Frans, M. L. McConnel and J. M. Harris, Anal. Chem., 1985, 57, 1552–1559 CrossRef CAS.
- F. J. Knorr and J. M. Harris, Anal. Chem., 1981, 53, 272–276 CrossRef CAS.
- A. K. Smilde, H. C. J. Hoefsloot, H. A. L. Kiers, S. Bijlsma and H. F. M. Boelens, J. Chemom., 2001, 15, 405 CrossRef CAS.
- P. J. Gemperline, J. Chem. Inf. Model., 1984, 24, 206 CrossRef CAS.
- B. G. M. Vandeginste, W. Derks and G. Kateman, Anal. Chim. Acta, 1985, 173, 253 CrossRef CAS.
- E. J. Karjalainen, Chemom. Intell. Lab. Syst., 1989, 7, 31 CrossRef CAS.
- R. Tauler and E. Casassas, Chemom. Intell. Lab. Syst., 1992, 14, 305 CrossRef CAS.
- P. Paatero, Chemom. Intell. Lab. Syst., 1997, 37, 23 CrossRef CAS.
- J.-H. Jiang, Y.-Z. Liang and Y. Ozaki, Chemom. Intell. Lab. Syst., 2003, 65, 51–65 CrossRef CAS.
- H. Gampp, M. Maeder, C. J. Meyer and A. D. Zuberbühler, Talanta, 1985, 32, 1133–1139 CrossRef CAS.
- M. Maeder, Anal. Chem., 1987, 59, 527–530 CrossRef CAS.
- E. R. Malinowski, J. Chemom., 1992, 6, 29–40 CrossRef CAS.
- W. Den and E. R. Malinowski, J. Chemom., 1993, 7, 89–98 CrossRef CAS.
- O. M. Kvalheim and Y. Z. Liang, Anal. Chem., 1992, 64, 936–946 CrossRef CAS.
- Y. Z. Liang, O. M. Kvalheim, H. R. Keller, D. L. Massart, P. Kiechle and F. Erni, Anal. Chem., 1992, 64, 946–953 CrossRef CAS.
- R. Manne, H. Shen and Y. Liang, Chemom. Intell. Lab. Syst., 1999, 45, 171–176 CrossRef CAS.
- H. Shen, R. Manne, Q. Xu, D. Chen and Y. Liang, Chemom. Intell. Lab. Syst., 1999, 45, 323–328 CrossRef CAS.
- J.-H. Jiang, S. Šašić, R.-Q. Yu and Y. Ozaki, J. Chemom., 2003, 17, 186–197 CrossRef CAS.
- E. R. Malinowski, J. Chemom., 1996, 10, 273–279 CrossRef CAS.
- R. Manne and B.r.-V. Grande, Chemom. Intell. Lab. Syst., 2000, 50, 35–46 CrossRef CAS.
- M. Wasim and R. G. Brereton, J. Chromatogr., A, 2005, 1096, 2–15 CrossRef CAS.
- H. Shen, C. Y. Airiau and R. G. Brereton, J. Chemom., 2002, 16, 469–481 CrossRef CAS.
- B. G. M. Vandeginste, D. L. Massart, L. M. C. Buydens, S. D. Jong, P. J. Lewi and J. Smeyers-Verbeke, Handbook of Chemometrics and Qualimetrics: Part B,, Elsevier, Amsterdam, 1998 Search PubMed.
- S. Masoum, C. Malabat, M. Jalali-Heravi, C. Guillou, S. Rezzi and D. Neil Rutledge, Anal. Bioanal. Chem., 2007, 387, 1499–1510 CrossRef CAS.
- N. P. V. Nielsen, J. M. Carstensen and J.r. Smedsgaard, J. Chromatogr., A, 1998, 805, 17–35 CrossRef CAS.
- T. Skov, F. van den Berg, G. Tomasi and R. Bro, J. Chemom., 2006, 20, 484–497 CrossRef CAS.
- E. R. Malinowski, Anal. Chim. Acta, 1982, 134, 129–137 CrossRef CAS.
- C. Y. Airiau, H. Shen and R. G. Brereton, Anal. Chim. Acta, 2001, 447, 199–210 CrossRef CAS.
- M. Wasim and R. G. Brereton, Chemom. Intell. Lab. Syst., 2004, 72, 133–151 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2012 |