Aquation and dimerization of osmium(II) anticancer complexes: a density functional theory study

Abstract

In this paper, the hydrolytic and aqueous solution chemistry of two half-sandwich Os^II arene complexes [(η⁶-p-cym)Os(pic)Cl] (1) and [(η⁶-p-cym)Os(mal)Cl] (2) (pic = 2-picolinic acid and mal = maltolate) have been investigated using density functional theory (DFT). For aquation (substitution of chloride by H₂O) of the complexes, three attacking models were explored, including two forms of side attack (A and B) and back attack C. Side attack A required the lowest free energy of activation of the three, both in the gas phase and in aqueous solution, suggesting that it best describes the hydrolysis of the complexes. Both the activation and reaction energies indicated faster aquation for 2 than 1, which was in accordance with previous experimental observations. With the side attack model of the complexes, it was found that the conformations of complexes had little effect on the aquation process. Moreover, mechanistic pathways have been obtained for the dimerization of aqua adducts. As for 1a, the ligand departure was the rate-determining step with an activation free energy of 26.1 kcal mol⁻¹, while for 2a, the first step of ring opening and protonation is rate-determining with a free energy of activation of 24.8 kcal mol⁻¹, suggesting that 1a was kinetically more stable toward dimerization. There were three factors presented to explain the stability of 1a: differences in HOMO/LUMO densities, the large activation energy of 1a, and stabilization of Os-pic bonding. This study assists in understanding the aqueous solution chemistry of the anticancer complexes and in the design of novel anticancer drugs.

---

Introduction

Platinum-based compounds are by far the most studied and widely used anticancer drugs in chemotherapy.¹ However, they exhibit high general toxicity leading to undesirable side-effects and inactivity against certain types of cancer cells.² This gives an impetus for the search for anticancer activity amongst complexes of other metals. Ruthenium-centered compounds are also well-suited for medicinal applications. Two compounds, trans-[RuCl₄(DMSO)(Im)] ImH (NAMI-A, Im = imidazole) and trans-[RuCl₄(Ind)₂] IndH (KP1019, Ind = indazole), are undergoing clinical trials.³ Currently, there is also considerable interest in developing osmium complexes as anticancer agents.^4–12 While osmium belongs to the same group as Ru, it is considered to be more (but not completely) inert compared to its analogues. Several groups have carried out a series of fruitful experiments for Os^II arene complexes and demonstrated that the aqueous solution behavior of Os^II arene complexes can be controlled by tuning the ancillary ligands, such as the chelating ligand YZ and the arene.^5–12 Sadler and coauthors investigated the aquation and biological activity of the types of [(η⁶-arene)Os(YZ)Cl] complexes (arene = biphenyl or p-cymene, YZ = ethylenediamine, picolinate, acetylacetonato, or maltolate).^6–12 The investigated Os^II arene complexes with N, O– and O, O– bidentate ligands hydrolyzed and reacted with nucleobases rapidly, such as complexes with the maltolate ligand, but were inactive toward cancer cells. This is attributable to the rapid hydrolysis and formation of an unreactive hydroxo-bridged dimer which was the only species present in aqueous solution at biologically relevant concentrations.^6–8 The mechanism has not yet been explicitly determined theoretically, but it was thought to depend strongly on the initial proton-assisted breakage of the Os–O bond, followed by Os–O (N) bond breakage. As opposed to the O, O– and N, O– bidentate ligands, Os-centered complexes employing 2-picolinate as the “YZ” ligand exhibited enhanced stability with respect to dimerization and showed promising anticancer activity, comparable to that of carboplatin.^8–12

Modern quantum chemistry has given significant attention to platinum and ruthenium anticancer complexes with regard to solution phase chemistry and their interaction with nucleobases,^13,14 while the reactions and possibility of designing novel osmium complexes has been relatively ignored by theoreticians. The objective of this work is to explore detailed differences in solution chemistry of two structurally related Os^II complexes of the type [(η⁶-p-cym)Os(YZ)Cl] (η⁶-p-cym = 1-methyl-4-isopropylbenzene, YZ = 2-picolinic acid (pic) and maltolate (mal)) (Scheme 1), in an attempt to understand their contrasting biological activities. This work also explores the mechanism of unreactive hydroxo-bridged dimer formation for osmium arene complexes. Understanding the rate-limiting step of complex deactivation could provide a computationally simple structure–activity relationship in order to guide design and tuning of the Ar and YZ ligands of Os-centered complexes.

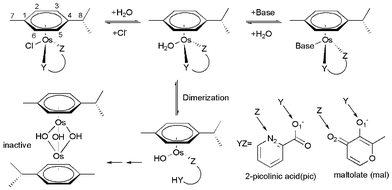Scheme 1 Reactions of osmium arene complexes.

Computational methods

In the present study, two complexes [(η⁶-p-cym)Os(pic)Cl] (1) and [(η⁶-p-cym)Os(mal)Cl] (2) were examined using DFT methods with the B3LYP hybrid functional,¹⁵ which has been demonstrated to be an effective tool for the theoretical studies of metal complexes,^16,17 with the 6-31G(d,p) basis sets for non-metal atoms and LanL2DZ for Os (labeled as B1).¹⁸ To refine energies for the reaction surfaces, single-point energies were further calculated in vacuo and in aqueous solution using the PCM continuum solvation method with the united atom Hartree–Fock (UAHF) parametrization¹⁹ and using larger basis sets 6-31+G(d,p) for non-metal atoms and LanL2DZ for Os (labeled as B2), as well as 6-311++G(d,p) for non-metal atoms and LanL2DZ-(f) for Os, (labeled as B3) i.e., the LanL2DZ basis set includes f polarization function (ξ_f = 0.886).²⁰ We have also calculated and compared the key structures and reaction barriers for aquation and subsequent open cycle processes using the BHandHLYP²¹ with B1 for the geometry and frequency calculations followed by single point energy refinement with BHandHLYP/B2.

Intrinsic reaction coordinate (IRC) calculations²² were used to further determine the correct transition states (characterized by one imaginary frequency and one negative eigenvalue). The reactant adduct and product adduct were obtained by following IRC of the corresponding transition state in both directions of the reaction path, followed by standard geometry optimizations. In all gas phase calculations, frequency calculations were carried out to verify the correct nature of the stationary points, and to extract the thermal energy contributions at 298.15 K and 1 atm. ΔG_a²⁹⁸, ΔH_a²⁹⁸ and ΔrG_r²⁹⁸, ΔrH_r²⁹⁸ were defined as the calculated energies of the transition state (TS) and product (P) relative to the energy of a reactant adduct (R), respectively.^13,14 All solvent-corrected enthalpies and free energies for the studied stationary points are displayed in the paper and the ESI.† Both enthalpy and free energy data give qualitatively similar results and conclusions for the investigated systems. Natural bond orbital (NBO)^23,24 analysis was performed at the B3LYP/B3//B3LYP/B1 level of theory. All calculations were carried out using the Gaussian 03 program.²⁵

Results and discussion

Conformation of the complexes

The structures of the complexes investigated may be conformationally complex because of the orientation and steric interactions between methyl and isopropyl (i-Pr) moieties in the p-cymene ligand and the YZ ligand. The p-cymene may perturb DNA structure in the major groove via steric interactions (i.e., upon binding of complexes to nucleobase, the methyl and i-Pr moieties on the arene ring may cause additional distortions to the structure of DNA).^9,12 In the literature, Gossens and coauthors reported eight conformations for the [(η⁶-p-cym)Ru(en)(Cl)]⁺ (en = ethylenediamine) system and qualitatively discussed the p-cymene and different diamine dihedral angle (NCCN) orientation in [(η⁶-p-cym)Ru(en)Cl]⁺.²⁶

Herein, stable conformers of each complex were obtained by rotating the p-cymene ligand as shown in Fig. S1.† In our rotation curves, the dihedral created by the terminal atom in the chloride, the osmium center, the carbon on the 4 position of the arene, and the methyne carbon of i-Pr are frozen. The rotational profiles were computed in both directions with respect to chelated ligands, labeled as A and B. By rotating the p-cymene ligand, various competing minima were obtained. After full geometry optimization for these minima, each complex gave rise to 6 possible stable conformers, respectively, as shown in Fig. 1. In all the conformers, p-cymene has the conformation resembling its isolated form in which the i-Pr hydrogen lies in the plane of the arene, and one methyl group points above and the other below this plane. The calculated energy global minima in vacuum of 1 were I, II and VI, in which the pic group slides to the side of cymene rings. Thus bulky chloride and pyridine had the least steric hindrance. As for 1, geometry optimizations starting directly from the crystal yielded IV, a point on the potential energy surface (PES) which is 0.6 kcal mol⁻¹ higher than the global minimum. Therefore we inferred that its stabilization may come from crystal packing effects. As for 2, the most stable were I, IV and VI, in which the mal group slid under the 7-methyl group of p-cymene. The structure of I was in agreement with the crystal structure of 2. The calculated results suggested that the energy difference between the conformers of chloro species was small (within 1.0 kcal mol⁻¹). There seemed to be no effective rotational barrier for rotation in the gas phase, especially for 2, as predicted by the approximate rotational energy barrier profile in Fig. S1† (4.3 and 1.4 kcal mol⁻¹ for 1 and 2, respectively). Experimental and theoretical investigations had reported a very low rotational energetic barrier of arene ligands in organometallic complexes (i.e., about 0.5 kcal mol⁻¹ in [(η⁶-benzene)Cr(CO)₃], about 2.5 kcal mol⁻¹ in [(η⁶-C₆H₆)Ru-{κ³-HB(pz)₃}]⁺).²⁷ Consequently, osmium complexes with this intrinsic conformational flexibility can rotate the p-cymene group readily to adapt to the DNA environment.²⁶

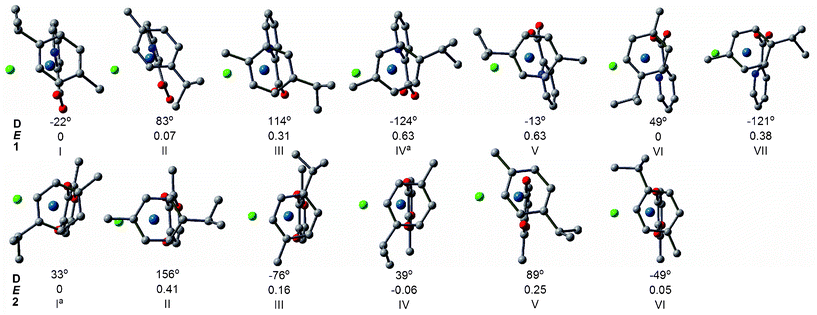Fig. 1 The relative energies E (in kcal mol⁻¹) and dihedral angles D (Cl-Os-C4-C8) of the optimized structures (top view) of conformers of 1 and 2 obtained at B3LYP/B1 level. The H atoms have been omitted for clarity.^a The preferred orientation of the crystal structure.^7,8

Activation of the Os^II complex: aquation reaction

Aqueous solution chemistry plays a fundamental role in potential biological and medical applications of osmium arene complexes. The aquation process (substitution of chloride by H₂O) of Os^II arene complexes is believed to be the key activation step before the drug reaches its intracellular target DNA. Herein, energies of the hydration reactions are explored both thermodynamically and kinetically.¹²

Aquation models. With respect to the orientation of the attacking water for the aquation of the complexes, we considered three attacking models (Fig. 2): one is side attack A, in which attacking water is from the chloride side and under the methyl group below the plane of the arene, therefore the bulky chloride atom is located in a place with less steric hindrance; the second is side attack B, where incoming water is from the chloride side opposite to side attack A. The third is back attack C, in which incoming water attacks from the opposite side of chloride. Specifically, R, TS and P relevant to pathways A, B and C are designated by the subscripts A, B, and C, respectively. Since there was little energy difference between various conformers as discussed above, those most relevant to the experiment crystal structures^7,8 (conformer IV for 1 and I for 2) are subsequently discussed.

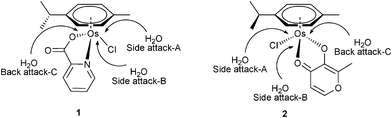Fig. 2 Three pathways of aquation for 1 and 2.

Structural characteristics. Fig. 3 shows the optimized structures for the species involved in the three pathways of aquation. The reaction model adopted is {[(η⁶-cym)Os(YZ)Cl]·H₂O} → [TS] → {[(η⁶-cym)Os(YZ)(H₂O)]⁺·Cl⁻}. Generally, the changes in the bond lengths of the ligands not directly involved in the substitution are only marginal between the different states (i.e., within 0.01–0.02 Å). The structures of the species involved in the corresponding aquation models are similar for 1-IV and 2-I. In the side attack A, the reactant of [(η⁶-p-cym)Os(YZ)Cl]·H₂O (R_A), the entering water molecule has formed hydrogen bonds with chloride and chelated oxygen. The vibrational mode of transition state (TS_A) demonstrates an angular vibrational mode between the leaving chloride and incoming water, with a decrease in the Os–OH₂ bond length, and a corresponding increase in the Os–Cl distance. In the structure of product, [(η⁶-cym)Os(YZ)(H₂O)]⁺·Cl⁻ (P_A), the Cl anion as ligand has been completely substituted by H₂O, which forms a bond with Os at a distance of 2.18 and 2.14 Å for 1 and 2, respectively.

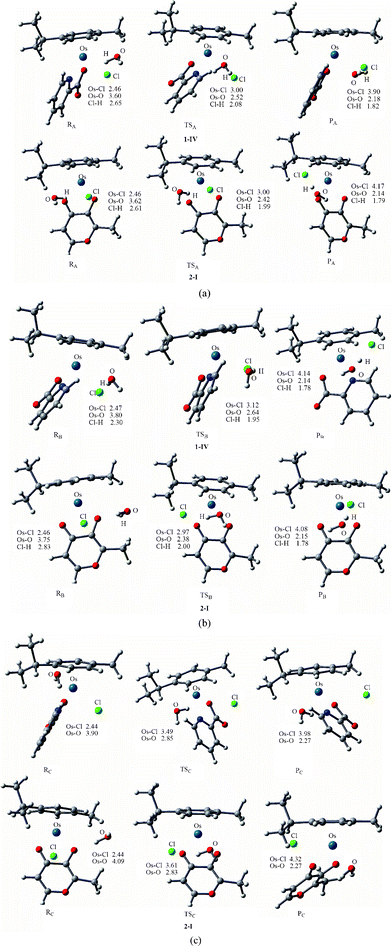Fig. 3 Optimized structures of the species (at B3LYP/B1 level) involved in the side attack A (a), side attack B (b) and back attack C (c). Bond length values are given in Å.

The transition states of complexes in side attack B (TS_B) are very similar to the vibrational mode of TS_A, in which the Os–Cl bond is breaking and the Os–O_wat bond is forming. As for path B of 1-IV, the incoming water is located on the pyridine side, thus there is no H-bond between the incoming water and pic to stabilize TS_B. Judging from the structural characteristics of side attack A and B, both of them could be described as associative, with the central Os atom being seven-coordinated. A similar structural characteristic of the hydrolysis process TS was also found for cisplatin, Ru^II arene complexes and their analogues.^{13a–c,14c,17}

Through analyzing the geometries of the species involved in the back attack C, we observed that the p-cymene and chelated ligands had to encounter a concerted “flip”, opening the way for the incoming water. This competes directly with chloride for a coordination site at the osmium center, thus the complexes encountered a large conformation change via back attack C. Interestingly, the Os–Cl and Os–O_wat distances (3.49/2.85 Å for 1-IV and 3.61/2.83 Å for 2-I) in the transition state of back attack (TS_C) are much longer than those of side attack transition states, suggesting that the reaction mechanism is more dissociative for back attack. The Os–Cl bonds in reactants of side attacks (R_A and R_B) (≈2.46 Å) are longer than that of the reactant of back attack (R_C) (2.44 Å), which could be regarded as a weak interaction indicative of partial solvation of the leaving chloride ligand by the incoming water. In addition, the Os–O_wat bond of the back attack product (P_C) (2.27 Å) is longer than that of products of side attack A (P_A) and B (P_B), in which the substituted chloride anion attracts the positively charged proton of coordinated water in side attack A and B, resulting in the partially deprotonation of coordinated water.

Energetics of the aquation process. Thermodynamic and kinetic results for three aquation paths in the gas phase and in solution are shown in Fig. 4 at the B3LYP/B3//B3LYP/B1 level of theory. In the gas phase, the back attack pathway implies significantly higher activation energy barriers than the side attack A and B pathways, ascribing to the large conformation change during the back attack process and the lack of H-bond. By adding the effect of the solvent (water), a highly polar solvent, the side/back energy difference found in the gas phase was reduced in the aqueous solution. This is because the water continuum drastically weakens the H-bond interactions with respect to the gas phase complex. The activation barrier for side attack A is lower than that of side attack B, as the bulky chloride occupied relatively less steric place in side attack A. It is concluded that the aquation process of the complexes mainly go through the side attack A. Our results indicated that a suitable model is crucial when describing drug hydrolysis.

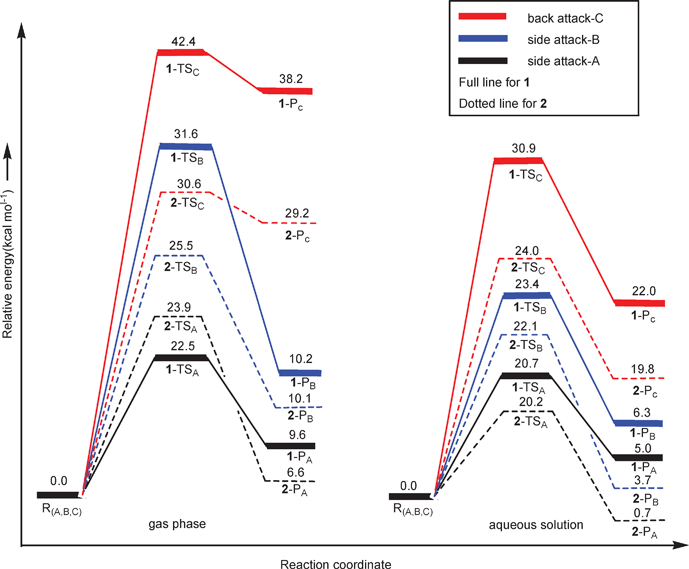Fig. 4 Free energy profiles (at B3LYP/B3//B3LYP/B1 level) of three pathways of the aquation process for complexes 1 and 2 in the gas phase and aqueous solution.

From the energy profiles presented in Fig. 4, we found that aquation of 1 required a free energy of activation larger than that of 2 in all the three pathways when using a solvation model. The computed free energy of activation of side attack A for 1 is 20.7 kcal mol⁻¹, in good agreement with the experimental activation energy which was measured to be 91.5 ± 3.0 kJ mol⁻¹ (21.9 ± 0.7 kcal mol⁻¹) in the temperature range 3–25 °C. 2 exhibits a slightly lower barrier of 20.2 kcal mol⁻¹ in comparison with 1, suggesting faster aquation of 2. The ΔrG_r²⁹⁸ of 2 is smaller than that of 1 by 4.3 kcal mol⁻¹, indicating that 2-P_A is thermodynamically more stable than 1-P_A. Our computations validate the faster hydrolysis of 2 both thermodynamically and kinetically in comparison with 1.⁷

Previous authors of studies on Ru-centered complexes of the type Ar(YZ)X suggested that BHandHLYP functionals may provide better results if π-stacking interactions occur between the Ar ligand and base.^14b Accordingly, reaction energies and activation barriers (single point values) were also computed at B3LYP and BHandHLYP levels with B2, both in gas phase and using PCM as shown in Table S1 and S3.† Performance of B3LYP is slightly better in comparison to the BHandHLYP functional. While in this investigation no strong intramolecular electronic interactions between the p-cymene and YZ ligands are expected, further testing of DFT functionals may be necessary if more structurally complex Ar ligands are to be employed.

Conformational effect on the aquation process. Previous studies of Ru and Os-centered piano stool complexes have not investigated whether the orientations of bound water and chlorine have any effect on the activation energies for the aquation reaction. The side attack A (in which the chloride is located in a place with least steric hindrance and the attacking water forms H-bonds with the chelated atom) was applied to various conformations of the complexes. However, path A is not a favored path for conformations I, VI and VII of 1, because the incoming water attacks in the pyridine side and there are no H-bonds between the incoming water and chelated atom. Therefore we utilized path B for I, VI and VII of 1. From Fig. 5, there was little effect on bond lengths in transition states of various conformations caused by steric effects of p-cymene. Moreover, the similarity of the vibrational modes of the transition states in various conformations suggested that aquation of the various conformations occurred by the same interchange associative mechanism.

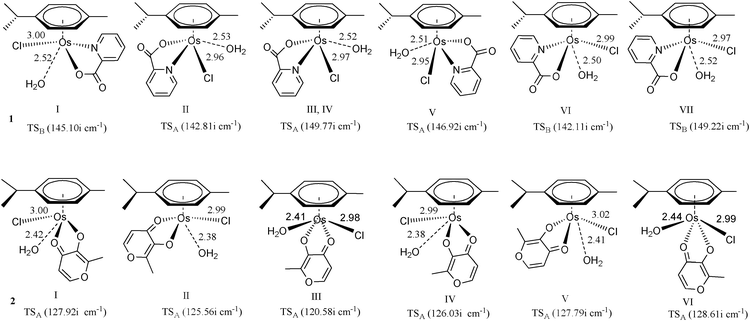Fig. 5 Optimized structures (at B3LYP/B1 level) of the transition state involved in the side attack for various conformations. Bond length values are given in Å.

From the data in Table 1, it was found that II of 1 and III of 2 had the lowest activation energies in the gas phase. In aqueous solution, II of 1 and III of 2 still exhibited the lowest activation energies among all the explored conformations. Overall, there were only subtle free energy differences of activation among aquation processes of various conformations. Therefore, it can be seen that the influence of conformation effect of Os^II arene complexes on activity is not as critical compared to the active cisplatin and inactive cisplatin conformer trans-diamminedichloroplatinum(II) (trans-DDP), for example.²⁸ DNA is believed to be the main target for the type of Os^II arene complexes with bidentate ligands. It forms monofunctional adducts with additional non-coordinative interactions, such as H-bonding and hydrophobic interactions, triggered by the introduction of extended arene rings into their versatile structures.^5–12 However, compared with cisplatin, trans-DDP is inactive because it has much faster dynamics. In addition, trans-DDP cannot form intrastrand cross-links between adjacent nucleotides, which are responsible for the antitumor activity of cisplatin.

Table 1 Estimation of activation ΔG_a²⁹⁸ and ΔrG_r²⁹⁸ reaction energies (kcal mol⁻¹) of various conformations investigated with side attack model for 1 and 2 (at B3LYP/B3//B3LYP/B1 level)

Complex		1						2
Conformation		I	II	III,IV	V	VI	VII	I	II	III	IV	V	VI
Model		PathB	PathA	PathA	PathA	PathB	PathB	PathA	PathA	PathA	PathA	PathA	PathA
ΔGa^298	Gas	24.9	22.3	22.5	22.4	23.6	25.4	23.9	24.6	23.1	24.2	25.4	24.4
ΔrGr^298	Gas	10.8	7.7	9.6	7.7	9.6	11.5	6.6	10.3	7.6	7.2	0.3	6.7
ΔGa^298	PCM	21.3	20.0	20.7	21.7	21.3	21.7	20.2	20.3	20.0	19.6	21.5	22.2
ΔrGr^298	PCM	5.2	4.2	5.0	6.1	4.2	6.4	0.7	2.8	3.0	1.1	0.2	2.8

---

Dimerization of aqua adducts

Although complex 1 and 2 both hydrolyze and show reactivity to nucleobases, only 1 was regarded as a promising anticancer agent, as the activated aqua adduct of 2 (2a) was unstable with respect to formation of the hydroxo-bridged dimer at micromolar concentrations.^7,8 Given the experimental observations of Sadler and coauthors, a detailed understanding of the dimerization mechanism has not yet been performed. Sadler has hypothesized that the mechanism of dimerization initially involves breakage of the Os–O1 bond, assisted by protonation, followed by Os–O(N)2 bond breakage. The aim in this part was to investigate how Os^II arene complexes with oxygen-chelating ligands were deactivated by dimer formation under biological test conditions.

As shown in Scheme 2 and 3 (Scheme 2 for 1a and Scheme 3 for 2a), the calculation model used was [(η⁶-p-cym)Os(YZ)(H₂O)]⁺, which were the products of the aquation of 1-IV and 2-I. Our computed mechanism for dimerization is as follows; in reactant RC·H₂O, O1 first accepts a proton from the coordinated water, while the chelated ring opens at the same time. Second, a solvent water molecule attacks the osmium and the chelated ligand departs, resulting in intermediate IM2. Subsequent deprotonation forms intermediate IM3. Finally, IM2 and IM3 associate (IM4) and then rearrange to form the triple-hydroxo-bridged dimer (PC).

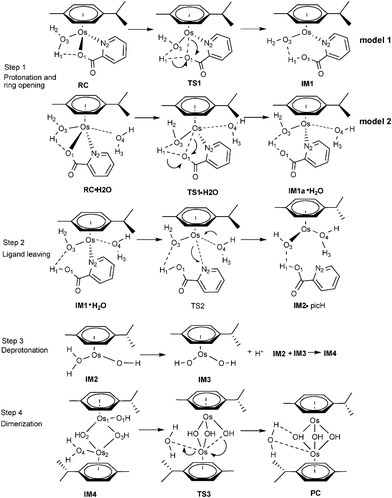Scheme 2 Proposed mechanism for the dimerization process for 1a.

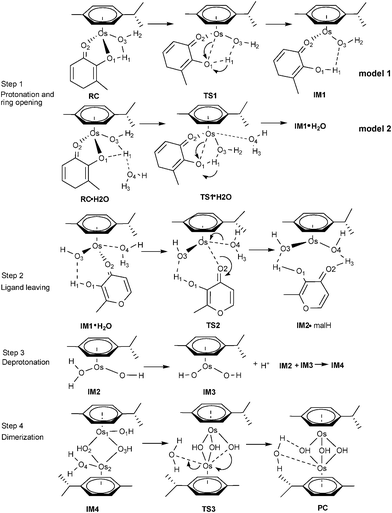Scheme 3 Proposed mechanism for the dimerization process for 2a.

As for the first step, two models were designed for the ring opening process. In the first model, the concerted reactions were studied for [(η⁶-p-cym)Os(YZ)(H₂O)]⁺. In the second model, extra solvent water was added to the system in order to better balance the reaction. The structures and energies of the first model of step 1 are compiled in Fig. S2.† In the first model, the calculated free energy of activation for the ring opening step of 1a is 18.9 kcal mol⁻¹, slightly larger than that of 2a (16.3 kcal mol⁻¹) in the gas phase. While in aqueous solution, it can be seen that the barrier of 1a significantly increased (to 24.5 kcal mol⁻¹), and 2a does not increase (16.3 kcal mol⁻¹). But after adding extra water (model 2), the trend of free energy of activation inverted, that was 2a higher than 1a, The extra solvent water was found to play a role in the ring opening process. Consequently, model 2 is more reasonable for describing the ring opening process, and energy profiles were based on model 2 in the following discussions.

Dimerization of 1a . The reaction mechanism is shown in Scheme 2. The optimized structures and free energy profiles for the deactivation process of 1a are collected in Fig. 6 and 7, respectively. The first step is a concerted step in which ring opening is concomitant with chelated oxygen protonation. In the RC·H₂O of 1a, the bond lengths of Os–O1 and O1–H1 are 2.07 and 2.12 Å, respectively. The transition state TS1·H₂O is characterized by an imaginary frequency of 97.29i cm⁻¹, in which the chelated oxygen of pic is leaving from Os while the hydrogen of coordinated water is approaching to the leaving oxygen of pic. The Os–O1 and O1–H1 bond lengths are 2.64 and 1.01 Å, respectively. In IM1a·H₂O, the Os–O1 bond length was elongated to 3.24 Å and O1–H1 was further shortened to 0.99 Å, suggesting that chelated oxygen of pic is protonated and completely broken away from Os. The bond distance variations indicated that these transition states are quite late with respect to hydrogen transfer. The nonbonded solvent water does not participate in hydrogen bonding with the Os complex. The activation barrier for this step is 16.3 kcal mol⁻¹ in the gas phase, but it increased by 4.4 kcal mol⁻¹ when in aqueous solution to become 20.7 kcal mol⁻¹.

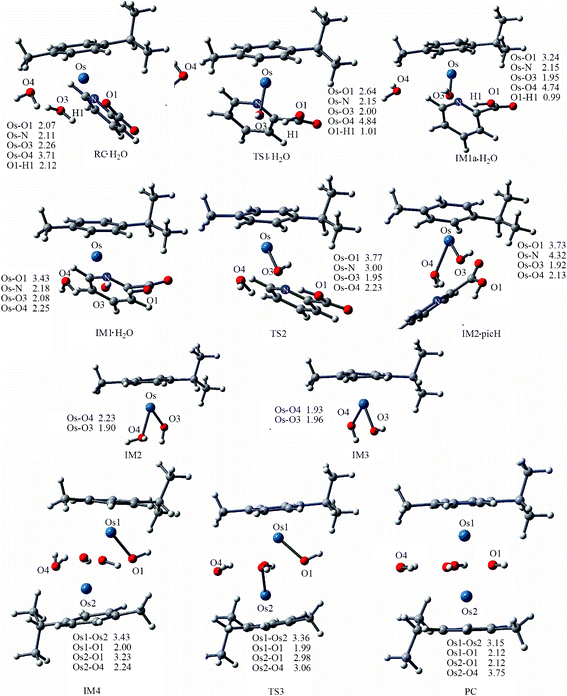Fig. 6 Optimized structures of the species involved in the dimerization of 1a. Bond length values are given in Å.

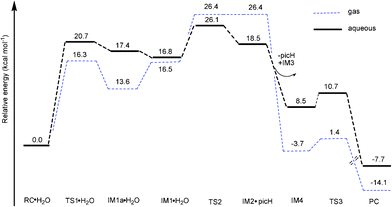Fig. 7 Free energy profiles (at B3LYP/B3//B3LYP/B1 level) of dimerization of 1a in gas phase and aqueous solution.

After the protonation and ring opening of the complex, the next step proposed was that a solvent molecule (water) substitutes the chelated ligand completely. In IM1·H₂O, the solvent molecule approached the Os center with R_Os-O4 being 2.25 Å, resulting in a slight stabilization by 0.6 kcal mol⁻¹. Departure of picH leads from IM1·H₂O to IM2•picH, through the transition state TS2, characterized by an imaginary frequency of 95.9i cm⁻¹. This process is the rate-determining step and the free energy of activation was determined to be 26.1 kcal mol⁻¹ as shown in Fig. 7. The high barrier to removal of the protonated pic ligand can be explained by the strong σ-bond between Os^II (d_z²) and nitrogen (p orbital) in pyridine as demonstrated by the MOs of 1a in Fig. 10 (vida infra).

After ligand departure, the subsequent steps, such as deprotonation and dimerization, are exergonic and qualitatively equivalent for 1a and 2a. It was interesting to note that the coordinated water in the triaqua benzene complex [Os(η⁶-benzene)(H₂O)₃]²⁺ was thought to be highly acidic (pK_a ≈ 2.3–3.4).²⁹ Subsequently, the two-leg intermediate IM2 with bound water would be easily deprotonated to form another intermediate IM3. Both of IM2 and IM3 were strongly nucleophilic and attractive, forming intermediate IM4. In the absence of any X-ray structural data, we tentatively suggested that IM4 should be formulated as the di-hydroxo-bridged cation (as shown in Scheme 2, 3 and Fig. 6), which is consistent with facile irreversible rearrangement to the final triple-hydroxo-bridged dimer (PC). In addition, similar double-bridged binuclear intermediates have been proposed elsewhere, such as [(C₆H₆)(OH)Ru(OH)₂Ru(H₂O)(C₆H₆)],³⁰ [Ru₂(η-C₆H₆)₂Cl₃]PF₆, [Ru₂(OH)₃(PR₃)₆]BPh₄³¹ and [Ru₂Cl₃(PR₃)₆]Cl.³² From Fig. 6 and 7, the dimerization proceeded via the transition state TS3 leading from IM4 to the formation of PC with a very low activation barrier of 2.2 kcal mol⁻¹ in solution. Analysis of the imaginary vibrational mode clearly indicated rupture of the bond between Os2 and water, and the simultaneous formation of an Os2-OH bond. The ΔrG_r²⁹⁸ of this step was quite lower, −7.7 kcal mol⁻¹, suggesting thermodynamic stability of the final product PC, a triple-hydroxo-bridged cation. Cymene rings in PC were fully staggered to reduce the steric hindrance. Reducing the cymene ligand to benzene and removing the hydroxo bridges, the PC structure has a pseudo C_s symmetry, in which Os-Os and Os-OH distances are 3.15 and 2.12 Å, respectively.

Dimerization of 2a . The complete reaction mechanism for dimerization of 2a is described in Scheme 3. The optimized structures and free energy profiles for the process are summarized in Fig. 8 and 9, respectively. In the optimized structure of RC·H₂O of 2a, the bond lengths of Os–O1 and O1–H1 are 2.09 and 2.37 Å, respectively. The transition state TS1·H₂O is characterized by an imaginary frequency of 153.3i cm⁻¹, in which the chelated oxygen of mal is leaving the Os while the hydrogen of the coordinated water is approaching the leaving oxygen of mal. The Os–O3 distance in TS1·H₂O (2.26 Å) is longer than in TS1 (2.03 Å), due to the effect of the extra solvent molecule, which is weakly bound to Os (R_Os-O4 = 2.42 Å). This process required a high activation energy of 24.8 kcal mol⁻¹ as shown in Fig. 9, indicated that it is the reaction rate-limiting step in the whole process, which agrees with the hypothesis of Sadler and coauthors.⁷ From the inspection of model 1 and 2 of this step, the extra water increases the barrier height of step 1 (16.5 kcal mol⁻¹, Fig. S3†), demonstrating the significant role played by the extra explicit solvent molecule.

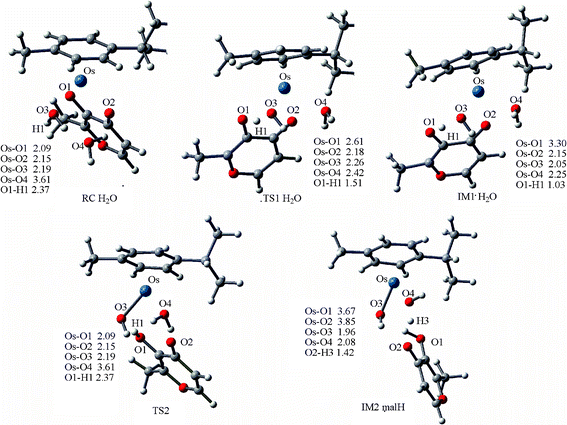Fig. 8 Optimized structures of the species involved in the dimerization of 2a, and IM2, IM3, IM4, TS3 and PC are compiled in Fig. 6. Bond length values are given in Å.

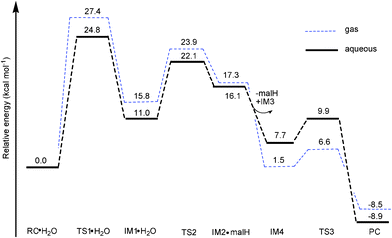Fig. 9 Free energy profiles (at B3LYP/B3//B3LYP/B1 level) of dimerization of 2a in gas phase and aqueous solution.

Ligand departure leads from IM1·H₂O to IM2·malH through a transition state, TS2. The computed free energy of activation is 23.9 kcal mol⁻¹ in the gas phase, as shown in Fig. 9. After solvation, the barrier decreased to 22.1 kcal mol⁻¹. In the conformation of the involved transition state, TS2·H₂O, characterized by a weak imaginary frequency of 50.8i cm⁻¹, the Os1-O2 bond distance lengthened from 2.15 to 3.02 Å but the Os1-O4 distance further shortened from 2.25 to 2.19 Å, suggesting that the malH is leaving and the solvent water is approaching closer to the Os. In the IM2·malH complex, the malH ligand has been completely substituted by H₂O, with a Os-O4 bond distance of 2.08 Å. The malH forms intermolecular interactions with O3 (R_O3-H1 = 1.76 Å) of the coordinated hydroxo and H3 (R_O2-H2 = 1.42 Å) of the water molecule, respectively. After ligand departure, the subsequent steps of 2a, such as deprotonation and dimerization, are greatly exergonic and qualitatively equivalent with 1a. The ΔrG_r²⁹⁸ of this step were −7.7 and −8.5 kcal mol⁻¹ for 1a and 2a, respectively. These findings suggested that the dimerization of 2a was thermodynamically more favored than 1a.

Based on the above proposed mechanisms, the overall dimer formation reaction proposed for 1a and 2a was shown in eqn (1).

2[(η⁶-p-cym) Os (YZ) H₂O]⁺ + H₂O → [(η⁶-p-cym) Os (u-OH₃) Os (η⁶-p-cym)]⁺ + 2YZ-H + H⁺ (1)

If the above mechanism is correct, the reaction rate should be dependent on the concentration of solvent water. Indeed, this was observed experimentally as the concentration of 2 was decreased, and ¹H-NMR peaks corresponding to hydroxo-bridged dimer and free maltolate ligand increased in intensity, whereas those for the aqua complex decreased in intensity.⁷ As shown in Fig. 7 and 9, the accumulated barrier of 1a (26.1 kcal mol⁻¹) is higher than 2a (24.8 kcal mol⁻¹), suggesting that 1a is less likely to dimerize. Moreover, all intermediates lie much higher in free energy with respect to RC·H₂O, which is consistent with experimental observation that there were no intermediates to dimerization detected in previous experimental work.⁷

Electronic properties of 1a and 2a . To understand the reactivity of 1a and 2a, we investigated the electronic structure of 1a and 2a. The isodensity surfaces of these orbitals for 1a and 2a are shown in Fig. 10. In the highest occupied molecular orbital (HOMO) of 1a, the contribution of pyridine of pic was small and there is σ bonding character between the d_z² atomic orbital (AO) of Os and the p_z of N in pyridine. The lowest unoccupied molecular orbital (LUMO) of 1a was mainly from d_xy of Os and π of pic, and there is π-bonding character between the d_xy of Os and p_y of N in pyridine of pic. As to 2a, it can be noted that the main contributions to the HOMO of 2a came from the d_x2-y2 of the Os atom and π-bonding of mal ligands. The main contributions to the LUMO were from d_x2-y2 of the Os atom and π*-bonding of mal ligands. In addition, there was an overlap between a p orbital of the O1 and an s orbital of the H in bound H₂O, indicating that O1 is more reactive than O2/N2 in the protonation. Analyzing the frontier MO energies, the energy gaps (difference in HOMO/LUMO eigenvalue) of 1a and 2a are 4.38 and 3.99 eV, respectively, demonstrating that 2a is more reactive than 1a, or rather that 1a is more stable than 2a.

Fig. 10 (a) Natural orbital diagram for [(η⁶-p-cym)Os(YZ)(H₂O)]⁺ (1a and 2a). (b) A schematic view of the orbital interaction between Os and chelated ligands (arene fragments were omitted).

A natural bond orbital (NBO) analysis for 1a and 2a (listed in Table 2),^23,24 shows the positive charge of Os in 1a was lower than that of 2a, suggesting that pic exhibited stronger electron donation ability than mal, therefore better stabilized electron deficient central Os^II cation. In addition, the charge of leaving O1 is more negative than that of O2/N2, further demonstrating that O1 protonation is facile.

Table 2 NBO charges of important atoms for 1a and 2a (e) at B3LYP/B3//B3LYP/B1 level.

Species	Os	O1	O(N)2	O3	H1	H2
1a	0.733	−0.724	−0.465	−0.849	0.520	0.507
2a	0.829	−0.731	−0.655	−0.847	0.510	0.504

---

Conclusions

In this study, two half-sandwich Os^II arene complexes 1 and 2 were investigated theoretically. 2 has been experimentally shown to be inactive toward cancer cells, despite its reactivity toward nucleobases. We have therefore explored differences in their solution chemistry in an attempt to understand their contrasting biological activities. Different conformations of the complexes together with their aqua adducts were explored from geometry optimization of the various competing minima by rotating p-cymene ligand and they were nearly energetically equivalent for various conformers.

Three attacking models were explored for aquation of the complexes, including two side attacks (A and B) and back attack C. Side attack A in which bulk chloride is located at a place with less steric hindrance has the lowest energy barrier of the three, both in the gas phase and in aqueous solution. With side attack A model, the aquation of 2 was both thermodynamically and kinetically more favored than 1, which is in agreement with the experimentally observed rapid hydrolysis of 2. The side attack computational model was applied to complexes and there was only a slight difference in the activation energies between conformers examined both in the gas phase and aqueous solution.

The calculations provided an overall mechanism of dimerization. Two models for the ring opening step were considered, and it was found that the model 2 with extra solvent water described the real reaction more reasonably. As for 1a, the ligand leaving was predicted to be the rate-determining step, while for 2a, the ring opening was a rate-determining step and subsequent steps exhibited quite low barriers. The accumulated barrier is higher for 1a than 2a, which was consistent with the experimental observation that 1a does not readily dimerize compared to 2a. Three effects were important to the stability toward dimer formation of 1a: Firstly, a significantly stronger HOMO bonding interaction was identified for 1a compared to 2a. Secondly, the energy gap of 1a is larger than 2a, suggesting that 1a is more stable. Thirdly, lower NBO charge on Os of 1a revealed better stabilization of the pic ligand.

The results reported here have implications for the mechanistic interpretation of aquation and dimerization processes for the osmium arene complexes, and indicated that the anticancer activity of 1a was partly due to its moderate aquation and stability against dimerization. In line with the findings obtained in this study, further work is now in progress aiming to explore the thermodynamics and kinetics processes for the binding of the hydrolyzed products of Os arene antitumor complexes to DNA bases.

Acknowledgements

We gratefully thank the National Natural Science Foundation of China (Grant Nos. 20725103, 20973204), the Guangdong Provincial Natural Science Foundation (No. 9351027501000003) to MZW and CYZ, and the Scholarship for International Young Scientists of the National Natural Science Foundation of China (Grant No. 20950110326) to NJD for financial support of this research. The High Performance Computing facility at the University of Memphis is also acknowledged.

References

1. (a) B. Rosenberg, L. VanCamp, J. E. Trosko and V. H. Mansour, Nature, 1969, 222, 385; (b) D. Lebwohl and R. Canetta, Eur. J. Cancer, 1998, 34, 1522; (c) K. Lemma, A. M. Sargeson and L. I. Elding, J. Chem. Soc., Dalton Trans., 2000, 1167; (d) R. R. Barefoot, J. Chromatogr., Biomed. Appl., 2001, 751, 205; (e) G. V. Kalayda, S. Komeda, K. Ikeda, T. Sato, M. Chikuma and J. Reedijk, Eur. J. Inorg. Chem., 2003, 4347; (f) P. Marques-Gallego, G. V. Kalayda, U. Jaehde, H. den Dulk, J. Brouwer and J. Reedijk, J. Inorg. Biochem., 2009, 103, 791; (g) R. Kipping, P. Kabolizadeh, F. Frezard, J. J. Ryan and N. P. Farrell, Mol. Cancer. Ther., 2007, 6, 3444s.
2. D. Wang and S. J. Lippard, Nat. Rev. Drug Discovery, 2005, 4, 307.
3. (a) G. Sava, A. Bergamo, S. Zorzet, B. Gava, C. Casarsa, M. Cocchietto, A. Furlani, V. Scarcia, B. Serli, E. Iengo, E. Alessio and G. Mestroni, Eur. J. Cancer, 2002, 38, 427; (b) S. Kapitza, M. Pongratz, M. A. Jakupec, P. Heffeter, W. Berger, L. Lackinger, B. K. Keppler and B. Marian, J. Cancer Res. Clin. Oncol., 2005, 131, 101; (c) V. Brabec and O. Novakova, Drug Resist. Updates, 2006, 9, 111; (d) A. V. Vargiu, A. Robertazzi, A. Magistrato, P. Ruggerone and P. Carloni, J. Phys. Chem. B, 2008, 112, 4401; (e) C. G. Hartinger, M. A. Jakupec, S. Zorbas-Seifried, M. Groessl, A. Egger, W. Berger, H. Zorbas, P. J. Dyson and B. K. Keppler, Chem. Biodiversity, 2008, 5, 2140; (f) A. Bicek, I. Turel, M. Kanduser and D. Miklavcic, Bioelectrochemistry, 2007, 71, 113; (g) N. Besker, C. Coletti, A. Marrone and N. Re, J. Phys. Chem. B, 2008, 112, 3871.
4. A. Egger, B. Cebrian-Losantos, I. N. Stepanenko, A. A. Krokhin, R. Eichinger, M. A. Jakupec, V. B. Arion and B. K. Keppler, Chem. Biodiversity, 2008, 5, 1588.
5. (a) P. J. Sadler and A. F. Peacock, Chem.–Asian J., 2008, 3, 1890; (b) A. M. Pizarro and P. J. Sadler, Biochimie, 2009, 91, 1198; (c) A. Levina, A. Mitra and P. A. Lay, Metallomics, 2009, 1, 458; (d) S. H. van Rijt and P. J. Sadler, Drug Discovery Today, 2009, 14, 1089; (e) H. K. Liu and P. J. Sadler, Acc. Chem. Res., 2011, 44, 349.
6. F. A. Peacock, A. Habtemariam, R. Fernandez, V. Walland, F. P. A. Fabbiani, S. Parsons, R. E. Aird, D. I. Jodrell and P. J. Sadler, J. Am. Chem. Soc., 2006, 128, 1739.
7. F. A. Peacock, M. Melchart, R. J. Deeth, A. Habtemariam, S. Parsons and P. J. Sadler, Chem.–Eur. J., 2007, 13, 2601.
8. F. A. Peacock, S. Parsons and P. J. Sadler, J. Am. Chem. Soc., 2007, 129, 3348.
9. H. Kostrhunova, J. Florian, O. Novakova, A. F. A. Peacock, P. J. Sadler and V. Brabec, J. Med. Chem., 2008, 51, 3635.
10. S. H. van Rijt, A. F. A. Peacock, R. D. L. Johnstone, S. Parsons and P. J. Sadler, Inorg. Chem., 2009, 48, 1753.
11. S. H. van Rijt, A. J. Hebden, T. Amaresekera, R. J. Deeth, G. J. Clarkson, S. Parsons, P. C. McGowan and P. J. Sadler, J. Med. Chem., 2009, 52, 7753.
12. (a) S. H. van Rijt, A. Mukherjee, A. M. Pizarro and P. J. Sadler, J. Med. Chem., 2010, 53, 840; (b) S. H. van Rijt, H. Kostrhunova, V. Brabec and P. J. Sadler, Bioconjugate Chem., 2011, 22, 218.
13. Theoretical papers on platinum anticancer complexes: (a) Y. Zhang, Z. Guo and X. Z. You, J. Am. Chem. Soc., 2001, 123, 9378; (b) C. B. Zhu, J. Raber and L. A. Eriksson, J. Phys. Chem. B, 2005, 109, 12195; (c) L. A. S. Costa, W. R. Rocha, W. B. De Almeida and H. F. Dos Santos, J. Chem. Phys., 2003, 118, 10584; (d) M. H. Baik, R. A. Friesner and S. J. Lippard, J. Am. Chem. Soc., 2003, 125, 14082; (e) D. V. Deubel, J. Am. Chem. Soc., 2004, 126, 5999; (f) D. V. Deubel, J. Am. Chem. Soc., 2006, 128, 1654; (g) J. K. C. Lau and D. V. Deubel, J. Chem. Theory Comput., 2006, 2, 103; (h) M. E. Alberto, M. F. A. Lucas, M. Pavelka and N. Russo, J. Phys. Chem. B, 2009, 113, 14473; (i) M. F. A. Lucas, M. Pavelka, M. E. Alberto and N. Russo, J. Phys. Chem. B, 2009, 113, 831; (j) L. X. Zhou, J. Phys. Chem. B, 2009, 113, 2110; (k) T. Zimmermann, Z. Chval and J. V. Burda, J. Phys. Chem. B, 2009, 113, 3139.
14. (a) Theoretical papers on ruthenium anticancer complexes: D. V. Deubel and J. K. C. Lau, Chem. Commun., 2006, 2451; (b) K. Gkionis, J. A. Platts and J. G. Hill, Inorg. Chem., 2008, 47, 3893; (c) J. C. Chen, L. M. Chen, S. Y. Liao, K. C. Zheng and L. N. Ji, J. Phys. Chem. B, 2007, 111, 7862; (d) J. C. Chen, L. M. Chen, L. C. Xu, K. C. Zheng and L. N. Ji, J. Phys. Chem. B, 2008, 112, 9966; (e) J. Li, L. C. Xu, J. C. Chen, K. C. Zheng and L. N. Ji, J. Phys. Chem. A, 2006, 110, 8174; (f) M. E. Moret, I. Tavernelli and U. Rothlisberger, J. Phys. Chem. B, 2009, 113, 7737; (g) C. Gossens, I. Tavernelli and U. Rothlisberger, J. Phys. Chem. A, 2009, 113, 11888; (h) C. Gossens, I. Tavernelli and U. Rothlisberger, J. Am. Chem. Soc., 2008, 130, 10921.
15. (a) C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785; (b) E. Niecke, P. Becker, M. Nieger, D. Stalke and W. W. Schoeller, Angew. Chem., Int. Ed. Engl., 1995, 34, 1849.
16. (a) L. Simon and J. M. Goodman, Org. Biomol. Chem., 2011, 9, 689; (b) I. Chiorescu, D. V. Deubel, V. B. Arion and B. K. Keppler, J. Chem. Theory Comput., 2008, 4, 499; (c) D. Roy and R. B. Sunoj, Org. Biomol. Chem., 2010, 8, 1040.
17. Z. Futera, J. Klenko, J. E. Sponer, J. Sponer and J. V. Burda, J. Comput. Chem., 2009, 30, 1758.
18. (a) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270; (b) W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284; (c) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299.
19. (a) M. Cossi, G. Scalmani, N. Regar and V. Barone, J. Chem. Phys., 2002, 117, 43; (b) V. Barone and M. Cossi, J. Chem. Phys., 1997, 107, 3210.
20. W. Ehlers, M. Böhme, S. Dapprich, A. Gobbi, A. Höllwarth, V. Jonas, K. F. Köhler, R. Stegmann, A. Veldkamp and G. Frenking, Chem. Phys. Lett., 1993, 208, 111.
21. (a) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785; (b) A. D. Becke, J. Chem. Phys., 1993, 98, 1372.
22. (a) K. Fukui, Acc. Chem. Res., 1981, 14, 363; (b) C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154; (c) C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523.
23. (a) A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735; (b) A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899.
24. NBO analysis was performed using the NBO Version 3.1, as implemented in the Gaussian 03 package by E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, F. Weinhold.
25. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez, J. A. Pople, Gaussian, Inc., Wallingford CT, 2004.
26. C. Gossens, I. Tavernelli and U. Rothlisberger, J. Chem. Theory Comput., 2007, 3, 1212.
27. (a) S. Bhambri, A. Bishop, N. Kaltsoyannis and D. A. Tocher, J. Chem. Soc., Dalton Trans., 1998, 3379; (b) T. A. Albright, Acc. Chem. Res., 1982, 15, 149; (c) D. Braga, Chem. Rev., 1992, 92, 633.
28. B. A. Donahue, M. Augot, S. F. Bellon, D. K. Treiber, J. H. Toney, S. J. Lippard and J. M. Essigmann, Biochemistry, 1990, 29, 5872.
29. Y. Hung, W. Kung and H. Taube, Inorg. Chem., 1981, 20, 457.
30. T. Arthur, D. R. Robertson, D. A. Tocher and T. A. Stephenson, J. Organomet. Chem., 1981, 208, 389.
31. T. V. Ashworth, M. J. Nolte and E. Singleton, J. Chem. Soc., Chem. Commun., 1977, 936.
32. D. R. Robertson, T. A. Stephenson and T. Arthur, J. Organomet. Chem., 1978, 162, 121.

---

Footnote

† Electronic supplementary information (ESI) available: The rotational energy barrier profiles, kinetic and thermodynamical data for aquation and dimerization. Optimized geometries of all ground and transition states involved in this study. See DOI: 10.1039/c1ra00604e

---