The F⋯HO intramolecular hydrogen bond forming five-membered rings hardly appear in monocyclic organofluorine compounds†
Rodrigo A.
Cormanich
a,
Matheus P.
Freitas
*b,
Cláudio F.
Tormena
a and
Roberto
Rittner
a
aChemistry Institute, State University of Campinas, P.O. Box 6154, 13083-970, Campinas, SP, Brazil
bChemistry Department, Federal University of Lavras, P.O. Box 3037, 37200-000, Lavras, MG, Brazil. E-mail: matheus@dqi.ufla.br; Fax: +55 35 3829 1271; Tel: +55 35 3829 1891
First published on 5th March 2012
Abstract
This paper emphasizes that fluorine atoms in organic molecules need special geometric requirements to experience intramolecular hydrogen bonds (H-bonds). Calculations at the B3LYP/aug-cc-pVDZ theoretical level and using the quantum theory of atoms in molecules applied over a series of monocyclic compounds, which have similar C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(F)–C(OH)
C(F)–C(OH)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C fragments, predict that the F⋯HO intramolecular H-bond does not exist when forming five-membered rings. Indeed, it is shown that the geometric restrictions imposed by the rigid rings are the main reasons in preventing fluorine participating in such a F⋯HO intramolecular H-bond.
C fragments, predict that the F⋯HO intramolecular H-bond does not exist when forming five-membered rings. Indeed, it is shown that the geometric restrictions imposed by the rigid rings are the main reasons in preventing fluorine participating in such a F⋯HO intramolecular H-bond.
1. Introduction
The comprehension of long-range interactions in which the fluorine atom can participate is of general interest, since fluorine is often present in a wide range of important organic compounds, both in material and medicinal chemistry.1–5 However, these interactions are not closely analyzed in many cases, and the conformational preferences, as well as the through-space fluorine–hydrogen spin–spin coupling constant, are intuitively ascribed as being due to a possible stabilizing interaction, such as a hydrogen bond (H-bond) in organofluorine compounds.6–11 Notwithstanding, a stabilizing interaction is neither a necessary condition to establish a through-space coupling constant nor to explain conformational preferences of some systems, which are usually the result of a complex interplay of many interactions.12–15Actually, despite some arbitrary interpretations, it is well known that the organic fluorine atom is a poor hydrogen acceptor and can only form weak H-bonds due to the poor polarizability of its lone pairs, which arises as a consequence of the high electronegativity of the fluorine atom and the strong electrostatic nature of the δ+C–δ−F bond.16–18 Indeed, a fluorine atom bonded to carbon needs very short contacts with acidic hydrogen atoms, often shorter than the sum of the F and H van der Waals radii (∼2.65 Å),18,19 in order to act as a H-bond acceptor; hence, this distance criterion is not reliable to infer F⋯H H-bond formation in organofluorine compounds. Also, such H-bond interactions are interpreted to be non-directional, weak long-range interactions. Although F⋯H close contacts are observed in rare favorable cases for organofluorine compounds,20–22 a H-bond cannot be formed if an organic fluorine atom has to compete with better H-bond acceptors, like oxygen or nitrogen atoms.
Although an H-bond involving fluorine atoms is reported to be a very rare phenomenon, it is not uncommon to find interpretations for molecular structure and spectroscopic properties based on such an intramolecular H-bond, which has constraints imposed by conformational geometries that make close contact between fluorine and hydrogen atoms difficult, unlike most of the intermolecular interactions. Accordingly, it has been shown that the fluorine–hydrogen spin–spin coupling constants in 2-fluorophenol and 4-bromo-2-fluorophenol are not due to an intramolecular F⋯HO H-bond, which would give rise to a five-membered ring, but to an overlap of O–H and C–F electronic clouds.15 Indeed, it has been known for a long time that the optimal ring size for H-bond formation is a 7-membered ring; in fact, an intramolecular F⋯HO H-bond forming a 7-membered ring has been recently characterized for 2′-fluoroflavonol, which exhibited a calculated F⋯H–O bond angle of 149.5°.23
Thus, in order to evaluate the restrictions imposed on an effective intramolecular F⋯HO H-bond forming a five-membered ring, as in 2-fluorophenols, several monocyclic molecules (Fig. 1) with cis conformation relative to the H–O–C–C(F) dihedral angle, which has the possibility to form an intramolecular H-bond, were theoretically evaluated at the B3LYP/aug-cc-pVDZ level and using the quantum theory of atoms in molecules (QTAIM).24
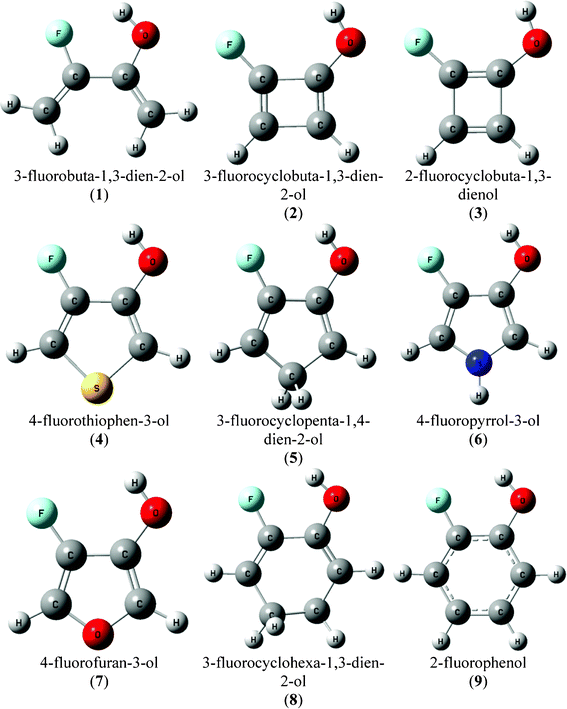 | ||
| Fig. 1 Geometric representations for the conformer A of compounds 1–9. | ||
2. Computational details
All calculations were carried out using the Gaussian 09 package of programs.25 Initially, a potential energy surface (PES) was built for 3-fluorobuta-1,3-dien-2-ol (compound 1; Fig. 1) at the B3LYP/aug-cc-pVDZ theoretical level, scanning the H–O–C–C(F) dihedral angle from 0° to 180° in steps of 10°. The cis and trans (A and B) energy minima were optimized at the B3LYP/aug-cc-pVDZ theoretical level, whose relative energies (0.00/2.48 kcal mol−1, respectively) are in good agreement with those obtained by CCSD(T)/aug-cc-pVDZ (0.00/2.39 kcal mol−1) and CCSD(T)/aug-cc-pVTZ (0.00/2.22) single point calculations. QTAIM calculations were performed using the resulting wave functions obtained from the B3LYP/aug-cc-pVDZ optimizations. QTAIM topological analyses, and the evaluation of the local properties and integral properties over the atomic basins (Ω), were carried out with the AIMALL program.26 The same aforementioned procedures performed for compound 1 were carried out for conformers A of the cyclic compounds 2–9 (Fig. 1).3. Results and discussion
Conformer A [cis H–O–C–C(F) dihedral angle arrangement] of compounds 1–9 would allow an intramolecular F⋯HO H-bond to form and, hence, calculations were carried out only for this conformer. The geometrical representations of all compounds under study are depicted in Fig. 1 and some selected geometrical parameters are listed in Table 1. Conformer A of 3-fluorobuta-1,3-dien-2-ol (1) has the shortest F⋯HO distance among all compounds studied (Table 1) and, therefore, it is firstly analyzed by means of QTAIM.| Compound | r(F⋯HO) | r(F⋯O) | ∠O–C–C(F) | ∠F–C–C(O) | ∠C–C(F)–C(O) | ∠C–C(O)–C(F) |
|---|---|---|---|---|---|---|
| 1 | 1.990 | 2.575 | 115.7 | 111.2 | 130.0 | 124.3 |
| 2 | 3.055 | 3.373 | 133.6 | 131.2 | 91.9 | 89.9 |
| 3 | 3.162 | 3.362 | 141.7 | 136.0 | 90.9 | 89.1 |
| 4 | 2.383 | 2.860 | 123.8 | 119.5 | 115.4 | 111.4 |
| 5 | 2.400 | 2.882 | 123.3 | 119.5 | 112.1 | 108.2 |
| 6 | 2.585 | 3.001 | 127.6 | 123.7 | 109.4 | 106.5 |
| 7 | 2.591 | 3.001 | 127.5 | 123.7 | 108.3 | 105.2 |
| 8 | 2.144 | 2.691 | 118.3 | 114.2 | 124.0 | 119.0 |
| 9 | 2.233 | 2.738 | 121.9 | 116.9 | 122.8 | 118.2 |
The QTAIM method is a rigorous electron density (ρ), interpretative methodology that can define unambiguously atoms as they exist in molecules and the interactions performed between such atoms.24,27,28 Even the weakest bonding interactions can be defined by the QTAIM through the so called bond paths (BPs), lines of maximum electron density linking neighboring nuclei of a molecular system in an equilibrium geometry, which, as repeatedly emphasized by Bader, is the sufficient and necessary condition for the definition of bonding between atoms.29–31 Because of this, QTAIM has been considered as the theoretical method that experienced the greatest advance in the study of chemical bonds in general, and in particular of the H-bond.32 H-bonds were characterized by following the criteria based on the QTAIM parameters developed by Koch and Popelier:33 a bond critical point (BCP) and a BP should be formed for each H-bond; the ρ and the ρ Laplacian values (∇2ρ) at the H-bond BCP (ρHBCP and ∇2ρHBCP) must lie in the range of 0.002 atomic units (au) to 0.04 au and +0.024 au to +0.139 au, respectively; and the H atom involved in the H-bond should have a loss of atomic charge [q(H)], an increased atomic energy [E(H)] and a decreased first dipole moment [M1(H)] and an atomic volume [V(H)] in comparison to that of a H atom not involved in a H-bond.
The molecular graph—the collection of BPs of a molecular system—for conformer A of 1 obtained by QTAIM is shown in Fig. 2. It shows a BCP and a BP referring to H-bond formation, i.e. QTAIM predicts the formation of a H-bond in compound 1, which is consistent with the close F⋯HO contact (1.990 Å; Table 1). The criteria established by Popelier were evaluated by using the hydroxyl hydrogen of conformer B in 1 (trans H–O–C–C(F) dihedral angle) as the reference H atom (that cannot form the F⋯HO H-bond), and the intramolecular F⋯HO H-bond of conformer A was characterized as a stable interaction (Table 2).
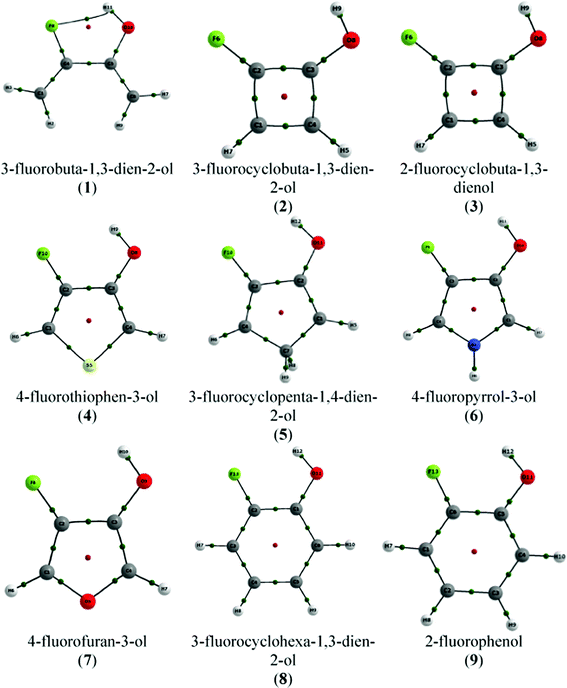 | ||
| Fig. 2 Molecular graphs of compounds 1–9 (conformers A). Green points represent bond critical points (BCP) and red points indicate ring critical points (RCP). | ||
| Conformer | ρ HBCP | ∇2ρHBCP | q(H) | E(H) | M1(H) | V(H) |
|---|---|---|---|---|---|---|
| A | 0.025 | +0.093 | +0.614 | −0.3413 | 0.149 | 17.760 |
| B | — | — | +0.591 | −0.3522 | 0.169 | 22.348 |
Since the F⋯HO H-bond is predicted to be formed in compound 1, the following question arises: why is a pentatomic F⋯HO intramolecular H-bond not formed in 2-fluorophenols,15 which have a similar C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(F)–C(OH)
C(F)–C(OH)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C fragment compared to 1? In order to find out the response to such a question, the geometric parameters of compound 1 were used as the standard to evaluate the cyclic compounds 2–9 depicted in Fig. 1 and Table 1.
C fragment compared to 1? In order to find out the response to such a question, the geometric parameters of compound 1 were used as the standard to evaluate the cyclic compounds 2–9 depicted in Fig. 1 and Table 1.
Interatomic distances r(F⋯HO) and r(F⋯O), and bond angles O–C–C(F) and F–C–C(O), which are the geometrical parameters that determine the proximity of F to the H(O) atom, are larger for all the cyclic compounds 2–9 in comparison to 1 (Table 1). Indeed, the values in Table 1 show an excellent parallelism between r(F⋯HO), r(F⋯O), O–C–C(F) and F–C–C(O) with the C–C(F)–C(O) and C–C(O)–C(F) bond angles for all the compounds, i.e., when the former parameter increases, the later decreases and vice versa. This parallelism is readily understandable, since the opening/closure of the O–C–C(F) and F–C–C(O) bond angles causes the closure/opening of the C–C(F)–C(O) and C–C(O)–C(F) bond angles, respectively, which in turn determines the r(F⋯HO) and r(F⋯O) values.
Since r(F⋯HO), r(F⋯O), O–C–C(F) and F–C–C(O) are those determining the F⋯H contact (together with the C–C(F)–C(O) and the C–C(O)–C(F) bond angles), we can expect that if the H-bond is formed in the monocyclic rings under study, it should be weaker than that formed in compound 1, bearing the closest F⋯H contact. Indeed, the QTAIM molecular graphs depicted in Fig. 2 predict that the F⋯HO H-bond is not formed in any of the compounds 2–9. 3-Fluorocyclobuta-1,3-dien-2-ol and 2-fluorocyclobuta-1,3-dienol (compounds 2 and 3, respectively) are those with the higher F⋯HO distance, due to the C–C(F)–C(O) and C–C(O)–C(F) bond angles of ca. 90°. In this way, the severe geometrical restriction caused by the four-membered ring to the C–C(F)–C(O) and C–C(O)–C(F) bond angles in compounds 2 and 3 hinders the contact between the F and H(O) atoms (in agreement with the r(F⋯HO), r(F⋯O), O–C–C(F) and F–C–C(O) geometrical parameters) and, therefore, the intramolecular F⋯HO H-bond cannot be formed in these compounds.
Similar effects can be observed for the remaining compounds: the geometrical restriction caused by the cyclic rings increases the F⋯HO distance, although to a smaller extent. An interesting effect of such an observation is experienced by the five-membered cyclic compounds 4–7, in which the values for r(F⋯HO), r(F⋯O), O–C–C(F) and F–C–C(O) are ordered as 4 < 5 < 6 ≈ 7, in agreement with the X atomic radius and X–C bond length (X = S, C, N and O; X–C bond length = 1.740 Å, 1.510 Å, 1.382 Å and 1.362 Å, respectively). Thus, closer F⋯H(O) contacts can be achieved for those compounds having bond angles capable of bending to higher values. Indeed, the less restricted six-membered compounds of 6-fluorohexa-1,5-dienol and 2-fluorophenol (8 and 9, respectively) are those with a F⋯H(O) contact and geometrical parameters that contribute towards a similar contact to 1. However, as suggested by our QTAIM calculations and earlier work based on experimental/theoretical results,15 an intramolecular F⋯HO H-bond forming a five-membered ring is not established in 2-fluorophenol. The difficult establishment of the pentatomic, intramolecular F⋯HO H-bond formation appears to be a general trend for other 2-fluorphenol derivatives (and even for 2–8 derivatives), since the ring C–C–C bond angles are nearly invariant with the nature of the substituent at the 3-, 4-, 5- or 6-positions, i.e., the geometrical restriction imposed by the rigid rings, which decreases the F⋯H contacts, is independent of the substituent. Indeed, this becomes evident when an intramolecular five-membered F⋯HO H-bond is evaluated on the basis of r(F⋯HO), r(F⋯O), O–C–C(F), F–C–C(O), C–C(F)–C(O) and C–C(O)–C(F) geometrical parameters in the crystal structures of nine 2-fluorophenol derivatives obtained from the Cambridge Structural Database (CSD)34 (tables, figures and references are listed in the ESI†). All the crystal compounds obtained from the CSD have similar geometrical parameters (which determine the F⋯H contact), also congruent to that calculated for 2-fluorophenol (9); therefore, an intramolecular five-membered F⋯HO H-bond is not formed in these compounds.
Similar results are found for Cl and Br derivatives (tables and figures in the ESI†), that is, while 3-halobuta-1,3-dien-2-ol (analog of 1) exhibits an intramolecular X⋯HO H-bond (X = halogen) in conformer A, the structures with small rings (analogs of 2–7) do not experience such an interaction due to geometrical restrictions. However, in contrast to fluorinated compounds, an intramolecular X⋯HO H-bond is formed for Cl and Br analogs in 8 and 9, which have the least geometrical restrictions among compounds 2–9. Indeed, the formation of the intramolecular X⋯HO H-bond in the Cl and Br derivatives in the 8 and 9 analogs highlights that organic fluorine is a bad proton acceptor in an intramolecular five-membered H-bond in comparison to Cl and Br atoms. Also, an unstable H-bond is estimated for the bromine derivatives 4 and 5 (ellipticity values in the HBCP of ∼3 and ∼8 au, respectively), but not for the chlorinated 5 and 6 derivatives. In this sense, the ring geometrical restrictions in compounds 5 and 6 are the borderline values for intramolecular X⋯HO H-bond formation in bromine derivatives, i.e., compounds with fewer geometric restrictions than 5 and 6 can form pentatomic intramolecular Br⋯HO H-bonds. Such a result is not experienced by the Cl derivatives 5 and 6, suggesting that the organic Br atom is a better proton acceptor than organic Cl, which in turn is a better proton acceptor than organic F in the formation of the intramolecular five-membered X⋯HO H-bond. Thus, the geometrical restrictions imposed by the ring size, which may be measured by the ring C–C–C bond angle values, is nearly independent of the halogen atom; consequently, the formation of the H-bond in Cl and Br analogs 8 and 9, and residual H-bond formation in the Br derivatives 5 and 6 indicate that the proton acceptor trend for organic halogens in the intramolecular five-membered X⋯HO H-bond is Br > Cl > F. These findings reinforce that geometric restrictions imposed by small (4–6) rigid rings dictate the formation of the intramolecular five-membered X⋯HO H-bond.
Another two approaches were carried out to support our findings. The first one was based on restricting the C–C(F)–C(O) and C–C(O)–C(F) geometrical parameters in 1 to 5° and 10° smaller than the value for the equilibrium geometry and then optimizing the remaining geometrical parameters; the second approach was to perform additional calculations for the less hindered 3-fluorocyclohepta-1,3-dien-2-ol (Fig. 3 and Table 3). The bending of the C–C(F)–C(O) and C–C(O)–C(F) bond angles to smaller values in conformer A of the aliphatic compound 1 was carried out to simulate the effect of the ring restriction over the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(F)–C(OH)
C(F)–C(OH)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C fragment. It is clear from Table 3 that r(F⋯HO), r(F⋯O), O–C–C(F) and F–C–C(O) increase when the C–C(F)–C(O) and C–C(O)–C(F) bond angles are frozen to −5° and to −10° (in a higher extent) relative to the equilibrium geometry of 1; consequently, the pentatomic intramolecular F⋯HO H-bond is not formed in these cases (Fig. 3). On the other hand, 3-fluorocyclohepta-1,3-dien-2-ol exhibits nearly the same geometrical parameters which determine the F⋯H(O) contact in 1 (compare values in Table 1 and 3) and, accordingly, QTAIM predicts the intramolecular H-bond in 3-fluorocyclohepta-1,3-dien-2-ol (conformer A) with about the same strength of that in 1 (ρHBCP of 0.025 for both compounds) (Fig. 3).
C fragment. It is clear from Table 3 that r(F⋯HO), r(F⋯O), O–C–C(F) and F–C–C(O) increase when the C–C(F)–C(O) and C–C(O)–C(F) bond angles are frozen to −5° and to −10° (in a higher extent) relative to the equilibrium geometry of 1; consequently, the pentatomic intramolecular F⋯HO H-bond is not formed in these cases (Fig. 3). On the other hand, 3-fluorocyclohepta-1,3-dien-2-ol exhibits nearly the same geometrical parameters which determine the F⋯H(O) contact in 1 (compare values in Table 1 and 3) and, accordingly, QTAIM predicts the intramolecular H-bond in 3-fluorocyclohepta-1,3-dien-2-ol (conformer A) with about the same strength of that in 1 (ρHBCP of 0.025 for both compounds) (Fig. 3).
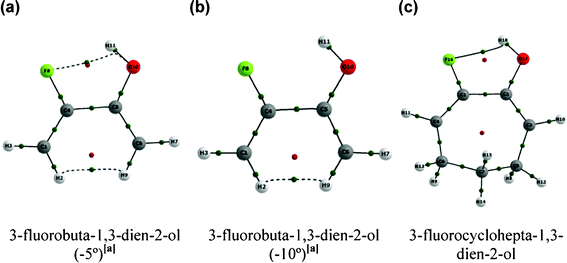 | ||
| Fig. 3 Molecular graphs for the hypothetical cases in which the C–C(F)–C(O) and C–C(O)–C(F) bond angles were frozen to (a) −5° and (b) −10° relative to the equilibrium geometry of 3-fluorobuta-1,3-dien-2-ol (1). (c) Molecular graph for 7-fluorocyclohepta-1,6-dienol. Green points represent BCPs and red points indicate RCPs. | ||
Remarkably, the geometrical parameters and the QTAIM results are in agreement and indicate that the absence of the pentatomic intramolecular H-bond in cyclic compounds is due to geometric restrictions occasioned by the rigid rings, which do not allow a sufficient contact between the F and H(O) atoms. Both the hypothetical case in which the C–C(F)–C(O) and C–C(O)–C(F) bond angles are frozen to smaller values than the equilibrium geometry in 1 and the H-bond formation in a less rigid 7-membered ring (3-fluorocyclohepta-1,3-dien-2-ol) support such results.
4. Conclusions
In comparison to the aliphatic 3-fluorobuta-1,3-dien-2-ol (1), the C–C(F)–C(O) and C–C(O)–C(F) bond angles in cyclic compounds are more strained, bending the O–C–C(F) and F–C–C(O) angles to higher values, which, consequently, decreases the contact between the F and H(O) atoms by increasing the r(F⋯HO) and r(F⋯O) distances. Indeed, the poor H-bond acceptor organic fluorine atom cannot form a pentatomic intramolecular F⋯HO H-bond in small (4–6 atomic members) cyclic compounds due to the geometric restrictions imposed by these rings.Overall, the present study shows that the F⋯H H-bond involving organic fluorine atoms is often overestimated in the literature and that rigorous evaluation is necessary to confirm its formation; simple chemical intuition, determination/estimation of a fluorine–hydrogen distance shorter than the sum of their van der Waals radii and identification of fluorine–hydrogen spin–spin coupling constants (as exemplified in 2-fluorophenols) are not conclusive probes for the F⋯H H-bond. Ultimately, we hope that the understanding of the requirements for long-range interactions involving organic F atoms provided by our outcomes may assist drug and material developments.
Acknowledgements
The authors are grateful to FAPESP and FAPEMIG for financially supporting this research and for a scholarship (to R.A.C.), and to CNPq for the fellowships (to M.P.F., C.F.T. and R.R.).References
- K. Müller, C. Faeh and F. Diederich, Science, 2007, 317, 1881 CrossRef.
- S. Purser, P. R. Moore, S. Swallow and V. Gouverneur, Chem. Soc. Rev., 2008, 37, 320 RSC.
- W. K. Hagmann, J. Med. Chem., 2008, 51, 4359 CrossRef CAS.
- A. Tressaud, J. Fluorine Chem., 2011, 132, 651 CrossRef CAS.
- K. Reichenbächer, H. I. Süss and J. Hulliger, Chem. Soc. Rev., 2005, 34, 22 RSC.
- T. J. Barbarich, C. D. Rithner, S. M. Miller, O. P. Anderson and S. H. Strauss, J. Am. Chem. Soc., 1999, 121, 4280 CrossRef CAS.
- D. L. Bryce and R. E. Wasylishen, J. Mol. Struct., 2002, 602–603, 463 CrossRef CAS.
- L. Hennig, K. Ayala-Leon, J. Angulo-Cornejo, R. Richter and L. Beyer, J. Fluorine Chem., 2009, 130, 453 CrossRef CAS.
- A. J. Mountford, S. J. Lancaster, S. J. Coles, P. N. Horton, D. L. Hughes, M. B. Hursthouse and M. E. Light, Inorg. Chem., 2005, 44, 5921 CrossRef CAS.
- I. Alkorta, J. Elguero and G. S. Denisov, Magn. Reson. Chem., 2008, 46, 599 CrossRef CAS.
- M. L. Senent, A. Niño, C. Muñoz-Caro, Y. C. Semeyers, R. Dominguez-Gomez and J. M. Orza, J. Phys. Chem. A, 2002, 106, 10673 CrossRef CAS.
- R. H. Contreras, J. E. Peralta, C. G. Giribet, M. C. R. De Azua and J. C. Facelli, Annu. Rep. NMR Spectrosc., 1993, 27, 255 CrossRef CAS.
- D. Cremer and J. Gräfenstein, Phys. Chem. Chem. Phys., 2007, 9, 2791 RSC.
- R. A. Cormanich, L. C. Ducati and R. Rittner, Chem. Phys., 2011, 387, 85 CrossRef CAS.
- R. A. Cormanich, M. A. Moreira, M. P. Freitas, T. C. Ramalho, C. P. A. Anconi, R. Rittner, R. H. Contreras and C. F. Tormena, Magn. Reson. Chem., 2011, 49, 763 CAS.
- J. A. K. Howard, V. J. Hoy, D. O'Hagan and G. T. Smith, Science, 1996, 52, 12613 CAS.
- D. O'Hagan, Chem. Soc. Rev., 2008, 37, 308 RSC.
- J. D. Dunitz and R. Taylor, Chem.–Eur. J., 1997, 3, 89 CrossRef CAS.
- E. Carosati, G. Sciabola and S. Cruciani, J. Med. Chem., 2004, 47, 5114 CrossRef CAS.
- J. A. K. Howard, V. J. Hoy, D. O'Hagan and G. T. Smith, Tetrahedron, 1996, 52, 12613 CrossRef CAS.
- J. D. Dunitz, Chem. Bio. Chem., 2004, 5, 614 CrossRef CAS.
- H. F. Bettinger, ChemPhysChem, 2005, 6, 1169 CrossRef CAS.
- T. A. O. Fonseca, M. P. Freitas, R. A. Cormanich, T. C. Ramalho, C. F. Tormena and R. Rittner, Beilstein J. Org. Chem., 2012, 8, 112 CrossRef CAS.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon, Oxford, 1990 Search PubMed.
- Gaussian 09, Revision B.01, M. J. Trucks, G. W. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, D. J. Fox, Gaussian, Inc., Wallingford CT, 2009.
- AIMAll (Version 11.10.16), Todd A. Keith, TK Gristmill Software, Overland Park KS, USA, 2011, http://aim.tkgristmill.com/.
- R. F. W. Bader, Chem. Rev., 1991, 91, 893 CrossRef CAS.
- R. F. W. Bader, J. Phys. Chem. A, 1998, 102, 7314 CrossRef CAS.
- R. F. W. Bader, Chem.–Eur. J., 2006, 12, 2896 CrossRef CAS.
- R. F. W. Bader, J. Phys. Chem. A, 2009, 113, 10391 CrossRef CAS.
- R. F. W. Bader, J. Phys. Chem. A, 2010, 114, 7431 CrossRef CAS.
- S. J. Grabowski, Chem. Rev., 2011, 111, 2597 CrossRef CAS.
- U. Koch and P. L. A. Popelier, J. Phys. Chem. A, 1995, 99, 9747 CAS.
- F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c2ra00039c |
| This journal is © The Royal Society of Chemistry 2012 |
