On the interaction of uranyl with functionalized fullerenes: a DFT investigation

Abstract

Understanding the interaction between uranyl and C₆₀ can be useful for nuclear waste management processes. In this paper, we have investigated the binding of uranyl with bare C₆₀ as well as functionalized C₆₀ using density functional theory. It is observed that, the uranyl is only weakly bound to bare C₆₀. On the contrary, functionalization of C₆₀ with malonate ligand is shown to increase its binding ability to uranyl species. Further, we notice that pH could play an important role in the binding of uranyl at the malonate site. Our calculated geometries are in close agreement with the experimental data of the malonate uranyl complex. Further, based on the calculated binding energies, we show that a chelate type binding is more favorable in comparison to bidentate carboxylate binding.

---

Introduction

Due to the ever increasing demand for energy, nuclear energy is emerging as an indispensable source of alternate energy. Uranium, Neptunium and Plutonium are commonly encountered elements in the nuclear fuel cycle. The generation of nuclear power, however, comes with the penalty in the form of challenges associated with the disposal of radioactive nuclear wastes from the spent fuel. The radiation and toxicity generated from such nuclear waste contaminate the aquatic and geological systems which is of primary concern.

However, there exist alternate ways of converting the toxic highly soluble U^VI species to insoluble U^IV species by means of electron transfer mechanisms. In fact, cytochrome c₇ type bacteria present in D. Acetoxitans,¹ iron-sulfur containing mineral surfaces (hematite)² and humic acids³ derived from natural organic matter does convert U^VI to U^IV in an efficient manner via electron transfer processes.

Fullerene chemistry grew very rapidly during the last two decades due to the remarkable redox and energy storage properties associated with it.^4–6 Furthermore, fullerene derivatives can be used as biologically active compounds in medicinal chemistry. Due to the poor solubility of C₆₀, its application involving aqueous phase chemical processes has been hindered. Major efforts have, however, been invested to improve the solubility of C₆₀ fullerene in aqueous phase. To this end, chemical functionalization bearing hydrophilic functional groups,⁷ encapsulation of C₆₀ within γ-cyclodextrin⁸ and incorporation of C₆₀ in micelles⁹ have improved the solubility in an aqueous environment. It is now being recognized that carbon nanotubes can also be a useful material for waste management processes.^10–20

On the theoretical side, there has been a large increase in the number of computational investigations of actinide complexes, particularly those of uranium.^22–31 The electronic structure and molecular geometry of the di-oxo cation of the three elements U, Np, and Pu have been studied at the Hartree Fock (HF),²⁶ density functional theory (DFT)^23,24,27,29 as well as correlated ab initio levels.^22,28 In addition to the requirement of using high levels of theory and basis sets, modelling actinide ions is also quite challenging because of the need to account for solvation and relativisitic effects at some level. Fortunately, the DFT approach, with incorporation of relativistic effect via small core pseudo-potentials in conjunction with continuum solvation model seems to be sufficient and cost-effective. As far as accuracy of the results is concerned, calculations at this level are at least semi-quantitative.²⁹

To this end, theoretical studies have also modelled these cations, especially uranyl, using various methods for the inclusion of aqueous solvation effects including variants of continuum models as well as by explicitly including the solvent molecules. The most studied structures are those which arise when the uranyl ion is hydrated, with the penta-aqua form being generally preferred to be the dominant species.²⁵ The effect of bulk solvent is usually included via a continuum model, but there is an increasing interest in considering the actual nature of interaction with the nearest solvent molecules.^29,30 Vazquez et al. modeled the uranyl acetate, carbonate and malonate complexes of uranyl in solution using DFT.³¹ We have recently investigated the interaction of uranyl with functionalized carbon nanotubes and found that the binding of uranyl is strong in the functionalized case than the unfunctionalized counterpart.³²

Hence, there is need for further calculations in order to understand in more details the binding behavior of uranyl with nanostructures, which might help us in designing new nanomaterials that can be efficiently used for nuclear waste management. In this paper, we investigate the structures, vibrational frequencies and binding affinities of uranyl to malonate functionalized C₆₀ in 1 : 1 and 1 : 2 ratio of functionalized C₆₀ (malonate:uranyl) through DFT based calculations.

Computational details

All the geometries are optimized using BP86 functional in conjunction with def-TZVP basis for uranium, def2-TZVP basis for oxygen (of UO₂) and def2-SV(P) basis set for the remaining atoms. For uranium, the core electrons are modeled with def-MWB pseudopotential. For energetics, we have used B3LYP functional with the same basis sets. Solvation effects are incorporated using COSMO continuum solvation model (using ε = 80) as implemented in TURBOMOLE.³³ Such a cost effective strategy saves computational time and the predicted structures, vibrational spectra and redox properties are comparable to the experimental data.²⁹

Results and discussion

(i) Binding of uranyl at bare C₆₀

We first present our results on binding of uranyl to bare C₆₀ prior to considering functionalization. In Fig. 1, we have shown the five different binding sites of uranyl to C₆₀. The first two binding sites are at the hexagonal carbon rings, where the uranyl can bind in two different orientations which is either parallel (μ^2-||) or perpendicular (μ^2-⊥) with respect to the C–C bond at the junction of two hexagons of C₆₀ (Fig. 1). Similarly, we have made attempts to optimize the structures of the uranyl bound at the pentagonal carbon in both μ^2-⊥ and μ^2-|| modes with respect to the junction of the hexagon–pentagon bond of C₆₀. However, the minimum energy structures are obtained only for the μ^2-⊥ binding site, which will be discussed hereafter. In the fourth binding site, the uranyl ion can bind symmetrically to the pentagonal ring (μ⁵) of the carbon atoms. Finally, we have also confined the uranyl inside the C₆₀ cage.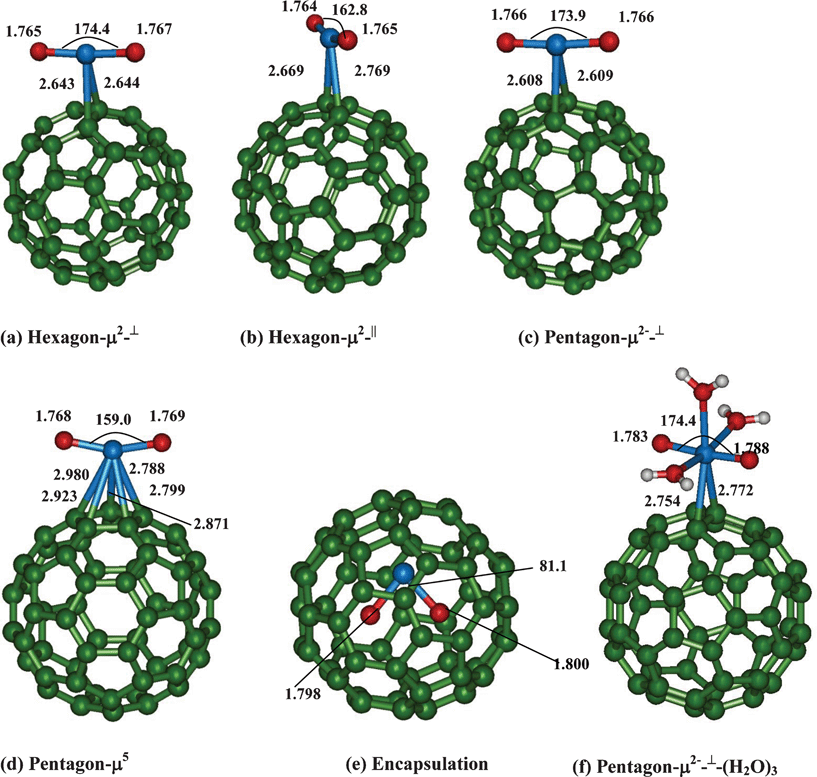

Fig. 1 Binding of uranyl at various sites to bare C₆₀ fullerene.

For both hexagon and pentagon μ^2⊥ binding, the calculated U=O bond lengths (∼1.766 Å) and O=U=O (∼174.0°) bond angle are very similar. However, for the uranyl binding at the hexagon μ^2|| binding mode, a strong bending of O=U=O (162.8°) is noted which is rather surprising. Within the three μ² coordinations, the U–C bond lengths are somewhat shorter (by 0.06 Å) when uranyl binds at the pentagonal ring system (pentagon μ^2⊥) as compared to the hexagons. Further, the two U–C bond lengths are symmetric for the μ^2⊥ binding mode at both hexagons and pentagon ring systems.

For the μ⁵-binding, the uranyl bond lengths and bond angles are slightly elongated (∼0.002 Å) and more bent (by 4°) as compared to the three μ²-binding sites. The distances between U and C (of C₆₀) for all the above four binding modes (excluding the encapsulation mode) have also been presented in Fig. 1. Between μ² and μ⁵, the U–C bond strength for the latter species is weaker as indicative from their bond lengths. Attempts were even made to optimize the structure of the uranyl at the hexagonal ring system with μ⁶-binding. Unfortunately, we were unable to get the minimum energy species, due to the spontaneous formation of the μ² coordination mode with the hexagons. Finally for the uranyl encapsulated species, the linear uranyl is much more elongated (1.798 Å) and very strongly bent (81.1°) as compared to other three binding sites.

All the four structures are characterized as minima and we find that the calculated vibrational spectra (symmetric (ν_sym) as well as asymmetric (ν_asym)) are slightly red shifted as compared to the penta-aqua–uranyl complex (Table 1). For instance, the calculated ν_sym and ν_asym of μ⁵ is about 20–25 cm⁻¹ lower in energy as compared to the penta-aquo–uranyl complex. For the encapsulated uranyl adduct, this stretching is further reduced (854 cm⁻¹ and 923 cm⁻¹) due to U=O bond elongation. For the μ² binding motifs, the calculated vibrational spectra are only slightly downshifted as compared to the penta-aquo–uranyl complex.

Table 1 Structural parameters and vibrational frequencies of uranyl complex bound to malonate functionalized C₆₀

	Binding mode	U=O (Å)	O=U=O (°)	U–OMal (Å)	U–OH2O (Å)	U=Oνsym (cm^−1)	U=Oνasym (cm^−1)
[U^VIO2(C60–Mal–H2)(H2O)3]^2+	μ^1-Carboxylate	1.787	174.5	2.305	2.437–2.603	836.2	930.5
[U^VIO2(C60–Mal–H2)(H2O)3]^2+	μ^2-Chelate	1.788	173.9	2.404, 2.465	2.473–2.485	836.2	930.2
[U^VIO2(C60–Mal–H)(H2O)3]^1+	μ^2-Carboxylate	1.792	172.0	2.389, 2.391	2.482–2.497	831.4	926.2
[U^VIO2(C60–Mal–H)(H2O)3]^1+	μ^2-Chelate	1.795	172.1	2.197–2.470	2.497–2.549	825.4	918.7
[U^VIO2(C60–Mal)(H2O)3]^0	μ^2-Carboxylate	1.801	168.1	2.341	2.504–2.530	821.5	909.3
[U^VIO2(C60–Mal)(H2O)3]^0	μ^2-Chelate	1.809	167.7	2.222, 2.228	2.512–2.586	809.1	891.5
[(U^VIO2)2(C60–Mal)(H2O)3]^2+	(μ^2)2-Carboxylate	1.792, 1.788	173.4	2.400–2.408	2.479–2.486	829.6, 836.5	927.2, 929.2

---

Binding energies are calculated using the following equation,

[UO₂]²⁺ + C₆₀→ [UO₂–C₆₀]²⁺

Between the four species, pentagon-μ^2-⊥ binding is the most stable species and the binding energy (COSMO-B3LYP) is found to be −6.27 kcal mol⁻¹. Hexagon-μ^2-|| is the least stable amongst the four binding patterns considered and the binding energy is estimated to be +4.93 kcal mol⁻¹. It is also noted that hexagon-μ^2-|| is less stable by 12.28 kcal mol⁻¹ in comparison to the most preferred structure (pentagon-μ^2-⊥). For the encapsulated adduct the binding energy is found to be 100.45 kcal mol⁻¹ and it is less stable by 66.45 kcal mol⁻¹ from the pentagon-μ^2-⊥ structure. Further, the calculated binding is marginally favorable for hexagon-μ^2-⊥ (−2.21 kcal mol⁻¹) and unfavorable for pentagon-μ⁵ (+2.55 kcal mol⁻¹). The weak binding of uranyl to C₆₀ can be attributed to the inability of C₆₀ to donate the charge to the lowest unoccupied molecular orbital (LUMO) of uranyl. As the charges of the carbons are very small (−0.001 to −0.005 au), the cation binding is very weak. Further, the binding efficacy of uranyl at various sites to bare C₆₀ can be attributed to the extent of charge transfer from uranyl to C₆₀. Indeed, it is known that in the case of metal atom-C₆₀ interactions, charge transfer usually occurs from the metal centre to the C₆₀ moiety, thus the metal atom attains partial ionic character.³⁴ This concept has been successfully utilized in the field of hydrogen storage using metal decorated fullerenes. However, in our case, due to the di-positive charge of the uranyl species, further electron transfer from uranyl to C₆₀ is highly unlikely. We find that the electron flow is from C₆₀ fullerene to the uranyl species. Our Mülliken charge analysis does confirm the above statement. For instance, as compared to bare uranyl, the positive charge on the uranyl moiety for the most stable pentagon-μ^2-⊥ species is smaller (1.28e⁻) as compared to least stable hexagon-μ^2-|| species (1.36e⁻). The electron accepting nature of the C₆₀ fullerene predominantly governs the fullerene chemistry, where the fullerene acts as a dienophile (electron acceptor) and forms favourable addition adducts with electron rich molecules like dienes.³⁵ For these cases, the most preferable site of additions at the hexagonal junctions [6,6]. Conversely, in our case, we find that the [6,5] junctions is the preferable site of binding to uranyl. This signifies the basic differences between the interactions of C₆₀ fullerene with different species.

As uranyl ion exists in aqueous phase with five water molecules, we have optimized a structure of uranyl with three water molecules bound to C₆₀ (considering the most stable structure pentagon-μ^2-⊥). The calculated uranyl bond lengths (1.783 Å) are lengthened due to the additional coordination of water molecules. However, the uranyl binding energies are unfavorable by more than 40 kcal mol⁻¹, probably because the solvation energy of the uranyl ion is very high prior to C₆₀ binding as compared to the adduct. We have also made attempts to optimize the structure of uranyl binding to C₆₀ by keeping all five water molecules. Although the binding energies have reduced from 40 kcal mol⁻¹ to ∼18 kcal mol⁻¹, the relative trend is still the same. We note that the equatorial penta-coordination is only preferred over the hepta-coordination. The two additional water molecules are only interacting via hydrogen bonding with the coordinated water molecules (of the first coordination sphere).

Further, for effective separation, uranyl ion will be in aqueous phase and C₆₀ will be in organic phase of the system. By attaching C₆₀ with organic functional groups (such as malonate), one can increase the solubility of C₆₀ and make it a better binder of uranyl in aqueous phase. From this part of the discussion it is quite clear that interaction of bare uranyl (along with explicitly hydrated species) with C₆₀ is unfavorable. Hence, in the forthcoming sections, we focus on binding of uranyl with malonate functionalized C₆₀.

(ii) Binding of uranyl at functionalized C₆₀

Functionalization of C₆₀ with carboxylic group such as malonic acid can improve the solubility and the strength of uranyl binding affinity to C₆₀.²¹ We have functionalized C₆₀ with a dicarboxylic acid, (malonic acid) and considered the uranyl binding to neutral, anionic and di-anionic form of malonate functionalized C₆₀. All the three types of complexes which differ in the protonation states of carboxylic acid group are expected to be formed at different pH conditions. At low pH (pH = 1–3), both the carboxylate functional group will be protonated, and in semi-acidic pH (pH = 3–6), either one of the functional group is expected to be protonated (mono-anionic form), whereas at high pH (7–10), both the carboxylates will be deprotonated creating a di-anionic form.³⁶

We have considered uranyl binding to mono-dentate (neutral), bi-dentate (in both anionic forms) or chelate (all three forms) binding motifs of malonate functionalized C₆₀ (Fig. 2, 3, 4).

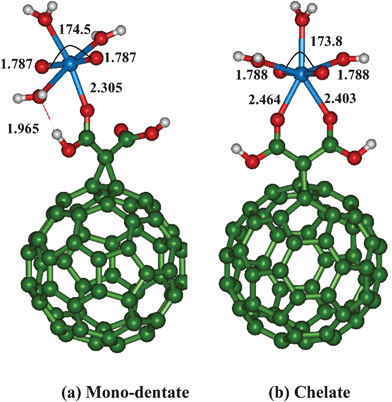Fig. 2 Binding of uranyl with neutral malonic acid functionalized C₆₀ fullerene.

Fig. 3 Binding of uranyl with mono-anionic malonate functionalized C₆₀ fullerene.

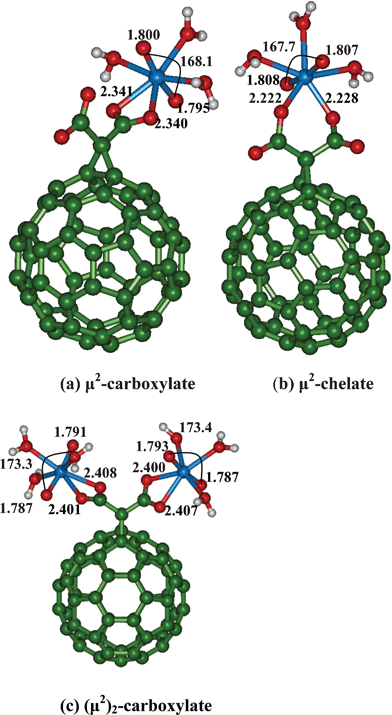Fig. 4 Binding of uranyl with di-anionic malonate functionalized C₆₀ fullerene.

For uranyl binding to neutral malonate functionalized C₆₀ (Fig. 2), we find that the U=O axial bond length is slightly longer for the chelate binding mode as compared to the mono-dentate binding mode. Similarly, the O=U=O bond angle is somewhat more bent (by 1°) in the chelate mode as compared to the same in mono-dentate binding. For mono-dentate carboxylate binding, during geometry optimization, we find that one water molecule is automatically detached from uranyl (2.751 Å) and now forms a hydrogen bonding with the carboxylate group of malonic acid if we consider tetra-aquo–uranyl with penta-coordination mode. Hence, we have considered only a tetra coordination site of uranyl (tri-aquo complex) with the mono-dentate carboxylate binding. This structure is characterized as minima (Fig. 2) and the geometrical parameters are given in Table 1.

For the mono-dentate carboxylate binding, the equatorially coordinated water molecule is hydrogen bonded (1.965 Å) to the carboxylate group, whereas in the case of chelate binding, no such weak interactions are noticed (Fig. 2). Further, asymmetric binding of two carboxylate oxygens to uranyl (2.404 Å and 2.465 Å) is noticed for chelating binding mode. Further, out of the monodentate and chelate modes, the latter uranyl binding mode is more favorable by ∼10 kcal mol⁻¹.

For both mono-anionic and di-anionic species, we have considered two types coordination modes, one is of chelate type which we refer as μ²-chelate and the other is the symmetric bidentate carboxylate site denoted as μ²-carboxylate. The notation carboxylate or chelate μ² arises from whether the bonded oxygen comes from the same carboxylic acid moiety or from two different carboxylic acids present in malonate.

As compared to the neutral malonic acid, the U=O bond length are slightly weaker by 0.01 Å for both μ² binding modes in case of corresponding mono-anionic form. Similarly, the O=U=O bond angle is also more bent by 2° in the latter binding sites. Between the two coordination modes, the μ²-carboxylate binding site is somewhat more stable by ∼3 kcal mol⁻¹ as compared to the μ²-chelate binding site. Here again, we find the asymmetric U–O bond length (2.197 Å and 2.470 Å) is noted for chelate binding site due to the differing charges present on the oxygen atoms of the two carboxylates. Due to the strong coordination of malonate to uranyl, the coordinated water molecules become weakly bound (2.497–2.549 Å).

At high pH conditions, the coordination of uranyl will be at the completely deprotonated sites of malonate. Similar to the mono-anionic form, here we have two μ²-forms which are either bi-dentate μ²-carboxylate or μ²-chelate binding modes. Due to the double negative charge of the ligand, the binding of uranyl is expected to be stronger. Indeed, the U=O bond length is more elongated (by 0.01 Å) as compared to the mono-anionic form and 0.02 Å with respect to neutral malonate form. Between the two binding sites, the μ²-chelate binding is stronger and energetically more favorable by ∼17 kcal mol⁻¹ as compared to the μ²-carboxylate binding mode. The stronger binding of asymmetric μ² mode to uranyl is also reflected in the O=U=O bond angle, which is more bent (167°) as compared to the μ² carboxylate binding. Due to the strong coordination of negative charged ligand, we find that the water molecules are loosely bound (2.512 Å–2.586 Å).

If the concentration of uranyl is high, then the binding of uranyl to functionalized C₆₀ in 1 : 2 (C₆₀ : uranyl) is possible. We have optimized this species (Fig. 4(c)), where the two uranyl ions bind via μ²-bidentate carboxylate functional groups of malonate. As compared to the μ²-carboxylate binding of malonate to one uranyl, we find that the binding of uranyl is somewhat weak which are reflected in the reduction of of U=O bond length (1.792 Å) and the extent of bending of O=U=O bond angle being small (173.4°).

(iii) Vibrational frequencies

The favourable binding of functionalized C₆₀ to uranyl will lead to elongation of U=O bond as compared to penta-aqua–uranyl complex, and this weakening in the bond strength will be reflected in the vibrational frequencies corresponding to symmetric (ν_sym) and asymmetric (ν_asym) stretching of the U=O bond. For all the complexes, the calculated U=O ν_sym and ν_asym stretching modes (Table 1) are red-shifted as compared to the penta-aqua–uranyl complex. However, the extent of red-shift of the malonate–uranyl complex varies depending on the protonation state of the carboxylate group of the malonate.

Hence, at high pH (fully depronated), the uranyl bond lengths are elongated by more than 0.02 Å as compared to low pH (doubly protonated). Correspondingly, the uranyl stretching frequencies are downshifted by more than 25 cm⁻¹. Between the two bidentate coordination modes, (carboxylate and chelate binding modes), both υ_sym and υ_asym μ²-binding are red shifted by nearly 20 cm⁻¹. Hence, the vibrational frequencies of the uranyl bond can be used as a “fingerprint” to identify the type of coordination mode and the protonation state of malonate ligand can be understood at least semi-quantitatively.

(iv) Binding energies

The binding energy for the functionalized C₆₀ to uranyl is evaluated using the following equation,

[UO₂(H₂O)₅]²⁺ + [Mal–H_n–C₆₀]ⁿ⁻² → [UO₂–Mal–H_nC₆₀–(H₂O)₃]ⁿ + (H₂O)₂

We note that the formation of [UO₂(H₂O)₃]²⁺ from [UO₂(H₂O)₅]²⁺ is an endothermic process (36 kcal mol⁻¹). The calculated binding energies (B3LYP/COSMO) for the neutral malonic acid to uranyl are unfavorable for both mono-dentate (19.1 kcal mol⁻¹) and chelate (9.5 kcal mol⁻¹) binding modes. However, for the case of mono-anionic and di-anionic malonate species (which are considered to be present in semi-neutral and high pH), the uranyl affinities are strongly favorable. For instance, for the mono-anionic malonate binding to uranyl, the calculated binding energies are −14.6 kcal mol⁻¹ and −12.0 kcal mol⁻¹ for μ²-carboxylate and chelate modes respectively. For the di-anionic species, the uranyl binding energies are strongly favorable for both μ²-carboxylate (−28.8 kcal mol⁻¹) and chelate modes (−46.0 kcal mol⁻¹). Similar to our earlier discussion, the possibility of binding of uranyl with all five water molecules and malonate is tested. We again find that two water molecules disassociated from uranyl and are weakly interacting with the coordinated water molecules. Further, the overall stabilization energy is not altered significantly. Hence, only penta-coordination mode of uranyl (with three water molecules) is favoured for both functionalized and bare C₆₀.

Finally, in the case of 2 : 1 uranyl complex with deprotonated malonate, we find the binding energies to be somewhat weak (20 kcal mol⁻¹ per uranyl) as compared to 1 : 1 ratio (28 kcal mol⁻¹). Hence, we propose that favorable and efficient uranyl binding to malonate functionalized C₆₀, is possible at high pH conditions.

We now compare our results with those of the recent experimental study using spectrophotometric measurements. Rao et al.³⁷ carried out experiments (EXAFS) on complexation behavior of uranium(VI) with malonate at different temperatures and at differing pH (3.5 and 5.2). Our geometric predictions of uranyl bond lengths are in close agreement with those of the experimental data. Particularly, the calculated U=O bond lengths from low pH (3.5) to semi-acidic pH (5.2), we find the elongation of 0.01 Å to be in close agreement with the experimental findings. In agreement with the experimental proposal, our calculations also suggest that chelate type binding with three equatorial water molecules is favored.

In the case of free malonate, more than one malonate molecule can interact with uranyl molecule. However, due to the presence of the C₆₀ molecule, steric hindrance restricts the formation of such species which is again consistent with the experimental data.³⁸

Conclusions

In this paper, we have considered the interactions between C₆₀ and uranyl using DFT based calculations. The effect of pH is incorporated by carrying out calculations by varying the protonation states of malonate. Our calculations suggest that uranyl binding with bare C₆₀ is not possible due to unfavorable binding energies. Upon functionalizing with malonate, the uranyl binding strength is improved upon increasing the pH of the medium. Further, we propose that chelate type binding is more favorable as compared to carboxylate binding. Our calculated geometries are also in close agreement with the experimental data. Although the formation of 2 : 1 and 3 : 1 ratio of malonate with uranyl are possible, it is highly unlikely to be formed in the case of malonate functionalized C₆₀ due to steric hindrance. Functionalized fullerenes can be considered as an ideal building block for the design of materials and our study demonstrates that favourable binding of uranyl species with functionalized fullerenes may chart the road map for developing materials for effective nuclear waste management.

Acknowledgements

N.K.J gratefully acknowledges a senior research fellowship from Homi Bhabha National Institute, Department of Atomic Energy, India. The authors also acknowledge supercomputing facility of BARC for providing high performance parallel computing facility. S.K.G acknowledges DST-India for Sir J. C Bose fellowship and also support from the INDO-EU project MONAMI.

References

1. D. R. Lovley, E. J. P. Phillips, Y. A. Gorby and E. Landa, Nature, 1991, 350, 413–416.
2. G. Lefevre, S. Noinville and M. Fedoroff, J. Colloid Interface Sci., 2006, 296, 608–613.
3. P. M. Shanbhag and G. R. Chopping, J. Inorg. Nucl. Chem., 1981, 43, 3369–3372.
4. M. S. Dresselhaus, G. Dresselhaus and P. C. Eklund, Science of Fullerenes and Carbon Nanotubes, Academic Press, New York, 1996, 870–917.
5. F. Giacalone and N. Martin, Chem. Rev., 2006, 106, 5136–5190.
6. S. A. Claridge, A. W. Castleman, Jr., S. N. Khanna, C. B. Murray, A. Sen and P. S. Weiss, ACS Nano, 2009, 3, 244–255.
7. I. Lamparth and A. Hirsch, J. Chem. Soc., Chem. Commun., 1994, 1727–1728.
8. D. M. Guldi, H. Hungerbuehler and K.-D. Asmus, J. Phys. Chem., 1995, 99, 13487–13493.
9. Y. N. Yamakoshi, T. Yagami, K. Fukuhara, S. Sueyoshi and N. Miyata, J. Chem. Soc., Chem. Commun., 1994, 517–518.
10. D. M. Guldi, J. Phys. Chem. A, 1997, 101, 3895–3900.
11. F. Belloni, C. Kutahyali, V. Rondinella, P. Carbol and T. Wiss, Environ. Sci. Technol., 2009, 43, 1250–1255.
12. J. Hu, C. Chen, X. Zhu and X. Wang, J. Hazard. Mater., 2009, 162, 1542–1550.
13. O. Moradi, K. Zare and M. Yari, Int. J. Nano Dim., 2011, 1, 203–220.
14. J. P. Ruparelia, S. P. Duttagupta, A. K. Chatterjee and S. Mukherji, Desalination, 2008, 232, 145–156.
15. M. A. Atieh, O. Y. Bakather, B. S. Tawabini, A. A. Bukhari, M. Khaled, M. Alharthi, M. Fettouhi and F. A. Abuilaiwi, J. Nanomater., 2010, 2010, 1.
16. O. Moradi, K. Zare, M. Monajjemi and H. Aghaie, Fullerenes, Nanotubes, Carbon Nanostruct., 2010, 18, 285–302.
17. N. Thamavaranukup, H. A. Hoppe, L. Ruiz-Gonzalez, P. M. F. J. Costa, J. Sloan, A. Kirkland and M. L. H. Green, Chem. Commun., 2004, 1686–1687.
18. X. Wang, C. Chen, W. Hu, A. Ding, D. Xu and X. Zhou, Environ. Sci. Technol., 2005, 39, 2856–2860.
19. P. Wang, Patent Article. IPC8 Class: AG21F906FI, USPC, 2007, 588 18.
20. A. Schierz and H. Zanker, Environ. Pollut., 2009, 157, 1088–1094.
21. J. Soto-Guerrero and J. Havel, Polyhedron, 2003, 22, 1085–1090.
22. V. Vallet, U. Wahlgren, B. Schimmelpfennig, Z. Szabo and I. Grenthe, J. Am. Chem. Soc., 2001, 123, 11999–12008.
23. G. Schreckenbach, P. J. Hay and R. L. Martin, J. Comput. Chem., 1999, 20, 70–90.
24. N. Kaltsoyannis, Chem. Soc. Rev., 2003, 32, 9–16.
25. M. Bühl, R. Diss and G. Wipff, J. Am. Chem. Soc., 2005, 127, 13506–13507.
26. J. S. Craw, M. A. Vincent, I. H. Hillier and A. L. Wallwork, J. Phys. Chem., 1995, 99, 10181–10185.
27. G. A. Shamov and G. Schreckenbach, Acc. Chem. Res., 2010, 43, 19–29.
28. D. Hagberg, G. Kalstrom, B. J. Roos and L. Gagliardi, J. Am. Chem. Soc., 2005, 127, 14250–14256.
29. J. A. Austin, M. Sundararajan, M. A. Vincent and I. H. Hillier, Dalton Trans., 2009, 5902–5909.
30. P. J. Hay, R. L. Martin and G. Schreckenbach, J. Phys. Chem. A, 2000, 104, 6259–6270.
31. J. Vazquez, C. Bo, J. M. Poblet, J. de Pablo and J. Bruno, Inorg. Chem., 2003, 42, 6136–6141.
32. M. Sundararajan and S. K. Ghosh, J. Phys. Chem. A, 2011, 115, 6732–6737.
33. TURBOMOLE V6.0 2009, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com..
34. K. R. S. Chandrakumar and S. K. Ghosh, Nano Lett., 2008, 8, 13.
35. P. Jayapal, M. Sundararajan, G. Rajaraman and P. Venuvanalingam, J. Phys. Org. Chem., 2008, 21, 146.
36. R. Colsenet, C. Gardiennet, B. Henry and P. Tekely, Angew. Chem., Int. Ed., 2002, 41, 4743–4745.
37. L. Rao, J. Jiang, P. Zanonato, P. Di Bernardo and A. Y. Garnov, Radiochim. Acta, 2002, 90, 581–588.
38. Y. Zhang, D. Collison, F. R. Livens, M. Helliwell, F. Heatley, A. K. Powell, S. Wocadlo and H. Eccles, Polyhedron, 2002, 21, 81–96.

---