Adsorption of an anionic dye from aqueous medium by organoclays: equilibrium modeling, kinetic and thermodynamic exploration
Adarsh S.
Bhatt
,
Praful L.
Sakaria
,
Manu
Vasudevan
,
Radheshyam R.
Pawar
,
N.
Sudheesh
,
Hari C.
Bajaj
* and
Haresh M.
Mody
*
Discipline of Inorganic Materials and Catalysis, Central Salt & Marine Chemicals Research Institute (CSIR-CSMCRI), Council of Scientific & Industrial Research (CSIR), Gijubhai Badheka Marg, Bhavnagar – 364 002, Gujarat, India. E-mail: hmmody@csmcri.org; hcbajaj@csmcri.org; Fax: +91 278 2567562; Tel: +91 278 2471793
First published on 24th July 2012
Abstract
Adsorption of an anionic dye, remazole brilliant blue R (RBBR) from aqueous solution, on organically modified attapulgite (ATP) and bentonite (BNT) clays was investigated. Beneficiated attapulgite and bentonite clay samples were modified by the cationic surfactant cetyltrimethylammoniumbromide (CTAB) by the ion exchange method. The efficiency of these adsorbents for the uptake of RBBR was examined by a series of adsorption isotherms using a batch technique at three different temperatures. A modified Freundlich equation has been proposed to describe the isotherms and compared with Langmuir, Freundlich and Redlich–Peterson (RP) models. Predicated values of RBBR adsorbed on modified clay using Freundlich, modified Freundlich, and RP models were identical along with the normalized standard deviation for all three models. These values were lower than those of Langmuir model. Values of r2 for RP and modified Freundlich were found to be identical and better than that of Langmuir for all the isotherms. Adsorption of RBBR followed a pseudo second order kinetic model. Negative values of free energy change, ΔG indicated spontaneity of the adsorption of RBBR on both of organoclays. An increase in adsorption of RBBR with an increase in temperature may be attributed to activated adsorption and hence an endothermic process. This was further supported by positive values of heat of adsorption, ΔH. The adsorption capacity of modified attapulgite is lower than that of modified bentonite. However, considering the requirement of CTAB for modification of the clay, attapulgite is the more economical adsorbent than modified bentonite.
1. Introduction
India, one of the largest producers and end users of dyes and pigments, caters for the dye requirements of a variety of industrial segments.1 The big consumers of dyes are textile, dyeing, paper and pulp, tannery and paint industries. The effluents of these industries as well as dye manufacturing industries lead to water pollution. The effluents discharged from such industries are contaminated with dyes and have a high chemical oxygen demand (COD).1–8 The majority of organic dyes are hazardous to aquatic life and disturb the natural equilibrium through reducing aquatic diversity and photosynthetic activity by blocking the passage of light through water.3,4,9,10 Dyes are also an objectionable pollutant due to their toxicity to human beings1–4,9–15 and therefore the removal of dyes from effluent before their discharge is important.Removal of dyes from effluent is a costly affair, since the dyes are generally stable under the influence of light, heat and oxidizing agents. Also, the major problem with reactive dyes is their poor biodegradability under aerobic environment.16,17 Although, a number of successful treatment systems have been designed such as flocculation, coagulation, precipitation, adsorption, membrane filtration, electrochemical techniques, ozonization, sedimentation, reverse osmosis, fungal degradation and photo degradation etc., these methods have certain disadvantages such as high capital and operational costs or secondary sludge disposal problems. Amongst the techniques mentioned, the adsorption technique currently appears to offer the best potential for overall treatment due to cost effectiveness, high efficiency, simple operation and easy recovery/reuse of adsorbent.1–5,9–28
Activated carbon is a structurally homogenous material of very high surface area with microporosity, hence it offers a very high adsorption capacity and is widely used as an adsorbent in many industrial processes.16–18,20,22 However, due to the relatively high cost of activated carbon, there is a growing need to develop low cost, efficient and easily available adsorbents for the removal of dyes.4,9–11,16,17 A host of natural materials have been explored for dye adsorption, which include wood, coal, banana, pith, rice husk, deoiled soya, fly ash, blast furnace slag, red mud, bottom ash, maize cob, bagasse fly ash etc.4,11,13 Ali and Gupta29 reported a protocol for the development of low cost adsorbents from waste materials for the removal of pollutants.
Various bio-wastes such as coconut husk, saw dust, rice straw, were also used to prepare cheap carbon materials for their application as adsorbents for the removal of dyes.14–18,20,21 Some clays such as sepiolite,22 palygorskite,30 kaolinite,31 acid activated bentonite32 and Ti-exchanged bentonite33 were investigated for the adsorption of different dye molecules. Surfactant modified clay minerals such as bentonite,1,3,6,9,14 palygorskite, also known as attapulgite,7,8 hectorite12 and sepiolite16,18 were also reported as adsorbents for the same purpose. Chitosan/organo-montmorillonite composite material was reported for the adsorption of congo red dye.23
In present study the efficiency of surfactant modified attapulgite and bentonite clays was compared as adsorbents for the removal of RBBR dye from an aqueous solution to understand adsorption behavior in terms of equilibrium isotherms, thermodynamic parameters and adsorption kinetics.
2. Experimental
2.1. Raw material and reagents
The attapulgite and bentonite clays were collected from the Bhavnagar and Kutch districts of Gujarat state, India, respectively, sodium polyacrylate (SPA) (GRAID 4500) was purchased from M/s Micro Polyionics Pvt. Ltd. Ahmedabad, Gujarat, India. Cetyltrimethylammoniumbromide (CTAB) was purchased from Sigma-Aldrich, USA. A commercial textile dye remazol brilliant blue R (MF: C22H16N2Na2O11S3, MW: 626.55 g mol−1, λmax: 592 nm) was from obtained from Acros Organics. De-ionized water was obtained from an Elix Gradient A10 Millipore water purification system.2.2. Beneficiation of raw clay samples
Beneficiation of raw clay samples was carried out by a sedimentation technique. Attapulgite clay lumps were soaked overnight in an aqueous solution of SPA at 7.5% (w/v) with a SPA to clay mass ratio of 0.0275. A homogeneous dispersion of clay was obtained by vigorous stirring for 1 h with a top stirrer. For the beneficiation of bentonite clay, a known quantity (1% w/v) of raw bentonite lumps were suspended in de-ionized water, allowed to swell overnight, and stirred vigorously by a top stirrer for 30 min. Suspensions of both the clays were allowed to stand for 4 h for the sedimentation of non clay and heavy matter, followed by decantation of the supernatant by siphoning. The solids from both the supernatants were separated by centrifugation (KUBOTA-6500) at 8000 rpm for 20 min at 20 °C and dried at 80 °C. Purified samples were designated as ATP and BNT for attapulgite and bentonite respectively. The cation exchange capacity (CEC) of both the samples was determined by the standard ammonium acetate method at pH 7.34 The CEC of ATP and BNT was 14 and 85 meq/100 g of sample respectively.2.3. Preparation of organoclays
The organo-attapulgite/bentonite was prepared by a cation exchange reaction. A known mass of the beneficiated clay sample was suspended in an aqueous solution of CTAB to obtain 1% w/v of clay concentration, where the CTAB/CEC of clay ratio (meq/meq) was kept at 1. The suspension was stirred at room temperature for 24 h. The organoclay was separated by filtration and washed repeatedly till removal of the bromide ion (AgNO3 test). The samples were dried at 105 °C, ground and passed through a 100 mesh BSS sieve. The resulting organo-attapulgite and organo-bentonite samples were designated as ATPOC and BNTOC respectively.2.4. Characterization methods
Powder X-ray diffractograms were recorded with a Philips X'Pert MPD X-ray powder diffractometer using Cu-Kα (λ = 1.54056 Å) radiation with scan speed of 0.04°/s in a 2θ range of 7–37. The BET-surface areas of the ATP, BNT, ATPOC and BNTOC were determined by N2 adsorption at liquid nitrogen temperature (∼77 K) using ASAP2010C (Micromeritics, USA). Scanning Electron Micrographs of samples were recorded using a Leo microscope (model 1430) operating at an acceleration voltage of 20 kV and a working distance of 14 mm with 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000x magnification.
000x magnification.
2.5. Adsorption isotherm of RBBR on ATPOC and BNTOC
The adsorption study of RBBR on ATPOC and BNTOC was carried out by batch equilibrium experiments. A known mass (∼0.2 g) of adsorbent was suspended in 50 mL RBBR solutions of different concentration in a stoppered 100 mL flask and kept under isothermal conditions in a shaking water bath (Julabo-SW23) at 150 rpm at the desired temperature. The initial concentration of RBBR in the solution was varied in the range of 50–1000 mg L−1. The adsorption study was carried out at 30, 45 and 60 °C. The concentration of dye in the solution was determined spectrophotometrically at 592 nm (UV 2550 spectrophotometer, Shimadzu) after an equilibrium time of 12 h. The amount of dye adsorbed Qe (mg g−1), was calculated by eqn (1).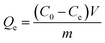 | (1) |
Where, Qe = amount of RBBR adsorbed on adsorbent at equilibrium (mg g−1), C0 = initial concentration of RBBR in solution (mg L−1), Ce = concentration of RBBR in solution at equilibrium (mg L−1), m = mass of adsorbent used (g) and V = volume of RBBR solution (L).
2.6. Kinetic study
In experiments of batch kinetic adsorption, a known mass of (0.2 g) of adsorbent and 50 mL dye solution of known concentration (∼488 mg L−1) were placed in a stoppered 100 ml conical flask and kept under isothermal conditions in a shaking water bath (Julabo-SW23) at 150 rpm at 30 ± 2 °C. At different time intervals, the solution was separated from the adsorbent material and the concentration of dye in the solution was analyzed spectrophotometrically at 592 nm using a UV-visible spectrophotometer (UV 2550 Shimadzu). The amount of dye adsorbed, Qt (mg g−1) at time t on the adsorbent, was calculated by eqn (1).3. Results and discussion
3.1. Characterization
 | ||
| Fig. 1 Powder X-ray diffraction pattern of ATP, BNT, ATPOC, and BNTOC. | ||
3.2. Batch equilibrium study
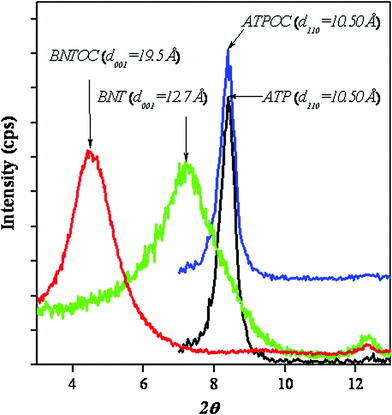
The effect of initial concentration of RBBR on adsorption was studied by taking known quantities of adsorbents with different concentrations of aqueous dye solution. Adsorption isotherms of RBBR on ATPOC and BNTOC at 30, 45, and 60 °C are shown in Fig. 2. At all the three temperatures, both the samples showed H2C type adsorption isotherms, according to the classification of Giles et al.35,36 The nature of the isotherms for both the organically modified clays showed a very high affinity for the dye molecules. Additionally, both the samples showed 100% dye removal at all three temperatures, indicating the H type nature followed by a long rising linear branch of C type, demonstrating partition distribution of dye molecules between solution and adsorbents.9,35,36 Further, with an increase in adsorption temperature, dye adsorption capacity increased for both the adsorbents, which is in concurrence with the adsorption of anionic dyes on organo-bentonite3,9 and organo-attapulgite.8 However, a reverse trend has also been reported for cationic surfactant modified bentonite5,6 and sepiolite.16,18 Though, there was a significant difference in specific the BET surface areas of ATPOC and BNTOC (Table 1), initially for ATPOC at 30 °C and for BNTOC at all the three temperatures, the value of dye adsorption at 100% dye removal capacity (Ce = 0 mg L−1) was found to be almost similar (∼27 mg g−1). After that the nature of isotherms changed to C type from H type. This high affinity for dye molecules can be attributed to the hydrophobic interaction between dye molecules and the incorporated long alkyl chains of the cetyltrimethylammonium cation.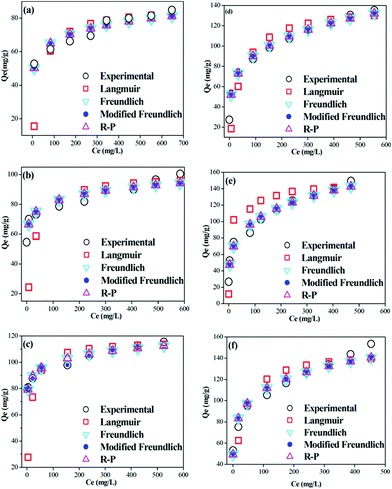 | ||
| Fig. 2 Adsorption isotherms of RBBR adsorption on ATPOC at 30 °C (a), 45 °C (b), 60 °C (c) and on BNTOC at 30 °C (d), 45 °C (e), 60 °C (f). | ||
Attapulgite is a non-swelling clay with an interwoven fibrous morphology (Fig. 3a). After modification with CTAB, fibers were bound together by surfactant molecules to form closely packed aggregates as shown in the SEM of ATPOC (Fig. 3b). These aggregates, having a hydrophobic surface, provide effective adsorption sites on which the dye is adsorbed. The hydrophobic surface area offered by ATPOC might be equivalent to the surface area offered by the BNTOC, as at 30 °C, the amount of dye adsorption at Ce = 0 was almost same. In case of ATPOC, dye adsorption at 100% dye removal (Ce = 0) increased linearly with an increase in temperature (Fig. 4). This phenomenon can be explained on the basis of a hypothesis given for the adsorption of gases in microporous carbon materials called the activated process.37 Usually, adsorption is exothermic; hence, equilibrium mass adsorbed at any given relative pressure for adsorption to the surface of a solid should increase with decreasing temperature. Contrary, it is often observed that the adsorption increases with temperature, indicating a non-equilibrium condition at lower temperature. The observations may be rationalized by considering barriers to diffusion which may only be overcome by a sufficient thermal energy; such a situation arises when the pore size or constriction approaches the size of adsorbate molecules and through which adsorbate molecule passes.37
 | ||
| Fig. 3 SEM images of ATP (a), ATPOC (b), BNT (c), and BNTOC (d). | ||
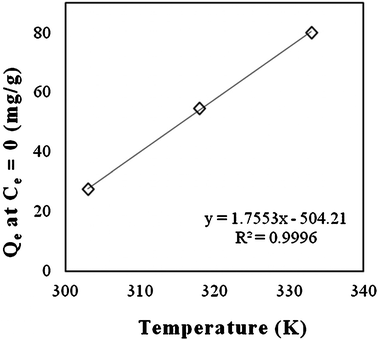 | ||
| Fig. 4 Effect of temperature on dye adsorption by ATPOC at 100% dye removal capacity. | ||
In the present study, modification of attapulgite with CTAB resulted in closely packed aggregate formation wherein there could be pores/constriction of sizes nearly equivalent to that of dye molecules and therefore the diffusion of dye molecules to the core of those aggregates required higher thermal energy. Therefore, with an increase in temperature, increase in the adsorption capacity at 100% dye removal (Ce = 0) was observed. Whereas, in the case of BNTOC, temperature did not affect the dye adsorption at 100% dye removal (Ce = 0), which might be due to a different arrangement of bentonite clay particles consisted of stacks of layers (Fig. 3c). CTAB cations were intercalated between the layers of the bentonite forming a hydrophobic lamellar type structure with little porosity (Table 1, Fig. 3d). However, in both the cases, at higher equilibrium concentration of the isotherms, an increase in dye adsorption was observed with temperature. This might be due to a higher partitioning rate of dye molecules in organophilic clays.
3.3. Equilibrium modeling
In order to describe the isotherms (Fig. 2), initially Langmuir and Freundlich models were used, details of the model equations are given in Table 2. Values of correlation coefficients and other parameters are summarized in Table 3. Generally, for the evaluation of best fit, values of correlation coefficients (r2) of linear plots of different models are considered.1,3,4,6–17 Values of r2 of a linear plot of the Langmuir model were found to be better than that of the Freundlich model for both the adsorbents at all three temperatures except for BNTOC at 30 °C. However, the difference between the experimental values of dye adsorbed and values calculated by the Freundlich model were significantly less than those calculated by the Langmuir model, particularly in the region of lower equilibrium concentration. For the evaluation of best fit, this difference in terms of normalized standard deviation (Δq), an important parameter, is calculated by eqn (2).18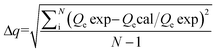 | (2) |
| Langmuir Isotherm 1–7,9–11,38–40 | ||
|---|---|---|
| a C e = dye concentration at equilibrium (mg L−1); Qe = equilibrium adsorption capacity (mg g−1); KL = Langmuir adsorption constant (L mg−1); Qm = maximum adsorption capacity (mg g−1); KF = Freundlich constant (L g−1); nF = heterogeneity factor of adsorption sites (dimensionless); KMF = modified Freundlich constant (L g−1); nMF = heterogeneity factor of the adsorbent sites (dimensionless); KRP = constant that is varied to maximize the linear correlation coefficient (r2), (L g−1); α = constant (mg L−1)−β; β = Redlich–Peterson exponent (dimensionless). | ||
| Non linear form | Linear form | Slope and intercept |
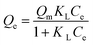
|
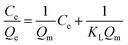
|
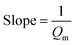
|
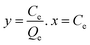
|
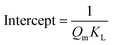
|
|
| Freundlich Isotherm 1–7,9–11,38–40 | ||
| Non linear form | Linear form | Slope and intercept |
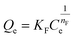
|
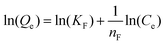
|
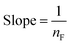
|
| y = ln(Qe) x = ln(Ce) | Intercept = lnKF | |
| Modified Freundlich | ||
| Non linear form | Linear form | Slope and intercept |
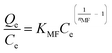
|
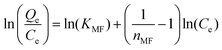
|
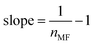
|
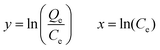
|
Intercept = lnKMF | |
| Redlich–Peterson 41,42 | ||
| Non Linear Form | Linear Form | Slope and Intercept |
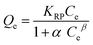
|
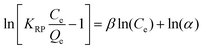
|
Slope = β |
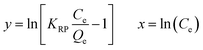
|
Intercept = ln(α) | |
| Parameters | ATPOC | BNTOC | ||||
|---|---|---|---|---|---|---|
| 303 (K) | 318 (K) | 333 (K) | 303 (K) | 318 (K) | 333 (K) | |
| Langmuir | ||||||
| r 2 | 0.992 | 0.992 | 0.998 | 0.988 | 0.982 | 0.984 |
| Q m (mg g−1) | 86.96 | 100.00 | 116.28 | 140.85 | 153.85 | 153.85 |
| K L (L mg−1) | 0.028 | 0.040 | 0.077 | 0.022 | 0.024 | 0.032 |
| R L | 0.11 | 0.08 | 0.04 | 0.08 | 0.07 | 0.06 |
| Δq | 0.272 | 0.263 | 0.243 | 0.248 | 0.315 | 0.340 |
| Freundlich | ||||||
| r 2 | 0.911 | 0.867 | 0.957 | 0.995 | 0.948 | 0.966 |
| n F | 9.19 | 12.32 | 13.89 | 4.72 | 4.83 | 6.17 |
| K F (L g−1) | 40.16 | 56.18 | 71.61 | 34.68 | 39.43 | 52.12 |
| Δq | 0.050 | 0.047 | 0.025 | 0.022 | 0.062 | 0.064 |
| Modified Freundlich | ||||||
| r 2 | 0.998 | 0.999 | 0.999 | 0.999 | 0.998 | 0.999 |
| n MF | 9.19 | 12.32 | 13.89 | 4.72 | 4.83 | 6.17 |
| K MF (L g−1) | 40.16 | 56.18 | 71.61 | 34.68 | 39.43 | 52.12 |
| Δq | 0.050 | 0.047 | 0.025 | 0.022 | 0.062 | 0.064 |
| Redlich–Peterson | ||||||
| r 2 | 0.998 | 0.999 | 0.999 | 0.999 | 0.998 | 0.999 |
| K RP (L g−1) | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| α (L mg−1) | 0.009 | 0.006 | 0.005 | 0.011 | 0.009 | 0.007 |
| β | 0.891 | 0.919 | 0.928 | 0.788 | 0.793 | 0.838 |
| Δq | 0.050 | 0.047 | 0.025 | 0.022 | 0.062 | 0.064 |
Where, N = the number of data points; Qe exp = experimental value of quantity adsorbed (mg g−1); Qe cal = calculated value of quantity adsorbed (mg g−1).
The Langmuir equation assumes that the surface of adsorbent is energetically homogeneous whereas, the Freundlich equation accounts for a multisite adsorption isotherm for heterogeneous surfaces and is characterized by the heterogeneity factor 1/n.5,6,9,10,19 Considering the best fit with respect to the value of r2 of the Langmuir model, the surface of the adsorbent should be homogeneous, but the difference in the calculated and experimental values of the dye adsorbed, particularly at lower equilibrium concentration, cannot be explained on the basis of the Langmuir model. Values of normalized standard deviation of Freundlich model were less than those of the Langmuir model, with lower r2 values. This discrepancy can be explained considering the adsorption behavior of the dye on the organo clays. Initially, due to hydrophobic interaction of very high affinity at zero equilibrium concentration, adsorption of dye molecules tends to form a monolayer and near the inflection point region, surface heterogeneity was created. At higher equilibrium concentration, the monolayer of dye molecules resulted in the surface homogeneity and in this region, the C type nature of the isotherms was observed. Looking at the isotherms, maximum data points of adsorption were lying in this region and hence the r2 values for Langmuir were near unity.
We have attempted to correlate standard free energy change (ΔG) of adsorption with each equilibrium concentration, Ce, and derived a new equation, which could describe the isotherms of the present work in terms of correlation coefficient, r2, as well as normalized standard deviation, (Δq). It is well established that the equilibrium constant Kc of adsorption depends on the thermodynamic parameters and is related to standard free energy change (ΔG) as shown in eqn (3).3,6
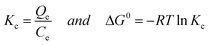 | (3) |
Where, Qe = quantity of dye adsorbed at equilibrium (mg g−1), Ce = equilibrium concentration (mg L−1); ΔG°= standard free energy change of adsorption, R = gas constant (0.008314 kJ mol−1 K−1); T = temperature in Kelvin (K).
A plot of lnKcvs. lnCe showed a linear relation (Fig. 5) with values of r2 near to unity for both the adsorbents at all three temperatures (Table 3).
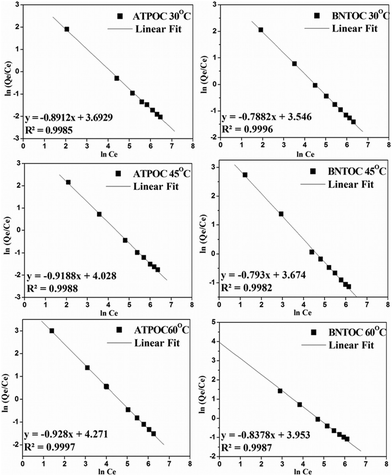 | ||
| Fig. 5 Linear fit for the modified Freundlich model for the adsorption of RBBR at different temperatures on organoclays. | ||
The values of normalized standard deviation (Δq) were found to be identical with those calculated by the Freundlich equation. The linear equation obtained for a new model from this relation is shown in Table 2. This linear equation can be converted into a non linear form as shown in Table 2. Values of adsorption calculated using KMF and nMF by linear and nonlinear forms of a new equation were found identical. These results showed the validity of the nonlinear form of the equation. This equation is similar to the Freundlich equation and has been designated as the modified Freundlich equation. Values of parameters, KMF and nMF, calculated using the modified Freundlich equation for all six isotherms were identical with those of values calculated using the Freundlich equation. The values of r2 of the linear plots for all six isotherms were better than those of the Langmuir and Freundlich models. This indicated that the modified Freundlich equation can be used in place of the Freundlich equation which showed better fit with respect to values of the correlation coefficient, r2.
Results of isotherms analyzed by the Redlich–Peterson (RP) equation (Table 2) using KRP = 1 are summarized in Table 3. It is worth noting that the calculated values of quantity adsorbed using the RP model were identical with those of the Freundlich and modified Freundlich equations and hence values of normalized standard deviation were identical (Fig. 2 and Table 3). The value of r2 of the RP model was also exactly matching with the modified Freundlich model. The Freundlich and modified Freundlich models were found to be appropriate for describing the isotherms of dye adsorption on ATPOC and BNTOC. Freundlich parameters, KF and nF indicate the capacity and intensity of adsorption respectively. If a value for nF = 1, the adsorption is linear, for nF < 1, the adsorption is chemisorption, and for nF > 1, the adsorption is a favorable physical process.1,3,5,6,8–10 This can be applicable to the constant nMF of the modified Freundlich model. Values of nF and nMF were in the range of 9 to 14 for ATPOC and 4 to 6 for BNTOC (Table 3) and increased with an increase in temperature, indicating the favored increase of adsorption with temperature.8,9,14
The separation factor, RL an important parameter indicating the favorability of the adsorption based on the Langmuir equation is calculated using eqn (4).
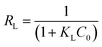 | (4) |
Where KL is the Langmuir constant and C0 is the highest initial dye concentration (mg L−1). The value of RL indicates the type of adsorption either to be unfavourable (RL > 1), linear (RL = 1), favorable (0 < RL < 1) or irreversible (RL = 0).1,3,5–7,12,14,16,18–22 Values of RL were found to be favorable for all the isotherms as they were between 0 and 1 (Table 3) and decreased from 0.11 to 0.04 for ATPOC and from 0.08 at to 0.06 for BNTOC with an increase in temperature from 303 K to 333 K. These results showed that the affinity of adsorbent for RBBR increased with an increase in temperature.
3.4. Distribution coefficient and % removal capacity of adsorbents for RBBR from solution
The distribution coefficient Kd is an important parameter for estimating the affinity of the adsorbent for adsorbate in aqueous solution. The distribution coefficients for five different initial concentrations were calculated for the adsorption of RBBR on ATPOC and BNTOC at three different temperatures using eqn (5)41,43 and the results are summarized in Table 4.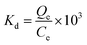 | (5) |
| C 0 (mg L−1) | C e (mg L−1) | Q e (mg g−1) | K d (mL g−1) | % Removal of RBBR | |
|---|---|---|---|---|---|
| ATPOC 30 °C | 109.64 | 0.00 | 27.34 | ∞ | 100.00 |
| 328.75 | 82.68 | 61.43 | 742.91 | 74.85 | |
| 548.19 | 269.35 | 69.47 | 257.91 | 50.87 | |
| 766.70 | 446.74 | 79.99 | 179.05 | 41.73 | |
| 987.73 | 646.38 | 84.87 | 131.30 | 34.56 | |
| ATPOC 45 °C | 219.26 | 0.00 | 54.62 | ∞ | 100.00 |
| 328.75 | 35.72 | 73.15 | 2047.51 | 89.13 | |
| 548.19 | 219.20 | 81.96 | 373.90 | 60.01 | |
| 766.70 | 406.81 | 89.97 | 221.16 | 46.94 | |
| 987.73 | 583.48 | 100.51 | 172.26 | 40.93 | |
| ATPOC 60 °C | 320.00 | 0.00 | 80.00 | ∞ | 100.00 |
| 548.19 | 155.22 | 97.85 | 630.42 | 71.69 | |
| 766.70 | 328.26 | 109.17 | 332.58 | 57.19 | |
| 987.73 | 524.64 | 115.54 | 220.23 | 46.88 | |
| BNTOC 30 °C | 109.64 | 0.00 | 27.34 | ∞ | 100.00 |
| 328.75 | 33.76 | 73.64 | 2181.13 | 89.73 | |
| 548.19 | 152.90 | 98.33 | 643.11 | 72.11 | |
| 766.70 | 301.09 | 116.40 | 386.61 | 60.73 | |
| 987.73 | 462.46 | 130.73 | 282.68 | 53.18 | |
| BNTOC 45 °C | 106.74 | 0.00 | 26.63 | ∞ | 100.00 |
| 320.06 | 18.97 | 74.94 | 3949.98 | 94.07 | |
| 533.70 | 122.90 | 102.44 | 833.57 | 76.97 | |
| 746.43 | 243.84 | 125.65 | 515.28 | 67.33 | |
| 961.61 | 403.19 | 139.54 | 346.08 | 58.07 | |
| BNTOC 60 °C | 106.74 | 0.00 | 26.67 | ∞ | 100.00 |
| 320.06 | 18.31 | 75.40 | 4117.58 | 94.28 | |
| 533.70 | 111.38 | 105.21 | 944.65 | 79.13 | |
| 746.43 | 241.45 | 126.12 | 522.34 | 67.65 | |
| 961.61 | 386.23 | 143.84 | 372.43 | 59.83 |
Where, Qe = amount of RBBR adsorbed on adsorbent at equilibrium (mg g−1), Ce = concentration of RBBR in solution at equilibrium (mg L−1), and Kd = the distribution coefficient.
The data in Table 4 indicated that with an increase in initial concentration, as expected the values of Kd decreased for both the adsorbents at all the three temperatures. It was observed that with an increase in temperature, the value of distribution coefficient for both the adsorbents increased, indicating that the affinity of adsorbents increased for RBBR with temperature. For higher initial concentrations, values of Kd were higher for BNTOC than those of ATPOC for all the three temperatures.
Percentage removal of RBBR from aqueous solution at different initial concentrations for both the adsorbents at different temperatures was calculated by eqn (6)41,43 and the results are given in Table 4.
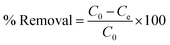 | (6) |
Where, C0 = initial concentration of RBBR in solution (mg L−1), Ce = concentration of RBBR in solution at equilibrium (mg L−1).
An increase in initial concentration corresponding to 100% removal of RBBR dye increased with an increase in temperature from 30 to 60 °C for ATPOC, whereas this value remained constant for BNTOC at all the three temperatures.
3.5. Thermodynamic parameters (ΔG°, ΔH°, ΔS°) for RBBR adsorption
The effect of temperature on RBBR adsorption was studied at 30, 45, and 60 °C. The thermodynamic parameters; change in Gibb's free energy (ΔG°), enthalpy (ΔH°), and entropy (ΔS°) of the adsorption process of RBBR onto ATPOC and BNTOC were calculated from the eqn (3), (7) and (8).| ΔG° = ΔH° − TΔS° | (7) |
| ∴ −RTlnKc = ΔH° − TΔS° | (8) |
The Freundlich/modified Freundlich constants KF and KMF were used as Kc. lnKF and lnKMF are intercepts of the linear plots of the Freundlich/modified Freundlich model and the value of lnKF and lnKMF is nothing but the value of lnKc (eqn (1)) at equilibrium concentration, Ce = 1 mg L−1. The values of enthalpy change (ΔH°) and entropy change (ΔS°) were calculated from the slope and intercept respectively of the linear plot of lnKcversus 1/T as presented in Fig. 6.
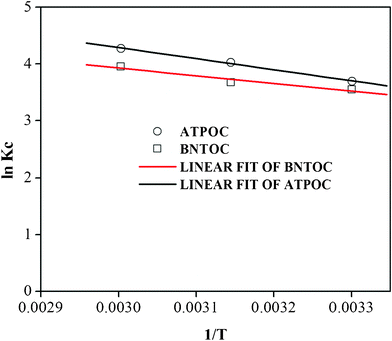 | ||
| Fig. 6 Plots of lnKcvs. 1/T for RBBR adsorption on ATPOC and BNTOC. | ||
Values of thermodynamic parameters are listed in Table 5. The positive value ΔH showed that the adsorption process of the RBBR on ATPOC and BNTOC was endothermic. However, the negative value ΔG decreased with an increase in temperature, indicating spontaneity of the adsorption process for both the adsorbents which was more favorable at higher temperatures.
| Adsorbent | r 2 | ΔH° (kJ mol−1) | ΔS° (kJ mol−1 K−1) | −ΔG° (kJ mol−1) | ||
|---|---|---|---|---|---|---|
| 30 °C | 45 °C | 60 °C | ||||
| ATPOC | 0.9957 | 16.2 | 0.084 | 9.33 | 10.59 | 11.86 |
| BNTOC | 0.9446 | 11.3 | 0.067 | 8.86 | 9.86 | 10.86 |
Similar results have been reported for the adsorption of dyes on organo-bentonite,3 organo-attapulgite8 and kaolinite.31 The value of ΔG for both the adsorbents was in the range of ∼−9 to ∼−12 kJ mol−1, which was well within the range of physisorption (−20 to 0 kJ mol−1).
Values of ΔS were positive for both the adsorbents. Increase in entropy for adsorption in the liquid phase has been reported by many researchers.3,5,8,20,31,44 Normally, adsorption of gases leads to a decrease in entropy due to the orderly arrangement of the gas molecules on a solid surface. However, adsorption of solute from the solution on a solid surface is a complex phenomenon and the entropy of the system is determined by degree of freedom of adsorbate (solute) and solvent molecules. The positive value of entropy could be due to the affinity of the organoclay for RBBR and desorption of water molecules from the surface of adsorbents.8,20,31
3.6. Effects of contact time and adsorption dynamics of RBBR
The quantity of RBBR adsorbed, Qt, was calculated at different time intervals using eqn (1) and plotted as a function of time in Fig. 7a. It can be seen that adsorption capacity of both the adsorbents for RBBR increased with increasing contact time. The adsorption equilibrium time was 300 and 360 min for ATPOC and BNTOC, respectively. In order to describe the kinetic behavior, pseudo-first-order, (eqn (9)) and pseudo-second-order, (eqn (10)) models were used. Linear forms of eqn (9) and (10) are given as eqn (11) and (12) respectively:1,3,5–10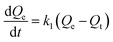 | (9) |
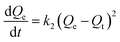 | (10) |
| ln(Qe − Qt) = lnQe − k1t | (11) |
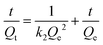 | (12) |
![The effect of contact time on adsorption of RBBR on ATPOC and BNTOC at 30 °C (a) [the line shows the predicated values] and (b) plot of pseudo second order kinetic model.](/image/article/2012/RA/c2ra20347b/c2ra20347b-f7.gif) | ||
| Fig. 7 The effect of contact time on adsorption of RBBR on ATPOC and BNTOC at 30 °C (a) [the line shows the predicated values] and (b) plot of pseudo second order kinetic model. | ||
Where, Qt and Qe = adsorption capacity at time t and at equilibrium respectively (mg g−1); k1 = rate constant of the pseudo first order adsorption (min−1); k2 = rate constant of the pseudo second order adsorption (g mg−1 min−1).
Values of Qe, k1, and correlation coefficient r2 were evaluated from the linear plot of ln(Qe − Qt) vs. t (figure not shown) for the pseudo first order model. Similarly, a plot of t/Qtvs. t (Fig. 7b) was used for evaluation of Qe, k2 and r2 for pseudo second order kinetics. Results were analyzed by calculating normalized standard deviation for both the kinetic models and the results are summarized in Table 6. Values of the correlation coefficient, r2 for both the adsorbents were near to unity, and calculated Qe values matched well with the experimental value for the pseudo second order model, demonstrating that adsorption of RBBR onto ATPOC and BNTOC followed a pseudo second order rate expression. The values of normalized standard deviation for the pseudo second order model were less than those of the pseudo first order model. This also indicated that the pseudo second order kinetic model was a better fit than that of the pseudo first order. Similar results have been reported for adsorption of dyes on organo-bentonite,1,3,5,6,9,14 organo-attapulgite7,8 and organo-sepiolite.16,18
| Parameters | ATPOC | BNTOC |
|---|---|---|
| Pseudo first order model | ||
| k 1 (×10−3 min−1) | 9.4 | 4.4 |
| Correlation coefficient r2 | 0.9531 | 0.9307 |
| Q e (cal) mg g−1 | 21.26 | 24.04 |
| Δq | 2.64 | 0.821 |
| Pseudo second order model | ||
| k 2 (×10−3 g mg −1 min−1) | 1.4 | 0.73 |
| Correlation coefficient r2 | 0.9996 | 0.9983 |
| Q e (cal) mg g−1 | 64.10 | 91.74 |
| Δq | 0.092 | 0.150 |
4. Conclusion
The purified Indian attapulgite and bentonite clay samples were modified with the cationic surfactant cetyltrimethylammonium bromide and evaluated for their adsorption capabilities for the removal of RBBR dye from aqueous solution by a batch method. ATPOC and BNTOC showed H2C type isotherms.A modified Freundlich equation has been proposed, which gave values of all the parameters identical to those of the Freundlich model with values of r2 near to one and better than the Langmuir model. On the basis of these results, it can be concluded that the Freundlich equation can be replaced by the modified Freundlich which gave better values of r2 than that of the Freundlich with identical values of other Freundlich parameters. The same was true for the RP model when the value KRP was taken as one.
The adsorption of RBBR on ATPOC and BNTOC was increased with an increase in temperature, where the maximum uptake of the dye was 119 mg g−1 and 153 mg g−1, respectively, at 60 °C and ∼1000 mg L−1 initial dye concentration. A pseudo second order kinetic model explained the rate of adsorption of RBBR on both the adsorbents. The thermodynamic parameters ΔG°, ΔH° and ΔS° indicated the spontaneity of the adsorption process even at higher temperature. The positive value of ΔH° showed the endothermic nature of the adsorption. The increase in entropy may be rationalized on the basis of randomness near the solid/solution interface region.
Apparently ATPOC showed less adsorption capacity than that of BNTOC, however, with respect to CTAB being used for the preparation of the organoclay, ATPOC is more economical than that of BNTOC.
Acknowledgements
The authors are thankful to the Council of Scientific & Industrial Research (CSIR), for financial support through network project NWP-0010. They are also thankful to the Analytical Science Division for providing assistance. MV, RP and NS thanks CSIR, New Delhi for the award of Senior Research Fellowship.References
- P. Baskaralingam, M. Pulikesi, D. Elango, V. Ramamurthi and S. Sivanesan, J. Hazard. Mater., 2006, 128, 138 CrossRef CAS.
- V. K. Gupta, P. J. M. Carrott, M. M. L. Ribeiro Carrott and Suhas, Crit. Rev. Environ. Sci. Technol., 2009, 39, 783 CrossRef.
- A. Khenifi, Z. Bouberka, F. Sekrane, M. Kameche and Z. Derriche, Adsorption, 2007, 13, 149 CrossRef CAS.
- V. K. Gupta, B. Gupta, A. Rastogic, S. Agarwald and A. Nayaka, J. Hazard. Mater., 2011, 186, 891 CrossRef CAS.
- A. Ozcan, C. Omeroglu, Y. Erdogan and A. S. Ozcan, J. Hazard. Mater., 2007, 140, 173 CrossRef.
- A. S. Ozcan, B. Erdem and A. Ozcan, J. Colloid Interface Sci., 2004, 280, 44 CrossRef.
- H. Chen and J. Zhao, Adsorption, 2009, 15, 381 CrossRef CAS.
- J. Huang, Y. Liu, Q. Jin, X. Wang and J. Yang, J. Hazard. Mater., 2007, 143, 541 CrossRef CAS.
- Z. Bouberka, A. Khenifi, F. Sekrane, N. Bettahar and Z. Derriche, Chem. Eng. J., 2008, 136, 295 CrossRef.
- V. K. Gupta, I. Ali and V. K. Saini, J. Colloid Interface Sci., 2007, 315, 87 CrossRef CAS.
- V. K. Gupta, A. Mittal, V. Gajbe and J. Mittal, Ind. Eng. Chem. Res., 2006, 45, 1446 CrossRef CAS.
- P. Baskaralingam, M. Pulikesi, V. Ramamurthi and S. Sivanesan, Appl. Clay Sci., 2007, 37, 207 CrossRef CAS.
- V. K. Gupta, I. Ali, Suhas and D. Mohan, J. Colloid Interface Sci., 2003, 265, 257 CrossRef CAS.
- A. S. Ozcan, B. Erdem and A. Ozcan, Colloids Surf., A: Physiochem. Eng. Aspects, 2005, 266, 73 CrossRef.
- V. K. Gupta, R. Jain and S. Varshney, J. Hazard. Mater., 2007, 142, 443 CrossRef CAS.
- A. Ozcan and A. S. Ozcan, J. Hazard. Mater., 2005, 125, 252 CrossRef.
- V. K. Gupta and I. Ali, Environ. Sci. Technol., 2008, 42, 766 CrossRef CAS.
- A. Ozcan, E. M. Oncu and A. S. Ozcan, J. Hazard. Mater., 2006, 129, 244 CrossRef.
- I. A. W. Tan, A. L. Ahmad and B. H. Hameed, J. Hazard. Mater., 2008, 154, 337 CrossRef CAS.
- M. J. Iqbal and M. N. Ashiq, J. Hazard. Mater., 2007, 139, 57 CrossRef CAS.
- P. K. Malik, J. Hazard. Mater., 2004, 113, 81 CrossRef CAS.
- A. S. Ozcan, S. Tetik and A. Ozcan, Sep. Sci. Technol., 2004, 39, 301 CrossRef.
- L. Wang and A. Wang, J. Chem. Technol. Biotechnol., 2007, 82, 711 CrossRef CAS.
- V. K. Gupta, R. Jain, A. Mittal, M. Mathur and S. Sikarwar, J. Colloid Interface Sci., 2007, 309, 464 CrossRef CAS.
- N. T. Sivakumar, T. Molly, N. Kalithasan, H. C. Bajaj and R. J. Tayade, Chem. Eng. J., 2011, 169, 126 CrossRef.
- V. K. Gupta, S. K. Srivastava and R. Tyagi, Water Res., 2000, 34, 1543 CrossRef CAS.
- V. K. Gupta, R. Jain and S. Varshney, J. Colloid Interface Sci., 2007, 312, 292 CrossRef CAS.
- V. K. Gupta, I. Ali, T. A. Saleh, A. Nayak and S. Agarwal, RSC Adv., 2012, 2, 6380 RSC.
- V. K. Gupta and I. Ali, Nat. Protoc., 2007, 1, 2661 CrossRef.
- A. Al-Futaisi, A. Jamrah and R. Al-Hanai, Desalination, 2007, 214, 327 CrossRef CAS.
- D. Ghosh and K. G. Bhattacharyya, Appl. Clay Sci., 2002, 20, 295 CrossRef CAS.
- A. S. Ozcan and A. Ozcan, J. Colloid Interface Sci., 2004, 276, 39 CrossRef CAS.
- C. C. Wang, L. C. Juang, T. C. Hsu, C. K. Lee, J. F. Lee and F. C. Huang, J. Colloid Interface Sci., 2004, 273, 80 CrossRef CAS.
- T. D. Oulton, Encyclopaedia of industrial chemical analysis, F. D. Mell and L. S. Ettre (Ed.), Interscience Publisher, 1970, 10, 109 Search PubMed.
- C. H. Giles, A. P. D'silva and I. A. Easton, J. Colloid Interface Sci., 1974, 47, 766 CrossRef CAS.
- C. H. Giles, T. H. Macewan, S. N. Nakhwa and D. Smith, J. Chem. Soc., 1960, 3973 Search PubMed.
- S. J. Gregg and K. S. W. Sing, Adsorption, Surface Area and Porosity, second ed., Academic Press, London, 1982 Search PubMed.
- V. K. Gupta, A. Mittal, L. Kurup and J. Mittal, J. Colloid Interface Sci., 2006, 304, 52 CrossRef CAS.
- V. K. Gupta and A. Rastogi, J. Hazard. Mater., 2009, 163, 396 CrossRef CAS.
- V. K. Gupta, A. Rastogi and A. Nayak, J. Colloid Interface Sci., 2010, 342, 135 CrossRef CAS.
- R. A. Jacques, R. Benrnardi, M. Caovila, E. C. Lima, F. A. Pavan, J. C. P. Vaghetti and C. Airoldi, Sep. Sci. Technol., 2007, 42, 591 CrossRef CAS.
- V. K. Gupta, I. Ali and V. K. Saini, Water Res., 2007, 41, 3307 CrossRef CAS.
- V. Manu, P. L. Sakaria, A. S. Bhatt, H. M. Mody and H. C. Bajaj, Ind. Eng. Chem. Res., 2011, 50, 11432 CrossRef.
- S. Lyubchik, A. Lyubchik, O. Lygina, S. Lyubchik and I. Fonseca, Comparison of the Thermodynamic Parameters Estimation for the Adsorption Process of the Metals from Liquid Phase on Activated Carbons, Thermodynamics-Interaction Studies-Solids, Liquids and Gases, J. C. Moreno-Pirajan (Ed.), ISBN: 978-953-307-563-1, InTech, 2011, pp. 95–122 Search PubMed.
| This journal is © The Royal Society of Chemistry 2012 |
