Magnetic field-induced alignment of nanoparticles in electrospun microfibers
Kristen E.
Roskov
a,
Jessie E.
Atkinson
c,
Lyudmila M.
Bronstein
c and
Richard J.
Spontak
*ab
aDepartment of Chemical & Biomolecular Engineering, North Carolina State University, Raleigh, North Carolina 27695, USA
bDepartment of Materials Science & Engineering North Carolina State University, Raleigh, North Carolina 27695, USA. E-mail: Rich_Spontak@ncsu.edu
cDepartment of Chemistry, Indiana University, Bloomington, Indiana 47405, USA
First published on 16th April 2012
Abstract
We report on the facile and switchable alignment of superparamagnetic iron oxide nanoparticles measuring ∼18 nm in diameter in electrospun microfibers. Application of a magnetic field perpendicular to the electric field employed during electrospinning yields polymeric microfibers with nanoparticles aligned in one-dimensional arrays, thereby providing control over when and where the nanoparticles align. According to electron microscopy, the length over which alignment is desired can be judiciously selected, thereby making these nanomaterials excellent candidates for nanotechnologies requiring nanoscale alignment on-demand. Concurrent alignment of the electrospun fibers using established procedures provides a viable route to organic/inorganic materials possessing anisotropic properties that reflect multiscale alignment.
Introduction
Previous efforts to achieve nanoparticle alignment in polymeric matrices have relied on a variety of process strategies, such as three-dimensional superlattices,1 deoxyribonucleic acid2 or block copolymer3 templating, surface nanolithography,4 electrostatic desalting transition,5 and surface chemical modification.6 Electrospinning is a rapidly developing fabrication technique that produces solid polymeric fibers with diameters ranging from several tens of nanometers up to several microns, a high surface-area-to-volume ratio, and the potential for porosity at multiple length scales.7,8 As such, it provides an attractive approach to the formation of nano/microscale polymeric fibers containing nanoparticles that are spatially restricted. Further control over nanoparticle positioning can be achieved within such fibers by post-crystallization of the polymer matrix,9 the electric field employed during electrospinning,10 development of a polymeric nanostructure via self-assembly,11 or strategic use of coaxial electrospinning.12 These methodologies and others, however, depend on the intrinsic nature of the polymer matrix and/or the processing conditions associated with electrospinning, and are not intrinsically switchable. Here, we postulate that control over the location and alignment of nanoparticles within electrospun fibers can be achieved through the straightforward use of an external electromagnetic field applied during electrospinning. As with electrospinning, several design issues, such as the strength of the magnet and its orientation/position with respect to the onset of the polymer jet at the Taylor cone, warrant consideration. Unlike other approaches intended to align nanoparticles during electrospinning, an external magnetic field can be applied and removed at any time, thereby permitting switchable alignment that can be pulsed. As a consequence of the switchable alignment, the magnetic properties of the nanoparticles can be correspondingly changed from superparamagnetic to ferromagnetic,13 which may allow for future read-write capability.Existing nanotechnologies that require aligned nanoparticle arrays include surface-enhanced Raman scattering (SERS) substrates for use in ultrasensitive analytical tools,14 micromechanical sensors,15 nanoscale barcodes,16 and protein separation.17 Prior studies have shown that magnetic fields can be applied during the electrospinning of polymer/nanoparticle systems to improve alignment of the fibers, but not of the nanoparticles within the fibers. Parallel-positioned permanent magnets with field strengths ranging from 25 to 120 mT have been placed, for instance, on the collector plate during the electrospinning of polymer fibers containing Fe3O4 nanoparticles to align the electrospun fibers.18 Deflection of entire fibrous mats generated by electrospinning and containing magnetite nanoparticles in the presence of a magnetic field has also been observed.10 In addition, magnetic fields have also been used to control the spatial arrangement of nanoscale objects within bulk, not electrospun, polymer matrices. Magneto-polymer nanocomposite particles measuring 200 nm in diameter are, for instance, reported19 to align in hydrogel nanocomposites under a magnetic field of 1.5 T. Even multi-wall carbon nanotubes dispersed in a monomer precursor are found20 to align when exposed to an external magnetic field during matrix polymerization. The use of an external magnetic field has likewise been found to have an effect on biological systems by organizing cell rods, seeded on magnetically susceptible fiber bundles, into three-dimensional tissue constructs.21 In the spirit of these prior observations, the objective of the present work is to create one-dimensional, periodic arrays of magnetic nanoparticles in electrospun polymer fibers by applying a magnetic field, in conjunction with an electric field, during electrospinning.
Experimental
ε-Polycaprolactone (PCL) with a molecular weight of 80 kDa according to the manufacturer was provided by Solvay (Warrington, England). Reagent-grade chloroform for electrospinning was obtained from Fisher Scientific (Fairlawn, NJ). Iron oxide nanoparticles with an average diameter of 17.6 nm were prepared by thermal decomposition of iron oleate in the presence of oleic acid as the capping agent in a high-boiling hydrocarbon, eicosane, according to the procedure described elsewhere.22,23 X-ray diffraction data confirmed that the as-synthesized nanoparticles are crystalline and contain mostly wüstite (Fe(1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x)O) and some spinel (most likely Fe3O4),22 but at the same time, they are superparamagnetic iron oxide nanoparticles (SPIONs) according to magnetic measurements.24 The resultant SPIONs were precipitated with a mixture of acetone and hexane and then separated by centrifugation and suspended in chloroform at concentrations between 10 and 50 mg mL−1. Suspensions for electrospinning were prepared by first dissolving PCL in chloroform and then adding appropriate amounts of the SPION suspension to yield 5 wt% PCL at three different SPION concentrations: 0.5, 1.0 and 2.5 vol%.
x)O) and some spinel (most likely Fe3O4),22 but at the same time, they are superparamagnetic iron oxide nanoparticles (SPIONs) according to magnetic measurements.24 The resultant SPIONs were precipitated with a mixture of acetone and hexane and then separated by centrifugation and suspended in chloroform at concentrations between 10 and 50 mg mL−1. Suspensions for electrospinning were prepared by first dissolving PCL in chloroform and then adding appropriate amounts of the SPION suspension to yield 5 wt% PCL at three different SPION concentrations: 0.5, 1.0 and 2.5 vol%.
The in-house electrospinning unit, operated at 8 kV, employed a syringe pump and an Al collection target. The separation distance was 12 cm, and the solution flow rate varied from 10 to 35 μL min−1. A horseshoe electromagnet (Edmund Scientific, Tonawanda, NY) was connected to a 6 V battery to generate a 26 mT magnetic field, which corresponds to the most uniform field as measured by a DC magnetometer (Alphalab Inc., Salt Lake City, UT). As schematically depicted in Fig. 1, the magnet was positioned parallel to and below the syringe needle. Electrospun fibers were collected with and without the magnetic field onto the Al plate, as well as onto carbon-coated transmission electron microscopy (TEM) grids taped to the plate. To discern the distribution of SPIONs within the PCL fibers, TEM was performed on a field-emission Hitachi HF2000 microscope operated at 200 kV. The magnetic behavior of aligned7 fiber mats was examined on a Quantum Design MPMS superconducting quantum interference device (SQUID) for fibers electrospun from PCL dissolved in a 30 mg mL−1 SPION suspension. Magnetization curves were recorded at 300 K from fiber mats with an average mass of 1.5 mg. The magnetizing field strength for embedded samples ranged from −20 to +20 kOe, whereas saturation was reached at 6 kOe as the field strength varied from −80 to 80 kOe for unembedded SPIONs.
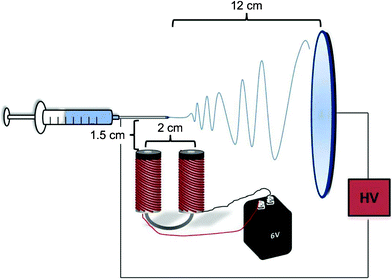 | ||
| Fig. 1 Schematic illustration of the magnetic field-assisted electrospinning setup used in this study. Note the position of the electromagnet, which yields a magnetic field that is perpendicular to the electric field employed during electrospinning. | ||
Results and discussion
The polymer solution concentration, separation distance and voltage used to electrospin PCL fibers have been judiciously selected to yield microfibers with diameters ranging from 100 to 500 nm so that their interior morphologies could be explored by TEM. Field-emission scanning electron microscopy (SEM) results (provided in the ESI) confirm that these PCL microfibers with and without SPIONs possess an average diameter of ∼300 nm. The microfibers exhibit slight dimpling on their surface, and very few bead defects containing large SPION aggregates (most likely formed by nanoparticles with insufficient surface functionalization in the suspension reservoir) develop. In the absence of an applied magnetic field, SPIONs measuring 17.6 nm in diameter appear to be randomly distributed throughout the PCL microfibers, as seen in the TEM images provided in Fig. 2 for microfibers differing in SPION concentrations: 0.5 vol% (Fig. 2a) and 2.5 vol% (Fig. 2b). A TEM image of the SPIONs drop cast from suspension is included in the inset of Fig. 2a for reference. Since these SPIONs are coated with oleic acid, which is fairly compatible with PCL, relatively little aggregation is observed in the PCL microfibers. Few small SPION aggregates, not evident in these images but found in other specimens, appear as spheroidal clusters with no preferential orientation. Complementary energy-dispersive spectroscopy (data provided in the ESI) reveals that few, if any, SPIONs reside on the surface of the microfibers. | ||
| Fig. 2 TEM images of randomly dispersed SPIONs in electrospun PCL microfibers varying in SPION concentration (in vol%): (a) 0.5 and (b) 2.5. A TEM image of SPIONs measuring 17.6 nm in diameter and drop cast from chloroform is included in the inset of (a). The scalemarker in the inset corresponds to 50 nm. | ||
An electromagnet is selected for the present study since it generates a magnetic field only when an electric current is flowing, in which case the magnetic field can be immediately terminated by stopping the current. Since the objective of this study is to create aligned arrays of magnetic nanoparticles on-demand and since many types of nanoparticles with various degrees of magnetic susceptibility exist, we have elected to use superparamagnetic nanoparticles due to their ability to respond to an external magnetic field but remain nonresponsive when the field is removed.25 In the field-induced alignment experiments, the degree to which SPIONs respond to an externally applied magnetic field governs the extent to which alignment will occur. For a spherical particle, the magnetic moment (mp) is related to particle size by26
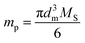 | (1) |
The syringe portrayed in Fig. 1 is positioned within several centimeters of the open end of the horseshoe electromagnet (where the magnetic field lines are the most concentrated). The optimal distance is ∼1.5 cm, which suggests that this position identifies where the magnetic field is the most uniform. The distance between the poles of the magnet is 2 cm, with one pole placed directly under the Taylor cone (the reasons for which are discussed later) and the other located 2 cm closer to the collection plate. Although the horseshoe shape of the electromagnet increases the strength of the magnet, we recognize that the field is not uniform. Another factor influencing the ability of the SPIONs to align in electrospun microfibers is their concentration in the suspension reservoir. The attractive forces between two SPIONs whose dipole moments are aligned must be sufficient to overcome the matrix viscosity for particle alignment to ensue, and the magnitude of such forces depends on the interparticle distance, which relates to the particle concentration.27 A sensitivity analysis for 17.6 nm SPIONs reveals that a minimum SPION concentration of ca. 0.05 vol% is required for discernible alignment in the present study. At higher concentrations, the interparticle distance decreases and greater attraction, or chaining, between neighboring SPIONs occurs. The maximum SPION concentration is set by other considerations, namely, suspension conductivity and viscosity, as well as undesirable SPION aggregation.
Examples of aligned SPIONs measuring 17.6 nm in diameter in electrospun PCL microfibers at a concentration of 0.5 vol% are presented in Fig. 3. In all cases, the electromagnet is connected first, followed by the high-voltage power supply for electrospinning. The 6 V battery remains outside the electric field to prevent the possibility of a short circuit. In images such as the one displayed in Fig. 3a, the SPIONS remain aligned in one-dimensional arrays parallel to the fiber surface over lengths exceeding 1.5 μm insofar as the electromagnet remains active. These long arrays are visible in most microfibers of a mat collected on a TEM grid, and they appear on multiple grids used to collect the same sample. In Fig. 3b (including the inset), the effect of the magnetic field is not constant (most likely due to the reasons discussed below), which results in shortened, but nonetheless highly aligned, SPION arrays of variable thickness. Although such arrays constitute the predominant feature when the magnetic field is applied, some randomly distributed SPIONs remain. Fine adjustment of both electrospinning conditions and solution properties has been unable to resolve this lack of positional uniformity within the microfibers. Possible reasons for this shortcoming are three-fold: (i) the magnetic field produced by the horseshoe-shaped magnet is inherently not uniform; (ii) instabilities in the jet,28 coupled with fiber whipping that occurs between the Taylor cone and the collection plate; and (iii) nanoparticles residing in the Taylor cone, as previously reported.1 All of these considerations could result in fibers that vary in position with respect to the applied magnetic field. The net result is that the strength of the magnetic field, and thus the uniformity and contiguity of SPION alignment, simultaneously vary. One way to enhance the spatial characteristics of SPION arrays is by aligning the microfibers between electrodes instead of generating a random mat of microfibers on a collection plate.29 However achieved, improved control over the position of the fiber within the field is ultimately expected to promote uniform SPION alignment that can be pulsed or otherwise induced on-demand.
 | ||
| Fig. 3 TEM images of magnetic field-aligned SPIONs, measuring 17.6 nm in diameter, in PCL microfibers illustrating long, contiguous arrays in (a), and shorter arrays in (b). The scalemarker in the inset corresponds to 100 nm. | ||
Unlike ferromagnetic materials, magnetization of the superparamagnetic SPIONs under investigation only occurs under an external magnetic field. When this field is removed, the net magnetization of the SPION dispersion drops close to zero. The magnetization (M) behavior of SPIONs measuring 17.6 nm in diameter is presented as a function of magnetizing field strength (H) at 300 K in the SQUID hysteresis plot shown in Fig. 4a. The value of MS for the unembedded SPIONs is 38.8 emu g−1, whereas that for SPIONs encapsulated within electrospun PCL microfibers is sharply lowered to 0.77–0.94 emu g−1. This nontrivial reduction in MS for the SPIONs residing in electrospun PCL microfibers with and without an external magnetic field is due largely to the decreased mobility of the SPIONs, a result that has been previously reported for embedded nanoparticles.30–32 If the matrix viscosity is sufficiently high, only the magnetic moment of a SPION can rotate in the presence of an external field, but the SPION itself may be unable to do so. In light of these results, the applied magnetic field must be positioned in the vicinity of the Taylor cone formed during electrospinning (where solvent remains and the matrix viscosity is relatively low). This location has been selected in this work to maximize the ability of the external magnetic field to induce SPION alignment in electrospun PCL microfibers.
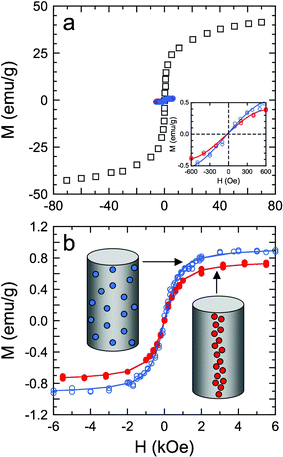 | ||
| Fig. 4 Magnetization (M) hysteresis curves at 300 K as a function of the magnetizing field strength (H) for SPIONs measuring 17.6 nm in diameter. In (a), the hysteresis curves are measured from unembedded SPIONs (□), as well as randomly dispersed and magnetically aligned SPIONs in electrospun PCL microfibers (blue and red, respectively). The inset shows magnetization hysteresis curves recorded for the embedded SPIONS at low fields and ambient temperature. In (b), the hysteresis curves from the SPIONs embedded in PCL microfibers (see the corresponding diagrams) are fitted to eqn (2) in the text (solid lines) to discern the saturation magnetization and mean dipole moment from each dataset. | ||
According to Fig. 4, the SPIONs alone and embedded in PCL exhibit a superparamagnetic loop characterized by a minimum coercivity and a remanent magnetization at room temperature. The mean magnetic moment (μ) and MS are extracted from each hysteresis curve by fitting the data to the Langevin function,33viz.,
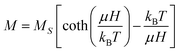 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PCL in the suspension prior to electrospinning by the mass of the fiber mat (∼1.5 mg). Therefore, the corresponding MS values are sensitive to the SPION populations present. With the possibility of aggregated SPION clusters forming in suspension or during electrospinning, the calculated SPION mass in a given specimen may not be sufficiently accurate to permit direct comparison. In contrast, values of μ are not sensitive to the mass present and reveal an interesting trend that is amenable to computational modeling: the mean magnetic moment increases with increasing SPION alignment.
PCL in the suspension prior to electrospinning by the mass of the fiber mat (∼1.5 mg). Therefore, the corresponding MS values are sensitive to the SPION populations present. With the possibility of aggregated SPION clusters forming in suspension or during electrospinning, the calculated SPION mass in a given specimen may not be sufficiently accurate to permit direct comparison. In contrast, values of μ are not sensitive to the mass present and reveal an interesting trend that is amenable to computational modeling: the mean magnetic moment increases with increasing SPION alignment.
Conclusions
Nanoscale alignment of SPIONs with a mean diameter of 17.6 nm has been achieved through the use of magnetic field-assisted electrospinning. In this case, an electromagnetic field of 26 mT is applied perpendicular to the electric field required for electrospinning, resulting in microfibers that contain one-dimensional arrays of SPIONs. In the present system investigated, a SPION concentration of greater than 0.05 vol% is required to induce discernible alignment. The arrays thus produced can extend beyond 1 μm under a constant magnetic field, or they can be controllably shortened by varying the magnetic field. The latter finding suggests that it may be possible in the future to write information to individual microfibers on the basis of array lengths. Moreover, alignment of the electrospun microfibers through the use of various established methods can yield nanocomposites with multiscale (i.e., nanoscale and macroscale) anisotropic properties.36 Complementary SQUID measurements at ambient temperature reveal that the saturation magnetization is significantly lower for SPIONs in electrospun fibers with or without magnetic field-induced alignment than for unembedded SPIONs. Improving alignment, however, appears to increase the mean magnetic moment, which provides evidence that nanoscale alignment of SPIONs affects their intrinsic physical properties.Acknowledgements
This work was supported by a National Science Foundation Graduate Research Fellowship (K. E. R.), a North Carolina Space Grant, and the NATO Science for Peace Program (L. M. B) and Indiana University Faculty Research Program (L. M. B.). We thank Professor Frank Tsui (University of North Carolina at Chapel Hill) for use of his SQUID, and Mr. Matt Wolboldt for insightful discussions.References
- M. Miyauchi, T. J. Simmons, J. J. Miao, J. E. Gagner, Z. H. Shriver, U. Aich, J. S. Dordick and R. J. Linhardt, ACS Appl. Mater. Interfaces, 2011, 3, 1958–1964 CAS.
- R. C. Mucic, J. J. Storhoff, C. A. Mirkin and R. L. Letsinger, J. Am. Chem. Soc., 1998, 120, 12674–12675 CrossRef CAS.
- L. A. Harris, J. D. Goff, A. Y. Carmichael, J. S. Riffle, J. J. Harburn, T. G. St Pierre and M. Saunders, Chem. Mater., 2003, 15, 1367–1377 CrossRef CAS.
- T. Tsirlin, J. Zhu, J. Grunes and G. A. Somorjai, Top. Catal., 2002, 19, 165–170 CrossRef CAS.
- M. Yan, J. Fresnais, S. Sekar, J. P. Chapel and J. F. Berret, ACS Appl. Mater. Interfaces, 2011, 3, 1049–1054 CAS.
- Y. Xiong, Q. W. Chen, N. Tao, J. Ye, Y. Tang, J. S. Feng and X. Y. Gu, Nanotechnology, 2007, 18, 345301 CrossRef.
- W. J. Li, C. T. Laurencin, E. J. Caterson, R. S. Tuan and F. K. Ko, J. Biomed. Mater. Res., 2002, 60, 613–621 CrossRef CAS.
- D. H. Reneker and I. Chun, Nanotechnology, 1996, 7, 216–223 CrossRef CAS.
- G. M. Kim, A. Wutzler, H. J. Radusch, G. H. Michler, P. Simon, R. A. Sperling and W. J. Parak, Chem. Mater., 2005, 17, 4949–4957 CrossRef CAS.
- A. Wang, H. Singh, T. A. Hatton and G. C. Rutledge, Polymer, 2004, 45, 5505–5514 CrossRef.
- B. B. Wang, B. Li, J. Xiong and C. Y. Li, Macromolecules, 2008, 41, 9516–9521 CrossRef CAS.
- T. Song, Y. Z. Zhang, T. J. Zhou, C. T. Lim, S. Ramakrishna and B. Liu, Chem. Phys. Lett., 2005, 415, 317–322 CrossRef CAS.
- A. K. F. Dyab, M. Ozmen, M. Ersoz and V. N. Paunov, J. Mater. Chem., 2009, 19, 3475–3481 RSC.
- P. Peng, Y. Z. Chen, Y. F. Gao, J. Yu and Z. X. Guo, J. Polym. Sci., Part B: Polym. Phys., 2009, 47, 1853–1859 CrossRef CAS.
- C. Goubault, P. Jop, M. Fermigier, J. Baudry, E. Bertrand and J. Bibette, Phys. Rev. Lett., 2003, 91 Search PubMed.
- J. M. Nam, S. J. Park and C. A. Mirkin, J. Am. Chem. Soc., 2002, 124, 3820–3821 CrossRef CAS.
- P. S. Doyle, J. Bibette, A. Bancaud and J. L. Viovy, Science, 2002, 295, 2237–2237 CrossRef CAS.
- D. Y. Yang, B. Lu, Y. Zhao and X. Y. Jiang, Adv. Mater., 2007, 19, 3702–3706 CrossRef CAS.
- J. Nunes, K. P. Herlihy, L. Mair, R. Superfine and J. M. DeSimone, Nano Lett., 2010, 10, 1113–1119 CrossRef CAS.
- T. Kimura, H. Ago, M. Tobita, S. Ohshima, M. Kyotani and M. Yumura, Adv. Mater., 2002, 14, 1380–1383 CrossRef CAS.
- W. Y. Lee, W. Y. Cheng, Y. C. Yeh, C. H. Lai, S. M. Hwang, C. W. Hsiao, C. W. Huang, M. C. Chen and H. W. Sung, Tissue Eng., Part C, 2011, 17, 651–661 CrossRef CAS.
- L. M. Bronstein, X. Huang, J. Retrum, A. Schmucker, M. Pink, B. D. Stein and B. Dragnea, Chem. Mater., 2007, 19, 3624–3632 CrossRef CAS.
- L. M. Bronstein, J. E. Atkinson, A. G. Malyutin, F. Kidwai, B. D. Stein, D. G. Morgan, J. M. Perry and J. A. Karty, Langmuir, 2011, 27, 3044–3050 CrossRef CAS.
- E. V. Shtykova, X. Huang, N. Remmes, D. Baxter, B. D. Stein, B. Dragnea, D. I. Svergun and L. M. Bronstein, J. Phys. Chem. B, 2007, 111, 18078–18086 CAS.
- A. K. Gupta and M. Gupta, Biomaterials, 2005, 26, 3995–4021 CrossRef CAS.
- D. Jiles, Introduction to Magnetism and Magnetic Materials. Chapman and Hall: Boca Raton, 1998; Vol. 2 Search PubMed.
- V. Russier, C. Petit and M. P. Pileni, J. Appl. Phys., 2003, 93, 10001–10010 CrossRef CAS.
- D. H. Reneker, A. L.Yarin, H. Fong and S. Koombhongse, J. Appl. Phys., 2000, 87, 4531–4547 CrossRef CAS.
- D. Li, Y. L. Wang and Y. N. Xia, Nano Lett., 2003, 3, 1167–1171 CrossRef CAS.
- D. Zhang, A. B. Karki, D. Rutman, D. R. Young, A. Wang, D. Cocke, T. H. Ho and Z. H. Guo, Polymer, 2009, 50, 4189–4198 CrossRef CAS.
- M. Bayat, H. Yang and F. Ko, Polymer, 2011, 52, 1645–1653 CrossRef CAS.
- J. H. Zhu, S. Y. Wei, X. L. Chen, A. B. Karki, D. Rutman, D. P. Young and Z. H. Guo, J. Phys. Chem. C, 2010, 114, 8844–8850 CAS.
- P. Langevin, Annal. Chim. Phys., 1905, 5, 70–127 Search PubMed.
- J. I. Park, Y. W. Jun, J. S. Choi and J. Cheon, Chem. Commun., 2007, 5001–5003 RSC.
- C. Petit, V. Russier and M. P. Pileni, J. Phys. Chem. B, 2003, 107, 10333–10336 CrossRef CAS.
- K. E. Roskov, K. A. Kozek, W.-C. Wu, R. K. Chhetri, A. L. Oldenburg, R. J. Spontak and J. B. Tracy, Langmuir, 2011, 27, 13965–13969 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2012 |
