Ligand exchange processes on solvated beryllium cations VII – water exchange on cationic [Be(H₂O)₃(Lⁿ)]²⁺ⁿ (Lⁿ: 4-O-Py⁻, Py, 4-(Py)-Py⁺, 3,5-(Py)₂-Py²⁺, 3,4,5-(Py)₃-Py³⁺)

Abstract

The water exchange reactions on [Be(H₂O)₃(Lⁿ)]²⁺ⁿ (Lⁿ: 4-O-Py⁻, Py, 4-(Py)-Py⁺, 3,5-(Py)₂-Py²⁺, 3,4,5-(Py)₃-Py³⁺) were investigated through quantum chemical calculations (B3LYP/6-311+G**). While in all cases an associative interchange mechanism was found, the associative character was found to increase with increasing charge on the overall system, which in turn is governed by the charge on the ligand Lⁿ. Including the CPCM solvent model into the system decreases the amplitude of the energetic effects, but leaves the general trend intact. Furthermore, the binding energy of a fourth water molecule and the overall exchange activation energy were found to increase with the overall charge on the system. The structures are also influenced by the charge, but to a smaller extent. The Be–O distances to the second coordination sphere water molecule and the distances to the entering/leaving water molecules in the transition state are significantly shortened in the higher charged systems. These effects can be attributed to electrostatic interactions.

---

Introduction

Starting in prehistoric times, humans have always been fascinated by the vibrant green colour of an emerald, a gem variety of the mineral beryl. Beryl is a beryllium aluminium cyclic silicate (Be₃Al₂(SiO₃)₆) containing traces of chromium or vanadium ions, which create the enchanting green colour.

Today scientists are attracted by the outstanding physical and chemical properties of beryllium, even though, or maybe because, it is not an essential element for any known living organism. Among the numerous unique properties of metallic beryllium are the highest melting point (1287 °C) of all light metals and the extraordinary flexural behaviour, resulting in a mode of elasticity approximately 50% higher than that of steel. Current applications of beryllium in non-nuclear areas are mostly based on alloys containing up to 2.5% of beryllium.^1–3 Applications take advantage of the materials' low tendency to fatigue or show corrosion, their high thermal and electrical conductivity, and their high strength, hardness and absence of magnetism. Therefore, such alloys find uses in springs, electrical contacts, gyroscopes and magnetic resonance imaging equipment.

Applications of pure beryllium include optical mirrors for military applications or high-end telescopes like the Spitzer Space Telescope or the planned James Webb Space Telescope, as beryllium can withstand the low temperatures in space better than glass.⁴

However, the usefulness of beryllium is reduced by the toxicity of beryllium compounds. Even if beryllium's toxicity is a topic currently under discussion⁵ the complete absence of any known successful treatment for beryllium poisoning or any form of berylliosis (chronic beryllium disease (CBD))⁶ limits applications. Just like its toxicity, the kinetic pathways of most chemical processes incorporating beryllium ions are determined by the beryllium ionic equilibria in water. Therefore, detailed knowledge of the coordination chemistry of Be²⁺ in aqueous solution is an absolute prerequisite for the effective design of Be(II)-specific chelating agents and other advanced beryllium chemistry.^7–9

Be²⁺ possesses some rather interesting features which lends itself conveniently to quantum chemical studies: it has the smallest ionic radius (0.35 Å) of all metal cations, exhibits tetrahedral coordination (shown both by way of calculations¹⁰ and experiments^11–13), and a body of kinetic and mechanistic data published by Merbach et al.¹⁴ exist that can be used to evaluate computational results.

Solvation of a beryllium salt will result in the formation of solvent-coordinated beryllium ions. These beryllium ions are surrounded by a second solvation sphere bound to the first coordination sphere either electrostatically or, if available, by hydrogen bonding. Solvent molecules exhibit mobility between the two solvent coordination spheres. The mechanism of this exchange can be rationalized within the Langford and Gray¹⁵ theory on rate-limiting mechanisms. Specifically, the mechanism can follow one of the extreme pathways, associative (A) and dissociative (D) mechanisms, in which an intermediate with either increased or decreased coordination number is formed (see Scheme 1). Half way between these extremes, the pathway follows the interchange (I) mechanism (see Scheme 1) that forms only a single transition state without the formation of a pronounced intermediate. The interchange mechanism, in turn, is usually divided into the three modes: I_a, I, and I_d, depending on whether the reaction is leaning towards pronounced bond formation, or bond breakage.

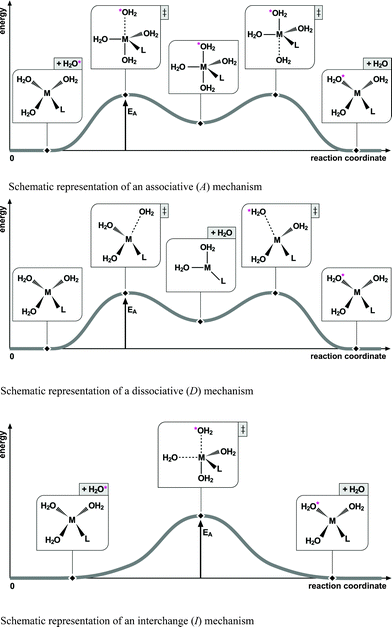Scheme 1 Schematic representations of the three exchange mechanisms rationalized with Langford and Gray's theory on rate-limiting mechanisms adapted to tetra-coordinated metal ions.

The most important solvent in both nature and technology is water. Therefore, an understanding of water exchange reactions is an important prerequisite to understand the reactivity of metal ions in solution. Starting out from the kinetic measurements of Merbach et al.,¹⁴ we calculated the solvent exchange reaction barriers and characteristics of solvated Be²⁺, using modern quantum mechanical methods and focusing on small solvent molecules with O and N donor atoms, viz. H₂O, H₂CO, CO₂, NH₃, HCN, N₂, etc. These consistently exhibited an associative interchange water exchange pathway.¹⁶ This same type of mechanism was found in our recent study on the water exchange on [Be(H₂O)₃(X)]⁺ (X = F, Cl, Br, OH, CN, NCNCN)¹⁷ as well. Analogous studies with different neutral ligands X (e.g., NH₃, Py, HCN, etc.)¹⁸ and with neutral chelating ligands like dimethoxyethane¹⁹ revealed, that the examined ligands do not influence the associative interchange mechanism and are therefore to be considered spectator ligands. The only observable influence is that of the overall charge of the complex on the activation barrier, independent of the nature of the donor atom in X. Analogous results were obtained for the exchange of water and ammonia on the beryllium dications coordinated by the chelating ligands crown ether (12-crown-4)²⁰ and imidazole.²¹

Here we present the results of quantum-chemical calculations for the water-exchange mechanism on the four-coordinate complexes of the type [Be(H₂O)₃(Lⁿ)]²⁺ⁿ (Lⁿ: 4-O-Py⁻, Py, 4-(Py)-Py⁺, 3,5-(Py)₂-Py²⁺, 3,4,5-(Py)₃-Py³⁺) (see Scheme 2). These pyridine based ligands were chosen to investigate the influence of differently-charged ligands on the water exchange on cationic beryllium complexes. Pyridine derivatives as coordinating ligands are ideal in this case, as they do not distort the results, neither by the formation of additional hydrogen bonds, nor any other forms of steric or electronic imbalance, due to the used ligands' C₂ symmetry. While positively charged ligands seem to be uncommon, 1-(pyridine-4-yl)pyridinium is well known experimentally,^22–24 and both 1,1′-(pyridine-3,5-diyl)dipyridinium and 1,1′,1′′-(pyridine-3,4,5-triyl)tripyridinium should be accessible via Weiss' SASAPHOS protocol.²⁵

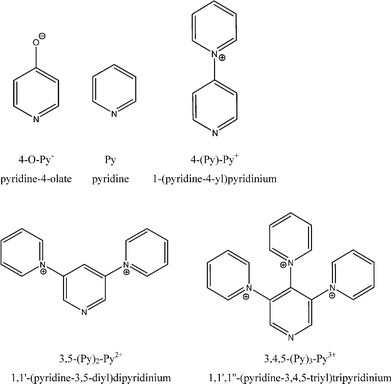Scheme 2 The investigated ligand systems Lⁿ.

Results and discussion

Whereas experimental methods are restrained to an ensemble of molecules under realistic conditions, quantum-chemical calculations allow us to focus on a single molecule along with a few solvent molecules. In this study we have chosen to restrict ourselves to the complex itself and the first coordination sphere as basic molecule, adding one additional solvent molecule to mimic the second coordination sphere.

Based on these quantum chemical model calculations, we observed an interchange type of mechanism (see Fig. 1) in all investigated systems. As expected, the addition of a fourth water molecule to [Be(H₂O)₃(Lⁿ)]²⁺ⁿ turned out to be exothermic in all cases. Even though this reaction is quite artificial, the assumption of a reaction in the gas phase can provide a first insight into the system not available to the experimental chemist (see Table 1, Fig. 2). The systems investigated here exhibit a continuous increase in energy for this part of the reaction from [Be(H₂O)₃(4-O-Py)]⁺ to [Be(H₂O)₃(3,4,5-(Py)₃-Py)]⁵⁺. Maybe somewhat unexpectedly, even the CPCM(G09) energy values show an increase from the mono-cationic via the di-cationic to the oligo-cationic species. Interestingly, the energy released during the formation of [Be(H₂O)₃⋯H₂O(Py)]²⁺ is lower than that released in the formation of [Be(H₂O)₄⋯H₂O]²⁺. This can be attributed to the smaller number of non-hydrogen atoms in [Be(H₂O)₄]²⁺ and the extra stabilization caused by an additional water molecule.

Fig. 1 Calculated (B3LYP/6-311+G**) reaction pathway for the water exchange at [Be(H₂O)₃(3,5-(Py)₂-Py)]⁴⁺.

Fig. 2 Correlation of the ligand and the complex charge, and the calculated (RB3LYP/6-311+G**) energies for the removal/addition of one additional water molecule simulating the second coordination sphere of [Be(H₂O)₃(Lⁿ)]²⁺ⁿ (circles). Correlation of the complex charge and the calculated (RB3LYP/6-311+G**) activation energies for the water exchange reaction (squares).

Table 1 Calculated relative energies for the addition of a fourth water molecule and water-exchange on [Be(H₂O)₃(Lⁿ)]²⁺ⁿ

L^n:	Method^a	[Be(H2O)3(L^n)]^2+n +H2O [kcal mol^−1]	[Be(H2O)3⋯H2O(L^n)]^2+n [kcal mol^−1]	[Be(H2O)4(L^n)]^2+n (ts) [kcal mol^−1]
a B3LYP: RB3LYP/6-311+G** + ZPE (RB3LYP/6-311+G**). MP2(full): RMP2(full)/6-311+G**//RB3LYP/6-311+G** + ZPE (RB3LYP/6-311+G**). CPCM (G03): B3LYP(CPCM)/6-311+G**//RB3LYP/6-311+G** + ZPE (RB3LYP/6-311+G**). CPCM (G09): B3LYP(CPCM)/6-311+G**//RB3LYP/6-311+G** + ZPE (RB3LYP/6-311+G**).
4-O-Py^−	B3LYP	+18.0	0.0	+11.2
n: −1	MP2(full)	+19.3	0.0	+8.7
	CPCM(G09)	+8.8	0.0	+13.8
Py	B3LYP	+25.6	0.0	+15.5
n: 0	MP2(full)	+26.3	0.0	+11.9
	CPCM(G09)	+10.0	0.0	+13.6
4-(Py)-Py^+	B3LYP	+30.4	0.0	+18.2
n: +1	MP2(full)	+31.0	0.0	+14.3
	CPCM(G09)	+10.5	0.0	+13.9
3,5-(Py)2-Py^2+	B3LYP	+34.9	0.0	+21.0
n: +2	MP2(full)	+35.5	0.0	+16.7
	CPCM(G09)	+10.3	0.0	+14.4
3,4,5-(Py)3-Py^3+	B3LYP	+39.0	0.0	+23.6
n: +3	MP2(full)	+39.4	0.0	+19.3
	CPCM(G09)	+10.4	0.0	+14.8
H2O	B3LYP	+29.2	0.0	+15.6
	MP2(full)	+29.3	0.0	+12.6
	CPCM(G03)^26c	+15.6	0.0	+9.4
	CPCM(G09)	+9.9	0.0	+13.5

---

As in our previous studies, we applied B3LYP/6-311+G** for the geometry optimization and the determination of the zero point energy. To evaluate the derived energies we applied MP2(full)/6-311+G** energy calculations on the B3LYP/6-311+G** structures. Except for the well-known underestimation of activation energies by MP2, a well-known and well documented phenomenon,²⁶ the energies for the addition of a fourth water molecule are nearly identical. Therefore we will discuss in the following, if not otherwise noted, the B3LYP/6-311+G** energy values only.

As anticipated from previous results, the binding of a fourth water molecule to [Be(H₂O)₃(Lⁿ)]²⁺ⁿ (Lⁿ: 4-O-Py⁻, Py, 4-(Py)-Py⁺, 3,5-(Py)₂-Py²⁺, 3,4,5-(Py)₃-Py³⁺) influences the reactivity of the complexes. Both the energy released from the addition of a fourth water molecule and the activation energy of the water exchange reaction increase linearly with increasing charge on the complex (see Table 1, Fig. 2).

This result can be clearly attributed to the influence of the charge on the system and the increasing electrostatic interaction from the ligand. CPCM(G09) values support this finding as they show a much smaller increase in energy due to partial simulation of a solvent.

In addition to the influence on the energy values, the charge on the ligand Lⁿ has an influence on geometric parameters (see Table 2 and Table 3). As shown in Fig. 3 (also see Table 2), the Be-N bond lengths increase linearly with increasing ligand charge. This behavior is easily understood as the system trying to separate charges with the same algebraic sign. Interestingly, the Be–N bond lengths increase slightly from [Be(H₂O)₂(Lⁿ)]²⁺ⁿ to [Be(H₂O)₃⋯H₂O(Lⁿ)]²⁺ⁿ to the transition state.

Fig. 3 Correlation between the calculated (RB3LYP/6-311+G**) Be–N bond lengths and the charges on the ligands or charges on the complexes: (circles) [Be(H₂O)₃(Lⁿ)]²⁺ⁿ (slope: 0.067, intercept (charge of Lⁿ): 1.665, intercept (charge of [Be(Lⁿ)(H₂O)₃]²⁺ⁿ: 1.531); (squares) [Be(H₂O)₃⋯H₂O(Lⁿ)]²⁺ⁿ (slope: 0.069, intercept (charge of Lⁿ): 1.675, intercept (charge of [Be(Lⁿ)(H₂O)₃]²⁺ⁿ): 1.537); (diamonds) [Be(H₂O)₄(Lⁿ)]²⁺ⁿ (ts) (slope: 0.077, intercept (charge of [Be(Lⁿ)(H₂O)₃]²⁺ⁿ): 1.677, intercept (charge n): 1.523).

Table 2 Calculated (B3LYP/6-311+G**) structural parameters for the investigated systems^a

L^n: d [Å]	Be–L	[Be(H2O)3(L^n)]^2+n	[Be(H2O)3⋯H2O(L^n)]^2+n	[Be(H2O)4(L^n)]^2+n (ts)
a B3LYP: Structure based on RB3LYP/6-311+G** optimization.
4-O-Py^−	Be–N	1.59	1.60	1.59
n: −1	Be–O	1.69, 1.70, 1.70	1.68, 1.70, 1.71, 3.49	1.66, 1.66
	Be–Ots	-.-	-.-	2.20
Py	Be–N	1.68	1.69	1.70
n: 0	Be–O	1.68, 1.68, 1.68	1.66, 1.66, 1.69, 3.45	1.66, 1.66
	Be–Ots	-.-	-.-	2.08
4-(Py)-Py^+	Be–N	1.73	1.74	1.75
n: +1	Be–O	1.67, 1.67, 1.68	1.65, 1.66, 1.69, 3.42	1.66, 1.66
	Be–Ots	-.-	-.-	2.06
3,5-(Py)2-Py^2+	Be–N	1.79	1.80	1.81
n: +2	Be–O	1.67, 1.67, 1.66	1.64, 1.65, 1.69, 3.37	1.66, 1.66
	Be–Ots	-.-	-.-	2.04
3,4,5-(Py)3-Py^3+	Be–N	1.87	1.89	1.92
n: +3	Be–O	1.66, 1.66, 1.66	1.63, 1.64, 1.68, 3.33	1.66, 1.66
	Be–Ots	-.-	-.-	2.01
H2O	Be–O	1.65, 1.65, 1.65, 1.65	1.64, 1.64, 1.66, 1.66, 3.39	1.68, 1.65
	Be–Ots	-.-	-.-	2.00

---

Table 3 Calculated (B3LYP/6-311+G**) angles for the investigated systems^a

L: d [Å]	Angle	[Be(H2O)3(L^n)]^2+nC1	[Be(H2O)3⋯H2O(L^n)]^2+nC1	[Be(H2O)4(L^n)]^2+n (ts) C2
a B3LYP: Structure based on RB3LYP/6-311+G** optimization.
4-O-Py^−	N–Be–O	119.7, 110.3, 110.3	117.2, 108.9, 118.5, 123.7	95.7, 95.7, 122.5, 122.5
n: −1	O–Be–O	103.1, 110.6, 102.5	99.6, 104.7, 104.8	168.5, 87.1, 87.1,114.9
	O–OHB–O	-.-	55.9	-.-
Py	N–Be–O	117.0, 109.7, 109.8	115.0, 108.4, 116.4, 132.0	95.2, 95.2, 118.9, 118.9
n: 0	O–Be–O	111.5, 104.4, 104.3	100.4, 110.2, 105.9	169.6, 87.5, 87.5, 122.1
	O–OHB–O	-.-	56.3	-.-
4-(Py)-Py^+	N–Be–O	114.6, 110.0, 111.8	116.0, 108.6, 113.2, 135.4	95.9, 95.9, 117.0, 117.0
n: +1	O–Be–O	108.6, 105.0, 106.4	100.8, 112.1, 105.8	168.2, 87.3, 87.3, 126.1
	O–OHB–O	-.-	56.6	-.-
3,5-(Py)2-Py^2+	N–Be–O	109.9, 112.2, 112.7	112.6, 108.2, 115.1, 138.9	96.4, 96.4, 115.6, 115.6
n: +2	O–Be–O	107.3, 105.4, 109.0	101.1, 112.8, 106.9	167.2, 87.3, 87.3, 128.8
	O–OHB–O	-.-	56.7	-.-
3,4,5-(Py)3-Py^3+	N–Be–O	109.7, 110.1, 112.0	111.8, 113.6, 106.9, 139.4	96.2, 96.2, 113.8, 113.8
n: +3	O–Be–O	107.0, 111.3, 106.7	101.6, 113.6, 109.4	167.7, 87.5, 87.5, 132.3
	O–OHB–O	-.-	57.1	-.-
H2O	N–Be–O	-.-	-.-	-.-
	O–Be–O	110.2, 108.3, 110.1, 108.3, 110.1, 110.0	102.4, 108.6, 108.6, 116.5, 116.5, 104.8, 127.6, 127.6	94.3, 94.3, 113.1, 113.1, 171.4, 88.3, 88.3, 133.9
	O–OHB–O	-.-	56.8	-.-

---

In contrast to the strongly affected Be–N bonds, the influence on the Be–O bond lengths is quite a bit smaller (Table 2). The largest influence is found on the second coordination sphere water molecules in [Be(H₂O)₃⋯H₂O(Lⁿ)]²⁺ⁿ and the entering and leaving water molecules in the transition state (see Table 2 and Fig. 4).

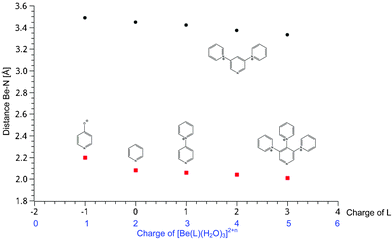Fig. 4 Correlation between the calculated (RB3LYP/6-311+G**) Be-O bond lengths for water in the second coordination sphere (circles) and the entering/leaving water in the transition state (squares) and the charge on the complexes.

Comparing the angles along the ascending charges only very small and hardly significant changes can be observed (see Table 3). If they follow a trend at all, then the marginal alterations go along continuously with the increasing charge, e.g. visible in the O–O_HB–O angle for the hydrogen-bonded water molecule in the second coordination sphere.

A comparison between the Be–O distances in [Be(H₂O)₃(Lⁿ)]²⁺ⁿ and in the transition state (see Table 4) shows that [Be(H₂O)₃(4-O-Py)]⁺ has the largest bond elongation for the leaving/entering water molecules, with a value of 0.50 Å, or 29%, while the smallest bond elongation is found in [Be(H₂O)₃(3,4,5-(Py)₃-Py)]⁵⁺ (0.35 Å, 21%). This shows that the increase in positive charge on the complex binds the exchanging water molecules tighter and increases the associative character of the interchange mechanism. Therefore the ligands Lⁿ: 4-O-Py⁻, Py, 4-(Py)-Py⁺, 3,5-(Py)₂-Py²⁺, and 3,4,5-(Py)₃-Py³⁺ cannot be considered to be spectator ligands, as they affect the energies along the reaction pathway and even the reaction mechanism itself with their charge and the resulting electrostatic attraction.

Table 4 Be–OH₂ bond length differences between the Be–OH₂ distance of the exchanging H₂O in the transition state [Be(H₂O)₄(Lⁿ)]²⁺ⁿ and [Be(H₂O)₃(Lⁿ)]²⁺ⁿ (RB3LYP/6-311+G**)

L^n	4-O-Py^−	Py	4-(Py)-Py^+	3,5-(Py)2-Py^2+	3,4,5-(Py)3-Py^3+	H2O^17
a Δd(Be–O) = d(Be–Ots in [Be(H2O)4(L^n)]^2+n) − d(Be–OH2O in [Be(H2O)3(L^n)]^2+n).
Δd(Be–O)^a [Å]	0.50	0.40	0.39	0.37	0.35	0.35
%	29%	24%	23%	22%	21%	21%

---

Since all ligands Lⁿ are aromatic heterocyclic systems, an obvious question is the potential influence of the aromaticity on the water exchange reaction, and vice versa. At first glance aromatic systems appear to be able to elicit an influence on the reaction, particularly in the context of the ongoing discussion on certain motifs like non-innocent ligands,²⁷ non-innocent anions,²⁸etc. As the largest difference in the Be-L bond length was found in [Be(H₂O)₃(3,4,5-(Py)₃-Py)]⁵⁺, we examined the aromaticity along the reaction path with NICS calculations.²⁹

As seen in Table 5, the pyridinium substituents on the pyridine moiety show no significant differences for the NICS(0) and NICS(1) values. A small change can be seen in the NICS values of the central and coordinating pyridine ring, but that change does not correlate linearly with the Be–N distances, which increase from [Be(H₂O)₃(3,4,5-(Py)₃-Py)]⁵⁺ to the transition state. Therefore, we do not attribute this small effect to the water exchange reaction. The origin is more likely to be found in the small differences in rotational angles between the central pyridine ring and the pyridinium substituents.

Table 5 Exemplary calculated (RB3LYP/6-311+G**) NICS(0) and NICS(1) values for [Be(H₂O)₃(3,4,5-(Py)₃-Py)]⁵⁺, [Be(H₂O)₃⋯H₂O(3,4,5-(Py)₃-Py)]⁵⁺ and [Be(H₂O)₄(3,4,5-(Py)₃-Py)]⁵⁺

		NICS(0)	NICS(1)
[Be(H2O)3(3,4,5-(Py)3-Py)]^5+	central Pyridine	−8.42	−8.74
	Py^+3. position	−6.84	−9.59
	Py^+4. position	−7.46	−9.99
	Py^+5. position	−6.85	−9.61
[Be(H2O)3⋯H2O(3,4,5-(Py)3-Py)]^5+	central Pyridine	−8.71	−9.23
	Py^+3. position	−7.09	−9.58
	Py^+4. position	−7.51	−9.92
	Py^+5. position	−7.17	−9.67
[Be(H2O)4(3,4,5-(Py)3-Py)]^5+	central Pyridine	−8.57	−8.88
	Py^+3. position	−6.91	−9.60
	Py^+4. position	−7.44	−9.96
	Py^+5. position	−6.91	−9.60

---

Conclusion

The investigation of the water exchange reaction on [Be(H₂O)₃(Lⁿ)]²⁺ⁿ (Lⁿ: 4-O-Py⁻, Py, 4-(Py)-Py⁺, 3,5-(Py)₂-Py²⁺, 3,4,5-(Py)₃-Py³⁺) shows an interchange mechanisms in all cases. The associative character of the mechanism is influenced by the charge on the complexes, which in turn is governed by the charge on the ligands. In addition to the character of the reaction mechanism, the energy for the addition of a fourth water molecule and the activation energy are influenced by the charge on the complexes. The bond lengths between Be–N and Be–O are also influenced, but to a smaller extent. In the case of Be–O, this is most obvious for the Be–O distance to the second coordination sphere water molecule and the distance to the entering/leaving water molecules in the transition state. These effects can be attributed to electrostatic interactions. After inclusion of model solvent effects, the strength of the energetic effects decreases notably, but the general trends remain the same.

Quantum chemical methods

All structures were fully optimized at the B3LYP/6-311+G** level³⁰ and characterized by computation of vibrational frequencies. Gas phase reaction energies were evaluated by MP2(full)/6-311+G** single point calculations (all electrons were included in the correlation treatment).³¹In an earlier study we have proven that the obtained results are nearly identical to those of so called high accuracy methods (G1, G2 and G3).¹⁷ The influence of bulk solvent was probed by single point calculations using the CPCM formalism^32,33 with water as solvent, i.e., B3LYP(CPCM:H₂O)/6-311+G**//B3LYP/6-311+G**. As DFT, in particular B3LYP, is well-suited for NMR³⁴ and NICS calculations,²⁹ we also applied B3LYP/6-311+G**//B3LYP/6-311+G** for the NICS calculations. The Gaussian 09 suite of programs was used throughout.³⁵

Acknowledgements

We are indebted to Prof. Dr Rudi van Eldik for his support of our work, and would like to thank Prof. Dr Tim Clark for hosting this work in the CCC, and the Regionales Rechenzentrum Erlangen (RRZE) for a generous allotment of computer time. M. W. would like to thank Prof. Dr Dirk Zahn for his support, which is most appreciated. This article is dedicated to Professor Günter Grampp on the occasion of his 65th birthday.

References

1. R. Puchta, Nat. Chem., 2011, 3, 416.
2. M. D. Rossman, O. P. Preuss and M. B. Powers, Beryllium: Biomedical and Environmental Aspects, Williams and Wilkins, Baltimore, 1991.
3. For the historical development of beryllium alloys see: I. McNeill, An Encyclopaedia of the History of Technology, Routledge, London, 1990.
4. J. Gardner, J. Mather, M. Clampin, R. Doyon, M. Greenhouse, H. Hammel, J. Hutchings, P. Jakobsen, S. Lilly, K. Long, J. Lunine, M. Mccaughrean, M. Mountain, J. Nella, G. Rieke, M. Rieke, H.-W. Rix, E. Smith, G. Sonneborn, M. Stiavelli, H. Stockman, R. Windhorst and G. Wright, Space Sci. Rev., 2006, 123, 485–606.
5. (a) J. R. Bill, D. G. Mack, M. T. Falta, L. A. Maier, A. K. Sullivan, F. G. Joslin, A. K. Martin, B. M. Freed, B. L. Kotzin and A. P. Fontenot, J. Immunol., 2005, 175, 7029–7037; (b) K. J. Cummings, A. B. Stefaniak, M. A. Virji and K. Kreiss, Environ. Health Perspect., 2009, 117, 1250–1256; (c) L. S. Newman, Sarcoidosis, 1995, 12, 7–19; (d) L. Richeldi, R. Sorrentino and C. Saltini, Science, 1993, 262, 242–244; (e) B. L. Scott, T. M. McCleskey, A. Chaudhary, E. Hong-Geller and S. Gnanakaran, Chem. Commun., 2008, 2837–2847; (f) C. Strupp, Ann. Occup. Hyg., 2011, 55, 30–42; (g) C. Strupp, Ann. Occup. Hyg., 2011, 55, 43–56; (h) Z. Wang, G. M. Farris, L. S. Newman, Y. Shou, L. A. Maier, H. N. Smith and B. L. Marrone, Toxicology, 2001, 165, 27–38; (i) Z. Wang, P. S. White, M. Petrovic, O. L. Tatum, L. S. Newman, L. A. Maier and B. L. Marrone, J. Immunol., 1999, 163, 1647–1653.
6. P. F. Wambach and J. C. Laul, J. Chem. Health Saf., 2008, 15, 5–12.
7. H. Schmidbaur, Coord. Chem. Rev., 2001, 215, 223–242.
8. L. Alderighi, P. Gans, S. Midollini and A. Vacca, Adv. Inorg. Chem., 2000, 50, 109–172.
9. B. L. Scott, T. M. McCleskey, A. Chaudhary, E. Hong-Geller and S. Gnanakaran, Chem. Commun., 2008, 2837–2847.
10. S. S. Azam, T. S. Hofer, A. Bhattacharjee, L. H. V. Lim, A. B. Pribil, B. R. Randolf and B. M. Rode, J. Phys. Chem. B, 2009, 113, 9289–9295.
11. W. W. Rudolph, D. Fischer, G. Irmer and C. C. Pye, Dalton Trans., 2009, 6513–6527.
12. Y. Inada, Y. Nakayama and S. Funahashi, J. Solution Chem., 2004, 33, 847–862.
13. (a) F. Kraus, S. A. Baer, M. R. Buchner and A. J. Karttunen, Chem.–Eur. J., 2012, 18, 2131–2142; (b) F. Kraus, M. B. Fichtl and S. A. Baer, Z. Naturforsch., 2009, 64b, 257–262.
14. (a) P. A. Pittet, G. Elbaze, L. Helm and A. Merbach, Inorg. Chem., 1990, 29, 1936–1942; (b) J. Frahm and H.-H. Füldner, Ber. Bunsenges. Phys. Chem., 1980, 84, 173–176.
15. C. H. Langford and H. B. Gray, Ligand Substitution Processes, W. A. Benjamin, New York, 1965.
16. R. Puchta, N. van Eikema Hommes and R. van Eldik, Helv. Chim. Acta, 2005, 88, 911–922.
17. A. Budimir, M. Walther, R. Puchta and R. van Eldik, Z. Anorg. Allg. Chem., 2011, 637, 515–522.
18. A. Budimir, M. Walther and R. Puchta, submitted.
19. M. Walther, C. Dücker-Benfer and R. Puchta, Z. Anorg. Allg. Chem., 2011, 637, 1736–1740.
20. R. Puchta and R. van Eldik, Z. Anorg. Allg. Chem., 2008, 634, 735–739.
21. R. Puchta and R. van Eldik, Z. Anorg. Allg. Chem., 2008, 634, 1915–1920.
22. J. V. Brenčič, B. Čeh and I. Leban, Z. Anorg. Allg. Chem., 1988, 565, 163–170.
23. A. Angeloni, P. C. Crawford, A. G. Orpen, T. J. Podesta and B. J. Shore, Chem.–Eur. J., 2004, 10, 3783–3791.
24. S. I. Gorelsky, A. B. Ilyukhin, P. V. Kholin, V. Y. Kotov, B. V. Lokshin and N. V. Sapoletova, Inorg. Chim. Acta, 2007, 360, 2573–2582.
25. R. Weiss, F. Pühlhofer, N. Jux and K. Merz, Angew. Chem., 2002, 114, 3969–3971.
26. (a) See e.g. W. J. Hehre, L. Radom and P. von Ragué Schleyer, Ab Initio Molecular Orbital Theory, Wiley, New York, 1986; (b) D. H. Ess and K. N. Houk, J. Phys. Chem. A, 2005, 109, 9542–9553; (c) R. Puchta, E. Pasgreta and R. van Eldik, Adv. Inorg. Chem., 2009, 61, 523–571.
27. (a) D. Coucouvanis, A. R. Paital, Q. Zhang, N. Lehnert, R. Ahlrichs, K. Fink, D. Fenske, A. Powell and Y. Lan, Inorg. Chem., 2009, 48, 8830–8844; (b) A. Kumar Das, B. Sarkar, C. Duboc, S. Strobel, J. Fiedler, St. Záliš, G. Kumar Lahiri and W. Kaim, Angew. Chem., 2009, 121, 4306–4309.
28. P. Illner, R. Puchta, F. W. Heinemann and R. van Eldik, Dalton Trans., 2009, 2795–2801.
29. (a) P. von Ragué Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. van Eikema Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318; (b) P. von Ragué Schleyer, H. Jiao, N. J. R. van Eikema Hommes, V. G. Malkin and O. L. Malkina, J. Am. Chem. Soc., 1997, 119, 12669–12670; (c) P. von Ragué Schleyer, M. Manoharan, Z.-X. Wang, B. Kiran, H. Jiao, R. Puchta and N. J. R. van Eikema Hommes, Org. Lett., 2001, 3, 2465–2468; (d) Z. Chen, Ch. S. Wannere, C. Corminboeuf, R. Puchta and P. von Ragué Schleyer, Chem. Rev., 2005, 105, 3842–3888; (e) H. Fallah-Bagher-Shaidaei, Ch. S. Wannere, C. Corminboeuf, R. Puchta and P. von Ragué Schleyer, Org. Lett., 2006, 8, 863–866.
30. (a) P. J. Stephens, F. J. Devlin, C. F. Chablowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627; (b) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652; (c) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789.
31. H. Hofmann, E. Hänsele and T. Clark, J. Comput. Chem., 1990, 11, 1147–1150.
32. V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001.
33. M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681.
34. N. J. R. van Eikema Hommes and T. Clark, J. Mol. Model., 2005, 11, 175–185.
35. Gaussian 09, Revision A.02, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, D. J. Fox, J. A. Pople, Gaussian, Inc., Wallingford CT, 2009.

---