Framework reconstruction between hR8 and cI16 germaniums: A molecular dynamics study

Abstract

Using molecular dynamics simulations and a Density Functional based Tight Binding method, the metastable germanium allotropes hR8 and cI16 are shown to interconvert by means of two sets of quasi-1D chains. The first set hosts sequences of S_N2 inversions of Ge tetrahedral centers, and represents the activated step. The second set does not imply any reconstruction, but assists the first one in propagating the reconstruction. The overall process is commenced by bond nucleation, followed by chain formation and reconstruction into either structure. A novel intermediate metastable phase is visited in the process. Elementary steps of chemical reactivity are accessible due to the appropriate time and spatial resolution of the methods used. This paves the way for a chemical understanding of structure reconstruction and metastable phase formation in solid materials.

---

Introduction

Tetrahedral structures are among the most versatile in terms of structural variety.¹ Group IV elements are by chemical valence keen to adopt a rich and surprising polymorphism. However, our capacity of directing novel covalent bond geometries is still limited by an incomplete understanding of the rules governing the formation of metastable phases.^2a This entails an understanding, as complete as possible, of the transformation kinetics and microscopic mechanisms associated with material synthesis.^2b This knowledge is needed to judge the synthesizability of a particular compound, which is not ensured by barely ascertaining that a particular compound can exist in principle. The quest for microscopic mechanisms is nowadays greatly empowered by methods able to provide the appropriate time and space resolution and the mandatory backtracking of the time evolution of a system to key elementary atomistic steps of material reactivity. While the resolution of experimental setups is greatly increasing, major breakthrough for material synthesis can be expected from routinely including the atomistic level of detail into designing synthetic approaches. Simple systems, and chemical elements in particular, represent the perfect ground on which an initial grammar of reactivity rules can be commenced.

Germanium has been intensively investigated, especially in recent years.^3–5 Many appealing technological properties are being discovered. While homologue Si has been the classical element for electronics, Ge is again receiving increased attention for its comparatively higher intrinsic electron mobility suitable for faster electronics, for photoluminescence and band-gap tunability, for its easier integration into semiconductor devices, and for superconducting properties.⁴ Squeezed under moderate pressure, germanium transforms from four-connected diamond type (cF8, sp. gr. Fd3̄m) into denser, high-symmetry structures with increasing coordination numbers .²

From mild oxidation of precursor Zintl compounds germanium can be obtained in the allotropic clathrate II structure (cF136, sp. gr. Fd3̄m),⁵ which is known in host–guest compounds⁶ for thermoelectric applications.⁷ Under pressure, cF136 transforms into β-tin type (tI4, sp. gr. I4₁/amd) and γ-silicon type (cI16, sp. gr. Ia3̄) over an intermediate, with only the moderately denser structure of trigonal symmetry, hR8 (sp. gr. R3̄),^3b which is also accessible from another metastable phase, tP12 (sp. gr. P4₁2₁2).^3c The hR8 Ge allotrope comprises four-coordinated Ge only, while 2 different sites Ge1 (Wyckoff position 6c) and Ge2 (Wyckoff position 18f) are indicated by the crystallographic analysis.^3b This contrasts with cF8, tI4 or cI16, which can be generated from one site only.

In the extended phase diagram of germanium, hR8 is at the gateway between denser (cF8, tI4, cI16) and open-framework (cF136) structures.^3b The hR8 structure may in fact be decomposed into a Ge2 framework hosting Ge1 guest chains.^3b Under compression, a structural evolution towards higher symmetric structures is common. Site splitting rarely occurs and when it does so, it is the case in exotic metals like for example Ti.⁸ Beyond the bare crystallographic data, we interpreted this as a manifestation of chemical reactivity and we moved on to unfolding the chemically relevant steps responsible for this differentiation. Clearly, a particular rearrangement of covalent bonds into a different pattern is controlling the formation and stability of a metastable phase here.

Using state-of-art molecular dynamics techniques combined with density-functional tight-binding (DFTB) level of theory⁹ for expressing interatomic forces, we have investigated the mechanism connecting hR8 to cI16, two intriguing structural patterns, and group IV (Si, Ge) characteristic assemblies (Fig. 1), which appear in the Ge phase diagram as metastable phases.

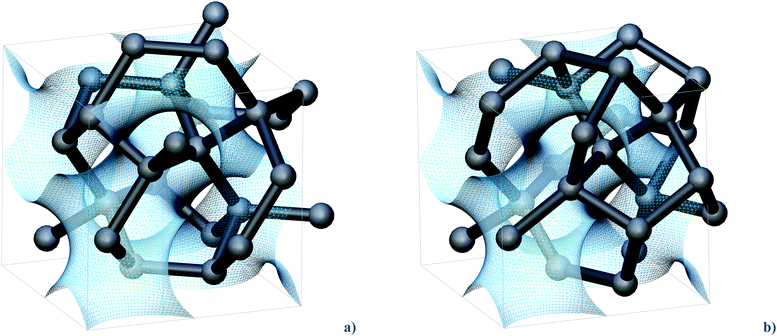Fig. 1 Crystal structures of the (a) cI16 and (b) hR8 Ge allotropes (hR8 is represented in a pseudo-cubic cell for better comparison with cI16). Their networks follow the shape of the gyroid (transparent blue), except for a set of bonds, which trespass the surface in a way that is peculiar for cI16 and hR8, respectively. Flipping these bonds formally converts cI16 into hR8. One such flip is visible in the foreground, causing inversion of a Ge tetrahedron.

The investigation of phase transition mechanisms remains a very important but challenging task.¹⁰ This is due to the specificities of the phenomenon of phase transition, which is difficult to assess both experimentally and by theory. Recent computational methods allow for shedding light onto transformation mechanisms and reactive intermediates, though.¹¹ A detailed atomistic map of reactive events that transform one structure into the other is the commencement of a chemical understanding of phase transitions in crystalline matter, now overdue .¹²

Symmetry provides, to some extent, guidance thanks to group–subgroup relationships.¹³ However, in a situation of framework reconstruction, relevant details of bond nucleation stay undisclosed. Heuristic matching of minimal surfaces (or approximants thereof) with crystalline matter has a long record of stimulating examples.¹⁴ The networks of cI16 and hR8 develop around the gyroid,¹⁵ a surface of intrinsic Ia3̄d symmetry. All Ge atoms are found on either side of the surface, as well as the majority of covalent bonds. Only some Ge–Ge bonds trespass the gyroid, in a way that is different and characteristic for cI16 and hR8, respectively (Fig. 1). Chemical intuition suggests that the process of their mutual structural rearrangement is “economical” and well-balanced in terms of bond-breaking and bond-forming patterns. However, how does the transformation of a framework into another one actually work, and what is the role of chemistry therein, given that covalent bonds have to be re-formed? These are the questions we address in this work.

Computation methods

Molecular dynamics simulations

Molecular dynamics (MD) is a powerful method for mechanistic investigations, and has found extensive use in chemistry, recently.¹⁶ However, in the presence of activation energy barriers, the efficiency of standard MD approaches is limited.¹⁷ To reliably determine reaction pathways for solid–solid transformations, Transition Path Sampling molecular dynamics (TPS) has a proven record of successes.¹⁸ If an initial transition path (ITP) can be worked out, which is able to connect the initial and final states of the transition, TPS can iteratively drive the ITP towards a most probable transformation regime. This is realized as a combination of MD and Monte Carlo (MC) simulation steps.¹⁹ The random walk is performed in the space of trajectories, instead of the space of configurations of a typical MC simulation. A new path is generated from a previous one, requiring the forward move (old-to-new) to be exactly balanced by the reverse move (new-to-old). The MD layer is used as a propagator. For a given trajectory, at a randomly chosen time slice, small momentum perturbations are introduced, followed by propagation forwards and backwards in time.¹⁹ Provided the trajectory stays in the regime of phase transition, the new trajectory is accepted with a probability proportional to the ratio of the distribution probabilities of the perturbed to the pristine time slice. Otherwise, a new perturbation move is made. Upon acceptance, the new trajectory becomes the old one, and the process is iterated. If the ITP is derived from a symmetry-based model, the converged calculation regime after TPS is typically characterized by nucleation and growth.

The hR8 → cI16 phase transition was investigated with TPS. The iterations were performed within the NPT ensemble (p = 12 GPa, T = 300 K) and implemented by applying momentum modifications on selected trajectory snapshots, keeping total energy, momentum and angular momentum unchanged according to the shooting scheme.¹⁹ The pressure corresponded to the equilibrium pressure of the DFTB potential, which fulfills the condition E₁ + pV₁ = E₂ + pV₂, where the indices distinguish between hR8 and cI16. Propagating the new configuration in both directions of time provided a new trajectory that was examined for the hR8–cI16 (or cI16–hR8) process, respectively. If this condition was not met, the trajectory was rejected and the shooting process iterated. The distinction between initial and final state was made based on coordination sequences (see below). MD simulations were carried out using DFTB,⁹ Γ-point-only module of the CP2K package.²⁰ The accuracy of electronic density representation was checked against DFTB k-point calculations.²¹ The Ge DFTB energetic score is in agreement with DFT- local-density approximation (DFT-LDA) calculations (Table S2, ESI†),²² but the equilibrium volumes are slightly overestimated.

The time step t = 0.2 fs ensured a good time reversibility. The mechanistic analysis was based on more than 50 transition pathways collected after trajectory convergence. The latter was inferred from the stability of the mechanistic features emerging during TPS MD. Different from the initial, concerted mechanistic models, the stable regime shows local events of bond flipping.

Construction of the model

The ITP was constructed based on matching the two allotropes (cI16 and hR8) in a common R3̄ space group within an 8-atom rhombohedral unit cell. Clearly, subgroup degradation was only necessary for the cI16 phase (Ia3 → R3̄). The simulation box was chosen as a supercell obtained from a minimal one by the transformation matrix (022/202/220), which resulted in a pseudo-cubic cell with 128 atoms. To quantitatively differentiate between the networks, we calculated coordination sequences (up to the 5th shell), which were also used to monitor structure evolution in the TPS simulations. Recall that a coordination sequence²³ is a set of integers {n₁, n₂, …n_i, …}, where n_i indicates the number of atoms separated from a central one by a minimal path of i bonds. For cI16 the coordination sequence reads (for each atom): {4, 12, 27, 49, 77, …}. In hR8, Ge1 sites are characterized by the sequence {4, 12, 24, 51, 72, …} while Ge2 sites show a denser environment {4, 12, 26, 49, 77, …}. Coordination sequences clearly discriminate between the two structures starting from the 3rd coordination sphere. Within this model, bond changes are taking place along three directions ([1̄11], [11̄1], [111̄]), without preference. Along [111] no bond breaking is observed. The reconstruction as the model codes it is thus “degenerate” in 3 directions.

Wannier functions

Wannier centers and Wannier orbitals were used to characterize bond evolution during phase transitions. The Fourier transform of Bloch states into Wannier functions is defined up to a phase factor. Characteristic of a Wannier function are its center and spread. A convenient set of maximally localized Wannier functions (MLWFs)²⁴ was obtained by minimizing the total quadratic spread of the Wannier orbitals, implemented in the WANNIER90 program.²⁵ For the MLWFs of Fig. 5, sp³ projection functions were used. This choice consistently produces four “bonds” in cI16 and hR8, and is sensitive to bond elongation/shortening.²⁶

Results and discussion

In the converged TPS regime, a typical transformation path shows structural variations along two directions only, distinguished by colors (red and blue) in Fig. 2. The reconstruction relates two distinct groups of localized bond systems, which are similarly oriented in the initial and final structures, Fig. 2a,d.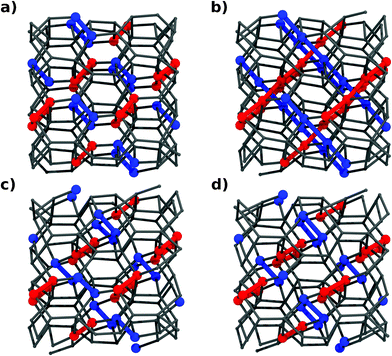

Fig. 2 Configurations appearing along the transformation. (a) Ge(cI16), (b) reactive intermediate, (c) a novel metastable phase Ge(hR32) and (d) Ge(hR8). Bonds changing from one structure to the other are highlighted in blue, while red ones show stretching along the trajectory, but they are never completely broken. (c) and (d) differ only by some bonds. They are nonetheless two distinct local minima on the chemical landscape of Ge.

Striking is the formation of two sets of Ge chains around the transition reactive intermediate (Fig. 2b). These chains, which result from the condensation of isolated bonds, are tilted with an angle of ∼60° against each other and are entangled and interconnected into a web. Blue chains are oriented along [1̄11] (referred to as the simulation box) (Fig. 2b) and are responsible for the transformation hR8 ↔ cI16 by shortening and elongating alternate sets of bonds. Red chains (along [111]), on the contrary, are forming in the course of the transition but do not rearrange from one structure into the other. Localized “red” bonds, similarly dislocated in both limiting structures, are momentarily resonating into a chain structure.

Along the transition, an intermediate, four-connected, metastable configuration is visited (hR32) (Fig. 2c), isosymmetric with hR8 but requiring certain bonds within some of the reactive [1̄11] chains to be flipped. Details on this novel metastable configuration, quenchable to ambient pressure based on phonon calculations and finite temperature molecular dynamics simulations (DFTB/DFT), can be found in the ESI section.†

The blue-marked dumbbells in hR8 (Fig. 2d) involve Ge1 sites only, while red ones are made by Ge2 sites. Red and blue become equivalent in cI16. Changes within blue chains are thus responsible for site differentiation. Their difference is rooted in the steps around the reactive intermediate, which we are analyzing in detail now.

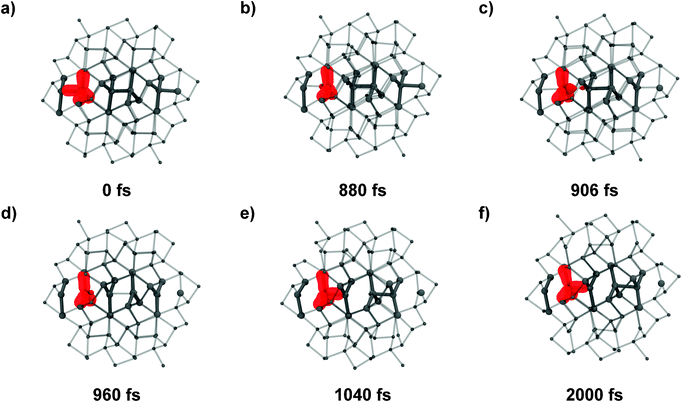
The bond flip mechanism among different reactive (blue) chains as well as within a single chain is markedly asynchronous. Fig. 3 shows a close-up of the bond reorganization of a single chain as a function of time. Noteworthy is the formation of trigonal-bipyramidal geometries at Ge, suggesting sp² + p hybridized states like they are caused by a S_N2 reaction sequence mechanism, in which tetrahedral sp³-hybridized Ge atoms get inverted. Most notable is the generation of an almost regularly spaced sequence of sp² Ge atoms. This sequence undergoes rapid rearrangements with the formation of new bonds, characteristic either of Ge(hR8) or Ge(cI16), respectively. Single bonds “nucleate” from a roughly equally spaced arrangement, triggering a sequence of bond-forming and bond-breaking events.

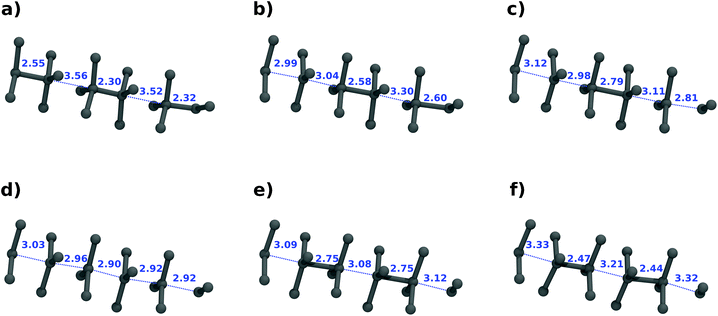Fig. 3 Transition mechanism for a single reaction chain (in blue in Fig. 1). Snapshots of the trajectory are shown at 0.0 (a), 880 (b), 906 (c), 960 (d), 1040 (e), 2000 (f) fs.

A global characterization of all bond changes along a trajectory is achieved by calculating Wannier functions centers (WFCs).²⁴ Two atoms are associated with a single WFC (within a so-called “association length”) in the presence of a chemical bond. Upon bond breaking, the WFC disappears or becomes shifted. For the characterization of the transition trajectories with respect to chemical bond changes, the motion of WFCs was monitored along the time coordinate of framework reconstruction. The shift of a bond within a chain (Fig. 3) is reflected into a jump in WFC relative position (Fig. 4). Just one snapshot every 20 fs was considered near the relaxed hR8 and cI16 phases. In the intermediate region, a finer time resolution (every 2 fs) was necessary. The displacement of Wannier centers serves here as collective order parameter.

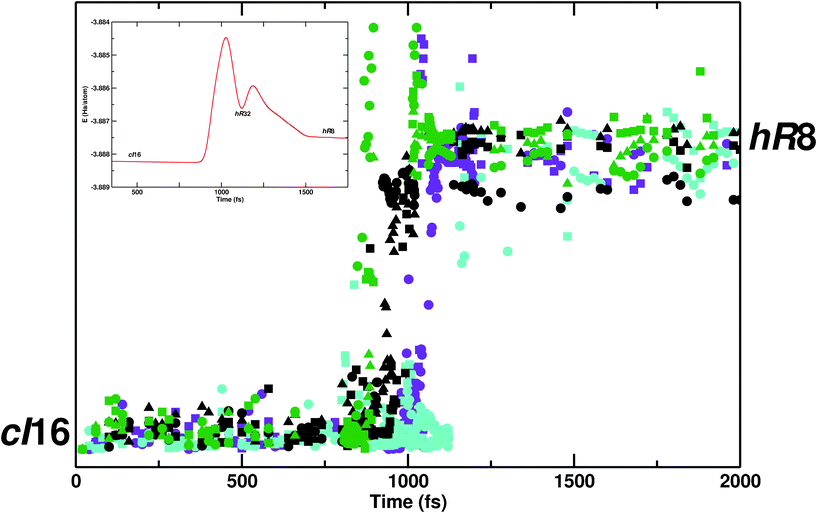Fig. 4 Evolution of WFC relative distances, calculated for each bond and each reactive chains (four blue chains in Fig. 2b) along the time coordinate of the framework reconstruction transition. Different colors (green, black, purple and turquoise) refer to distinct chains, while distinct symbols (square, circle and triangle) refer to different bonds within a single chain. Inset: potential energy profile with hR32 as the intermediate phase. Zeroth time frame is arbitrary set. The y axis corresponds to relative displacements of WFC along the transition and is used here as an order parameter, able to distinguish between initial and final states.

Fig. 4 shows the time evolution of WFCs within every reactive chain. Different reactive chains are distinguished by color (green, black, purple and turquoise), while bonds within a chain are marked by symbols. Clearly, the total reconstructive process is discontinuous on the timescale of the simulation. Chain bond flippings occur at different moments in the whole material, as indicated by the mutual offset of the sigmoidal curves. For each color, different symbols jump at different times, denoting non-concerted bond shifts within chains, as already highlighted in the close-up of Fig. 3. Therefore, the overall bond rearrangement process spans quite a large time window: the first bond flip occurs at ∼750 fs while the last one is at ∼1200 fs. The green curves refer to the chain of Fig. 3. As the first bond gets broken (green circle), the other bonds in the same chain start rearranging (green square, triangle), followed after some delay by bond shifts in neighboring chains (black, purple and turquoise). The larger WFC fluctuations around 850 fs (Fig. 4, green chain) and 1000 fs (green and purple chains) coincides with the formation of red chains, which is taking place just before breakage/formation of reactive (black and purple) chains, and less markedly ahead of the last chain reshuffling (∼1200 fs).

This is echoed in the changes of phonon frequencies along the transition. The stretching mode of the first flipping bond becomes negative at t = ∼750 fs, at the onset of bond nucleation (green curve and circles in Fig. 4). At ∼800 fs also, the frequency associated with black squares flips and turns negative, rapidly followed by other reactive chain modes. At 950 fs, in correspondence with the first fluctuation of the green curve (circle), the modes associated with the red, non-reactive chains become unstable and keep showing negative frequencies till 1050 fs, past the second fluctuation value of green and violet curves. The maximal wavenumbers of the red chains (−75 cm⁻¹) are considerably smaller than the blue chain modes (−270 cm⁻¹). Nonetheless they strongly influence phase transition by spreading the initial instability associated with single bond nucleation events over the whole material via chemical bonds.

The inset of Fig. 4 shows the potential energy profile along the reaction coordinate for a representative trajectory. For the hR8 → cI16 transformation, hR32 is initially formed, which is structurally and energetically similar to hR8, before a major reconstruction towards cI16 takes place. This allows splitting of the overall reconstruction into two “elementary” steps, hR8 → hR32, followed by hR32 → cI16. The intermediate can be formed thanks to the asynchrony of chain reconstruction, as hR8 and hR32 differ by just a few bonds. To the extent that this solid transformation can indeed be understood as a set of “molecular” steps, the Hammond postulate,²⁷ may warrant some guidance. The hR32 intermediate is structurally and energetically closer to hR8 and is formed first. The second step involves more bond reshuffling and a larger activation barrier, as it contains the core of the reconstructions. On forming hR32 first, hR8 would be the kinetic product, cI16 the thermodynamic one.

To visualize the sp³ → (sp² + p) → sp³ sequence of re-hybridization around Ge inside reactive chains, Wannier functions were calculated, Fig. 5. In cI16 (t = 0 fs) four-bonded Ge shows four equal sp³ Wannier functions. Around t = 880 fs, the first bond is broken, under formation of a trigonal planar center (3 Wannier functions) and of a lone pair along the chain (contracted Wannier function, associated with one Ge only). Geometry fluctuations cause the lone pair to slightly expand and contract again (t = 880–960 fs) while the intermediate arrangement is maintained. Eventually, a new bond is formed under inversion of the pristine tetrahedral arrangements at t = 960–1040 fs. This is indicated by a rapid change of spread and shape of the corresponding Wannier function along the chain axis. Minor rearrangements lead to hR8 at t = 2000 fs.

Fig. 5 sp³-projected, maximally-localized Wannier functions for the Ge atom at which the transition is commenced. The evolution of bonds (transparent lobes) and lone pair (opaque lobe) are shown at different snapshots. For clarity, only the positive lobe of the MLWFs is rendered. The chain and time frames are the same as in Fig. 3. Zeroth time frame was set at cI16.

Quasi-regularly spaced chains appeared in the intermediate regions of the phase transition reconstruct by symmetrically pairing atoms into alternating localized bonds in a sort of Bond Density Wave (BDW),²⁸ reminiscent of a 1D Peierls distortion. Nonetheless, our analysis has shown that different modes coexist while the networks reconstruct. Particularly, no chain acts as a truly isolated 1D system, as a non-reactive “red” mode is supporting bond rearrangement. While the rearrangement of a single chain may be termed “Peierls-patterned”, a 1D chain is not acting here as the fundamental instability controlling the process.

The effect of periodic boundary conditions needs careful consideration when studying nucleation geometries. However, we believe our results to be transferable to larger systems, as the initial “nucleus” was determined to be a single bond switching, which can occur anywhere within a reactive chain. Furthermore, the non-concerted character of the bond shuffling process allows for the formation of an intermediate metastable structure (hR32), which we expect to be detectable in high-pressure experiments with an appropriate (de)compression protocol. This would represent a rare case of experimental verifiability of a solid–solid phase transition mechanism, and a major step towards controlling reactivity in the solid state.

In conclusion, by atomistic simulations we have characterized the hR8 to cI16 phase transition as a chemical isomerization reaction, which is taking place in the solid state. Sets of reactive chains are formed in the intermediate transition region. Within such reactive channels, distinct sets of bonds can rearrange from one structural pattern into the other one. Framework reconstruction is commenced by local bond nucleation, which is propagated along chains. The propagation step is assisted by a second set of chains, which is forming around the transition state only, but which is not accommodating any event of bond breakage or bond formation. In the reactive chains, bonds are reshuffled by Ge sp³ tetrahedra inversions, with the formation of intermediate trigonal-planar geometries known from S_N2 type reactions.

Acknowledgements

The DFG, Deutsche Forschungsgemeinschaft, is gratefully acknowledged for funding within SPP 1415. We are grateful to ZIH, Dresden for the generous allocation of computational resources. We thank Arnold Guloy for critically reading the manuscript. Discussions with Ulrich Schwarz are thankfully acknowledged. SL wishes to thank Nicola Marzari (EPFL, Lausanne) and Ali Hassanali (USI, Lugano) for inspiring discussions on Wannier functions.

References

1. M. M. J. Treacy, K. H. Randall, S. Rao, J. A. Perry und and D. J. Chadi, Z. Kristallogr., 1997, 212, 768–791.
2. (a) J. N. Wickham, A. B. Herhold and A. P. Alivisatos, Phys. Rev. Letters, 2000, 84, 924–926; (b) P. F. McMillan, Nat. Mater., 2002, 1, 19–25.
3. (a) R. J. Nelmes, M. I. McMahon, N. G. Wright and D. R. Allan, Phys. Rev. B: Condens. Matter, 1993, 48, 9883–9886; (b) U. Schwarz, A. Wosylus, B. Böhme, M. Baitinger, M. Hanfland and Yu. Grin, Angew. Chem., Int. Ed., 2008, 47, 6790–6793; (c) A. Wosylus, Yu. Prots, W. Schnelle, M. Hanfland and U. Z. Schwarz, Naturforsch. B, 2008, 63, 608.
4. X.-J. Chen, C. Zhang, Y. Meng, R.-Q. Zhang, H.Q. Lin, V. Struzhkin and H.-K. Mao, Phys. Rev. Lett., 2011, 106, 135502.
5. A. Guloy, R. Ramlau, Z. Tang, W. Schnelle, M. Baitinger and Yu. Grin, Nature, 2006, 443, 320.
6. (a) A. Guloy, Z. Tang, R. Ramlau, B. Böhme, M. Baitinger and Yu. Grin, Eur. J. Inorg. Chem., 2009, 2455–2458; (b) J. S. Kasper, P. Hagenmuller, M. Pouchard and C. Cros, Science, 1965, 150, 1713–1714; (c) S. Bobev and S. C. Sevov, J. Am. Chem. Soc., 1999, 121, 3795–3796.
7. G. S. Nolas; J. W. Sharp; H. J. GoldsmidThermoelectrics: Basic Principles and New Materials Developments, Springer-Verlag, Heidelberg, 2001.
8. R. Demchyna, S. Leoni, H. Rosner and U. Z. Schwarz, Z. Kristallogr., 2006, 221, 420–434.
9. G. Seifert, D. Porezag and T. Frauenheim, Int. J. Quantum Chem., 1996, 58, 185.
10. K. Jacobs, D. Zaziski, E. C. Scher, A. B. Herhold and A. P. Alivisatos, Science, 2001, 293, 1803–1806.
11. S. Leoni; S. E. Boulfelfel in Modern Methods of Crystal Structure Prediction; Oganov, A., Ed.; Wiley, 2010, pp. 181-221.
12. (a) S. E. Boulfelfel, G. Seifert, Yu. Grin and S. Leoni, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 014110; (b) S. E. Boulfelfel, A. Oganov and S. Leoni, Sci. Rep., 2012, 2, 471.
13. H. Katze, U. Bismayer and P. Toledano, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 134105.
14. (a) H.-G. von Schnering and R. Nesper, Angew. Chem., Int. Ed. Engl., 1987, 26, 1059–1080; (b) R. Nesper and Yu. Grin, Z. Kristallogr., 2011, 226, 692–710.
15. (a) A. H. Schoen, Infinite periodic minimal surfaces without self-intersections; NASA Technical Note No. D-5541: Washington, DC, 1970; (b) S. Leoni and I. A. Baburin, Z. Kristallogr., 2011, 226, 678–683; (c) mathworld.wolfram.com/Gyroid.html. .
16. (a) E. B. Moore and V. Molinero, Nature, 2011, 479, 506–508; (b) J.-Y. Raty, E. Schwegler and S. A. Bonev, Nature, 2007, 449, 448–451; (c) T. Li, D. Donadio, L. M. Ghiringhelli and G. Galli, Nat. Mater., 2009, 8, 726–730; (d) R. Z. Khaliullin, H. Eshet, T. D. Kühne, J. Behler and M. Parrinello, Nat. Mater., 2011, 10, 693–697.
17. D. Frenkel; B. SmitUnderstanding Molecular Simulation: From Algorithm to Applications, 2nd. ed., Elsevier, 2001.
18. (a) M. Grünwald, E. Rabani and C. Dellago, Phys. Rev. Lett., 2006, 96, 255701; (b) S. Leoni, Chem.–Eur. J., 2007, 13, 10022–10029; (c) S. Leoni, R. Ramlau, K. Meier, M. Schmidt and U. Schwarz, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 19612–19616.
19. (a) P. G. Bolhuis, C. Dellago and D. Chandler, Faraday Discuss., 1998, 110, 421; (b) C. Dellago, P. G. Bolhuis and P. L. Geissler, Lect. Notes Phys., 2006, 703, 349.
20. http://cp2k.berlios.de 2011.
21. B. Aradi, B. Hourahine and T. Frauenheim, J. Phys. Chem. A, 2007, 111, 5678.
22. G. Seifert, T. Köhler, Z. Hajnal and T. Frauenheim, Solid State Commun., 2001, 119, 653–657.
23. M. O'Keeffe and B. G. Hyde, Crystal Structures. I. Patterns and Symmetry. Washington, DC: Mineralogical Society of America, 1996, 7 Chapter.
24. N. Marzari and D. Vanderbilt, Phys. Rev. B: Condens. Matter, 1997, 56, 12847–12865.
25. A. A. Mostofi, J. R. Yates, Y.-S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2008, 178, 685–699.
26. P. Fitzhenry, M. M. M. Bilek, N. A. Marks, N. C. Cooper and D. R. J. McKenzie, J. Phys.: Condens. Matter, 2003, 15, 165–173.
27. G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334–338.
28. M.-H. Whangbo, J. Chem. Phys., 1981, 75, 4983.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c2ra20837g

---