Visualizations of charge transfer for the model of poly(3,4-alkylenedioxythiophene)s in neutral and various oxidation states

Abstract

The charge transfer mechanisms of the poly(3,4-alkylenedioxythiophene)s model in neutral and various oxidation states are theoretically investigated, which is stimulated by the recent experimental reports [C. Lin, et al., J. Am. Chem. Soc. 2011, 133, 11339.]. Due to the difference of charge distribution on different units at various oxidation states, the bond lengths of inter-units are significantly different. The properties of excitons and polarons in poly(3,4-alkylenedioxythiophene)s model in neutral and various oxidation states were revealed by quantum chemical calculations. In particular, simultaneous use of different correlation plots in atomic site representation and transition densities in real space representation reveals the electronic structure and spatial localization of the elementary excitations. Theoretical results state that the charge transfer mechanisms for neutral and oxidation states are significantly different. The theoretical results promote deeper understanding for the structural, optical and electronic properties of poly(3,4-alkylenedioxythiophene)s model, and will offer crucial hints for the rational design of novel transparent conductive poly(3,4-alkylenedioxythiophene)s and relative polymers.

---

Introduction

As a class of conducting and electroactive polymer, Poly(3,4-alkylenedioxythiophene)s have attract great attention across academia and industry, because they have high and quite stable conductivities, a high degree of optical transparency as a conductor, and the ability to rapidly switch between conducting and doped and insulating neutral state.¹ Among them, poly(3,4-ethylenedioxythiophene) (PEDOT) has been the most successful material from both a fundamental and practical perspective,^1,2 because PEDOT has been proved to be highly transparent, and could be used as stable positively oxidized (p-doped) conductive states film under ambient conditions.^2,3

In order to understand the structural, optical, and electronic of these PXDOTs, it is important to study the well defined oligomers with various conjugation lengths.⁴ Though the length of the oligomers has reached up to five repeated EDOT units,⁵ the limited solubility hampers the synthesis of the longer oligomers. To study the properties of them in more electron oxidation states, the longer repeat units are needed. ⁶ Very recently, a series of 3,4-propylenedioxythiophene (ProDOT) oligomers (nPHex) with dihexyl side chains and methylthio end-capping up to the dodecamer length was synthesized as a model of PXDOTs, and the structural, optical, and electronic properties of a series of ProDOT oligomers in neutral and various oxidation states were investigated experimentally by Lin and coworkers.⁷ So for deeper understanding the properties of PXDOTs at various oxidized states, the theoretical studies on the structural, optical, and electronic properties are very important to understand the properties of PXDOTs at various oxidized states, which would benefit for the rational design of other transparent conductive PXDOTs.

In this paper, we theoretically characterize the structural, optical, and electronic properties of ProDOT dodecamer (as a model of PXDOTs) in neutral and various oxidation states, as the model of PXDOTs. Firstly, the structure of the ProDOT dodecamer (shown in Fig. 1) in neutral and various oxidation states was studied with density functional theory (DFT). Secondly, the optical and electronic properties are investigated with time-dependent DFT method together with a set of extensive multidimensional visualization techniques. Lastly, the conclusions are derived.

Fig. 1 Molecular structure of ProDOT dodecamer.

II. Methods

All the quantum chemical calculations were done with Gaussian 09 software.⁸ The geometry of the neutral and oxidized ProDOT dodecamer at ground state were optimized by the density functional theory (DFT) method,⁹ B3LYP functional,^10,11 and 6-31G(D) basis set. The electronic transitions were calculated with time-dependent DFT (TD-DFT),¹² B3LYP functional and 6-31G(D) basis set. Visualizations of charge transfer and electron-hole coherence on electronic transitions were done with charge difference density^13–15 and transition density matrix,^{13,14,16–20} respectively. The transition dipole moments were visualized with transition density.^{13,14,21–26}

III. Results and discussion

3.1 Oxidation effect at ground state

Firstly, the various oxidation states of this molecule were optimized using DFT, from which the influence of the oxidation effect on the molecular structure and charge distribution at ground state were investigated theoretically. As can be seen from Fig. 2, we can see that two methylthios end-capping strongly influences the charge distribution on the two adjacent EDOT units, which results in positive charges on the methylthio end-capping which are much larger than those on the two adjacent EDOT units. While for the inner EDOT units (units 3–12), the influence of oxidation effect upon charge distributions can be also qualitatively analyzed. which can be described as: (1), for the neutral case, there is an almost net charge distributed on them; (2) for the +2e case, there is about 0.18 positive charge equally distributed on these units; (3) for the +4e case, net positive charges distributed on them increase gradually (from 0.2 to 0.35) from inner to outer units, which means that net positive charges have a tendency of moving from the center to the outer units; and (4) for the +6e case, net positive charges distributed on them firstly decrease from two center units to two adjacent two outer units, then increase to adjacent three units, and lastly decrease again. So, charge distributions on the units are strongly influenced by the oxidations.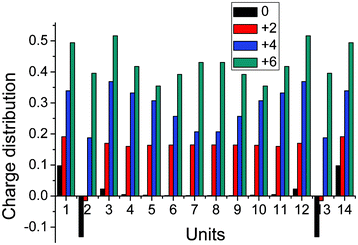

Fig. 2 Milliken charge distribution on different units at optimized neutral and positive ground state geometries.

Furthermore, the bond length of inter units adjusted by the oxidation effect are also studied, which can be seen from Fig. 3. For the neutral ProDOT dodecamer, the bond lengths of inter units are almost equal , except for the two outer units influenced by the side chains of –SCH₃. For the +2e ProDOT dodecamer, the bond length of the inter units becomes smaller from outer units to inner units. Different behavior can be found for the higher oxidized states. In detail, for the +4e ProDOT dodecamer, the bond length of inter units becomes larger from the outer units to the inner units, except for the two outer parts influenced by the side chains. While for the +6e ProDOT dodecamer, the bond length of inter units becomes larger and then smaller from outer units to inner units. Simply, this can be summarized as: there are two periods for the variation of inter bond length for +4e ProDOT dodecamer; while there is one period for the variation of inter bond length for +6e ProDOT dodecamer. So, for higher oxidized states, the periods of the variation of inter bond length will be smaller.

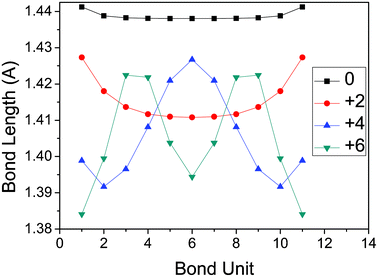Fig. 3 The variation of inter bond length for neutral and higher oxidized states of the ProDOT dodecamer.

3.2 Oxidation effect on excited state properties

The electronic transition of the neutral and charged ProDOT dodecamer were calculated and compared with the experimental results (see Table 1). It is found for neutral and +2e ProDOT dodecamer, the calculated results are very consistent with the experimental values. While for +4e ProDOT dodecamer and +6e ProDOT dodecamer, the calculated values are slightly higher than the experimental results. To further investigate the oxidation effect on the excited state properties of neutral and charged ProDOT dodecamer, the charge difference density of this molecule was calculated.

Table 1 The calculated lowest transition energies (eV) with oscillator strengths (parenthesis) for the neutral and charged ProDOT dodecamer

	0		+2		+4		+6
	Exp	Cal	Exp	Cal	Exp	Cal	Exp	Cal
S1	2.34	2.37 (1.87)	0.68	0.69 (0.73)	0.75	1.06 (0.91)	0.76	1.06 (0.95)

---

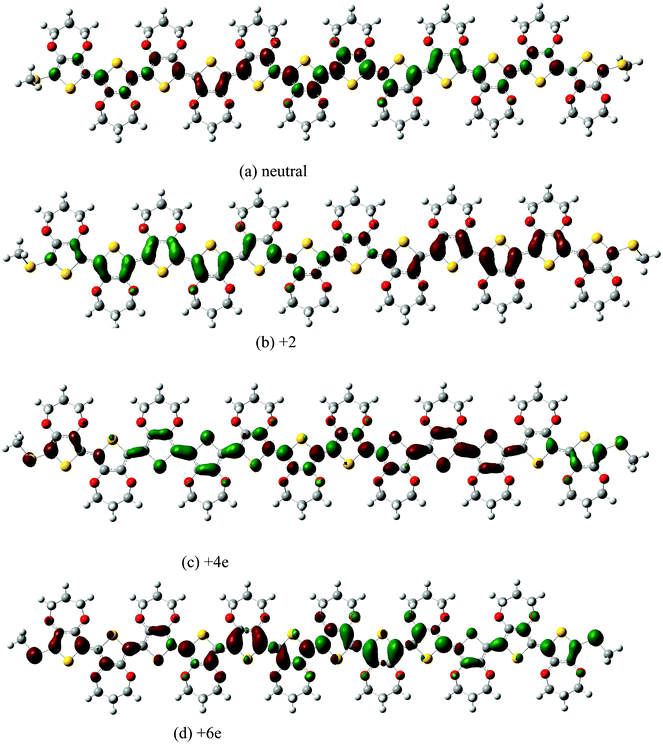
The charge difference density shown in Fig. 4, allows us to follow the change of the static charge distribution upon excitation. For the neutral ProDOT dodecamer, it is found that electrons and holes are delocalized on the whole units, though densities of electrons and holes become weaker on the two methylthios end-capping. In the case of the +2 charged ProDOT dodecamer, the excited hole resides mainly at the ends of the ProDOT dodecamer. If one compares this to the charge distribution of the polaronic species in the ground state shown in Fig. 2, one can find that the excitation tends to compensate for the extra charge localization. This indicates that the hole density becomes more similar to that of a free charge carrier in the valence band. In other words, the electron becomes free. For the +4e charged ProDOT dodecamer, the excited hole mainly resides at the center units. Also when comparing this to the charge distribution in the ground state (see Fig. 2), one finds that the electron hole density becomes similar to that of a free charge carrier in the conduction band. By considering the results of the +2e and +4e ProDOT dodecamer, the charge distribution on the ground state and orientation of charge transfer on excitation are completely opposite to each other. According to the results of the +6 charged ProDOT dodecamer mentioned above, the bond length and charge distribution of the inter units are separated into two centers in the ground state. Similarly, we can see that there are also two centers for charge transfer of the excited state, which can be characterized by the holes distributing on the two centers and the net charges localizing on the two centers slightly. So it is reasonable to suggest that charge transfer on excitation can compensate for charge localization at the ground state, when combined with the charge distribution and the orientation of charge transfer together.

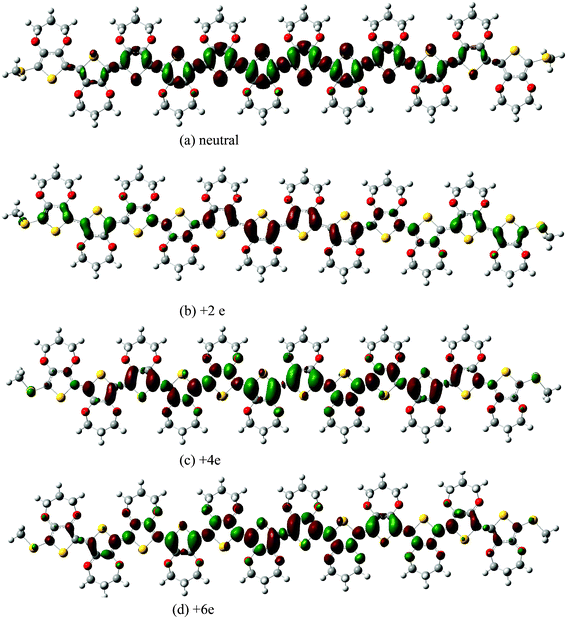Fig. 4 Charge difference density of neutral and charged ProDOT dodecamer.

The same features can also be found in the atomic site representation from the plots of |Q|² and |P|² shown in Fig. 5. In the transition density matrix, |Q|² measures the delocalization of the exciton as a whole; while |P|² describes the oscillation of the electron and hole from the atomic sites A–B and vice versa. These plots can be interpreted in terms of collective electronic oscillations along the conjugated chain. For the first excited state in neutral ProDOT dodecamer, the occupations of both matrices, |Q|² and |P|², are concentrated along the diagonal. This indicates that the oscillations of electrons and holes take place over only a few neighboring groups, the excitation as a whole, however, is delocalized over the conjugated chain, though with a slight concentration to the monomeric units in the center. This is a typical signature for the Frenkel-exciton. The corresponding plots for the +2e species are quite different. The occupation for |Q|² is concentrated in the diagonal corners, while for |P|², A–B are in the off-diagonal corners. In particular the latter means spacious charge oscillations from one end of the oligomer to the other. Generalized to polymers in +2e species, nearly free oscillating motion of two holes in the conduction band can be indicated. In this way the lowest electronic transition of the charged species can be seen as an ‘‘intra-band’’ excitation. The corresponding plots for the +4e and +6e species are similar to those of the +2e species, but the size of delocalization and size of the inter unit charge transfer are larger. So, for +4e and +6e species, there are the nearly free oscillating motion of two holes in the conduction band, which can be also seen as an ‘‘intra-band’’ excitation.

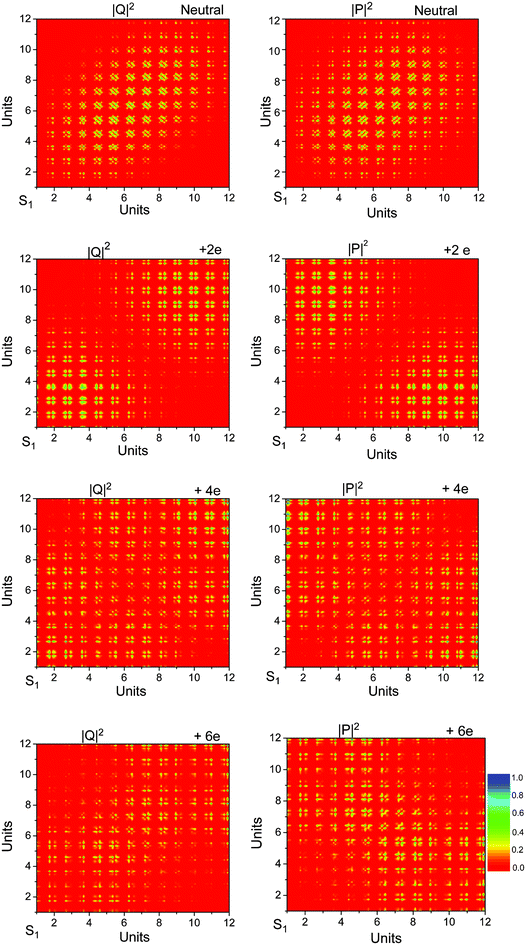Fig. 5 Transition density matrix of neutral and charged ProDOT dodecamer.

The real space transition densities for the first excited state of neutral and charged species show significantly different characteristic features, which can be easily seen from Fig. 6. The transition density for the lowest excited state of the neutral ProDOT dodecamer alternates in sign on the conjugated chain, while that of the +2e ProDOT dodecamer is divided into two regions with a constant sign and a node in the central ring. Thus the charged ProDOT dodecamer represent mesoscopic dipole antennae, while the neutral polymers should rather be represented by a series of small transition dipoles—one per monomeric unit. For the +4e ProDOT dodecamer, there are two nodes in the central ring, which separate the whole molecule into two sub-transition densities; furthermore, these two sub-transition densities are similar with the transition density for +2e ProDOT dodecamer, respectively. For the +6e ProDOT dodecamer, the transition density is similar to the +2e ProDOT dodecamer, which is also divided into two regions with a constant sign and a node in the central ring.

Fig. 6 Transition density matrix of neutral and charged ProDOT dodecamer.

IV. Conclusion

The structural, optical, and electronic properties of the model of PXDOTs in neutral and various oxidation states were theoretically characterized using TD-DFT together with a set of extensive multidimensional visualization techniques. Charge difference density revealed that the excitation tends to compensate the extra charge localization on the ground state. The significant difference between the transition dipole moments of neutral and charged ProDOT dodecamer can be easily seen from the transition density.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (grants 90923003, 21271095 and 11274149) and the Program of Shenyang Key Laboratory of Optoelectronic materials and technology (Grant No. F12-254-1-00). L. X. Xia Thanks for the Program for Liaoning Excellent Talents in University, China (LR2012001), the Shenyang Natural Science Foundation, China (F12-265-4-00 and F10-230-4-00), the Program for Shengyang Excellent Talents, and the Liaoning University 211-Projects of the third period. We also thank for the Natural Science Foundation of Liaoning Province, China (Grant No. 20111035, 20121032 and 201102080) and Liaoning Provincial Department of Education Project (Grant No. L20111003). Y. Li thanks for the Fundamental Research Funds for the Central Universities (grant no: DL12BB19).

References

1. L. Groenendaal, G. Zotti, P. H. Aubert, S. M. Waybright and J. R. Reynolds, Adv. Mater., 2003, 15, 855–879.
2. L. Groenendaal, F. Jonas, D. Freitag, H. Pielartzik and J. R. Reynolds, Adv. Mater., 2000, 12, 481–494.
3. G. Heywang and F. Jonas, Adv. Mater., 1992, 4, 116.
4. D. Wasserberg, S. C. J. Meskers, R. A. J. Janssen, E. Mena-Osteritz and P. J. Bauerle, J. Am. Chem. Soc., 2006, 128, 17007–17017.
5. K. Müllen and G. Wegner, Electronic Materials: The Oligomer Approach, Wiley: Chichester, U.K., 1998.
6. D. Wasserberg, S. C. J. Meskers, R. A. J. Janssen, E. Mena-Osteritz and P. J. Bäuerle, J. Am. Chem. Soc., 2006, 128, 17007–17017.
7. C. Lin, T. Endo, M. Takase, M. Iyoda and T. J. Nishinaga, J. Am. Chem. Soc., 2011, 133, 11339.
8. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E.; Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, et al.Gaussian 09, Revision A.02; Gaussian, Inc.: Wallingford, CT, 2009.
9. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B687.
10. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
11. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785.
12. E. K. U. Gross and W. Kohn, Phys. Rev. Lett., 1985, 55, 2850–2582.
13. M. T. Sun, Chem. Phys., 2006, 320, 155.
14. Y. Li, T. Pullerits, M. Y. M. T. Zhao and J. Sun, J. Phys. Chem. C, 2011, 115, 21865.
15. (a) W. J. D. Beenken and T. J. Pullerits, J. Phys. Chem. B, 2004, 108, 6164; (b) Y. R. Fang, Y. Z. Li, H. X. Xu and M. T. Sun, Langmuir, 2010, 26, 7737.
16. S. Mukamel, S. Tretiak, T. Wagersreiter and V. Chernyak, Science, 1997, 277, 781–787.
17. E. Zojer, P. Buchacher, F. Wudl, J. P. Cornil, J. Calbert, J. L. Bredas and G. J. Leising, Chem. Phys., 2000, 113, 10002.
18. J. Rissler, H. Bassler, F. Gebhard and P. Schwerdtfeger, Phys. Rev. B: Condens. Matter, 2001, 64, 045122.
19. W. Barford and D. Trembath, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 165418.
20. S. Tretiak and S. Mukamel, Chem. Rev., 2002, 102, 3171.
21. W. J. D. Beenken and T. J. Pullerits, J. Phys. Chem. B, 2004, 108, 6164–6169.
22. B. P. Krueger, G. D. Scholes and G. R. J. Fleming, J. Phys. Chem. B, 1998, 102, 5378.
23. M. T. J. Sun, Chem. Phys., 2006, 124, 054903.
24. M. T. Sun, L. W. Liu, Y. Ding and H. X. Xu, J. Chem. Phys., 2007, 127, 084706.
25. M. T. Sun, Y. Ding and H. X. Xu, J. Phys. Chem. B, 2007, 111, 13266.
26. S. Liu, X. Zhao, Y. Li, X. Zhao and M. Chen, J. Chem. Phys., 2009, 130, 234509.

---