Face-to-face stacking of dianionic quinoid rings in crystals of alkali salts of 2,5-dihydroxyquinone in view of π-system polarization†
Krešimir
Molčanov
*a,
Biserka
Kojić-Prodić
a,
Darko
Babić
ab and
Jernej
Stare
c
aRudjer Bošković Institute, Bijenička 54, HR-10000, Zagreb, Croatia. E-mail: kmolcano@irb.hr; Tel: +385 1 4561025
bDepartment of Chemistry, Faculty of Science, Horvatovac 102a, HR-10000, Zagreb, Croatia
cNational Institute of Chemistry, Hajdrihova 19, SI-1001, Ljubljana, Slovenia
First published on 18th October 2012
Abstract
A series of alkali (M+ = K+, NH4+, Rb+ and Cs+) salts of 2,5-dihydroxyquinone [M2+ (C6H4O4)2−] was prepared and their structures were determined by X-ray structure analysis. A less-common type of π-stacking of dianionic quinoid rings in face-to-face fashion (no offset) is observed. However, in the potassium salt of this series the stacking motif of the dianionic quinoid rings is in a herring-bone pattern, usually observed in the stacking of aromatics. The different types of crystal structures, induced by varied cations, are discussed in terms of the relative energies calculated by the DFT method. The structural features observed were reproduced by the calculations. The stacking of the quinoid rings is assisted by dispersion interactions.
Introduction
The interactions between stacked aromatic rings are extensively studied and characterised as π-stacking forces or π⋯π interactions.1–8 According to the most recent analysis of these forces based on experimental and theoretical findings Martinez and Iverson9 advocate for reconsideration of the term ‘π-stacking’. They provide evidence that these interactions should be viewed as ones occurring between polarised π-systems, i.e. interactions of electron rich vs. electron deficient regions.However, the stacking of quinoid rings has been little studied. It was documented only recently in the crystals of some simple alkali salts of chloranilic acid (3,6-dichloro-2,5-dihydroxyquinone)10–12 and bromanilic acid (3,6-dibromo-2,5-dihydroxyquinone).13 The two types of planar rings, aromatic and quinoid, have different electronic structures:14 the former have delocalised π electrons and all C–C bonds almost equal (Fig. 1a), whereas quinoid rings reveal well-distinguishable single and double bonds (Fig. 1b). Thus, stacking interactions between these rings are different to those in aromatics. Energetically the most favoured arrangement of aromatic rings is either offset parallel or T-shaped,7,15 however, neutral and monoanionic quinoid rings can appear in face-to-face parallel arrangement (no offset).10,12,13 Dianionic rings of chloranilates and bromanilates have a more pronounced electron delocalisation and favour offset stacking (Fig. 1c).11–13 The observed stacking can be understood as the overlapping of electron-rich and electron-deficient units between the polarised π-systems.
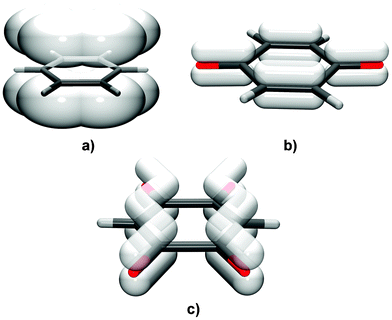 | ||
| Fig. 1 The distribution of π-electrons in (a) aromatic rings, (b) neutral quinoid rings and (c) DHQ2− anions. While aromatics comprise a delocalised (conjugated) system over the whole ring, in neutral quinoid rings π-bonds are essentially localised. DHQ2− (and similar chloranilate and bromanilate dianions) comprise two delocalised systems separated by single C–C bonds. | ||
Forced face-to-face stacking of aromatic rings has a potential use in the design of organic semiconducting materials.16,17 A synthetic approach has been used to control the organisation of aromatic rings of semiconductor molecules in the solid state supporting face-to-face π-stacking where π-orbital overlap is reliably enforced by stronger hydrogen bonds.16,17 However, quinoid rings can self-assemble into face-to-face π-stacks without directed chemical modifications.10,12,13
The present study is dealing with an unsubstituted analogue of chloranilic and bromanilic acid, 2,5-dihydroxyquinone (DHQ, Scheme 1). The main difference between DHQ and its halogen analogues is the lack of bulky, electronegative substituents. Electron density in the DHQ quinoid ring is therefore slightly higher than in its halogenated analogues, whereas the polarity of C–H bonds is reversed compared to C–Cl and C–Br bonds.
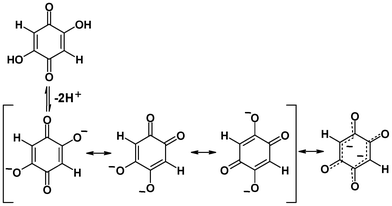 | ||
| Scheme 1 Dissociation of 2,5-dihydroxybenzoquinone (DHQ). DHQ2− has two delocalised systems separated by the two single C–C bonds. | ||
Results and discussion
The salts of alkali cations (K+, NH4+, Rb+, and Cs+) and 2,5-dihydroxybenzoquinonate dianions were prepared and their crystal structures determined and discussed in view of their dianion stacking and the interactions responsible for the motifs detected. Their crystal packings are not isostructural. Crystal packings of all studied salts exhibit a 3D-network via cation–dianion interactions. The two homologous salts, (NH4)2DHQ and Rb2DHQ crystallise in the orthorhombic space group Ibam, whereas K2DHQ appears in the monoclinic space group P21/c, and Cs2DHQ in the orthorhombic space group Cmmm (see Experimental section). The crystal structures of Li2DHQ·2H2O18 and (NH4)2DHQ, both with similar packing densities, exhibit extensive hydrogen bonds using the proton donor functionalities of crystal water molecules and of ammonium cations, respectively.Molecular structure and symmetry of 2,5-dihydroxybenzoquinone anion (DHQ2−)
Molecular symmetry of the DHQ2− dianion is D2h. In crystal structures, the crystallographic symmetry of the DHQ2− can be different. In the series studied the anions possess a crystallographic symmetry: Ci in K2DHQ; C2h in Li2DHQ·2H2O,18 (NH4)2DHQ, and Rb2DHQ; in Cs2DHQ the anion is disordered and located in a special position with the crystallographic symmetry D2h. The crystal structure of Li2DHQ·2H2O was published by Xiang et al.18 during our research on the herein presented series. The structure of the lithium–homologue was redetermined by us (ESI†) and it is briefly discussed and compared to other members of the series. There are two symmetry-independent anions in Li2DHQ·2H2O. According to the bond lengths (Table 1, Fig. 2) dianions comprise two delocalised systems separated by single C–C bonds (Scheme 1, Table 1). This structure is analogous to the dianion of chloranilic acid (3,6-dichloro-2,5-dihydroxybenzoquinone)11,19 and bromanilic acid (3,6-dibromo-2,5-dihydroxybenzoquinone).13 The DHQ2− in Cs2DHQ is disordered: atoms C1 and O1 are located on a twofold axis, therefore atoms O2 and H of the quinoid ring are disordered over two positions (Fig. 3).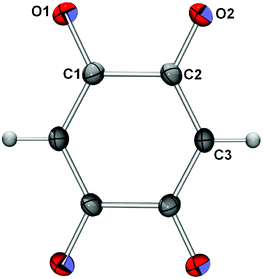 | ||
| Fig. 2 ORTEP-320 drawing of a DHQ2− in K2DHQ. The centroid of the ring coincides with a crystallographic inversion centre. The atomic numbering scheme is applied to all structures discussed, except that of Cs2DHQ. Displacement ellipsoids are drawn at the probability level of 50% and hydrogen atoms are depicted as spheres of arbitrary radii. | ||
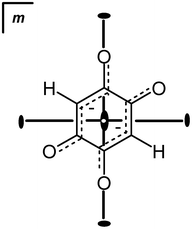 | ||
| Fig. 3 Nature of the disorder of the DHQ2− ring in Cs2DHQ. The crystallographic symmetry of the DHQ2− ring: the centroid of the ring is at (1/2, 0, 1/2), a special position with symmetry mmm; atoms C1 and O1 are located on a crystallographic twofold axis (site symmetry m2m), while atoms C2 and O2 are located in a mirror plane (site symmetry m). Therefore, C2, O2 and the hydrogen atom (which could not be located due to disorder) are disordered about a twofold axis: at each position of O2 (with population parameters for O2 and H of 0.25). ORTEP drawing of the disordered molecule is deposited into ESI.† | ||
| Li2DHQ·2H2O | K2DHQ | Rb2DHQ | (NH4)2DHQ | ||
|---|---|---|---|---|---|
| A ring | B ring | ||||
| a The geometry of the anion in Cs2DHQ is not realistic due to disorder and is not included. b The symmetry operators given in the table are: (i) −x, y, 1 − z; (ii) 1 − x, y, 1 − z; (iii) −1 − x, 1 − y, 1 − z; (iv) −x, −y, z. | |||||
| C1–C2 | 1.537(2) | 1.536(2) | 1.543(2) | 1.541(5) | 1.529(4) |
| C2–C3 | 1.391(3) | 1.397(2) | 1.398(2) | 1.381(7) | 1.395(4) |
| C1–C3b | 1.396(3)i | 1.394(3)ii | 1.402(2)iii | 1.407(5)iv | 1.392(4)iv |
| C1–O1 | 1.261(2) | 1.264(2) | 1.252(2) | 1.257(7) | 1.253(3) |
| C2–O2 | 1.264(2) | 1.254(2) | 1.258(2) | 1.263(6) | 1.271(3) |
| C3–H3 | 1.00(3) | 0.99(3) | 0.97(2) | 1.12(6) | 1.04(4) |
Crystal packing and π-stacking of 2,5-dihydroxybenzoquinone dianions (DHQ2−)
The striking feature of the crystal packing is face-to-face π-stacking of the dianionic rings with no offset (Table 2, Fig. 4–7). The space group symmetry and location of the quinoid rings on special positions correspond to strictly planar and parallel stacks with no offset. An exception is the packing of K2DHQ, where rings stack in an aromatic-like fashion with a large centroid distance and a considerable offset resulting in a herring-bone pattern (Fig. 8). In our previous studies of similar compounds, alkali chloranilates10–12 and bromanilates,13 we observed the stacking of neutral and monoanionic rings with no offset, while dianions were arranged in offset stacks.11–13![Crystal packing of Li2DHQ·2H2O18 viewed in the directions (a) [010] and (b) [001]. Lithium cations are depicted as spheres of arbitrary radii. DHQ2− anions are located on a crystallographic mirror plane and are therefore parallel.](/image/article/2013/CE/c2ce26119g/c2ce26119g-f4.gif) | ||
| Fig. 4 Crystal packing of Li2DHQ·2H2O18 viewed in the directions (a) [010] and (b) [001]. Lithium cations are depicted as spheres of arbitrary radii. DHQ2− anions are located on a crystallographic mirror plane and are therefore parallel. | ||
![Crystal packing of Rb2DHQ viewed in the directions: (a) [001] and (b) [100]. Rubidium cations are depicted as spheres of arbitrary radii. DHQ2− anions are located on a crystallographic mirror plane and are therefore strictly parallel.](/image/article/2013/CE/c2ce26119g/c2ce26119g-f5.gif) | ||
| Fig. 5 Crystal packing of Rb2DHQ viewed in the directions: (a) [001] and (b) [100]. Rubidium cations are depicted as spheres of arbitrary radii. DHQ2− anions are located on a crystallographic mirror plane and are therefore strictly parallel. | ||
![Crystal packing of (NH4)2DHQ viewed in the direction [001]. DHQ2− anions are located on a crystallographic mirror plane and are therefore parallel.](/image/article/2013/CE/c2ce26119g/c2ce26119g-f6.gif) | ||
| Fig. 6 Crystal packing of (NH4)2DHQ viewed in the direction [001]. DHQ2− anions are located on a crystallographic mirror plane and are therefore parallel. | ||
![Crystal packing of Cs2DHQ viewed in the direction [001]. Caesium cations are depicted as spheres of arbitrary radii. Disordered DHQ2− anions are located on a crystallographic mirror plane and are therefore parallel.](/image/article/2013/CE/c2ce26119g/c2ce26119g-f7.gif) | ||
| Fig. 7 Crystal packing of Cs2DHQ viewed in the direction [001]. Caesium cations are depicted as spheres of arbitrary radii. Disordered DHQ2− anions are located on a crystallographic mirror plane and are therefore parallel. | ||
![Crystal packing of K2DHQ viewed in the directions: (a) [100] and (b) [001]. Offset dianions form a herringbone pattern. Potassium cations are depicted as spheres of arbitrary radii.](/image/article/2013/CE/c2ce26119g/c2ce26119g-f8.gif) | ||
| Fig. 8 Crystal packing of K2DHQ viewed in the directions: (a) [100] and (b) [001]. Offset dianions form a herringbone pattern. Potassium cations are depicted as spheres of arbitrary radii. | ||
| π⋯π | Cga⋯Cg/Å | α b | β c | Cg⋯plane (Cg2)/Å | Offset/Å | Symm. op. on Cg2 |
|---|---|---|---|---|---|---|
| a Cg = centre of gravity of the aromatic ring. b α = angle between planes of two aromatic rings. c β = angle between Cg⋯Cg line and normal to the plane of the first aromatic ring. | ||||||
| Li2DHQ·2H2O | ||||||
| C1A → C3A⋯C1B → C3Bi | 3.2209(1) | 0 | 0 | 3.2209(1) | 0 | −1/2 + x, −1/2 + y, z |
| K2DHQ | ||||||
| C1 → C3ii⋯C1 → C3ii | 3.9251(9) | 0 | 29.30 | 3.4229(6) | 1.921 | −2 − x, 1 − y, 1 − z |
| (NH4)2DHQ | ||||||
| C1 → C3iii⋯C1 → C3iii | 3.5130(6) | 0 | 0 | 3.5129(6) | 0 | x, −y, −1/2 − z |
| Rb2DHQ | ||||||
| C1 → C3iii⋯C1 → C3iii | 3.6154(2) | 0 | 0 | 3.6154(2) | 0 | x, −y, −1/2 − z |
| Cs2DHQ | ||||||
| C1 → C2vi⋯C1 → C2iv | 3.888(5) | 0 | 0 | 3.888(5) | 0 | 1/2 + x, 1/2 + y, z |
A qualitative explanation can be based on the electronic structures of the species involved (Scheme 1, Fig. 1): neutral molecules and dianions comprise well-defined single and double bonds; therefore, they can avoid repulsion between electron-rich regions and maximise attraction between electron-rich and electron-deficient regions simply by stacking without offset.10,12 In halogen-substituted dianions, comprising two delocalised systems, repulsion between electron-rich regions cannot be avoided, and therefore halogen-derivatives form offset stacks.11–13 Moreover, the repulsion of two doubly negatively charged rings is much stronger. Therefore, the face-to-face stacking of dianionic DHQ2− rings came as a surprise. While the interplanar distances in halogen derivatives10–13 are about 3.2 Å, considerably shorter than the sum of the van der Waals radii for carbon (3.5 Å), interplanar separation between DHQ2− rings is greater than 3.5 Å, indicating much stronger repulsion.
DHQ, lacking large partially negatively charged halogen atoms, is less sterically hindered (Fig. 9) than its halogen analogues. Therefore, it can pack more closely. While contiguous hydrogen chloranilate and hydrogen bromanilate (Fig. 9a and b) rings are in staggered orientations, the DHQ2− rings are almost perfectly eclipsed (Fig. 9c). Such an arrangement allows maximised attractions between electron-rich and electron-deficient regions not only of the quinoid core, but also of C–O and C–H bonds (Fig. 9c). The additional attraction between the antiparallel dipoles of C–O and C–H bonds also contributes to the total interaction. On the other hand, stacked chloranilates and bromanilates in staggered orientation allow attractive interactions of the quinoids only (Fig. 9a and b). However, such enhanced attractions are only a part of the picture and alone can not overcome the significant repulsion of doubly charged rings. The most important contribution is probably the compensation of the negative charges by cation–anion interactions.
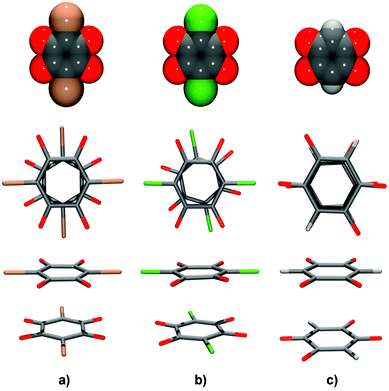 | ||
| Fig. 9 Pairs of contiguous quinoid rings in face-to-face stacks: (a) hydrogen bromanilate monoanions13 in a staggered arrangement, (b) hydrogen chloranilate monoanions10 in a partially staggered arrangement and (c) DHQ dianions in an eclipsed arrangement. To illustrate the bulkiness of halogen substituents, models of the anions using van der Waals spheres are shown in the upper row. | ||
Unlike previously described chloranilates with an extensive network of hydrogen bonds,10–12 in the DHQ salts only hydrogen bonds are present in Li2DHQ·2H2O and (NH4)2DHQ where water molecules and ammonium cations are proton donors and dianion oxygen atoms are acceptors. In other structures studied here there are C–H⋯O interactions between DHQ2−, only (Table 3). Thus, no competition exists between hydrogen bonding and stacking. Since similar types of stacks are observed in the structures with extensive hydrogen bonding [Li2DHQ·2H2O, (NH4)2DHQ, chloranilates10,12 and bromanilates13] and in those lacking hydrogen bonding (Rb2DHQ, Cs2DHQ), one can conclude that an impact of hydrogen bonds over the stacking arrangements is not of primary influence. Steric factors appear to have a crucial role in stabilising or destabilising the stacks. The different environments of DHQ2− in the structures of potassium and rubidium salts (Fig. 10 and 11, respectively) illustrate the impact of cation size on anion packing in crystals. In the potassium salt with a herring-bone motif each dianion is surrounded with ten cations: each ortho-positioned O1 and O2 function as bidentate bridging groups to five K+ (Fig. 10 and ESI,† Fig. S6). However, in the crystal structure of the rubidium salt each of the stacked dianions is embedded into the environment of twelve Rb+. Each pair of ortho-positioned O1 and O2 of a dianion acts as a bidentate bridging group to six cations.
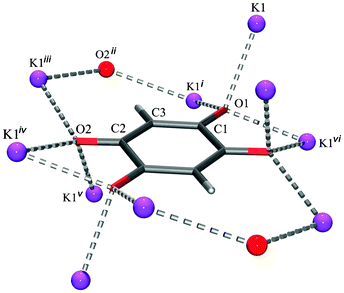 | ||
| Fig. 10 Environment of the DHQ2− dianion in K2DHQ. Symmetry operators: (i) −x, −y, −z; ii) x, −y + 3/2, z + 1/2; (iii) −x, y + 1/2, −z + 1/2; (iv) −x, −y + 1, −z + 1; (v) −x + 1, y + 1/2, −z + 3/2; (vi) x + 1, y, z. | ||
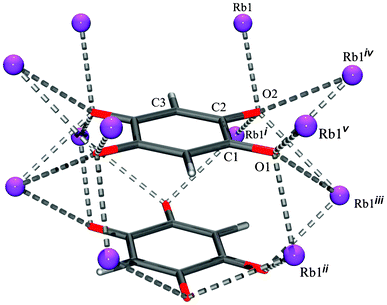 | ||
| Fig. 11 Environment of the DHQ2− dianion in Rb2DHQ. Symmetry operators: (i) x, y, −z; (ii) x + 1/2, y + 1/2, z + 1/2; (iii) −x + 1/2, −y + 1/2, z + 1/2; (iv) −x + 1/2, −y + 1/2, −z + 1/2; (v) x + 1/2, y + 1/2, −z + 1/2. | ||
| D–H/Å | H⋯A/Å | D⋯A/Å | D–H⋯A/° | Symm. op. on A | |
|---|---|---|---|---|---|
| Li2DHQ·2H2O | |||||
| O5–H5A⋯O1A | 0.94(3) | 2.06(3) | 2.8209(17) | 137(2) | 1/2 + x, −1/2 + y, z |
| O5–H5A⋯O2A | 0.94(3) | 2.33(3) | 3.1701(16) | 148(2) | 1/2 + x, −1/2 + y, z |
| O5–H5B⋯O2A | 0.90(2) | 1.95(2) | 2.8280(17) | 164(2) | 1 − x, y, 1 − z |
| K2DHQ | |||||
| C2–H2⋯O1 | 0.97(2) | 2.59(2) | 3.565(2) | 178.3(13) | x, 3/2 − y, 1/2 + z |
| (NH4)2DHQ | |||||
| N1–H1A⋯O2 | 0.88(3) | 2.05(3) | 2.915(2) | 166(2) | x, y, z |
| N1–H1B⋯O1 | 0.85(3) | 2.12(3) | 2.938(2) | 161(3) | 1/2 − x, 1/2 − y, 1/2 + z |
| C3–H3⋯O2 | 1.04(4) | 2.29(4) | 3.323(3) | 168(3) | −1/2 + x, 1/2 − y, −z |
| Rb2DHQ | |||||
| C3–H3⋯O2 | 1.12(6) | 2.22(7) | 3.323(6) | 171(5) | −1/2 + x, 1/2 − y, −z |
In (NH4)2DHQ, Rb2DHQ and Cs2DHQ the centroid separation distances are proportionally larger with the increased cation size (Table 2). The stacks of quinoid rings in these three structures reveal no offset but they have larger intrastack distances than in their halogenated homologues.10–13 The enlarged separation distance between stacked rings reduces the inter-ring repulsions.
However, Li2DHQ·2H2O crystallises as a dihydrate where hydrogen bonds stabilise the crystal packing; probably, the small size of the lithium cation could not be sufficient to stabilise the crystal packing and anhydrous crystals were not obtained. In its crystal packing stacks of dianions the shortest Cg⋯Cg separation distance is 3.2209(1) Å (no offset, Table 2).
Comparison of stacking types in the crystal structures of M2DHQ salts by DFT calculations
We tried to explain the differences in stacking types of DHQ2− in the crystal structures of M2DHQ salts by DFT calculations. Initially, we focused onto the stacking types displayed in the crystal structures of K2DHQ – hereafter referred to as type A, and Rb2DHQ – referred to as type B. We assumed that each salt can form stable structures of both types and that the more stable one – with lower energy – occurs in reality. The structures of M2DHQ, M = K, Rb, Cs, were optimized starting from the experimental structures of K2DHQ and Rb2DHQ as the initial geometry templates, with M+ ions replacing K+ and Rb+, respectively. The optimization of Cs2DHQ that was initiated from the structure type A ended up in a third structure – hereafter referred to as type C. It is similar to the type B inasmuch as having also face-to-face stacks of DHQ2− anions. In contrast to the B-type, in which the orientation of the C–H bonds along the stacked anions strictly alternates, the stacked anions in C are all parallel. The type C can be produced from type B by shifting the alternate layers of coplanar DHQ2− anions along the vector [0.5, 0.5, 0]. The optimization of K2DHQ and Rb2DHQ structures was repeated starting with the initial geometry of type C as well.As the pure Na2DHQ could not be prepared, we tried to predict its hypothetical structure as the most stable among the A, B and C types. On the other hand, the above procedure did not involve the NH4 cation since the quasi-octahedral coordination of oxygen atoms around the cation in the potassium salt is obviously unsuitable for the ammonium ion. In contrast, the octa-coordination polyhedron in Rb2DHQ (ESI,† Fig. S7) has 4 out of 8 apices in almost tetrahedral arrangement, favourable for hydrogen bonding to NH4+, and in agreement with the experimentally found structure of (NH4)2DHQ. This was considered sufficient to explain the structure of (NH4)2DHQ.
The calculated parameters of the unit cells are in good agreement with the experimental data (ESI,† Table S2). The energy of the K2DHQ structure obtained from the experimental geometry (type A) is 27.3 kJ mol−1 lower than the alternative structure derived from Rb2DHQ (type B). Similarly for Rb2DHQ, the energy of the type B structure was 10.6 kJ mol−1 lower than the type A structure. These results mean that the experimental structures of K2DHQ and Rb2DHQ are successfully predicted by calculation. The energies of type B and type C structures of Cs2DHQ are quite close, with the energy of the C-structure only 2.3 kJ mol−1 lower than the B-structure. Taking into account the structural similarity of types B and C and ease of transformation between them, the energy of a mixed structure with consecutive pairs of DHQ layers randomly being of B- or C-type, should not be significantly different from the fully ordered types B and C. This agrees with precisely the same character of the experimentally found disorder in the Cs2DHQ structure. Besides, optimisation of Rb2DHQ, initiated from the C-type, resulted in energy that was 10.1 kJ mol−1 higher than the B-type, in agreement with the fully ordered experimental structure. Similarly, the structure of K2DHQ initiated from the C-type was higher in energy by 27.2 kJ mol−1 than the A-type.
Interaction energy of the stacked pair of DHQ2− dianions and evaluation of the dispersion component
The interaction energy was calculated by using various types of model chemistry and for three distinct models – the isolated pair of dianions, the same pair in the field of explicit point charges located at the positions of cations and anions in the crystal structure and, finally, the pair of neutral DHQ molecules. Calculated energies are listed in Table 4.| Method | (DHQ2−)2 isolated | (DHQ2−)2 69 858 point charges | (DHQ)2 isolated |
|---|---|---|---|
| HF | 244.3 | 276.9 | 5.5 |
| B3LYP | 242.5 | 274.4 | 3.7 |
| M06 | 237.6 | 264.4 | −2.8 |
| B97D | 235.3 | 266.4 | −4.6 |
| MP2 | 235.9 | 267.9 | −4.4 |
The interaction between the stacked pair of DHQ2− dianions is largely repulsive. Evidently, the interaction is dominated by the repulsive electrostatic force between the negatively charged DHQ2− entities. However, the most interesting result is the subtle, yet significant difference between the HF and B3LYP methodologies on one side and M06, B97D and MP2 on the other. Namely, interaction energies calculated with the latter set are consistently (by 5–9 kcal mol−1) less repulsive than with the former. The difference can likely be attributed to the dispersion component of the interaction. While the HF and traditional DFT methods such as B3LYP are notorious for their lack of dispersion, the novel functionals such as Truhlar's M06 and Grimme's B97D offer improved support for the dispersion component; the same is true of the ab initio MP2 methodology.
The inclusion of explicit charges at their crystallographic positions influences the calculated interaction energy, making it even more repulsive. The sensitivity of the energy to the size of the array of surrounding charges is considerable when the surrounding shell of charges is relatively small, but the 100 Å cluster of charges provides practically convergent values of the interaction energy. Interestingly, the difference in interaction energy between the dispersion-deficient and dispersion-supported methodologies remains virtually identical, the latter yielding by about 7 kcal mol−1 less repulsive interaction. The insensitivity of the relative values supports the view that the origin of difference between the two groups lies in dispersion rather than in electrostatics or polarization.
Finally, in order to remove the predominant electrostatic component, we considered a pair of neutral DHQ molecules. While the HF and B3LYP methods suggest a slightly repulsive interaction, it becomes attractive with the methods with enhanced dispersion. Again, the differences are in the range between 6.5 and 10 kcal mol−1, suggesting that the dispersion forces can provide a decisive shift in the interactions that govern the alignment of DHQ rings.
The presented results provide evidence that, while the main interaction in the crystal is electrostatic, there is a relatively small but noticeable amount of dispersion component in the intermolecular interaction between the DHQ2− rings. Dispersion probably assists the observed face-to-face stacking of the rings. While quantitative determination of the dispersion component is probably beyond the reach and the scope of the present work, the present calculations clearly suggest that the attractive dispersion component is likely significant enough for the observed alignment of the rings.
Conclusions
A series of alkali (M+ = K+, NH4+, Rb+ and Cs+) salts of 2,5-dihydroxyquinone [M2+(C6H4O4)2−] was prepared and their structures determined by X-ray structure analysis. A novel type of face-to-face π-stacking without the offset of dianionic quinoid rings is observed. The factors affecting stacking of DHQ2− (dianions) are related to their electronic structures and the size, and polarisability of cations. The eclipsed orientation of DHQ2− rings in a stack (Fig. 9c) allows maximised attractions between electron-rich and electron-deficient regions of the quinoid ring, but also of C–O and C–H bonds (Fig. 9c). The additional attraction between antiparallel dipoles of C–O and C–H bonds also contributes to the total interaction. The strong attractions between C–O and C–H bonds of the two contiguous rings significantly contribute to the stability of the face-to-face arrangement, whereas the repulsions in these structures can be minimised by enlargement of ring separation distance within the stack, which is controlled by the size of NH4+, Rb+ and Cs+ (Table 2). Calculations by methodologies with different support for the dispersion component indicate that the attractive dispersion interaction between the stacked quinoid rings is in the range between 5 and 10 kcal mol−1, enhancing the stacking of the otherwise ionic entities at a close distance. For the salt structure with the relatively small K+, the face-to-face stacking is not optimal and a herring-bone type of stacking occurs. The relative energies of the crystal packings (including stacking types observed with different alkali cations), calculated by DFT method, revealed the lower values for the X-ray-structures. Other notable features in the crystal structures, like structural disorder in Cs2DHQ, were also explained by computational results.The self-organisation of 2,5-dihydroxyquinone dianions through dispersion interactions, leading to stacking, can be used in crystal engineering, and in the design of functional materials.
Experimental
All samples were prepared by slow evaporation of an aqueous solution containing 2,5-DHQ (Sigma-Algdich, p.a. grade) and an equivalent amount of alkali carbonate (Sigma-Aldrich, Merck, Kemika, all p.a. grade).Single crystal measurements were performed on an Oxford Diffraction Xcalibur Nova R (microfocus Cu tube) at room temperature. Program package CrysAlis PRO21 was used for data reduction. The structures were solved using SHELXS9722 and refined with SHELXL97.22 The models were refined using the full-matrix least squares refinement; all non-hydrogen atoms were refined anisotropically. Hydrogen atoms were located in a difference Fourier map and refined as free entities. Molecular geometry calculations were performed by PLATON,23 and molecular graphics were prepared using ORTEP-3,20 and CCDC-Mercury.24 Crystallographic and refinement data for the structures reported in this paper are shown in Table 5.
The computations were performed with the Gaussian 09.25 Electronic structure was calculated by the DFT method, and the exchange and correlation energies were evaluated with the PBE26 functional. Optimization was performed without any constraints, including all the molecular and the cell parameters. In order to reduce computational cost, the optimizations were performed with primitive cells. The computational parameters for periodic boundary conditions were automatically set up by the program,25 with numbers of k-points ranging between 112 and 148 and the number of replicated cells between 279 and 423.
The choice of the basis sets was quite important since the standard basis sets ordinarily used for molecules resulted in computational failures.27 It was remedied by using all-electron basis sets published on the Crystal Resources webpage.27 The basis consisted28 of contracted Gaussian-type functions of the form s(8)s(2)s(1)p(1) for element H, s(6)sp(1)sp(1)sp(1)sp(1)d(1) for element C, s(6)sp(2)sp(1)d(1) for elements N and O, s(8)sp(5)sp(1)sp(1) for element Na, s(8)sp(6)sp(5)sp(1)sp(1)d(3) for element K, s(9)sp(7)sp(6)d(5)d(1)sp(3)sp(1) for element Rb and s(9)sp(7)sp(6)d(6)sp(3)d(3)d(1)sp(3)sp(1)sp(1) for element Cs, where the letters give shell-type and the number in brackets gives the number of primitive Gaussians in each shell contraction. The exponents and contraction coefficients are reported in the Computational details in ESI.†
Calculations of interaction energy of an isolated stacked pair of dianionic quinoid rings were performed by the Gaussian 09 program using the 6-31++G(d,p) basis set and various quantum methodologies, including the functionals B3LYP,29,30 Grimme's B97D31 and Truhlar's M06,32 the latter two being improved for dispersion. In addition, the plain Hartree–Fock methodology and the perturbational correlation method MP233,34 were also used. The models included two neighbouring DHQ2− rings taken from the experimental geometry of (NH4)2DHQ. Effects of surroundings were modelled by an array of point charges of +1.0 and −2.0, corresponding to the positions of centroids of NH4+ and DHQ2− entities in the crystal lattice, respectively, within the nearest 100 Å from the stacked dimer (a total number of 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 858 point charges). In addition to the deprotonated DHQ2− ions, stacked pairs of neutral DHQ molecules were also considered. The neutral model was created by appending two hydrogen atoms to each of the DHQ2− anions. The interaction energies were corrected for the basis set superposition error by the standard counterpoise protocol, as implemented in Gaussian 09.
858 point charges). In addition to the deprotonated DHQ2− ions, stacked pairs of neutral DHQ molecules were also considered. The neutral model was created by appending two hydrogen atoms to each of the DHQ2− anions. The interaction energies were corrected for the basis set superposition error by the standard counterpoise protocol, as implemented in Gaussian 09.
| Compound | K2DHQ | (NH4)2DHQ | Rb2DHQ | Cs2DHQ |
|---|---|---|---|---|
| Empirical formula | C6H2K2O4 | C6H10N2O4 | C6H2Rb2O4 | C6H2Cs2O4 |
| Formula wt/g mol−1 | 216.28 | 174.16 | 309.02 | 403.89 |
| Crystal dimensions/mm | 0.25 × 0.04 × 0.03 | 0.21 × 0.07 × 0.06 | 0.23 × 0.16 × 0.04 | 0.15 × 0.12 × 0.10 |
| Space group | P21/c | Ibam | Ibam | Cmmm |
| a/Å | 3.92510(10) | 8.2507(9) | 8.1716(4) | 8.2553(11) |
| b/Å | 11.2358(3) | 12.4085(13) | 12.4680(5) | 12.8490(16) |
| c/Å | 8.3337(2) | 7.0259(12) | 7.2307(3) | 3.8880(4) |
| α (°) | 90 | 90 | 90 | 90 |
| β (°) | 102.757(3) | 90 | 90 | 90 |
| γ (°) | 90 | 90 | 90 | 90 |
| Z | 2 | 4 | 4 | 2 |
| V/Å3 | 358.457(16) | 719.30(16) | 736.69(6) | 412.41(9) |
| D calc/g cm−3 | 2.004 | 1.608 | 2.786 | 3.252 |
| μ/mm−1 | 11.470 | 1.172 | 17.029 | 68.746 |
| Θ range (°) | 6.72–76.09 | 6.44–75.41 | 6.48–75.48 | 6.37–76.18 |
| T/K | 293 (2) | 293 (2) | 293 (2) | 293 (2) |
| Radiation wavelength | 1.54179 (Cu Kα) | 1.54179 (Cu Kα) | 1.54179 (Cu Kα) | 1.54179 (Cu Kα) |
| Diffractometer type | Xcalibur Nova | Xcalibur Nova | Xcalibur Nova | Xcalibur Nova |
| Range of h, k, l | −4 < h < 4; −14 < k < 11; −10 < l < 10 | −7 < h < 10; −12 < k < 15; −8 < l < 8 | −9 < h < 10; −13 < k < 15; −4 < l < 9 | −10 < h < 8; −15 < k < 16; −4 < l < 4 |
| Reflections collected | 2524 | 772 | 850 | 1318 |
| Independent reflections | 737 | 386 | 407 | 274 |
| Observed reflections (I ≥ 2σ) | 700 | 324 | 333 | 253 |
| Absorption correction | Multi-scan | Multi-scan | Multi-scan | Multi-scan |
| R int | 0.0273 | 0.0225 | 0.0213 | 0.0972 |
| R(F) | 0.0294 | 0.0569 | 0.0433 | 0.0550 |
| R w(F2) | 0.0845 | 0.1873 | 0.1216 | 0.1534 |
| Goodness of fit | 1.119 | 1.122 | 1.130 | 1.102 |
| H atom treatment | Free | None | Free | None |
| No. of parameters | 59 | 47 | 40 | 25 |
| No. of restraints | 0 | 3 | 0 | 0 |
| Δρmax, Δρmin (eÅ−3) | 0.352, −0.274 | 0.338, −0.496 | 0.789, −1.057 | 2.168, −1.912 |
Acknowledgements
This work was supported by Ministry of Science, Education and Sports of Croatia (grants nos. 098-1191344-2943 and 098-0982915-2942), Slovenian Research agency (program group P1-0012) and Slovenian–Croatian bilateral collaboration (grant for 2012/2013).References
- C. A. Hunter and J. K. M. Sanders, J. Am. Chem. Soc., 1990, 112, 5525–5534 CrossRef CAS.
- C. A. Hunter, Angew. Chem., Int. Ed. Engl., 1993, 32, 1584–1586 CrossRef.
- C. A. Hunter, Chem. Soc. Rev., 1994, 23, 101–109 RSC.
- M. L. Głowka, D. Martynowski and K. Kozłovska, J. Mol. Struct., 1999, 474, 81–89 CrossRef.
- C. Janiak, J. Chem. Soc., Dalton Trans., 2000, 3885–3896 RSC.
- J. W. Steed, J. L. Atwood, Supramolecular Chemistry, J. Wiley & Sons, Chichester, U.K., 2nd edn, 2009 Search PubMed.
- C. A. Hunter, K. R. Lawson, J. Perkins and C. J. Urch, J. Chem. Soc., Perkin Trans., 2001, 2, 651–659 Search PubMed.
- E. A. Mayer, R. K. Castellano and F. Diedrich, Angew. Chem., Int. Ed., 2003, 42, 1210–1250 CrossRef.
- C. R. Martinez and B. L. Iverson, Chem. Sci., 2012, 3, 2191–2201 RSC.
- K. Molčanov, B. Kojić-Prodić and A. Meden, CrystEngComm, 2009, 11, 1407–1415 RSC.
- K. Molčanov, B. Kojić-Prodić and A. Meden, Croat. Chim. Acta, 2009, 82, 387–396 Search PubMed.
- K. Molčanov, I. Sabljić and B. Kojić-Prodić, CrystEngComm, 2011, 13, 4211–4217 RSC.
- K. Molčanov and B. Kojić-Prodić, Acta Crystallogr., Sect. B: Struct. Sci., 2012, 68, 57–65 Search PubMed.
- S. Hünig, Pure Appl. Chem., 1990, 62, 395–406 CrossRef.
- M. O. Sinnokrot and C. D. Sherrill, J. Phys. Chem. A, 2006, 110, 10656–10668 CrossRef CAS.
- A. N. Sokolov, T. Friščić and L. R. MacGillivray, J. Am. Chem. Soc., 2006, 128, 2806–2807 CrossRef CAS.
- M. Bendikov, F. Wudl and D. F. Perepichka, Chem. Rev., 2004, 104, 4891–4945 CrossRef CAS.
- J. Xiang, C. Chang, M. Li, L. Yuan and J. Sun, Cryst. Growth Des., 2008, 8, 280–282 CAS.
- K. Molčanov and B. Kojić-Prodić, CrystEngComm, 2010, 12, 925–939 RSC.
- L. J. Farrugia, J. Appl. Crystallogr., 1997, 30, 565 CrossRef CAS.
- CrysAlis PRO, Oxford Diffraction Ltd, U.K., 2007 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., 2008, A64, 112–122 CrossRef CAS.
- A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7–13 CrossRef CAS.
- C. F. Macrae, P. R. Edgington, P. McCabe, E. Pidcock, G. P. Shields, R. Taylor, M. Towler and J. van de Streek, J. Appl. Crystallogr., 2006, 39, 453–457 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr.,J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.2, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- (a) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–68 CrossRef CAS; (b) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- http://www.tcm.phy.cam.ac.uk//∼mdt26/crystal.html, last time accessed on August 22, 2012.
- M. Towler, An introductory guide to Gaussian basis sets in solid-state electronic structure calculations, European Summer School ′′Ab initio modelling in solid-state chemistry′′, Torino, September 2000; available at: http://www.tcm.phy.cam.ac.uk/∼mdt26/basis_sets/basis_sets_2000.ps, last time accessed on August 22, 2012 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- M. Head-Gordon, J. A. Pople and M. J. Frisch, Chem. Phys. Lett., 1988, 153, 503–506 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details on redetermination of Li2DHQ·2H2O, ORTEP drawings of DHQ2− anions and cation coordination spheres; parameters of DFT-optimised unit cells and computational details. CCDC 889125–889129. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c2ce26119g |
| This journal is © The Royal Society of Chemistry 2013 |
