Supramolecular architecture of molecular crystals possessing shearing mechanical properties: columns versus layers

Abstract

The supramolecular architectures of crystals of substituted benzenes possessing shearing mechanical properties have been analyzed from the viewpoint of energy of intermolecular interactions. It is demonstrated that suggested earlier layered structure of these crystals do not correspond to the character of intermolecular interactions. Analysis of the topology of intermolecular interactions indicates that the crystals have a columnar supramolecular architecture with weak interactions between the columns. The presence of shearing mechanical properties is caused by localization of intercolumnar interactions within some layers and a relatively small (less than 12 kcal mol⁻¹) barrier of shift of molecules within this layer.

---

Introduction

Usually molecular crystals are quite brittle solids which are destroyed under any mechanical stress. However, during the last decade, the existence of crystals for which mechanical stress in some specific directions results in shearing or bending deformations without destruction of the crystal was demonstrated.¹ Presence of such unusual mechanical properties is caused by the specific supramolecular architecture of these crystals. In particular, for the crystals with shearing deformations, it was suggested that the formation of strongly bonded layers is responsible for the possibility of a smooth shift of one part of the crystal with respect to another part due to weak interactions between the layers, in a similar way to graphite. Such crystal structure is common for symmetrically substituted halogen derivatives of benzene^2,3 where layers are formed due to intermolecular halogen bonds while only stacking interactions are observed between layers. Such interactions have relatively weak dependence on the shift of aromatic rings with respect to each other, providing quite a smooth shift of layers. Thus, it was concluded¹ that the structural model of the molecular crystals possessing shearing mechanical properties includes strongly bonded flat layers with quite smooth interactions between them. Validity of this model was confirmed by the investigation of the mechanical properties of polymorphs of 6-chloro-2,4-dinitroaniline.⁴ It was found that only polymorphs with layered structures meeting these requirements may undergo shearing and bending mechanical deformations.

However, it should be noted that conclusions about the relationship between the character of intermolecular interactions and mechanical properties of these crystals were made on the basis of a traditional geometric approach to the detection of non-bonded contacts. Recently,⁵ it was demonstrated that such an approach may lead to significant errors in the determination of a basic structural motif (BSM) of crystal packing especially in the case of an absence of strong intermolecular interactions in the crystal phase. For example, in the crystals of bicyclic aziridines⁶ it was found that the energy of interaction of the basic molecule (BM) located in the asymmetric part of the unit cell (reference molecule) with some neighboring molecules belonging to the first coordination sphere of the BM is higher in the absence of any shortened intermolecular contacts than for the dimers bonded by weak C–H⋯N or similar hydrogen bonds.

Influence of halogen bonds on the crystal structure strongly depends on the strength of such interactions.^7–9 Usually halogen bonds represent rather weak intermolecular interactions. Investigation of the crystal structure of halogen substituted trityl alcohols clearly demonstrated¹⁰ that the energy of intermolecular interactions in dimers bonded by the O–H⋯π hydrogen bond is more than twice that for halogen bonded dimers. An even more significant difference was found for the crystals with stacking interactions. Analysis of the supramolecular architecture of the crystal of 2-(4-iodophenyl)-1,10-phenanthroline demonstrated¹¹ that halogen bonds do not play a primary role in organization of the crystal structure. The crystal consists of stacked columns of molecules while the interactions between the columns are almost isotropic despite the presence of the N⋯I halogen bonds. Recently, preference of stacking interactions over halogen bonds was experimentally detected for solutions.¹² Even in the case of strong halogen bonds, the energy of these interactions becomes only comparable with the energy of stacking interactions.¹³

Based on these data it is difficult to believe the conclusion about strongly bonded layers formed by halogen bonds in the crystals of halogenated benzenes undergoing shearing mechanical deformations. Taking into account the presence of the aromatic ring in these molecules it is possible to suppose that the basic structural motif of these crystals should be based on stacking between substituted benzene rings as the strongest interactions. Therefore we analysed the supramolecular architecture of the crystals of seven benzene derivatives based on the energies of intermolecular interactions instead of interatomic distances. Results of the calculations clearly demonstrate that all crystals have a columnar structure. The presence of shearing mechanical properties is not caused by the layered structure of the crystal but the character of interactions between neighboring columns which are located near planes of molecules belonging to different columns.

Methodology

Crystal structures of all compounds under consideration (Scheme 1, Table 1) were extracted from the Cambridge Crystal Structure Database¹⁴ (release 2011).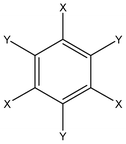

Scheme 1 General chemical formula of substituted benzenes under consideration.

Table 1 Numbering, substituents and CCDC refcodes of molecules under consideration

Structure	X	Y	Refcode	Ref.
1	Br	CH3	PUZHIB	15
2	Cl	CH3	ZEPDAZ	16
3	I	Br	UCENOG01	2
4	I	Cl	UCEPAU	2
5	I	CH3	SAQZOY	17
6	Cl	Cl	HCLBNZ12	2
7	Cl	CN	BAFJOH	18

---

The molecular structures of the molecules under consideration have been taken from X-ray diffraction data except the lengths of the C–H bonds. It is well known that lengths of the X–H bonds obtained from X-ray diffraction data are systematically shorter as compared to the real values.¹⁹ Therefore, before calculations of intermolecular interaction energies the lengths of the C–H bonds were established as 1.089 Å.

The first coordination sphere of the basic molecule located in the asymmetric part of the unit cell, had been determined using the “Molecular Shell Calculation” option implemented in the Mercury program²⁰ (version 2.4.6). This option makes it possible to find all molecules for which the distance between the atoms of the basic molecule and its symmetric equivalents are shorter than the van der Waals radii sum plus 1 Å at least for one pair of atoms.

In order to calculate the energy of interaction between the molecules in each dimer formed by the basic molecule, the positions of all atoms were taken from X-ray diffraction data and positions of the hydrogen atoms were normalized as mentioned above. Energy of the interaction between the molecules in each dimer was obtained by single point calculations as the difference between the energy of a dimer and the energy of monomers and it has been corrected for basis set superposition error using Boys–Bernardi counterpoise procedure.²¹ The total energy of the interactions of the basic molecule with its environment in the crystal was determined as the sum of pairwise interactions with each molecule of the first coordination sphere. All calculations were performed within Density Functional Theory²² with BLYP functional^23,24 augmented by empirical dispersion correction²⁵ and def2-TZVP basis set using ORCA program.²⁶ It was demonstrated that BLYP-D method may be used for description of dispersion interactions between molecules.²⁷ Complete results of the calculation are listed in Tables S1–S7, ESI.†

Graphic representation of the topology of intermolecular interactions in the crystals was done using energy-vector diagrams (or “hedgehogs”) of intermolecular interactions.²⁸ According to this approach the interaction between each pair of the molecules corresponds to two vectors originating from the geometric center of one molecule and oriented towards the geometric center of the second molecule. The length of these vectors is proportional to the energy of intermolecular interactions between two molecules. In the case of the strongest interaction, these two vectors form straight lines connecting geometrical centers of the molecules forming the most strongly bonded dimer. The length of the vectors of intermolecular interactions was calculated using eqn (1):

L_i = (R_iE_i)/2E_str (1)

where L_i is length of the vector corresponding to the interaction of the basic molecule with the molecule i, R_i is a distance between geometrical centers of interacting molecules, E_i is an energy of intermolecular interactions between these molecules and E_str is an energy of the strongest interaction of basic molecule with the molecule belonging to its first coordination sphere.

The degree of dimerization (DD) describes inhomogeneity of intermolecular interactions within the column. It is calculated using the following equation:

DD = 100 × (E₂/E₁ − 1) (2)

where E₁ and E₂ are the energies of interaction of the basic molecule with two neighbours within the column (E₂ > E₁).

Corrugation of columns may be characterized by angle between the energy vectors directed from the geometrical center of the basic molecule towards geometrical centers of two neighboring molecules within the column (corrugation angle φ). Degree of corrugation (DC) may be described using following equation:

DC = 100 × (1 − φ/180°) (3)

Results and discussion

Results from the calculations clearly demonstrate that the most strongly bonded dimers in all structures under consideration are formed due to stacking interactions (Table 2). The energy of the interaction between the molecules in such dimers is more than 4–5 times higher when compared to other dimers. Moreover, halogen bonded dimers have an interaction energy smaller than four of the most strongly bonded dimers in all structures except 5 (Table 2). This indicates that the halogen–halogen interactions play a minor role in the formation of the basic structural motif of crystals. It should be noted that there is an increase in the energy of stacking interactions with an increase in size and atomic number of halogen (Tables 2 and 3).

Table 2 Symmetry codes, energy of interaction of basic molecule with neighboring molecule (E_int), intermolecular contact and its characteristics for 4 molecules belonging to first coordination sphere of basic molecule with the highest values of intermolecular interaction energy in crystals under consideration (for full list of dimers see Tables S1–S7, ESI†). Molecules belonging to column as basic structural motifs are highlighted in bold

Str.	Symmetry code	E int, kcal mol^−1	Contact	Dist.,^a Å	Angle,^b °
a Distance between planes of benzene rings for stacking interactions and between interacting atoms for halogen bonds. b Angle between planes of benzene rings for stacking interactions and the C–X⋯Y angle for halogen bonds.
1	1 − x, −y, −z	−14.28	Stacking	3.60	0
			C–H⋯Cl	2.99	171.0
	−x, −y, −z	−12.53	Stacking	3.61	0
	1 − x, −y, −1 − z	−2.93
	−x, 1 − y, −z	−2.39
2	1 − x, 2 − y, −z	−15.35	Stacking	3.61	0
	−x, 2 − y, −z	−14.96	Stacking	3.62	0
	−x, 2 − y, −1 − z	−2.85
	1 − x, 3 − y, 1 − z	−2.84
3	−x, −y − z	−16.02	Stacking	3.76	0
	1 − x, −y, −z	−15.56	Stacking	3.80	0
	1 − x, −y, −1 − z	−3.24
	−x, −1 − y, 1 − z	−3.07
4	2 − x, −y, 1 − z	−14.80	Stacking	3.58	0
	1 − x, −y, 1 − z	−14.43	Stacking	3.60	0
	1 − x, −y, 2 − z	−2.89
	2 − x, 1 − y, −z	−2.82
5	2 − x, −y, 1 − z	−16.31	Stacking	3.66	0
	1 − x, −y, 1 − z	−16.08	Stacking	3.66	0
	x, 1 + y, −1 + z	−4.70	C–I⋯I	3.78	119.7
			C–Br⋯I	3.80	125.8
	x, −1 + y, 1 + z	−4.68	C–I⋯Br	3.80	126.4
			C–I⋯I	3.80	176.6
6	x, −1 + y, z	−12.18	Stacking	3.45	0
	x, 1 + y, z	−12.18	Stacking	3.45	0
	−1 + x, 1 + y, z	−1.75
	1 + x, −1 + y, z	−1.75
7	−0.5 + x, 0.5 − y, 1 − z	−5.61	C–N⋯π(C3)	3.14	141.3
	0.5 + x, 0.5 − y, 1 − z	−5.61	C–N⋯π(C3)	3.14	141.3
	x, y, −1 + z	−5.14
	x, y, 1 + z	−5.14

---

Table 3 Number of molecules belonging to the first coordination sphere of basic molecule (FCS), total energy (kcal mol⁻¹) of interactions of basic molecule with its first coordination sphere (E_tot), with molecules belonging to strongly bonded column (E_BSM), average value for interactions with molecules belonging to neighbouring column (E_inter) and ratio between energies of interactions of basic molecule with molecules belonging to the same and neighbouring basic structural motif (ER = E_BSM/E_inter)

Structure	FCS	E tot	E BSM	E inter	ER
1	13	−47.66	−26.81	−3.48	7.7
2	14	−52.98	−30.31	−3.78	8.0
3	14	−58.51	−31.58	−4.49	7.0
4	14	−54.76	−29.23	−4.25	6.9
5	14	−66.90	−32.38	−5.75	5.6
6	14	−42.51	−24.36	−3.02	8.1
7	14	−56.26	−18.30	−6.33	2.9

---

It should be noted that the crystal structures 1–5 have the same architecture. Domination of stacking interactions results in the formation of stacked columns along the [1 0 0] crystallographic axis. The energy of interaction of basic molecules with neighbors within the column is 5–8 times higher than the average energy of interactions to molecules belonging to surrounding columns (Table 3). Columns are packed in a more or less isotropic way in all crystals in terms of energies of intermolecular interactions. This means that it is impossible to recognize any layer formed by considerably stronger bonded columns (Fig. 1). Thus, all crystals under consideration have clear columnar supramolecular architectures instead of layered ones as was suggested earlier.¹

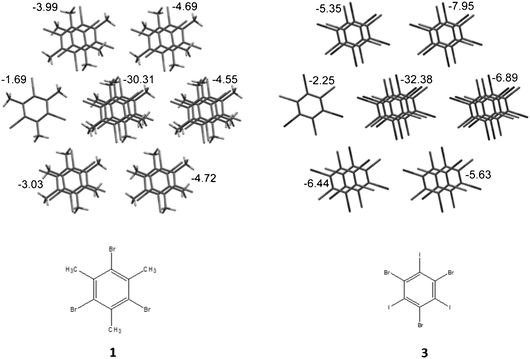Fig. 1 Packing of stacked columns in crystals 1 and 3. Numbers near columns indicate the energy of interaction of the basic molecule with neighbors within the column (for central column) and with molecules belonging to each neighboring column.

The results of the calculations demonstrate that the energy of the interaction of BM with two neighbors within the column are not equal. This indicates some inhomogeneity of columns from an energetic viewpoint. In the case of considerable differences in energy of interaction of BM with two neighbors within the column it is possible to say about columnar packing of stacked dimers as it was found recently for crystal structure of substituted quinoline.¹¹ Such a situation may be characterized by values of degree of dimerization within the column (eqn (2)). Results of calculation demonstrated (Tables 2 and 4) that all crystal structures under consideration except 1 are characterized by almost zero degrees of dimerization of columns. This value does not exceed 3%. Only in the case of structure 1 is the dimerization degree more than 10%. However, even in this case it is only possible to comment on the trend of dimerization but not about the real presence of strongly bonded dimers within columns. It is likely that low degrees of dimerization of columns are a prerequisite for unusual mechanical properties of these crystals.

Table 4 Degree of dimerization (DD) within strongly bonded columns, angle between energy vectors directed from basic molecules towards neighbouring molecules within the column (φ) and degree of corrugation of columns (DC)

Structure	DD, %	φ, °	DC, %
1	14.0	178.0	1.0
2	2.6	154.5	14.2
3	3.0	150.8	16.2
4	2.6	150.0	16.7
5	1.4	151.4	15.9
6	0.0	180.0	0.0
7	0.0	69.7	61.3

---

More information about the supramolecular architecture of crystals under consideration may be obtained from analysis of packing of energy-vector diagrams (EVD) of molecules or hedgehogs of intermolecular interactions. In all cases, packing of hedgehogs clearly demonstrates the columnar structure of crystals with relatively weak interactions between columns (Fig. 2). These columns are slightly corrugated except structure 2 (Fig. 2).

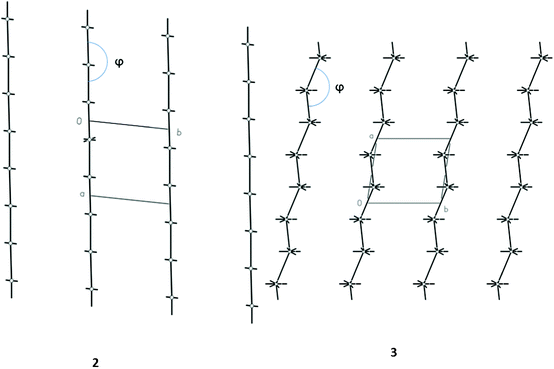Fig. 2 Typical packing of hedgehogs of intermolecular interactions in crystals 2 and 3 illustrating straight and slightly corrugated columns in the crystals.

Analysis of packing of EVD makes it possible to suggest some quantitative characteristics of packing. In particular this concerns corrugation of columns. Degree of corrugation may be described by the angle between energy vectors directed from the geometrical center of the basic molecule towards the geometrical centers of two neighboring molecules within the column (angle φ, Fig. 2) or by deviation of this angle from linearity (see DC values in Table 4). In all structures the value of the φ angle is higher than 150° and the degree of corrugation is less than 17%. Therefore, it is possible to conclude that strongly bonded columns in the crystals under consideration have a rod-like or almost rod-like shape. This creates suitable conditions for tight packing of columns.

Another interesting feature of the crystals under consideration is directionality of intermolecular interactions between neighboring columns. The hedgehogs of intermolecular interactions demonstrate that the interactions between the basic molecule and the molecules of neighboring columns are localized mainly near the equatorial plane of the angle formed by the longest energy vectors (Fig. 3). This corresponds to specific packing of the columns where the molecules of neighboring columns form layers which are parallel to (1 0 0) the crystallographic plane as it was described earlier.^1–4 In other words the geometrical centers of the basic molecule and its the closest neighbors belonging to six neighboring columns are located within the same plane. Such arrangement of strongly bonded columns is caused by directionality of weak halogen–halogen interactions which are maximal at the co-planar arrangement of the molecules. However, the specific feature of crystals of trihalogenbenzenes is the absence of considerable interactions between the basic molecule and the molecules from neighboring columns located above and under symmetrical equivalents of BM. For example, columnar structures were also found for crystals of some fused hydrocarbons.²³ However, considerable energy vectors directed towards all three closest molecules of each neighboring column were observed. This leads to the shift of one column with respect to another column. It is probably that such features of the crystals under consideration are caused by a weakness of intercolumnar interactions. However, this creates favorable conditions for the shift of one layer with respect to another due to the rather smooth character of interlayer interactions.

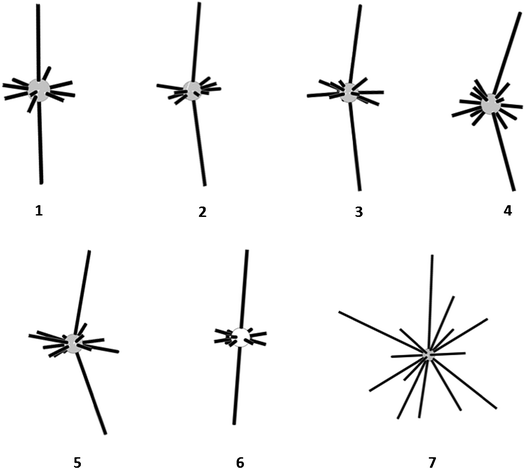Fig. 3 Hedgehogs of intermolecular interactions in crystals of halogenated benzenes

In order to estimate the energetics of mechanical shearing in crystals under consideration the energy of shift of one molecule with respect to the fragment of layer formed by the basic molecule and nine molecules from neighboring columns (Fig. 4) of crystal 2 was calculated. The molecule was shifted in four directions which are parallel to the (1 0 0) crystallographic plane. The energy of system was obtained by single point calculations by BLYP-D3/def2-TZVP method for geometries taken from experiment and eight shifted locations of molecule with respect to layer, with shift being equal to distance between equivalent positions of molecule divided by eight. The results of the calculations demonstrate that the energy barrier for the shift of the molecule from one crystallographic position to another does not exceed 11 kcal mol⁻¹ (Fig. S1, ESI†). Moreover, the change of energy during movement molecules along the [0 0 1] and [0 1 1] crystallographic axes is about 6 kcal mol⁻¹ only. This indicates that shearing deformation of crystals really does not require significant amounts of energy at correct directionality of mechanical pressure. It should be noted that changes of energy do not include relaxation of geometry of molecule during shift which may be quite considerable, for example, due to the rotation of methyl groups. Therefore these values may be considered only as an upper limit for energy of shift. Moreover accounting of geometry relaxation may lead to equalization of energy changes during molecule shift towards different directions which are parallel to the layer plane.

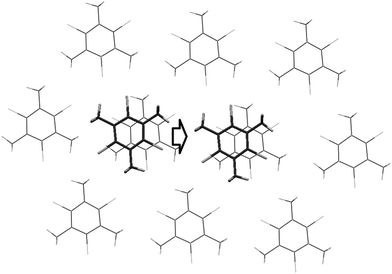Fig. 4 Model system for estimation of energy change during shift of molecule with respect to layer.

Thus, it is possible to suggest that specific organization of crystal possessing shearing mechanical properties should include the presence of homogeneous stacked columns with a relatively small degree of corrugation and near isotropic packing of columns in such a way that intercolumnar interactions are rather weak and localized mainly within one plane leading to a layered arrangement of molecules belonging to neighboring columns. It is possible to assume that such a way of packing of columns results from the presence of halogens in positions 1, 3 and 5 of the benzene ring and other substituents which are able to form halogen or hydrogen bonds in positions 2, 4 and 6. In order check this assumption we analyzed the crystal structure of hexachlorobenzene 6 and 1,3,5-chloro-2,4,6-cyanobenzene 7 containing the same pattern of halogen substitution but other different substituents. In both cases it is possible to expect formation of the Cl⋯Cl or N⋯Cl halogen bonds stabilize the same type of column packing.

The results of the calculations demonstrate that crystal 6 also has a columnar structure (Tables 2–4, Fig. 5) with perfectly homogeneous and straight columns. However packing of these columns differ from other trihalobenzenes considered above. Two columns located within the (0 0 1) crystallographic plane are obtained by translation of columns containing the BM by simple translation along the [1 0 0] direction. The other four neighboring columns are shifted with respect to the column containing the BM along the [0 1 0] crystallographic axis (Fig. 5). Therefore, the basic molecule has the two closest neighboring molecules belonging to each of these columns (see dimers 7–14 in Table S6, ESI†) with the same distance from their geometrical centers to the geometrical center of BM. Thus, the geometrical centers of the basic molecule and its 10 closest neighbors belonging to six neighboring columns do not lie within one plane in contrary to the crystal structures 1–5.

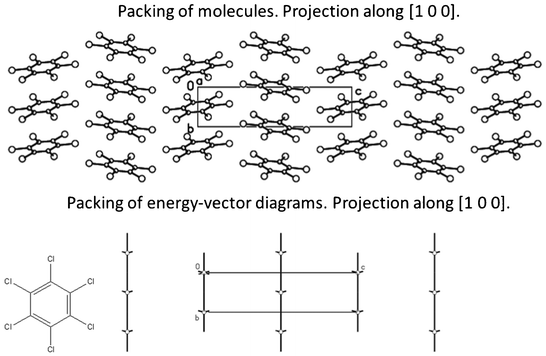Fig. 5 Packing of stacked columns in crystal 6 displayed as packing of molecules and energy-vector diagrams (hedgehogs of intermolecular interactions).

Based on these data it is possible to suppose that substituents in positions 2, 4 and 6 of the benzene ring must differ from the halogen atom in positions 1, 3 and 5. Otherwise columns are packed with a shift along the axis of the columns.

However, analysis of the supramolecular architecture of the crystal of 1,3,5-trichloro-2,4,6-tricyanobenzene 7 (Fig. 6) shows that the nature and characteristics of substituents also play a very important role. In general it is possible to expect that the nitrogen atom of the cyano group may form halogen bonds with the chlorine atoms of neighboring molecules. The results of calculations demonstrate that the most strongly bonded dimer is stabilized by electrostatic interactions between the negatively charged nitrogen atom of one molecule and the positively charged carbon atom of the benzene ring bonded to the cyano group of the other molecule (Table 2). Such character of interactions between molecules results in significant inclination of benzene rings of two molecules with the angle between their mean plane being 54°. This leads to the formation of strongly corrugated columns with a corrugation angle less than 70° (Table 4). These columns are perfectly homogeneous (degree of dimerization is zero) but the energy of interactions of the basic molecule with neighbors within the column are only slightly higher than the highest energy of interaction with molecules belonging to neighboring columns (Tables 2 and 3). Therefore it is possible to conclude that the crystal of 7 also has a columnar structure but it is significantly less pronounced with completely different column character when compared to other trihalobenzenes mentioned above.

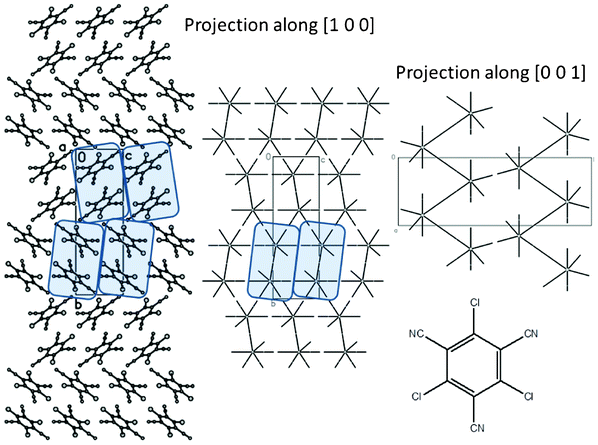Fig. 6 Packing of molecules and hedgehogs of intermolecular interactions in crystal of 7. Corrugated columns are highlighted.

The most probable reason of such big differences in the crystal structure of 7 and other trihalobenzenes is different lengths of bonds to substituents. The distance between the carbon atom of the benzene ring and the nitrogen atom of the cyano group (2.55 Å) is significantly longer than even the longest C–I bond (2.10 Å). This creates steric clashes for the formation dense enough crystal packing with planar location of molecules of neighboring columns leading also to deformation of columns themselves.

Conclusions

Analysis of the crystal structure of a set of substituted 1,3,5-trihalobenzenes based on the topology of intermolecular interactions indicates that all of them have similar supramolecular architectures. However, the basic structural motif of these crystals is not a halogen bonded layer as it was suggested before^1–4 but a strongly bonded stacked column. The supramolecular architecture of all crystals has some general features namely i) rod-like highly homogeneous columns as basic structural motifs; ii) almost completely isotropic packing of columns; iii) the location of the strongest intercolumnar interactions within one plane leads to planar arrangement of molecules from neighboring columns. These crystal structures can be considered to belong to one structural type of molecular crystal which may be called trihalobenzene types of crystal structure.

Typical features of the supramolecular architecture of such crystals creates suitable conditions for shearing mechanical deformations of crystals. The presence of strongly bonded rod-like columns in an orthogonal direction with respect to mechanical stress prevents molecules from out-of-plane moves during shearing deformation. Isotropic packing of columns provides uniform distribution of mechanical stress among neighboring molecules within the layer. Absence of considerable inclined intercolumnar interactions as well as the well-known flat character of the potential energy surface for stacked dimers makes interactions between layers quite smooth. This leads to relatively small energy barrier values for the shift of one molecule with respect to the layer which is less than 12 kcal mol⁻¹. Thus, analysis of the supramolecular architecture of molecular crystals based on the topology of intermolecular interactions makes it possible to classify crystal structures as belonging to the same structural type of molecular crystals and to predict mechanical properties of crystals.

However, analysis of crystal structure of hexachlorobenzene and 1,3,5-trichloro-2,4,6-tricyanobenzene indicates a strong requirement also to characterize substituents. The presence of the same substituents in all positions of the benzene ring or considerable differences in the geometry of substituents (difference in C–Halogen bond and C⋯N distance for cyano group) results in violation of the topology of intermolecular interactions. This leads to the formation of crystal structures which do not meet the structural criteria for crystals with shearing mechanical properties. However, these data create a background for the purposeful design of crystals with prescribed properties.

References

1. C. M. Reddy, G. R. Krishna and S. Ghosh, CrystEngComm, 2010, 12, 2296.
2. C. M. Reddy, M. T. Kirchner, R. C. Gundarakaram, K. A. Padmanabhan and G. R. Desiraju, Chem.–Eur. J., 2006, 12, 2222.
3. T. T. T. Bui, S. Dahaoui, C. Lecomte, G. R. Desiraju and E. Espinosa, Angew. Chem., Int. Ed., 2009, 48, 3838.
4. C. M. Reddy, S. Basavoju and G. R. Desiraju, Chem. Commun., 2005, 2439.
5. I. S. Konovalova, S. V. Shishkina, B. V. Paponov and O. V. Shishkin, CrystEngComm, 2010, 12, 909.
6. V. V. Dyakonenko, A. V. Maleev, A. I. Zbruyev, V. A. Chebanov, S. M. Desenko and O. V. Shishkin, CrystEngComm, 2010, 12, 1816.
7. G. M. Espallargas, F. Zordan, L. A. Marin, H. Adams, K. Shankland, J. van de Streek and L. Brammer, Chem.–Eur. J., 2009, 15, 7554.
8. R. J. Santos-Contreras, F. J. Martınez-Martınez, N. A. Mancilla-Margalli, A. L. Peraza-Campos, L. M. Morın-Sanchez, E. V. Garcıa-Baez and I. I. Padilla-Martınez, CrystEngComm, 2009, 11, 1451.
9. D. Henschel, T. Hamann, O. Moers, P. G. Jones and A. Blaschette, Z. Naturforsch., 2005, 60, 645.
10. D. Schollmeyer, O. V. Shishkin, T. Rühl and M. O. Vysotsky, CrystEngComm, 2008, 10, 715.
11. O. V. Shishkin, V. V. Dyakonenko, A. V. Maleev, D. Schollmeyer and M. O. Vysotsky, CrystEngComm, 2011, 13, 800.
12. Y. Zhang, B. Ji, A. Tian and W. Wang, J. Chem. Phys., 2012, 136, 141101.
13. H. Li, Y. Lu, Y. Liu, X. Zhu, H. Liu and W. Zhu, Phys. Chem. Chem. Phys., 2012, 14, 9948.
14. F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380.
15. E. Bosch and C. L. Barnes, Cryst. Growth Des., 2002, 2, 299.
16. M. Tazi, J. Meinnel, M. Sanquer, N. Nusimovici, F. Tonnard and R. Carrie, Acta Crystallogr., Sect. B: Struct. Sci., 1995, 51, 838.
17. A. Boudjada, O. Hernandez, J. Meinnel, M. Mani and W. Paulus, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2001, 57, 1106.
18. D. Britton, Cryst. Struct. Commun., 1981, 10, 106.
19. P. Coppens, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 1638.
20. C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, L. Rodriguez-Monge, R. Taylor, J. van de Streek and P. A. Wood, J. Appl. Crystallogr., 2008, 41, 466.
21. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553.
22. R. G. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, Oxford University Press, New York, 1989.
23. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098.
24. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785.
25. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
26. F. Neese, ORCA 2.8.0, Universitaet Bonn, Germany, 2010.
27. W. Hujo and S. Grimme, J. Chem. Theory Comput., 2011, 7, 3866.
28. O. V. Shishkin, V. V. Dyakonenko and A. V. Maleev, CrystEngComm, 2012, 14, 1795.

---

Footnote

† Electronic supplementary information (ESI) available: Values of pairwise interaction energies and parameters for visualization of intermolecular interactions are listed in Tables S1–S7. See DOI: 10.1039/c2ce26126j

---