A quantum-mechanical study of the adsorption of prototype dye molecules on rutile-TiO₂(110): a comparison between catechol and isonicotinic acid

Abstract

In this work we present a theoretical investigation of the attachment of catechol and isonicotinic acid to the rutile-TiO₂(110) surface. These molecules can be considered as prototypical dyes for use in Grätzel type dye sensitised solar cells (DSCs) and are often employed as anchoring groups in both organic and organo-metallic sensitisers of TiO₂. Our study focuses on determining the lowest energy adsorption mode and discussing the electronic properties of the resultant hybrid interface by means of density functional theory (DFT) calculations using the hybrid exchange (B3LYP) functional. We find that both molecules adsorb dissociatively at the TiO₂ surface giving a type II (staggered) heterojunction. Compared to isonicotinic acid, catechol, due to the greater hybridisation of its molecular orbitals with the states of the substrate, is seen to enhance performance when employed as an anchoring group in dye sensitised solar cells.

---

I. Introduction

Nanocrystalline dye-sensitised solar cells (DSCs), designed originally by O'Regan and M. Grätzel,^1,2 have attracted great interest because of their high efficiency and thus potential application as cost-effective alternatives to present day silicon-based pn-junction photovoltaic devices. In conventional photovoltaic systems, the semiconductor assumes the tasks of both light absorption and charge-carrier transport, whereas in DSCs the two tasks are separated: a dye molecule attached to the surface of a wide band gap semiconductor (typically TiO₂) absorbs light, while the semiconductor is responsible for the charge-carrier transport. Charge separation occurs at the interface between the dye and the semiconductor by photo-induced electron injection from the dye to titanium dioxide (TiO₂). The dye is necessary, because the two commonly used TiO₂ phases (rutile and anatase) absorb only a small fraction of the solar spectrum; the optical band gap is 3.03 eV^3,4 for the rutile phase and 3.18 eV^3,5 for the anatase phase. To obtain large photocurrents, DSCs are realised by employing thin layers of highly porous TiO₂, whose extremely high surface area facilitates high levels of dye loading and thus photoelectron generation. The structure is then immersed in an electrolyte solution containing a redox couple, such as the triiodide–iodide system, which, after electron injection, restores the original state of the dye by electron donation.

For an effective sensitisation of the substrate it is important that the dye–oxide heterostructure generates a so-called type II (or staggered) heterojunction or, in other words, that the HOMO (highest occupied molecular orbital) of the dye is in the semiconductor gap and the LUMO (lowest unoccupied molecular orbital) is above the conduction band minimum. In this arrangement the electron–hole separation is achieved through the hybrid interface either by direct electron photoinjection from the HOMO of the dye molecule to the conduction band of the oxide or, indirectly, by first excitation of an electron from the HOMO to the LUMO of the dye followed by electron injection into the semiconductor conduction band.

Recently small molecules, such as catechol, have attracted considerable attention in the realisation of DSCs.^6–11 Catechol is used as an anchoring group for organic and organometallic dyes because of its efficient adsorption onto TiO₂via formation of a strong adsorbate–substrate complex.^6,7 Catechol has also been directly employed as a sensitiser for DSC since the TiO₂–catechol interface realises a type II hybrid junction.^8–12 In the UV-vis absorption spectrum for catechol adsorption onto TiO₂ anatase nanoparticles,¹² an absorption peak at ∼2.88 eV (∼430 nm) is observed and is interpreted as evidence of the HOMO level of the molecule in the TiO₂ band gap. In the case of catechol adsorbed at the rutile (110) surface absorption occurs at 2.4 eV as deduced from UV photoemission and inverse photoemission spectroscopy (UPS and IPS) measurements under ultra-high vacuum.¹⁰ Another prototypical dye often used as an anchoring group in metallorganic-dyes (e.g. N₃)¹³ is isonicotinic acid; this presents similar properties to that of the catechol molecule in terms of anchoring/coupling to TiO₂ surfaces.

Ab initio simulations have been employed to unravel the structural and electronic properties of several organic/inorganic interfaces in the case of various inorganic substrates^14–16 and several theoretical methods have been exploited to investigate the electronic properties of the catechol–TiO₂ heterojunction. Density functional theory (DFT) and time dependent DFT (TDDFT) methods have been applied to study the interface structure and excited states for various models of the surfaces including a TiO₂-cluster^8,11 and a single Ti atom;^9,10 periodic DFT calculations (based on generalised gradient approximation – GGA – functionals for exchange and correlation) have been used for studying the anatase-TiO₂(101)¹⁷ and rutile-TiO₂(110) surfaces¹⁸ functionalised with catechol molecules. In order to classify the heterojunction, a method, which computes accurate adsorption energies and a reasonable description of the electronic structure and optical absorption spectrum, is required. Previous periodic DFT calculations, based on GGA functionals, provide a poor representation of the bulk band gap and it is unclear how well surface energy level alignments are described. Cluster models of the surface converge slowly with respect to the cluster size and so great care is required in drawing conclusions from calculations on small clusters. Concerning the isonicotinic acid–TiO₂ heterojunction, there have been two previous theoretical investigations using hybrid-exchange DFT; upon adsorption of isonicotinic acid onto anatase TiO₂¹⁹ and onto rutile TiO₂,²⁰ the HOMO level was found to be in the energy gap while the LUMO level falls in the conduction band. Yet, it has to be noted that in the published study²⁰ no complete geometry optimization of the combined substrate–adsorbate system was performed and that the adsorption geometry was based on a previous work on formic acid attached to the TiO₂ surface.²⁰

In order to gain deeper insight into the structural and electronic properties of the two heterostructures and to allow for a comparative study between the two heterojunctions (by considering also the relaxation effects upon adsorption), periodic hybrid-exchange DFT calculations based on the B3LYP functional are suitable. This approach provides an accurate description of the structural energetics and of the electronic structure (i.e. band gap and band offset) for periodic systems,^21–34 particularly for transition metal oxides, and the implementation in the CRYSTAL code is computationally efficient for large periodic systems.³⁵ The aim of this study is to address the binding of catechol and of isonicotinic acid to the rutile-TiO₂(110) surface in terms of geometry, stability and electronic structure, using hybrid-exchange DFT. We compare in detail the interaction of these two molecules with TiO₂: strong binding of the anchoring group not only serves to put the sensitiser in place, but also to control the interfacial electronic coupling between the organic molecule and the semiconductor, thus influencing solar cell efficiency. Although anatase-TiO₂ is currently preferred over the rutile phase when realising DSCs, we focused our study on rutile because it presents some advantages over anatase: it is chemically more stable, can potentially be produced more cheaply and has superior light-scattering properties because of the higher refractive index. Moreover, the performance of rutile in DSCs has been shown to be comparable to that of anatase at one sun light intensity.³⁶ In particular, the rutile-TiO₂(110) face has been selected, because it is the most stable surface of rutile and thus dominates the surface area of equilibrium crystallites; it is also the best microscopically characterised surface of TiO₂.¹⁸

The paper is organised as follows: in Section II the computational details are provided. In Section III the results are discussed in terms of energetics (i.e. binding energies, acidity of the functional groups, bond distances and bond natures between the adsorbate and the substrate) and in terms of electronic structure (i.e. band alignment, band gap states, electron coupling between the molecule and the surface). Conclusions are drawn in Section IV.

II. Computational details

All calculations have been performed using the CRYSTAL09 software package,^37,38 based on the expansion of the crystalline orbitals as a linear combination of a local basis set (BS) consisting of atom-centred Gaussian orbitals. The titanium and oxygen atoms are described by a triple valence all-electron BS: an 86-411G** contraction (one s, four sp and two d shells) and an 8-411G* contraction (one s, three sp and one d shells), respectively;³⁹ the most diffuse sp (d) exponents are α^Ti = 0.3297(0.26) and α^O = 0.1843(0.6) Bohr⁻². These basis sets were developed in previous studies of the bulk and surfaces of titania in which a systematic hierarchy of all-electron basis sets was used to quantify the effects of using a finite BS.^40,41 Both adsorbed molecules are described by a 6-31G** contraction,⁴² where the valence electrons of the carbon and nitrogen atoms are described by two sp shells and one d shell (in the case of the H atom two s shells and one p shell are used), in order to ensure a similar level of accuracy.

Electron exchange and correlation are approximated using the B3LYP hybrid exchange functional, as indicated in Section I. Matrix elements of the exchange and correlation potentials and the energy functional are integrated numerically on an atom-centred grid of points. The integration over radial and angular coordinates is performed using Gauss–Legendre and Lebedev schemes, respectively. A pruned grid consisting of 99 radial points and 5 sub-intervals with (146, 302, 590, 1454, 590) angular points has been used for all calculations (the XXLGRID option implemented in CRYSTAL09).³⁷ The geometry optimisation was initially performed using a smaller grid (LGRID) and then refined using the XXLGRID. This ensures numeral stability both for the bulk and the slab calculations. This grid converges the integrated charge density to an accuracy of about ×10⁻⁶ electrons per unit cell. The Coulomb and exchange series are summed directly and truncated using overlap criteria with thresholds of 10⁻⁷, 10⁻⁷, 10⁻⁷, 10⁻⁷ and 10⁻¹⁴ as described previously.^37,43 Reciprocal space sampling for the bulk structure was performed on a Pack–Monkhorst net with a shrinking factor IS = 8 along each periodic direction. In the bulk, this grid corresponds to 75 k-points in the irreducible Brillouin zone of the bulk crystal and to 25 in that of the surface unit cell. The self-consistent field procedure was converged up to a tolerance in the total energy of ΔE = 1 × 10⁻⁷E_h per unit cell.

Structural optimisation of both the bulk cell parameters and internal coordinates was performed using the Broyden–Fletcher–Goldfarb–Shanno scheme. Convergence was determined from the root-mean-square (rms) and the absolute value of the largest component of the forces. The thresholds for the maximum and the rms forces (the maximum and the rms atomic displacements) have been set to 0.00045 and 0.00030 (0.00180 and 0.0012) in atomic units. Geometry optimisation was terminated when all four conditions were satisfied simultaneously. The predicted structural parameters, with the deviation from those observed⁴⁴ in parentheses, are: a_bulk = b_bulk = 4.639 Å (1.1%), c_bulk = 2.979 Å (0.9%) and u = 0.306 (0.5%) where the O atom is at the fractional position (u,u,0). These values are consistent with those predicted in previous calculations.^3,23,26,41 With regards to the surface,³⁸ a 9-atomic-layer (9AL) slab cut from the bulk has been used, since it represents a good compromise between the surface description and the computational cost. When increasing the slab thickness from 9AL to 15AL, the electronic structure is unaffected in terms of the contributions to the valence and conduction bands in the projected density of states. The corresponding lattice parameters are a_slab = 2.979 Å ([001] direction of the bulk) and b_slab = 6.561 Å ([11̄0] direction of the bulk). In comparing the electronic structure of various adsorption modes, it is important to note that, as 2D periodic boundary conditions are used, all energies are referred to vacuum zero V_es(z) = 0 when z = ∞, where V_es is the electrostatic potential and z is the distance from the surface. Projection of density of states onto orbital and atomic contributions was performed using Mulliken analysis.

Adsorption has been investigated by initially placing the molecule with its symmetry plane perpendicular to the surface plane. The distance between the two anchoring oxygen atoms in both molecules is comparable to the separation between the two undercoordinated titanium atoms along a_slab, therefore the molecule is likely to be coordinated to two surface Ti atoms and thus a 3 × 1 supercell, containing three surface Ti atoms, has been adopted to ensure that adsorbates are separated by at least one empty surface site (see Fig. 1 and 2). In addition, it should be noted that molecules were adsorbed symmetrically on both sides of the two-dimensionally periodic slab as this ensures more rapid convergence of the structure and total energy with respect to slab thickness. The binding energy (BE) per molecule of the adsorbate–substrate system was computed with respect to the isolated molecule and the clean surface. The counterpoise correction to the binding energy was applied to take into account the basis set superposition error (BSSE), details of which are documented in ref. 45 and 46. The BE reported does not take into account either the vibrational component of the free energy or London dispersion contributions to the bonding. At room temperature the former are expected to be insignificant compared to the BE reported in Table 1 (see ref. 47) and the latter are expected to be a small correction to the binding interaction which is dominated by ionic and covalent contributions.

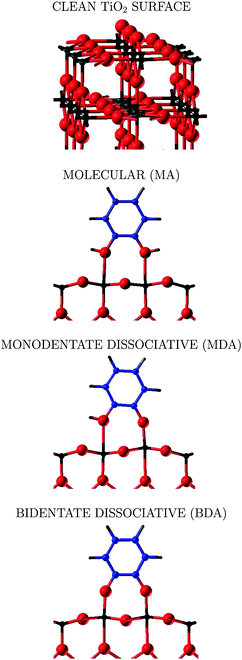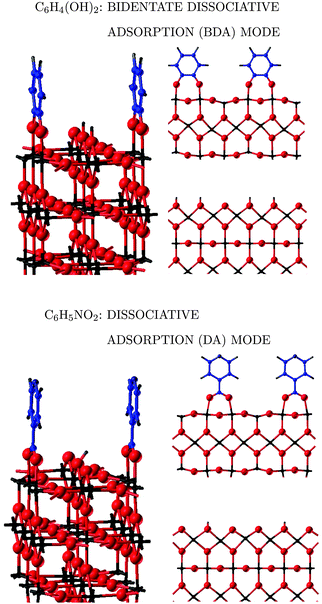
Fig. 1 Ball and stick representation of the adsorption modes of the catechol molecule on the rutile TiO₂(110) surface: (top) clean rutile-TiO₂ surface; (middle) molecular adsorption mode (MA) and monodentate dissociative adsorption (MDA); (bottom) bidentate dissociative adsorption (BDA). Ti atoms are represented in black, O in red, C in blue, and H in grey. In the case of the MA and BDA, one and two hydrogen atoms, respectively, are missing, since adsorbed above the bridging oxygen atoms O_s, which do not appear in this atomic layer, see Fig. 2.

Fig. 2 Ball and stick representation of catechol and isonicotinic acid adsorbed at the rutile (110) surface in the lowest energy configuration. Ti atoms are represented in black, O in red, C in blue, N in dark blue, and H in grey. Left: prospective view, right: side view of two different atomic layers, one containing the molecule and one containing the released hydrogen atoms.

Table 1 Binding energy (BE) of the adsorbate–substrate complex with respect to the clean surface and the isolated molecule for the adsorption geometries considered. The bond distances between the atoms of the molecule (O_m and H) and the surface atoms are reported; Ti_s and O_s are the outermost Ti and O atom of the surface; O_s,ap is the apical oxygen atom bonded to Ti_s, see Fig. 1

	Adsorption mode	BE/eV	d Om−Tis/Å	d Tis−Os,ap/Å	d Om−H/Å	d Os−H/Å
Catechol	MA	−0.359	2.342/2.347	1.907/1.893	0.967/0.967	—
	MDA	−1.452	2.381/1.820	1.871/2.380	0.966	0.961
	BDA	−1.756	1.831/1.834	2.202/2.249	—	0.961/0.961
Isonicotinic acid	MA	−0.457	3.943/2.184	1.815/2.014	0.971	—
	DA	−1.906	2.033/2.059	2.069/2.049	—	0.967

---

III. Results

The binding energy of the adsorbate–substrate system with respect to the clean surface and the isolated molecule is analysed for the catechol and the isonicotinic acid along with the structural changes induced by the adsorption in Section III.A, while the electronic properties of the resulting hybrid interfaces are discussed in Section III.B. The acidity of the molecules, the ionicity of the oxygen atom and the electron conjugation between the adsorbed molecule and the substrate are used to shed light on the structural and electronic properties of the two heterojunctions in both Sections III.A and III.B.

A. Structure and energetics

The clean rutile TiO₂(110) surface is characterised by the presence of fivefold-coordinated titanium (Ti_s) and twofold-coordinated “bridging” oxygen atoms (O_s). The Ti_s ions, being undercoordinated, react with adsorbing species. There are various possible adsorption modes depending on the molecule: catechol C₆H₄(OH)₂ (benzene-1,2-diol according to the IUPAC notation) has two hydroxyl groups that can form a bond with the TiO₂(110) surface. In Fig. 1 the typical adsorption modes previously discussed in the literature are represented: molecular (MA), monodentate (MDA) and bidentate (BDA) dissociative. In the MA case, the molecule adsorbs with the two molecular oxygen atoms pointing towards two Ti_s atoms of the surface, the two hydroxyl groups remaining intact. In the MDA mode, the adsorbed molecule is half-deprotonated, as one of the hydroxyl groups breaks and the corresponding oxygen atom bonds strongly to the fivefold coordinate Ti atom; the released hydrogen atom binds to the nearest two-coordinated O_s. In the BDA, both –OH groups of catechol deprotonate and attach to two five-coordinated Ti atoms; the two released H atoms form two hydroxyl groups with two nearest O_s. In the case of the isonicotinic acid C₆H₅NO₂ (pyridine-4-carboxylic acid according to IUPAC notation), which is characterised by the presence of a carboxyl group, two adsorption modes are considered: molecular (MA) in which the [double bond splayed left]C=O group coordinates with a Ti_s species and dissociative (DA) in which the carboxyl group releases its hydrogen atom to an O_s site and the –COO⁻ group bridges two Ti_s surface ions (see Fig. 2).

In Table 1, the binding energy⁴⁶ of the adsorbate–surface system with respect to the clean surface and the isolated molecule (BE) is given for both molecules. In both cases, the dissociative adsorption corresponds to the lowest energy configuration. The isonicotinic acid binds more strongly to the surface (BE_DA = −1.906 eV) than the catechol (BE_BDA = −1.756 eV). This is as one would expect from the higher acidity of the carboxyl group of the isonicotinic acid, which releases H more easily than catechol. In the case of catechol, there is a clear trend in the BE as a function of the deprotonation, the BDA being more stable than the MDA: BE_BDA < BE_MDA < BE_MA, in agreement with previous theoretical studies.¹⁸ This trend can be rationalised in terms of the bond distance between the atoms of the molecule and of the rutile surface and in terms of the displacement of the outermost surface atoms, bonded to the molecule.

The distances between the five-coordinated Ti atoms and each of the two oxygen atoms of the molecule, d_Om−Tis, are reported in Table 1. In the dissociative adsorption the molecule forms shorter bonds with the surface atoms than in the molecular (MA) adsorption. In the MDA configuration of catechol, the d_Om−Tis are about 1.8 and 2.4 Å, respectively, for the deprotonated oxygen atom and for the intact hydroxyl group (both oxygen atoms belonging to the molecule), while for the BDA case both d_Om−Tis are about 1.8 Å; correspondingly, the BE increases from −1.452 to −1.756 eV. The values of d_Om−Tis and the BE for the various adsorption modes are also a consequence of the ionicity of the oxygen atom in the molecule; the more ionic the O atom, the shorter the d_Om−Tis, with the deprotonated oxygen atom more ionic (more negative) than the hydroxyl oxygen one. In the isonicotinic acid, the [double bond splayed left]C=O group plays an important role in the interaction between the molecule and the surface, especially in the MA case. In fact, the value of d_Om−Tis = 2.184 Å for the [double bond splayed left]C=O group is smaller than d_Om−Tis = 3.943 Å for the OH group, whose interaction with the surface is negligible. However, this value (d_Om−Tis = 2.184 Å) is larger than d_Om−Tis for the deprotonated oxygen atom in both adsorbed molecules. Therefore, there is a decrease in d_Om−Tis with increasing O ionicity, when moving from the O ion in –OH to that in [double bond splayed left]C=O, –O⁻ of the isonicotinic acid and –O⁻ of catechol (refer to the next subsection for a detailed analysis in terms of the electronic structure).

In order to understand the structural modifications occurring upon adsorption, it is useful to consider the relaxation of the clean surface, as a reference. With respect to a surface defined by cutting a slab from an optimised bulk geometry, the Ti_s moves inwards by 0.14 Å to increase effective coordination with neighbouring O ions. In the optimised crystal bulk, the TiO₆ octahedron is characterised by two long apical (d_Ti−Oap = 2.01 Å) and four short equatorial (d_Ti−Oeq = 1.98 Å) oxygen bonds. At the clean relaxed TiO₂ surface the distance between the outermost Ti and its neighbouring apical oxygen, d_Tis−Os,ap, is shorter (1.853 Å), due to the under coordination of Ti_s, as reported in a previous work.²⁶ When the adsorbed molecule saturates the fivefold coordinated Ti atoms (Ti_s) at the rutile surface, one of the most significant effects is that Ti_s moves outwards to restore a bulk-like coordination. In catechol a shorter d_Om−Tis ≈ 1.8 Å for the deprotonated oxygen atom and a consequent larger d_Tis−Os,ap ≈ 2.3 Å can be understood in terms of the extension of the delocalisation of the π-electrons of the benzene ring over the Ti_s atoms. For isonicotinic acid this effect does not occur and the distances, d_Om−Tis and d_Tis−Os,ap, are similar and very close to the value in the bulk (d_Ti−Oap = 2.01 Å). In Table 1, the hydrogen–oxygen distance is also reported. The distance between the H atom released by the molecule and the two-coordinated bridging oxygen atom, d_Os−H, is close to the molecular distance, d_Om−H.

In summary, the binding energy and the bond distance of the anchoring functional groups of a dye at the TiO₂ surface can be rationalised in terms of the acidity and of the ionicity of the molecular oxygen atom, and in terms of a secondary factor related to the electron conjugation with the surface. These effects are also important in their influence on the electronic structure of the heterojunctions formed.

B. Electronic structure

In order to rationalize the behaviour of the two adsorbed molecules, the different alignment of the molecular states with respect to the semiconductor bands has to be taken into account. With this aim, the total density of states and the projections onto the atomic contribution are presented in Fig. 3 and 4.⁴⁸ The lower (below –23 eV) and the upper (in the range of –15 eV and –6 eV) valence bands have predominantly O-2s and O-2p character with some hybridisation with Ti-3d orbitals, while the lower conduction band (above −5 eV) has Ti-3d character. Upon adsorption, the molecular states, attributed to the π orbitals in the catechol, appear in the TiO₂ band gap above the top of VB; while in the isonicotinic acid case a σ state, mainly due to carbon and nitrogen atoms, is evident at the top of VB for dissociative mode only. These abovementioned HOMO states (both π and σ) are useful as a reference, since their energies with respect to the vacuum level are not significantly affected by adsorption, when compared to the isolated molecule, as shown in Fig. 3 and 4. A shift of the valence band offset of the semiconductor is instead evident, especially when the DOS for the molecular mode is compared with the superposition of the DOS for the isolated molecule and the clean TiO₂ surface. This shift is generated by the dipole of the absorbed molecule and is significantly smaller for dissociative adsorption.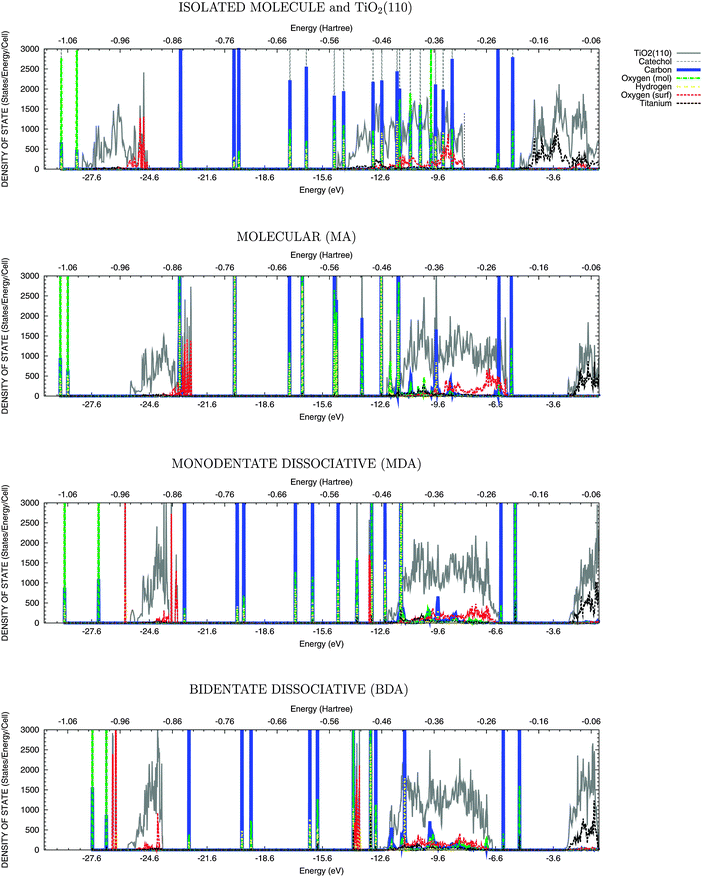

Fig. 3 DOS for various adsorption modes of the catechol molecule onto the rutile TiO₂(110) surface. From top to bottom panel: superposition of the DOS for the isolated molecule and the clean TiO₂ surface; Molecular Adsorption (MA); Monodentate Dissociative Adsorption (MDA); Bidentate Dissociative Adsorption (BDA). The lower and the upper valence bands and the occupied molecular states appear below ∼−5 eV (−0.2 Hartree).

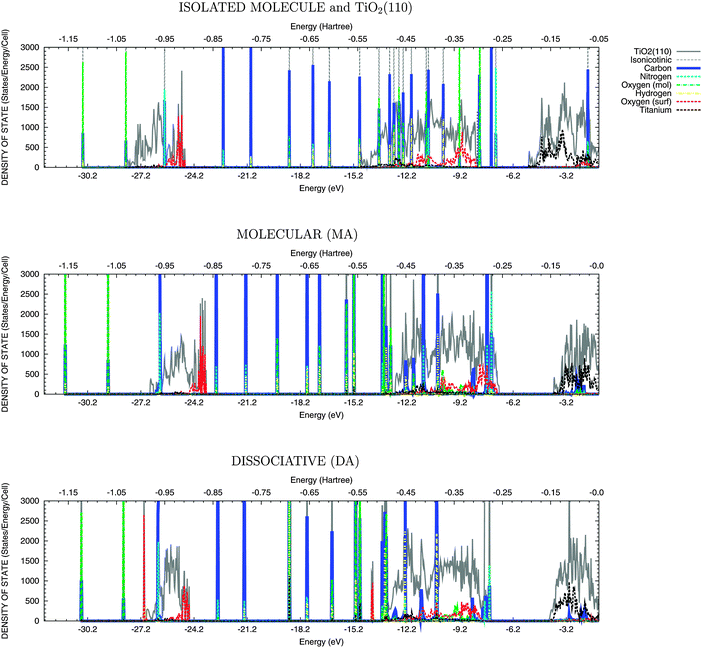Fig. 4 DOS for various adsorption modes of the isonicotinic acid molecule onto the rutile TiO₂(110) surface. From top to bottom panel: superposition of the DOS for the isolated molecule and the clean TiO₂ surface; Molecular Adsorption (MA); Dissociative Adsorption (DA). The lower and the upper valence bands and the occupied molecular states appear below ∼−5 eV (−0.2 Hartree).

The electronic structure is analysed in Table 2 in terms of the energy difference (ΔE^unocc,occ) between the highest occupied (E^occ) and the lowest unoccupied (E^unocc) states of the adsorbate–substrate system and in terms of the energy difference for the molecular HOMO–LUMO transition (ΔE^LUMO,HOMO). As expected, ΔE^unocc,occ and ΔE^LUMO,HOMO are dependent on both the adsorbed molecule and the adsorption mode. For catechol, there is a decrease in ΔE^unocc,occ when moving from the molecular (ΔE^unocc,occ = 2.90 eV) to the two dissociative modes (ΔE^unocc,occ = 2.78 eV for MDA and 2.35 eV for BDA). This decrease is due to the presence of the HOMO state above the top of the valence band of TiO₂, as described above. These energy differences can be used to interpret the UPS and IPS measurements, characterised by a peak around 2.4 eV binding energy,^10,18 similar to the calculated BDA case. For isonicotinic acid, no states appear above the valence band in disagreement with a previous study,²⁰ where a similar level of theory was adopted but no geometrical relaxation of the substrate–adsorbate system was performed. This is consistent with the decrease in energy separation between the HOMO and the top of the valence band when comparing the superimposed DOS with the MA case (first and second panel from top in both Fig. 3 and 4).

Table 2 The calculated energy difference ΔE between the highest occupied (E^occ) and the lowest unoccupied (E^unocc) states for the clean surface, the isolated molecules and the various adsorption modes. In the column E^LUMO–E^HOMO, the star indicates that the value of the electronic transition, HOMO → LUMO, is affected by the hybridization of LUMO with the conduction band states and by the consequent dispersion in energy of this state. In the last column, the type of electronic transition is reported: for instance, for the clean surface ΔE is the difference between the bottom of the conduction band (CB) and the top of the valence band (VB) and for the isolated molecules ΔE is the HOMO–LUMO difference. In addition, the symmetry of the state corresponding to the HOMO (π or σ) is given in parentheses

	ΔE^unocc,occ	ΔE^LUMO,HOMO	Transition
	E ^unocc–E^occ/eV	E ^LUMO−E^HOMO/eV	occ → unocc
Clean TiO2	2.90	—	VB → CB
Isolated catechol	5.86	5.88	HOMO(π) → LUMO
MA catechol	2.90	5.55*	HOMO(π) → CB
MDA catechol	2.78	5.24*	HOMO(π) → CB
BDA catechol	2.35	4.84*	HOMO(π) → CB
Isolated isonicotinic acid	5.21	5.20	HOMO(σ) → LUMO
MA isonicotinic acid	3.07	4.82*	VB → CB
DA isonicotinic acid	3.35	4.55*	HOMO(σ) → CB

---

The HOMO has been investigated by using a localization procedure based on the Wannier functions. The contributions (c^WF) of the atoms involved in the HOMO are reported in Table 3 for the adsorbed catechol. It is evident that this state is due to the 2p orbitals (perpendicular to the plane of the molecule) of the two C atoms close to the surface and to the 2p orbitals of the O atom directly connected to C. This occurs in all the adsorption modes, but there is an additional contribution of the Ti-3d orbital, overlapping with the 2p of the O atom. The increase in c^WF_Ti as a function of the number of oxygen deprotonated is also related to the decrease in the distance O–Ti and to the stronger BE, discussed in Section III.A. The hybridisation between Ti_s and O_m is not only evident from the but also from the overlap population for q_Tis−Om, given in Table 4. In the case of the catechol, q_Tis−Om increases when the deprotonation occurs, as evident when comparing MA (q_Tis−Om = 0.03|e| Bohr⁻³) and BDA (q_Tis−Om = 0.10|e| Bohr⁻³) with MDA. For isonicotinic acid, the reduced conjugation of the molecule with the surface explains the lower population (q_Tis−Om = 0.07|e| Bohr⁻³) compared to catechol. Generally it appears that catechol is more strongly electronically coupled as an anchoring group with the oxide substrate than isonicotinic acid and thus likely to be more effective for photo-induced electron injection, when employed as a dye molecule.

Table 3 Wannier function contributions c^WF of the atoms (the two C atoms closer to the surface, the two O atoms of the molecule directly bond to them and the Ti atoms, originally fivefold coordinated) involved in the HOMO for the catechol on TiO₂(110) in the various adsorption modes

	HOMO
MA catechol	0.189/0.188	0.112/0.115	—/—
MDA catechol	0.188/0.171	0.091/0.142	—/0.029
BDA catechol	0.170/0.170	0.123/0.120	0.025/0.024

---

Table 4 The Mulliken populations for the atoms involved in bonding between the molecule and the surface for catechol and isonicotinic acid; the charge associated to the Ti atoms, originally fivefold coordinated, the C atoms closer to the surface, the O atoms of the hydroxyl groups and the double bond with the C atom are reported in the first column. In the last column the overlap population associated with the Ti_s–O_m bond is reported. Unit: |e| Bohr⁻³

	q Cm	q Om	q Tis	q Tis−Om
Clean TiO2(110)	—	—	2.130	—
Isolated catechol	0.291/0.285	−0.527/−0.564	—	—
MA catechol	0.350/0.348	−0.567/−0.562	2.144/2.143	0.026/0.025
MDA catechol	0.300/0.344	−0.578/−0.710	2.152/2.140	0.024/0.105
BDA catechol	0.295/0.295	−0.711/−0.710	2.142/2.146	0.104/0.104
Isolated Isonicotinic acid	0.500	−0.466/−0.428	—	—
MA isonicotinic acid	0.583	−0.529/−0.405	2.108/2.159	−0.001/0.043
DA isonicotinic acid	0.593	−0.581/−0.613	2.149/2.147	0.066/0.070

---

IV. Conclusions

In this work different adsorption modes of the catechol and the isonicotinic acid molecules onto the rutile TiO₂(110) surface have been analysed in terms of geometry, binding energy and electronic structure within a hybrid-exchange DFT framework. The calculations demonstrate that for both molecules the dissociative adsorption (fully deprotonated) is the thermodynamically favoured mode of adsorption due to saturation of two fivefold coordinated Ti atoms at the surface and formation of two Ti_s–O bonds with partial covalent character. Bond formation and bond distances can be rationalised in terms of acidity and ionicity of the functional groups responsible for the molecular attachment. Upon adsorption, in the most stable configuration the HOMO of both molecules occurs in the energy gap of the TiO₂ substrate while the LUMO lies above the top of the conduction band, generating a type II heterojunction that makes these systems suitable for applications in DSC. In the case of catechol the HOMO state originates from a hybridisation of the delocalised π orbitals of the benzene ring with the 3d-states of the substrate titanium atoms, while the HOMO of the isonicotinic acid corresponds to a σ orbital of the N–C bond. In the former case the larger electron coupling between the molecule and the oxide is expected to facilitate electron injection from the dye to the TiO₂ and thus larger photocurrent during DSC operation. For this reason our results indicate that catechol will be a better anchoring group with respect to isonicotinic acid although being characterised by a slightly lower binding energy.

Finally, we found that the adsorption of both the organic molecules considered here gives rise to a positive shift of the TiO₂ bands (both VB and CB) with respect to the vacuum level (or equivalently to the hydrogen redox potential). This shift, which is mostly determined by the molecular dipole and by the type of bonds formed with the substrate, is important since the position of the oxide CB determines the solar cell open circuit voltage (the higher is the positive shift the larger is V_oc). This observation highlights the need to tune the dipole of the dye (and of the co-adsorbent often used during DSC realisation to avoid dye aggregation) to molecularly engineer the electronic properties of the hybrid interface and enhance solar cell performances.

Acknowledgements

This work made use of the high performance computing facilities of Imperial College London and – via membership of the UK's HPC Materials Chemistry Consortium funded by EPSRC (EP/F067496) – of HECToR, the UK's national high-performance computing service, which is provided by UoE HPCx Ltd at the University of Edinburgh, Cray Inc and NAG Ltd, and funded by the Office of Science and Technology through EPSRC's High End Computing Programme. One of the authors, F.R., also acknowledges the TYC for providing financial assistance through the Junior Research Fellowship (JRF).

References

1. B. O'Regan and M. Grätzel, Nature, 1991, 353, 737.
2. M. Grätzel, J. Photochem. Photobiol., C, 2003, 4, 145 , ISSN 1389-5567.
3. F. Labat, P. Baranek, C. Domain, C. Minot and C. Adamo, J. Chem. Phys., 2007, 126, 154703 , pages 12.
4. H. Tang, F. Lévy, H. Berger and P. E. Schmid, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 7771.
5. H. Tang, H. Berger, P. Schmid, F. Lvy and G. Burri, Solid State Commun., 1993, 87, 847 , ISSN 0038-1098.
6. R. Mosurkal, J.-A. He, K. Yang, L. A. Samuelson and J. Kumar, J. Photochem. Photobiol., A, 2004, 168, 191 , ISSN 1010-6030.
7. C. R. Rice, M. D. Ward, M. K. Nazeeruddin and M. Gratzel, New J. Chem., 2000, 24, 651.
8. P. Persson, R. Bergstrm and S. Lunell, J. Phys. Chem. B, 2000, 104, 10348.
9. W. R. Duncan and O. V. Prezhdo, J. Phys. Chem. B, 2005, 109, 365.
10. S. Rangan, J. P. Theisen, E. Bersch and R. A. Bartynski, Appl. Surf. Sci., 2010, 256, 4829.
11. R. Sanchez-de Armas, M. A. San-Miguel, J. Oviedo, A. Marquez and J. F. Sanz, Phys. Chem. Chem. Phys., 2011, 13, 1506.
12. J. Moser, S. Punchihewa, P. P. Infelta and M. Graetzel, Langmuir, 1991, 7, 3012.
13. A. L. A. Parussulo, M. F. G. Huila, K. Araki and H. E. Toma, Langmuir, 2011, 27, 9094.
14. A. Terentjevs, G. Cicero and A. Catellani, J. Phys. Chem. C, 2009, 113, 11323.
15. Y. Kanai, G. Cicero, A. Selloni, R. Car and G. Galli, J. Phys. Chem. B, 2005, 109, 13656.
16. V. Scrinivasan, G. Cicero and J. C. Grossman, Phys. Rev. Lett., 2008, 101, 185504.
17. L.-M. Liu, S.-C. Li, H. Cheng, U. Diebold and A. Selloni, J. Am. Chem. Soc., 2011, 133, 7816.
18. S.-C. Li, J.-g. Wang, P. Jacobson, X.-Q. Gong, A. Selloni and U. Diebold, J. Am. Chem. Soc., 2009, 131, 980.
19. M. Nilsing, P. Persson and L. Ojame, Chem. Phys. Lett., 2005, 415, 375 , ISSN 0009-2614.
20. P. Persson, S. Lunell and L. Ojame, Chem. Phys. Lett., 2002, 364, 469 , ISSN 0009-2614.
21. D. Muñoz, N. M. Harrison and F. Illas, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 085115.
22. J. Muscat, A. Wander and N. Harrison, Chem. Phys. Lett., 2001, 342, 397.
23. G. Mallia and N. M. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 165201.
24. N. C. Wilson, S. P. Russo, J. Muscat and N. M. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 024110.
25. G. Mallia, R. Orlando, M. Llunell and R. Dovesi, in Computational Materials Science, ed. C. Catlow and E. Kotomin, IOS Press, Amsterdam, 2003, vol. 187 of series NATO SCIENCE SERIES, III: Computer and Systems Sciences, pp. 102–121.
26. J. Scaranto, G. Mallia, S. Giorgianni, C. Zicovich-Wilson, B. Civalleri and N. Harrison, Surf. Sci., 2006, 600, 305 , ISSN 0039-6028.
27. F. Corà, M. Alfredsson, G. Mallia, D. Middlemiss, W. Mackrodt, R. Dovesi and R. Orlando, in Principles and Applications of Density Functional Theory in Inorganic Chemistry II, N. Kaltsoyannis and J. McGrady, Springer, Berlin/Heidelberg, 2004, vol. 113, pp. 171–232.
28. G. C. De Fusco, B. Montanari and N. M. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 220404.
29. L. Ge, J. H. Jefferson, B. Montanari, N. M. Harrison, D. G. Pettifor and G. A. D. Briggs, ACS Nano, 2009, 3, 1069.
30. G. C. De Fusco, L. Pisani, B. Montanari and N. M. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 085201.
31. L. Liborio, G. Mallia and N. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 245133.
32. C. L. Bailey, L. Liborio, G. Mallia, S. Tomić and N. M. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 205214.
33. L. M. Liborio, C. L. Bailey, G. Mallia, S. Tomic and N. M. Harrison, J. Appl. Phys., 2011, 109, 023519 , pages 9.
34. E. A. Ahmad, L. Liborio, D. Kramer, G. Mallia, A. R. Kucernak and N. M. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 085137.
35. I. J. Bush, S. Tomi, B. G. Searle, G. Mallia, C. L. Bailey, B. Montanari, L. Bernasconi, J. M. Carr and N. M. Harrison, Proc. R. Soc. London, Ser. A, 2011, 467, 2112.
36. N.-G. Park, J. van de Lagemaat and A. J. Frank, J. Phys. Chem. B, 2000, 104, 8989.
37. R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison and I. J. Bush, et al., CRYSTAL09, Università di Torino, Torino, 2010.
38. R. Dovesi, B. Civalleri, E. Orlando, C. Roetti and V. R. Saunders, Reviews in Computational Chemistry, John Wiley & Sons, Inc., Wiley-VCH, 2005, vol. 21.
39. J. Muscat, PhD Thesis, University of Manchester, 1999.
40. J. Muscat, N. M. Harrison and G. Thornton, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 2320.
41. J. Muscat, V. Swamy and N. M. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 224112.
42. https://bse.pnl.gov/bse/portal .
43. C. Pisani, R. Dovesi and C. Roetti, Hartree–Fock Ab Initio Treatment of Crystalline Systems, Springer Verlag, Heidelberg, 1988, vol. 48.
44. J. K. Burdett, T. Hughbanks, G. J. Miller, J. W. Richardson and J. V. Smith, J. Am. Chem. Soc., 1987, 109, 3639.
45. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553.
46. J. Scaranto, G. Mallia and N. Harrison, Comput. Mater. Sci., 2011, 50, 2080.
47. K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 035406.
48. The DOS plots for the surfaces are plotted with respect to atomic zero and thus the variations in peak positions and Fermi energies can legitimately be interpreted in terms of changes in the surface dipole and workfunction.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c2cp42078c

---