Hybrid density functional–molecular mechanics calculations for core-electron binding energies of glycine in water solution
Johannes
Niskanen
*ab,
N.
Arul Murugan
a,
Zilvinas
Rinkevicius
ac,
Olav
Vahtras
a,
Cui
Li
d,
Susanna
Monti
e,
Vincenzo
Carravetta
d and
Hans
Ågren
a
aDivision of Theoretical Chemistry & Biology, School of Biotechnology, Royal Institute of Technology, S-106 91 Stockholm, Sweden. E-mail: jniskan@theochem.kth.se
bDepartment of Physics, University of Helsinki, P.O. Box 64, FI-00014 University of Helsinki, Finland
cKTH Royal Institute of Technology, Swedish e-Science Research Center (SeRC), S-100 44, Stockholm, Sweden
dCNR – Institute of Chemical and Physical Processes, Area della Ricerca, via G. Moruzzi 1, I-56124 Pisa, Italy
eCNR – Institute of Chemistry of Organometallic Compounds, Area della Ricerca, via G. Moruzzi 1, I-56124 Pisa, Italy
First published on 19th November 2012
Abstract
We report hybrid density functional theory–molecular mechanics (DFT/MM) calculations performed for glycine in water solution at different pH values. In this paper, we discuss several aspects of the quantum mechanics–molecular mechanics (QM/MM) simulations where the dynamics and spectral binding energy shifts are computed sequentially, and where the latter are evaluated over a set of configurations generated by molecular or Car–Parrinello dynamics simulations. In the used model, core ionization takes place in glycine as a quantum mechanical (QM) system modeled with DFT, and the solution is described with expedient force fields in a large molecular mechanical (MM) volume of water molecules. The contribution to the core electronic binding energy from all interactions within and between the two (DFT and MM) parts is accounted for, except charge transfer and dispersion. While the obtained results were found to be in qualitative agreement with experiment, their precision must be qualified with respect to the problem of counter ions, charge transfer and optimal division of QM and MM parts of the system. Results are compared to those of a recent study [Ottoson et al., J. Am. Chem. Soc., 2011, 133, 3120].
1 Introduction
Synchrotron facilities provide techniques to study the structure and properties of liquid and solid state systems both at the atomic and molecular level. Modern synchrotron radiation sources provide intense radiation within a narrow, adjustable photon energy band with well-defined polarization, making them ideal tools for X-ray and UV photoelectron spectroscopies (XPS, UPS). Electron spectroscopy for chemical analysis (ESCA), introduced by Siegbahn and co-workers,1,2 is an example of a spectroscopy that has been greatly promoted in scope and precision by synchrotron radiation. The fundamental idea behind ESCA is that the chemical environment leaves detectable shifts and photoline structure for each element or molecule that can be interpreted in terms of local electronic configuration, conformational arrangement and environmental effects.Earlier development of electron spectroscopy enabled measurements of core-electron spectra in solution. However, as the electron detection itself demands high vacuum, most of the sample preparation techniques rely nowadays on the liquid-jet principle,3,4 where a jet of studied solution is shot through the interaction region. Recently, Ottoson and co-workers5 have performed, by this method, an exhaustive core-electron spectroscopy study of glycine in water solution and analyzed accurately, both experimentally and theoretically, the role played by charge transfer in core electron binding energies. Other liquid-phase X-ray spectroscopic studies of glycine6,7 have also been reported as well as gas-phase XPS experiments in the valence8–11 and core12–14 region.
A variety of electronic structure methods are now available to address core electron binding energies and chemical shifts of large quantum systems, like Δ-self-consistent-field (ΔSCF),15,16 ΔKohn–Sham (ΔKS),17,18 and transition state methods.19–21 Environmental effects are commonly treated either by dielectric continuum,22 supermolecular23,24 or statistical models,25,26 where in the latter case the nonbonded solvent interaction (n.b. electrostatic and polarization) is treated parametrically in terms of statistical distribution functions. Although quantum supramolecular models in combination with classical molecular dynamics simulations can provide an accurate description of solvent effects, they are computationally very demanding, and thus impractical for large systems and when a great number of configurations are needed to have a realistic description of the environmental perturbation. It is therefore timely to test core electron binding energy calculations with the now available multiscale modeling methods including coupled quantum-classical representations. Such modeling is based on the idea that quantum description is critical for some part of the system while classical models may perform well for other parts, thus allowing treating quantum phenomena in large systems that evolve on nanosecond timescales. Full electrostatic and polarization interactions within and between the two parts are accounted for in the property calculations, here the core electron binding energy. As photo-electron emission is a vertical process, the final state electronic relaxation takes place on a time scale that is negligible with respect to the molecular motion, which implies that a sequential approach for structure and property evaluation is effective.
Motivated by recent advances in the multiscale modeling techniques, we take the glycine molecule as our test system to study the performance of the sequential density functional theory/molecular mechanics (DFT/MM) approach for evaluation of core-electron ESCA shifts. Like all other amino acids, glycine exists in a zwitterionic form in aqueous solution at normal pH. Depending on the pH value, the molecule can accept an extra proton through the carboxyl group or deprive a proton from the ammonium group to transform to a cationic or an anionic form, respectively, while the neutral form of glycine is absent in aqueous solutions. There are many reports on the microsolvation of zwitterionic and neutral forms of glycine in water,27–29 whereas the ionic cases were not studied in detail. However the pH-dependent evolution of the microsolvation structure of the other two forms of glycine is an interesting topic best probed, theoretically, with the quantum mechanical Car–Parrinello molecular dynamics (CPMD) approach. In this work, we applied hybrid Car–Parrinello QM/MM molecular dynamics (CP-QM/MM MD) techniques to study accurately the microsolvation structure of glycine in its zwitterionic, cationic and anionic forms. Binding energy evaluation for C1s and N1s core-electrons was then performed through a snapshot-based DFT/MM method, although for studying the charge transfer effect (Section 3.5), a supermolecular approach was also applied. In our discussion, we also pay attention to the convergence behaviour of the results with respect to the interaction distance and granulation of the interaction. Moreover, two opposite cases for the ionic liquid modeling are considered: close-lying counter-ion and the limit of infinite dilution.
2 Theory and computations
2.1 Hybrid Car–Parrinello QM/MM molecular dynamics
A sequential multiscale approach, consisting of hybrid CP-QM/MM MD runs, followed by property evaluation for each selected snapshot was used in the simulations. Before reporting the details of the simulations, some important aspects considering the simulation of XPS energetics will be clarified in order to give the reader a more definite picture of the problems encountered during spectra simulations.In the present simulations the total charge of the anionic and cationic forms of glycine was neutralized by adding a positively or negatively charged counter-ion. As long as the box is large enough, in many cases this does not cause any difference. However, in photoemission for a one molecule-one counterion situation this is not the case. As there is a clear origin for photoionization and only one ion, ergodicity, the full sampling of the accessible phase space, is hard to obtain in the MD run. We also point out that, without screening, the potential by the counterion is of type 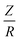 (in a.u.) and therefore a considerable contribution to binding energy can be expected: at a distance of 15 Å, the result is approximately 1 eV.
(in a.u.) and therefore a considerable contribution to binding energy can be expected: at a distance of 15 Å, the result is approximately 1 eV.
The MD simulations were carried out in an isothermal-isobaric ensemble (NPT). Except for the zwitterionic form of glycine, a counter-ion was also included to neutralize the system. Approximately 9000 solvent molecules were included in all these glycine–solvent systems. The initial molecular geometry for glycine was obtained from optimization at the B3LYP30/6-31+G*31–33 level and the charges were derived using a CHELPG method as implemented in Gaussian-09.34 Glycine was then solvated with explicit water molecules, which were modeled with the TIP3P force-field.35 A general Amber force field (GAFF)36 was used to describe the non-bonded interaction of glycine. The time step used for the integration of nuclear equation of motion was 1 fs. All three ionic systems were equilibrated in a canonical ensemble for a total time scale of 1 ns. The final configurations from this equilibration runs were then taken as the initial configuration for the subsequent CP-QM/MM MD simulations. In the CP-QM/MM MD calculation, only the glycine molecule (in its different ionic forms) was treated at the DFT level while the remaining solvent molecules and neutralizing ions were treated using the molecular mechanics force-field as in the above-described MD simulations. The CP-QM/MM Hamiltonian accounts for the electrostatic and non-bonded interactions between the QM and MM subsystems, and it thus includes the solvent polarization effect on the solute molecular geometry and electronic charge distribution. The CP-QM/MM MD calculation was started with a quenching run that relaxes the solute–solvent system to a local minimum in the Born–Oppenheimer potential energy surface. Subsequently, the calculation involved a scaling run and a run with a Nose thermostat where the latter run allows the system to evolve in the canonical ensemble. In the CP-QM/MM MD the time step for integration of equation of motion was 2 a.u. and the simulations were carried out for a total time scale of 3–6 ps.
To probe the two opposite cases of the counter-ion distance distribution, we performed two CP-QM/MM MD runs, starting from classical MD snapshots with different counter-ion–glycine separations. The first CP-QM/MM MD run was started from a classical MD snapshot with a close-lying counter-ion and in the second run, the ion was far from the solute. To simulate infinite dilution in the binding energy evaluation for the distant-ion run, the distance of the ion was large enough to neglect its contribution. The timescale of the CP-QM/MM MD run was rather small, and the counter-ion was almost immobile inside the simulation box.
2.2 Binding energy calculations
For evaluation of core-electron binding energies, hybrid open-shell density functional theory DFT/MM and the ΔKS procedure were utilized. The open-shell DFT method used for the binding energy calculations is discussed in more detail in ref. 37 and 38. As all the studied forms of glycine are initially closed-shell systems, the current case deals with spin singlet and doublet states. To avoid variational collapse, the final state relaxation was performed in a two-step procedure; firstly the core hole orbital was frozen and then relaxed with other occupied orbitals frozen.39 Such a relaxation scheme is valid, although not strictly variational, and the contribution for the second cycle in this iteration scheme is negligible. A local development version of the DALTON code package,40 with open-shell implementation for DFT/MM, was used.Augmented correlation-consistent polarized core-valence triple zeta (aug-cc-pCVTZ)Dunning's basis sets41,42 were used for computations. The DFT calculations were performed with the B3LYP30 exchange-correlation functional following the choice of Ottoson and co-workers.5 In their study, a reasonable agreement with the experiment was observed.
In the MM region of each snapshot, 5 different MM force field parametrizations for the water molecules and the counter-ion were used. The force fields are the same as used in ref. 43, the key features of which are also listed in Table 1.
![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) denote partial charges, dipoles, quadrupoles, octupoles, isotropic polarizability and first order polarizabilities
denote partial charges, dipoles, quadrupoles, octupoles, isotropic polarizability and first order polarizabilities
| q | d | Q | O | α iso |
![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif)
|
|
|---|---|---|---|---|---|---|
| a Distributed over hydrogen and oxygen atoms and OH bond midpoints. | ||||||
| MM-0 | 3 | — | — | — | — | — |
| MM-1 | 3 | — | — | — | 1 | — |
| MM-2 | 3 | — | — | — | 3 | — |
| MM-3 | 3 | 5 | 5 | — | — | 5 |
| MM-4 | 3 | 5 | 5 | 5 | — | 5 |
For MM-0, only partial charges of the atomic centers are used. The molecular isotropic polarizability αiso is added to the oxygen atom in MM-1. In MM-2, three first order polarizabilities ![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) , one for each atom, are used instead, and in MM-3 (and MM-4) the point charges are augmented with static dipoles, quadrupoles (octopoles), and polarizability tensors
, one for each atom, are used instead, and in MM-3 (and MM-4) the point charges are augmented with static dipoles, quadrupoles (octopoles), and polarizability tensors ![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) in the atoms and the middle points of the O–H bonds. These MM force fields form a systematic hierarchical ladder in the classical treatment of the MM molecules. Convergence with respect to the cut-off radius for the waters included in the MM region was studied in the MM-0 and MM-1 frameworks.
in the atoms and the middle points of the O–H bonds. These MM force fields form a systematic hierarchical ladder in the classical treatment of the MM molecules. Convergence with respect to the cut-off radius for the waters included in the MM region was studied in the MM-0 and MM-1 frameworks.
In addition to bare solute-DFT–solvent-MM calculations, two different computational approaches were applied to evaluate the effect of charge transfer between the solute and solvent molecules. First, we calculated by ΔKS the binding energy for clusters containing the amino acid in the zwitterionic form and a small number of water molecules. Second, explicit water molecules were included in the DFT part of the ΔKS DFT/MM calculation performed for the snapshots of the distant-ion CP-QM/MM MD runs for all three forms of glycine.
3 Results and discussion
In this section the results of the microsolvation structure from CP-QM/MM MD simulations are analyzed and convergence with respect to the DFT/MM modeling framework is discussed. Then the binding energies are provided and briefly discussed.3.1 pH dependent microsolvation in glycine
Microsolvation of glycine in its neutral and zwitter-ionic forms was previously studied by other authors.27–29 Here the microsolvation of the zwitterion, cation and anion is also addressed. The solvation shell structure is discussed in terms of radial-distribution functions (RDFs); the results are depicted in Fig. 1.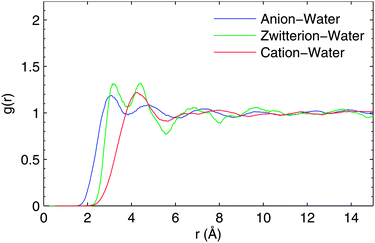 | ||
| Fig. 1 The center-of-mass radial distribution function for anionic, zwitter-ionic and cationic glycine in water solvent. For details, see the text. | ||
As seen in Fig. 1, the first solvation shell appears, for all forms of glycine, between 3–6.2 Å. However, the peak positions shift towards a larger r value in the cation. The position of the first peak appears at 3.1, 3.2 and 4.2 Å for the anionic, zwitterionic and cationic forms, respectively. This can be attributed to an increasing molecular volume of the different ionic forms. Moreover, for the anion and the zwitterion, the first solvation shell has a bimodal distribution caused by the difference in the distance of the amino and carboxyl groups from the molecular CM. The single peak of cationic RDF is due to strong hydrogen bonding to the positive amino group, whereas the first peak in the bimodal RDF of anionic and zwitterionic glycine indicates hydrogen bonding to oxygens of the carboxylate group, located closer to the molecular CM.
The average number of solvent molecules in the first solvation shell is 32, 23 and 21 for anionic, zwitterionic and cationic glycine respectively. One could have anticipated an increasing trend along increase in the molecular volume of the ionic forms. However, as the opposite is observed, the total charge is concluded to play the dominant role in building up the solvation shell structure. This is especially evident in the case of the cationic form where a smaller number of molecules are present in the first solvation shell, due to the absence of the carboxyl-originating peak at 3 Å in the RDF of Fig. 1. The solvation shell structure is not affected significantly beyond 9 Å for any of the three considered forms.
Concerning the number of waters coordinated with specific polar groups (such as carboxyl and amino groups in glycine), it is convenient to use solute-atom–CMwater RDF. This also allows a more detailed comparison with the solvation shell structure already discussed for zwitter-ionic glycine by ab initio molecular dynamics calculations.28 The X–CMwater RDFs (X = O, N, H in polar groups) are presented in Fig. 2.
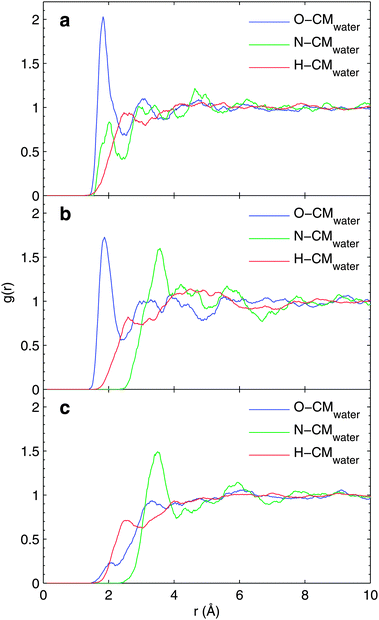 | ||
| Fig. 2 Solute atom-solvent center of mass radial distribution function for (a) anionic, (b) zwitter-ionic and (c) cationic glycine in water solution. For details, see the text. | ||
In the case of anionic and zwitterionic glycine, the first coordination shell around the O and H atoms appears similar while the first coordination shell around N is shifted by about 1.5 Å because of the protonation of the amino group. Simultaneously, the peak height of N–CMwater increases indicating more symmetric hydrogen bonding to the positive amino group of zwitterionic glycine. As H–CMwater RDF does not change in this transition, the corresponding hydrogen bonding length and strength remain constant. Thus the appearance of the lowest peak in N–CMwater of anionic glycine indicates most likely direct hydrogen bonding to N, which is then blocked by the added proton in the zwitterionic and cationic cases. This is seen as a suppression of this peak for zwitterionic and cationic glycine and by an increase in the height of the remaining peak. The reduction of peak structure and an increase in one peak of the RDF is a clear evidence of more symmetric hydrogen bonding to the amino group – all water molecules bind via H of the amino group and none of them binds directly to N. For zwitterionic and cationic forms, the N–CMwater and H–CMwater RDFs remain the same as the protonation of the amino group is not modified in this step.
As seen in the O–CMwater RDF, the closest-lying peak around 2 Å is highly suppressed when a proton is added to the carboxyl group (cationic form), making it neutral. This analysis confirms the on/off hydrogen bonding in the carboxyl group along its protonation state, suggested earlier by the molecular center-of-mass RDF. All in all, changes in the local solvation shell structure with respect to the protonation state of the glycine molecule are clearly indicated by the solute-atom–CMwater RDF.
The present results can be compared with data reported in the literature.28 For pointing out differences and similarities, we have only considered the case of zwitter-ionic glycine and only for the solvation structure around the carboxyl group oxygens. The average number of waters connected to these oxygen atoms is 2.2 from the earlier study while a value of 2.6 was obtained by the present study. The difference can be explained easily since in full ab initio MD the dispersion interaction between solute–solvent subsystems is not accounted while in the CP-QM/MM MD it is included. This results in an increased number of solvents in the coordination shell. We also point out that in a recent report on the semicontinuum based calculation of core-electron chemical shifts for glycine,5 a coordination number of 3 for these oxygen atoms was considered.
3.2 MM-cutoff convergence
We have also investigated the convergence of the evaluated binding energy values with respect to different sizes of the MM region included in the binding energy calculations. To study the effect of the used cut-off radius for binding energies, MM-0 and MM-1 force fields for the solvent molecules were used. The analysis is based on one snapshot only, from the close-counter-ion runs and the resulting binding energy curves are presented in Fig. 3, for N1s (a) and C1s (b and c) hole states.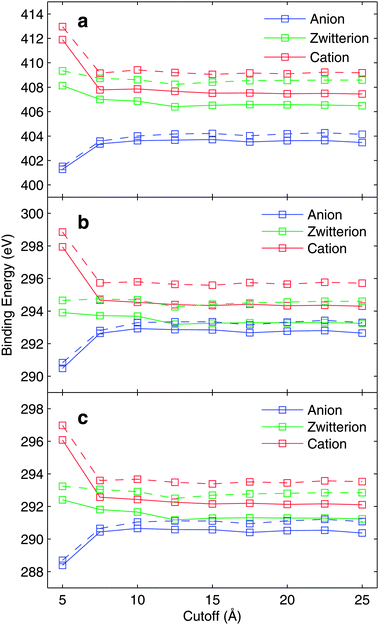 | ||
| Fig. 3 The convergence of (a) N, (b) CCOO, and (c) CCH2 core-electron binding energies with respect to MM-cutoff radius. The solid line represents the MM-1 force field and the broken line represents the MM-0 force field. The results are based on one snapshot only. For details see text. | ||
As seen from the figure, a substantial change in the core-electron binding energies is observed only for small cut-off radii in the case of anionic and cationic glycine; this is partly due to the counter-ion located close to the molecule. More modest variations in the zwitterionic binding energy curve as a function of cut-off radius are seen. Based on Fig. 3 we conclude that the cut-off radius of 10 Å is sufficient.
The convergence behaviour can qualitatively be analyzed by the two major contributions to binding energy and chemical shift; initial state electrostatic contribution and final state polarization. Both of them evidently depend critically on the distribution of solvent molecules. In a uniform continuum the polarization is limited to the Born value of a charged molecule with a specific radius merged (shift relating as inverse effective radius) into a solvent characterized by its dielectric constant. In the absence of ions the electrostatic contribution relates mostly to the first solvation shell structure, while more distant contributions tend to cancel out in a well sampled solvent. Therefore the cutoff curves give important evidence when a supermolecular model can be expected to hold for describing core ionization binding energies.
These two contributions can be studied by comparing the bare-electrostatics model (MM-0 force field), and the polarizable model including isotropic polarizability for the water molecules (MM-1 force field). As Fig. 3 displays the convergence with respect to electrostatics, the binding-energy difference between MM-1 and MM-0, evaluated for the same snapshot, can be considered to be representing the dielectric polarization contributions. Strictly speaking this is not the case as in the MM-0 force field slightly larger partial charges for the water molecule are used in order to implicitly account for polarization effects in the solid state environment.
Fig. 4 depicts the dielectric contribution to the core electron binding energies evaluated in the manner described above. As the total binding energy as a function of cutoff radius converges to slight oscillations in Fig. 3, the dielectric contribution depicted in Fig. 4 converges very slowly. The binding energy curves in Fig. 3 show very similar behaviour for electrostatics-only (MM-0) and polarization-included (MM-1) models.
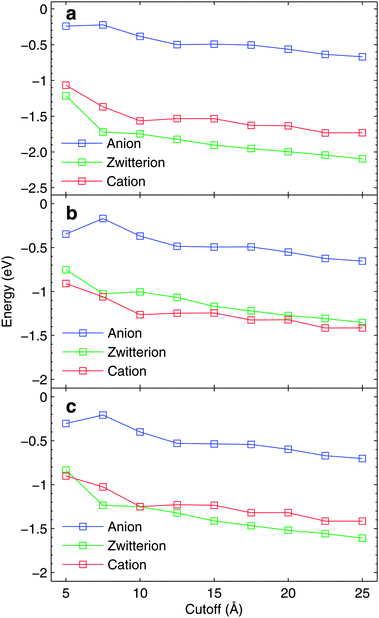 | ||
| Fig. 4 The dielectric contributions to (a) N, (b) CCOO, and (c) CCH2 core-electron binding energies with respect to MM-cutoff radius. The results are based on one snapshot only using MM-1 force field. For details see text. | ||
Although presented in much more magnified range of values, the fully converged dielectric contribution would require a cutoff radius definitely larger than 25 Å, causing a significant increase in the required computational resources. As the dielectric contribution shows a monotonical trend towards lower binding energies due to relaxation, it can be expected that the results with 15 Å cutoff overestimate slightly the binding energies. For cationic and zwitterionic glycine, the dielectric contributions are larger than for the anionic case.
3.3 MM-convergence
To test the convergence with respect to the used MM force field, simulations with different MM models (0–4) were carried out and 20 snapshots with a cut-off radius of 15 Å were extracted and used for the final analysis. The average binding energies are reported in Table 2. The results are based on CP-QM/MM MD runs where the counter-ion is located very close to the cationic or anionic glycine.| Anion | Zwitterion | Cation | |
|---|---|---|---|
| N (MM-0) | 404.59 | 408.44 | 409.08 |
| N (MM-1) | 403.85 | 406.89 | 407.41 |
| N (MM-2) | 404.15 | 407.12 | 407.64 |
| N (MM-3) | 404.24 | 407.09 | 407.54 |
| N (MM-4) | 404.24 | 407.07 | 407.52 |
| CCOO (MM-0) | 293.66 | 294.29 | 296.05 |
| CCOO (MM-1) | 293.07 | 293.31 | 294.62 |
| CCOO (MM-2) | 293.54 | 293.60 | 294.75 |
| CCOO (MM-3) | 293.76 | 293.75 | 294.78 |
| CCOO (MM-4) | 293.78 | 293.75 | 294.75 |
| CCH2 (MM-0) | 291.30 | 292.46 | 293.50 |
| CCH2 (MM-1) | 290.68 | 291.29 | 292.05 |
| CCH2 (MM-2) | 291.02 | 291.50 | 292.19 |
| CCH2 (MM-3) | 291.13 | 291.53 | 292.12 |
| CCH2 (MM-4) | 291.13 | 291.51 | 292.10 |
For the transfer from the MM-3 to the MM-4 model, the maximal deviation for the average of the 20 snapshots is only 0.03 eV. The major shift occurs going from MM-0 to MM-1, which reflects the large effect of the final state polarization, which is typically 1–2 eV for organic molecules. We see, as expected, different contributions of the polarization between cations, zwitterions and anions, where the former shows the largest effect. The Coulomb and polarization contributions to the solvation shift of ionization energies of charged molecular systems are in general of comparable importance. These quantities add cooperatively for the total shift; negatively for the cations and positively for the anions. This results in a quite substantial cationic shift, while in all cases the anion shifts end up being only a few tenths of an eV. The zwitterionic shifts seem to be intermediate between the cationic and the anionic shifts in all cases. Moving from MM-1 to MM-2 reflects the role of polarizability decomposition in the solvent molecules. As indicated from earlier studies on XPS chemical shifts using simple decomposition schemes,44–46 this gives additions to the shift in order of a couple of tenths of an eV and only due to the solvent molecules close to the DFT region. Therefore, we conclude that the MM-2 model is suitable for binding energy analysis with the accuracy that the used DFT/MM approach can provide in the current case.
To study the statistical convergence in the simulation, we calculated the running standard deviation σ for the core-electron binding energies for 100 snapshots extracted from the CP-QM/MM MD trajectory. The curves are presented in Fig. 5 for N1s and C1s hole states, respectively. For both close-counter-ion and distant-counter-ion CP-QM/MM MD runs, clear convergence is seen.
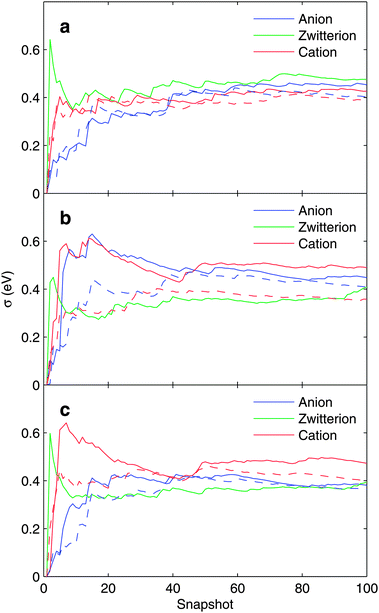 | ||
| Fig. 5 Running standard deviation σ (in eV) for (a) N, (b) CCOO, and (c) CCH2 core-electron binding energies. The solid line represents the case of a distant counter-ion and the broken line represents the case of a close-lying counter-ion. For details see text. | ||
3.4 Core-electron binding energies
As discussed in the introduction, there are two limit cases for simulations of anionic and cationic glycine, the close-lying counter-ion, and the limit of infinite distance. This is, of course, a naive interpretation as in reality the solution contains a large number of ions and cations. Applying this simple one-ion approximation, we modeled the two cases as the extreme values. The results, obtained as the average over the 100 snapshots for the MM-4 force field and 15 Å cutoff, are presented in Table 3.| Anion | Zwitterion | Cation | |
|---|---|---|---|
| N (close counter-ion) | 404.36 | 407.17 | 407.47 |
| N (distant counter-ion) | 403.57 | — | 407.78 |
| N exp. | 404.30 | 406.81 | 406.91 |
| CCOO (close counter-ion) | 293.91 | 293.87 | 294.78 |
| CCOO (distant counter-ion) | 293.16 | — | 295.30 |
| CCOO exp. | 293.22 | 293.55 | 294.53 |
| CCH2 (close counter-ion) | 291.20 | 291.62 | 292.06 |
| CCH2 (distant counter-ion) | 290.44 | — | 292.50 |
| CCH2 exp. | 290.67 | 291.43 | 291.88 |
As seen from the table, the shifts of the zwitterionic case vary in the range 0.2 eV–0.4 eV. The experimental N1s and C1s core electron binding energies for anionic glycine are all in between the values obtained with close and distant counter-ions. For cationic glycine, the calculated values overestimate slightly the experimental values.
Of course like for any quantum chemical method, the absolute binding energies for DFT are more sensitive to parametrization (density functional and basis set in the present case) than for the chemical shifts, which are obtained for different nonequivalent atoms and phase space configurations. We evaluated the energy shifts with respect to the zwitterionic form from our simulations; the results are presented in Table 4.
| Anion | Cation | |
|---|---|---|
| N (close counter-ion) | −2.8 | 0.29 |
| N (distant counter-ion) | −3.6 | 0.61 |
| N exp. | −2.5 | 0.10 |
| CCOO (close counter-ion) | 0.04 | 0.91 |
| CCOO (distant counter-ion) | −0.71 | 1.43 |
| CCOO exp. | −0.33 | 0.98 |
| CCH2 (close counter-ion) | −0.42 | 0.44 |
| CCH2 (distant counter-ion) | −1.18 | 0.89 |
| CCH2 exp. | −0.76 | 0.45 |
It is evident from Table 4 that the chemical shifts for anionic and cationic glycine with respect to the zwitterionic form vary drastically between the runs with different counter-ion distances. For N1s, the shifts are overestimated by the calculations, especially for distant counter-ions, and for carbon atoms the experimental values fall in between the two opposite cases studied – the close-lying and infinitely far counter-ions. As the glycine molecule provides a nice test case containing two non-equivalent C atoms, we also evaluated explicitly their chemical shift with respect to each other for both counter-ion distances, close and distant. The results are presented in Table 5.
| Anion | Zwitterion | Cation | |
|---|---|---|---|
| Close counter-ion | 2.71 | 2.25 | 2.72 |
| Distant counter-ion | 2.72 | — | 2.80 |
| Exp. | 2.55 | 2.12 | 2.65 |
Table 5 shows that the chemical shift between CCH2 and CCOO is not very sensitive to the molecule–counterion distance.
Lastly, we studied line widths produced by the phase-space sampling and vertical binding energy evaluation. From the standard deviation σ of the statistical core-electron binding energy distribution, the full widths at half maximum (FWHM) of the corresponding Gaussian distribution can be calculated by
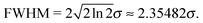 | (1) |
| Anion | Zwitterion | Cation | |
|---|---|---|---|
| N (close counter-ion) | 0.950 | 1.121 | 0.925 |
| N (distant counter-ion) | 1.067 | — | 1.004 |
| N exp. FWHM | 1.20 | 1.40 | 1.45 |
| CCOO (close counter-ion) | 0.964 | 0.962 | 0.843 |
| CCOO (distant counter-ion) | 1.055 | — | 1.153 |
| CCOO exp. FWHM | 1.05 | 1.07 | 1.10 |
| CCH2 (close counter-ion) | 0.855 | 0.929 | 0.946 |
| CCH2 (distant counter-ion) | 0.898 | — | 1.114 |
| CCH2 exp. FWHM | 1.10 | 1.10 | 1.17 |
Comparing the estimated FWHM values to the experimental ones, we first notice that the distant-ion runs always yield larger numbers. This is at first sight somewhat contradictory since small displacements in the ion–molecule distance are relatively larger for the close-lying counter-ion. The obtained values do not include life-time broadening (approximately 0.1–0.2 eV), quantized vibrational structure (Franck-Gondon profile), and the experimental broadening of the photoelectron line. As in the CP-QM/MM MD simulations the molecules are treated flexible, zero-point averaging contributions are represented in a classical sense in addition to broadening due to electronic structure variation with respect to the sample conformations. Thus the final spectrum is built up by the superposition of vertical core-electron excitations over the sampled conformation, thus leaving out the Franck–Condon effect. Therefore the obtained values are expected to be somewhat smaller than the experimental ones, which really is the case.
3.5 Charge transfer
Since charge transfer between the solute and solvent plays a role in the solvation energetics, it is expected to contribute also in the final state electronic relaxation of the system after core-electron ionization. As the molecule subject to ionization loses one electron in a timescale too quick for the nuclear rearrangement, charge transfer from the solvent to ionic state is expected to reduce the binding energy of the core-electron. So far in this study we have used a pure solute-DFT–solvent-MM representation for the DFT/MM calculations. As charge transfer between the two parts, DFT and MM, is not accounted for only the internal molecular screening of the core hole was included in the model. If such screening takes intermolecular contributions a more general supermolecular model is called to include closest solvation molecules to the DFT part of the system. To evaluate charge transfer between the solute and the solvent, two approaches were chosen. First, supermolecular cluster calculations were performed and second, straightforward extension of the DFT region, to cover also the closest water molecules in the DFT/MM calculation, was performed.The cluster geometries were obtained from previous equilibrium MD simulations using the ‘‘cluster’’ code included in GROMACS to select representative structures from the trajectories generated by the MD simulations. With a cutoff value of 8 from glycine, we got 10 average structures representing the trajectory of 100 frames used for DFT/MM. For each of such averaged structures, we then selected a cluster with glycine plus all the water molecules within 4.5 Å from the N atom in the NH3+ group or within 4.5 Å from the C atom in the COO− group, corresponding to an average number of 33 water molecules for each cluster. The resulting clusters are depicted in Fig. 6.
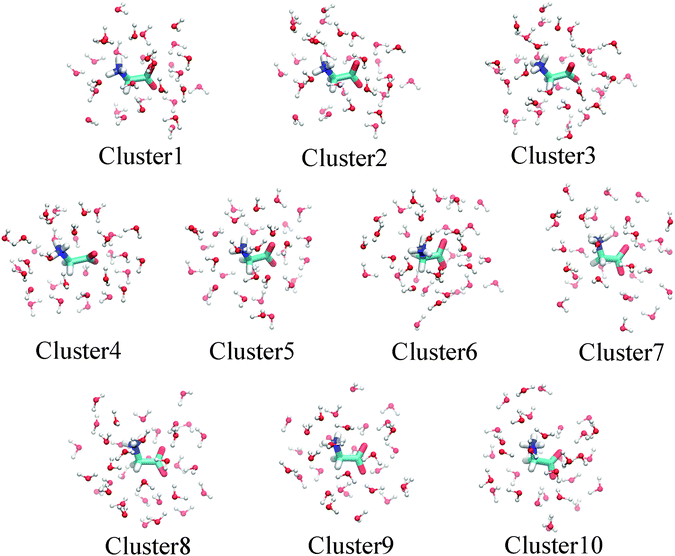 | ||
| Fig. 6 Structure of selected clusters used in the supermolecular binding energy evaluation. For details see the text. | ||
The core ionization potentials for each of the 10 clusters were calculated using the DALTON code.40 From the energy of the ground and core ionized state, the photoemission spectra (XPS) were simulated considering the intensity proportional to the number of configurations explored by the MD simulation and associated with a specific structure (cluster). The computed bar spectra in Fig. 7 and 8 show a rather large statistical spreading in energy, but the contribution of cluster 6, where the glycine zwitterion is surrounded by 35 water molecules, is dominant because it represents about 50% of the configurations sampled by the MD.
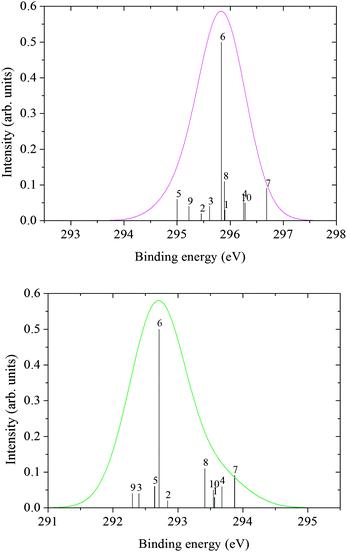 | ||
| Fig. 7 C XPS spectra from cluster ΔKS calculations: COO (top), CH2 (bottom). | ||
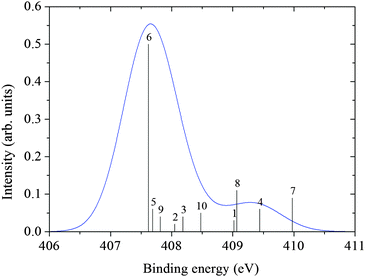 | ||
| Fig. 8 N XPS spectrum from cluster ΔKS calculations. | ||
Our second approach to charge transfer is simple extension of the DFT regime in DFT/MM to cover closest solvent molecules. In this work, we performed a series of calculations including 6 water molecules, closest to the N and C (carboxyl) atoms, explicitly in the DFT region. For these solvent water molecules the 6-31+G* basis set31–33 was used, and the MM-2 force field was utilized for the other waters within the 15 Å cutoff radius. As the difference between the MM-2 and MM-4 is quite small (≈10 meV according to Table 2), this choice was made to reduce the computation time needed. The 100 snapshots of the runs with distant counter-ion were used, but due to non-converging core-hole states, a maximum of 3 snapshots were not used in calculation of the average values presented in Table 7.
| Anion | Zwitterion | Cation | |
|---|---|---|---|
| N (distant counter-ion) | 403.28 | 406.84 | 407.40 |
| N exp. | 404.30 | 406.81 | 406.91 |
| CCOO (distant counter-ion) | 292.85 | 293.70 | 295.25 |
| CCOO exp. | 293.22 | 293.55 | 294.53 |
| CCH2 (distant counter-ion) | 290.23 | 291.52 | 292.45 |
| CCH2 exp. | 290.67 | 291.43 | 291.88 |
The first observation about explicit-DFT solvent molecules is that the results are very close to those of MM-4 without any explicit water molecules. As the MM-2 and MM-4 yield very similar results, it can therefore be concluded that charge transfer does not alter the obtained results to a large extent. Typical relaxation originating from the charge transfer from the closest 6 waters is about 20 meV in magnitude, always downwards in energy as expected.
| N | CCH2 | CCOO | |
|---|---|---|---|
| Neutral | 405.58 (+0.18) | 293.09 (+0.79) | 296.70 (+1.50) |
| Exp.14 (gas phase) | 405.40 | 292.30 | 295.20 |
| Zwitterion | 411.14 (+4.33) | 293.89 (+2,46) | 294.70 (+1.15) |
| Zwitterion + 35 waters | 407.62 (+0.81) | 292.71 (+1.28) | 295.83 (+2.28) |
| Zwitterion + MM-4 (15 Å cutoff) | 407.17 (+0.36) | 291.62 (+0.19) | 293.87 (+0.32) |
| Zwitterion + 6 waters + MM-2 (15 Å cutoff) | 406.84 (+0.03) | 291.52 (+0.09) | 293.70 (+0.15) |
| Exp.5 (solution) | 406.81 | 291.43 | 293.55 |
The data in Table 8 show the variation of the N, CCH2 and CCOO binding energies going from glycine in the gas phase to glycine in water solution at neutral pH. The first change that may be considered is the migration of the proton from the carboxylic group to the amino group in order to pass from the neutral glycine to the zwitterionic glycine. Since the zwitterion is stable only in the presence of the solvent, calculations were performed at a molecular geometry derived from cluster 6 after removing the water molecules. As it could be expected, the conversion of neutral glycine to a strongly polarized molecule has large initial state effects on the core binding energies. When comparing the values for zwitterionic and neutral glycine (third and first row in Table 8) we find that the N core binding energy of the protonated amino group (NH3+) in the zwitterion increases by about 6 eV while the core binding energy of the carbon atom of the carboxylate group CCOO decreases by about 2 eV. Only a minor effect is observed for CCH2 because it is only indirectly affected by the proton transfer. As previously mentioned, the stabilization of the zwitterionic form is due to the presence of the water molecules.
The water molecules also have a different stabilization effect on the charged initial state, strongly polarized but totally neutral, and on the final core ionized cationic state, that is accomplished mainly by a structural relaxation and polarization of the solvent and a solute–solvent charge transfer. A predominant final state effect can be anticipated and it is actually confirmed by the cluster calculations in the fourth row of the table. As a consequence all the binding energies decrease in comparison to those of the bare zwitterion obtained in the absence of the solvent; their deviations from the experimental (solution) data are appreciable but, except for a common energy shift, they are in line with the deviations (see first row) previously found14 for glycine in the gas phase. A cluster calculation includes, in the limit of the approximated method employed, all the stabilization effects mentioned above but, of course, gives only a partial representation of the solvent: namely the first solvation shell in present calculations. Extending the model to the second or third shell would be computationally demanding already for glycine and rapidly prohibitive for large molecules in solution. The alternative way here investigated, based on a force-field representation of the solvent molecules, leads to the result collected in the fifth row of Table 8. Instead of charge transfer, intermolecular coulombic and polarization effects can be attributed to most of the binding energy shift caused by the solvent environment. This conclusion becomes even clearer when the results from the DFT/MM calculation with extended DFT region are considered (sixth row in Table 8). As discussed above, the effect of charge transfer in the model used is of order 20 meV.
In addition to charge transfer, for core ionization there is an additional, mostly overlooked, effect that comes into play; the coupling between internal core hole relaxation and external solvent interaction. Such coupling introduces a more complete contraction and screening around the core hole and has been indicated to contribute several tenths of an eV for molecules like water and benzene.46 This coupled relaxation is recapitulated by a full quantum representation, while it is not caught by the PCM model and probably not by single solute DFT/MM models, being included in the two models with explicit water molecules in Table 8.
4 Conclusions
The hybrid density functional theory–molecular mechanics method is to date the most general method, albeit hitherto untested, for simulations of core electron energies and their chemical shifts. DFT/MM provides an atomically granulated representation over a substantial portion of the solution (in this work 25 Å) only limited by the capability of the classical dynamics simulation model. Full contribution to the binding energy shifts from interaction within and between the DFT and MM parts is accounted for, while charge transfer between the two parts is neglected. In this paper, a multiscale modeling DFT/MM technique was applied to model the structure and core-electron binding energies for the glycine molecule in aqueous solution. The three different forms of the glycine molecule according to the protonation state were considered: anionic, zwitterionic and cationic.Molecular dynamics simulations allowed identification of some salient structural variations, important for binding energies and their shifts. The solvation shell structures show clear alternation of hydrogen bonding with respect to the protonation state of the polar amino and carboxyl groups. The NH3 group shows more uniform hydrogen bonding lengths than NH2 since the symmetrically located protons block direct bonding to N. In addition, the carboxyl group was found to exhibit a clear on/off feature in hydrogen bonding when being protonated neutral.
The DFT/MM approach, integrating the main contributions to the binding energy shifts, like initial state electrostatic and final state polarization, allows for an evaluation when a more expedient supermolecular quantum model can hold. The cutoff for the solvent molecules is clearly system dependent, for instance anion shifts converge slower than cationic shifts. As XPS probes the configurations of ionic solutions effectively, such studies depend on a careful sampling of the phase space. In the particular case studied the role and positions of counterions serve as a crucial, and complicating, feature not present in “normal” organic photoionization. By comparing two opposite cases of counterion influence, we find the role of such ions to be decisive for reliable binding energy evaluation: the results show strong dependency, in both absolute values and ESCA shifts, between different forms of glycine. As the charge transfer between DFT–MM divisions is neglected in the model, an explicit quantum chemical method for the first solvation shell was tested in two models, a cluster approach and an extended DFT region in the DFT/MM.
Comparison allowed assigning a couple of tens of eV to charge transfer (both solvational and core hole induced), leading to the conclusion that in the current case the main solvent effects originate from Coulombic interaction and solvent polarization. Therefore, at least for qualitative evaluation of binding energies, a single solute DFT model is viable for the DFT/MM approach.
Acknowledgements
This work was supported by a grant from the Swedish National Infrastructure for Computing (SNIC) for the project “Multiphysics Modeling of Molecular Materials”, SNIC 023/07-18. J.N. would like to thank Jenny and Antti Wihuri foundation for financial support.References
- K. Siegbahn, C. Nordling, A. Fahlman, R. Nordberg, K. Hamrin, J. Hedman, G. Johansson, T. Bergmark, S.-E. Karlsson, I. Lindgren and B. Lindberg, ESCA – Atomic Molecular, and Solid State Structure Studied by means of Electron Spectroscopy, Almqvist & Wiksells, 1967 Search PubMed.
- K. Siegbahn, C. Nordling, G. Johansson, J. Hedman, P. F. Heden, K. Hamrin, U. I. Gelius, T. Bergmark, L. O. Werme, R. Manne and Y. Baer, ESCA Applied to free molecules, North-Holland, 1969 Search PubMed.
- B. Winter and M. Faubel, Chem. Rev., 2006, 106, 1176 CrossRef CAS and references therein.
- B. Winter, Nucl. Instrum. Methods Phys. Res., Sect. A, 2009, 601, 139 CrossRef CAS.
- N. Ottoson, K. J. Børve, D. Spångberg, H. Bergersen, L. Sæthre, M. Faubel, W. Pakapanich, G. Öhrwall, O. Björneholm and B. Winter, J. Am. Chem. Soc., 2011, 133, 3120 CrossRef.
- B. M. Messer, C. D. Cappa, J. D. Smith, K. R. Wilson, M. K. Gilles, R. C. Cohen and R. J. Saykally, J. Phys. Chem. B, 2005, 109, 5375 CrossRef CAS.
- B. M. Messer, C. D. Cappa, J. D. Smith, W. S. Drisdell, C. P. Schwartz, R. C. Cohen and R. J. Saykally, J. Phys. Chem. B, 2005, 109, 21640 CrossRef CAS.
- T. P. Debies and J. W. Rabalais, J. Electron. Spectrosc. Relat. Phenom., 1974, 3, 315 CrossRef CAS.
- L. Klasinc, J. Electron Spectrosc. Relat. Phenom., 1976, 8, 161 CrossRef CAS.
- P. H. Cannington and N. S. Ham, J. Electron Spectrosc. Relat. Phenom., 1979, 15, 79 CrossRef CAS.
- P. H. Cannington and N. S. Ham, J. Electron Spectrosc. Relat. Phenom., 1983, 32, 139 CrossRef CAS.
- A. R. Slaughter and M. S. Banna, J. Phys. Chem., 1988, 92, 2165 CrossRef CAS.
- O. Plekan, V. Feyer, R. Richter, M. Coreno, M. de Simone, K. C. Prince and V. Carravetta, J. Electron Spectrosc. Relat. Phenom., 2007, 155, 47 CrossRef CAS.
- O. Plekan, V. Feyer, R. Richter, M. Coreno, M. de Simone, K. C. Prince and V. Carravetta, J. Phys. Chem. A, 2007, 111, 10998 CrossRef CAS.
- P. S. Bagus, Phys. Rev., 1965, 139, A619 CrossRef.
- P. S. Bagus, O. Coolbaugh, S. P. Kowalczyk, G. Pacchioni and F. Parmegian, J. Electron Spectrosc. Relat. Phenom., 1990, 51, 69 CrossRef CAS.
- L. Triguero, L. G. M. Pettersson and H. Ågren, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 8097 CrossRef CAS.
- L. Triguero, O. Plashkevych, L. G. M. Pettersson and H. Ågren, J. Electron Spectrosc. Relat. Phenom., 1999, 104, 195 CrossRef CAS.
- J. C. Slater, Adv. Quantum Chem., 1972, 6, 1 CrossRef CAS.
- D. P. Chong, Chem. Phys. Lett., 1995, 232, 486 CrossRef CAS.
- D. P. Chong, J. Chem. Phys., 1995, 103, 1842 CrossRef CAS.
- H. Ågren, C. Medina Llanos and K. V. Mikkelsen, Chem. Phys., 1986, 115, 43 CrossRef.
- M. Arbman, H. Siegbahn, L. Pettersson and P. Siegbahn, Mol. Phys., 1985, 54, 1149 CrossRef CAS.
- H. Ågren and V. Carravetta, Mol. Phys., 1985, 55, 901 CrossRef.
- H. Ågren and H. Siegbahn, J. Chem. Phys., 1984, 81, 488 CrossRef.
- H. Ågren and H. Siegbahn, Chem. Phys., 1985, 95, 37 CrossRef.
- C. A. Aikens and M. S. Gordon, J. Am. Chem. Soc., 2006, 128, 12835 CrossRef CAS.
- J. Sun, D. Bousquet, H. Forbert and D. Marx, J. Chem. Phys., 2010, 133, 114508 CrossRef.
- S. M. Bachrach, J. Phys. Chem. A, 2008, 112, 3722 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213 CrossRef CAS.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. v. R. Schleyer, J. Comput. Chem., 1983, 4, 294 CrossRef CAS.
- M. J. Frisch,G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al- Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzlez and J. A. Pople, Gaussian 03, Revision B.04, Gaussian, Inc., Pittsburgh, PA, 2003 Search PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926 CrossRef CAS.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157 CrossRef CAS.
- J. Niskanen, V. Carravetta, O. Vahtras, H. Ågren, H. Aksela, E. Andersson, L. Hedin, P. Linusson, J. H. D. Eland, L. Karlsson, J.-E. Rubensson and R. Feifel, Phys. Rev. A, 2010, 82, 043436 CrossRef.
- J. Niskanen, E. Andersson, J. H. D. Eland, P. Linusson, L. Hedin, L. Karlsson, R. Feifel and O. Vahtras, Phys. Rev. A, 2012, 85, 023408 CrossRef.
- H. J. Aa. Jensen, P. Jørgensen and H. Ågren, J. Chem. Phys., 1987, 87, 451 CrossRef.
- DALTON, a molecular electronic structure program, Release 2.0, 2005, see http://daltonprogram.org/ Search PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1995, 103, 4572 CrossRef CAS.
- Z. Rinkevicius, N. Arul Murugan, J. Kongsted, K. Aidas, A. H. Steindal and H. Ågren, J. Phys. Chem. B, 2011, 115, 4350 CrossRef CAS.
- C. Medina-Llanos and H. Ågren, Phys. Rev. B, 1988, 38, 11785 CrossRef CAS.
- K. Mikkelsen, H. Ågren, H. J. Aa. Jensen and T. Helgaker, J. Chem. Phys., 1988, 89, 3086 CrossRef CAS.
- C. Medina-Llanos, H. Ågren, K. V. Mikkelsen and H. J. Aa. Jensen, J. Chem. Phys., 1989, 90, 6422 CrossRef CAS.
| This journal is © the Owner Societies 2013 |
