A combined high-field EPR and quantum chemical study on a weakly ferromagnetically coupled dinuclear Mn(III) complex. A complete analysis of the EPR spectrum beyond the strong coupling limit†
Marius Reteganab, Marie-Noëlle Collomba, Frank Neeseb and Carole Duboc*ac
aUniversité Joseph Fourier Grenoble 1/CNRS, Département de Chimie Moléculaire, UMR-5250, Laboratoire de Chimie Inorganique Redox, Institut de Chimie Moléculaire de Grenoble FR-CNRS-2607, BP-53, 38041 Grenoble Cedex 9, France. E-mail: carole.duboc@ujf-grenoble.fr
bMax-Planck-Institut für Bioanorganische Chemie, Stiftstr. 34-36, D-45470 Mülheim an der Ruhr, Germany
cLaboratoire National des Champs Magnétiques Intenses, CNRS, UPR 3228, 25 avenue des Martyrs, BP166, 38042 Grenoble, France
First published on 24th October 2012
Abstract
The electronic and magnetic properties of polynuclear complexes, in particular the magnetic anisotropy (zero field splitting, ZFS), the leading term of the spin Hamiltonian (SH), are commonly analyzed in a global manner and no attempt is usually made to understand the various contributions to the anisotropy at the atomic scale. This is especially true in weakly magnetically coupled systems. The present study addresses this problem and investigates the local SH parameters using a methodology based on experimental measurements and theoretical calculations. This work focuses on the challenging mono μ-oxo bis μ-acetato dinuclear MnIII complex: [Mn2III(μ-O)(μ-OAc)2L2](PF6)2 (with L = trispyrrolidine-1,4,7-triazacyclononane) (1), which is particularly difficult for EPR spectroscopy because of its large magnetic anisotropy and the weak ferromagnetic interaction between the two MnIII ions. High field (up to 12 T) and high frequency (190–345 GHz) EPR experiments have been recorded for 1 between 5 and 50 K. These data have been analyzed by employing a complex Hamiltonian, which encompasses terms describing the local and inter-site interactions. Density functional theory and multireference correlated ab initio calculations have been used to estimate the ZFS of the MnIII ions (DMn = +4.29 cm−1, EMn/DMn = 0.19) and the Euler angles reflecting the relative orientation of the ZFS tensor for each MnIII (α = −52°, β = 28°, γ = 3°). This analysis allowed the accurate determination of the local parameters: DMn = +4.50 cm−1, EMn/DMn = 0.07, α = −35°, β = 23°, γ = 2°. The spin ladder approach has also been applied, but only the parameters of the ground spin state of 1 have been accurately determined (D4 = +1.540 cm−1, E4/D4 = 0.107). This is not sufficient to allow for the determination of the local parameters. The validity and practical performance of both approaches have been discussed.
1. Introduction
Transition metal ion complexes are involved in many domains such as biology, catalysis, condensed matter physics and materials science. In view of understanding their chemical reactivity and/or their physical properties a large number of experimental techniques are used to characterize their electronic and magnetic properties. Although EPR spectroscopy is probably the best tool for measuring the magnetic anisotropy, conventional EPR spectrometers are usually inoperative in the case of paramagnetic metallic compounds because of too large D values (axial part of the zero field splitting, ZFS) or/and weak magnetic exchange interaction (J) in polynuclear systems (|J| ≈ or ≪ |ZFS|). Either the EPR signal is absent or the obtained data are too complex to be analyzed. Yet weakly coupled dimers can be found in areas as diverse as biochemistry and molecular magnetism, in addition to inorganic and bio-inorganic chemistry.On the other hand, high field and high frequency EPR spectroscopy (HF-EPR) has been successful in elucidating the magnetic anisotropy of mononuclear transition metal ion complexes with large ZFS1–7 and of strongly coupled high spin polynuclear clusters, including single molecule magnets.8–11 However, for these latter compounds, the goal of the reported studies was mainly the determination of the ZFS of the entire system, and no attempt was generally made to understand the various contributions to the anisotropy at the single-ion level. It can still be noticed that with the aim of performing rational synthesis, a few investigations using ligand field approaches have been reported to assess the contribution of the local metallic ion anisotropy.12–14
Several X- and/or Q-band-EPR investigations have been also performed on magnetically coupled dinuclear complexes with S > 1/2 metallic ions in order to reach such information, especially the ZFS of each metallic ion. These systems have been described as a Heisenberg spin ladder, for which |J| ≫ |ZFS|, and the ZFS of the paramagnetic spin states involved in the EPR spectra have been determined.15–23 The advantage of this approach is that a detailed analysis of the EPR spectra gives access to an estimate of these ZFS values. From these spin ladder parameters, the ZFS of each metallic ion can be also estimated by means of empirical equations.24 However, in most cases, the condition |J| ≫ |ZFS| was not met which makes the results of the analysis questionable.
To properly analyze EPR spectra of polynuclear complexes with relatively weak magnetic exchange interaction (relative to the ZFS), the spin ladder description cannot be used as the zero-field splitting interaction will mix the various multiplets. The complexes are then best described in terms of local spin-Hamiltonian parameters together with the parameters characterizing the magnetic interaction (foremost the isotropic Heisenberg exchange J, but also terms such as the anisotropic exchange, or, in mixed-valence cases, the double exchange B). Consequently, the parameters used to simulate the EPR spectra, especially the ZFS of each metallic ion, cannot be estimated by a simple analysis of the data. However, during this last decade, quantum chemistry made significant progresses to predict the ZFS of number of transition metal ions.2,25–34 The relative importance of the distinct contributions to the ZFS (spin–spin and spin–orbit coupling) can vary substantially between the different metallic ions. The complexity of the problem therefore requires the use of theoretical tools adapted to each case. We have been able to demonstrate that DFT calculations correctly reproduce the measured ZFS of the MnII ion.35,36 For the MnIII ion, on the other hand, we have shown that ab initio complete active space self-consistent field (CASSCF) calculations are required because they are able to explicitly treat the excited spin states of different spin than the ground state. Unlike predicted by popular ligand field arguments, the spin–orbit coupling of these spin-flip states with the ground state makes the dominant contribution to the zero-field splitting in this case.4,37–39
In the present work, our main objective was to properly analyze EPR spectra of a weakly exchanged coupled polynuclear complex by means of a methodology based on the crucial use of theoretical calculations. A second focus of this work was to gain insight into the conditions under which the spin ladder approach is no longer valid. We will focus on the challenging example of the mono μ-oxo bis μ-acetato dinuclear manganese(III) complex: [Mn2III(μ-O)(μ-OAc)2L2](PF6)2 (with L = trispyrrolidine-1,4,7-triazacyclononane) (1). This system is particularly difficult for EPR spectroscopy because it shows large magnetic anisotropy as well as a weakly ferromagnetic interaction between the two MnIII ions (Fig. 1).40 Indeed, the high-spin d4 configuration of MnIII together with its relatively high oxidation state thus provides particularly large Jahn–Teller distortions with |D| values expected in the range of 2–5 cm−1. Our strategy was to obtain a complete set of HF-EPR spectra at variable temperature using a multifrequency approach, corresponding to the first EPR data obtained on a dinuclear MnIII complex. Then, by quantum chemistry, the ZFS parameters of each MnIII ion were calculated and used as initial values in fitting the experimental HF-EPR data. These data were also fitted using the spin ladder approach in order to reveal the success and limitations of this approach. Finally, the quality of the theoretical predictions will be critically assessed.
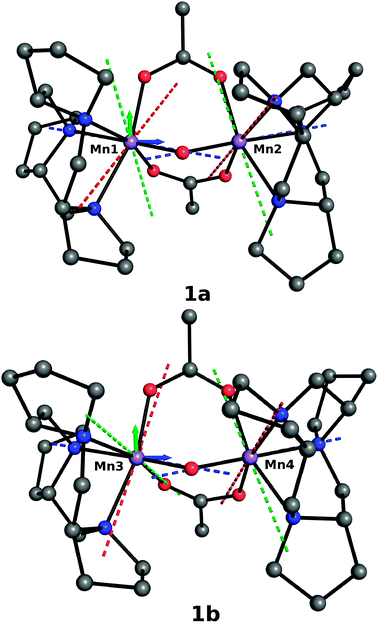 | ||
| Fig. 1 Principal axes of the DA and DB-tensors for the two dimers (1a and 1b) present in the X-ray structure (dashed lines). Dxx, Dyy, Dzz are red, green and blue respectively. | ||
2. Theory
2.1. The spin Hamiltonian
For the present manganese(III) dinuclear, the appropriate phenomenological spin Hamiltonian (excluding hyperfine coupling terms) is:| Ĥ = μBB·gA·ŜA + ŜA·DA·ŜA + μBB·gB·ŜB + ŜB·DB·ŜB + ŜA·DAB·ŜB | (1) |
ŜA·DAB·ŜB = −2JŜA·ŜB + ŜA·D·ŜB + ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0064_20d1.gif) ·ŜA × ŜB ·ŜA × ŜB | (2) |
![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0064_20d1.gif) is the Dzyaloshinskii–Moriya vector.41
is the Dzyaloshinskii–Moriya vector.41There are two experimentally undistinguishable contributions to the symmetrical part of the interaction: (i) the dipole–dipole interaction, which is a direct through space interaction between the two magnetic centers, and generally regarded as the most important contribution, and (ii) the spin–orbit contribution, also called the anisotropic exchange. If the separation between the two ions is large compared to the spatial extension of the dipoles themselves, we can approximate the spin–spin dipolar component by a classical interaction. The matrix elements of the DAB tensor are given by:
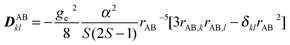 | (3) |
Following Moriya, the antisymmetric coupling in a complex that presents C2 symmetry does not vanish and is perpendicular to the two-fold rotation axis of the molecule.41
2.2. The spin ladder approach
In the strong exchange limit, i.e. the isotropic interaction outweighs the local anisotropic terms; the total spin quantum number S remains a good quantum number for the AB pair. In this case, the dinuclear complex is described as a spin ladder defined in terms of total spin S, where S can take values:| |SA − SB| ≤ S ≤ SA + SB | (4) |
| ES = −J[S(S + 1) − SA(SA + 1) − SB(SB + 1)] | (5) |
| ĤS = μBB·gS·Ŝ + Ŝ·DS·Ŝ | (6) |
| gS = cAgA + cBgB | (7) |
| DS = dADA + dBDB + dABDAB | (8) |
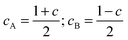 | (9) |
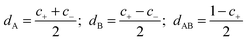 | (10) |
2.3. The on-site spectroscopic parameters
The interaction of the molecular magnetic dipole moment with an external magnetic field, i.e. the molecular Zeeman effect, is described by the g-tensor, and can be computed by solving the coupled-perturbed self-consistent field (CP-SCF) equations.The elements of the g-tensor can be calculated as a sum of four contributions:
| gkl = geδkl + ΔgRMCδkl + ΔgGCkl + ΔgOZ/SOCkl | (11) |
The zero-field splitting, which is parameterized by the D-tensor, describes the removal of the state degeneracy for systems with S > 1/2 in the absence of an applied magnetic field, and enters the following phenomenological Hamiltonian:
| HZFS = Ŝ·D·Ŝ | (12) |
| HZFS = D[Ŝz2 − ⅓S(S + 1)] + E(Ŝx2 − Ŝy2) | (13) |
D = ½(−Dxx − Dyy + 2Dzz) = ![[/]](https://www.rsc.org/images/entities/char_e0ee.gif) Dzz Dzz | (14) |
| E = ½(Dxx − Dyy) | (15) |
| |Dzz| > |Dyy| > |Dxx| | (16) |
From first principles, the D-tensor can be written as a sum of first- and second-order perturbational terms. For a single determinant ground state, the spin–spin coupling (SSC) contribution to the D-tensor is given by the equation of McWeeny and Mizuno:44
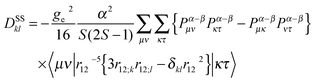 | (17) |
The treatment of the SOC part is somewhat more complicated. This is due to the fact that SOC mixes states of different multiplicity. The quantum mechanical form of these equations has been derived in 1998.25 The translation into a linear response formalism has only been attempted much more recently.45 Following the same line of thoughts, Van Wüllen has recently suggested a minor modification of the original formalism which amounts to using the same prefactor 1/S(2S − 1) for all contributions to the ZFS tensor.46 In our experience, either DFT based treatment is of limited predictive power. From a number of previous studies,3,37,39,47–49 we came to the conclusion that the calculation of the ZFS in transition metal complexes is best done on the basis of multireference ab initio treatments together with quasi-degenerate perturbation theory (QDPT) for the treatment of the SOC and SS interactions. This is a more suitable approach since, in contrast to DFT methods, the magnetic sublevels of all multiplets can be explicitly taken into account. The most efficient variant that incorporates at least the leading effects of dynamic electron correlation employs second order N-electron valence perturbation theory (NEVPT2), a strongly contracted form of second-order many body multireference perturbation theory.50–52 In cases where the ZFS is substantial, this treatment has been proven to be successful if at least the d–d excited multiplets are included in the treatment.53
2.4. The exchange coupling constant
The isotropic exchange interaction was modeled by the Heisenberg–Dirac–van Vleck (HDvV) Hamiltonian:| Ĥ = −2JŜA·ŜB | (18) |
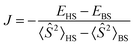 | (19) |
3. Materials and methods
3.1. Sample preparation
Complex 1 was synthesized according to the published procedure.40 The HF-EPR spectra have been recorded on a polycrystalline powder pellet to afford magnetic orientation of crystals.3.2. EPR measurements
HF-EPR spectra were recorded on a laboratory made spectrometer.58 Gunn diodes operating at 95 GHz and 115 GHz and equipped with a second- and third-harmonic generator have been used as the radiation source. The magnetic field was produced by a superconducting magnet (0–12 T).3.3. EPR simulations
The HF-EPR spectra were simulated with the Easyspin program.59 Due to the high complexity of the experimental spectra the fitting procedure was conducted on a limited number of peaks. Consequently, we have taken into account only the peaks for which our initial guess from quantum mechanical calculations provided an unambiguous determination (see main text for details). Subsequently we minimized the root mean square error of these peaks relative to experimental values. Finally the entire spectra were simulated.3.4. Computational details
Broken-symmetry DFT calculations were performed with the hybrid meta-GGA TPSSh functional.66 The coulomb and exchange parts were evaluated with the “chain-of-spheres” (RIJCOSX) algorithm.67 Increased integration grids (Grid4 and Gridx4 in ORCA convention) and tight SCF convergence criteria were used. Subsequently, the exchange coupling constants were computed with the Yamaguchi equation.
The exchange pathways are discussed by an analysis of the magnetic orbitals. Unambiguous identification of these orbitals was achieved on the basis of the corresponding orbital transformation (COT) of Amos and Hall.28,68,69 This transformation of canonical orbitals into corresponding orbitals leaves the broken symmetry determinant invariant and has the additional property that each spin-up orbital has a nonzero overlap with only a single spin-down orbital. The magnitude of the spatial overlap can serve as an indicator of the strength of the interactions in the system.
4. Results
4.1. Multifrequency high field EPR study
As no signal could be observed at 4.2 K on the powder X- and Q-band EPR spectra of complex 1, a high-field and high frequency EPR (HF-EPR) investigation has been carried out. The multifrequency HF-EPR study was achieved over a temperature range of 5–50 K, between 190 and 345 GHz, using a magnetic field up to 12 T. Fig. 2a, 3a and 4a illustrate the temperature and the frequency dependence of the resulting HF-EPR spectra. EPR transitions are spread over the entire range from 0 to 12 T at all frequencies. The shape of the transitions and their resolution point the fact that, due to the design of the home-built multifrequency HF-EPR spectrometer, the spectra correspond to a mixture of in-phase and out-of-phase signals. Therefore no quantitative analysis of the line intensity can be properly done but qualitative analysis can be performed which allows determination of the spin Hamiltonian parameters. It should be noted that above 25 K, the general appearance of the spectra no longer changes, only the overall intensity decreases. A weak transition located at g = 2 (10.2 T at 285 GHz and 8.2 T at 230 GHz) corresponding to a small amount of mononuclear MnII impurities is observed at low temperature.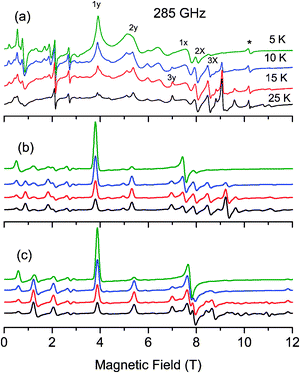 | ||
| Fig. 2 Experimental (a) and simulated (b–c) EPR powder spectra recorded at 285 GHz and at different temperatures. The simulated b spectra have been calculated by diagonalizing the 25 × 25 matrix (eqn (1)), and the simulated c spectra with the spin ladder approach taking into account the S = 4 and S = 3 spin states. | ||
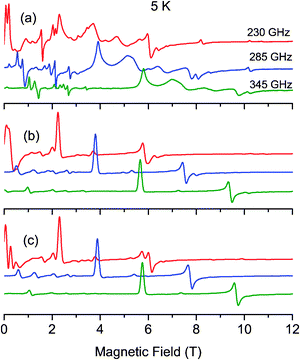 | ||
| Fig. 3 Experimental (a) and simulated (b–c) EPR powder spectra recorded at 5 K and at different frequencies. The simulated b spectra have been calculated by diagonalizing the 25 × 25 matrix (eqn (1)), and the simulated c spectra with the spin ladder approach taking into account the S = 4 spin state. | ||
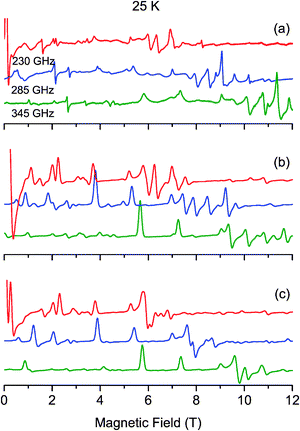 | ||
| Fig. 4 Experimental (a) and simulated (b–c) EPR powder spectra recorded at 25 K and at different frequencies. The simulated b spectra have been calculated by diagonalizing the 25 × 25 matrix (eqn (1)), and the simulated c spectra with the spin ladder approach taking into account the S = 4 and S = 3 spin states. | ||
The most intense and resolved EPR features are observed at low temperature in the low field region (below 4 T). They are assigned to “forbidden” transitions because (i) their intensity is enhanced as the EPR frequency decreases, (ii) they are located in the low field part of the spectra where strong-field limit conditions are not reached (ZFS ≫ gβB) and, (iii) more importantly, their field position dependency as a function of the frequency matches to a g value much greater than 2.
4.2. Theoretical calculations
| Mn–Ooxo | Mn–Na | Mn–OAc | Mn–Nb | Mn–OAc* | Mn–Nc | Mn–Ooxo–Mn | |
|---|---|---|---|---|---|---|---|
| a N in trans position from Ooxo.b N in trans position from OAc.c N in trans position from OAc*.d Structural parameters issued from ref. 36.e This work. | |||||||
| Mn1d | 1.785 | 2.141 | 2.053 | 2.228 | 2.063 | 2.217 | 122.93 |
| Mn2d | 1.821 | 2.111 | 2.021 | 2.193 | 2.130 | 2.223 | |
| Mn3d | 1.796 | 2.106 | 1.996 | 2.152 | 2.136 | 2.274 | 121.60 |
| Mn4d | 1.804 | 2.146 | 2.025 | 2.160 | 2.166 | 2.221 | |
| Mn (opt)e | 1.827 | 2.145 | 2.019 | 2.186 | 2.163 | 2.272 | 120.62 |
For high spin MnIII complexes, the anisotropy of the Zeeman interaction is very small leading to g-values close to 2. Already at the DFT level of theory the predicted g-values confirmed this lack of anisotropy with gx, gy and gz being equal to 1.998, 2.000, and 2.004, respectively, thus no further ab initio calculations were performed for this property.
Our previous systematic investigation on mononuclear MnIII complexes has shown that the best DFT-based approach for the calculation of the ZFS parameters corresponds to the combination of the coupled-perturbed (CP) approach for the spin–orbit coupling (SOC) part of the D-tensor, and the spin unrestricted natural orbital (UNO) variant for the calculation of the spin–spin coupling (SSC) part of D.39 This combination has been used in this work for predicting the ZFS parameters of the heterodinuclear models. All results are reported in Table 2. The DFT calculations predict a positive sign of D in all cases, consistent with the compressed tetragonal distortion of the octahedra observed in the X-ray structure of 1. This is quite unusual for MnIII, which is predominantly found in elongated octahedral geometry. Only two mononuclear MnIII complexes with a positive D value combined with a compressed tetragonal distortion have been described yet.4,72 As expected for a MnIII ion, the DSOC value represents the main contribution to D. On the other hand, the contribution of the spin–spin term (DSSC ∼ +0.35 cm−1) is not negligible since it represents about 16% of the total D value. Nevertheless, even with the corrected prefactors for the spin-flip term that enter the evaluation of the DSOC contribution,37 previous studies have shown that the DFT results consistently underestimate the calculated value of D.4,39 Consequently, the calculation of the ZFS parameters was also be handled at a multiconfigurational ab initio level. The resulting D values (between +3.69 and +4.10 cm−1) are noticeably larger than that calculated by DFT. We have also included dynamic correlation into the calculation by dressing the QDPT matrix with diagonal energies calculated with the NEVPT2 scheme. In the present case, the use of NEVPT2 energies increases the SOC contribution by about 20%, in agreement with previous reports,25,73 leading to total D values in the range of +4.14 to +4.30 cm−1. It should be noted that this effect was of minor importance in our previous systematic study on MnIII.39 In the absence of a macrocycle ligand, it has been experimentally observed by HF-EPR that the magnitude of D increases with the number of oxygenated-based ligands: 3.29 < |DN6| < 3.50; |DN4O2| = 3.52; |DN2O4| = 4.50; 4.35 < |DO6| < 4.52 cm−1.4,72,74–77 The predicted D values for the different optimized heterodinuclear MnIIIGaIII structures are therefore consistent with a MnIII ion in a N3O3 environment.
| Complex | Center | Method | D | E/D | DSSC | DSOC | α | β | γ |
|---|---|---|---|---|---|---|---|---|---|
| 1a | Mn1 | BP86 | 2.39 | 0.03 | 0.37 | 2.02 | −21 | 27 | 1 |
| SA-CASSCF | 4.14 | 0.02 | 0.46 | 3.67 | −28 | 28 | 0 | ||
| NEVPT2 | 4.76 | 0.02 | 0.46 | 4.30 | −28 | 28 | 0 | ||
| Mn2 | BP86 | 2.31 | 0.12 | 0.36 | 1.95 | 43 | 27 | 180 | |
| SA-CASSCF | 4.02 | 0.12 | 0.45 | 3.56 | 46 | 28 | 180 | ||
| NEVPT2 | 4.60 | 0.11 | 0.45 | 4.14 | 46 | 28 | 180 | ||
| 1b | Mn3 | BP86 | 2.17 | 0.23 | 0.34 | 1.83 | −51 | 27 | 2 |
| SA-CASSCF | 3.72 | 0.24 | 0.43 | 3.29 | −53 | 28 | 1 | ||
| NEVPT2 | 4.23 | 0.22 | 0.43 | 3.80 | −52 | 28 | 1 | ||
| Mn4 | BP86 | 2.17 | 0.22 | 0.34 | 1.83 | 50 | 27 | 178 | |
| SA-CASSCF | 3.84 | 0.21 | 0.43 | 3.41 | 52 | 27 | 178 | ||
| NEVPT2 | 4.39 | 0.19 | 0.43 | 3.96 | 52 | 27 | 177 | ||
| 1opt | Mn | BP86 | 2.15 | 0.20 | 0.35 | 1.80 | −51 | 27 | 3 |
| SA-CASSCF | 3.83 | 0.21 | 0.44 | 3.39 | −52 | 28 | 3 | ||
| NEVPT2 | 4.29 | 0.19 | 0.44 | 3.85 | −52 | 28 | 3 |
In addition to the magnitude of the D tensor components, the calculations also provided the orientation of their eigenframe with respect to the molecular frame, which can be expressed a set of three Euler angles, α, β and γ, summarized in Table 2. Interestingly the angle α, which specifies the orientation of the x and y principal axes of the ZFS tensor with respect to the molecular frame, presents a large variation among the metal centers, as can be seen more clearly from Fig. 1. Most probably this can be related to the particular local coordination environment of each MnIII ion in 1 that leads to principal axes of the anisotropy tensor that are not aligned along the metal–ligand bond, in contrast to Mn(H2O)6, in which it is the case. No attempts were made to further investigate the origin of this difference for both the magnitude or the orientation of the D tensor. Indeed, in our previous systematic study on mononuclear MnIII complexes, we have shown that the SA-CASSCF method permits an excellent prediction of D,39 we thus deemed that the values obtained for the symmetric dimer can be considered as a reasonable guess for our fitting procedure, while restraining all parameters within the limits of the data calculated from X-ray geometries. As previously emphasized this considerably reduces the parameter space employed in the spectral simulations which is an essential ingredient of our approach.
At the chosen theoretical level, both approaches give a ferromagnetic complex, with J equal to 8.5 cm−1 and 15.1 cm−1 for the “single geometry” and the “adiabatic” approach, respectively. Given the previously reported errors of approximately 30 cm−1 for the calculation of J,78 the present results are quite satisfactory. Interestingly, previous calculations on dinuclear MnIII complexes that present the same bridges (μ-O, 2μ-OAc) were unable to predict the correct sign for the coupling constant, most probably owing to the fact that J is very sensitive to structural parameters (vide infra).80,81
Inspection of the pairs of magnetic orbitals, resulted from a corresponding orbital transformation, offers a pictorial representation of the exchange interactions in the system. The subset of the magnetic orbitals for the current system gives rise to four superexchange pathways, one with significantly larger overlap integral (Sαβ = 0.206) (Fig. 5). In line with previous studies,82 we notice that the μ-O bridge facilitates the magnetic coupling mainly through an out-of-plane π interaction, while the μ-OAc bridge impedes the superexchange interaction.
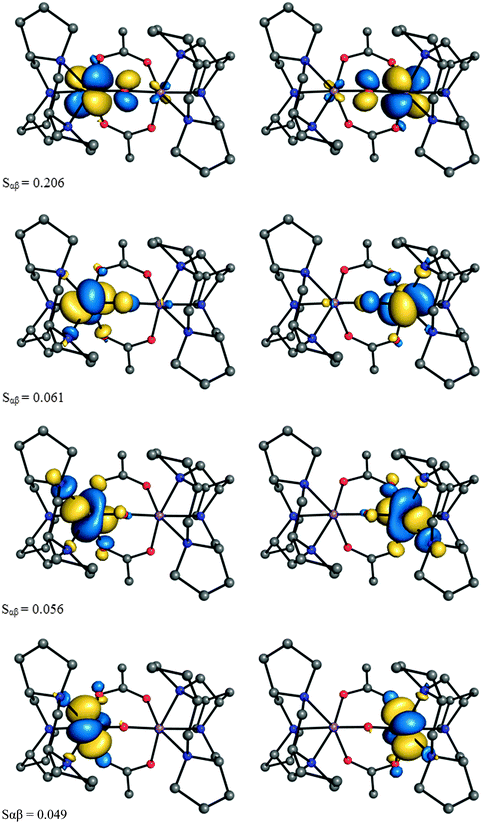 | ||
| Fig. 5 Magnetic orbital pairs of 1opt and their overlap integral. | ||
Given the nature of the superexchange pathways, it is expected for the coupling constant to be sensitive to structural modifications involving the μ-O bridge, i.e. the Mn–Ooxo distance and Mn–Ooxo–Mn angle. Indeed, the nature of the coupling constant in oxo-bridged manganese(III) dinuclears varies from weakly ferromagnetic, as in the case of the current complex (r(Mn–Ooxo) = 1.80 Å, ∠(Mn–Ooxo–Mn) = 122°), to strongly antiferromagnetic, J = −120 cm−1, in a quasi linear dinuclear (r(Mn–Ooxo) = 1.76 Å, ∠(Mn–Ooxo–Mn) = 168°).83 In order to evaluate the magneto-structural correlations for such MnIII dinuclears, we calculated the coupling constant for a series of geometries in which only the position of the bridging oxygen atom was moved along the C2 axis of the complex. The plot of J as obtained for the “single geometry” approach versus δ, which represents the ratio of the Mn–Ooxo–Mn angle and Mn–Ooxo distance for the different optimized geometries, is presented in Fig. 6. The magnitude of J is smoothly reduced as δ becomes larger, which eventually means that a shorter Mn–Ooxo distance or a larger Mn–Ooxo–Mn angle tends to decrease the magnitude of the ferromagnetic coupling, in agreement with the experimental data. Interestingly, for the largest value of δ, which corresponds to an Mn–Ooxo–Mn angle of 123.9° and an Mn–Ooxo distance equal to 1.798 Å, the calculated J values pass into the antiferromagnetic regime (Table S2, ESI†). In light of these results, it becomes evident that the coupling constant is highly sensitive to small structural variations, and hence the theoretical results cannot hope to lead to better than qualitative agreement with experiment. However, the structural differences between the two dimers observed in the X-ray structure are not sufficient to lead to J values, which would cause the splitting of EPR lines, but they may explain in part the significant width of the experimental EPR lines.
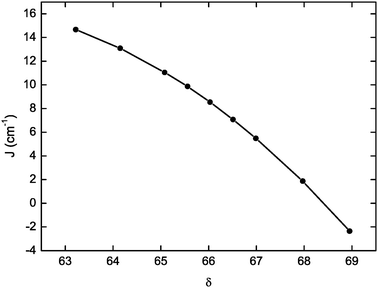 | ||
| Fig. 6 Representation of the variation of the magnetic exchange coupling interaction J as a function of the δ parameter, defined in the text, for various geometries derived from 1opt. | ||
4.3. Analysis and simulation of the HF-EPR spectra by diagonalizing the full Hamiltonian
In the case of complex 1, the appropriate spin Hamiltonian operator is described by eqn (1). Since the predicted ZFS values of each MnIII ion are of the same order of magnitude as the isotropic magnetic exchange interaction, the simulations were performed by diagonalization of the full 25 × 25 complex Hamiltonian matrix. Since all interactions that enter the spin Hamiltonian must be expressed in the same coordinate system, the tensors that parameterize these interactions had to be rotated into a common frame. We chose the axes of the dipolar part of the D tensor which, in the present case, are related to the molecular geometry, i.e. the Dzz component is aligned with the vector that connects the two metal centers, and Dyy is perpendicular to the (Mn, Mn, Ooxo) plane.Initially, the parameters used for simulating the HF-EPR spectra given in Table 3 are: (i) the DMn and EMn values and the Euler angles reflecting the relative orientation of the ZFS tensor for each MnIII ion calculated with NEVPT2 corrected SA-CASSCF, (ii) the isotropic exchange interaction experimentally measured, and (iii) the dipole–dipole interaction described by the eigenvalues of the D tensor calculated from eqn (3). Concerning the description of the magnetic interaction between the two MnIII ions (eqn (2)), the spin–orbit contribution to its symmetrical part and the antisymmetric exchange described by Dzyaloshinskii–Moriya have been neglected since these contributions should be weak in magnitude with respect to the dipole–dipole interaction, which in turn is the smallest contribution among the ones included. Furthermore, we have chosen to use the experimental J value, which corresponds to the average of the J values corresponding to the two dimers characterized by X-ray diffraction present in the sample. High-order anisotropy terms to describe the MnIII ions have not been considered to avoid over-parameterization. Besides, their magnitude should be negligible in energy compared to the other contributions considered in the simulation process.
| DMn | EMn/DMn | α | β | γ | |
|---|---|---|---|---|---|
| Initial | 4.29 | 0.19 | −52 | 28 | 3 |
| Fitted | 4.50 | 0.07 | −35 | 23 | 2 |
Although the resulting simulated spectra reproduce the overall shape of the experimental data (Fig. S1, ESI†), an optimization of the set of parameters was performed. The fitting procedure requires a qualitative analysis of the spectra, performed based on the energy diagrams calculated with the initial parameters (Table 3). Several transitions have been considered, namely the Zeeman levels that are most populated at low temperature under the magnetic field along the x and y axes (identified in Fig. 2a). Notice that since in complex 1 the sign of D is positive, the fundamental transitions along x and y are expected to be located at the lower field compared to the center of the spectra (g = 2).84 In contrast, at low temperature, with the magnetic field range used in the present HF-EPR experiments, the fundamental transition along the z axis cannot be observed.
During the fitting process, we noticed that, as expected, the position of the transitions is sensitive to the ZFS values of the MnIII ions. However, the transition positions are also noticeably dependent on the Euler angle α, thus highlighting the importance of properly describing the relative orientation of the local anisotropy tensors of each metallic ion. Conversely, the interaction parametrized by DAB is too weak to have a noticeable effect on the simulated spectra (Fig. S2, ESI†).
To assess the quality of a simulation, two criteria have been considered, namely the transition position and the evolution of its intensity as a function of temperature. Fig. 2b, 3b and 4b present simulated HF-EPR spectra at different frequencies and temperatures using the best set of fit parameters given in Table 3. The simulated spectra reproduce the overall shape of the experimental data well. The only exception is one broad feature located at 5.0 T, 6.6 T and 8.5 T at 230 GHz, 285 GHz and 345 GHz, respectively. All of our attempts to reproduce or to interpret this feature have failed and thus it has not been taken into account in our analysis. At low temperature, the first transitions along the y and x axes (1x and 1y in Fig. 2a) are at 3.88 and 7.62 T, respectively. As soon as the temperature increases, their intensity decreases for the benefit of the features at 5.36 and 7.92 T assigned to the second transitions along the y and x axes, respectively. From the energy diagrams (Fig. S3 and S4, ESI†) calculated with the fitted parameters (Table 3), the main features of the spectra can then be attributed as far as transitions between “pure” Zeeman, namely with a magnetic field above 3.5 T, are concerned. In addition, at 230 GHz, it was possible at 5 K to observe a z transition at 10.2 T (Fig. 3a and b), which is nicely reproduced in the simulated spectra, confirming the accuracy of the optimized parameters. The sign of DMn has been also confirmed. A negative DMn-value leads to HF-EPR spectra inconsistent with the experimental data, while a positive value allows to nicely reproduce the evolution of the intensity of the transitions as a function of temperature.
4.4 Analysis and simulation of the HF-EPR spectra using the spin ladder approach
In general, the spin ladder approach should be used only if the isotropic magnetic exchange interaction is the dominant parameter, i.e. |J| ≫ |DMn|. Although it is not the case in complex 1 (J ≈ DMn), we will use this approximation to conclude the pertinence of this description in such a case.Complex 1, in which the two high spin MnIII ions (S = 2) are coupled via a ferromagnetic interaction, is characterized by a ground spin state S = 4, implying that, in the spin ladder description, the EPR transitions observed at low temperature arise from transitions belonging to the S = 4 spin state. From eqn (8), the EPR parameters of the S = 4 spin state can be calculated using the DMn, EMn and DAB values predicted by the theoretical study. Three sets of ZFS parameters for S = 4 (D4 and E4/D4) are then obtained (Table 4), leading to close values (less than 5% of difference for D4). These parameters have been used to simulate the HF-EPR spectra and to calculate the energy diagrams of the nine Zeeman levels of the nonet along the three magnetic axes in order to give access to an assignment of the different transitions on the experimental spectra. To perform a fit of the experimental data, the first three transitions (|4,−4〉 → |4,−3〉; |4,−3〉 → |4,−2〉; |4,−2〉 → |4,−1〉) belonging to the y axis have been taking into account using their field position at 285 and 345 GHz (3.88, 5.36 and 6.99 T/5.80, 7.31 and 9.04 T, respectively). The values that have been obtained for D4 and E4/D4 given in Table 4 are close to initial values and lead to spectra that well-simulated the low-temperature data in agreement with the fact that only the S = 4 ground spin state is involved. When increasing temperatures, new transitions are observed whose origin does not belong to the S = 4 state. To interpret the appearance of these features, the first excited S = 3 spin state has to be taken into account. By the same procedure, the D3 and E3/D3 values have been determined (Table 4). Spectra calculated with the appropriate weight for each spin state (using the experimental J value) as a function of the temperature are shown in Fig. 2c and 4c. While the low temperature experimental data were quite well reproduced, it is not the case for the data recorded at higher temperatures. To improve the simulation, we adjusted both the ZFS parameters of the S = 3 spin state and the weight of each spin state in a reasonable range of values, but the resulting spectra did not lead to a better agreement with the experimental data.
5. Discussion and conclusion
In the present manuscript, we report on the determination of the electronic structure of a dinuclear MnIII compound, characterized by large magnetic anisotropy and weak ferromagnetic interaction between the two metallic ions. Two methods have been considered to analyze the multifrequency HF-EPR data in order to extract the local spin Hamiltonian parameters. In the first one, a complex Hamiltonian has been employed that includes terms describing the local and inter-site interactions. This method involves the evaluation of all matrix elements of the spin Hamiltonian in the basis set of uncoupled spin states. The resulting 25 × 25 complex matrix was subsequently diagonalized in order to obtain all its eigenvalues, i.e. energy levels. This should be appropriate whatever the magnitude of the exchange coupling constant J, and in the present case allows for an excellent interpretation of all HF-EPR spectra recorded in a large range of temperatures.In addition, the spin ladder approach has been investigated. For the present system it is only successful for the analysis of the experimental data that were recorded at the lowest temperatures. Nevertheless as soon as the temperature increases, it fails since the transitions arising from the excited state manifolds overlap with the ones from the ground state. Under these circumstances, only the parameters of the ground spin state of 1 can be precisely determined, which means that the determination of the local parameters of the metal centers is impossible. Thus, our investigation clearly shows that although the spin ladder approach is probably the more convenient and straightforward, it cannot be applied with confidence to the case of weakly exchanged coupled polynuclear complexes.
The zero field splitting parameter (DMn) of the MnIII ion obtained from fitting the experimental spectra was +4.50 cm−1, consistent with a N3O3 environment in a compressed octahedral geometry.4,72,74–76 This value does not deviate significantly from our best estimate obtained from theoretical calculations, despite the fact that we relied on a pragmatic and rather approximate method for its calculations, i.e. by substituting one of the MnIII atoms with a GaIII. Therefore, the local ZFS values in a polynuclear complex can be in principle evaluated via theoretical calculations by considering each metallic center separately.
Finally we also found that the prediction of the exchange coupling remains very challenging in the case of weakly coupled systems. At most, one can expect to rationalize a trend for a series of polynuclear complexes, while an accurate prediction of the absolute value of the Heisenberg coupling constant cannot be expected, especially in the framework of density functional theory. In the special case of dinuclear μ-oxo MnIII complexes, it has been proposed that the J value is sensitive to the nature of the octahedral distortion around the MnIII ions: for an octahedron that is compressed in the direction of the oxo-bridge a ferromagnetic interaction should be expected between the MnIII ions, while for an elongated octahedron, depending on the rhombicity of the system, antiferro- or ferro-magnetic interactions could result.85–87 In addition, recent studies reported by the group of Corbella have shown that the π- or σ-acid character of the ligand can also affect J.88 However, this correlation appears to be invalid for a nearly linear dinuclear μ-oxo MnIII complex, characterized by an antiferromagnetic coupling (J = −120 cm−1) in which the two metallic ions display compressed octahedral geometry.83 Based on the nature of the superexchange pathways evidenced in complex 1, the present work demonstrates that another important structural factor that can notably influence the nature and the magnitude of J is the Mn–Ooxo–Mn angle together with the Mn–Ooxo distance. A systematic study taking into account all available experimental data would be necessary to define the minimal set of structural parameters required to predict J.
The present work clearly shows how fruitfully experimental and theoretical techniques can be combined. In the present case the theoretical calculations proved to be an essential tool to predict very good initial values of all EPR parameters and their eigenframes. This was necessary in order to arrive at successful fits to the experimental data. The importance of previous systematic studies in order to determine the appropriate methodology to calculate the ZFS of the metallic ion is also highlighted. Work is in progress in our groups to generalize this approach to other dinuclear complexes with different metallic ions or Mn ions at various oxidation states.
Acknowledgements
MR, MNC and CD thank the Agence Nationale pour la Recherche (Grant No. ANR-05-JCJC-0171-01) for financial support.References
- J. Krzystek, A. Ozarowski and J. Telser, Coord. Chem. Rev., 2006, 250, 2308–2324 CrossRef CAS.
- C. Duboc, T. Phoeung, S. Zein, J. Pécaut, M. N. Collomb and F. Neese, Inorg. Chem., 2007, 46, 4905–4916 CrossRef CAS.
- S. Ye, F. Neese, A. Ozarowski, D. Smirnov, J. Krzystek, J. Telser, J.-H. Liao, C.-H. Hung, W.-C. Chu, Y.-F. Tsai, R.-C. Wang, K.-Y. Chen and H.-F. Hsu, Inorg. Chem., 2010, 49, 977–988 CrossRef CAS.
- Q. Scheifele, C. Riplinger, F. Neese, H. Weihe, A. L. Barra, F. Juranyi, A. Podlesnyak and P. L. W. Tregenna-Piggott, Inorg. Chem., 2008, 47, 439–447 CrossRef CAS.
- C. Duboc and M. N. Collomb, Chem. Commun., 2009, 2715–2717 RSC.
- J. Krzystek, D. C. Swenson, S. A. Zvyagin, D. Smirnov, A. Ozarowski and J. Telser, J. Am. Chem. Soc., 2010, 132, 5241–5253 CrossRef CAS.
- A.-L. Barra, A. Dossing, T. r. Morsing and J. Vibenholt, Inorg. Chim. Acta, 2011, 373, 266–269 CrossRef CAS.
- D. Gatteschi, A. L. Barra, A. Caneschi, A. Cornia, R. Sessoli and L. Sorace, Coord. Chem. Rev., 2006, 250, 1514–1529 CrossRef CAS.
- P. L. Feng, C. C. Beedle, C. Koo, J. Lawrence, S. Hill and D. N. Hendrickson, Inorg. Chim. Acta, 2008, 361, 3465–3480 CrossRef CAS.
- S. Piligkos, H. Weihe, E. Bill, F. Neese, H. El Mkami, G. M. Smith, D. Collison, G. Rajaraman, G. A. Timco, R. E. P. Winpenny and E. J. L. McInnes, Chem.–Eur. J., 2009, 15, 3152–3167 CrossRef CAS.
- J. Dreiser, O. Waldmann, G. Carver, C. Dobe, H.-U. Güdel, H. Weihe and A.-L. Barra, Inorg. Chem., 2010, 49, 8729–8735 CrossRef CAS.
- A. V. Palii, S. M. Ostrovsky, S. I. Klokishner, B. S. Tsukerblat, C. P. Berlinguette, K. R. Dunbar and J. R. Galan-Mascaros, J. Am. Chem. Soc., 2004, 126, 16860–16867 CrossRef CAS.
- S. Piligkos, J. Bendix, H. Weihe, C. J. Milios and E. K. Brechin, Dalton Trans., 2008, 2277–2284 RSC.
- M. Nakano and H. Oshio, Chem. Soc. Rev., 2011, 40, 3239–3248 RSC.
- B. Epel, K.-O. Schäfer, A. Quentmeier, C. Friedrich and W. Lubitz, JBIC, J. Biol. Inorg. Chem., 2005, 10, 636–642 CrossRef CAS.
- C. Duboc-Toia, H. Hummel, E. Bill, A.-L. Barra, G. Chouteau and K. Wieghardt, Angew. Chem., Int. Ed., 2000, 39, 2888–2890 CrossRef CAS.
- T. Howard, J. Telser and V. J. DeRose, Inorg. Chem., 2000, 39, 3379–3385 CrossRef CAS.
- S. Blanchard, G. Blain, E. Riviere, M. Nierlich and G. Blondin, Chem.–Eur. J., 2003, 9, 4260–4268 CrossRef CAS.
- S. Blanchard, G. Blondin, E. Riviere, M. Nierlich and J. J. Girerd, Inorg. Chem., 2003, 42, 4568–4578 CrossRef CAS.
- A. P. Golombek and M. P. Hendrich, J. Magn. Reson., 2003, 165, 33–48 CrossRef CAS.
- R. Carmieli, T. M. Larsen, G. H. Reed, S. Zein, F. Neese and D. Goldfarb, J. Am. Chem. Soc., 2007, 129, 4240–4252 CrossRef CAS.
- P. ter Heerdt, M. Stefan, E. Goovaerts, A. Caneschi and A. Cornia, J. Magn. Reson., 2006, 179, 29–37 CrossRef CAS.
- V. V. Semenaka, O. V. Nesterova, V. N. Kokozay, V. V. Dyakonenko, R. I. Zubatyuk, O. V. Shishkin, R. Boca, J. Jezierska and A. Ozarowski, Inorg. Chem., 2010, 49, 5460–5471 CrossRef CAS.
- A. Bencini and D. Gatteschi, Electron Paramagnetic Resonance of Exchange Coupled Systems, Springer-Verlag, Berlin, 1990 Search PubMed.
- F. Neese and E. I. Solomon, Inorg. Chem., 1998, 37, 6568–6582 CrossRef CAS.
- M. R. Pederson and S. N. Khanna, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 9566–9572 CrossRef CAS.
- R. Boca, Coord. Chem. Rev., 2004, 248, 757–815 CrossRef CAS.
- F. Neese, in Calculation of NMR and EPR Parameters, ed. M. B. M. Kaupp and V. G. Malkin, Wiley-VCH, Heidelberg, 2004 Search PubMed.
- K. Ray, A. Begum, T. Weyhermuller, S. Piligkos, J. van Slageren, F. Neese and K. Wieghardt, J. Am. Chem. Soc., 2005, 127, 4403–4415 CrossRef CAS.
- R. Reviakine, A. V. Arbuznikov, J. C. Tremblay, C. Remenyi, O. L. Malkina, V. G. Malkin and M. Kaupp, J. Chem. Phys., 2006, 125, 054110 CrossRef.
- C. Duboc, M. N. Collomb, J. Pécaut, A. Deronzier and F. Neese, Chem.–Eur. J., 2008, 14, 6498–6509 CrossRef CAS.
- F. Neese, Coord. Chem. Rev., 2009, 253, 526–563 CrossRef CAS.
- R. Maurice, R. Bastardis, C. de Graaf, N. Suaud, T. Mallah and N. Guihery, J. Chem. Theory Comput., 2009, 5, 2977–2984 CrossRef CAS.
- R. Maurice, N. Guihery, R. Bastardis and C. de Graaf, J. Chem. Theory Comput., 2009, 6, 55–65 CrossRef.
- C. Duboc, M. N. Collomb and F. Neese, Appl. Magn. Reson., 2010, 37, 229–245 CrossRef.
- J. Rich, C. E. Castillo, I. Romero, M. Rodríguez, C. Duboc and M. N. Collomb, Eur. J. Inorg. Chem., 2010, 3658–3665 CrossRef CAS.
- F. Neese, J. Am. Chem. Soc., 2006, 128, 10213–10222 CrossRef CAS.
- S. Romain, C. Duboc, F. Neese, E. Rivière, L. R. Hanton, A. G. Blackman, C. Philouze, J.-C. Leprêtre, A. Deronzier and M.-N. Collomb, Chem.–Eur. J., 2009, 15, 980–988 CrossRef CAS.
- C. Duboc, D. Ganyushin, K. Sivalingam, M.-N. Collomb and F. Neese, J. Phys. Chem. A, 2010, 114, 10750–10758 CrossRef CAS.
- C. Bolm, N. Meyer, G. Raabe, T. Weyhermuller and E. Bothe, Chem. Commun., 2000, 2435–2436 RSC.
- T. Moriya, Phys. Rev., 1960, 120, 91–98 CrossRef CAS.
- F. Neese, J. Phys. Chem., 2001, 115, 11080 CrossRef CAS.
- W. E. Blumberg, in In The Magnetic Resonance in Biological Systems, ed. A. Ehrenberg, B. G. Malmström and T. Vänngård, Pergamon Press, Oxford, 1967, pp. 119–133 Search PubMed.
- R. McWeeny and Y. Mizuno, Proc. R. Soc. London, Ser. A, 1961, 259, 554–577 CrossRef CAS.
- F. Neese, J. Chem. Phys., 2007, 127, 164112 CrossRef.
- S. Schmitt, P. Jost and C. v. Wullen, J. Chem. Phys., 2011, 134, 194113 CrossRef.
- R. Maurice, C. de Graaf and N. Guihery, J. Chem. Phys., 2010, 133, 084307 CrossRef.
- D. Maganas, S. Sottini, P. Kyritsis, E. J. J. Groenen and F. Neese, Inorg. Chem., 2011, 50, 8741–8754 CrossRef CAS.
- M. Atanasov, D. Ganyushin, D. A. Pantazis, K. Sivalingam and F. Neese, Inorg. Chem., 2011, 50, 7460–7477 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J. P. Malrieu, Chem. Phys. Lett., 2001, 350, 297–305 CrossRef CAS.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J. P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J. P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153 CrossRef CAS.
- M. Orio, D. Pantazis and F. Neese, Photosynth. Res., 2009, 102, 443–453 CrossRef CAS.
- L. Noodleman, J. Chem. Phys., 1981, 74, 5737–5743 CrossRef CAS.
- L. Noodleman and E. R. Davidson, Chem. Phys., 1986, 109, 131–143 CrossRef.
- K. Yamaguchi, Y. Takahara and T. Fueno, in Applied Quantum Chemistry, ed. V. H. Smith, H. F. Schaefer III and K. Morokuma, D. Reidel Publishing Company, Boston, 1986 Search PubMed.
- T. Soda, Y. Kitagawa, T. Onishi, Y. Takano, Y. Shigeta, H. Nagao, Y. Yoshioka and K. Yamaguchi, Chem. Phys. Lett., 2000, 319, 223–230 CrossRef CAS.
- A. L. Barra, L. C. Brunel and J. B. Robert, Chem. Phys. Lett., 1990, 165, 107–109 CrossRef CAS.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- V. N. Staroverov, G. E. Scuseria, J. M. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137 CrossRef CAS.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- A. T. Amos and G. G. Hall, Proc. R. Soc. London, Ser. A, 1961, 263, 483–493 CrossRef.
- H. F. King, R. E. Stanton, H. Kim, R. E. Wyatt and R. G. Parr, J. Chem. Phys., 1967, 47, 1936 CrossRef CAS.
- S. Zein, C. Duboc, W. Lubitz and F. Neese, Inorg. Chem., 2008, 47, 134–142 CrossRef CAS.
- S. Zein and F. Neese, J. Phys. Chem. A, 2008, 112, 7976–7983 CrossRef CAS.
- C. Mantel, A. K. Hassan, J. Pécaut, A. Deronzier, M. N. Collomb and C. Duboc-Toia, J. Am. Chem. Soc., 2003, 125, 12337–12344 CrossRef CAS.
- D. Ganyushin and F. Neese, J. Chem. Phys., 2006, 125, 024103 CrossRef.
- J. Krzystek, G. J. Yeagle, J. H. Park, R. D. Britt, M. W. Meisel, L. C. Brunel and J. Telser, Inorg. Chem., 2003, 42, 4610–4618 CrossRef CAS.
- A. L. Barra, D. Gatteschi, R. Sessoli, G. L. Abbati, A. Cornia, A. C. Fabretti and M. G. Uytterhoeven, Angew. Chem., Int. Ed. Engl., 1997, 36, 2329–2331 CrossRef CAS.
- G. Aromi, J. Telser, A. Ozarowski, L. C. Brunel, H. M. Stoeckli-Evans and J. Krzystek, Inorg. Chem., 2005, 44, 187–196 CrossRef CAS.
- J. Limburg, J. S. Vrettos, R. H. Crabtree, G. W. Brudvig, J. C. d. Paula, A. Hassan, A.-L. Barra, C. Duboc-Toia and M.-N. Collomb, Inorg. Chem., 2001, 40, 1698–1703 CrossRef CAS.
- M. Orio, D. A. Pantazis, T. Petrenko and F. Neese, Inorg. Chem., 2009, 48, 7251–7260 CrossRef CAS.
- N. Cox, W. Ames, B. Epel, L. V. Kulik, L. Rapatskiy, F. Neese, J. Messinger, K. Wieghardt and W. Lubitz, Inorg. Chem., 2011, 50, 8238–8251 CrossRef CAS.
- X. G. Zhao, W. H. Richardson, J. L. Chen, J. Li, L. Noodleman, H. L. Tsai and D. N. Hendrickson, Inorg. Chem., 1997, 36, 1198–1217 CrossRef CAS.
- T. C. Brunold, D. R. Gamelin and E. I. Solomon, J. Am. Chem. Soc., 2000, 122, 8511–8523 CrossRef CAS.
- D. A. Pantazis, V. Krewald, M. Orio and F. Neese, Dalton Trans., 2010, 39, 4959 RSC.
- C. A. Kipke, M. J. Scott, J. W. Gohdes and W. H. Armstrong, Inorg. Chem., 1990, 29, 2193–2194 CrossRef CAS.
- A. Abragam and B. Bleaney, in Electron Paramagnetic Resonance of Transition Ions, Oxford University, New York, 1970 Search PubMed.
- J. B. Vincent, K. Folting, J. C. Huffman and G. Christou, Biochem. Soc. Trans., 1988, 16, 822–823 CAS.
- R. Hotzelmann, K. Wieghardt, U. Florke, H. J. Haupt, D. C. Weatherburn, J. Bonvoisin, G. Blondin and J. J. Girerd, J. Am. Chem. Soc., 1992, 114, 1681–1696 CrossRef CAS.
- M. Corbella, R. Costa, J. Ribas, P. H. Fries, J.-M. Latour, L. Ohrström, X. Solans and V. Rodriguez, Inorg. Chem., 1996, 35, 1857–1865 CrossRef CAS.
- M. Corbella, V. Gomez, B. Garcia, E. Rodriguez, B. Albela and M. A. Maestro, Inorg. Chim. Acta, 2011, 376, 456–462 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c2cp42955a |
| This journal is © the Owner Societies 2013 |
