Screening of carbonaceous nanoporous materials for capture of nerve agents†
Piotr
Kowalczyk
*a,
Piotr A.
Gauden
b,
Artur P.
Terzyk
b and
Alexander V.
Neimark
c
aNanochemistry Research Institute, Department of Chemistry, Curtin University of Technology, P.O. Box U1987, Perth, 6845 Western Australia, Australia. E-mail: Piotr.Kowalczyk@curtin.edu.au; Tel: +61 8 9266 7800
bDepartment of Chemistry, Physicochemistry of Carbon Materials Research Group, N. Copernicus University, Gagarin St. 7, 87-100 Torun, Poland
cDepartment of Chemical and Biochemical Engineering, Rutgers, The State University of New Jersey, 98 Brett Road, Piscataway, New Jersey 08854-8058, USA
First published on 31st October 2012
Abstract
A strategy for combined experimental and computational screening of candidate carbonaceous materials for capturing highly volatile nerve agents at ambient temperature using physisorption. Based on theoretical calculations of Henry constants and zero-coverage adsorption enthalpies for sarin and DMMP (its common stimulant) adsorbed in model slit-shaped carbon pores at 298 K, we found the following. Slit-shaped carbon pores with pore width ∼0.5 nm are optimal for agent adsorption due to strong confinement of adsorbed molecules. Agent adsorption enthalpy at zero coverage computed for optimal pore width is very high and reaches ∼83 kJ mol−1. Widening of pore width above ∼1 nm results in a significant decrease of the Henry constant and zero-coverage adsorption enthalpy (∼44 kJ mol−1). Polydispersity of studied candidate carbonaceous materials strongly affects adsorption capacity for DMMP under the operating conditions. The optimal carbonaceous adsorbent, pitch-based P7 activated carbon fiber, adsorbed ∼100 μg g−1 DMMP at 0.03 μg m−3. Commercial Norit activated carbon adsorbed only ∼20 μg g−1 DMMP at 0.03 μg m−3. Surprisingly, a small shift of the pore size distribution towards wider micropores has a great impact on agent adsorption. Because the adsorption enthalpies computed at zero coverage weakly dependent on pore size, the heat released during agent adsorption is similar for all studied candidate adsorbents (i.e. ∼55–60 kJ mol−1).
I. Introduction
Protection against readily accessible nerve agents (e.g. tabun, sarin, soman, VX, and others) is of major social concern. Thus, there is a need to provide efficient carbonaceous materials (adsorbents) that remove highly toxic nerve agent vapors by physical adsorption.1–15 Unfortunately, the broad range of toxic agents, environmental conditions and types of carbonaceous materials simply does not allow laboratory testing of every possible combination. In this regard, screening of candidate carbonaceous materials for efficient capturing of highly toxic nerve agents is of undoubted interest for both military and civilians.(RS)-Propan-2-yl methylphosphonofluoridate (i.e., sarin or GB) is a chemical warfare nerve agent. Near ambient temperature, sarin is highly volatile liquid, so that inhalation as well as absorption through the skin poses a great threat.1 Highly toxic sarin vapor is clear, colorless, and highly soluble in fat and water. Very small concentration of sarin vapor in air, i.e. ∼0.09 mg dm−3, causes death via respiratory failure, which in turn is caused by increased airway resistance (bronchorrhea, bronchoconstriction), respiratory muscle paralysis, and most importantly, loss of central respiratory drive.1
Since the First World War, respirators with a cartridge filled with carbonaceous adsorbents (i.e., activated charcoals, activated carbons, and activated carbon fibers) have been used for capturing highly volatile nerve agents. No metal impregnants (such as famous Cu–Cr–Ag catalysts) are needed to breakdown these toxic substances because they are strongly physisorbed near ambient temperature.1 However, tailoring the pore size and pore surface chemistry of the carbon microstructure may increase the adsorption effectiveness significantly.1–5,16,17 Traditional carbonaceous materials are noncrystalline porous solids with heterogeneous structure of pores. Depending on the pore size (for slit-shaped carbon pores, pore width, H, is recommended), all pores are divided into three main groups. Following the International Union of Pure and Applied Chemistry (IUPAC) terminology,18 micropores are the smallest pores with the pore width H < 2 nm. The enhanced solid–fluid potential in micropores (i.e., surface energy) is much larger than the thermal energy of adsorbed molecules at room temperature. Consequently, molecules tend to congregate in the deep potential wells of narrow carbon micropores. As such, a large micropore volume is required to enhance the adsorption capacity towards organophosphorous vapors.
Dimethyl methyl phosphonate (DMMP) and tert-butylbenzene (TBB) used as stimulants for sarin and sulfur mustard (mustard gas or HD) capturing via physisorption.1–5 Gun'ko and co-workers2 showed that the dynamics characteristics of carbonaceous materials measured at low breakthrough concentration of DMMP–TBB (∼10−5 mg dm−3) have revealed nonlinear effects caused by many factors, including pore size distributions, presence of water, oxidation or reduction of carbon surfaces, etc. However, Branton et al.19 showed that adsorption and dynamics of DMMP in porous materials correlated with the micropore volume. Thus, one can argue that the optimal carbonaceous adsorbent towards DMMP capturing is the one with the highest micropore volume. Note however, that total micropore volume for DMMP adsorption is poorly defined. This is because it contains contributions from carbon pores of various sizes.20–23 Moreover, we should bear in mind that micropore volume is “available” or “accessible” volume measured indirectly.20–23 This parameter depends on the effective size of the adsorbate molecule (i.e., probe molecule) used in porosimetry measurements.21,24 That is why direct correlation of the experimental DMMP adsorption capacity with the micropore volume “accessible” for N2 at 77 K can lead to inconsistent and incorrect conclusions.
These experimental results raise a question of whether a simple relation exists between the pore structure and the equilibrium adsorption of phosphor-organic agents at low concentrations. Adsorption equilibria provide the necessary information to determine the amount of adsorbed compound per unit mass of adsorbent for given vapor concentration and operating temperature. Therefore, the microscopic insight into DMMP and sarin equilibrium adsorption at low concentrations and ambient temperature is absolutely necessary in order to make progress in the study of agent transport in the adsorbent bed. Although we acknowledge the importance of H2O adsorption in carbonaceous materials as well as surface chemistry of pores, these effects are not considered in this article.
The problem of agent adsorption on carbonaceous materials is not only of topical practical importance for optimized protection technologies, but it is also a challenging and long-studied problem in the adsorption science. When pores are so tight that they can accommodate just one or two agent molecules in their cross-section, even subtle differences between molecules can make a significant impact on adsorption. As such, our work represents a case study and the methodology that we put forward can be generalized to other adsorption systems, including computer aided design of novel adsorbents for capture of toxic industrial chemicals.
The primary goal of this work is to establish a relationship between the agent (exemplified by sarin and DMMP) adsorption capacity measured at low concentrations and the distribution of pore sizes of realistic carbonaceous materials. Thus, we would like to answer the following question: what is the pore structure of carbonaceous material that maximizes the equilibrium agent adsorption capacity at low concentrations and ambient temperature? To answer this question and shed some light on the experimental puzzles associated with the dynamics of agent propagation through the carbon bed, we propose a systematic approach combining the experimental knowledge and theoretical calculations. First, we develop a reliable method for the evaluation of the distribution of the surface area over slit-shaped carbon pore width from N2 porosimetry at 77 K. Next, we implement a novel algorithm for calculation of the DMMP/sarin Henry constant and zero-coverage adsorption enthalpy for single slit-shaped carbon pore width. Finally, we combine the experimental pore size distributions with theoretical calculations of Henry constants to account for the polydispersity of carbonaceous materials.
II. Carbonaceous materials
Three kinds of carbonaceous materials were investigated. Pitch-based P7 activated carbon fiber (ACF) supplied by Osaka Gas Corporation was selected as model homogenous microporous material.25–28 Two samples of carbonaceous films (C875 and Cox)29 prepared from cellulose were selected as model materials characterized by molecular sieve properties. Finally, two samples of commercialized granular activated carbons (Norit and D55/2)22,23 were selected to account for the polydispersion of carbon pores. N2 adsorption isotherms at 77 K on studied carbonaceous materials were previously measured using the volumetric method. The molar volume of liquid N2 of 34.666 cm3 mol−1, and the density of 0.808 g cm−3, was used for conversion of STP (Standard Temperature and Pressure) volume of adsorbed N2 into liquid one. Adsorption and textural properties of studied microporous materials evaluated from measured N2 adsorption isotherms were published elsewhere.22,23,25,29III. Theory
Agent adsorption at infinite dilution
For dilute DMMP vapor the experimental adsorption is proportional to the pressure, the proportionality constant, KH (Henry's law constant) is given by,30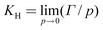 | (1) |
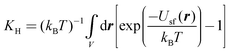 | (2) |
For the slit-shaped pore composed of structureless semi-infinite adsorbing walls, the theoretical expression given by eqn (2) can be rewritten as follows,32
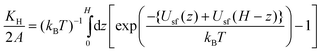 | (3) |
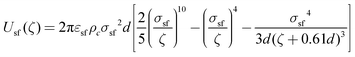 | (4) |
Eqn (3) and (4) can be easily implemented when one considers the adsorption of the spherical particle (e.g. noble gas atom, methane treated as a spherical quasi-particle, etc.) on structurally homogenous carbonaceous material (e.g. defect-free graphite crystal, carbonaceous materials composed of uniform pores, etc.).34,35 To describe phosphor-organic agent (DMMP and sarin) adsorption on real carbonaceous porous materials we have to take into account the molecular shape of the agent molecule and the pore size polydispersity of the adsorbing carbonaceous material.
In the current work we proposed the following algorithm. First, we selected the Transferable Potentials for Phase Equilibria (TraPPE)36 force-field to correctly represent the studied dimethylmethylphosphonates. As has been recently shown by Potoff and co-workers, the TraPPE force-field correctly reproduced the vapor–liquid coexistence curve for studied nerve agents and stimulants.36 Obviously, the grand state geometry of agent molecules cannot be used for the calculation of Henry's law constant at finite temperatures. Therefore, we simulated liquid DMMP and sarin at 293 K in the constant pressure ensemble (NPT) by the Monte Carlo method.37 This allows us to sample the Boltzmann distribution of bond and torsional angles at studied temperature. The equilibrated configurations of 200 DMMP and sarin molecules were then recorded and stored in database.
By considering the interactions between M-dispersion centers of agent molecules and crystalline slit-shaped graphitic-like pores (assuming pair-additive interactions), we rewrite eqn (3) as follows,
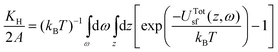 | (5) |
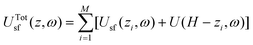 | (6) |
The enthalpy of adsorption computed at zero coverage, Qst (θ = 0), can be obtained from the well-known expression,30–32
Qst (θ = 0) = R[dln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KH/d(1/T)] KH/d(1/T)] | (7) |
So far, we have limited our considerations to the adsorption of DMMP and sarin molecules in a single crystalline slit-shaped carbon pore at infinite dilution. Real carbonaceous materials are structurally heterogeneous.21 Distribution of pore sizes strongly affects various properties of these materials, including adsorption and separation of fluids. To account for the polydispersity we average the Henry constant and enthalpy of adsorption computed at zero coverage by using the experimental pore size distribution.
Having a normalized pore size distribution function, J(x), we performed the averaging as follows,39
 | (8) |
| a = KHp | (9) |
| c = p/RT | (10) |
Details of nonlocal density functional theory, pore size analysis, and validation of the Metropolis–Ulam Monte Carlo integration algorithm against experimental measurements are documented in ESI.†
IV. Results and discussion
Knowledge of the pore size distribution of carbonaceous materials is one of the most important factors that impact the efficiency of nerve agent adsorption from the gas phase. Narrow pores are able to adsorb more toxic molecules because of the enhanced solid–fluid interaction potential, whereas very wide pores can be treated as two independent graphitic surfaces with low adsorption capacity. Fig. 1–3 show the histograms of pore widths for studied carbonaceous materials computed from N2 adsorption isotherms measured at 77 K and the NLDFT method. The fitting of experimental N2 adsorption isotherms measured at 77 K by theoretical model is very good. Taking into account the IUPAC classification of pores,18 all studied carbonaceous materials are microporous (i.e., pore widths are less than 2 nm). Pitch-based P7 ACF has a homogenous microporous structure. Pore size distribution with maximum of ∼0.5 nm decreases exponentially. Wider micropores (i.e., pore size above ∼1.5 nm) have negligible contribution to the total surface of the P7 ACF sample. It is worth pointing out that P7 ACF contains very high fraction of the smallest micropores accessible to N2 (called ultramicropores) with a pore width of ∼0.5 nm. We would like to stress that ACFs are disordered materials. They are consisting of a complex network of elongated pores embedded in an amorphous matrix. Although the pore morphology is ill-defined, the presence of slit-shaped and ellipsoid-shaped graphitic pores has been revealed from high resolution transmission electron microscopy. Studied carbonaceous films possess a well-tailored micropore structure with a negligibly small contribution from the mesopores. Remarkable narrow and sharp pore size distribution with a pore size of 0.55–0.6 nm indicates the sieving properties of these materials. Note however, that the pore size distributions computed for carbonaceous films are shifted to wider micropores as compared to the P7 ACF sample. Therefore the fraction of ultramicropores with a pore width of <0.5 nm is negligible for both carbonaceous films. Norit and D55/2 activated carbons are microporous adsorbents with similar bimodal pore size distributions and large surface areas (see Fig. 3 and Table 1). We notice a high-intensity peak exhibited by both activated carbons in the 0.55–0.6 nm pore width range. The second low-intensity peak exhibited by both activated carbons is at around a pore width of 1.2 nm. Norit activated carbon contains a low fraction of small mesopores with a pore width in the 4.5–5.3 nm range. However, their contribution to the total surface area is very small. Total surface areas computed from the NLDFT method for all studied carbonaceous materials are displayed in Table 1. As would be expected, the NLDFT method generates higher values of total surface areas as compared to apparent ones computed from the standard BET method. On the other hand, NLDFT and high-resolution αs methods generate comparable values of the total surface areas. These observations are fully consistent with the previous work.29 A great advantage of the NLDFT method over the high-resolution αs method is that it gives the surface area distribution over the pore width. We believe that this information is crucial in many areas of surface science, including adsorption and catalysis. One may have large total surface area that is only accessible for a small fraction of crystal size of catalysis or adsorbates with a particular molecular size. We would like to point out that within a current implementation of the NLDFT method the total surface area of ill-defined porous material does not depend strongly on the value of the regularization parameter (see Fig. 1 and Fig. S4–S6 in ESI†). Notice that either under-smoothing or over-smoothing does not change the value of the total surface area significantly. We believe that this feature of the proposed numerical method is important for practical calculations of PSD from noisy and incomplete experimental data. | ||
| Fig. 1 Upper panel: NLDFT pore size distribution of pitch-based p7 ACF. The inner panel presents the fitting of N2 experimental adsorption isotherm at 77 K (open circles) by the NLDFT method (solid line). Middle panel: the L-curve plot used for selection of an optimal value of the regularization parameter, λ = 0.0011. Bottom panel: variation of the total surface area with the value of the regularization parameter. Stotal = 999 m2 g−1 corresponds to the optimal value of regularization parameter computed from the L-curve. | ||
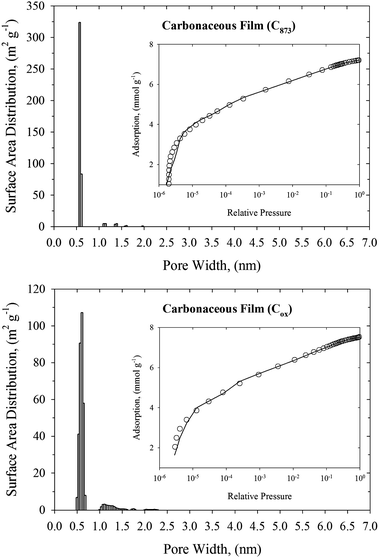 | ||
| Fig. 2 NLDFT pore size distributions of carbonaceous films (upper panel: C875, and bottom panel: Cox). The inner panels present the fitting of N2 experimental adsorption isotherm at 77 K (open circles) by the NLDFT method (solid line). | ||
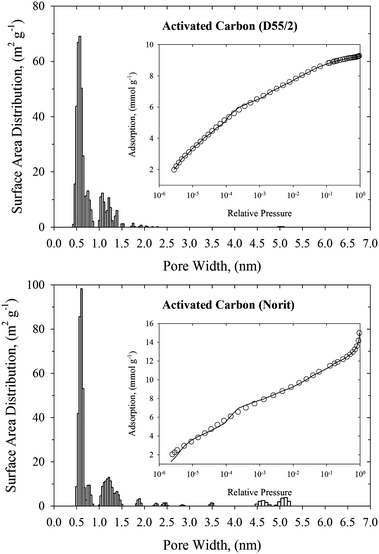 | ||
| Fig. 3 NLDFT pore size distributions of commercialized activated carbons (upper panel: D55/2, and bottom panel: Norit). The inner panels present the fitting of N2 experimental adsorption isotherm at 77 K (open circles) by the NLDFT method (solid line). | ||
| Carbonaceous material | C873 | Cox | Norit | P7 | D55/2 |
|---|---|---|---|---|---|
| S BET (m2 g−1) | 478 | 520 | 837 | 668 | 616 |
| S c (m2 g−1) | 627 | 661 | 893 | 856 | 759 |
| S NDFT (m2 g−1) | 705 | 690 | 943 | 816 | 999 |
Fig. 4 depicts the Henry constants and zero-coverage adsorption enthalpies computed for DMMP and sarin adsorbed in slit-shaped carbon pores of various sizes at 293 K. Indeed, the adsorption properties of DMMP and sarin at infinite dilution of adsorbed phase are very similar. Observed similarities between adsorption equilibrium of sarin and DMMP are consistent with experimental measurements1 and recent works.40,41 Because DMMP is commonly used in both static and dynamics adsorption measurements, we further focus on the DMMP adsorption.
 | ||
| Fig. 4 Henry constants (upper panel) and zero-coverage adsorption enthalpies (bottom panel) computed for DMMP and sarin adsorbed in slit-shaped graphitic carbon pores at 293 K. | ||
In Fig. 5 (upper and middle panel) we showed the calculated Henry constant vs. pore width for 278, 293, and 400 K. A couple of things are immediately apparent. The Henry constant is reduced with the operating temperature. However, the shape of this relation is temperature-independent. Therefore, the pore width of ∼0.5 nm is an optimal for adsorption of DMMP, whereas slit-shaped carbon pores with pore widths greater than ∼1 nm are not effective for nerve agent adsorption. Due to significant contribution from repulsive dispersion interactions, the Henry constants in very narrow slit-shaped carbon pores with pore widths lower than ∼0.5 nm are also reduced (see clear maxima displayed in Fig. 4 and 5). To account for the polydispersity we averaged our theoretical results using the experimental PSDs (see bottom panel in Fig. 5). This figure indicates that the adsorption of DMMP, as compared at infinite dilution and 293 K, is the highest for the pith-based P7 ACF followed by D55/2 activated carbon. The adsorption capacity towards DMMP at infinite dilution and 293 K is significantly reduced for remaining carbonaceous materials, e.g.: Norit activated carbon, Cox and C873 carbonaceous films. These important predictions can be explained by different fraction of slit-shaped carbon pores with pore widths close to ∼0.5 nm in experimental PSDs. We note that homogenous carbonaceous films are composed of slit-shaped carbon pores with pore widths greater than 0.5 nm (see Fig. 2). Their micropores are accessible to DMMP molecules, but they are too large to provide high adsorption capacity at infinite dilution of adsorbed phase. Similarly, the fraction of the smallest micropores is very low for Norit activated carbon (see Fig. 3). Therefore, we concluded that controlling of the fraction of slit-shaped pores with pore widths ∼0.5 nm is crucial for efficient adsorption of nerve agents near ambient temperature (Fig. 6).
 | ||
| Fig. 5 Upper and middle panel: Henry constants for DMMP adsorbed in slit-shaped graphitic carbon pores at 273, 293, and 400 K. Bottom panel: Henry constants for DMMP adsorbed on studied carbonaceous materials at 293 K. | ||
 | ||
| Fig. 6 Linear Henry isotherms for DMMP adsorbed on studied carbonaceous materials at 293 K. The adsorbed amount is expressed in units of μg m−2 (upper panel) and μg g−1 (bottom panel). The range of DMMP concentrations in the bulk phase was chosen arbitrary. | ||
Broad PSDs smeared out the pore size dependence of the Henry constant that inevitably reduce the adsorption of nerve agents at infinite dilution, as is shown in Fig. 6. Note that pitch-based P7 ACF adsorbed ∼100 μg g−1 DMMP at 0.03 μg m−3. A commercialized Norit activated carbon sample adsorbed only ∼20 μg g−1 DMMP at 0.03 μg m−3. Surprisingly, a small shift of PSD towards wider micropores has a great impact on DMMP adsorption under studied operating conditions. As has been shown by Nikolaev1 and Dubinin and co-workers,42,43 the breakthrough time measured in the region of low concentrations is longer for adsorbents with higher adsorption capacity. Moreover, it has been shown that ACFs have better access to the surface area and the faster the rate of adsorption kinetics as compared to commercially used activated carbons.21 A short pathway of gas molecules from gas phase to micropores explains the fast adsorption kinetic of ACFs. Taking into account adsorption kinetic measurements and current equilibrium calculations, we state that pitch-based ACF is a potential candidate adsorbent for protection against nerve agents.
To quantify the strength of the interaction of the DMMP molecules with studied carbonaceous materials, we calculated their zero-coverage DMMP adsorption enthalpy from the variation of the Henry constant with temperature and experimental PSDs. The high values of zero-coverage adsorption enthalpy ∼55–61 kJ mol−1 indicate strong physisorption of DMMP molecules in crystalline graphitic micropores (see Fig. 7). Note that reported heat of DMMP vaporization ∼54 kJ mol−1 is lower than computed zero-coverage adsorption enthalpy. Indeed, microscopic snapshots reveal a strong confinement of the DMMP molecule in very narrow carbon nanopores (see Fig. 7). The adsorbed DMMP molecule fits perfectly between graphitic pore walls that maximize the solid–fluid potential energy. Experimental results on hexane, DMMP, and N2 adsorption on BLP activated carbon supported our theoretical calculations. Karwacki concluded:17 “hexane and DMMP adsorption equilibria are remarkably similar to the N2. Although some scatter exists, the trend shows that each adsorbate occupies about the same pore volume for a given relative pressure”. Thus, branched DMMP molecules penetrate very small micropores accessible to the smallest quasi-spherical N2 ones. Interestingly, in great contrast to the Henry constant, we found that zero-coverage adsorption enthalpy weekly depends on PSD. To explain this result we presented the variation of zero-coverage adsorption enthalpy with the slit-shaped carbon pore width at 293 K (see Fig. 7). Very high adsorption heat ∼83 kJ mol−1 (for pore width ∼0.5 nm) decreases very quickly with the widening of slit-shaped carbon pore size. For pore widths greater than ∼1 nm, the heat released during DMMP physisorption is close to that corresponding to the open graphite surface (∼44 kJ mol−1). However, the key observation is that the zero-coverage DMMP adsorption enthalpy at 293 K does not change with the pore size significantly. For instance, it drops about 25% for slit-shaped carbon pores between 0.5 and 0.6 nm (see Fig. 4). On the other hand, Henry's constant is very sensitive to even the very small changes in the pore size. It drops more than two orders of magnitude for slit-shaped carbon pores between 0.5 and 0.6 nm (see Fig. 4). Thus, the impact of the polydispersity on the zero-coverage DMMP adsorption enthalpy at 293 K is weak. Interestingly, the isosteric heat of DMMP adsorption on PCC coal-based carbon44 (a BET surface area of 1198 m2 g−1) at finite pore loadings is ∼84 kJ mol−1, which is comparable with current theoretical calculations. Note that coals are consisted of very narrow micropores.44 Direct comparison of theoretical results with adsorption experiment should be taken with some caution. DMMP is a highly polar molecule, and as many warfare agents, is acidic in nature.40,41 Therefore, pore surface chemistry may enhance adsorption affinity. This and other aspects of nerve agent capture by physisorption will be subject of our future works.
 | ||
| Fig. 7 Upper panel: dependence of the zero-coverage DMMP adsorption enthalpy on slit-shaped carbon pore width computed at 293 K. Inner panel shows the low-energetic configurations of DMMP molecules computed from the Metropolis–Ulam Monte Carlo method. Bottom panel: zero-coverage adsorption enthalpies computed for DMMP adsorbed on studied carbonaceous materials at 293 K. | ||
V. Conclusions
A novel methodology for prediction of low-pressure linear adsorption of nerve agents on carbonaceous materials from experimental pore size distribution and theoretical Henry constant is presented. Tailoring the pore size of candidate adsorbents is crucial for efficient capturing of highly toxic agent vapors. In general, it appears that slit-shaped carbon pores with pore widths around ∼0.5 nm are optimal for DMMP and sarin capture by physisorption. Strong confinement of agent molecules adsorbed in small carbon ultramicropores is supported by the high value of the zero-coverage adsorption enthalpy (∼83 kJ mol−1) and configurational low-energy snapshots. Theoretical calculations revealed that widening the pore size and polydispersity has a significant negative effect on capturing of DMMP under operating conditions. Interestingly, small micropores with pore widths greater than ∼1 nm have similar agent adsorption properties at infinite dilution as an open graphite surface. For carbonaceous materials studied in this work, the zero-coverage DMMP enthalpy at 293 K weekly depends on the pore size distribution, which has an important implication for selection of the potential candidate adsorbents for nerve agent capture.Acknowledgements
P.K. acknowledges partial support from the Office of Research & Development, Curtin University of Technology, Grant CRF10084. P.K. acknowledges partial support from the Australian Academy of Science, Scientific Visits to Japan 2011-12. P.G. and A.P.T. acknowledge the use of the computer cluster at Poznan Supercomputing and Networking Centre and Networking Centre and the Information and Communication Technology Centre of the Nicolaus Copernicus University (Torun). P.K. acknowledges the use of the EPIC computer cluster (ivec.org.au). P.K. acknowledges Prof. J. J. Potoff (Wayne State University, USA) for fruitful comments about TraPPE force field. A.V.N. acknowledges support from the DTRA grant HDTRA1-08-1-0042.References
- K. M. Nikolaev, Facilities of Individual and Collective Protection, Military Academy of Chemical Protection, Moscow, 1976 (in Russian) Search PubMed.
- V. M. Gun'ko, D. Palijczuk, R. Leboda, J. Skubiszewska-Zieba, R. Szmigielski and S. Zietek, J. Colloid Interface Sci., 2006, 294, 53–68 CrossRef CAS.
- L. A. Jonas, Carbon, 1978, 16, 115–119 CrossRef CAS.
- Activated Carbon Surfaces in Environmental Remediation, ed. T. J. Bandosz, Elsevier Ltd., Oxford, 2006 Search PubMed.
- V. M. Gun'ko, V. V. Turov, J. Skubiszewska-Zieba, R. Leboda, M. D. Tsapko and D. Palijczuk, Appl. Surf. Sci., 2003, 214, 178–189 CrossRef CAS.
- V. B. Fenelonov, Porous Carbon, Nauka, Novosibirsk, 1995 (in Russian) Search PubMed.
- P. Lodewyckx and E. F. Vansant, Am. Ind. Hyg. Assoc. J., 1999, 60, 612–617 CrossRef CAS.
- P. Lodewyckx and E. F. Vansant, Am. Ind. Hyg. Assoc. J., 2000, 61, 461–468 CrossRef CAS.
- E. Ustinov, N. S. Polyakov, K. M. Nikolaev and M. M. Dubinin, Russ. Chem. Bull., 1986, 35, 888–892 CrossRef.
- Y. H. Yoon and J. H. Nelson, Am. Ind. Hyg. Assoc. J., 1992, 53, 303–316 CrossRef CAS.
- D. Palijczuk, V. M. Gun'ko, R. Leboda, J. Skubiszewska-Zieba and S. Zietek, J. Colloid Interface Sci., 2002, 250, 5–17 CrossRef CAS.
- J. Wu, Modelling adsorption of organic compounds on activated carbon, Solfjädern Offset AB, Umeå, 2004 Search PubMed.
- P. Lodewyckx, G. O. Wood and S. K. Ryu, Carbon, 2004, 42, 1351–1355 CrossRef CAS.
- G. O. Wood, Carbon, 2002, 40, 1883–1890 CrossRef CAS.
- L. A. Jonas and J. A. Rehrmann, Carbon, 1973, 11, 59–64 CrossRef CAS.
- Q. Meng, D. C. Doetschman, A. K. Rizos, M.-H. Lee and J. Schulte, Environ. Sci. Technol., 2011, 45, 3000–3005 CrossRef CAS.
- Ch. J. Karwacki, Recirculation filter unit for the M28 simplified collective protection systems: adsorption equilibria of candidate nonwoven microporous media. www.dtic.mil/cgi-bin/GetTRDoc?AD=ADA379406.
- K. S. W. Sing, D. H. Everett, R. A. W. Haul, L. Moscou, R. A. Pierotti, J. Rouquérol and T. Siemieniewska, Pure Appl. Chem., 1985, 57, 603–619 CrossRef CAS.
- P. J. Branton, K. G. McAdam, M. G. Duke, Ch. Liu, M. Curle, M. Mola, Ch. J. Proctor and R. H. Bradley, Adsorpt. Sci. Technol., 2011, 29, 117–138 CrossRef CAS.
- P. I. Ravikovitch, A. Vishnyakov, R. Russo and A. V. Neimark, Langmuir, 2000, 16, 2311–2320 CrossRef CAS.
- H. Marsh and F. Rodriguez-Reinoso, Activated Carbon, Elsevier Ltd., Oxford, 2006 Search PubMed.
- P. Kowalczyk, V. N. Gun'ko, A. P. Terzyk, P. A. Gauden, H. Rong, Z. Ryu and D. D. Do, Appl. Surf. Sci., 2003, 206, 67–77 CrossRef CAS.
- P. Kowalczyk, A. P. Terzyk, P. A. Gauden, R. Leboda, E. Szmechtig-Gauden, G. Rychlicki, Z. Ryu and H. Rong, Carbon, 2003, 41, 1113–1125 CrossRef CAS.
- A. V. Neimark, P. I. Ravikovitch and A. Vishnyakov, J. Phys.: Condens. Matter, 2003, 15, 347–365 CrossRef CAS.
- P. Kowalczyk, H. Tanaka, K. Kaneko, A. P. Terzyk and D. D. Do, Langmuir, 2005, 21, 5639–5646 CrossRef CAS.
- A. Tanaka, T. Iiyama, T. Ohba, S. Ozeki, K. Urita, T. Fujimori, H. Kanoh and K. Kaneko, J. Am. Chem. Soc., 2010, 132, 2112–2113 CrossRef CAS.
- K. Kaneko, R. F. Cracknell and D. Nicholson, Langmuir, 1994, 10, 4606–4609 CrossRef CAS.
- M. El-Merraoui, M. Aoshima and K. Kaneko, Langmuir, 2000, 16, 4300–4304 CrossRef CAS.
- A. P. Terzyk, P. A. Gauden, J. Zawadzki, G. Rychlicki, M. Wisniewski and P. Kowalczyk, J. Colloid Interface Sci., 2001, 243, 183–192 CrossRef CAS.
- D. Nicholson and N. G. Parsonage, Computer Simulation and the Statistical Mechanics of Adsorption, Academic Press, London, 1982 Search PubMed.
- J. A. Barker and D. H. Everett, Trans. Faraday Soc., 1962, 58, 1608–1623 RSC.
- J. E. Lane and T. H. Spurling, Aust. J. Chem., 1976, 29, 2103–2121 CrossRef CAS.
- W. A. Steele, Surf. Sci., 1973, 36, 317–332 CrossRef CAS.
- J. Liu and M. D. LeVan, Carbon, 2010, 48, 3454–3462 CrossRef CAS.
- J. Liu and M. D. LeVan, Carbon, 2009, 47, 3415–3423 CrossRef CAS.
- N. Sokkalingam, G. Kamath, M. Coscione and J. J. Potoff, J. Phys. Chem. B, 2009, 113, 10292–10297 CrossRef CAS.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Clarendon Press, Oxford, 1987 Search PubMed.
- N. Metropolis and S. Ulam, J. Am. Stat. Assoc., 1949, 44, 335–340 CrossRef CAS.
- S. Kondrat, C. R. Perez, V. Presser, Y. Gogotsi and A. A. Kornyshev, Energy Environ. Sci., 2012, 5, 6474–6479 CAS.
- A. Vishnyakov, G. Yu. Gor, M.-T. Lee and A. V. Neimark, J. Phys. Chem. A, 2011, 115, 5201–5209 CrossRef CAS.
- M.-T. Lee, A. Vishnyakov, G. Yu. Gor and A. V. Neimark, J. Phys. Chem. B, 2011, 115, 13617–13623 CrossRef CAS.
- M. M. Dubinin, K. M. Nikolaev, N. S. Polyakov and G. L. Pirozhkov, Russ. Chem. Bull., 1980, 29, 1211–1214 CrossRef.
- M. M. Dubinin, P. P. Zolotarev, K. M. Nikolaev, N. S. Polyakov, L. I. Petrova and L. V. Radushkevich, Russ. Chem. Bull., 1973, 22, 282–285 CrossRef.
- A. W. Loven, F. J. Vermillion, Adsorption–Desorption Properties of Sorbents. www.dtic.mil/dtic/tr/fulltext/u2/604116.pdf.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c2cp43366d |
| This journal is © the Owner Societies 2013 |
