Pyrazine excited states revisited using the extended multi-state complete active space second-order perturbation method†
Toru
Shiozaki‡
*a,
Clemens
Woywod
*b and
Hans-Joachim
Werner
*a
aInstitut für Theoretische Chemie, Universität Stuttgart, Pfaffenwaldring 55, D-70569 Stuttgart, Germany. E-mail: shiozaki@northwestern.edu; werner@theochem.uni-stuttgart.de; Fax: +49 711 68564442; Tel: +49 711 68564401
bCentre for Theoretical and Computational Chemistry, Department of Chemistry, University of Tromsø, N-9037 Tromsø, Norway. E-mail: woywod@ch.tum.de
First published on 25th October 2012
Abstract
We demonstrate that the recently developed extended multi-state complete active space second-order perturbation theory (XMS-CASPT2) [Shiozaki et al., J. Chem. Phys., 2011, 135, 081106] provides qualitatively correct potential energy surfaces for low-lying excited singlet states of pyrazine, while the potential energy surfaces of the standard MS-CASPT2 methods are ill-behaved near the crossing point of two reference potential energy surfaces. The XMS-CASPT2 method is based on the extended multi-configuration quasi-degenerate perturbation theory proposed earlier by Granovsky [J. Chem. Phys., 2011, 134, 214113]. We show that the conical intersection at the XMS-CASPT2 level can be described without artifacts if the entire method is invariant with respect to any unitary rotations of the reference functions. The photoabsorption spectra of the 11B3u and 11B2u states of pyrazine are simulated, based on a vibronic-coupling model Hamiltonian. The XMS-CASPT2 spectrum of the 11B3u band is found to be comparable to the one computed by a more expensive multireference configuration interaction (MRCI) method, while the XMS-CASPT2 simulation of the 11B2u band is slightly inferior to the MRCI one.
1 Introduction
There are many chemical processes that must be modeled by multireference electronic structure theories. Such processes include those related to state crossings and those dependent on global potential energy surfaces (PESs). Among others, the complete active space second-order perturbation (CASPT2) theories1–9 have been routinely used for such chemical applications. The CASPT2 method is based on a complete active space reference wavefunction and describes the so-called dynamical correlation using second-order perturbation theory. In CASPT2 the internal contraction scheme10,11 is mostly used to reduce the dependence of the computational effort on the number of reference configurations, while some other variants of multireference perturbation theory use uncontracted configuration state functions (CSFs) to expand the first-order wave functions.12–16 Recently,17 a CASPT2 method with density matrix renormalization group reference functions18,19 has also been reported. A concise review on the current status of CASPT2 can be found in ref. 20.One of the shortcomings of the CASPT2 method has been, however, that it is state-specific and it does not allow for a relaxation of the reference coefficients in the first-order wavefunction. This is problematic, especially near conical intersections and avoided crossings. In order to rectify this problem, a multi-state extension of the CASPT2 method (MS-CASPT2) has been developed by Finley et al.5 on the basis of the multi-configuration quasi-degenerate perturbation theory (MCQDPT),15 which was in turn based on earlier developments.21 In MS-CASPT2, a second-order effective Hamiltonian is diagonalized at the end, which allows for mixings of the zeroth and first-order wave functions of different nearly degenerate states. There are also similar approaches called generalized Van-Vleck perturbation theories.22,23
Although MS-CASPT2 improves the description of electronic structures around conical intersections and avoided crossings in comparison to the single state CASPT2, there are still many cases where MS-CASPT2 PESs become singular at crossing points.24 A remedy has been first proposed by Granovsky,25 who has proposed the ‘extended’ MCQDPT method, which is a generalization of the uncontracted MCQDPT of Nakano.15 An internally contracted CASPT2 variant has recently been implemented (XMS-CASPT2) by Shiozaki et al., together with its analytic nuclear energy gradients.26,27
The key idea in XMCQDPT and XMS-CASPT2 has been to use a zeroth-order Hamiltonian that is invariant with respect to any unitary rotations of the reference wavefunctions. For the second order energy, this is technically equivalent (see below) to use rotated reference functions, which diagonalize the Fock operator within the space spanned by the reference functions (or, the model space) when computing the perturbed wave functions. As a result, the computational cost of XMS-CASPT2 energy and nuclear gradient computations is the same as that of standard MS-CASPT2.
On the other hand, the XMS-CASPT2 method could introduce some shortcomings as well. For instance, the intruder state problems could be more pronounced, since in XMS-CASPT2 some states have a higher zeroth-order energy than in MS-CASPT2 due to diagonalization of the Fock operator. Furthermore, in rare cases when the reference functions span the complete active space, XMS-CASPT2 transforms eigenfunctions of the active space Hamiltonian back to CSFs, which is not desirable. Therefore, it is important to carefully examine the accuracy of the XMS-CASPT2 method.
In order to assess the quality of PESs computed by the XMS-CASPT2 approach we have in the current work employed this method to parametrize a vibronic coupling Hamiltonian for the 11B3u and 11B2u states of pyrazine. The strong vibronic interaction between these states is clearly manifested in the continuous wave (CW) photoabsorption and resonance Raman spectra. The 11B3u–11B2u coupling has in fact become a showcase example for the calibration of vibronic coupling models. Spectroscopic properties of the two vibronically coupled electronic states have been studied in detail both by experiment28–32 as well as by theory.33–49
We first present a summary of the XMS-CASPT2 theory (Section 2.1), followed by the methodology for the simulation of CW photoabsorption bands (Section 2.2). In Section 3.1 we show that the XMS-CASPT2 method provides smooth potential energy functions for the 11B3u and 11B2u states of pyrazine, which are free of artifacts and almost parallel to those computed by the multireference configuration-interaction approach, including the quasi-degenerate Davidson correction (MRCI+Q). In Section 3.2 it will be demonstrated that the invariant inclusion of level shifts50 in the XMS-CASPT2 theory is crucial for description of electronic structures near conical intersections. The simulations of the 11B3u and 11B2u photoabsorption bands performed with this model are discussed in Section 3.3 and compared with previous calculations, in particular ref. 48 and 49. Conclusions based on the computational results are given in Section 4.
2 Theoretical background
In this section, we briefly review the XMS-CASPT2 theory and the framework of computing photoabsorption spectra. For details, the readers are referred to ref. 26 and 48, respectively.2.1 XMS-CASPT2 theory
The main idea of the extended multistate multireference perturbation theories, first proposed by Granovsky,25 is to make the multistate theories invariant with respect to any unitary rotations of reference [i.e., complete-active-space self-consistent-field (CASSCF)] functions. As shown previously25,26 and herein, this is essential for a consistent simulation of conical intersections and avoided crossings.The invariant form of the XMS-CASPT2 amplitude equations and the effective Hamiltonian is
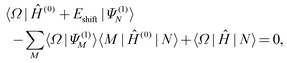 | (1) |
| (Heff)MN = ½(〈ΨM|Ĥ|N〉 + 〈M|Ĥ|ΨN〉) − Eshift〈Ψ(1)M|Ψ(1)N〉, | (2) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) |N〉 + |Ψ(1)N〉. The zeroth order Hamiltonian is defined as
|N〉 + |Ψ(1)N〉. The zeroth order Hamiltonian is defined as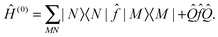 | (3) |
![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) is the projector
is the projector 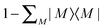 . If internally contracted functions are used for |Ψ(1)N〉, the first-order wave function for each state should be expanded in terms of the union of the internally contracted functions generated from all the references26,51 (the so-called MS-MR-CASPT2 scheme in MOLPRO52).
. If internally contracted functions are used for |Ψ(1)N〉, the first-order wave function for each state should be expanded in terms of the union of the internally contracted functions generated from all the references26,51 (the so-called MS-MR-CASPT2 scheme in MOLPRO52). ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) is the generalized Fock operator
is the generalized Fock operator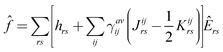 | (4) |
The level shift Eshift has been introduced into CASPT2 in order to circumvent intruder state problems.50 We have introduced the level shift in the XMS-CASPT2 amplitude equations [eqn (1)] in an invariant way with respect to any unitary rotation of reference functions. The proof of invariance is straightforward.25 Thanks to this invariance, one can transform the reference functions by means of a unitary matrix UMN so that 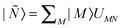 diagonalizes Ĥ(0), i.e.,
diagonalizes Ĥ(0), i.e.,
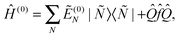 | (5) |
〈![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) |Ĥ(0)|Ñ〉 = δMNẼ(0)N. |Ĥ(0)|Ñ〉 = δMNẼ(0)N. | (6) |
〈Ω|Ĥ(0) − Ẽ(0)N + Eshift|![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) (1)N〉 + 〈Ω|Ĥ|Ñ〉 = 0, (1)N〉 + 〈Ω|Ĥ|Ñ〉 = 0, | (7) |
(Heff)MN = ½(〈![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) M|Ĥ|Ñ〉 + 〈 M|Ĥ|Ñ〉 + 〈![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) |Ĥ| |Ĥ|![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) N〉) − Eshift〈 N〉) − Eshift〈![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) (1)M| (1)M|![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) (1)N〉, (1)N〉, | (8) |
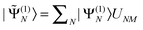 and
and ![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) N = |Ñ〉 + |
N = |Ñ〉 + |![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) (1)N〉. Note that the first-order wave functions are generally not orthogonal to each other, and the shift correction in the effective Hamiltonian is therefore only invariant if the full overlap matrix 〈
(1)N〉. Note that the first-order wave functions are generally not orthogonal to each other, and the shift correction in the effective Hamiltonian is therefore only invariant if the full overlap matrix 〈![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) (1)M|
(1)M|![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) (1)N〉 is included in the last term of (Heff)MN. Previously,26 we used only the diagonal (M = N) part of the correction term [the last term in eqn (8)], which was, in turn, the default choice for the standard MS-CASPT2 (which we hereafter denote ‘standard shifts’). The fully invariant inclusion has turned out to be of vital importance as we will see numerically later (hereafter denoted as ‘invariant shifts’).
(1)N〉 is included in the last term of (Heff)MN. Previously,26 we used only the diagonal (M = N) part of the correction term [the last term in eqn (8)], which was, in turn, the default choice for the standard MS-CASPT2 (which we hereafter denote ‘standard shifts’). The fully invariant inclusion has turned out to be of vital importance as we will see numerically later (hereafter denoted as ‘invariant shifts’).
The modification of the analytic nuclear energy gradient code due to the change of the level shift formula has been trivial. The computer code that implements the above methods is available in the latest release of MOLPRO.52 Other choices of the zeroth-order Hamiltonian, such as the so-called IPEA shift,53 can also be used in conjunction with XMS-CASPT2. However, the standard zeroth-order Hamiltonian has been used throughout the current work.
2.2 Simulation of 11B3u and 11B2u continuous wave absorption spectra
In this work, the vibronic coupling dynamics is treated in a quasi-diabatic electronic basis ({ΦN(r,Q)}N=1,2) since this simplifies numerical calculations. Here r denotes collectively the electronic coordinates and Q the set of vibrational normal coordinates. Φ1 and Φ2 correspond to the 11B3u and 11B2u excited states of pyrazine, respectively. The definition and generation of these quasi-diabatic states from the adiabatic wavefunctions ΨN is described in ref. 48. Expanding 〈ΦN(Q)|(Ĥ(Q)|ΦM(Q))〉 − V0(Q)δNM (Ĥ denotes the electronic Hamiltonian) around the S0 equilibrium geometry [Q = 0] to second order (except for bilinear terms) leads to the approximate two-state multimode matrix Hamiltonian of vibronic coupling theory (Table 1),54 in which γ(n)t and γ(n)10a are parameters corresponding to the diagonal elements of the matrix of second derivatives of the excitation energies of the 11B3u and 11B2u states with respect to the normal coordinates Qt and Q10a, respectively.![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) nuc is the nuclear kinetic energy operator, and V0(Q) is the nuclear ground-state potential of pyrazine in the harmonic approximation. Qi denotes a dimensionless normal coordinate. En are the vertical excitation energies, κ(n)t the first-order intrastate and λ10a the first-order 11B3u–11B2u interstate electron-vibrational coupling constants. The summation index t includes all five totally symmetric or “tuning” coordinates of pyrazine: Q1, Q2, Q6a, Q8a and Q9a. Tuning modes νt are characterized by modulating the energy gap between the two states.54 For symmetry reasons, only nuclear displacements that transform according to the Ag and B1g irreducible representations of the D2h point group can couple linearly to one-photon transitions into the 11B3u and 11B2u states. The parameters (κ(n)t, λ10a, γ(n)t and γ(n)10a) are computed by the same procedure as in ref. 48, see also below.
nuc is the nuclear kinetic energy operator, and V0(Q) is the nuclear ground-state potential of pyrazine in the harmonic approximation. Qi denotes a dimensionless normal coordinate. En are the vertical excitation energies, κ(n)t the first-order intrastate and λ10a the first-order 11B3u–11B2u interstate electron-vibrational coupling constants. The summation index t includes all five totally symmetric or “tuning” coordinates of pyrazine: Q1, Q2, Q6a, Q8a and Q9a. Tuning modes νt are characterized by modulating the energy gap between the two states.54 For symmetry reasons, only nuclear displacements that transform according to the Ag and B1g irreducible representations of the D2h point group can couple linearly to one-photon transitions into the 11B3u and 11B2u states. The parameters (κ(n)t, λ10a, γ(n)t and γ(n)10a) are computed by the same procedure as in ref. 48, see also below.
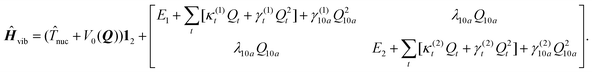
|
The photoabsorption line spectrum is computed using Fermi's golden rule,55
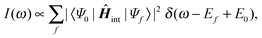 | (9) |
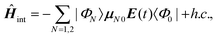 | (10) |
The eigenvalues of the approximate two-state matrix Hamilton operator Ĥvib [Table 1] are obtained by numerically solving the time-independent vibronic Schrödinger equation with a vibronic basis,56
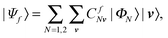 | (11) |
The ground state |Ψ0〉 of pyrazine is to a good approximation a Born–Oppenheimer product:
| |Ψ0〉 = |Φ0〉|0〉, | (12) |
| 〈Ψ0|Ĥint|Ψf〉 ∝ τ1Cf10 + τ2Cf20, | (13) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ2 of 1
τ2 of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.7 has been estimated by employing the same basis set (basis version 1) and active space definition as for the calculation of vibronic parameters in the present study. The oscillator strengths were computed by combining transition dipole moments and vertical excitation energies obtained at the CASSCF and CASPT2 levels of theory, respectively.47
4.7 has been estimated by employing the same basis set (basis version 1) and active space definition as for the calculation of vibronic parameters in the present study. The oscillator strengths were computed by combining transition dipole moments and vertical excitation energies obtained at the CASSCF and CASPT2 levels of theory, respectively.47
3 Numerical results
Our numerical demonstration in this section is threefold. In Section 3.1 we will first show that the artifacts one encounters with the standard MS-CASPT2 method in regions that are characterized by very small energy differences between two or more CASSCF reference states can be removed by using the new XMS-CASPT2 method. Secondly, in Section 3.2 we demonstrate the importance of the invariant inclusion of level shifts when the Fock operator has degenerate eigenvalues near state crossings. Finally, based on the two-state vibronic model, we simulate the CW photoabsorption spectra of the 11B3u and 11B2u states of pyrazine and compare the results to experiment as well as to previous theoretical spectra48,49 (Section 3.3).We have used Dunning's augmented triple-ζ basis set (aug-cc-pVTZ), without the diffuse functions of highest angular shells for each atom. In addition, we included four s-, three p-, and three d-type diffuse functions located at the center of mass of the molecule, whose exponents are s (0.021, 0.008, 0.0025, 0.0008), p (0.017, 0.009, 0.004), d (0.015, 0.008, 0.004). This basis set has been employed in the calculations reported in ref. 47 (basis version 1). In principle, the aug-cc-pVTZ basis set would be sufficient for the description of the 11Ag, 11B3u and 11B2u states of pyrazine, but we prefer this basis for consistency reasons.
The ground state geometry and force field have been determined by the single-state CASPT2 approach.57 The 11B3u and 11B2u excited states transform according to the Bu irreducible representation if the C2h point group applies to the nuclear frame. They are computed with state averaging and multi-state treatments within the reduced symmetry. The active space was constructed from 10 electrons in 8 orbitals (2 orbitals each in ag, au, bu, and bg within C2h symmetry).47–49 A level shift of 0.3 Eh was used to avoid intruder state problems.
Note that although the 11B3u and 11B2u excitations are frequently assigned as the S1 and S2 states at the ground state equilibrium geometry and the 11B3u state is indeed the S1 state, the true second excited state is of Au symmetry and 11B2u is in reality S3.47 We therefore use 11B3u and 11B2u to label these states in this article.
3.1 Excited state potential energy surfaces in the Franck–Condon region
First we present the PESs of the 11B3u and 11B2u states of pyrazine near the ground-state equilibrium geometry. Fig. 1 compares those computed by the standard MS-CASPT2 and those by XMS-CASPT2. Apparently, the PESs from MS-CASPT2 have artifacts around Q10a = 0 and Q6a = −0.5, whereas those from XMS-CASPT2 do not exhibit such erratic behavior. The artifacts are ascribed to the rotation of the reference functions due to a state crossing of the reference surfaces, as in the examples reported earlier.25,26 This is supported by Fig. 2, which shows the two-dimensional cut of the reference PESs along the Q6a and Q10a modes.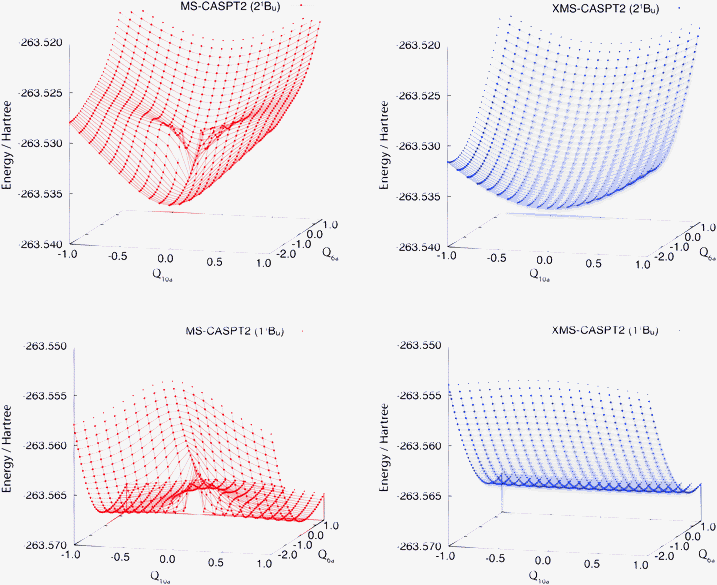 | ||
| Fig. 1 Potential energy surfaces of the adiabatic 11Bu and 21Bu states of pyrazine (using C2h labels) are shown in the Franck–Condon region. The electronic states are computed at the standard (left) and extended (right) MS-CASPT2 levels of theory. The nuclear coordinate space is spanned by Q6a and Q10a. Note that at Q10a = 0, MS- and XMS-CASPT2 give the same results due to symmetry. | ||
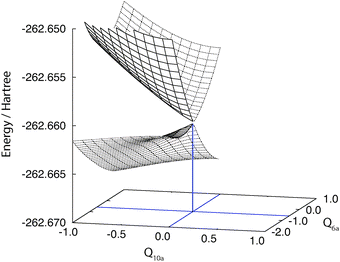 | ||
| Fig. 2 The state crossing of the SA-CASSCF potential energy surfaces, which coincides with the artifacts in the standard MS-CASPT2. The surfaces are symmetric with respect to the inversion of the Q10a axis. | ||
In Fig. 3 we present a one-dimensional cut of the same PESs along the Q10a coordinate computed by MS-CASPT2 and XMS-CASPT2, as well as by MRCI+Q.58,59 The curves computed by the standard MS-CASPT2 have an artificial dent near the equilibrium structure, which is not present in the MRCI+Q curves. The XMS-CASPT2 method removes this artifact and the curves are almost parallel to the one from MRCI+Q. At the equilibrium geometry, the MS-CASPT2 and XMS-CASPT2 energies become identical since the off-diagonal element of the Fock operator in the reference space (i.e., 〈M|![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) |N〉 with M ≠ N) is zero due to symmetry. Therefore, the difference in the separation of two excited states is ascribed to the insufficient treatment of dynamical correlation at the CASPT2 level (and not to the multi-state treatment). The quality of XMS-CASPT2 PESs will be tested in what follows.
|N〉 with M ≠ N) is zero due to symmetry. Therefore, the difference in the separation of two excited states is ascribed to the insufficient treatment of dynamical correlation at the CASPT2 level (and not to the multi-state treatment). The quality of XMS-CASPT2 PESs will be tested in what follows.
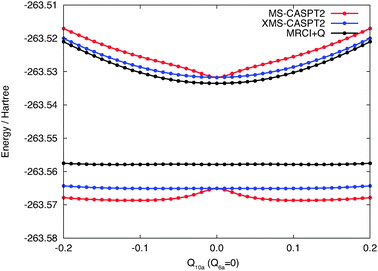 | ||
| Fig. 3 Potential energy curves along the Q10a mode computed by MS-CASPT2, XMS-CASPT2 and MRCI+Q. | ||
3.2 Conical intersection
Fig. 4 shows a one-dimensional cut of the same PESs along the Q10a mode near the conical intersection [Q6a = −3.9]. The lower panel corresponds to the zeroth-order energies (i.e., the eigenvalues of the Fock matrix in the reference space), showing that it has degenerate eigenvalues near the state crossing. The standard MS-CASPT2 has a smooth potential here (red curves). The erratic behavior of the XMS-CASPT2 surfaces with the standard level shift (black curves) is attributed to the degeneracy of the eigenvalues of the Fock matrix: at the Q10a = 0 geometry, the rotation angle in XMS is zero due to symmetry; but when the geometry is slightly distorted along the Q10a mode, the off-diagonal Fock elements become nonzero, while the difference between two diagonal elements remains small. This leads to significant rotation in XMS, and hence the artifact as shown in the upper panel of Fig. 4. This problem has been fixed by using the invariant level shift (blue curves). Note that the curves from XMS-CASPT2 with the standard and invariant level shifts become nearly identical apart from the crossing region. These observations are confirmed by the two-dimensional cuts in Fig. 5.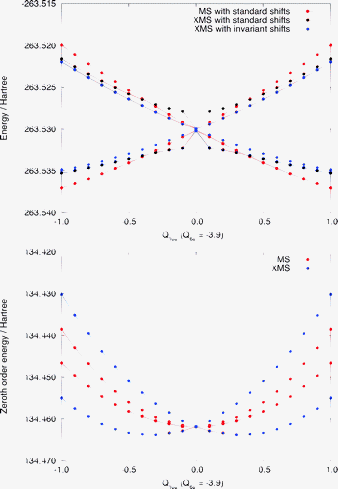 | ||
| Fig. 4 Upper panel: a one dimensional cut of the potential energy surfaces along the Q10a mode near the conical intersection (Q6a = −3.9), computed by MS-CASPT2 and XMS-CASPT2 with the standard and invariant level shift of 0.3 Eh. Lower panel: the zeroth-order energies along the same cut. | ||
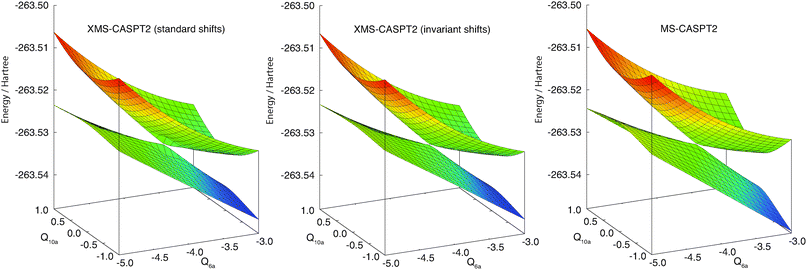 | ||
| Fig. 5 Two-dimensional maps with Q6a and Q10a around the conical intersection computed by MS-CASPT2 and XMS-CASPT2. Note that MS-CASPT2 and XMS-CASPT2 are identical when Q10a = 0 due to symmetry. | ||
3.3 Simulation of 11B3u and 11B2u continuous wave photoabsorption spectra
The parameters κ(n)t and γ(n)t for the 11B3u and 11B2u states evaluated with the single-state CASPT2 method are compiled in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 Since the 11B3u and 11B2u states cannot interact within D2h symmetry, a state-averaged treatment of both states is not necessary in this case. We have verified that the CASPT2 excitation energies of both states computed in the D2h point group are very insensitive to the optimization scheme applied to the reference functions: individually converged CASSCF wave functions yield single-state CASPT2 excitation energy functions that are almost identical to those obtained by MS-CASPT2 calculations based on reference functions that are obtained by including the 11B3u and 11B2u states with equal weights in the CASSCF energy functional.
60 Since the 11B3u and 11B2u states cannot interact within D2h symmetry, a state-averaged treatment of both states is not necessary in this case. We have verified that the CASPT2 excitation energies of both states computed in the D2h point group are very insensitive to the optimization scheme applied to the reference functions: individually converged CASSCF wave functions yield single-state CASPT2 excitation energy functions that are almost identical to those obtained by MS-CASPT2 calculations based on reference functions that are obtained by including the 11B3u and 11B2u states with equal weights in the CASSCF energy functional.
Since the MS-CASPT2 approach yields artifacts in the adiabatic PESs of the 11Bu and 21Bu states for nonzero displacements along Q10a in the vicinity of the degeneracy of the CASSCF reference states as we demonstrated above, a reliable determination of the Q10a vibronic coupling parameters is not possible. We therefore concentrate only on a comparison of spectra calculated using MRCI and XMS-CASPT2 parameters.
The κ(n)t parameters computed by XMS-CASPT2 show qualitative agreement with those by MRCI:49 for instance, κ(1)6a/κ(2)6a and κ(1)8a/κ(2)8a have similar values. However, the magnitude of the individual parameters differs significantly in some cases; the most pronounced example is κ(1)1 (MRCI: −0.0470 eV, CASPT2: −0.0299 eV). The set of vibronic coupling parameters for Ĥvib (Table 1) is completed by λ10a = 0.201 eV, γ(1)10a = −0.014 eV and γ10(2)a = −0.014 eV. λ10a, γ(1)10a, and γ(2)10a have been determined by a least-squares fit of the eigenvalues of the two-state model potential energy matrix as a function of Q10a at the XMS-CASPT2 level of theory. The XMS-CASPT2 parameters deviate only slightly from those obtained with the MRCI method (0.1825 eV, −0.0180 eV, −0.0180 eV, respectively).48
Fig. 6 and 7 show the observed, XMS-CASPT2, and MRCI photoabsorption spectra of the 11B3u and 11B2u states, respectively. The coherence-decay constants are set to T2 = 400 fs and T2 = 35 fs, respectively, to account for homogeneous broadening of the individual vibronic transitions. For a discussion of the microscopic origin of dephasing rates 1/T2 see, for instance, ref. 62. The theoretical spectra shown as solid lines in panel (b) of Fig. 6 and 7 have been blue-shifted by 0.165 eV and by 0.096 eV, respectively, in order to compensate for the underestimation of 0–0 transitions of both bands by the CASPT2 method. The MRCI-derived spectrum (solid line) is likewise red-shifted by 0.031 eV in Fig. 6(c). It is typical that CASPT2 underestimates excitation energies, while MRCI slightly overestimates them.
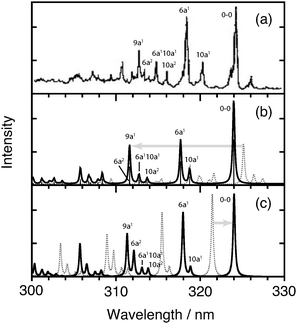 | ||
| Fig. 6 CW photoabsorption spectra of the 11B3u state: (a) experimental,61 (b) XMS-CASPT2, and (c) MRCI (based on ref. 49). Unshifted (dotted) and shifted (full) theoretical spectra are shown. See text for details. The assignments in the experimental spectrum are based on an analysis of both theoretical spectra, taking available information on experimental 11B3u frequencies into account. | ||
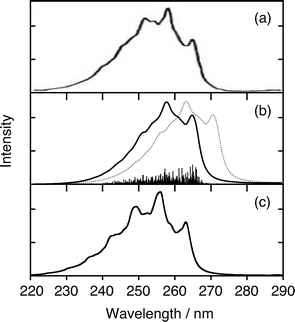 | ||
| Fig. 7 CW photoabsorption spectra of the 11B2u state: (a) experimental,31 (b) XMS-CASPT2, and (c) MRCI (based on ref. 49). Unshifted (dotted) and shifted (full) theoretical spectra are shown. See text for details. | ||
Note that the XMS-CASPT2 spectra in this work are computed with a vibronic model that slightly differs from the vibronic Hamiltonians used in the previous MRCI simulations.48,49 In ref. 48 a 4-mode model was used, which included the Q1, Q6a, Q9a tuning modes, as well as the Q10a coupling mode. In ref. 49 the 4-mode model was augmented by including also the Q8a, Q4, and Q14 modes, but the Q2 tuning mode was still neglected. In the current work we employ a 6-mode model that includes all five Ag tuning modes (Q1, Q2, Q6a, Q8a, Q9a), but neglects the quadratic effect of the out-of-plane displacements Q4 and Q14. Secondly, in this study the ground-state force field is consistently constructed by CASPT2, while a second-order Møller–Plesset (MP2) ground-state force field was used in ref. 49. Third, diagonal quadratic intrastate coupling terms with parameters γ(n)t have been introduced for the Ag vibrations, which were absent in the model of ref. 49.
The 11B3u and 11B2u MRCI absorption spectra shown in Fig. 6(c) and 7(c), respectively, have been calculated with the MRCI parameters and the 7-mode vibronic model reported in ref. 49. The 11B3u spectrum was not shown in ref. 49 and is published for the first time in this work.
Both XMS-CASPT2 and MRCI successfully reproduce the main vibronic features of the 11B3u band (Fig. 6). The XMS-CASPT2 spectrum appears to better describe the spacing between levels ν110a and ν16a and relative intensities of three pronounced excitations between 312 nm and 317 nm. These three resonances in the experimental spectrum have originally been attributed to vibronic levels ν102a, ν16aν110a and ν26a.31 An analysis of the strong transition at 311.59 nm in the XMS-CASPT2 spectrum reveals, however, that the intensity is derived from two nearly degenerate levels of B3u vibronic symmetry with an intensity ratio of 6.1 (ν19a) to 1.0 (ν26a). The present model therefore confirms the assignments of ref. 46 and 48 that the strong peak at around 312.5 nm in the experimental spectrum corresponds primarily to the quantum ν19a.
This suggests the following interpretation of Fig. 6(b) and (c): the XMS-CASPT2 calculation wrongly attributes a slightly higher energy to the overtone ν26a as compared to the fundamental of ν9a, and the small spacing between both transitions leads to an overestimation of the peak appearing at ca. 311.5 nm in Fig. 6(b). On the other hand, the MRCI model correctly predicts that the ν26a transition is red-shifted with respect to ν19a but strongly overestimates the intensity of ν26a. We emphasize again that in the MRCI simulation of ref. 49 an MP2 ground state potential and a slightly different vibronic model than in the current work were used. For a more detailed and consistent analysis one would need to compute all three MRCI and XMS-CASPT2 potentials on equal footing and carry out the simulations using the same vibronic model. This is beyond the scope of the present paper and will be the subject of future work.
The XMS-CASPT2 simulation of the 11B2u band is less satisfactory than the MRCI simulation (Fig. 7), although both electronic structure theories yield similar Q10a-related coefficients (λ10a, γ(1)10a and γ(2)10a). The vibronic models yield the following intersection points: Q1 = 6.8, Q6a = −3.7 (XMS-CASPT2) and Q1 = 5.4, Q6a = −3.9 (MRCI). This result implicates that the discrepancy between XMS-CASPT2- and MRCI-based spectra is partly owing to a substantial difference between the CASPT2- and MRCI-derived topologies of the 11B3u–11B2u degeneracy subspaces with respect to the location of the ground-state equilibrium geometry.
4 Conclusions
In this paper we have demonstrated that the recently developed XMS-CASPT2 method is a useful tool for the ab initio description of strongly coupled electronically excited states, even in cases where the standard MS-CASPT2 approach completely fails. For the pyrazine excited states that are considered here, the standard MS-CASPT2 gives a hump around the equilibrium geometry of the ground state that is associated with a CASSCF state crossing, while XMS-CASPT2 is free from such artifacts. We have also shown the importance of including the level shift in a way that is invariant with respect to unitary transformations of the reference functions.The smooth PES computed by XMS-CASPT2 has allowed us to examine the accuracy of the vibronic interaction strength of the 11B3u and 11B2u states of pyrazine, which was not possible with the standard MS-CASPT2 method. We have extended previous versions46,48,49 of the model Hamiltonian for nonadiabatic dynamics in the coupled 11B3u and 11B2u vibronic manifolds by including the diagonal quadratic intrastate coupling parameters γ(n)t for the Ag modes.
A comparison of the simulated 11B3u absorption bands by XMS-CASPT2 and by MRCI49 shows that while some aspects of the vibronic structure are improved in the XMS-CASPT2 spectrum, other features of the experimental envelope are better approximated by the MRCI-based approach. A more detailed analysis of the influence of the PESs and of the different vibronic models on the simulated spectra would require computation of an accurate MRCI PES for the electronic ground state, as well as extension of the existing MRCI potentials by the Q2 mode that was neglected in previous work.49 This will be the subject of future work.
We have also observed that the XMS-CASPT2 11B2u spectrum is slightly inferior to that computed with MRCI parameters, which can probably be ascribed to a lower accuracy of the XMS-CASPT2 potential energy surfaces. Nevertheless, we conclude that the XMS-CASPT2 method is a useful method for such simulations when the system of concern becomes so large that more accurate MRCI computations are too expensive.
Acknowledgements
This work has been supported by the Deutsche Forschungsgemeinschaft as part of the SimTech Cluster of Excellence at the University of Stuttgart. T.S. thanks the Japan Society for the Promotion of Science for financial support. C.W. has received continued support from the Mohn Foundation (Grant No. A32542) and the Centre for Theoretical and Computational Chemistry (CTCC) at the University of Tromsø. We acknowledge computational resources provided by Norwegian High Performance Computing (NOTUR).References
- B. O. Roos, P. Linse, P. E. M. Siegbahn and M. R. A. Blomberg, Chem. Phys., 1982, 66, 197–207 CrossRef CAS.
- K. Andersson, P.-Å. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483–5488 CrossRef CAS.
- K. Andersson, P.-Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226 CrossRef CAS.
- H.-J. Werner, Mol. Phys., 1996, 89, 645–661 CrossRef CAS.
- J. Finley, P.-Å. Malmqvist, B. O. Roos and L. Serrano-Andrés, Chem. Phys. Lett., 1998, 288, 299–306 CrossRef CAS.
- P. Celani and H.-J. Werner, J. Chem. Phys., 2000, 112, 5546–5557 CrossRef CAS.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS.
- F. Aquilante, P.-Å. Malmqvist, T. B. Pedersen, A. Ghosh and B. O. Roos, J. Chem. Theory Comput., 2008, 4, 694–702 CrossRef CAS.
- T. Shiozaki and H.-J. Werner, J. Chem. Phys., 2010, 133, 141103 CrossRef.
- W. Meyer, Methods of Electronic Structure Theory, Plenum, New York, 1977 Search PubMed.
- H.-J. Werner and E.-A. Reinsch, J. Chem. Phys., 1982, 76, 3144–3156 CrossRef CAS.
- K. Hirao, Chem. Phys. Lett., 1992, 190, 374–380 CrossRef CAS.
- K. Hirao, Chem. Phys. Lett., 1992, 196, 397–403 CrossRef CAS.
- K. Hirao, Chem. Phys. Lett., 1993, 201, 59–66 CrossRef CAS.
- H. Nakano, J. Chem. Phys., 1993, 99, 7983–7992 CrossRef CAS.
- S. Ten-no, Chem. Phys. Lett., 2007, 447, 175–179 CrossRef CAS.
- Y. Kurashige and T. Yanai, J. Chem. Phys., 2011, 135, 094104 CrossRef.
- D. Zgid and M. Nooijen, J. Chem. Phys., 2008, 128, 144116 CrossRef.
- D. Ghosh, J. Hachmann, T. Yanai and G. K.-L. Chan, J. Chem. Phys., 2008, 128, 144117 CrossRef.
- P. Pulay, Int. J. Quantum Chem., 2011, 111, 3273–3279 CrossRef CAS.
- B. Huron, J. P. Malrieu and P. Rancure, J. Chem. Phys., 1973, 58, 5745–5759 CrossRef CAS.
- Y. G. Khait, J. Song and M. R. Hoffmann, J. Chem. Phys., 2002, 117, 4133–4145 CrossRef CAS.
- T. J. Dudley, Y. G. Khait and M. R. Hoffmann, J. Chem. Phys., 2003, 119, 651–660 CrossRef CAS.
- L. Serrano-Andrés, M. Merchán and R. Lindh, J. Chem. Phys., 2005, 122, 104107 CrossRef.
- A. A. Granovsky, J. Chem. Phys., 2011, 134, 214113 CrossRef.
- T. Shiozaki, W. Győrffy, P. Celani and H.-J. Werner, J. Chem. Phys., 2011, 135, 081106 CrossRef.
- P. Celani and H.-J. Werner, J. Chem. Phys., 2003, 119, 5044–5057 CrossRef CAS.
- K. K. Innes, I. G. Ross and W. R. Moomaw, J. Mol. Spectrosc., 1988, 132, 492–554 CrossRef CAS.
- A. Bolovinos, P. Tsekeris, J. Philips, E. Pantos and G. Anditsopouluos, J. Mol. Spectrosc., 1984, 103, 240–256 CrossRef CAS.
- J. Kommandeur, W. A. Majewski, W. L. Meerts and D. W. Pratt, Annu. Rev. Phys. Chem., 1987, 38, 433–462 CrossRef CAS.
- I. Yamazaki, T. Murao, T. Yamanaka and K. Yoshihara, Faraday Discuss. Chem. Soc., 1983, 75, 395–405 RSC.
- M. H. Palmer and I. C. Walker, Chem. Phys., 1991, 157, 187–200 CrossRef CAS.
- P. Weber and J. R. Reimers, J. Phys. Chem. A, 1999, 103, 9821–9829 CrossRef CAS.
- Y. Li, J. Wan and X. Xu, J. Comput. Chem., 2007, 28, 1658–1667 CrossRef CAS.
- A. Raab, G. A. Worth, H.-D. Meyer and L. S. Cederbaum, J. Chem. Phys., 1999, 110, 936–946 CrossRef CAS.
- M. P. Fülscher, K. Andersson and B. O. Roos, J. Phys. Chem., 1992, 96, 9204–9212 CrossRef.
- K. Andersson, Theor. Chim. Acta, 1995, 91, 31–46 CAS.
- M. P. Fülscher and B. O. Roos, Theor. Chim. Acta, 1994, 87, 403–413 CrossRef.
- J. E. DelBene, J. D. Watts and R. J. J. Bartlett, J. Chem. Phys., 1997, 106, 6051–6060 CrossRef CAS.
- G. A. Worth, H.-D. Meyer and L. S. Cederbaum, J. Chem. Phys., 1996, 105, 4412–4426 CrossRef CAS.
- M. Schreiber, M. R. Silva-Junior, S. P. A. Sauer and W. Thiel, J. Chem. Phys., 2008, 128, 134110 CrossRef.
- M. R. Silva-Junior, M. Schreiber, S. P. A. Sauer and W. Thiel, J. Chem. Phys., 2010, 133, 174318 CrossRef.
- M. R. Silva-Junior, M. Schreiber, S. P. A. Sauer and W. Thiel, J. Chem. Phys., 2008, 129, 104103 CrossRef.
- S. P. A. Sauer, M. Schreiber, M. R. Silva-Junior and W. Thiel, J. Chem. Theory Comput., 2009, 5, 555–564 CrossRef CAS.
- N. Heider and S. F. Fischer, Chem. Phys., 1984, 88, 209–220 CrossRef CAS.
- L. Seidner, G. Stock, A. L. Sobolewski and W. Domcke, J. Chem. Phys., 1992, 96, 5298–5309 CrossRef CAS.
- C. Woywod, A. Papp, G. J. Halasz and A. Vibok, Theor. Chem. Acc., 2010, 125, 521–533 CrossRef CAS.
- C. Woywod, W. Domcke, A. L. Sobolewski and H.-J. Werner, J. Chem. Phys., 1994, 100, 1400–1413 CrossRef CAS.
- G. Stock, C. Woywod, W. Domcke, T. Swinney and B. S. Hudson, J. Chem. Phys., 1995, 103, 6851–6860 CrossRef CAS.
- B. O. Roos and K. Andersson, Chem. Phys. Lett., 1995, 245, 215–223 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Theor. Chim. Acta, 1992, 84, 95–103 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, G. Knizia and F. R. Manby, M. Schütz, et al., MOLPRO, version 2012.1, a package of ab initio programs, Cardiff, UK, 2012, see http://www.molpro.net Search PubMed.
- G. Ghigo, B. O. Roos and P.-Å. Malmqvist, Chem. Phys. Lett., 2004, 396, 142–149 CrossRef CAS.
- H. Köppel, W. Domcke and L. S. Cederbaum, Adv. Chem. Phys., 1984, 57, 59–246 CrossRef.
- A. Lami, C. Petrongolo and F. Santoro, Conical Intersections, World Scientific, Singapore, 2004, p. 705 Search PubMed.
- C. Cohen-Tannoudji, B. Diu and F. Laloe, Quantum mechanics, Wiley, New York, 1977, vol. 1 Search PubMed.
- K. Andersson, M. R. A. Blomberg, M. P. Fülscher, G. Karlström, R. Lindh, P.-Å. Malmqvist, P. Neogrády, J. Olsen, B. O. Roos, A. J. Sadlej, M. Schütz, L. Seijo, L. Serrano-Andrés, P. E. M. Siegbahn and P.-O. Widmark, MOLCAS Version 7.4, Lund University, Sweden, 2010 Search PubMed.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1988, 145, 514–522 CrossRef CAS.
- See ESI† for the computational details of photoabsorption spectra.
- M. Perić, S. D. Peyerimhoff and R. J. Buenker, Z. Phys. D: At., Mol. Clusters, 1992, 24, 177–198 CrossRef.
- W. Domcke and G. Stock, Adv. Chem. Phys., 1997, 100, 1–169 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c2cp43381h |
| ‡ Present address: Department of Chemistry, Northwestern University, 2145 Sheridan Road, Evanston, IL 60208, USA. |
| This journal is © the Owner Societies 2013 |
