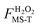Role of conformational structures and torsional anharmonicity in controlling chemical reaction rates and relative yields: butanal + HO2 reactions†
Jingjing
Zheng
,
Prasenjit
Seal
and
Donald G.
Truhlar
*
Department of Chemistry and Supercomputing Institute, University of Minnesota, Minneapolis, Minnesota 55455-0431, USA. E-mail: truhlar@umn.edu
First published on 24th September 2012
Abstract
Aldehyde–radical reactions are important in atmospheric and combustion chemistry, and the reactions studied here also serve more generally to illustrate a fundamental aspect of chemical kinetics that has been relatively unexplored from a quantitative point of view, in particular the roles of multiple structures and torsional anharmonicity in determining the rate constants and branching ratios (product yields). We consider hydrogen abstraction from four carbon sites of butanal (carbonyl-C, α-C, β-C and γ-C) by hydroperoxyl radical. We employed multi-structural variational transition state theory for studying the first three channels; this uses a multi-faceted dividing surface and allows us to include the contributions of multiple structures of both reacting species and transition states. Multi-configurational Shepard interpolation (MCSI) was used to obtain the geometries and energies of the potential energy surface along the minimum-energy paths, with gradients and Hessians calculated by the M08-HX/maug-cc-pVTZ method. We find the numbers of structures obtained for the transition states are 46, 60, 72 and 76respectively for the H abstraction at the carbonyl C, the α position, the β position and the γ position. Our results show that neglecting the factors arising from multiple structures and torsional anharmonicity would lead to errors at 300, 1000 and 2400 K of factors of 8, 11 and 10 for abstraction at the carbonyl-O, 2, 11 and 25 at the α-C position, 2, 23 and 47 at the β-C position, and 0.6, 8 and 18 at the γ-C position. The errors would be even larger at high temperature for the reverse of the H abstraction at the β-C. Relative yields are changed as much as a factor of 7.0 at 200 K, a factor of 5.0 at 298 K, and a factor of 3.7 in the other direction at 2400 K. The strong dependence of the product ratios on the multi-structural anharmonicity factors shows that such factors play an important role in controlling branching ratios in reaction mechanism networks.
Introduction
Aldehydes, such as butanal (common name: butyraldehyde), play an important role in the field of combustion chemistry. In combustion engines, aldehydes are produced as primary pollutants formed by partial oxidation of hydrocarbon fuels.1–7 They are also produced by the photo oxidation of hydrocarbons in the tropospheric zone of the earth's atmosphere. Acting as a precursor for free radicals, aldehydes react with OH radicals, which is one of the main initiating steps towards their atmospheric degradation.4 Hence, study of the reaction mechanisms of aldehyde–radical reactions is essential to understanding both atmospheric chemistry and combustion.Reaction rates for butanal reactions with radicals have been measured for OH,2–5 CH3,6,7 NO3,5 and O,7 but there is no experimental data for H atom abstraction reactions from butanal by hydroperoxyl radical, which is an important species at intermediate temperatures in ignition processes. These H abstraction reactions are an important source of H2O2, which can decompose to form two ˙OH radicals.
The objective of the present article is to provide reliable theoretical rate constants for the H-atom abstraction from three sites of butanal, carbonyl-C, α-C and β-C, to yield respectively butanoyl radical, 1-oxo-2-butyl radical and 4-oxo-2-butyl radical. In each case, hydrogen peroxide is also produced. The three reactions are:
CH3CH2CH2CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O + ˙O2H ↔ CH3CH2CH2C˙ O + ˙O2H ↔ CH3CH2CH2C˙![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O + H2O2 O + H2O2 | (R1) |
CH3CH2CH2CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O + ˙O2H ↔ CH3CH2C˙HCH O + ˙O2H ↔ CH3CH2C˙HCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O + H2O2 O + H2O2 | (R2) |
CH3CH2CH2CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O + ˙O2H ↔ CH3C˙HCH2CH O + ˙O2H ↔ CH3C˙HCH2CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O + H2O2 O + H2O2 | (R3) |
For completeness, we also studied the energetics and partition functions of the H-atom abstraction from the γ-C that yields 4-oxo-1-butyl radical. This reaction is
CH3CH2CH2CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O + ˙O2H → C˙H2CH2CH2CH O + ˙O2H → C˙H2CH2CH2CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O + H2O2 O + H2O2 | (R4) |
A key issue in calculating these reaction rates is the existence of multiple conformers of the reactants and the saddle points of the reactions. It is well known that it is important to consider all the conformational structures in analyzing a reaction mechanism. However, the purpose of conformational structure search is usually simply to find the global-minimum structures, and the higher-energy structures are not used in calculating enthalpies, entropies and free energies. Furthermore, although conformational searches for the low-energy structures of a stable molecule are common, it is much less common to try to locate all saddle point structures for a single reaction. Without finding all the conformational structures of the transition state of a reaction—or at least all the low-energy ones, a reaction barrier height can only be based on an arbitrarily selected saddle point, and this is not meaningful even if it is calculated by a high-level ab initio method. The existence of multiple conformational structures for both the reactants and the transition state has an important effect on the calculated reaction rates, but it is often ignored or treated in an incomplete way in studying reaction kinetics and thermodynamics, as for example in some earlier studies of hydrogen abstraction reactions.8–12
In the present paper, we will study the importance of multiple structures and torsional anharmonicity in determining reaction rates and reactivity of various channels (branching ratios) over a wide range of temperature of interest in atmospheric chemistry and in combustion. This study will show large errors when only the global minima of the reactant and transition state are used for calculations. Therefore we go beyond the standard textbook treatment in terms of a single structure of reactants and a single structure of the transition state, and we include multi-structural anharmonicity by using the recently proposed multi-structural variational transition state theory (MS-VTST).13,14
Theoretical overview
A global harmonic approximation to the potential energy surface is a quadratic potential that has only a single minimum. An internal rotation due to a torsional motion has a periodic potential energy function that usually has more than one local minimum, thereby generating multiple conformational structures. In the molecules and transition states considered in this article, the existence of multiple conformers for a given chemical species or transition state is a consequence of torsional anharmonicity. However, molecules with multiple torsions usually have coupled internal rotational motions, and the total number of structures is not simply a product of given numbers of minima for the various torsions. Therefore we find the structures by a multi-dimensional structure search that does not assume separable torsions. The effect of including all the structures in the partition function, each with its own harmonic or quasiharmonic partition function, is called multiple-structure anharmonicity. The effect of including the nonquadratic nature of the torsional potential energy function is called torsional potential anharmonicity. The combination of these two effects is called multi-structural anharmonicity. In this section we summarize the MS-VTST rate constant approximation13,14 which includes multi-structural anharmonicity in terms of the recent multi-structural torsions15,16 (MS-T) approximation.In textbooks, the transition state theory rate constant of a bimolecular reaction is usually given by17
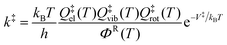 | (1) |
| ΦR = ΦRrelQRelQRvibQRrot | (2) |
In the present work, the electronic partition functions of HO2 and all the organic radicals are set to two to account the degenerate spin states of the radical, and the electronic partition functions of the closed-shell molecules are set equal to unity because they have no low-lying electronic states.
Variational transition state theory for a canonical ensemble is called canonical variational theory20–22 (CVT). The single-structure CVT rate constant including multidimensional tunneling (MT) may be written as23
| kSS-CVT/MT = κ(T)Γ(T)kSS-TST(T) | (3) |
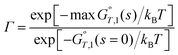 | (4) |
In most cases we choose the reaction path as the minimum-energy path (MEP) in isoinertial coordinates,27,28 and in particular, that is the choice made in the present article.
However, even for molecules that are moderately complex, one cannot generate all the low-energy structures by independent internal rotations, and so the above equations cannot treat the effect of multi-structural anharmonicity in the general case. There are two reasons for this. First, the normal modes do not correspond to individual torsions but often correspond to a mixture of two or more torsions and often also some low-frequency bends. Second, the total number of structures is often not the ideal number; for example, for n-heptane and isoheptane, there are respectively 4 and 3 relevant torsions (this excludes methyl torsions because they do not generate distinguishable structures due to symmetry), and since they are all threefold (two gauche and one trans), that ideally generates 34 = 81 and 33 = 27 structures; but the actual number of structures is 58 and 37, respectively.29 (Note that in the original paper,29 the number of structures of n-heptane was miscounted as 59, which affects the partition function about 2% at low temperature, e.g., 200 K.) The MS-T approximation15,16 uses internal coordinates and a coupled treatment of torsions and overall rotations to treat the transition from a low-T approximation corresponding to collection of local harmonic potentials to a high-T approximation corresponding to unhindered coupled internal rotations. The MS-T approximation replaces the separable product of Qvib and Qrot by a nonseparable conformational–rotational–vibrational partition function, Qcon-rovib. Incorporating the MS-T approximation into CVT in a convenient fashion yields multi-structural canonical variational theory with tunneling, with a bimolecular rate constant given by13,14,30
| kMS-CVT/MT = FMS-T(T)kSS-CVT/MT(T) | (5) |
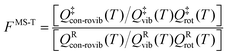 | (6) |
Note that the partition functions QXvib and QXrot (X = ‡ or R) are the same as those in eqn (1) so that these single-structure partition functions can be cancelled in the MS rate. The MS-T conformational–rovibrational partition function is given by15
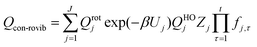 | (7) |
The multidimensional tunneling approximation employed in the present work is the small-curvature tunneling (SCT) approximation.24 In this approximation, κ is defined as the ratio of a thermally averaged approximate quantal transmission probability to a thermally averaged quasiclassical one, and the approximate quantal transmission probability takes account of both the multidimensional energy requirements of the vibrational modes transverse to the reaction coordinate and the corner-cutting tunneling induced by the multidimensional reaction-path curvature, which is treated in the small-curvature limit.21,22,25,26 The “quasiclassical” result is a calculation in which reaction-coordinate motion is classical, and motions transverse to the reaction coordinate are quantized (this is sometimes labeled as “semiclassical” or “hybrid” in other papers, but “quasiclassical” is the language we have settled on in recent years31 as that which is least subject to confusion). Then eqn (3) becomes
| kSS-CVT/SCT = κSCT(T)kSS-CVT(T) | (8) |
| kSS-CVT = Γ(T)k‡(T) | (9) |
Note that we use the κ and Γ calculated from only a single reaction path to represent these effects as resulting from all reaction paths. A more comprehensive treatment would be provided by multi-path variational transition state theory (MP-VTST),14,32 which involves the calculation of tunneling contributions and variational effects from more than one reaction path. But the MP-VTST approximation requires larger computational effort than the MS-VTST one, and we adopt MS-VTST here for this reason and because using a single reaction path provides a reasonable compromise approximation applicable to many reactions of large molecules. A case in which MS-VTST and MP-VTST have been compared for a smaller, but similar system is ethanol + OH.14 On the basis of our experience14,29,32 we believe that MS-VTST is a useful practical scheme, and it reasonable approximations can often be obtained without including multiple paths.
The conformational–rotational–vibrational partition functions are calculated by the MSTor16,33 program. The POLYRATE34 program is used to calculate reaction paths and single-structure reaction rate constants.
Potential energy surface
The potential energy surfaces needed for the dynamics calculation were obtained by density functional theory. First we calculated the forward barrier height, V‡f, energy of reaction ΔU, and reverse barrier height,| V‡r = V‡f − ΔU | (10) |
We also used a more approximate method, called the “jun–jun” approximation, to approach the quality of the CCSD(T)-F12a/jun-cc-pVTZ method. The jun–jun energy is defined as
| Ejun–jun = ECCSD(T)-F12a/jun-cc-pVDZ + (EMP2-F12/jun-cc-pVTZ − EMP2-F12/jun-cc-pVDZ) | (11) |
For butanal, butanoyl radical, 1-oxo-2-butyl radical and 4-oxo-2-butyl radical, the torsion angles that were used in searching for distinguishable structures are O5–C1–C2–C3 and C1–C2–C3–C4. For the three transition states, the torsional angles that yield distinct structures are O5–C1–C2–C3, C1–C2–C3–C4, O5–C1–H8–O6, C1–H8–O6–O7 and H8–O6–O7–H9 for the R1 TS; O5–C1–C2–C3, C1–C2–C3–C4, C1–C2–H9–O6, C2–H9–O6–O7 and H9–O6–O7–H8 for the R2 TS; O5–C1–C2–C3, C1–C2–C3–C4, C2–C3–H11–O6, C3–H11–O6–O7 and H11–O6–O7–O8 for the R3 TS; and O13–C11–C8–C5, C11–C8–C5–C1, C8–C5–C1–H2, C5–C1–H2–O14, C1–H2–O14–O15 and H2–O14–O15–H16 for the R4 TS. For independent and ideal torsions, the number of conformational structures would be 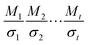 where Mτ and στ are respectively the periodicity and symmetry of torsion τ. However, the torsions are not ideal for most cases, for example, the periodicity of C1–C2 rotation in butanal is 3 when the torsion C1–C2–C3–C4 is in trans conformation, and it is 2 when the torsion C1–C2–C3–C4 is in a gauche conformation. The periodicity of one torsion thus depends on the conformation of the other torsions, and this circumstance clearly shows the coupling between torsions and the inapplicability of separable 1-D torsion methods. We found 7 structures for butanal, 7, 6 and 7, respectively, for butanoyl radical, 1-oxo-2-butyl radical and 4-oxo-2-butyl radical, and 46, 60, 72 and 76 structures for the corresponding TSs (R1–R4). All of these structures are included in eqn (6).
where Mτ and στ are respectively the periodicity and symmetry of torsion τ. However, the torsions are not ideal for most cases, for example, the periodicity of C1–C2 rotation in butanal is 3 when the torsion C1–C2–C3–C4 is in trans conformation, and it is 2 when the torsion C1–C2–C3–C4 is in a gauche conformation. The periodicity of one torsion thus depends on the conformation of the other torsions, and this circumstance clearly shows the coupling between torsions and the inapplicability of separable 1-D torsion methods. We found 7 structures for butanal, 7, 6 and 7, respectively, for butanoyl radical, 1-oxo-2-butyl radical and 4-oxo-2-butyl radical, and 46, 60, 72 and 76 structures for the corresponding TSs (R1–R4). All of these structures are included in eqn (6).
All harmonic vibrational frequencies calculated by the M08-HX/maug-cc-pVTZ method are scaled by a factor 0.976, which was previously determined as a value designed to give more accurate48 zero-point vibrational energies. This scale factor accounts both for the systematic difference between harmonic and actual zero-point energies and also for systematic errors in the electronic structure method. Since the zero-point vibrational energy is dominated by the high-frequency modes, using the scale factor effectively incorporates an estimate of the effect of the anharmonicity of high-frequency modes, but the optimized value of the scale factor is not much affected by the low-frequency modes since they make only a minor contribution to the zero-point vibration energy. Therefore, there is no significant issue of double counting the anharmonicity in including both the scale factor and the MS-T approximation, which primarily includes anharmonicity in low-frequency modes (the practical effect of using MS-T is that the low-frequency torsions are effectively replaced by classical partition functions using a reference potential16). The approach of scaling the frequency by an empirical constant is an approximation and it introduces some uncertainty, which is discussed elsewhere.48,49 Although methods for calculating anharmonic energy levels for polyatomic molecules from anharmonic potential energy functions are improving,50–52 as are path integral methods for calculating conformational–vibrational–rotation partition functions without calculating converged energy levels,53,54 actual calculations of converged vibrational partition functions for molecules with more than four atoms55–57 are still rare. Therefore, the procedures used here must be used without full tests of their accuracy for complex systems.
All density functional calculations were carried out with Gaussian0958 program. Molpro59 program was used for the CCSD(T)-F12 and MP2-F12 calculations.
Results and discussion
Structures
The naming of the structures is based on the notation we used previously.30Table 1 lists the naming conventions and labeling of structures for the convenience of the reader. To avoid confusions, one should distinguish two ways to order the structures, either by potential energy (zero-point exclusive energy) or by ground-state energy (zero-point inclusive energy). For butanal and butanoyl radical, these two kinds of energy ordering give different minimum-energy structures. In both of these cases, the CT conformer is the structure with the lowest ground-state energy, whereas the GM (i.e., the structure with lowest potential energy) is the optically active pair C−G− and C+G+. On the other hand, for 1-oxo-2-butyl radical, 4-oxo-2-butyl radical, and all of the TSs, the two kinds of energy ordering yield same minimum-energy structure, namely the C−A+, C+A− structures for 1-oxo-2-butyl radical, and the CT structure for 4-oxo-2-butyl radical. For the TS structures that lead to the formation of butanoyl radical, among 46 conformers, we found that the A−G+G+C−g− conformer and its mirror image have the lowest zero-point-inclusive and exclusive energies and correspond to the GM structure. In the case of TS structures leading to the formation of 1-oxo-2-butyl radical and 4-oxo-2-butyl radical, respectively, the C−T+G−C−g+, C+T−G+C+g− and C+G+g+C+g−, C−G−g−C−g+ structures are the lowest-energy structures for both ordering. All the GM structures are shown in Fig. 1.| Name convention | Abbreviation | Dihedral angle range (in deg)b |
|---|---|---|
| a The dihedral angles used for torsions are H1–O2–C3–C4, O2–C3–C4–C5 and C3–C4–C5–C6 for 1-butanol; H15–O14–C7–C5 and O14–C7–C5–H6 for 2-methyl-1-propanol; O2–C1–C4–C7 and C1–C4–C7–C10 for butanal. b (x, y) means x < τ < y. c This includes both −75 < τ < −30 and 30 < τ < 75. | ||
| cis | C | 0 |
| cis± | C± | (0, ±30) |
| gauche± | G± | (±30, ±75)c |
| g± | (±75, ±90) | |
| anti± | a± | (±90, ±105) |
| A± | (±105, ±150) | |
| trans± | T± | (±150, ±180) |
| trans | T | 180 |
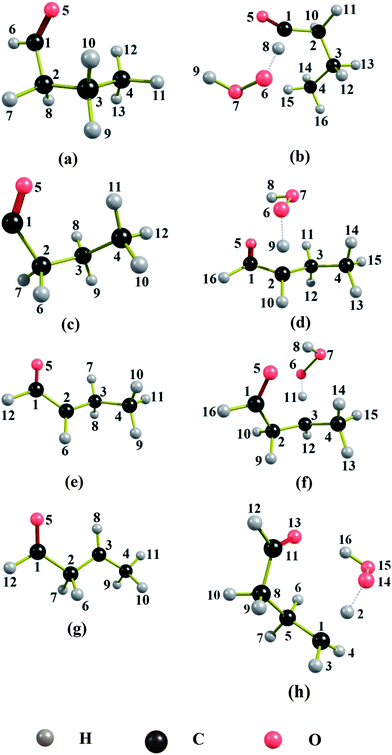 | ||
| Fig. 1 Global minimum structures of (a) butanal, (b) saddle point leading to the formation of butanoyl radical, (c) butanoyl radical, (d) saddle point leading to the formation of 1-oxo-2-butyl radical, (e) 1-oxo-2-butyl radical, (f) saddle point leading to the formation of 4-oxo-2-butyl radical, (g) 4-oxo-2-butyl radical and (h) saddle point leading to the formation of 4-oxo-1-butyl radical. | ||
The relative conformational energies of all of the structures are given in Tables S4 and S5 of the ESI.† The relative potential conformational energies of the structures of a given species lie within ranges of 1.20, 0.71, 1.92 and 1.13 kcal mol−1 for butanal and the product radicals (butanoyl radical, 1-oxo-2-butyl radical and 4-oxo-2-butyl radical), respectively. The small effective torsional barriers (1–8 kcal mol−1) of butanal when compared to the barrier heights (12–17 kcal mol−1) justifies the assumption of the MS-VTST theory that interconversion of conformers of the reactant is rapid compared to the rate of reaction. Note that any of the conformations of the reactant can give rise to any of the products, so this is a qualitatively different kind of reaction set than the ones envisioned by the Curtin–Hammett principle60 where each conformation is inconsistently assumed to lead to a different product.
The ranges of relative potential energy of the conformers of the TSs are larger than the ranges in the reactants and the products. For the TS that leads to the formation of butanoyl radical, the range is 2.58 kcal mol−1, while for the other three cases, the ranges are 4.78, 5.13 and 6.31 kcal mol−1, respectively (see Table S5 of the ESI†). Although the ranges are larger, there are also more low-energy conformers than for reactants or products. Thus there are respectively 40, 16, 12 and 12 conformers below 2 kcal mol−1 (with respect to their GMs) for the TSs for abstraction at the carbonyl, the α carbon, the β carbon and the γ carbon.
These two sets of benchmark-level calculations are presented in Table 2, where they are compared to the M08-HX/maug-cc-pVTZ calculations. The agreement is excellent with the mean unsigned deviation of the two benchmarks from each other for V‡f, V‡r and ΔU for the three reactions (nine quantities) being 0.40 kcal mol−1, and the mean unsigned deviation of M08-HX/maug-cc-pVTZ from CCSD(T)/CBS being only 0.58 kcal mol−1. We shall use M08-HX/maug-cc-pVTZ for all the remaining calculations in this paper. Note that the barrier heights calculated by the high-level methods in Table 2 are not the energy difference between the global minimum of reactant and the lowest-energy of saddle point. They are the energy difference between a representative conformer of reactant/product and a representative one of saddle point because the geometries used for validation were chosen before the complete conformational search for all the stationary points. The barrier heights calculated by the energy differences between the global minimum structure of reactant/product and the lowest-potential-energy saddle points are listed in Table 3.
| Electronic model chemistry | V ‡f | V ‡r | ΔU | MUEb |
|---|---|---|---|---|
| a In the context of the present table, “classical” means zero-point-exclusive. b The mean unsigned errors are calculated with respect to CCSD(T)-F12a/jun-cc-pVTZ method, which is labeled as CCSD(T)/CBS. c The structures of reactant, product, and saddle points used are those listed in Tables S5 and S61 respectively. In particular, butanal is structure 6; butanoyl radical is structure 6; 1-oxo-2-butyl radical is structure 1; 4-oxo-2-butyl radical is 1; TS of R1 is structure 27; TS of R2 is structure 1; and TS of R3 is structure 3. d In order to perform a consistent comparison, the benchmark results in this table are both calculated at geometries obtained by the M08-HX/maug-cc-pVTZ method. | ||||
| Abstraction of H atom from carbonyl-C to yield butanoyl radical (R1) | ||||
| M08-HX/maug-cc-pVTZ | 12.05 | 9.46 | 2.59 | 0.96 |
| jun–jund | 12.53 | 11.60 | 0.93 | 0.47 |
| CCSD(T)/CBSd | 12.28 | 10.90 | 1.38 | 0.00 |
| Abstraction of H atom from α-C to yield butanal-2-yl radical (R2) | ||||
| M08-HX/maug-cc-pVTZ | 16.01 | 13.17 | 2.84 | 0.34 |
| jun–jund | 16.86 | 13.41 | 2.45 | 0.33 |
| CCSD(T)/CBSd | 16.52 | 13.54 | 2.98 | 0.00 |
| Abstraction of H atom from β-C to yield butanal-2-yl radical (R3) | ||||
| M08-HX/maug-cc-pVTZ | 17.06 | 5.28 | 11.78 | 0.43 |
| jun–jund | 16.23 | 4.58 | 11.65 | 0.41 |
| CCSD(T)/CBSd | 16.84 | 4.63 | 12.21 | 0.00 |
| Reaction | V ‡f | V ‡r | ΔU |
|---|---|---|---|
| R1 | 12.13 | 9.06 | 3.07 |
| R2 | 17.20 | 13.17 | 4.03 |
| R3 | 17.93 | 4.95 | 12.98 |
| R4 | 19.67 |
Multi-structural anharmonicity
The factor FMS-T(T) in eqn (5) is called the reaction's multi-structural torsional anharmonicity factor,13 and eqn (6) can be rearranged such that it equals the ratio of the multi-structural anharmonicity factor13 of the conventional transition state (‡) divided by that of the reactants (R):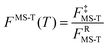 | (12) |
Table 4 presents the multi-structural anharmonicity factors of the reactants, the products, the transition states, and the reactions as functions of temperature. The table shows that FχMS-T values for reactants and products usually pass through a maximum as a function of temperature.
| T/K | Multi-structural anharmonicity factors | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F RMS-T | F P1MS-T | F P2MS-T | F P3MS-T |
|
F ‡,1MS-T | F ‡,2MS-T | F ‡,3MS-T | F MS-Tf,R1 | F MS-Tr,R1 | F MS-Tf,R2 | F MS-Tr,R2 | F MS-Tf,R3 | F MS-Tr,R3 | F MS-Tf,R4 | |
a P1: butanoyl radical, P2: 1-oxo-2-butyl radical, P3: 4-oxo-2-butyl radical.
b
 , , 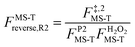 , , 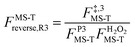 . .
|
|||||||||||||||
| 200 | 4.76 | 10.02 | 2.78 | 1.92 | 2.08 | 28.97 | 4.08 | 6.93 | 6.09 | 1.39 | 0.86 | 0.70 | 1.46 | 1.73 | 0.53 |
| 300 | 6.62 | 12.07 | 3.26 | 2.57 | 2.14 | 53.15 | 10.48 | 13.29 | 8.07 | 2.08 | 1.61 | 1.53 | 2.03 | 2.45 | 0.62 |
| 400 | 8.64 | 13.47 | 3.65 | 3.03 | 2.20 | 79.81 | 23.58 | 29.18 | 9.24 | 2.69 | 2.73 | 2.93 | 3.38 | 4.37 | 1.01 |
| 600 | 12.02 | 14.96 | 4.18 | 3.44 | 2.30 | 125.07 | 65.89 | 104.51 | 10.41 | 3.64 | 5.48 | 6.86 | 8.67 | 13.17 | 2.77 |
| 1000 | 15.22 | 15.01 | 4.59 | 3.27 | 2.35 | 169.82 | 173.22 | 353.45 | 11.16 | 4.82 | 11.38 | 16.11 | 23.22 | 46.02 | 7.94 |
| 1500 | 15.35 | 13.27 | 4.50 | 2.68 | 2.28 | 168.51 | 274.84 | 572.43 | 10.98 | 5.57 | 17.90 | 26.77 | 37.28 | 93.53 | 13.30 |
| 2400 | 12.82 | 10.00 | 3.88 | 1.84 | 2.09 | 123.97 | 326.38 | 599.79 | 9.67 | 5.93 | 25.46 | 40.28 | 46.79 | 155.81 | 17.57 |
The rate of change of FMS-T(T) with temperature increases in the order R1 < R2 < R3. The trend in the multi-structural effect can be explained considering the number of structures obtained for the TS, which also follows the above order, i.e., R1 (46 structures) < R2 (60 structures) < R3 (72 structures). This is consistent with eqn (6), where the ratio contains QMS-T‡,con-rovib(T) in the numerator, and this partition function involves a sum over all the structures of the TS. The multi-structural anharmonicity factors decrease after a certain temperature because the torsional potential corrections (Zj and fj,τ in eqn (7)) play a more important role than the multiple structure effect at high temperature. Examination of Table 4 shows that multi-structural anharmonicity is important for product ratios as well as for overall reaction rates.
When a molecule has multiple conformational structures, the often used approximation is to base thermodynamics and kinetics calculations on the global minimum. The global minimum is often the most important structure at low temperature; however, other low-energy structures could also be important,61 and even higher-energy structures can be important at high temperature or even at low temperature when one considers entropy as well as energy. It is interesting to examine this approximation by using the complex reactions of the present study. Fig. 2 plots, for each conformational structure, the contribution to the rotational–vibrational partition function of the species (including both stable species and transition states) normalized to that of the global-minimum contribution of that species. The purpose of this figure is to show the relative contributions to the partition function changes due to structural changes; therefore only one structure of a pair of mirror images is presented in Fig. 2 (e.g., butanal has 4 structures shown in Fig. 2; note that our definition of the global-minimum's contribution to the partition function has a contribution from only one structure even when global minimum structure is one of a pair of mirror images). The figure also shows (in blue, with the ordinate scale at the right) relative energies. The partition functions are plotted for 200 K and 1000 K. At 200 K, the partition function of butanal is dominated by the three lowest-energy structures (see Table S4 in the ESI†); however, the contribution from the global minimum is smaller than that from the third-lowest energy structure even at such a low temperature. At 1000 K, the higher-energy structures of butanal become more important, and the contribution from the global minimum is the smallest of all the structures. A similar trend is also found for the transition states of the three reactions, as shown in subplots (b), (c) and (d). For example, consider subplot (b) for the abstraction of H from the carbonyl C. Structure 19 has a potential energy 0.66 kcal mol−1 higher than the GM (see Table S5†), but its contribution is a factor of 2.2 higher at 200 K and 5.2 higher at 1000 K.
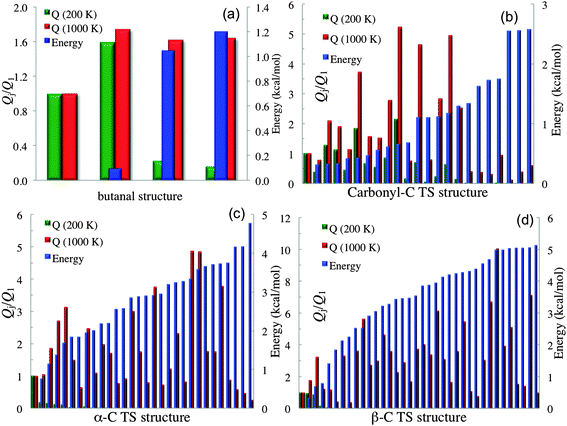 | ||
| Fig. 2 Rotational–vibrational partition function normalized to that of global minimum for each conformational structure with torsional anharmonicity as well as relative energy. The left vertical axis is the partition function normalized to the contribution of the lowest-energy structure; the right vertical axis is relative energy, and the first structure of each plot is the global minimum. Subplot (a) shows structures 1, 3, 4 and 6 for butanal. Subplot (b) shows structures 1, 3, …, 45 for the transition state for abstraction of H by HO2˙ from the carbonyl-C of butanal. Subplot (c) shows structures 1, 3, …, 59 for the transition state for abstraction of H by HO2˙ from the α-C of butanal. Subplot (d) shows structures 1, 3, …, 71 for the transition state for abstraction of H by HO2˙ from the β-C of butanal. | ||
The results show that the approximation of using the global minimum is generally not valid at high temperature, and sometimes it is not even a good approximation at low temperature. The reason for this is that high-energy structures usually have more floppy vibrational modes such that entropic contributions make them dominant at high temperature where entropy effects overcome the effect of the Boltzmann factor. An interesting observation made in the study of metal nanoparticles62 is that the lowest-energy structure is sometimes a highly symmetric structure with a small contribution to the conformational partition function; this is another example of where higher-energy structures tend to have higher entropy. Although it is well known that higher-energy structures become more important as the temperature is raised, the higher-energy structures are nevertheless ignored in many research articles dealing with kinetics, and the quantitative effect of including higher-energy structures has not been widely studied in the kinetics context.
The HO2 radical only has one conformational structure and no torsion, therefore the multi-structural anharmonicity factor for HO2 radical is 1.
Table 5 shows that reaction R4 has the smallest rates based on the conventional transition state theory using the MS-T partition functions (a table with more temperatures is given in the ESI as Table S13†). The contribution of R4 to total rate is less than 1% under 1000 K and less than 7% under 2400 K. Therefore in the rest of the paper, we will only discuss the rate constants for R1–R3, and for these reactions we will use a higher level of dynamics, in particular the MS-CVT/SCT method.
| T/K | R1 | R2 | R3 | R4 |
|---|---|---|---|---|
| 200 | 3.6 × 10−25 | 5.3 × 10−32 | 4.0 × 10−32 | 2.5 × 10−34 |
| 300 | 4.7 × 10−21 | 4.9 × 10−26 | 3.5 × 10−26 | 9.0 × 10−28 |
| 600 | 1.5 × 10−16 | 2.0 × 10−19 | 2.4 × 10−19 | 3.0 × 10−20 |
| 1000 | 2.1 × 10−14 | 2.6 × 10−16 | 4.8 × 10−16 | 1.1 × 10−16 |
| 1500 | 4.1 × 10−13 | 1.8 × 10−14 | 3.7 × 10−14 | 1.2 × 10−14 |
| 2400 | 5.9 × 10−12 | 7.6 × 10−13 | 1.5 × 10−12 | 6.4 × 10−13 |
Reaction path calculations
Calculation of a converged reaction-path Hamiltonian for a system of the size of the reactions R1–R3 in this article is very computationally expensive. A number of strategies have been proposed to reduce the computational cost of reaction path calculations.63–81 Some of these methods take advantage of the fact that although one needs a small step size to calculate an accurate MEP, one does not require full Hessian at each point on such a fine grid. The multi-configuration Shepard interpolation (MCSI)79,80,82–84 method has been used for some complex reactions. We found that the MCSI method usually yields a smooth potential energy along the MEP with moderate computational cost, for example, only 6–9 Hessians are needed for nonstationary points on reaction paths for reactions studied in this article. However, the vibrationally adiabatically ground-state potential curve obtained from MCSI is often bumpy, and sometimes it is difficult to obtain a smooth enough curve to produce the correct variational effect and tunneling contribution. This negative aspect of the MCSI method comes from two sources: (i) sometimes the interpolated Hessians are not precise enough to yield accurate vibrational frequencies along the reaction path, and a set of small errors in each of several vibrational frequencies sometimes adds up to a large error in a complex system; (ii) sometimes the approximate gradients from interpolation are not precise enough to be used in the transformation of the Hessian from Cartesian coordinates to internal coordinates, but this transformation of coordinates is necessary85,86 to obtain physical frequencies at nonstationary points along the reaction path. A straightforward strategy that overcomes this negative aspect of the MCSI method is to calculate gradients and Hessians by electronic structure method at points on the MEP (rather than obtaining them by Shepard interpolation). By using this strategy, we can use MCSI to calculate a well converged reaction path Hamiltonian with less effort than a straight direct dynamics calculation but more accurately than one would obtain by the original MCSI method, and we assume that the geometries and energies obtained along the MEP by the MCSI calculations are accurate enough. A favorable aspect of using this strategy (as compared to straight direct dynamics) is that all the Hessian calculations by an electronic structure method can be performed simultaneously. Note that Hessian calculation is the most expensive part of the whole dynamics calculation; therefore the parallelization of Hessian calculations reduces the wall-clock time significantly. The M08-HX/maug-cc-pVTZ electronic model chemistry was used to calculate reaction paths by the MCSI method, and the numbers of Hessians calculated by the M08-HX/maug-cc-pVTZ method along the reaction paths are 37 for R1, 66 for R2, and 28 for R3.For the generalized transition states studied in this article, there are many choices for a set of non-redundant internal coordinates to describe vibrations of the system. Choice of a set of non-redundant internal coordinates is crucial to obtain physically meaningful frequencies of nonstationary points along reaction path. For instance, the four atoms 1, 2, 5 and 16 (see Fig. 1(d)) become planar during part of the reaction path of reaction R2 (s = −0.450 to −1.125 Å); in this case, one need to choose two angles and one improper torsion for these four atoms instead of choosing three angles which can only be non-redundant set when the four atoms are not planar.
Thermal rate constants
No experimental or previous theoretical rate constant data are available for these reactions, and the present study constitutes a set of predictions. The calculated rate constants using the MS-CVT/SCT method are plotted in Fig. 3 for reactions R1–R3 and are given in Table 6. For comparison purposes, we also plot the rate constants calculated by the SS-CVT/SCT method in Fig. 3. Fig. 3 shows that the multiple-structure effects are significant at high temperatures for all reactions in both forward and reverse directions except the forward reaction of R1. The transition state of R1 has more low-energy structures than others, and its reactant has less low-energy structures than the products, therefore the forward reaction rate constants of R1 obtained by the MS-CVT/SCT method is about 6 times larger than that obtained by the SS-CVT/SCT method at T = 200 K. Even at temperatures of 400 K and lower, the forward SS-CVT/SCT and MS-CVT/SCT rate constants differ by as much as a factor of 9, whereas those for the reverse reactions differ by as much as a factor of 4.4. Above 400 K, the differences in the two kinds of calculations of rate constants are even larger, reaching factors of 40 and 156 for R2 and R3 respectively, by 2400 K. For reaction R1, the ratio between the forward SS-CVT/SCT and MS-CVT/SCT rate constants starts from 6 and reaches 11 at 1300 K and then decreases. For the reverse of reaction R3, the multistructural anharmonicity effect increases from a factor of 1.7 at 200 K to a factor of 156 at 2400 K. We see that the prototype textbook example of a single-structure transition state is qualitatively incorrect and that anharmonicity effects by no means cancel out when one ratios transition state partition functions to reactant ones.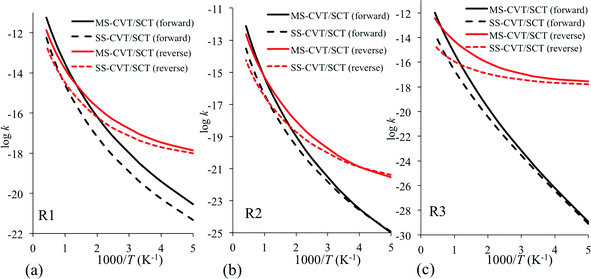 | ||
| Fig. 3 Forward and reverse rate constants obtained by the MS-CVT/SCT method for the H-atom abstraction by ˙O2H (a) from the carbonyl-C of butanal to form butanoyl radical, (b) from the α-C of butanal to form 1-oxo-2-butyl radical, and (c) from the β-C of butanal to form 4-oxo-2-butyl radical. In each of these reactions, hydrogen peroxide is also produced as the second product. | ||
| T/K | R1 | R2 | R3 |
|---|---|---|---|
| 200 | 2.86 × 10−21 | 9.85 × 10−26 | 1.15 × 10−29 |
| 250 | 3.94 × 10−20 | 3.09 × 10−24 | 6.30 × 10−27 |
| 298.15 | 2.84 × 10−19 | 4.84 × 10−23 | 4.91 × 10−25 |
| 300 | 3.04 × 10−19 | 5.33 × 10−23 | 5.68 × 10−25 |
| 400 | 6.80 × 10−18 | 4.28 × 10−21 | 2.97 × 10−22 |
| 500 | 6.71 × 10−17 | 1.05 × 10−19 | 2.09 × 10−20 |
| 600 | 3.90 × 10−16 | 1.21 × 10−18 | 4.67 × 10−19 |
| 800 | 4.96 × 10−15 | 4.10 × 10−17 | 3.20 × 10−17 |
| 1000 | 2.90 × 10−14 | 4.77 × 10−16 | 5.14 × 10−16 |
| 1300 | 1.84 × 10−13 | 6.28 × 10−15 | 8.21 × 10−15 |
| 1500 | 4.63 × 10−13 | 2.23 × 10−14 | 3.05 × 10−14 |
| 1800 | 1.33 × 10−12 | 9.79 × 10−14 | 1.36 × 10−13 |
| 2000 | 2.32 × 10−12 | 2.16 × 10−13 | 2.97 × 10−13 |
| 2400 | 5.67 × 10−12 | 7.62 × 10−13 | 1.01 × 10−12 |
The forward MS-CVT/SCT rate constants are fitted with the four-parameter expressions proposed by Zheng and Truhlar87
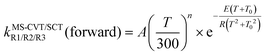 | (13) |
Because the reverse reactions are exothermic, we used the four-parameter expression in ref. 25 so that the rate constant is finite at 0 K.
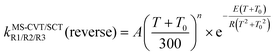 | (14) |
| Reactions | Directions | Fitting parameters | |||
|---|---|---|---|---|---|
| A | T 0 | n | E | ||
| a Eqn (13) is used for the forward reactions, and eqn (14) is used for the reverse reactions. b Units for A, T0 and E are cm3 molecule−1 s−1, K, and kcal mol−1, respectively. The parameter n is unitless. | |||||
| R1 | Forward | 1.968 × 10−15 | 195.48 | 4.387 | 4.546 |
| Reverse | 4.347 × 10−16 | 298.90 | 4.105 | 4.029 | |
| R2 | Forward | 1.680 × 10−17 | 203.79 | 5.942 | 6.604 |
| Reverse | 1.027 × 10−17 | 270.29 | 5.256 | 6.137 | |
| R3 | Forward | 2.071 × 10−16 | 136.75 | 5.226 | 9.791 |
| Reverse | 1.059 × 10−15 | 398.17 | 3.179 | 5.396 | |
Because the reverse reaction barrier heights are smaller than the forward reaction barrier heights for all three reactions (see Table 3), the reverse rate constants are much larger than the forward reaction rate constants at low temperatures. However, this trend is reversed at high temperature, i.e., forward reaction rates become larger at high temperatures. Here we define the temperature at which the forward and reverse reactions have the same rate, i.e., the temperature at which the equilibrium constant is 1, as the isoconcentration temperature. The MS method predicts a quite different isoconcentration temperature than the SS method. For example, the isoconcentration temperature is 720 K in the MS calculation, while SS one gives 1130 K. Therefore, the improvement by the MS method is not only in the absolute rate constants, but also in their temperature dependence and in equilibrium constants.
The Arrhenius activation energy is defined as the negative value of the slope of the curve ln k vs. 1/kBT.72 The activation energy derived from eqn (13) and (14) are respectively25,71
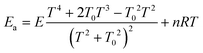 | (15) |
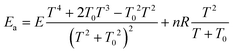 | (16) |
Table 8 lists the activation energies for the three reactions (forward and reverse) by using the SS-CVT/SCT and MS-CVT/SCT methods. The activation energies are temperature dependent because the curves shown in Fig. 3 have large curvature. The large curvatures of the Arrhenius plots are enhanced by two features of the reaction: (i) tunneling contributions mainly impact the temperature dependence at low temperatures, and (ii) the multiple-structure and torsional anharmonicity have large effects at high temperatures. For all temperatures listed in Table 7 the total effect of multi-structure and torsional anharmonicity increase the reaction rates for all three reactions in the forward and reverse directions except at 200 K, where the MS method lowers the reaction rate for reaction R2 by factors of 0.9 and 0.7 for the forward and reverse reactions respectively. However, Table 7 shows that activation energies given by the MS method are often larger than those given by the SS method. The physical interpretation of this is that the Arrhenius activation energy equals the average energy of reacting pairs of reactants minus the average energy of all pairs of reactants;88 and inclusion of multi-structural anharmonicity changes these averages.
| Forward | Reverse | |||
|---|---|---|---|---|
| T/K | SS | MS | SS | MS |
Reaction R1: CH
3
CH
2
CH
2
CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O + ˙O
2
H → CH
3
CH
2
CH
2
C˙ O + ˙O
2
H → CH
3
CH
2
CH
2
C˙![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O + H
2
O
2 O + H
2
O
2
|
||||
| 200 | 3.88 | 4.12 | 1.04 | 1.33 |
| 300 | 6.47 | 6.82 | 2.67 | 3.26 |
| 400 | 8.28 | 8.64 | 4.35 | 5.08 |
| 600 | 10.73 | 10.97 | 7.01 | 7.79 |
| 1000 | 14.46 | 14.42 | 10.64 | 11.40 |
| 1500 | 18.90 | 18.54 | 14.47 | 15.27 |
| 2400 | 27.03 | 26.11 | 21.29 | 22.23 |
Reaction R2: CH
3
CH
2
CH
2
CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O + ˙O
2
H → CH
3
CH
2
C˙HCH O + ˙O
2
H → CH
3
CH
2
C˙HCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O + H
2
O
2 O + H
2
O
2
|
||||
| 200 | 5.07 | 5.54 | 1.73 | 2.33 |
| 300 | 8.36 | 9.41 | 4.06 | 5.37 |
| 400 | 10.57 | 12.05 | 6.17 | 7.97 |
| 600 | 13.44 | 15.39 | 9.20 | 11.52 |
| 1000 | 17.73 | 20.12 | 13.29 | 16.04 |
| 1500 | 22.88 | 25.69 | 17.76 | 20.92 |
| 2400 | 32.33 | 35.91 | 25.86 | 29.79 |
Reaction R3: CH
3
CH
2
CH
2
CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O + ˙O
2
H → CH
3
C˙HCH
2
CH O + ˙O
2
H → CH
3
C˙HCH
2
CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O + H
2
O
2 O + H
2
O
2
|
||||
| 200 | 11.28 | 10.72 | 0.49 | 0.65 |
| 300 | 13.45 | 14.55 | 1.22 | 2.15 |
| 400 | 14.55 | 16.45 | 2.12 | 3.99 |
| 600 | 16.19 | 18.65 | 3.90 | 7.19 |
| 1000 | 19.53 | 22.22 | 6.89 | 11.10 |
| 1500 | 24.01 | 26.88 | 10.21 | 14.37 |
| 2400 | 32.47 | 35.73 | 16.13 | 19.67 |
The percentage yields of products R1 and R2 are plotted in Fig. 4(a). Because the percentage yield of R3 is close to that of R2 on the scale of Fig. 4(a), it is not plotted in Fig. 4(a) for better visualization. In the temperature range from 200 K to 2400 K, R1 is the dominant product. For instance, the percentage yield of R1 as calculated by the MS-CVT/SCT method is above 90% at temperatures below 1500 K. At high temperature, the difference between the results obtained by the MS-CVT/SCT method and the SS-CVT/SCT method becomes more noticeable on the scale of Fig. 4(a); for instance, at T = 2400 K, the percentage yield of R1 is 92 by MS-CVT/SCT and 76 by SS-CVT/SCT.
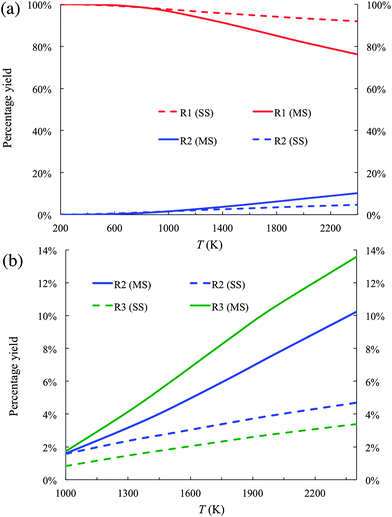 | ||
| Fig. 4 (a) Product branching fractions of the forward reactions R1 and R2 calculated by the SS-CVT/SCT (denoted as SS) and MS-CVT/SCT (denoted as MS) methods. (b) Product branching fraction of the forward reactions R2 and R3 calculated by the SS-CVT/SCT (denoted as SS) and MS-CVT/SCT (denoted as MS) methods. | ||
Fig. 4(b) shows the yields of R2 and R3 in the temperature range of 1000–2400 K. By only considering the global minimum structure in the rate calculations, i.e., by carrying out the calculations with SS-CVT/SCT, the yield of R2 is higher than that of R3. In the other words, the reactivity of the reaction sites of butanal would be predicted to be
| carbonyl-C > α-C > β-C |
This order of the reactivity is consistent with the forward barrier heights of these reactions as shown in Table 3. By considering contributions of all conformational structures to the reaction rate, the order of the reactivity below 1000 K remains the same as inferred from the global minima. However, the order of reactivity is changed for temperatures above 1000 K to
| carbonyl-C > β-C > α-C |
This shows that the reactivity of different channels depends not only on the classical barrier heights, but also on contributions of conformational structures to partition functions. Therefore reactivity that is inferred only by using classical barrier heights without considering temperature dependence is questionable; unfortunately this kind of basis for conclusions about reactivity appears frequently in the literature.
Fig. 5 plots the product ratios calculated by the SS-CVT/SCT and MS-CVT/SCT methods. Here we define the product ratios as [P1]/[P2], [P1]/[P3] and [P3]/[P2] respectively, where [Pi] (i = 1, 2, or 3) is the concentration of product of forward reactions R1–R3. Fig. 5 shows that the multi-structural torsional anharmonicity increases the product ratio [P1]/[P2] by a factor of 7 at 200 K, and decreases the ratio by a factor of 0.3 at 2400 K. The effects on product ratios due to the multi-structural torsional anharmonicity are significant both at low and high temperatures.
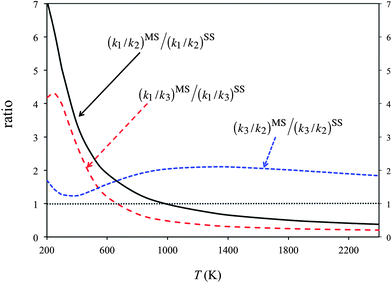 | ||
| Fig. 5 Percentage yields calculated by the SS-CVT/SCT (denoted as SS) and MS-CVT/SCT (denoted as MS) methods. For the SS calculations, the structure chosen is always the global minimum structure for reactants and products, that is, the structure with the lowest potential energy, and the structure chosen for the saddle point is always the structure with the lowest ground-state energy. Since the multi-structural anharmonicity effect is the deviation of these curves from unity, we denote unity by a thin dotted horizontal line in the figure. | ||
Fig. 6 shows the SCT transmission coefficients for R1, R2 and R3, and we tabulate this quantity for a range of temperature in Table S12 of the ESI.† The curves and the table reveal that all these reactions have very large tunneling contributions at temperatures below 600 K, especially reaction R2. The latter is explained by noting that reaction R2 has large barrier heights for both forward and reverse reactions, and also it has a narrow barrier in the vibrationally adiabatically potential energy curve (see Fig. S1 in ESI†).
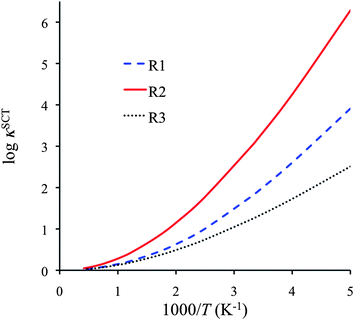 | ||
| Fig. 6 SCT transmission coefficients for reactions R1–R3 as function of reciprocal temperature. | ||
Conclusions
We performed calculations on the energetics and conformational structures for hydrogen abstraction from carbonyl-C, α-C, β-C and γ-C of butanal by ˙O2H and estimated the thermal rate constants for all the reaction except the γ-C channel by employing the recently developed MS-VTST method for the temperature range 200–2400 K. The MS-VTST approach is a convenient way to include contributions of more than one conformational structure for reacting species and transition states. Hence reliable rate constants for complex reactions of species with multiple torsions can be calculated. Most textbooks present gas-phase transition state theory in terms of the vibrational–rotational partition function of the lowest-energy saddle point, which would be correct for a transition state with a single conformational structure. However, even reactions of small molecules can have transition states with many saddle points. Here we find up to 76 structures for one of the reactions of C3H7CHO with HO2. Furthermore we find that multiple-structure anharmonicity and torsional anharmonicity can lead to factors as large as 8, 46 and 155 in calculated reaction rates at temperatures of 300 K, 1000 K and 2400 K, respectively. The multi-structural anharmonicity effects are quite different for the different abstraction reactions so that the changes of calculated absolute rate constants of each reaction are quite different when one takes account of these effects. As a consequence, the product ratios are affected significantly (up to a factor 7) by the multi-structural anharmonicity and also the order of reactivity of different reactive sites could be reversed by taking account the multi-structural anharmonicity.The effect of multi-structural torsional anharmonicity on product yields is quantitatively similar to the effect on branching ratios. For example, at 298 K, the yield of P2 decreases from 0.086% to 0.017%—a factor of 5.0 decrease. In contrast, at 2400 K the P2 yield is increased from 4.7% to 10.2%—a factor of 2.2 in the other direction, and the P3 yield increases from 3.4% to 13.6%, a factor of 4.0. The effects are largest at low temperature; for example the P2 and P3 yields decrease by factors of 4.0 and 7.0, respectively.
Acknowledgements
The authors are grateful to Dr Osanna Tishchenko for valuable contributions to the work. This work was supported in part by the U.S. Department of Energy, Office of Science, Office of Basic Energy Science, as part of the Combustion Energy Frontier Research Center under Award Number DE-SC0001198 and as part of grant no. DE-FG02-86ER13579. Some of the computations were performed as part of a Computational Grand Challenge grant at the Molecular Science Computing Facility in the William R. Wiley Environmental Molecular Sciences Laboratory, a national scientific user facility sponsored by the U.S. Department of Energy's Office of Biological and Environmental Research and located at the Pacific Northwest National Laboratory, operated for the Department of Energy by Battelle.References
- R. N. Birrell and A. F. Trotman-Dickenson, J. Chem. Soc., 1960, 2059 RSC.
- D. L. Singleton, R. S. Irwin and R. J. Cvetanović, Can. J. Chem., 1977, 55, 3321 CrossRef CAS.
- A. C. Lloyd, NBS Spec. Publ., 1979, 557, 27 CAS.
- G. J. Audley, D. L. Baulch and I. M. Campbell, J. Chem. Soc., Faraday Trans. 1, 1981, 77, 2541 RSC.
- J. A. Kerr and D. W. Sheppard, Environ. Sci. Technol., 1981, 15, 960 CrossRef CAS.
- D. H. Semmes, A. R. Ravishankara, C. A. Gump-Perkins and P. H. Wine, Int. J. Chem. Kinet., 1985, 17, 303 CrossRef CAS.
- C. Pagagni, J. Arey and R. Atkinson, Int. J. Chem. Kinet., 2000, 32, 79 CrossRef.
- A. Galano, J. R. Alvarez-Idaboy, G. Bravo-Pérezk and M. E. Ruiz-Santoyo, Phys. Chem. Chem. Phys., 2002, 4, 4648 RSC.
- A. A. Shestov, S. A. Kostina and V. D. Knyazev, Proc. Combust. Inst., 2005, 30, 975 CrossRef.
- J. Aguilera-Iparraguirre, H. J. Curran, W. Klopper and J. M. Simmie, J. Phys. Chem. A, 2008, 112, 7047 CrossRef CAS.
- G. Black and J. M. Simmie, J. Comput. Chem., 2010, 31, 1236 CAS.
- C.-W. Zhou, J. M. Simmie and H. J. Curran, Int. J. Chem. Kinet., 2012, 44, 155 CrossRef CAS.
- T. Yu, J. Zheng and D. G. Truhlar, Chem. Sci., 2011, 2, 2199 RSC.
- J. Zheng and D. G. Truhlar, Faraday Discuss., 2012, 157, 59 RSC.
- J. Zheng, T. Yu, E. Papajak, I. M. Alecu, S. L. Mielke and D. G. Truhlar, Phys. Chem. Chem. Phys., 2011, 13, 10885 RSC.
- J. Zheng, S. L. Mielke, K. L. Clarkson and D. G. Truhlar, Comput. Phys. Commun., 2012, 183, 1803 CrossRef CAS.
- S. Glasstone, K. J. Laidler and H. Eyring, The Theory of Rate Processes, McGraw-Hill, New York, 1941 Search PubMed.
- K. S. Pitzer, Quantum Chemistry, Prentice-Hall: Englewood Cliffs, NJ, 1953 Search PubMed.
- D. G. Truhlar, J. Comput. Chem., 1991, 12, 266 CrossRef CAS.
- B. C. Garrett and D. G. Truhlar, J. Chem. Phys., 1979, 70, 1593 CrossRef CAS.
- D. G. Truhlar and B. C. Garrett, Acc. Chem. Res., 1980, 13, 440 CrossRef CAS.
- D. G. Truhlar, A. D. Isaacson and B. C. Garrett, Theory of Chemical Reaction Dynamics, ed. M. Baer, CRC Press, Boca Raton, FL, 1985, vol. 4, p. 65 Search PubMed.
- M. Garcia-Viloca, J. Gao, M. Karplus and D. G. Truhlar, Science, 2004, 303, 186 CrossRef CAS.
- B. C. Garrett, D. G. Truhlar, R. S. Grev and A. W. Magnuson, J. Phys. Chem., 1980, 84, 1730 ( J. Phys. Chem. , 1983 , 87 , 4554 ) CrossRef CAS , erratum.
- Y.-P. Liu, G. C. Lynch, T. N. Truong, D.-h. Lu and D. G. Truhlar, J. Am. Chem. Soc., 1993, 115, 2408 CrossRef CAS.
- A. Fernandez-Ramos, B. A. Ellingson, B. C. Garrett and D. G. Truhlar, Rev. Comput. Chem., 2007, 23, 125 CrossRef CAS.
- D. G. Truhlar and A. Kuppermann, J. Am. Chem. Soc., 1971, 93, 1840 CrossRef.
- A. D. Isaacson and D. G. Truhlar, J. Chem. Phys., 1982, 76, 1380 CrossRef CAS.
- T. Yu, J. Zheng and D. G. Truhlar, Phys. Chem. Chem. Phys., 2012, 14, 482 RSC.
- P. Seal, E. Papajak and D. G. Truhlar, J. Phys. Chem. Lett., 2012, 3, 264 CrossRef CAS.
- M. Garcia-Viloca, J. Gao, M. Karplus and D. G. Truhlar, Science, 2004, 303, 186 CrossRef CAS.
- T. Yu, J. Zheng and D. G. Truhlar, J. Phys. Chem. A, 2012, 116, 297 CrossRef CAS.
- J. Zheng, S. L. Mielke, K. L. Clarkson and D. G. Truhlar, MSTor, University of Minnesota, Minneapolis, version 2011-3, 2011 Search PubMed.
- J. Zheng, S. Zhang, B. J. Lynch, J. C. Corchado, Y.-Y. Chuang, P. L. Fast, W.-P. Hu, Y.-P. Liu, G. C. Lynch, K. A. Nguyen, C. F. Jackels, A. F. Ramos, B. A. Ellingson, V. S. Melissas, J. Villà, I. Rossi, E. L. Coitino, J. Pu, T. V. Albu, R. Steckler, B. C. Garrett, A. D. Isaacson and D. G. Truhlar, POLYRATE, University of Minnesota, Minneapolis, version 2010-A, 2010 Search PubMed.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2008, 4, 1849 CrossRef CAS.
- J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2009, 5, 808 CrossRef CAS.
- X. Xu, I. M. Alecu and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 1667 CrossRef CAS.
- E. Papajak, H. Leverentz, J. Zheng and D. G. Truhlar, J. Chem. Theory Comput., 2009, 5, 1197 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007 CrossRef CAS.
- E. Papajak and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 10 CrossRef CAS.
- W. Klopper, F. R. Manby, S. Ten-No and E. F. Valeev, Int. Rev. Phys. Chem., 2006, 25, 427 CrossRef CAS.
- T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef.
- G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef.
- J. Zheng, X. Xu, H. R. Leverentz and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 3027 CrossRef.
- E. Papajak and D. G. Truhlar, J. Chem. Phys., 2012, 137, 064110 CrossRef.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618 CrossRef.
- I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 2872 CrossRef CAS.
- R. D. Johnson III, K. K. Irikura, R. N. Kacker and R. Kessel, J. Chem. Theory Comput., 2010, 6, 2822 CrossRef.
- J. M. Bowman, T. Carrington and H.-D. Meyer, Mol. Phys., 2008, 106, 2145 CrossRef CAS.
- S. Carter, A. R. Sharma, J. M. Bowman, P. Rosmus and R. Tarroni, J. Chem. Phys., 2009, 131, 224106 CrossRef.
- O. Christiansen, Phys. Chem. Chem. Phys., 2012, 14, 6672 RSC.
- S. Chempath, C. Predescu and A. T. Bell, J. Chem. Phys., 2006, 124, 234101 CrossRef.
- S. L. Mielke and D. G. Truhlar, J. Phys. Chem. A, 2009, 113, 4817 CrossRef CAS.
- J. M. Bowman, D. Wang, X. Huang, F. Huarte-Larrañaga and U. Manthe, J. Chem. Phys., 2001, 114, 9863 CrossRef.
- A. Chakraborty, D. G. Truhlar, J. M. Bowman and S. Carter, J. Chem. Phys., 2004, 121, 2071 CrossRef CAS.
- A. Chakraborty and D. G. Truhlar, J. Chem. Phys., 2006, 124, 184310 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. E. Gomperts, O. Stratmann, A. J. Yazyev, R. Austin, C. Cammi, J. W. Pomelli, R. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian Inc., Wallingford CT, Revision A.02, 2009 Search PubMed.
- H.-J. Werner, P. J. Knowles, F. R. Manby, M. Schütz, P. Celani, G. Knizia, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklaß, P. Palmieri, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang and A. Wolf, MOLPRO, University of Birmingham, Birmingham, version 2010.1, 2010 Search PubMed.
- J. I. Seeman, Chem. Rev., 1983, 83, 83 CrossRef CAS.
- D. Katsikadakos, Y. Hardalupas, A. M. K. P. Taylor and P. A. Hunt, Phys. Chem. Chem. Phys., 2012, 14, 9615 RSC.
- Z. H. Li, A. W. Jasper and D. G. Truhlar, J. Am. Chem. Soc., 2007, 129, 14899 CrossRef CAS.
- M. W. Schmidt, M. S. Gordon and M. Dupuis, J. Am. Chem. Soc., 1985, 107, 2585 CrossRef CAS.
- M. Page and J. W. McIver, Jr, J. Chem. Phys., 1988, 88, 922 CrossRef CAS.
- B. C. Garrett, M. J. Redmon, R. Steckler, D. G. Truhlar, K. K. Baldridge, D. Bartol, M. W. Schmidt and M. S. Gordon, J. Phys. Chem., 1988, 92, 1476 CrossRef CAS.
- K. K. Baldridge, M. S. Gordon, R. Steckler and D. G. Truhlar, J. Phys. Chem., 1989, 93, 5107 CrossRef CAS.
- C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154 CrossRef CAS.
- C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523 CrossRef CAS.
- M. Page, C. Doubleday and J. W. McIver, Jr, J. Chem. Phys., 1990, 93, 5634 CrossRef CAS.
- V. S. Melissas, D. G. Truhlar and B. C. Garrett, J. Chem. Phys., 1992, 96, 5758 CrossRef CAS.
- V. S. Melissas and D. G. Truhlar, J. Chem. Phys., 1993, 99, 1013 CrossRef CAS.
- W.-P. Hu, Y.-P. Liu and D. G. Truhlar, J. Chem. Soc., Faraday Trans., 1994, 90, 1715 RSC.
- V. S. Melissas and D. G. Truhlar, J. Phys. Chem., 1994, 98, 875 CrossRef CAS.
- J. C. Corchado, J. Espinosa-Garcia, W.-P. Hu, I. Rossi and D. G. Truhlar, J. Phys. Chem., 1995, 99, 687 CrossRef CAS.
- Y.-Y. Chuang and D. G. Truhlar, J. Phys. Chem. A, 1997, 101, 3808 ( J. Phys. Chem. A , 1997 , 101 , 8741 ) CrossRef CAS , erratum.
- J. Villà and D. G. Truhlar, Theor. Chem. Acc., 1997, 97, 317 CrossRef.
- J. C. Corchado, E. L. Coitiño, Y.-Y. Chuang, P. L. Fast and D. G. Truhlar, J. Phys. Chem. A, 1998, 102, 2424 CrossRef CAS.
- Y.-Y. Chuang, J. C. Corchado and D. G. Truhlar, J. Phys. Chem. A, 1999, 103, 1140 CrossRef CAS.
- Y. Kim, J. C. Corchado, J. Villa, J. Xing and D. G. Truhlar, J. Chem. Phys., 2000, 112, 2718 CrossRef CAS.
- T. V. Albu, J. C. Corchado and D. G. Truhlar, J. Phys. Chem. A, 2001, 105, 8465 CrossRef CAS.
- H. Lin, J. Pu, T. V. Albu and D. G. Truhlar, J. Phys. Chem. A, 2004, 108, 4112 CrossRef CAS.
- H. Lin, Y. Zhao, O. Tishchenko and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 1237 CrossRef CAS.
- O. Tischenko and D. G. Truhlar, J. Phys. Chem. A, 2006, 110, 13530 CrossRef.
- O. Tischenko and D. G. Truhlar, J. Chem. Theory Comput., 2009, 5, 1454 CrossRef.
- C. F. Jackels, Z. Gu and D. G. Truhlar, J. Chem. Phys., 1995, 102, 3188 CrossRef CAS.
- K. A. Nguyen, C. F. Jackels and D. G. Truhlar, J. Chem. Phys., 1996, 104, 6491 CrossRef CAS.
- J. Zheng and D. G. Truhlar, Phys. Chem. Chem. Phys., 2010, 12, 7782 RSC.
- D. G. Truhlar, J. Chem. Educ., 1978, 55, 309 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Optimized Cartesian coordinates (in Å) of all the structures of butanal (reactant), butanoyl radical, 1-oxo-2-butyl radical, 4-oxo-2-butyl radical (product radicals), hydroperoxyl radical, hydrogen peroxide, and six lowest-energy structures of the transition states leading to the formation of butanoyl radical, 1-oxo-2-butyl radical, 4-oxo-2-butyl radical and 4-oxo-1-butyl radical; relative conformational energies and local periodicities; conformational–rotational–vibrational partition functions and anharmonicity factors; more temperatures for Tables 2 and 3; and details of the density functional validations, the anharmonicity calculations, and the reaction paths. See DOI: 10.1039/c2sc21090h |
| This journal is © The Royal Society of Chemistry 2013 |