Partial slip at fluid–solid boundaries by multiparticle collision dynamics simulations
S.
Hanot
,
M.
Belushkin
and
G.
Foffi
*
Institute of Theoretical Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), CH-1015 Lausanne, Switzerland. E-mail: maxim.belushkin@epfl.ch; giuseppe.foffi@epfl.ch
First published on 17th October 2012
Abstract
The understanding of the exact boundary conditions at the interface between a solid and a fluid is becoming increasingly important, as the limitations of the no-slip boundary condition are becoming apparent, especially in micro- and nanofluidics applications. We present a systematic study of controlled partial-slip boundary conditions in multiparticle collision dynamics simulations. By studying a plane Poiseuille flow, we demonstrate that, in general, the slip length of the fluid strongly depends on the microscopic dynamics in the vicinity of the solid surface. We empirically derive the dependence of the slip length on the properties of the MPC fluid and of the wall, and demonstrate that the wall slip in this coarse-grained simulation approach is linearly correlated with the flux of momentum across the fluid–solid interface.
1 Introduction
Knowledge of the behaviour of a fluid in contact with a solid boundary is an important ingredient in the solution of hydrodynamic equations and, consequently, in the understanding of fluid dynamics. Macroscopically, the classical no-slip boundary condition proposed by Stokes is typically adopted. It dictates that the velocity of the fluid in contact with a solid boundary is equal to the velocity of the solid boundary. On microscopic and, more importantly, mesoscopic scales, however, violations of this condition become important.1,2 The resulting slip of a fluid at a surface is not only responsible for a change in fluid dynamics, but is also technologically important to influence flow friction.1While the general mechanisms responsible for generating surface slip remain unclear,1,3,4 it is known that the typical slip lengths encountered in applications range from several nanometres to micrometres,1,2 and that they depend strongly on properties of the fluid and the wall.1,4 While macroscopically such small lengths can indeed largely be ignored, in applications where channel sizes are on similar orders of magnitude in size, fluid dynamics may be significantly affected by the presence of slip.
As exact theoretical results are only available for a small class of problems relevant to micro- and nanofluidics, computer simulations are relied upon as a powerful predictive and exploratory tool.
The study of hydrodynamic interactions (HI) in computer simulations is a delicate topic that has attracted a lot of interest in the last few years. The main challenge is represented by the intrinsically many-body and long range origin of HI that make analytic solutions limited to few oversimplified cases. The situation becomes even more complicated when one is interested in mesoscopic objects embedded in a hydrodynamic fluid since the problems become multiscale. As a matter of fact this is a typical situation in soft matter where, for example, polymers or colloids are dynamically coupled to the solvent.
Historically the first method that implements HI in computer simulations was proposed in the pioneering work of Ermann and McCammon who used the Oseen tensor approximation of the hydrodynamic tensor in Brownian dynamics (BD) simulations.5 Several extensions to this work were based on more advanced approximations of the full hydrodynamic tensor. The drawback of these methods, like for example Stokesian dynamics,6 is that they can easily become computationally very expensive.
A different approach is based on the direct solution of the Navier–Stokes equation (NSE) with the appropriate boundary conditions. Several techniques based on a field treatment of the density, like fluid particle dynamics7 and related methods,8 have been proposed. In this case however, the Brownian nature of the mesoscopic particles is not built in a priori in the method and it is not clear how to implement different slip conditions at the interfaces.
A completely different approach is represented by lattice methods among which the most used is Lattice–Boltzmann (LB).9 In LB the solution of the NSE is based on a lattice-gas automata that uses movements that conserve momentum and energy locally. These are simple collision rules that make the simulation easily implemented and parallelized. The solid–fluid interface can be also implemented by proper modification of the collision rules.10 In the original formulation, there are no thermal fluctuations but this can be introduced with proper care.11 The modification of the slip length has been also recently discussed.12
Finally there are off-lattice methods, where the fluids possess both HI and thermal fluctuations. One of the most used methods is dissipative particle dynamics (DPD).13,14 This method is a modification of the standard molecular dynamics (MD) algorithm with particles interacting by soft potentials and a thermostat that conserves momentum locally. This method can be used to represent a solvent that can be coupled with a mesoscopic object. It is also possible to implement a fluid–solid interface with no-slip by proper modification of the algorithm.
In this work we will discuss the properties of the slip at the interfaces in multiparticle collision dynamics (MPC). This method belongs to the class of the off-lattice methods and is well-known for describing thermal fluctuations and hydrodynamics on coarse-grained length- and time-scales,15–17 even at very short times.18,19 There are several advantages for MPC with respect to other off-lattice methods like, for example, DPD. In MPC, the fluid is made of ideal particles and this makes it possible to calculate analytically the transport coefficients, like the viscosity or the self-diffusion coefficient, from the parameters of the simulations. In this way it is possible to tune a priori the properties of the solvent and this is a great advantage when comparing the numerical results with experimental situations. Another fundamental advantage is the fact that, differently from DPD, the particles of the fluid are non-interacting and consequently the algorithm scales as O(N) and can be easily parallelized.
In its most recent implementations, it has been shown that an MPC fluid relaxes toward the correct Gibbs equilibrium state with a monotonically increasing entropy as guaranteed by the existence of an H-theorem.20,21 Fluctuations are also taken properly into account as the fluctuation theorem is obeyed.22 All the aforementioned properties make MPC a very interesting method especially in soft matter simulations.
MPC was introduced only ten years ago and there are a lot of aspects that still have to be investigated. Investigations of fluid–solid boundary conditions within MPC to date, for example, have focused on eliminating slip at fluid–solid boundaries23,24 while no recipe has been devised to change the nature of the slip by modifying intrinsically the properties of the MPC collision rule.
Here, we present a systematic study of the possibility of tuning the slip length of an MPC fluid. We consider a planar Poiseuille flow in a channel. Working with a coarse-grained description of this system, in which the atomistic-level details are integrated out, we investigate the influence of the remaining parameters on the slip length. More specifically, we demonstrate the possibility of obtaining a wide range of slip length by changing properties of the system which influence the flux of momentum and energy across the fluid–wall interface.
2 Simulation protocol
In MPC, a cubic box of lateral size L is filled with N point-like particles, each having a mass m and continuous coordinates![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i and velocities
i and velocities ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) i. The simulation consists of two steps: propagation and collision. During the propagation step, the coordinates and velocities of each solvent particle i are updated according to Newton's equations of motion with a gravitational constant g and a collision time δt:
i. The simulation consists of two steps: propagation and collision. During the propagation step, the coordinates and velocities of each solvent particle i are updated according to Newton's equations of motion with a gravitational constant g and a collision time δt: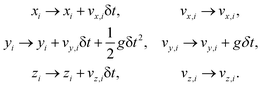 | (1) |
We consider periodic boundary conditions in the y- and the z-directions, and walls impermeable to the bulk fluid at x = 1 and x = L − 1. Collisions of fluid particles with a wall are treated with bounce-back rules: if, during the propagation step, the fluid particle crosses a wall, it is reflected from the wall, with its velocities reversed at the time of contact.
Following propagation, particles are sorted into collision cells of size a which form a cubic collision grid. Within each collision cell, the velocities of the particles are rotated with respect to the cell's centre-of-mass velocity by a fixed angle α around a randomly oriented rotation axis. To guarantee the Galilean invariance, the structure of the collision grid is shifted randomly at each collision step.25
Because of the random shift, walls do not necessarily coincide with collision cell boundaries, which results in partially filled cells. It is well-known that under this protocol, a finite slip length at the fluid–wall interface is generated.23,24 To model stick boundary conditions, it has been proposed that the volume internal to the walls be filled with ghost particles of the same density as the bulk fluid,23 and that the velocities of these wall particles be sampled from a Maxwell–Boltzmann distribution before each collision step. In fact, this method does not guarantee perfect no-slip conditions because the average center of mass of the particles in the wall does not always coincide with the wall. Winkler and Huang suggested a modification of this algorithm that guarantees perfect no-slip conditions.26
Our aim is to determine which coarse-grained system parameters influence the slip length of the fluid at the wall. To this end, we measure the flow velocity profile across the channel, vy,flow(x), of a fluid undergoing a planar Poiseuille flow. We choose a gravitationally driven flow as opposed to a pressure-driven flow to avoid perturbations of the flow profile along the length of the channel.27 Steady-state flow conditions are guaranteed by coupling a cell-level thermostat28 to the fluid. This is not strictly necessary since MPC is an energy conserving off-lattice method that can be used to represent temperature effects. In the present case, however, the use of non-isothermal dynamics would have implied to take care of other relevant time scales for heat diffusion, something that goes beyond the scope of this paper. For the effect of temperature on MPC we refer the reader to the very recent work of Lüsenbrink and Ripoll.29 We fit the obtained flow profile as done in previous studies,27 but allowing for a slip velocity,
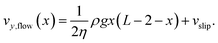 | (2) |
Here η denotes the shear viscosity of the solvent, L − 2 denotes the fact that the walls are located at x = 1 and x = L − 1, and vslip, the slip velocity, is then used to determine the slip length from the equation vy,flow(λ) = 0,
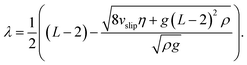 | (3) |
The fit parameters are the slip velocity vslip and the shear viscosity η. We keep the latter a fit parameter, and compare the results to the theoretical values calculated according to ref. 17.
We assume the standard normalization of MPC units: collision cell size a = 1, thermal energy kBT = 1 and fluid particle mass m = 1. Thus, the length is measured in units of a, time in units of 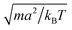 , density in units of m/a3, shear viscosity in units of
, density in units of m/a3, shear viscosity in units of 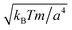 , and gravitational constant g in units of kBT/(ma). The parameters of the fluid – mass density ρ, collision time δt, collision angle α, and the parameters of the wall – the density of internal wall particles ρwall, and the gravitational constant g are varied to study their influence on the slip length. The bulk density of the fluid is fixed as a parameter at the beginning of the simulations and after that the number of MPC particles is conserved.
, and gravitational constant g in units of kBT/(ma). The parameters of the fluid – mass density ρ, collision time δt, collision angle α, and the parameters of the wall – the density of internal wall particles ρwall, and the gravitational constant g are varied to study their influence on the slip length. The bulk density of the fluid is fixed as a parameter at the beginning of the simulations and after that the number of MPC particles is conserved.
3 Results
3.1 Influence of wall properties
The flux of momentum and energy between the bulk fluid and the walls has two components: kinetic and collisional. The kinetic component arises in the propagation step of MPC. It is fixed by the bounce-back rules adopted and depends only on the bulk fluid properties – since the velocities of the internal wall particles are resampled before each collision step, the momentum they exchange with the walls during the propagation step need not be considered at all. The collisional contribution arises in the collision step of MPC and depends strongly on the density of the particles internal to the wall: at zero wall particle density, there is no flux of momentum across the wall during the collision step at all.As the slip length depends on the flux of energy and momentum,2–4 it is natural to assume that the density of wall particles will play a significant role. Indeed, considerable slip has been observed at zero density, and no-slip conditions have been achieved by matching wall particle density with bulk particle density.23,24
We investigate in detail the transition between the two limits by performing simulations at different wall particle densities. A typical set of obtained flow velocity profiles is shown in Fig. 1. The slip lengths measured from the flow profiles using eqn (3) for two different sets of fluid parameters are shown in Fig. 2. The slip length values do not depend either on the flow rate (Fig. 2, left) or on the channel size (Fig. 2, right), and do depend on properties of the bulk fluid and density of the wall particles (compare values in Fig. 2, left and right).
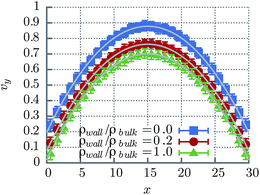 | ||
| Fig. 1 Flow velocity profiles for ρ = 10, δt = 0.05, α = 130° (η = 16.7), g = 0.01 for different values of ρwall for L = 32. Points are simulation results, and gray solid lines denote the fit of eqn (2). | ||
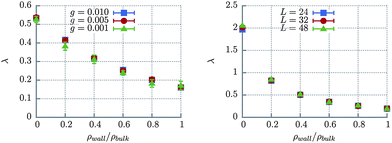 | ||
| Fig. 2 Slip length λ as a function of wall particle density ρwall for two different fluids. Results demonstrate that the slip length depends on fluid and wall properties, but not on the flow rate or system size. Error bars represent averaging errors over several hundred independent runs for each set of parameters. Left: L = 32, ρ = 5, δt = 0.1, α = 90° (η = 2.5), different values of g give the same results. Right: ρ = 10, δt = 0.05, α = 130° (η = 16.7), g = 0.01, different values of L give the same results. | ||
We observe that the slip length scales as the inverse of the density of wall particles, and does not identically vanish when the density of wall particles matches the density of the bulk fluid. However, in this limit, its value is sufficiently small to disregard the slip for most applications, since generally the smallest really meaningful length scale resolved in MPC is comparable to the size of one collision cell a.15
It is tempting to investigate the possibility of having a vanishing slip length. To this end, we perform simulations where the density of wall particles ρwall exceeds the bulk density ρ for L = 32, ρ = 5, δt = 0.1, α = 90° (η = 2.5), and g = 0.01. The results shown in Fig. 3 show that, in fact, λ appears to become negative at very large wall densities. Effectively, this implies that within a layer of some small thickness in the vicinity of the wall, the bulk fluid exhibits no net flow. This can be understood in terms of momentum exchange in the collision step: when the wall particle density is very high, the contribution of these particles makes the centre-of-mass velocities of all cells crossing the wall essentially zero. Therefore, it is the velocities of the bulk particles inside such cells that are rotated around a randomly oriented axis. This effectively randomizes the orientation of velocities of particles near the wall.
![Slip length for L = 32, ρ = 5, δt = 0.1, α = 90° (η = 2.5), and g = 0.01 as a function of ρwall for ρwall ∈ [0;10]ρ.](/image/article/2013/SM/c2sm26316e/c2sm26316e-f3.gif) | ||
| Fig. 3 Slip length for L = 32, ρ = 5, δt = 0.1, α = 90° (η = 2.5), and g = 0.01 as a function of ρwall for ρwall ∈ [0;10]ρ. | ||
For all the cases we confirmed that the temperature across the channel is uniform and that the viscosities obtained from the fits, η = 2.6 and η = 16.5, are in excellent agreement with the theoretical values of ηth = 2.5 and ηth = 16.7, respectively.
3.2 Influence of fluid properties
Properties of the fluid generally also play an important role in defining the slip length, and the MPC fluid is no exception to this rule. We performed simulations for 1760 different combinations of the basic MPC parameters. More specifically, we varied the solvent density ρ ∈ [5;15], collision angle α ∈ [90;160]° and collision time δt ∈ [0.01;0.1].We studied two conditions: the slip length at zero wall density ρwall = 0 and the slip length at wall density matching bulk density ρwall = ρ. For the latter, we find no dependence on the properties of the MPC fluid. We find a value of λ∣ρwall=ρ = 0.187 ± 0.003 for 880 different fluid parameters. Therefore, in this regime, one can generally assume no-slip conditions.
The slip length at zero wall density λ∣ρwall=0, on the other hand, exhibits a strong dependence on MPC parameters, especially on the collision time δt. Furthermore, the dependencies on the collision time δt and on the density ρ are monotonous within the parameter ranges studied, whereas the dependence on the collision angle α is not.
In order to provide a prescription for obtaining a well-defined slip length within MPC, we empirically find the following functional form for the slip length at zero wall density at a fixed collision angle α:
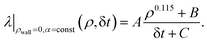 | (4) |
The parameters in eqn (4) obtained for the different collision angles studied are given in Table 1.
| α,o | A | B | C |
|---|---|---|---|
| 90 | 0.1159 | −0.6739 | 0.000272 |
| 100 | 0.1335 | −0.6831 | 0.000356 |
| 110 | 0.1244 | −0.5778 | 0.000772 |
| 120 | 0.1154 | −0.4731 | 0.000610 |
| 130 | 0.1167 | −0.4603 | 0.000584 |
| 140 | 0.1004 | −0.3168 | 0.000809 |
| 150 | 0.0796 | −0.0856 | 0.000371 |
| 160 | 0.0530 | 0.5004 | 0.000094 |
This functional form eqn (4) provides an excellent description of the measured values, as shown in Fig. 4 (left). This dependence on the solvent parameters vanishes in the limit of high wall particle densities, as discussed above and shown in Fig. 4 (right).
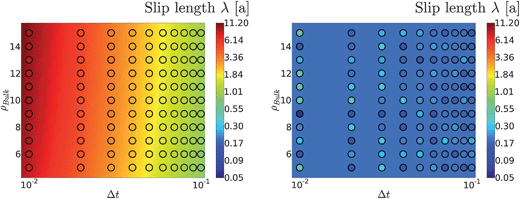 | ||
| Fig. 4 Left: dependence of slip length at ρwall = 0 on the fluid density ρ and collision time δt for α = 130°. The continuous color map corresponds to the empirically determined functional dependence eqn (4), with parameters given in Table 1. Right: the slip length at ρwall = ρbulk for the same fluid parameters is constant. The coloured points correspond to the values measured in simulations, and the color map shows the average value determined from 880 simulations with different parameters, λ∣ρwall=ρ = 0.187 ± 0.003. | ||
The physical origin of the wall slip in such a coarse-grained simulation approach lies in the rate of momentum flow across the fluid–solid interface. Indeed, we observe a linear relationship between the slip length and the measured flux of momentum across the fluid–wall boundary, Fig. 5.
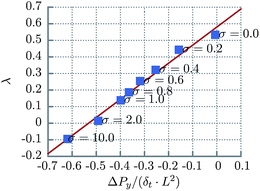 | ||
| Fig. 5 The slip length as a function of the measured flux of momentum across the wall. The solid line is a guide to the eye demonstrating the existence of a linear relationship. σ is the ratio of the wall density to the bulk density. | ||
These results also demonstrate that in the presence of solid boundaries an additional level of complexity in matching the results of simulations to experimental data arises. This stems from the fact that it is no longer sufficient to match dimensionless numbers such as the Schmidt and Reynolds numbers for the solvent, and the Peclet number for colloidal particles.15 Details of the interactions of the solid boundary with the solvent are also highly relevant in determining the fluid dynamics and, consequently, the flow friction. We remark that simulations in the typical regime where the density of wall particles matches the density of the bulk fluid essentially removes this dependence, and the resulting boundary conditions can be considered no-slip.
4 Conclusions
We have demonstrated that the slip length of a simple fluid at a solid interface can be varied by changing the flux of momentum across the interface. We have shown that well-defined slip lengths at a fluid–solid interface can be achieved in multiparticle collision dynamics simulations, and have quantified the dependence of the slip length on the parameters of the fluid and of the wall. The resulting slip length in general strongly depends on the properties of the fluid and of the wall, but not on the flow rate or on the system size. We have quantified the highly non-trivial dependence of the slip length on the parameters of the MPC fluid and of the wall.In this way, we have shown that within MPC the slip length is governed by the flux of momentum and energy across the interface, since the simulation protocol is coarse-grained and does not capture the molecular-level details of the underlying interactions.
We have decided to discuss Poiseuille flow because, in its extreme simplicity, it represents the first natural test case for which a lot of analytical results are available. However the idea laid down here can be easily extended to other situations. It is possible, for example, to treat the case of moving or accelerating surfaces. In this case one has to move the ghost particles according to the center of mass of the wall/interface and in this way it would be possible to generalize the methodology described here with the caveat of generalizing the collision rules. The case of a non-flat wall could also be treated similarly. In this case, the bounce-back rule has to be adapted and the number and size of collision cells have to be tuned. If the cells are too large with respect to the typical curvature of the surface, an averaged effect of the surface will act on the fluid. In contrast, reducing the size of the cell too much will make the method too computationally demanding.
MPC is a mesoscopic method that can access only mesoscopic length scales. It is natural to ask in which situation the method that we have laid down here can be used. MPC has proven to be quite successful in the study of colloidal systems. It has been used, for example, to discuss colloidal sedimentation30,31 and colloidal optical18 traps. In the case of colloidal particles of micrometer size embedded in a fluid, typical MPC simulations would be implemented with a typical cell size between 1/2 and 1/8 of the particle diameter.15 Under these conditions we can extract information above the length scales between 250 nm (for the first case) and 60 nm (for the second case). In their pioneering paper,32 Zhu and Granick have found that the slip length can grow up to 2 μm. In particular, they introduced a phenomenological parameter f* that is equal to unity for the perfect no-slip boundary condition while it is lower than one for increasing slip. They found f* as low as 0.1 for a film thickness in the regime we could investigate. It is clear that the method proposed here could be used to simulate colloids close to interfaces with a non-null slip length.
The method we have sketched here could be used to investigate experimental situations in which the presence of a wall with a non-zero slip length could have a particular importance. Besides traditional fields of applications, such as microfluidics and confined fluids, the effect of slip might have important consequences on the behavior of colloidal particles that are trapped by optical tweezers. In a recent paper, we have demonstrated that MPC can be used to give an insight into the behavior of optically trapped colloidal particles.18 Similar experiments were performed by Jannasch et al. in the presence of an interface.33 The authors interpreted their data using a frequency dependent and distance (from the wall) dependent drag coefficient that assumes interfaces with no-slip boundary conditions. This assumption has been criticized as a possible source of misinterpretation of the experimental data.34 This is an example of a situation in which the use of mesoscopic simulations could be used to clarify the situation by the possibility to tune the slip length.
To conclude, the topic of the slip-length in solid–fluid boundary conditions is extremely important and delicate to treat numerically. Here we have presented a possible route to tune the slip length in MPC simulations that could represent a valuable way to tackle the problem in situations like microfluidics, confinement and, especially, colloidal particles trapped in optical tweezers.
Acknowledgements
We are indebted for invaluable discussion to Roland Winkler. MB and GF acknowledge financial support by the Swiss National Science Foundation (grant no. PP0022_119006).References
- L. Bocquet and J.-L. Barrat, Soft Matter, 2007, 3, 685–693 RSC.
- E. Lauga, M. Brenner and H. Stone, Microfluidics: The No-Slip Boundary Condition. Handbook of Experimental Fluid Mechanics, Springer, 2007, pp. 1219–1240 Search PubMed.
- P. A. Thompson and S. M. Troian, Nature, 1997, 389, 360–362 CrossRef CAS.
- H. Brenner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 046309 Search PubMed.
- D. L. Ermak and J. A. McCammon, J. Chem. Phys., 2011, 84, 046309 Search PubMed.
- J. F. Brady and G. Bossis, Annu. Rev. Fluid Mech., 1988, 20, 111 CrossRef.
- H. Tanaka and T. Araki, Phys. Rev. Lett., 2000, 85, 1338 CrossRef CAS.
- Y. Nakayama and R. Yamamoto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 036707 CrossRef.
- A. Succi, The Lattice Bolzmann Equation for Fluid Dynamics and Beyond, Oxford University Press, Oxford, 2001 Search PubMed.
- A. J. C. Ladd, Phys. Rev. Lett., 1993, 70, 1339 CrossRef CAS.
- M. E. Cates, et al. , J. Phys.: Condens. Matter, 2004, 16, S3903 CrossRef CAS.
- N. K. Ahmed and M. Hecht, J. Stat. Mech.: Theory Exp., 2009, P09017 Search PubMed.
- P. J. Hoogerbrugge and J. M. V. A. Koelman, Europhys. Lett., 1992, 19, 155 CrossRef.
- P. Espanol and P. B. Warren, Europhys. Lett., 1995, 30, 191 CrossRef CAS.
- J. T. Padding and A. A. Louis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 031402 CrossRef CAS.
- R. Kapral, Adv. Chem. Phys., 2008, 140, 89–146 CAS.
- G. Gompper, T. Ihle, D. M. Kroll and R. G. Winkler, Advanced computer simulation approaches for soft matter sciences III, Adv. Polym. Sci., 2009, 221, 1–87 CAS.
- T. Franosch, M. Grimm, M. Belushkin, F. M. Mor, G. Foffi and L. Forró, Nature, 2011, 478, 85–88 CrossRef CAS.
- M. Belushkin, R. G. Winkler and G. Foffi, J. Phys. Chem. B, 2011, 115, 14263–14268 CrossRef CAS.
- A. Malevanets and R. Kapral, J. Chem. Phys., 1999, 110, 8605–8613 CrossRef CAS.
- T. Ihle and D. M. Kroll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 066705 CrossRef CAS.
- M. Belushkin, R. Livi and G. Foffi, Phys. Rev. Lett., 2011, 106, 210601 CrossRef CAS.
- A. Lamura and G. Gompper, Eur. Phys. J. E: Soft Matter Biol. Phys., 2002, 9, 477–485 Search PubMed.
- J. K. Whitmer and E. Luijten, J. Phys.: Condens. Matter, 2010, 22, 104106 CrossRef.
- T. Ihle and D. M. Kroll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 020201 CrossRef CAS.
- R. Winkler and C. Huang, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 130, 074907 Search PubMed.
- E. Allahyarov and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 036702 CrossRef CAS.
- C.-C. Huang, A. Chatterji, G. Sutmann, G. Gompper and R. G. Winkler, J. Comput. Phys., 2010, 229, 168 CrossRef CAS.
- D. Lüsenbrink and M. Ripoll, J. Chem. Phys., 2012, 136, 084106 Search PubMed.
- J. T. Padding and A. A. Louis, Phys. Rev. Lett., 2004, 93, 220601 CrossRef CAS.
- A. Wysocki, C. P. Royall, R. G. Winkler, G. Gompper, H. Tanaka, A. van Blaaderen and H. Löwen, Faraday Discuss., 2010, 144, 245 RSC.
- Y. Zhu and S. Granick, Phys. Rev. Lett., 2001, 87, 096105 CrossRef CAS.
- A. Jannasch, M. Mahamdeh and E. Schäffer, Phys. Rev. Lett., 2011, 107, 228301 Search PubMed.
- B. U. Felderhof, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 046303 Search PubMed.
| This journal is © The Royal Society of Chemistry 2013 |
