Topological defects in the buckling of elastic membranes
Chloe M.
Funkhouser
,
Rastko
Sknepnek
and
Monica
Olvera de la Cruz
*
Department of Materials Science and Engineering, Northwestern University, Evanston, Illinois 60208, USA. E-mail: m-olvera@northwestern.edu
First published on 11th October 2012
Abstract
We investigate the effects of topological defects on the low-energy shapes of single-component two-dimensional elastic membranes with spherical topology. The membrane is described as a closed, triangulated two-dimensional manifold embedded in three-dimensional space using a dynamic triangulation model, thus allowing the creation of topological defects. Low-energy structures and connectivities are explored using a Monte Carlo simulated annealing method while also constraining the internal volume of the membrane to simulate incompressible contents within the membrane, such as in colloidosomes and viruses. We find that since the volume constraint partially suppresses the buckling transition such that the buckled icosahedral shape has a reduced asphericity, defect scars are favorable over a larger range of elastic parameters of the membrane compared with systems having no constraint on volume.
1 Introduction
Membranes are integral components of countless biological systems. While biological membranes are typically in a liquid state, most commonly as lipid bilayers, membranes with a solid, elastic character are found in a variety of systems and can also be engineered in the laboratory. Examples of natural elastic membranes include virus capsids1,2 and bacterial carboxysomes composed of proteins.3,4 Elastic membrane vesicles can be created, for example, by cooling lipid vesicles below the gel transition temperature,5 by cross-polymerizing amphiphiles, or by coassembling particular mixtures of charged lipids.6 The solid character of the these membranes has profound effects on their physical properties7 and can lead to faceted structures.8,9 However we note that a mechanism for forming facets has been recently reported for liquid membranes as well.10,11 The faceted shapes observed for elastic membranes and surfaces are often icosahedral, particularly in single-component systems such as virus capsids and fullerenes. For multicomponent membranes, a variety of faceted structures can arise if the components have different mechanical properties.12,13 Morphologies can also be altered in response to adsorption of colloids14 or molecules such as DNA,15 in addition to local changes in solution composition.The morphologies of these elastic membrane systems can additionally be affected by their contents and environment, which can impose constraints on the membrane internal volume. For example, the permeability of colloidosomes can be controlled, such that the internal volume is fixed,16 by letting the colloidal particles crystallize on the surface of emulsion droplets where the immiscibility of the liquids inside and outside of the droplet constrain the volume. The DNA contained within a virus capsid also imposes constraints on the internal volume.
If the solid membrane wall is characterized by crystalline order, as in the case of viruses, fullerene structures,17 and colloidosomes,18,19 interesting phenomena arise as a consequence of the interplay between the long-range positional and orientational order and the curved geometry. Understanding this interplay in these two-dimensional crystalline systems has been a recent topic of active research interest, as reviewed in ref. 20.
In a planar geometry (or any geometry with zero Gaussian curvature) it is possible to form a long-range crystalline order that is not frustrated. For a system with an isotropic interparticle interaction potential, a close-packed hexagonal order is the ground state, meaning that each particle has exactly six equidistant nearest neighbors. In other words, it is possible to tessellate a plane with equilateral triangles. This is however not the case for curved surfaces with non-zero Gaussian curvature,21,22 and defects that disrupt translational and/or orientational order are necessarily present in the lattice even in the ground state. Particularly important defects are dislocations and disclinations as they produce long-range effects on the crystalline lattice. Dislocations are characterized by a Burger's vector defined to close a loop drawn around the defect, while disclinations are points with five- or sevenfold coordination in the otherwise sixfold-coordinated lattice. Analogous to electrostatics, disclinations are often referred to as topological charges, with fivefold disclinations having a topological charge 2π/6 and sevenfold disclinations carrying a −2π/6 charge. A dislocation can be thought of as a pair (dipole) of bound disclinations. Such topological charges not only interact with the Gaussian curvature of the surface, but also affect each other through their long-range distortions of the elastic medium. As a consequence, disclinations of the same charge will repel each other.
On a sphere (the simplest example of a curved surface with non-zero Gaussian curvature at any point), the total number of defects is determined by the topology dictating that any crystalline lattice has a topological charge of exactly 4π.23 Consequently, there are at least twelve (12(2π/6) = 4π) fivefold disclinations present in the ground state of a crystal on a spherical surface. These twelve positively charged disclinations repel each other and take a position that minimizes the total energy, i.e., they position themselves at the twelve vertices of an inscribed icosahedron.24 Also permitted are crystals with configurations satisfying N5–N7 = 12,21 where N5 (N7) is the number of five (seven)-coordinated sites.
Continuum elastic theory has been applied to investigate initially planar membranes with a single disclination while allowing changes in membrane geometry, finding that the topological defect can trigger an elastic instability and cause the membrane to buckle out of the plane.25 This buckling into a conical shape with the defect located at the apex can relieve the strain imposed on the lattice by the defect, since the system can lower its stretching energy at the expense of bending energy. Thus, whether this buckling occurs or not is determined by the competition25 between the stretching energy, which is ∝R2 and bending energy ∝log(R), with R being the disclination radius. A dimensionless parameter known as the Föppl–von Kármán (FvK) number,25 defined as γ = YR2/κ, where Y is the Young's modulus and κ is the bending modulus, characterizes the buckling behavior, where the defect will buckle if γ > 154.25
Similarly, for the necessary twelve fivefold disclinations on the surface of a sphere, the elastic energy can be lowered by forming twelve conical deformations. The icosahedral distribution of the defects will naturally lead to an icosahedral shape in the buckled state.9 The buckling transition is rounded and shifted to a higher value of γ due to screening by the spherical geometry.9 This simple mechanical argument can provide a plausible explanation for the prevalence of the icosahedral shapes among faceted structures typically found in nature.
For crystalline lattices on fixed spherical geometries, Bowick et al.24 have studied ground-state configurations as a function of the ratio of the defect core energy to the Young's modulus. For small core energies, the formation of excess disclination defects (i.e., defects in addition to the required twelve) can be favorable since they screen the strain introduced by the required twelve defects. For larger core energies, the twelve-defect ground state prevails since forming new defects is prohibitively expensive. Over a range of moderate core energies the ground state consists of twelve fivefold disclinations accompanied by finite-length grain boundaries (so-called scars), i.e., pairs of fivefold and sevenfold disclinations emanating from each required disclination. These scars have also been observed experimentally.26–29 Using dynamical triangulation and allowing surface deformations, a finite-temperature study by Kohyama and Gompper30 showed that these scars become fuzzy and shift the onset of the buckling transition to larger values of γ. Additionally, topological defects have been studied in relation to curvature for non-spherical geometries31,32 such as toroids.33
In this work, we study the competition between two strain-relieving mechanisms in solid elastic membranes (buckling and forming excess defects), focusing on ground states. These systems are studied both with and without constraining the internal volume of the membrane. We perform simulated annealing Monte Carlo optimization to investigate these ground-state structures, allowing changes in the membrane morphology as well as the connectivity of the surface network. These changes in connectivity permit the formation of disclination pairs beyond the required twelve, and we examine their stability in different regions of parameter space. We emphasize that we exclusively study ground-state properties of solid membranes and thus the allowance of changes in connectivity is a tool used solely to access low-energy-state configurations with excess defects. This is a distinctly different problem from that of liquid membranes at finite temperatures for which the identical “edge-flip” move is used to ensure that the membrane is fluid. Liquid membranes and the melting transition are not addressed in this work, and have been extensively studied in the past.30,34 Our model includes elastic effects, which are not present in liquid membranes, and we examine whether solid membranes in the ground state prefer to form buckled morphologies and/or excess defects to relieve the strain caused by the twelve required disclinations.
We compare systems with no constraints on internal volume with systems having a fixed volume. The effects of volume constraints on the buckling transition in crystalline membranes have been investigated in ref. 35 for networks with fixed connectivity, limited to have only twelve disclinations. We allow changes in connectivity in our model, and find that the volume constraint is an integral factor in determining the favorability of having excess disclinations.
2 Methods
The membrane is described as a two-dimensional surface embedded in three-dimensional space, i.e., it is described by a three-dimensional position vector r = r(x1,x2) parametrized by two surface coordinates (x1, x2). At each point of the surface we can assign a metric tensor with components defined as gij = ∂ir·∂jr, where ∂i denotes a partial derivative with respect to coordinate xi. The metric tensor determines the distance between two neighboring points measured along the surface and in general depends on the position on the surface. In continuum elastic theory,36,37 the elastic energy of a two-dimensional isotropic thin sheet can be written as a sum of stretching and bending energy, F = Fs + Fb, with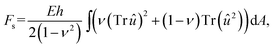 | (1) |
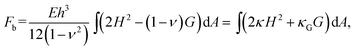 | (2) |
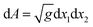 , where g is the determinant of the metric tensor; H is the mean curvature; κ= Eh3/(12(1 − ν2)) is the bending modulus; G is the Gaussian curvature, and κG = –Eh3/(12(1 + ν)) is the Gaussian bending modulus. The mean and Gaussian curvatures are defined in terms of the principle curvatures R1−1 and R2−1, as
, where g is the determinant of the metric tensor; H is the mean curvature; κ= Eh3/(12(1 − ν2)) is the bending modulus; G is the Gaussian curvature, and κG = –Eh3/(12(1 + ν)) is the Gaussian bending modulus. The mean and Gaussian curvatures are defined in terms of the principle curvatures R1−1 and R2−1, as 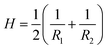 and G = 1/(R1R2), respectively. We note that the strain tensor can be understood as the deviation of the metric from that of the flat space, i.e.,
and G = 1/(R1R2), respectively. We note that the strain tensor can be understood as the deviation of the metric from that of the flat space, i.e., 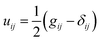 , where δij is Kronecker's delta symbol.
, where δij is Kronecker's delta symbol.
Any analytical treatment of the energy functional F = Fs + Fb (eqn (1) and (2)) in the presence of defects and fluctuating geometry would be intractable. Instead we resort to the numerical study of the ground-state properties of a discretized version of the continuum theory and introduce a discrete model of the membrane. We use simulated annealing Monte Carlo simulations to find low-energy configurations of the membrane. In this model, the closed membrane surface is represented as a triangular lattice having a minimum of twelve fivefold disclinations. The lattice is constructed using the method introduced by Caspar and Klug, where a triangulation is specified by a T – number defined in terms of a pair of positive integers (p,q), such that T = p2 + q2 + pq.1 Such a triangulation has a total of Nν = 10T + 2 vertices. In our simulations, we use a range of (p,q) pairs (12,3), (16,4), (24,1), and (25,0), creating structures with up to Nν = 6252 vertices in the (25,0) case. We note that the elastic parameters of the continuum theory are renormalized in the discrete model25,38 and the discrete description becomes equivalent to the continuum description in the limit where the length of the edges connecting vertices goes to zero.25
Within the discretized model the stretching energy ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) s is defined by assigning a harmonic spring to each edge with spring constant ε:
s is defined by assigning a harmonic spring to each edge with spring constant ε:
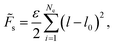 | (3) |
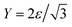 with ν = 1/3.7 The discrete bending energy
with ν = 1/3.7 The discrete bending energy ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) b is defined in terms of the normal vectors of two triangles sharing edge li, denoted as ni,1 and ni,2:
b is defined in terms of the normal vectors of two triangles sharing edge li, denoted as ni,1 and ni,2: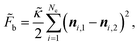 | (4) |
![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) is the discrete bending modulus, related to the continuum modulus as
is the discrete bending modulus, related to the continuum modulus as 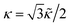 .7,25 We note that other discretizations of the bending energy have been proposed.7,39,40 The bending modulus
.7,25 We note that other discretizations of the bending energy have been proposed.7,39,40 The bending modulus ![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) has units of energy and throughout this paper it is used to set the energy scale in the model, i.e., we set
has units of energy and throughout this paper it is used to set the energy scale in the model, i.e., we set ![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) = 1. Lastly, in order to avoid unphysical configurations where the membrane crosses itself, the simulations additionally impose a soft-core repulsion on vertices of the form
= 1. Lastly, in order to avoid unphysical configurations where the membrane crosses itself, the simulations additionally impose a soft-core repulsion on vertices of the form![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) soft-core = Γ(exp(rmin − r − 1)) soft-core = Γ(exp(rmin − r − 1)) | (5) |
![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) edge-lim = Γ(exp(l − lmax − 1)) edge-lim = Γ(exp(l − lmax − 1)) | (6) |
![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) . We note that it is common to impose hard limits on the edge length,7 with
. We note that it is common to impose hard limits on the edge length,7 with 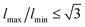 . Here we opt to relax that constraint and instead impose a soft but steep potential in order to allow moves at the early stages of the minimization process that would otherwise be rejected if the hard potential was used. As we are interested in obtaining low-energy configurations rather that exploring thermodynamic properties of the system, accepting unphysical configurations during the minimization process does not pose any problem as long as the final configuration is physical.
. Here we opt to relax that constraint and instead impose a soft but steep potential in order to allow moves at the early stages of the minimization process that would otherwise be rejected if the hard potential was used. As we are interested in obtaining low-energy configurations rather that exploring thermodynamic properties of the system, accepting unphysical configurations during the minimization process does not pose any problem as long as the final configuration is physical.
In some simulations, a constraint on the volume of the membrane is imposed, adding an extra term to the free energy:
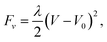 | (7) |
![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) acts to penalize any changes of the volume from its prescribed value V0. In all simulations we set V0 to the initial volume of the membrane structure. Volumes are calculated as described in ref. 35.
acts to penalize any changes of the volume from its prescribed value V0. In all simulations we set V0 to the initial volume of the membrane structure. Volumes are calculated as described in ref. 35.
The allowance of changes in the connectivity of the vertices composing the membrane network is a key element in the minimization procedure. Connectivity changes are accomplished using dynamic triangulation,7 and occur by iteratively “flipping” single edges, meaning that an edge shared by a pair of neighboring triangles is detached from its vertices and then connected to the two previously unshared vertices of the pair of triangles. With this method, the number of edges remains constant, as an edge can only be removed in conjunction with the creation of a new edge. In order to retain the triangular character of the network, an attempted edge flip that would leave a vertex with fewer than three neighbors is never accepted. By allowing changes in the connectivity, defects are able to develop beyond the twelve fivefold disclinations required for the closed surface. The twelve required disclinations will be referred to as required defects, while additional disclinations will be referred to as excess defects. We stress that the edge-flip moves are used as a tool to explore the low-energy configurations with excess defects rather than to simulate a liquid membrane.
Simulated annealing Monte Carlo simulations with 6 × 105 sweeps were performed with a series of linear and exponential cooling profiles in order to explore the energy landscape. The simulated annealing temperatures were determined as a function of the Young's modulus, such that low annealing temperatures were applied to simulations with low Young's moduli. We emphasize that the final simulated annealing temperatures imposed are sufficiently low such that the energy fluctuations are at most ≈10−4%. Therefore, we effectively study systems at zero temperature. Each sweep consisted of an attempt to move each vertex by at most 0.05l0 in a random direction, with moves accepted or rejected using Metropolis rules. Additionally, when changes in connectivity were permitted, an attempt was made to flip randomly selected edges every five sweeps using the same acceptance algorithm. This edge-flipping move is a tool used to allow the system to explore the energy landscape, permitting the formation of defects beyond the minimum twelve fivefold defects required by the spherical topology.
Simulations were performed with one of two setups: imposing no constraint on volume or imposing a constraint on volume penalizing changes from the initial volume (as in eqn (7)). For each of these setups, two subsets of simulations were performed, one with no excess defects and no changes in connectivity, and the other beginning with excess defects while attempting to make changes to the connectivity. There are thus four types of systems simulated, with and without volume constraint, and with and without excess defects. For those permitting excess defects, the initial structure was created using the following procedure. For four of the twelve required defects, one of their neighboring vertices was relocated to a randomly selected location elsewhere on the membrane surface and the regions surrounding both the old and new locations were retriangulated, introducing excess defects as illustrated in Fig. 1. We note that this procedure was necessary to form excess defects sufficiently far apart from each other. A simple edge-flip move generates two fivefold and two sevenfold defects next to each other. Such a configuration has to overcome a large energy barrier for the defects to unbind and in a simulation it is typically quickly annihilated.
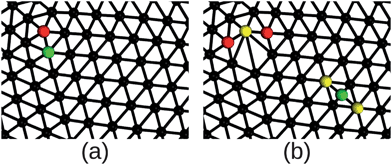 | ||
| Fig. 1 Illustration of the triangulation before (a) and after (b) a vertex neighboring a fivefold disclination is relocated to a randomly selected location. This is done for four vertices to produce the initial condition for simulations permitting changes in connectivity. The vertex that is relocated in shown in green, while fivefold disclinations are shown in red and sevenfold disclinations in yellow. Images were generated with the Visual Molecular Dynamics (VMD) package41 and rendered with Tachyon ray-tracer.42 | ||
In order to investigate the nature of the buckling transition with respect to FvK number, simulations for each of the four setups were performed for a range of FvK numbers by keeping the radius and discrete bending modulus fixed at R0 = 20.79l0 and ![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) = 1, respectively, and varying ε, to obtain FvK numbers (γ) in the range of log10γ = [0.76,5.6]. Additional simulations using different R0 but preserving that l0 = 1 were performed to examine how the results depend on the ratio of R/l0.
= 1, respectively, and varying ε, to obtain FvK numbers (γ) in the range of log10γ = [0.76,5.6]. Additional simulations using different R0 but preserving that l0 = 1 were performed to examine how the results depend on the ratio of R/l0.
3 Results and discussion
We investigate how changes in connectivity and geometry affect excess defects and the buckling transition. We determine the range of material parameters for which excess defects are energetically favorable. Additionally, we look into how these aspects are affected by constraining the volume enclosed by the membrane. Throughout the following discussion, we report results from simulated annealing Monte Carlo simulations of the (p, q) = (25, 0) structure that arrive at low-energy configurations, which may not necessarily be ground states, but are reproducible and typical. We refer to these states as optimal structures.The buckling transition from a sphere to an icosahedron can be identified as the FvK number corresponding to a rapid increase in asphericity. Asphericity is a measure of the deviation of a shape from a sphere (where an asphericity of zero corresponds to a perfect sphere), defined as9
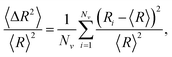 | (8) |
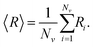 | (9) |
Fig. 2a presents plots of asphericity vs. FvK number for the four systems simulated, and for clarity those same systems divided based on the volume constraint are presented in Fig. 2b and c. The plots in Fig. 2b and c each show two curves that represent systems with and without excess defects. Additionally, the bending and stretching energy per vertex are plotted against the same range of FvK numbers in Fig. 2d and e to illustrate their relative contributions to the total energy. The asphericity plot showing all four systems highlights differences arising from the volume constraint; the buckling transition appears to be slightly shifted to higher FvK numbers when there is a fixed volume. Since the volume constraint provides an additional driving force for the shape to be spherical, the membrane remains spherical for a larger range of FvK numbers, shifting the location of the buckling transition. Also, the maximum value of asphericity reached with the fixed volume is significantly lower than that reached in the other case. This is because the transition from a sphere to an icosahedron involves a reduction in volume,35 and therefore with the volume fixed the shape cannot reach a perfect icosahedron. We observe that the faces of the icosahedron remain slightly curved, never achieving the planar character observed in the absence of constraint, and similarly that the edges of the icosahedron are softer with the volume constraint, both leading to a morphology with reduced asphericity.
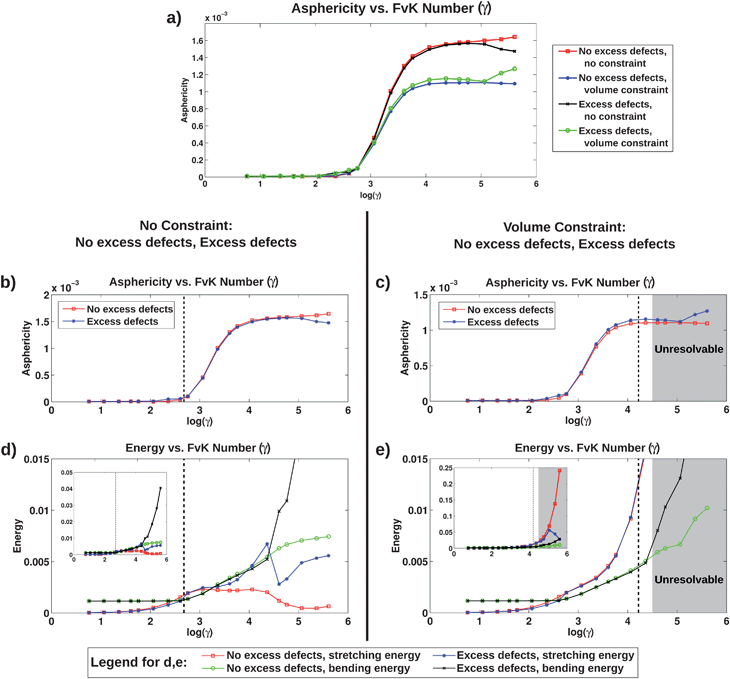 | ||
Fig. 2 Plots of asphericity, bending, and stretching energies per vertex in units of ![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) vs. FvK number. (a) Asphericity vs. FvK number for all four systems simulated, as indicated in the legend to the right; (b and c) asphericity vs. FvK number with the same data as in (a), but plotted separately with no constraint (b) and with the volume constraint (c); (d and e) stretching and bending energies vs. FvK number, again plotted separately based on volume constraint. In (d) and (e), the inset shows the full range of the data, while the larger plot shows a smaller range to better present the details at lower energies. In (b–e), the dashed lines indicate the threshold below which the system with excess defects was found to have lower total energy than the system with no excess defects. For the fixed volume plots, the shading indicates data from simulations where structures formed with features that were too small to be properly resolved. vs. FvK number. (a) Asphericity vs. FvK number for all four systems simulated, as indicated in the legend to the right; (b and c) asphericity vs. FvK number with the same data as in (a), but plotted separately with no constraint (b) and with the volume constraint (c); (d and e) stretching and bending energies vs. FvK number, again plotted separately based on volume constraint. In (d) and (e), the inset shows the full range of the data, while the larger plot shows a smaller range to better present the details at lower energies. In (b–e), the dashed lines indicate the threshold below which the system with excess defects was found to have lower total energy than the system with no excess defects. For the fixed volume plots, the shading indicates data from simulations where structures formed with features that were too small to be properly resolved. | ||
Examining the asphericity curves in Fig. 2b and c, which each directly compare systems with and without excess defects, we find that the buckling transition occurs at approximately the same FvK number in both cases with and without the volume constraint. We therefore conclude that the presence of excess defects does not alter the membrane morphology. While it has been reported that the buckling transition is shifted to higher FvK numbers in the presence of excess defects at finite temperature,30 the defect fractions we observe in the optimal structures we simulate are small enough that this shift does not occur, or is very minimal. At finite temperatures, thermal fluctuations create excess defects. However, for the ground-state systems studied here, excess defects only form when their strain-shielding effects more than compensate for their associated core energy. We speculate that this is the reason that we do not observe a shift in the buckling transition. The location of the buckling transition is not observed to shift when systems with different radius are compared (data not shown), although we find that excess defects are less favorable when R/l0 is smaller, since the core energy of a defect is larger for small R/l0 as shown by Bowick et al.24
Comparing systems with and without a volume constraint, we find that excess defects are favored for different ranges of the FvK number. Throughout the following discussion, we will refer to FvK numbers well below the buckling transition (≲102) as “low,” FvK numbers near the buckling transition (≈102 to 104) as “mid-range,” and FvK numbers well above the buckling transition (≳104) as “high.” For systems with no constraint on volume, excess defects are energetically favorable at FvK numbers below the approximate value where the buckling transition begins, as shown by the dashed line in Fig. 2b and d. The coincident location of these two transitions means that the FvK number for which a sphere is no longer the most favorable shape is also where excess defects become unfavorable. Therefore we do not observe any alignment of buckling with defect scars, as both are not observed for any single FvK number. On the energy plot for these systems, this threshold is where the two stretching energy curves cross. Below the threshold, the stretching energy with no excess defects is lower than that with excess defects, while the opposite is true above the threshold. It is not until larger FvK numbers (log(γ) ≈ 4.6) that the bending energy with excess defects surpasses the bending energy with no excess defects, and thus the stretching energy is the dominant energy contribution in determining the transition where excess defects are no longer favorable.
For systems with a fixed volume, excess defects are found to be energetically favorable for a much larger range of FvK numbers than with no constraint, as indicated by the dashed line in Fig. 2c and e. However, while excess defects are favorable, they are sparse and the fraction of vertices with more or less than six neighbors is still extremely low (0.5–3.4%). For large FvK numbers, in the shaded region in Fig. 2c and e, isolated regions of the membrane deformed into structures with length scales comparable to l0, i.e., too small to be accurately resolved by the discretization, and thus we cannot draw conclusions from those simulation results. We note that the energy contribution from the volume constraint (eqn (7)) is included in the total energy calculation, however this energy is approximately equal to zero in all simulations as the multiplier λ is large enough such that the volume remains nearly equal to V0, and thus it is not included in the plots in Fig. 2e.
Fig. 3 presents a plot of the number of excess defects vs. FvK number for the results with a volume constraint. We observe a sharp decrease in the number of excess defects at the buckling transition, above which the number of excess defects levels off. The positive slope of the curve at low FvK numbers (≲102) is a result of the edge-length limit imposed, where at very low FvK numbers (≈101) many Monte Carlo moves that would lead to new excess defects would also lead to edges that violate the length limit and are thus rejected. At FvK numbers below but approaching the buckling transition (≈101.5 to 102), the relative penalty for stretching is such that the length limit is imposed much less often, and more excess defects are created. In the absence of the edge-length limit, we would expect the maximum number of excess defects to occur at the lowest FvK number. Above the buckling transition, at very high FvK numbers, the membranes formed unresolvable structures, and thus we do not analyze this data.
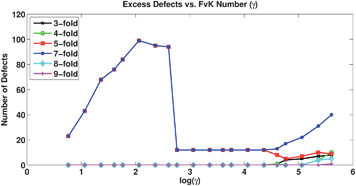 | ||
| Fig. 3 Number of excess defects vs. FvK number for systems with a constrained volume, showing a sharp decrease at the location of the buckling transition (log(γ) ≈ 2.5). | ||
An icosahedral shape with roughly the same surface area as a sphere has a volume approximately 10% smaller. Therefore, for the membrane to buckle from a sphere to an icosahedron, the volume must be reduced. For FvK numbers below the buckling transition, where the shape remains a sphere, excess defects are expected to be favorable since the volume constraint has little effect and the results should be the same as in the absence of the constraint. However, excess defects are also favorable at FvK numbers above the buckling transition, since the constraint opposes the formation of an icosahedron with perfectly planar facets, highly bent edges, and sharp corners. With changing connectivity, the configurations formed have small clusters of defects located at the edges and corners of the icosahedral shape, which shield the strain from the required fivefold disclinations that would drive the buckling. With a lower affinity for buckling, there is less frustration originating from the volume constraint with excess defects, and the stretching and bending energies are lower.
While systems with and without a volume constraint have similar bending energy profiles, with fixed volume the stretching energy continuously increases through the buckling transition. Without fixing the volume, the stretching energy approaches zero at high FvK numbers, as the morphology approaches a perfect icosahedron with all edges having equal length. By fixing the volume, a perfect icosahedral structure cannot form even though the Young's modulus is very large, and thus the stretching energy penalty becomes correspondingly very large.
Fig. 4 presents plots of total energy, stretching energy, and bending energy from three representative simulations with no volume constraint, at low, moderate, and high FvK numbers: log(γ) = 1.36, 3.36, and 5.36 (with ε = 0.04![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) /l02, 4
/l02, 4![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) /l02, and 400
/l02, and 400![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) /l02, respectively). For each of the three cases, surface plots are used to show the energetic contributions on the membrane surface, while the two-dimensional projection plots show total energy, with the locations of fivefold and sevenfold disclinations marked in red and white, respectively. First, it is clear from the surface renderings that at low FvK numbers a sphere is optimal, at high FvK numbers an icosahedron is optimal, and at FvK numbers near the buckling transition, a shape resembling an icosahedron but with softer edges and corners is optimal. For the low FvK number results shown in Fig. 4a, the bending energy has small fluctuations but is relatively uniform, as the colorbar values cover a small range. The regions with slightly higher bending energy correspond to locations with sevenfold disclinations, with the highest bending energy at single dislocations. There are twelve clusters or scars of defects, and each of these have one more fivefold disclination than sevenfold, and overall tend to give a slightly lower bending energy. The stretching energy is relatively low and uniform, but with spikes located at every disclination regardless of the type. The total energy then reflects that there are spikes at each defect, but they are smaller in locations where there are scars having an extra fivefold disclination.
/l02, respectively). For each of the three cases, surface plots are used to show the energetic contributions on the membrane surface, while the two-dimensional projection plots show total energy, with the locations of fivefold and sevenfold disclinations marked in red and white, respectively. First, it is clear from the surface renderings that at low FvK numbers a sphere is optimal, at high FvK numbers an icosahedron is optimal, and at FvK numbers near the buckling transition, a shape resembling an icosahedron but with softer edges and corners is optimal. For the low FvK number results shown in Fig. 4a, the bending energy has small fluctuations but is relatively uniform, as the colorbar values cover a small range. The regions with slightly higher bending energy correspond to locations with sevenfold disclinations, with the highest bending energy at single dislocations. There are twelve clusters or scars of defects, and each of these have one more fivefold disclination than sevenfold, and overall tend to give a slightly lower bending energy. The stretching energy is relatively low and uniform, but with spikes located at every disclination regardless of the type. The total energy then reflects that there are spikes at each defect, but they are smaller in locations where there are scars having an extra fivefold disclination.
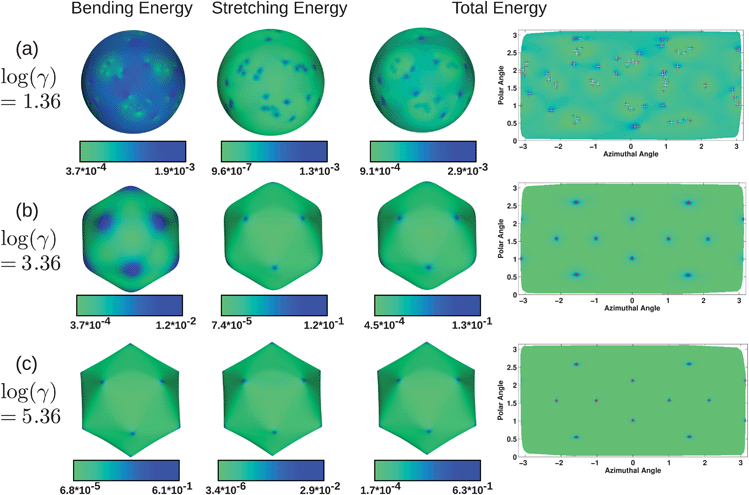 | ||
Fig. 4 Bending, stretching, and total energy in units of ![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) for three systems with no volume constraint, with excess defects at log(γ) = 1.36 (a), and no excess defects with log(γ) = 3.36 (b) and log(γ) = 5.36 (c). Fivefold disclinations are shown in red and sevenfold in white. The right column shows projection plots of the entire surface, showing the same data (total energy) as on the surface in the third column. At different values of the FvK number, the relative contributions from the bending and stretching energies vary. for three systems with no volume constraint, with excess defects at log(γ) = 1.36 (a), and no excess defects with log(γ) = 3.36 (b) and log(γ) = 5.36 (c). Fivefold disclinations are shown in red and sevenfold in white. The right column shows projection plots of the entire surface, showing the same data (total energy) as on the surface in the third column. At different values of the FvK number, the relative contributions from the bending and stretching energies vary. | ||
For the mid-range FvK number results shown in Fig. 4b, the bending energy is largest at the rounded corners of the icosahedron, and gradually decreases toward the centers of the rounded faces. The stretching energy reaches a maximum value that is an order of magnitude larger than the maximum bending energy, and is highly localized at the defects. Since the stretching energy is significantly larger than the bending energy, it dominates the total energy plot, which qualitatively resembles the stretching energy plot although the peaks are slightly more diffuse as a result of the bending energy.
Lastly, for the high FvK number results in Fig. 4c, the maximum bending energy is higher than for either of the other structures at lower FvK numbers, and similarly the minimum bending energy is lowest. This is a result of the almost perfectly planar faces and highly bent corners of the icosahedron. The edges of the icosahedron also have a relatively large bending energy, although it is still small compared to the energy at the corners. The stretching energy has minimum and maximum values that are lower than for the mid-range FvK number case since the stretching caused by the defects is largely relieved by the faceted structure of the icosahedron. The bending now dominates the total energy and the peaks in energy are highly localized where the defects sit, which is where the highly bent corners also reside.
To further illustrate the shapes we observe, Fig. 5 presents surface plots of the membrane networks and two-dimensional projections plotting mean curvature. All of these plots additionally label fivefold and sevenfold disclinations. As was evident in the energy plots in Fig. 4, the defects tend to cluster or line up in scars. While the mean curvature for the system with the lowest FvK number is nearly constant, there are variations correlated with the locations of the defects as was apparent in the bending energy in Fig. 4a. For log(γ) = 3.36 in Fig. 4b, the mean curvature is clearly related to the locations of the defects, where the rounded corners of the icosahedron align with the defects such that each defect is at the center of a region with relatively high mean curvature. Lastly, when log(γ) = 5.36, the range of mean curvature is the largest of all three systems, with very low curvature in the nearly planar faces of the icosahedron, and very high curvature at the corners where the defects are located. In this particular case, some of vertices located precisely at the corners of the icosahedron actually bend the membrane inward, which is why some of the defects marked in red at the corners appear smaller. The system became trapped in this state with slightly crumpled corners; the energy of such a configuration is very similar to that of a perfect icosahedron, although the barrier to switch between the two configurations is very energetically costly and is too large for the Monte Carlo procedure to overcome in a reasonable simulation time.
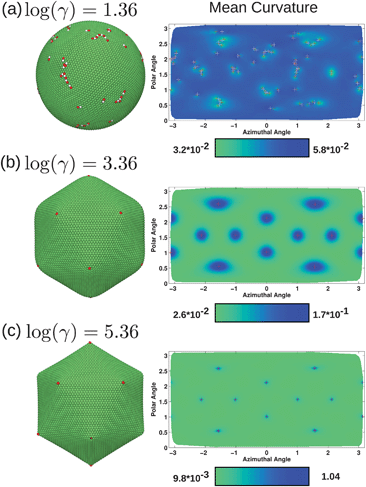 | ||
| Fig. 5 Final configurations and mean curvature in units of l0−1 for three systems with no volume constraint, with excess defects at log(γ) = 1.36 (a), and no excess defects at log(γ) = 3.36 (b) and log(γ) = 5.36 (c). Fivefold disclinations are shown in red and sevenfold in white, on both the surface plots and two-dimensional projections of the surface plotting mean curvature. When excess defects are present, they arrange to form dislocations and lines of defects. As the structure buckles, excess defects are no longer favorable. | ||
4 Conclusions
In this work we have studied how the presence of excess topological defects affects the optimal shapes reached by elastic membranes as a function of their material properties and volume constraint. We also investigated which regions of parameter space favor excess defects. Regarding the first point, we find that permitting changes in connectivity and the presence of excess defects yields the same morphologies as when the connectivity is fixed; in both cases we observe only spheres, icosahedra, and morphologies transitioning between these. We also find that the buckling transition between these shapes is largely unaffected by the presence of excess defects in the optimal structures we observe. While excess defects are found to be energetically favorable in some cases, they are present at a low enough fraction such that the buckling transition can still be characterized by the FvK number as it was in the absence of excess defects. However, when an additional constraint is imposed on the internal volume of the membrane, we observe shapes with a reduced asphericity compared with perfect icosahedra. This is because the imposed volume constraint tends to disfavor deviations from a spherical shape.With no constraint on the internal volume, excess defects are favorable at low FvK numbers up to the onset of the buckling transition. These defects also form lines or scars, similar to those reported in ref. 24 and 26–30. Low FvK numbers correspond to relatively low penalties for stretching, such that the screening effects of the excess defects make them favorable since the stretching energy penalty resulting from their distortion of the lattice is small. In terms of bending energy alone, excess defects are favored for almost the entire range of FvK numbers; it is the stretching energy that causes them to be unfavorable at higher FvK numbers, and it is thus the more influential energetic contribution in determining the stability of excess defects. We note that the current study does not address the very interesting problem of defect dynamics.43–47
We find that fixing the internal volume of the membrane alters the results significantly. Icosahedra that form at high FvK numbers have facets that bulge outward slightly instead of being planar, and the corners have lower curvature (i.e., they appear less sharp). This causes the asphericity to plateau at a lower value than for systems with no volume constraint, since the buckling transition to icosahedral shapes is partially suppressed. The fixed-volume cases also favor excess defects both below and above the buckling transition. Since the buckling transition is driven by the required twelve fivefold disclinations, but is opposed by the fixed volume constraint, the shielding effects of the excess defects are favorable even when buckling occurs. Defects tend to segregate to the corners and edges of the icosahedron, making the morphology less faceted and thus more favorable in the presence of the volume constraint. This finding that the volume constraint affects the favorability of excess defects may have implications for colloidosomes. Since we find that the excess defects are favorable with a constrained volume, if the degree of permeability could be tuned to adjust the amount of defects, the mechanical strength and flexibility of the colloidosome could be adjusted. Colloidosomes have potential for encapsulation in drug delivery, for example, and with control over such mechanical properties, the resistance to mechanical loads or the release of the contents triggered by defined shear rates can be tuned.16
Overall we have found that at low FvK numbers, forming excess defects is the preferred mechanism for relieving the strain associated with the required twelve fivefold disclinations, while at high FvK numbers, bucking is the preferred mechanism. When the internal volume is constrained, the buckled shapes have a reduced asphericity, and defect scars are favorable over a wider range of FvK numbers both above and below the bucking transition.
Acknowledgements
Numerical simulations were performed using the Northwestern University High Performance Computing Cluster Quest. RS and MO acknowledge the financial support of US Department of Energy Award DEFG02-08ER46539. CF and MO were funded by the Office of the Director of Defense Research and Engineering (DDR&E) and the Air Force Office of Scientific Research (AFOSR) under Award no. FA9550-10-1-0167.References
- D. L. D. Caspar and A. Klug, Cold Spring Harbor Symp. Quant. Biol., 1962, 27, 1–24 CrossRef CAS.
- Stuctural Biology of Viruses, ed. W. Chiu, R. M. Burnett and R. L. Garcea, Oxford University Press, New York, 1997 Search PubMed.
- T. O. Yeates, C. A. Kerfeld, S. Heinhorst, G. C. Cannon and J. M. Shively, Nat. Rev. Microbiol., 2008, 6, 681–691 CrossRef CAS.
- C. V. Iancu, D. M. Morris, Z. Dou, S. Heinhorst, G. C. Cannon and G. J. Jensen, J. Mol. Biol., 2010, 396, 105–117 CrossRef CAS.
- M. Dubois, B. Deme, T. Gulik-Krzywicki, J.-C. Dedieu, C. Vautrin, S. Desert, E. Perez and T. Zemb, Nature, 2001, 411, 672–675 CrossRef CAS.
- M. A. Greenfield, L. C. Palmer, G. Vernizzi, M. Olvera de la Cruz and S. I. Stupp, J. Am. Chem. Soc., 2009, 131, 12030–12031 CrossRef CAS.
- D. R. Nelson, T. Piran and S. Weinberg, Statistical Mechanics of Membranes and Surfaces, World Scientific Singapore, 2nd edn, 2004 Search PubMed.
- T. A. Witten and H. Li, Europhys. Lett., 1993, 23, 51 CrossRef.
- J. Lidmar, L. Mirny and D. R. Nelson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 051910 CrossRef.
- C. A. Haselwandter and R. Phillips, Phys. Rev. Lett., 2010, 105, 228101 CrossRef.
- C. A. Haselwandter and R. Phillips, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 061901 CrossRef.
- G. Vernizzi, R. Sknepnek and M. Olvera de la Cruz, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 4292–4296 CrossRef CAS.
- R. Sknepnek, G. Vernizzi and M. Olvera de la Cruz, Soft Matter, 2012, 8, 636 RSC.
- A. Saric and A. Cacciuto, Soft Matter, 2011, 7, 1874 RSC.
- E. Raspaud, M. Olvera de la Cruz, J. L. Sikorav and F. Livolant, Biophys. J., 1998, 74, 381–393 CrossRef CAS.
- A. D. Dinsmore, M. F. Hsu, M. G. Nikolaides, M. Marquez, A. R. Bausch and D. A. Weitz, Science, 2002, 298, 1006–1009 CrossRef CAS.
- D. J. Srolovitz, S. A. Safran, M. Homyonfer and R. Tenne, Phys. Rev. Lett., 1995, 74, 1779–1782 CrossRef CAS.
- N. Tsapis, E. R. Dufresne, S. S. Sinha, C. S. Riera, J. W. Hutchinson, L. Mahadevan and D. A. Weitz, Phys. Rev. Lett., 2005, 94, 018302 CrossRef CAS.
- S. S. Datta, H. C. Shum and D. A. Weitz, Langmuir, 2010, 26, 18612–18616 CrossRef CAS.
- M. J. Bowick and L. Giomi, Adv. Phys., 2009, 58, 449–563 CrossRef CAS.
- S. Sachdev and D. R. Nelson, J. Phys. C: Solid State Phys., 1984, 17, 5473–5489 CrossRef.
- V. Vitelli, J. B. Lucks and D. R. Nelson, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12323–12328 CrossRef CAS.
- T. Frankel, The Geometry of Physics: An Introduction, Cambridge University Press, 2011 Search PubMed.
- M. J. Bowick, D. R. Nelson and A. Travesset, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 8738 CrossRef CAS.
- H. S. Seung and D. R. Nelson, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 1005–1018 CrossRef.
- A. R. Bausch, M. J. Bowick, A. Cacciuto, A. D. Dinsmore, M. F. Hsu, D. R. Nelson, M. G. Nikolaides, A. Travesset and D. A. Weitz, Science, 2003, 299, 1716–1718 CrossRef CAS.
- T. Einert, P. Lipowsky, J. Schilling, M. J. Bowick and A. R. Bausch, Langmuir, 2005, 21, 12076–12079 CrossRef CAS.
- P. Lipowsky, M. J. Bowick, J. H. Meinke, D. R. Nelson and A. R. Bausch, Nat. Mater., 2005, 4, 407–411 CrossRef CAS.
- W. T. M. Irvine, V. Vitelli and P. M. Chaikin, Nature, 2010, 468, 947–951 CrossRef CAS.
- T. Kohyama and G. Gompper, Phys. Rev. Lett., 2007, 98, 198101 CrossRef.
- V. Vitelli and A. M. Turner, Phys. Rev. Lett., 2004, 93, 215301 CrossRef.
- A. Hexemer, V. Vitelli, E. J. Kramer and G. H. Fredrickson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 051604 CrossRef CAS.
- L. Giomi and M. J. Bowick, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 010601 CrossRef.
- T. Kohyama, D. M. Kroll and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 061905 CrossRef CAS.
- A. Siber, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 061915 CrossRef.
- L. D. Landau and E. M. Lifshitz, Theory of Elasticity, Butterworth-Heinemann, London, 3rd edn, 1995 Search PubMed.
- B. Audoly and Y. Pomeau, Elasticity and Geometry – From Hair Curls to the Non-linear Response of Shells, Oxford University Press, Oxford, UK, 2010 Search PubMed.
- B. Schmidt and F. Fraternali, J. Mech. Phys. Solids, 2012, 60, 172 CrossRef.
- G. Gompper and D. M. Kroll, J. Phys. I, 1996, 6, 1305–1320 CrossRef.
- P. B. S. Kumar, G. Gompper and R. Lipowsky, Phys. Rev. Lett., 2001, 86, 3911–3914 CrossRef.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS.
- J. Stone, MSc thesis, Computer Science Department, University of Missouri-Rolla, 1998.
- M. Bowick, H. Shin and A. Travesset, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 021404 CrossRef.
- I. S. Aranson, S. Scheidl and V. M. Vinokur, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 14541–14547 CrossRef CAS.
- M. Karttunen, M. Haataja, K. R. Elder and M. Grant, Phys. Rev. Lett., 1999, 83, 3518–3521 CrossRef CAS.
- P. Sharma and X. Zhang, Phys. Lett. A, 2006, 349, 170–176 CrossRef CAS.
- H. Popova and A. Milchev, J. Chem. Phys., 2008, 129, 215103–215111 CrossRef.
| This journal is © The Royal Society of Chemistry 2013 |
