DOI:
10.1039/C2SM26758F
(Paper)
Soft Matter, 2013,
9, 69-81
Non-lamellae structures of coil–semiflexible diblock copolymers
Received
30th July 2012
, Accepted 21st September 2012
First published on 12th October 2012
Abstract
We investigate the self-assembly of coil–semiflexible block copolymers in 2D positional space by using self-consistent field theory (SCFT) based on the wormlike chain model for the semiflexible block and the Gaussian chain model for the coil block. A highly accurate and efficient operator splitting pseudospectral algorithm is adopted to cope with the computational intricacy of solving modified diffusion equations for the propagators of wormlike chains. Within the framework of anisotropic Maier–Saupe orientational interactions and isotropic Flory–Huggins interactions, the phase diagram including isotropic, smectic-C, and further appended non-lamella structures is constructed for the coil–semiflexible block copolymers in the region of coil volume fractions from 0.6 to 0.8. Hexagonal packed pucks and rhombic pucks formed by the semiflexible block with major orientation perpendicular to their nearest neighbors in the latter are discovered at relatively high coil fractions and strong orientational interactions. We also study the influence of chain rigidity on the phase behavior of coil–semiflexible block copolymers.
I. Introduction
Benefiting from the ability of achieving well-defined long-range ordered nanoscale structures and specific orientational ordering, the self-assembly of coil–semiflexible block copolymers has attracted much attention in recent years for enormous applications in a wide variety of technologies such as organic optoelectronic devices,1–3 nanolithography,4 biotechnology,5–7 and high-performance polymer resins.8 The rigidity of rod-like polymer chains mainly originates from π-conjugation, helical secondary structure, or aromatic groups into polymer blocks. By coupling the microphase separation and orientation interactions, various self-assembled structures can be obtained for coil–semiflexible block copolymers. In the past couple of decades, a number of intriguing phases had been observed in rod–coil block copolymer solution or melts. Chen et al. observed morphologies characterized as ‘wavy’, ‘arrow-head’ and ‘zigzag’ from poly-hexyl isocyanate-polystyrene (PHIC-PS) block copolymers by the solvent-casting technique.9,10 Olsen and Segalman observed a new phase consisting of rectangular rod nanodomains packed onto a hexagonal lattice and a unique order–order transition between hexagonal and lamellar phases in moderately segregated PPV-b-PI (polyalkoxyphenylenevinylene-b-isoprene).11 Besides that, a number of intriguing phases including straight lamellae, perforated lamellae,12 hexagonal stripes,13–15 pucks,14,16 spheres,17,18 cylindrical,19–21 and bicontinuous cubic22–24 were detected in rod–coil block copolymers by using different techniques and experimental facilities.
Technological applications of coil–semiflexible block copolymers strongly depend on their self-assembled nanostructures thus theoretical understanding of their phase behavior is desirable. The self-consistent field theory (SCFT) has proven to be very successful in understanding the thermodynamic equilibrium structures for coil–coil block copolymers based on the Gaussian chain model.25–28 It is natural that the SCFT should be expected as a powerful tool for the self-assembly of block copolymers with chain rigidity. However, its numerical implementations are still far from perfect. Therefore, in this paper, we mainly focus on extending the SCFT theoretical frame to AB diblock copolymers composed of flexible coil block A and semiflexible block B with tunable rigidity. The conformation of semiflexible chains can be described by the wormlike chain model which constrains segments to a constant contour length, L, and weighs the configuration based on the curvature of the segments and a dimensionless bending modulus κ. Within the wormlike chain model, the state of a segment is specified by its position r and orientation u. In this case, the chain conformation requires that the chain propagator q(r,u,s) has two additional internal coordinates describing the segment orientation compared to the propagator q(r,s) in the Gaussian chain model. Several efficient numerical methods have been well established for q(r,s) of the Gaussian chain model,29–31 however, numerical solving of the diffusion equation for the chain propagator of the wormlike chain presents considerable computational challenges due to the extra internal coordinates. To date, the extension of SCFT to rod–coil systems is quite limited and most of those previous studies are based on either further assumptions of complete rigidity or ignorance of orientational interactions between rods.32–34 In our previous works,35,36 we developed a real-space numerical implementation to solve the diffusion equation of q(r,u,s), in which the unit vector u is described on a triangulated unit spherical surface and the angular Laplace operator on q(r,u,s) is calculated using a finite volume method.37 We studied in detail the liquid crystalline (LC) phases including isotropic, nematic, smectic-A, smectic-C, and with the help of high-performance GPU devices, we explored the phase diagram of the coil–semiflexible block copolymer in 2D positional space, in which the tetragonally packed non-lamellar phase emerged, under Onsager-type excluded-volume interactions. Furthermore, we reported a study on the self-assembly of coil–semiflexible melt under the Maier–Saupe type orientational potential, instead of the Onsager-type employed previously, and chemical unlike repulsion between rods and coils modeled by Flory–Huggins interactions.38 A hybrid numerical approach is introduced to solve the modified diffusion equations in 1D positional space for coil–semiflexible diblock copolymers. In such cases the properties of thermotropic liquid crystalline can be studied because both of these two enthalpic interactions are temperature dependent, thus it provides more convenient means to understand the phase behavior of block copolymers used in real applications.
The progress of the numerical solution method of SCFT based on the wormlike chain model, namely solution of the diffusion equation with the orientation freedom, has been reviewed in our previous work.35 Very recently, Kumar and Ganesan investigated the phase behavior of coil–semiflexible diblock copolymers with the methodology of self-consistent Brownian dynamics simulation. They use Brownian dynamics simulation to obtain the chain conformations and thus avoid numerical solving of the modified diffusion equations based on the wormlike chain model.39 Jiang and Chen investigated the interfacial properties between isotropic and nematic phases by using SCFT based on the wormlike chain model along with Onsager orientational interaction.40 This work developed an improved numerical method for solving q(r,u,s) by using the stable Crank–Nicholson algorithm, which contains a numerical error of the second order in the step length of the time-like variable s. This method takes advantage of a software package SPHEREPACK involving convenient analysis and synthesis of spherical-harmonics functions and inverted Laplacian on the spherical surface. Later on, they adopted a more accurate split-step pseudospectral numerical algorithm to solve the modified diffusion equations for the chain propagator q(r,u,s) and to investigate the influence of the persistency on the phase diagram.41 Although they assumed that the orientation variable u is axial-symmetric and reduced it to 1D for simplicity, it is still a celebrating improvement for the solution of chain propagator including the segment orientation freedom.
In this paper, we employ a highly efficient and accurate pseudospectral method for solving modified diffusion equations based on the wormlike chain model which combines the operator splitting algorithm and pseudospectral treatment of the orientational Laplacian operator with spherical-harmonic space. In the SCFT model, the coil and semiflexible blocks of the copolymer are described by the Gaussian chain and wormlike chain model respectively, the Maier–Saupe-type potential and Flory–Huggins interactions are used to model the enthalpic energy term like what we did in our previous paper.38 The high numerical stability of this algorithm allows us to perform SCFT calculations in 2D positional space to search non-lamellar ordered LC phases formed by coil–semiflexible diblock copolymers. We specially obtained the non-lamellar phases assembled by coil–semiflexible copolymers and constructed a phase diagram for high asymmetric composition conditions with the coil composition fA ≥ 0.6.
II. Theoretical model and numerical algorithm
We model coil–semiflexible diblock copolymers as a combination of a flexible coil block A with NA segments of a statistical segment length a, and a semiflexible block B with NB segments of a statistical length b and a diameter d. The SCFT model is considered for incompressible melt with n such AB diblock copolymer chains occupying a volume V. The volume fractions of coil and semiflexible blocks are thus fA = NA/(NA + NB) and fB = 1 − fA, respectively. The theoretical framework is the same as our previous paper for the SCFT model of the coil–semiflexible diblock copolymers,38 however the current paper adopts more accurately and efficiently numerical solution of the diffusion equation for the chain propagator of semiflexible blocks. Therefore we only briefly present the SCFT equations of the system as follows:| | | wA(r) = χNϕB(r) + ξ(r) | (1) |
| | | wB(r) = χNϕA(r) + ξ(r) | (2) |
| | 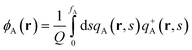 | (3) |
| | 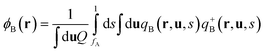 | (4) |
| | 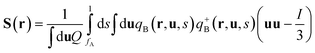 | (5) |
where ϕA(r) and ϕB(r) are local volume fractions of the coil and semiflexible segments. χ is the Flory–Huggins interaction parameter describing the isotropically chemical unlike interactions between segments A and B and μ is the Maier–Saupe-type anisotropic orientation interaction which favors the alignment of the segments with chain rigidity. Q is the partition function of a single chain under an external potential resulting from other interaction polymer chains and wA(r) and wB(r) are the external fields exerted on the coil and semiflexible species. The local orientational order parameter tensor S(r) and the corresponding self-consistent field M(r) are spatial dependent, symmetric and traceless, 3 × 3 matrices. ξ is a Lagrange multiplier that ensures the incompressibility of the melt. The partition function Q is calculated as 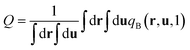 , where the chain propagators qA(r,s) and qB(r,u,s) are the probability density of finding the s-th segment from the coil end s = 0 at position r and with the segment orientation u for qB(r,u,s). They satisfy modified diffusion equations:
, where the chain propagators qA(r,s) and qB(r,u,s) are the probability density of finding the s-th segment from the coil end s = 0 at position r and with the segment orientation u for qB(r,u,s). They satisfy modified diffusion equations:| | 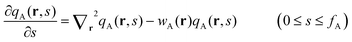 | (8) |
| | 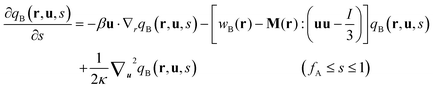 | (9) |
with the initial conditions qA(r,0) = 1 and qB(r,u,fA) = qA(r,fA). Similarly a set of conjugate propagators q+A(r,s) and q+B(r,u,s) also satisfy eqn (8) and (9), where s starts from the semiflexible end s = 1 with the initial conditions of q+B(r,u,1) = 1 and 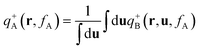 . In the above expressions, all spatial lengths are scaled by the radius of gyration of the diblock copolymer chains, Rg = a(N/6)1/2. A parameter β = bN/a(N/6)1/2 is introduced to describe the size asymmetry between the two blocks. Moreover, the bending modulus κ = λ/L is introduced to weigh the chain's rigidity, where λ is the persistence length over which the orientation of a polymer persists and L is the constrained chain contour length. The Helmholtz free energy of the system in the unit of nkBT (with kB being the Boltzmann constant) can be given by:
. In the above expressions, all spatial lengths are scaled by the radius of gyration of the diblock copolymer chains, Rg = a(N/6)1/2. A parameter β = bN/a(N/6)1/2 is introduced to describe the size asymmetry between the two blocks. Moreover, the bending modulus κ = λ/L is introduced to weigh the chain's rigidity, where λ is the persistence length over which the orientation of a polymer persists and L is the constrained chain contour length. The Helmholtz free energy of the system in the unit of nkBT (with kB being the Boltzmann constant) can be given by:| | 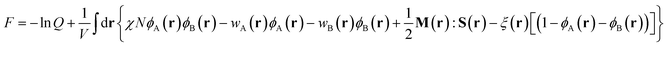 | (10) |
Eqn (1)–(7) constitute a set of SCFT equations describing the equilibrium state of self-assembled coil–semiflexible diblock copolymers. The solving procedure is standard: randomly generates wA(r), wB(r) and S(r) to obtain the chain propagator qA(r,s), q+A(r,s), qB(r,u,s) and q+B(r,u,s) by solving modified diffusion eqn (8) and (9). Subsequently the densities ϕA(r) and ϕB(r) viaeqn (4) and (5) were calculated and the fields wA(r), wB(r) and S(r) with the new density were updated. This procedure repeats until the difference between two successive fields, |wnewi(r) − woldi(r)| < 10−5 (i = A, B), i.e., the energy and field of the system are self-consistent.
In fact, solving the modified diffusion equation (eqn (9)) to obtain the chain propagators qB(r,u,s) and q+B(r,u,s) is the most time consuming and difficult step. Here we specifically employ the operator splitting pseudospectral method for semiflexible blocks, which has been proven as an efficient and accurate way for the chain propagators qA(r,s) and q+A(r,s) of Gaussian chains.42 Formally, eqn (9) can be solved by integrating along the contour variable from s to s + Δs.43
| | qB(r,u,s + Δs) = exp(Δs![[script L]](https://www.rsc.org/images/entities/char_e144.gif) )qB(r,u,s) )qB(r,u,s) | (11) |
where the linear operator is split into three parts
![[script L]](https://www.rsc.org/images/entities/char_e144.gif)
=
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) W
W +
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) C
C +
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) D
D: potential term
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) W
W = −[
wB(
r) −
M(
r):(
uu −
I/3)], advective term
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) C
C = −
βu·∇
r and diffusive term
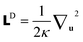
. Then it is straightforward to show
eqn (11) by explicit Taylor expansion in
eqn (12)| | qB(r,u,s + Δs) = exp(0.5Δs![[script L]](https://www.rsc.org/images/entities/char_e144.gif) W)exp(0.5Δs W)exp(0.5Δs![[script L]](https://www.rsc.org/images/entities/char_e144.gif) C)exp(Δs C)exp(Δs![[script L]](https://www.rsc.org/images/entities/char_e144.gif) D)exp(0.5Δs D)exp(0.5Δs![[script L]](https://www.rsc.org/images/entities/char_e144.gif) C)exp(0.5Δs C)exp(0.5Δs![[script L]](https://www.rsc.org/images/entities/char_e144.gif) W)qB(r,u,s) + O(Δs3) W)qB(r,u,s) + O(Δs3) | (12) |
Obviously, the advantage of this method is that the error only amounts to an order of Δs3 or higher. To implement this solving strategy, we need to find ways to apply ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) W,
W, ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) C and
C and ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) D operators to qB(r,u,s) numerically. In the pseudospectral algorithm developed by Rasmussen and Kalosakas44 for solving eqn (8), the operator exp(−0.5Δsw(r)) is applied in real space and exp(Δs∇r2) is applied to q(r,s) in Fourier space separately. This method is known to be unconditionally stable and highly accurate, allowing a relatively large time step length Δs. This pseudospectral method can be easily immigrated to our problems.
D operators to qB(r,u,s) numerically. In the pseudospectral algorithm developed by Rasmussen and Kalosakas44 for solving eqn (8), the operator exp(−0.5Δsw(r)) is applied in real space and exp(Δs∇r2) is applied to q(r,s) in Fourier space separately. This method is known to be unconditionally stable and highly accurate, allowing a relatively large time step length Δs. This pseudospectral method can be easily immigrated to our problems. ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) C and
C and ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) D are diagonals in Fourier representation and spherical harmonic representation respectively, thus eqn (12) can be solved by the following 5 steps:
D are diagonals in Fourier representation and spherical harmonic representation respectively, thus eqn (12) can be solved by the following 5 steps:
| | qBn+1/5 = exp(0.5Δs![[script L]](https://www.rsc.org/images/entities/char_e144.gif) W)qBn W)qBn | (13) |
| | qBn+2/5 = ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) −1[(cos(0.5Δsβu·ik) + isin(0.5Δsβu·ik)) −1[(cos(0.5Δsβu·ik) + isin(0.5Δsβu·ik))![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) (qBn+1/5)] (qBn+1/5)] | (14) |
| | 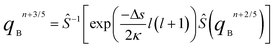 | (15) |
| | qBn+4/5 = ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) −1[(cos(0.5Δsβu·ik) + isin(0.5Δsβu·ik)) −1[(cos(0.5Δsβu·ik) + isin(0.5Δsβu·ik))![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) (qBn+3/5)] (qBn+3/5)] | (16) |
| | qBn+1 = exp(0.5Δs![[script L]](https://www.rsc.org/images/entities/char_e144.gif) W)qBn+4/5 W)qBn+4/5 | (17) |
where the operator
![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif)
denotes the Fourier forward transform converting a function in spatial (real space
r) description into associated Fourier space
k and
![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) −1
−1 denotes the corresponding inverse Fourier transform turning a function in the Fourier space
k into real space
r. Similarly,
Ŝ and
Ŝ−1 denote spherical harmonic analysis and synthesis for a function in the real space
u(
θ,
φ) and its associated spherical harmonic space
lm.
This scheme was originally proposed by Fredrickson43 in 2006 but was implemented in 2011.41 By taking advantage of free software packages FFTW45 and SPHEREPACK,46eqn (9) can be solved efficiently with an overall operation count O(MrMlat2Mlonlog Mlon), where Mr is a spatial discrete grid points number, Mlat and Mlon are the latitude and longitude discrete grid points number on a unit spherical surface. In this paper we will implement this operator splitting pseudospectral method in 2D spatial variation of polymer density to further explore phase behavior of coil–semiflexible block copolymers including the non-lamellar structure. The 2D space is denoted by the yz plane with Ly × Lz lattice points with periodic boundary conditions in y− and z− directions. We minimize the free energy F with respect to both Ly and Lz to eliminate the energy penalty caused by the constraint of simulation box size. The final stable phase structure is thus determined as the one having the lowest free energy independent of the initial conditions. The spatial discretization is specified by Δy = Δz = 0.1Rg and the contour discretization as Δs = 0.01 to ensure that the phase structure is reliable. In this way, a 2D space phase diagram is constructed in the fA–χN plane. The computation is performed on Lenovo R510 clusters with Intel Xeon E5420 CPUs, and a typical calculation with Mr = 64 × 64, Mu = 11 × 20, and N = 100 takes about 16 hours to reach the solution convergence (5 × 103 iterations).
III. Results and discussion
This paper focuses on the phase behavior of coil–semiflexible diblock copolymers dependent on the parameters including isotropic Flory–Huggins interaction parameter χN, anisotropic Maier–Saupe interaction μN, coil volume fraction fA, geometry asymmetry parameter β and chain rigidity parameter κ related to the persistence length of the semiflexible block κ = λ/L. To intuitively compare with our previous work,38 we specify the ratio of μ and χ as μ/χ = 4, i.e. μ and χ have the fixed scaling ratio relationship with temperature T. The rigidity parameter of the semiflexible block is fixed to κ = 10 in the current article except special explanation. The phase diagram with calculation of composition inhomogeneity in 1D positional space under this parameter set was shown in our previous paper38 by using a hybrid numerical algorithm to solve SCFT equations for the semiflexible chain. In this article we are more interested in 2D morphologies that occurred in asymmetric composition diblock copolymers. In our explored parameters, non-lamellae structures can possibly emerge in the range from fA = 0.6 to fA = 0.8. Different LC phases can be distinguished in terms of two order parameters: the position-dependent densities ϕA(r) and ϕB(r) and the orientational order parameters for the semiflexible block ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) 2,v(r) characterizing the orientational structure:
2,v(r) characterizing the orientational structure:| | 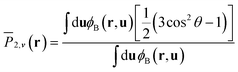 | (18) |
where θ is the angle between a segment axis and the arbitrarily specified statistical orientation direction v. We also compute a scalar orientational order parameter: 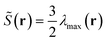 to quantify the overall degree of orientational order, where λmax(r) is the maximum eigenvalue corresponding to eigenvector vmax(r) (denoting the orientational direction) of the orientation tensor S(r)/ϕB(r).
to quantify the overall degree of orientational order, where λmax(r) is the maximum eigenvalue corresponding to eigenvector vmax(r) (denoting the orientational direction) of the orientation tensor S(r)/ϕB(r). ![[S with combining tilde]](https://www.rsc.org/images/entities/b_char_0053_0303.gif) (r) varies from 0 indicating perpendicular orientation to 1 indicating completely ordered alignment and 0 indicating free of orientation. To further illustrate the detailed structure of LC phases, the density distribution for the segment at s along the chain, in terms of the spatial position r, irrespective of the orientation of the segment u, φ(r,s) is given as:
(r) varies from 0 indicating perpendicular orientation to 1 indicating completely ordered alignment and 0 indicating free of orientation. To further illustrate the detailed structure of LC phases, the density distribution for the segment at s along the chain, in terms of the spatial position r, irrespective of the orientation of the segment u, φ(r,s) is given as:| | 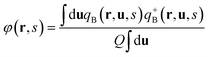 | (19) |
A. Puck phase
In comparison to the flexible chains, the configuration of wormlike chains depends not only on the location of segments, but also on the orientation directions of the mesogens. We can predict the conformation of wormlike chains in an equilibrium state via analyzing orientation of LC blocks and density distributions of specific segments including the free end of the semiflexible block, and the conjunction point of coil and semiflexible blocks based on the SCFT simulations. The blocks with relatively high rigidity tend to pack parallel or antiparallel to the nematic direction n to relieve the steric constraint. Therefore many phases which are common in the self-assembly of coil–coil block copolymers such as sphere and bicontinuous phases47 are not observed for the coil–semiflexible system, but instead various layered structures with specific chain orientation are found.35 When LC blocks form the non-continuous phase like the puck domain, the arrangement of rod blocks is a topic of great interest and has not yet been understood perfectly. In this section, we try to reveal the regime and inside details of self-assembled coil–semiflexible block copolymers through our 2D SCFT calculations.
We observe the puck phase at high values of χN for relatively high coil volume fractions in the phase diagram. Fig. 1a shows a typical puck phase in a one-unit-cell calculation box with width (ly = 5.8Rg) and height (lz = 3.4Rg) under fA = 0.7, χN = 14 and β = 4. The puck phase in Fig. 1a is very similar to the hexagonal cylinder (HC) phase without orientational order self-assembled by coil–coil block copolymers. The puck shape formed by the semiflexible block in the coil matrix is elliptical but with almost same lengths of major and minor axes. The angle Θ between two primitive vectors of the Bravais lattice marked a1 and a2 in Fig. 1a is 119.1°, and the magnitude ratio is |a1|/|a2| = 0.98. This structure is thus very close to the hexagonal lattice, however its C6 symmetry is reduced by the anisotropic pucks with C2 symmetry. We approximately denote this phase as hexagonal puck (HP). In our previous paper,35 we found another type of non-lamellar phase with tetragonal packing elliptical pucks of the C2mm group in the coil matrix under the Onsager excluded-volume interaction. Similar puck phases with bigger ratio of long to short axis occurred at high asymmetric composition in previous theoretical works.32,48 In this case the interfacial energy of the system is higher than that of HP in Fig. 1a. In these works, the block is completely a rigid rod, and hence the orientational packing of the rigid segments dominates leading to the puck phase with strongly anisotropic shape bearing high stretching entropy penalty of the coil blocks. However, in our current work the configuration adjusting of the semiflexible blocks allows us to form compromised structures which can release both the coil-stretching energy and packing frustration of semiflexible blocks. A hexagonally packed phase of rectangular nanodomains in the coil matrix was found at high coil fractions and high geometrical asymmetry between rods and coils in the rod–coil (PPV-b-PI) system experimentally found by Olsen and Segalman.11 It should be noticed that in their experiments the rods are oriented randomly with quite low orientation degree due to weak orientational interaction between rigid blocks whereas Flory–Huggins unlike interaction between rods and coils dominates the assembly, resulting in the microphase segregated morphology more like that observed in coil–coil self-assembly. In contrast, the orientational order parameter distribution ![[S with combining tilde]](https://www.rsc.org/images/entities/b_char_0053_0303.gif) (r) in Fig. 1b exhibits a quite strong orientation degree in semiflexible block domains, indicating that the semiflexible blocks are highly orientated along the nematic director n. Therefore, another question is raised: is it possible for semiflexible blocks with high chain rigidity ordering to form an almost circular shape without suffering expensive bending energy?
(r) in Fig. 1b exhibits a quite strong orientation degree in semiflexible block domains, indicating that the semiflexible blocks are highly orientated along the nematic director n. Therefore, another question is raised: is it possible for semiflexible blocks with high chain rigidity ordering to form an almost circular shape without suffering expensive bending energy?
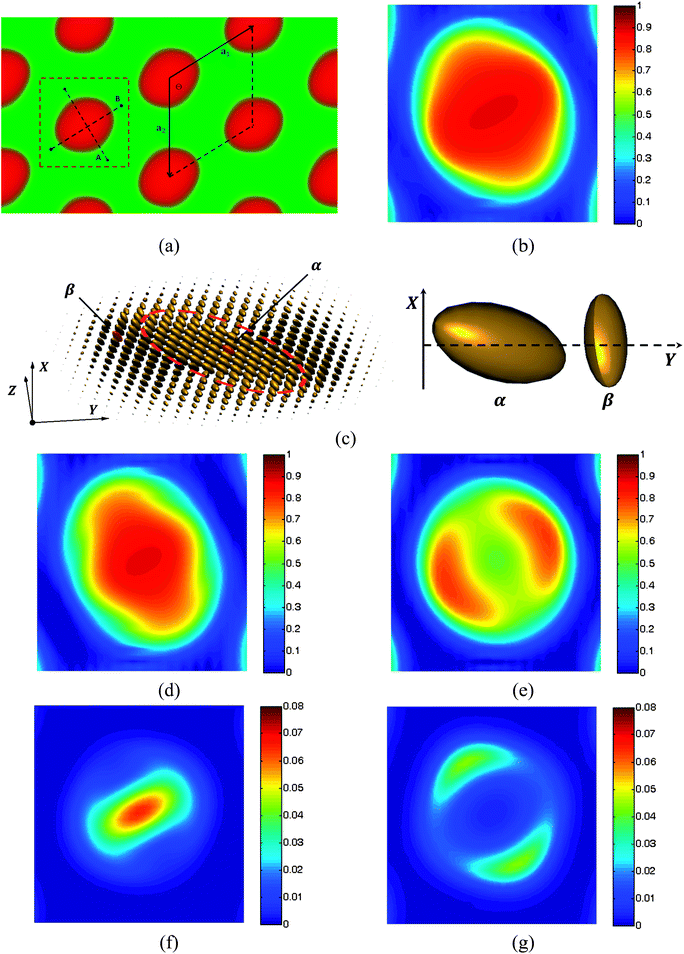 |
| | Fig. 1 (a) Representative hexagonal packed rod pucks in a coil matrix at coil volume fraction fA = 0.7 for χN = 14, μN = 56 and β = 4, where red and green colors represent semiflexible blocks and coil blocks, respectively. The linear dimensions of the unit cell are replicated two times in each direction for clear presentation. Dashed line A shows the nematic direction at point α and line B is perpendicular to line A. (b) Orientation degree of the semiflexible blocks, 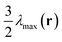 . (c) Visualization of tensor field S(r) by plotting the Gaussian ellipsoids.55 The orientation of the ellipsoid is determined by the eigenvectors of the two-order tensor and the magnitude of the three axes of each ellipsoid is controlled by the eigenvalues. (d) Orientation degree of the semiflexible blocks, . (c) Visualization of tensor field S(r) by plotting the Gaussian ellipsoids.55 The orientation of the ellipsoid is determined by the eigenvectors of the two-order tensor and the magnitude of the three axes of each ellipsoid is controlled by the eigenvalues. (d) Orientation degree of the semiflexible blocks, ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) 2,vmax(rα)(r), which counted along major eigenvector at point α; (e) 2,vmax(rα)(r), which counted along major eigenvector at point α; (e) ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) 2,vmax(rβ)(r) counted along major eigenvector at point β. (f) Segment density distributions at the semiflexible terminal φ(r,s = 1) and (g) at the coil–semiflexible junction φ(r,s = fA). The area shown in (b–f) corresponds to that inside the red dashed square in (a). 2,vmax(rβ)(r) counted along major eigenvector at point β. (f) Segment density distributions at the semiflexible terminal φ(r,s = 1) and (g) at the coil–semiflexible junction φ(r,s = fA). The area shown in (b–f) corresponds to that inside the red dashed square in (a). | |
Our 2D SCFT calculations enable us to study the detailed structure of the puck phase for understanding the formation of such phase for coil–semiflexible block copolymers. We visualized the tensor field S(r) in Fig. 1c to demonstrate the orientational information of the semiflexible blocks inside the puck domain. It is found that the orientation directions are not uniform in space. In the center of the puck, namely the shuttle-like area denoted by the dashed circle in Fig. 1c, the orientation direction is clearly different from that in the side parts. We use the nematic directions nα and nβ on the points α (representing the center area of the puck) and β (representing the side area) in Fig. 1c, to represent the directions of the two areas inside the puck, respectively. The eigenvector of S(r) on α and β are vmax(rα) = (0.547,0.40,0.737) and vmax(rβ) = (0.908,0.164,0.393), and the angle between them is about 32°. Furthermore, the orientational degree distribution ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) 2,v(r) counted along nα and nβ according to eqn (18) is shown in Fig. 1d and e. From these figures, we could see that the highly orientated area in Fig. 1d is slimmer than that in Fig. 1b and two crescent areas with high orientational degree occur in Fig. 1e, which is complementary to Fig. 1d. This result is consistent with Fig. 1c. Furthermore, the segment density of the semiflexible block terminal, φ(r,s = 1), has a peak in the center of the puck, as shown in Fig. 1f, and the coil–semiflexible conjunction points, φ(r,s = fA) are mainly aggregated in the poles of the shuttle as shown in Fig. 1g, further confirming the above mentioned structure of semiflexible blocks in the puck.
2,v(r) counted along nα and nβ according to eqn (18) is shown in Fig. 1d and e. From these figures, we could see that the highly orientated area in Fig. 1d is slimmer than that in Fig. 1b and two crescent areas with high orientational degree occur in Fig. 1e, which is complementary to Fig. 1d. This result is consistent with Fig. 1c. Furthermore, the segment density of the semiflexible block terminal, φ(r,s = 1), has a peak in the center of the puck, as shown in Fig. 1f, and the coil–semiflexible conjunction points, φ(r,s = fA) are mainly aggregated in the poles of the shuttle as shown in Fig. 1g, further confirming the above mentioned structure of semiflexible blocks in the puck.
Profiles of density and orientation degree and segments density along lines A and B are shown in Fig. 2a and b as a quantitative confirmation of Fig. 1d–g. The line A is in the direction of the projection of nα on the yz plane, which is recognized as the nematic direction of the puck and also the major axis of the ellipse, and the line B is perpendicular to A and denoted as the minor axis of the ellipse. It is seen that the width of the puck in the line A direction is 1.83Rg (measured with full-width-half-maximum, FWHM), which is about one time larger than the projection length of the semiflexible block in the calculation plane, 1.2Rg × cos θ = 0.97Rg (θ = 36.7° is the angle between vmax(rα) and the yz plane). The orientational order parameter counted along nβ shows two peaks at the two ends of line B as shown in Fig. 2a, illustrating the difference of orientation direction between point β and the center of the puck. Fig. 2b shows that the segment density φ(r,s) for s = 1,fA,0.5 + 0.5fA corresponding to the semiflexible terminals, the junction of two blocks, and the mid-point of semiflexible blocks, respectively. φ(r,s = fA) and φ(r,s = 0.5 + 0.5fA) show two peaks along line A separated by a distance of 1.9Rg and 0.9Rg, respectively, and φ(r,1) has only one maxima in the center of the puck. Combining this result with the above discussed orientation direction in the center of the puck, we conclude that semiflexible blocks form a shuttle-like area of bilayer smectic-C in the center of the puck, along with two crescent shaped areas of nematic orientated along nβ aside of the center. We thus figure the segment arrangement scheme of the puck formed by coil–semiflexible diblock copolymers in Fig. 2c for intuitive understanding. Several possible schemes were also proposed by Williams and Fredrickson49 in 1992 and the stabilities of those structures were calculated analytically. The arrangement scheme proposed in Fig. 2c is more likely a modified bilayer puck model defined in ref. 48. This structure is driven by minimizing the coil stretching entropy penalty while releasing packing frustration of semiflexible segments with high rigidity. We should note that the arrangement scheme is just a prediction under 2D situation. Very recently Kriksin and Khalatur50 proposed several novel 3D structures assembled by coil–rigid rod diblock copolymers including hexagonally (HEX) packed chiral columnar phase, zigzag-like phases, etc., by performing a SCFT calculation. This greatly encourages us to explore such phases and we are working on parallel algorithms and hope to do systematical 3D space calculations in further studies.
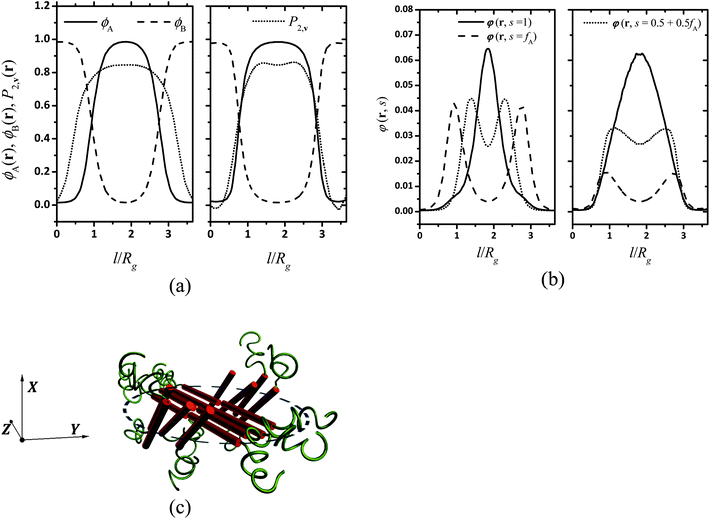 |
| | Fig. 2 Profiles of (a) density and orientation degree and (b) segments density for a puck domain corresponding to Fig. 1a along line A (shown on the left-hand side) and line B (shown on the right-hand side). The orientational order parameters ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) 2,v(r) in (a) on the left and right side are counted in directions nα and nβ, respectively. Line A is the projection of nα on the yz plane, which is recognized as the nematic direction of the puck and also the major axis of the ellipse, and line B is perpendicular to A. (c) Schematic representation of segments arrangement in a single puck domain (marked as a blue circle) suggested by Fig. 1c–g. 2,v(r) in (a) on the left and right side are counted in directions nα and nβ, respectively. Line A is the projection of nα on the yz plane, which is recognized as the nematic direction of the puck and also the major axis of the ellipse, and line B is perpendicular to A. (c) Schematic representation of segments arrangement in a single puck domain (marked as a blue circle) suggested by Fig. 1c–g. | |
A circle-like phase in 2D and its corresponding cylinder-like phase in 3D are much more complicated for coil–semiflexible block copolymers because the aggregation of rods has packing anisotropy. The formation of the puck phase determined by the interfacial energy, the entropic penalty of coil stretching and rods packing energy refers to four terms of information: the shape, size, relative position and intersection angle of semiflexible-rich aggregates. The former three are discussed in detail by Matsen in ref. 52, but the last one is a special issue for coil–semiflexible block copolymer aggregates. Alignment of semiflexible blocks breaks the symmetry of cylinder phase and leads to the distribution of conjunction points of two components around the puck, i.e., the possibility of joint point of coil and semiflexible blocks is high near the center as shown in Fig. 1f and g, thus changing the space requirement of coils in different directions. Consequently the optimized packing strategy should include not only the size and position of pucks but also the relative angle between the major directions. Intuitively we find that the most favorable packing strategy is either puck with all major axes (such as nα in Fig. 1) parallel to each other (HP), as shown in Fig. 1a, or with major axes perpendicular to their nearest neighbors (R90P) as shown in Fig. 3a. This feature of R90P can be demonstrated using the quiver image as shown in Fig. 3b, in which the vectors are the projection of vmax(r) on the yz plane and their magnitudes are equal to the ![[S with combining tilde]](https://www.rsc.org/images/entities/b_char_0053_0303.gif) (r). It is clear that the major axes of two nearest neighbor pucks are perpendicular to each other. It should also be noticed that the long-range packing structure of R90P is not hexagonal, instead with a rhombic packing structure of the P2gg group in a centered rectangular lattice. Thus we name this phase as rhombic puck (R90P), and the principle of this change will be discussed as follows. The segment alignment of semiflexible blocks in R90P is also in agreement with that in Fig. 2e. Similar phenomena were also observed for flexible block copolymers by Li and coworkers who discussed the interaction between chiral helixes with different rotation degrees in the double helices-on-cylinder (H2C) phase formed by ABC triblock copolymers.51 The interplay between helixes induced by chain frustration is similar to the current case, and from their work, we see that the free energy of Ha2C phases with different rotations of the hexagonal helical supercylinders is different. The stability comparison between HP and R90P phases will be shown later and we also calculated the phase diagram region they occupied in Section B.
(r). It is clear that the major axes of two nearest neighbor pucks are perpendicular to each other. It should also be noticed that the long-range packing structure of R90P is not hexagonal, instead with a rhombic packing structure of the P2gg group in a centered rectangular lattice. Thus we name this phase as rhombic puck (R90P), and the principle of this change will be discussed as follows. The segment alignment of semiflexible blocks in R90P is also in agreement with that in Fig. 2e. Similar phenomena were also observed for flexible block copolymers by Li and coworkers who discussed the interaction between chiral helixes with different rotation degrees in the double helices-on-cylinder (H2C) phase formed by ABC triblock copolymers.51 The interplay between helixes induced by chain frustration is similar to the current case, and from their work, we see that the free energy of Ha2C phases with different rotations of the hexagonal helical supercylinders is different. The stability comparison between HP and R90P phases will be shown later and we also calculated the phase diagram region they occupied in Section B.
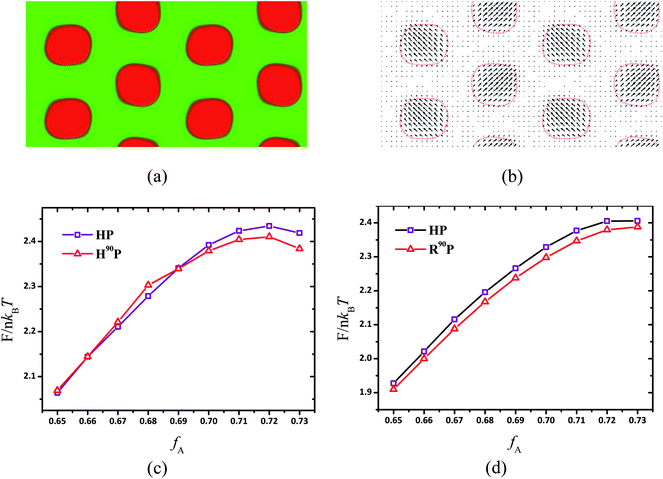 |
| | Fig. 3 (a) R90P phase obtained at fA = 0.7 for χN = 16, μN = 64 and β = 10, where the red and green colors represent semiflexible and coil blocks, respectively. The linear dimensions of the unit cell are replicated two times in each direction for clear presentation. (b) Quiver scheme of major eigenvector vmax(r) and the arrow direction and length represent the direction of projection of vmax(r) on the yz plane and the value of major eigenvalue λmax(r), respectively. Free energy F in the units of nkBT as a function of fA for HP (open square) and H90P (open triangle) phase at χN = 12, μN = 48 for β = 4 (c) and for β = 10 (d). | |
B. Phase diagram
We constructed the phase diagrams of coil–semiflexible diblock copolymers in the plane of χN versus the volume fraction of coil block fA under β = 4 as shown in Fig. 4a and β = 10 as shown in Fig. 4b. For each certain fixed composition, the final stable phase is determined as the one having the lowest free energy by comparing the free energy of various phases including isotropic, smectic-C, HP and R90P phases. The symbols in Fig. 4 represent the calculated transition points, and the transition lines separating two different phases are simply a guide for the eyes. As a supplement to our previous 1D phase diagram only layered structure included,38 we only vary fA from fA = 0.6 to fA = 0.8 in which non-lamellar phases occur. Moreover, we did not distinguish mono-layer and bilayer smectic phases in this article because these issues were systematically discussed in our previous work.38 In the phase diagrams, typical LC phases are obtained including isotropic, smectic-C and especially non-lamellar puck phase by taking advantage of our 2D SCFT calculations with full 3D orientation u taken into consideration. In Fig. 4, phase transitions including isotropic to smectic-C, isotropic to puck, and puck to smectic-C are observed, which is in agreement with previous theoretical and experimental works.11,49 As expected, a significant difference between 2D and 1D phase diagrams is in the region with large values of χN for relatively high coil fractions occupied by the non-lamellar phase. When χN increases, isotropic to HP and isotropic to R90P transition is obtained like the isotropic to hexagonal cylinder transition in coil–coil diblock copolymers at asymmetric composition.
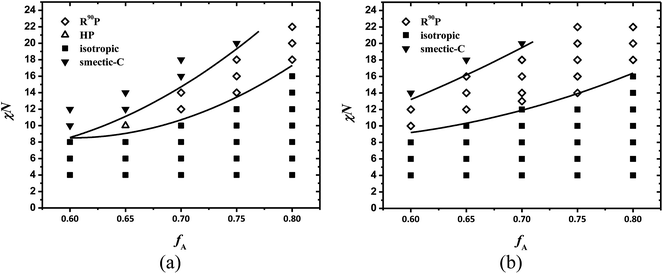 |
| | Fig. 4 Phase diagrams of coil–semiflexible diblock copolymers in the fA–χN plane at μ/χ = 4. The solid lines are a guide to the eye. (a) β = 4 and (b) β = 10. | |
The case of β = 4: in this case, the isotropic-smectic-C boundary intersects with the puck one at critical volume fraction fA,crit = 0.65. The isotropic–puck transition occurs at χN = 10 for fA,crit = 0.65, and rises as fA increases. For larger χN, the smectic-C phase appears in the region of 0.65 ≤ fA ≤ 0.75. The order–disorder transition (ODT) line in Fig. 4a is significantly lower when compared with coil–coil diblock copolymers, as denoted in previous theoretical works,41,52 in which both blocks have the same rigidity. Like coil–coil diblock copolymers, the emergence of the puck phase is mainly driven by favoring high spontaneous curvature for asymmetrical composition of diblock copolymers. The orientational interaction between semiflexible blocks just transforms the circle like domain into ellipse with the rods packing as shown in Fig. 2c.
The HP phase only emerges in the region of 0.65 ≤ fA < 0.7 and changes to R90P as fA increases. The free energy comparison of these two phases under parameters χN = 12, μN = 48 and β = 4 is shown in Fig. 3c. When fA < 0.7, the HP is more favorable with the free energy slightly lower than R90P, and for fA ≥ 0.7, the R90P phase is more stable and the energy difference ΔF between HP and R90P phase becomes larger as fA increases. This transition is mainly induced by the stretching entropy effect of the coils. As we discussed above, the pucks formed by semiflexible blocks are anisotropic in shape and the conjunction points of coil and semiflexible blocks are distributed inhomogeneously around the puck. Obviously coils near the puck poles (such as the ends of line A in Fig. 1a) are more concentrated, thus the space requirements in this direction are more urgent than those in the minor axis (line B in Fig. 1a) direction of the puck. The R90P phase can make use of the space more efficiently by allowing the coil-concentrated poles of the pucks to interlace with each other to relieve the packing frustration. This can be proven by our calculations, e.g., the optimal size of the unit cell is 5.8Rg × 3.0Rg for the R90P phase whereas 5.8Rg × 3.4Rg for the HP phase, under fA = 0.7, χN = 14 and β = 4, indicating that coils are less stretched in the structure of R90P. Meanwhile, as a result of chain-packing optimization of coils, the Bravais lattice of the R90P phase is no longer hexagonal but rectangular instead. Thus the HP phase occurs under relatively low coil fraction in which phase segregation is dominated by enthalpy effects and the R90P phase occurs at high coil volume fractions because stretching entropy of coils plays a key role.
The case of β = 10: the phase behavior of coil–semiflexible block copolymers can be strongly influenced by the geometry asymmetry parameter β. Comparing with the phase diagram for β = 4, the puck area is remarkably enlarged for diblock copolymers with β = 10. The fA,crit decreases to fA < 0.6 while the ODT boundary remains in the region of 0.65 ≤ fA ≤ 0.8. The puck to smectic-C boundary moves higher as β is enlarged, resulting in the puck area being very close to the area of the hexagonal cylinder phase for coil–coil diblock copolymers. This phenomenon is reasonable. The domain size of self-assembled structures, including lamellar phases like smectic-C and non-lamellar phases like the puck, is highly related to the length and shape of semiflexible blocks, especially for chains with quite large rigidity under the current conditions. The packing consideration of the longer rigid blocks forces the system to adopt morphologies with large period, in which coils are stretched. The greater entropy penalty of coils leads to the formation of structures with larger spontaneous curvature like puck, rather than smectic phases. This can also be verified with the size comparison between puck phases with different values of β. The size of the calculation box with one R90P unit under fA = 0.7, χN = 14 and μN = 56 is 5.8Rg × 3.0Rg for β = 4, whereas 8.2Rg × 4.0Rg for β = 10, which is significantly larger in size than the previous one. It is clear that in the case of large β, the larger domain size of the structures leads to a greater conformational entropy loss of coils and tends to the formation of non-lamellar phases.
Another difference from the chain stretching effect of coils in the phase diagram for β = 10 is that all puck phase is R90P rather than HP in the case of β = 4. The free energy comparison of these two phases for a series of fA under χN = 12, μN = 48 and β = 10 is presented in Fig. 3b, which clearly shows that the free energy of the R90P phase is significantly lower than HP. Furthermore, we confirm the isotropic to puck transition order by examining the free energy variation vs. χN at fA = 0.7 as shown in Fig. 5a and b for β = 4 and β = 10, respectively. From Fig. 5, as χN increases, the free energy of the isotropic phase increases linearly while that of the puck phase decreases. A notable discontinuous point emerges at the phase transition, indicating a first order phase transition like most disorder–order phase transitions for the liquid crystalline system. In the system with large β, the conformational entropy penalty of coils dominates the free energy of the system, while the interfacial enthalpy penalty is negligible. This will bring about many unexpected changes to the phase diagrams of coil–semiflexible block copolymers. The parameter β is experimentally determined not only by its polymerization degree but also by the shape of the monomers of the copolymers. This result indicates that understanding the self-assembled structures of coil–semiflexible block copolymers should also take the influence of geometrical asymmetry of two blocks into consideration.
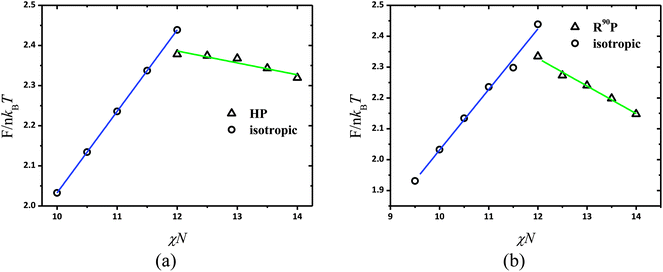 |
| | Fig. 5 Free energy F in the units of nkBT at fA = 0.7 according to SCFT calculations for isotropic (open circle) and puck (open triangle) phases as a function of χN. (a) β = 4 and (b) β = 10. | |
C. Influence of κ on the phase diagram
Due to the computational intricacy, it is difficult to obtain a full 5-dimensional (χN, μN, fA, κ, β) phase diagram for the self-assembly of coil–semiflexible copolymers completely. As discussed above, we fix the rigidity module of the semiflexible blocks to κ = 10, namely a quite large rigid semiflexible block, to focus on the effect of the temperature (χN and μN) and the size asymmetry ratio β on the liquid crystalline behavior of coil–semiflexible copolymers. In fact, the rigidity, i.e. the persistent length in current work, also plays an important role in the self-assembled procedure. In our theoretical framework, the wormlike chain model is employed to describe the semiflexible polymer blocks, and thus the chain rigidity can be considered directly. The diagrams of coil–semiflexible diblock copolymers with rigidity near the flexible limit (κ = 0.02 ≪ 1), and intermediate rigidity κ = 0.2 and κ = 0.4 and β = 10 in the region of 0.2 ≤ fA ≤ 0.8 are constructed as shown in Fig. 6a–c, respectively.
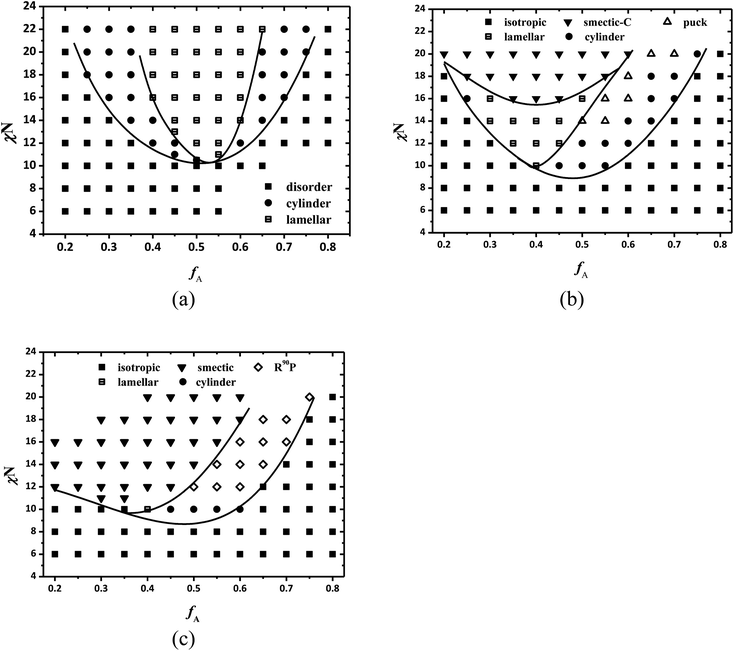 |
| | Fig. 6 Phase diagrams of semiflexible diblock copolymers with various rigidities in the fA–χN plane at β = 10 for (a) κ = 0.02, (b) κ = 0.2 and (c) κ = 0.4. Smectic-A and smectic-C phases are not distinguished in this diagram and the solid lines are a guide to the eye. | |
In the case of small rigidity (κ = 0.02), the calculated phase diagram almost perfectly reproduces that of coil–coil diblock copolymers based on the Gaussian chain model. The ODT occurs at χN ≈ 10.7 under symmetric composition which is very close to the RPA prediction of χN = 10.5 for coil–coil diblock copolymers.53 The boundary of disorder to hexagonal cylinder transition and hexagonal cylinder to lamellae transition is approximately symmetric about fA = 0.5. As the rigidity increases, the LC phases like smectic-C and the puck phase which are discussed above also appear in the phase diagram for κ = 0.2 when segregation intensity is strong. The phase behavior of the copolymers becomes more complicated under the medium rigidity condition. As can be seen in Fig. 6b, the ordered non-LC phases including lamellae and hexagonal cylinder exist when χN and thus μN (enthalpic interactions) are relatively small, and their transitions to LC phases, e.g. cylinder to puck, lamellae to smectic-C, are also observed as χN increases. This indicates that the assembled structures can switch between ordered isotropic phases and anisotropic LC phases by adjusting the temperature, remarkably enriching the phase structures assembled from block copolymers with some degree of chain rigidity. With larger persistence length of the semiflexible block, the lamellar phase is more favored for B-rich component, thus the phase diagram shows high asymmetry and the hexagonal packed coil cylinders in the semiflexible matrix almost disappear in the phase diagram. For larger rigidity (κ = 0.4), the phase behavior tends to approach coil–rod block copolymers. The semiflexible-rich area in the phase diagram is mainly occupied by smectic phases and the R90P phase appears in the non-lamellar region at relatively large χN instead of the hexagonally packed cylinder phase.
The persistence length influences the self-assembly of coil–semiflexible block copolymers from two aspects: the arrangement of semiflexible segments and the conformation entropy contribution of semiflexible blocks to the free energy of the system. It is intuitive for the first issue that as κ increases, the packing consideration of semiflexible blocks restrains the system to form morphologies similar to those detected in coil–rigid rod block copolymers, e.g. smectic-A or smectic-C, puck, which has been widely discussed both theoretically and experimentally. The latter issue is reduced for block copolymers with two blocks of the same chain rigidities because the ratio of conformational entropy of two blocks is only controlled by fA, and is mostly ignored for the coil–rod system because the conformational entropy of rods is negligible when compared with that of coils. However, in the current case the change of conformation entropy term of semiflexible blocks will lead to two special observations in the phase diagrams. Firstly, in Fig. 6b, the cylindrical morphology in which semiflexible block forms the non-continuous phase appears even for fA ≤ 0.5. This phase which is quite similar to hexagonal cylinders with high constant mean curvature is driven by minimizing the packing frustration of the majority component.54 In the current situation the conformation entropy of semiflexible blocks is significantly lower than its flexible counterpart due to its rigidity even though its volume fraction is over 0.5. Therefore, there is no reverse cylindrical phase (cylinders formed by semiflexible blocks) found in the diagram. It is a unique phenomenon and a similar issue was also indicated by Kumar and Ganesan.39
Secondly, the critical χN, (χN)*, at which LC behavior starts to appear, has a minimum point in the phase diagram when κ = 0.2, while (χN)* is monotonically proportional to fA in the case of relatively large κ. The clear point temperature is determined by the competition between conformational entropy of semiflexible blocks and the Maier–Saupe potential. It is obvious that for rod-like polymers, of which persistence length λ ≫ L and thus conformational entropy is negligible, the clear point temperature will rise as fA decreases due to the dominated Maier–Saupe-type anisotropic interactions. However, it is different in the case of coil–semiflexible copolymers with intermediate rigidities. The entropy penalty caused by uniform alignment, i.e. LC, becomes more pronounced as fA decreases for semiflexible blocks with a given relatively small λ. Consequently a minimum (χN)* is determined by the balance of the contribution of conformational entropy and Maier–Saupe potential to the free energy. Fig. 6 and 4a qualitatively demonstrate the influence of the persistence length upon the self-assembled morphologies of diblock copolymers. The calculation denotes that coil–semiflexible diblock copolymers with the same component volume fractions but different molecular weights can have totally different assembled performances.
We also demonstrate the equilibrium structures under fA = 0.6, χN = 10 and β = 10 for copolymers with κ = 0.2, κ = 0.4 and κ = 10, respectively as shown in Fig. 7 as an example. We find that when the semiflexible blocks are relatively flexible (κ = 0.2 and κ = 0.4), non-liquid crystal structures including isotropic and HC phase free of orientation emerge, and the phase behavior is similar to the coil–coil block system. However, even though there is no pronouncing liquid crystalline behavior in such situation, the rigidity still contributes to the phase segregation strength. The ODT is lowered as the rigidity κ is increased from 0.2 to 0.4. As expected, the critical point (χN)* of the emergence of LC behavior also reduces for larger κ = 10.
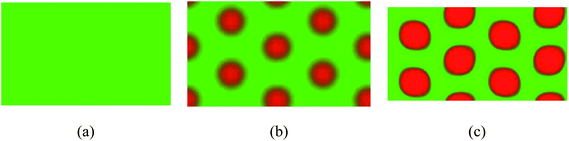 |
| | Fig. 7 Coil–semiflexible block copolymers self-assemble into different structures such as isotropic in (a), HC in (b) and R90P in (c) by varying the rigidity of block B under fA = 0.6, χN = 10 and β = 10. Red and green colors represent the semiflexible and coil components. (a) κ = 0.2; (b) κ = 0.4; (c) κ = 10. | |
IV. Conclusion
In this work, we study the phase behavior of coil–semiflexible diblock copolymers by adopting the SCFT framework based on the wormlike chain and Gaussian chain models for describing the semiflexible and coil blocks, respectively. An operator splitting algorithm is implemented to cope with the computational intractability for the numerical solution of the modified diffusion equations for five-dimensional chain propagator q(r,u,s) in 2D position (r) space. The self-assembly of coil–semiflexible copolymers depends on Flory–Huggins interactions χN, anisotropic orientational Maier–Saupe-type interactions μN, coil volume fraction fA, size asymmetry parameter β, and chain rigidity parameter κ. We mainly focus on non-lamellar phases assembled by diblock copolymers with asymmetric composition. Two novel puck phases, in which semiflexible blocks are phase segregated as hexagonal packed elliptical islands, are observed in a relatively high coil fraction region of the 2D phase diagram. Both the morphology and the long term ordering of puck phases are investigated in detail and a reasonable arrangement scheme of semiflexible blocks inside the puck meets the requirements of both minimization of the interface and ordered alignments of semiflexible blocks. Phase diagrams including non-lamellar structures are constructed as a function of the coil volume fraction fA and Flory–Huggins interaction parameter χN in the region of 0.6 ≤ fA ≤ 0.8 for different values of β, which plays an important role in the phase behavior. In general, large β tends to form the puck phase with the coils being more stretched, whereas small β prefers layered structures. The isotropic to non-lamellar transition is also confirmed as a first order transition which is consistent with previous experimental and theoretical reports.11,35 Moreover, we demonstrate the significant changes of the phase behaviors of coil–semiflexible block copolymers caused by tuning chain rigidity κ from near the flexible limitation (κ = 0.02) to the intermediate region (κ = 0.2 and κ = 0.4). This calculation further supplements the understanding of the self-assembly of coil–semiflexible block copolymers in 5-dimensional (fA, χN, μN, κ, β) parameter space.
Acknowledgements
We thank financial support from the National Basic Research Program of China (grant no. 2011CB605700). Funds from the NSF of China (grant no. 20990231 and 91127033) are also acknowledged.
References
- R. A. Segalman, B. McCulloch, S. Kirmayer and J. J. Urban, Macromolecules, 2009, 42, 9205–9216 CrossRef CAS.
- X. Yang and J. Loos, Macromolecules, 2007, 40, 1353–1362 CrossRef CAS.
- J. S. Liu, E. Sheina, T. Kowalewski and R. D. McCullough, Angew. Chem., Int. Ed., 2001, 41, 329–332.
- Z. H. Nie and E. Kumacheva, Nat. Mater., 2008, 7, 277–290 CrossRef CAS.
- J. C. M. van Hest, Polym. Rev., 2007, 47, 63–92 Search PubMed.
- J. Huang, C. W. P. Foo and D. L. Kaplan, Polym. Rev., 2007, 47, 29–62 Search PubMed.
- A. J. Simnick, D. W. Lim, D. Chow and A. Chilkoti, Polym. Rev., 2007, 47, 121–154 Search PubMed.
- Y. Pae and F. W. Harris, J. Polym. Sci., Part A: Polym. Chem., 2000, 38, 4247–4257 CrossRef CAS.
- J. T. Chen, E. L. Thomas, C. K. Ober and G. P. Mao, Science, 1996, 273, 343–346 CrossRef CAS.
- J. T. Chen, E. L. Thomas, C. K. Ober and S. S. Hwang, Macromolecules, 1995, 28, 1688–1697 CrossRef CAS.
- B. D. Olsen and R. A. Segalman, Macromolecules, 2007, 40, 6922–6929 CrossRef CAS.
- M. Lee, B. K. Cho, H. Kim, J. Y. Yoon and W. C. Zin, J. Am. Chem. Soc., 1998, 120, 9168–9179 CrossRef CAS.
- K. K. Tenneti, X. Chen, C. Y. Li, Y. Tu, X. Wan, Q. Zhou, I. Sics and B. S. Hsiao, J. Am. Chem. Soc., 2005, 127, 15481–15490 CrossRef CAS.
- J. Ryu, N. Oh, W. Zin and M. Lee, J. Am. Chem. Soc., 2004, 126, 3551–3558 CrossRef CAS.
- C. Y. Li, K. K. Tenneti, D. Zhang, H. Zhang, X. Wan, E. Chen, Q. Zhou, A. Carlos, S. Igos and B. S. Hsiao, Macromolecules, 2004, 37, 2854–2860 CrossRef CAS.
- B. K. Cho, Y. W. Chung and M. Lee, Macromolecules, 2005, 38, 10261–10265 CrossRef CAS.
- N. Sary, L. Rubatat, C. Brochon, G. Hadziioannou and R. Mezzenga, Macromol. Symp., 2008, 268, 28–32 CrossRef CAS.
- N. Sary, C. Brochon, G. Hadziioannou and R. Mezzenga, Eur. Phys. J. E: Soft Matter Biol. Phys., 2007, 24, 379–384 Search PubMed.
- C. Dai, W. Yen, Y. Lee, C. Ho and W. Su, J. Am. Chem. Soc., 2007, 129, 11036–11038 CrossRef CAS.
- X. L. Chen and S. A. Jenekhe, Macromolecules, 2000, 33, 4610–4612 CrossRef CAS.
- J. G. Wang, G. P. Mao, C. K. Ober and E. J. Kramer, Macromolecules, 1997, 30, 1906–1914 CrossRef CAS.
- M. Lee, B. K. Cho, Y. S. Kang and W. C. Zin, Macromolecules, 1999, 32, 7688–7691 CrossRef CAS.
- M. Lee, B. Cho, H. Kim, J. Yoon and W. Zin, J. Am. Chem. Soc., 1998, 120, 9168–9179 CrossRef CAS.
- M. Lee, B. K. Cho, H. Kim and W. C. Zin, Angew. Chem., Int. Ed., 1998, 37, 638–640 CrossRef CAS.
- E. Helfand, J. Chem. Phys., 1975, 62, 999–1005 CrossRef CAS.
- E. Helfand and A. M. Sapse, J. Chem. Phys., 1975, 62, 1327–1331 CrossRef CAS.
- E. Helfand and Y. Tagami, J. Chem. Phys., 1972, 57, 1812–1813 CrossRef.
- E. Helfand and Y. Tagami, J. Polym. Sci., Part B: Polym. Lett., 1971, 9, 741–746 CrossRef CAS.
- R. B. Thompson, K. O. Rasmussen and T. Lookman, J. Chem. Phys., 2004, 120, 31–34 CrossRef CAS.
- F. Drolet and G. H. Fredrickson, Phys. Rev. Lett., 1999, 83, 4317–4320 CrossRef CAS.
- M. W. Matsen and M. Schick, Phys. Rev. Lett., 1994, 72, 2660–2663 CrossRef CAS.
- V. Pryamitsyn and V. Ganesan, J. Chem. Phys., 2004, 120, 5824–5838 CrossRef CAS.
- W. Li and D. Gersappe, Macromolecules, 2001, 34, 6783–6789 CrossRef CAS.
- M. W. Matsen and C. Barrett, J. Chem. Phys., 1998, 109, 4108–4118 CrossRef CAS.
- J. Gao, W. Song, P. Tang and Y. Yang, Soft Matter, 2011, 7, 5208–5216 RSC.
- W. D. Song, P. Tang, H. D. Zhang, Y. L. Yang and A. C. Shi, Macromolecules, 2009, 42, 6300–6309 CrossRef CAS.
- P. Tang, F. Qiu, H. Zhang and Y. Yang, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 16710 Search PubMed.
- W. D. Song, P. Tang, F. Qiu, Y. L. Yang and A. C. Shi, Soft Matter, 2011, 7, 929–938 RSC.
- N. A. Kumar and V. Ganesan, J. Chem. Phys., 2012, 136, 101101 Search PubMed.
- Y. Jiang and J. Z. Y. Chen, Macromolecules, 2010, 43, 10668–10678 CrossRef CAS.
- Y. Jiang, W. Zhang and J. Z. Y. Chen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 41803 Search PubMed.
- G. Tzeremes, K. O. Rasmussen, T. Lookman and A. Saxena, Phys. Rev. E, 2002, 65, 1777–1783 Search PubMed.
-
G. H. Fredrickson
2006
.
- K. O. Rasmussen and G. Kalosakas, J. Polym. Sci., Part B: Polym. Phys., 2002, 40, 1777–1783 CrossRef CAS.
- M. Frigo and S. G. Johnson, Proc. IEEE, 2005, 93, 216–231 CrossRef.
- J. C. Adams and P. N. Swarztrauber, Mon. Weather Rev., 1999, 127, 1872–1878 Search PubMed.
- M. W. Matsen, J. Phys.: Condens. Matter, 2002, 14, R21–R47 CrossRef CAS.
- G. Yang, P. Tang, Y. Yang and Q. Wang, J. Phys. Chem. B, 2010, 114, 14897–14906 CrossRef CAS.
- D. R. M. Williams and G. H. Fredrickson, Macromolecules, 1992, 25, 3561–3568 CrossRef CAS.
- Y. A. Kriksin and P. G. Khalatur, Macromol. Theory Simul., 2012, 21, 382–399 Search PubMed.
- W. Li, F. Qiu and A. Shi, Macromolecules, 2011, 45, 503–509 Search PubMed.
- M. W. Matsen, J. Chem. Phys., 1996, 104, 7758–7764 CrossRef CAS.
- L. Leibler, Macromolecules, 1980, 13, 1602–1617 CrossRef CAS.
- M. W. Matsen and F. S. Bates, J. Chem. Phys., 1997, 106, 2436–2448 CrossRef CAS.
- A. Barmpoutis, B. C. Vemuri, T. M. Shepherd and J. R. Forder, IEEE Trans. Med. Imag., 2007, 26, 1537–1546 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2013 |
Click here to see how this site uses Cookies. View our privacy policy here. 
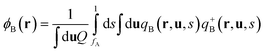
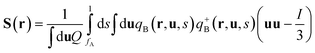
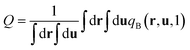 , where the chain propagators qA(r,s) and qB(r,u,s) are the probability density of finding the s-th segment from the coil end s = 0 at position r and with the segment orientation u for qB(r,u,s). They satisfy modified diffusion equations:
, where the chain propagators qA(r,s) and qB(r,u,s) are the probability density of finding the s-th segment from the coil end s = 0 at position r and with the segment orientation u for qB(r,u,s). They satisfy modified diffusion equations: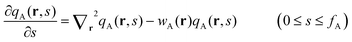
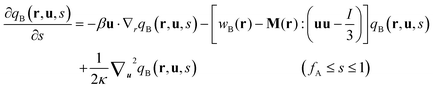
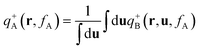 . In the above expressions, all spatial lengths are scaled by the radius of gyration of the diblock copolymer chains, Rg = a(N/6)1/2. A parameter β = bN/a(N/6)1/2 is introduced to describe the size asymmetry between the two blocks. Moreover, the bending modulus κ = λ/L is introduced to weigh the chain's rigidity, where λ is the persistence length over which the orientation of a polymer persists and L is the constrained chain contour length. The Helmholtz free energy of the system in the unit of nkBT (with kB being the Boltzmann constant) can be given by:
. In the above expressions, all spatial lengths are scaled by the radius of gyration of the diblock copolymer chains, Rg = a(N/6)1/2. A parameter β = bN/a(N/6)1/2 is introduced to describe the size asymmetry between the two blocks. Moreover, the bending modulus κ = λ/L is introduced to weigh the chain's rigidity, where λ is the persistence length over which the orientation of a polymer persists and L is the constrained chain contour length. The Helmholtz free energy of the system in the unit of nkBT (with kB being the Boltzmann constant) can be given by: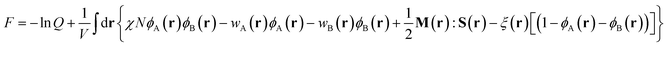
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) )qB(r,u,s)
)qB(r,u,s)![[script L]](https://www.rsc.org/images/entities/char_e144.gif) =
= ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) W +
W + ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) C +
C + ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) D: potential term
D: potential term ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) W = −[wB(r) − M(r):(uu − I/3)], advective term
W = −[wB(r) − M(r):(uu − I/3)], advective term ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) C = −βu·∇r and diffusive term
C = −βu·∇r and diffusive term 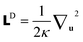 . Then it is straightforward to show eqn (11) by explicit Taylor expansion in eqn (12)
. Then it is straightforward to show eqn (11) by explicit Taylor expansion in eqn (12)![[script L]](https://www.rsc.org/images/entities/char_e144.gif) W)exp(0.5Δs
W)exp(0.5Δs![[script L]](https://www.rsc.org/images/entities/char_e144.gif) C)exp(Δs
C)exp(Δs![[script L]](https://www.rsc.org/images/entities/char_e144.gif) D)exp(0.5Δs
D)exp(0.5Δs![[script L]](https://www.rsc.org/images/entities/char_e144.gif) C)exp(0.5Δs
C)exp(0.5Δs![[script L]](https://www.rsc.org/images/entities/char_e144.gif) W)qB(r,u,s) + O(Δs3)
W)qB(r,u,s) + O(Δs3)![[script L]](https://www.rsc.org/images/entities/char_e144.gif) W,
W, ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) C and
C and ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) D operators to qB(r,u,s) numerically. In the pseudospectral algorithm developed by Rasmussen and Kalosakas44 for solving eqn (8), the operator exp(−0.5Δsw(r)) is applied in real space and exp(Δs∇r2) is applied to q(r,s) in Fourier space separately. This method is known to be unconditionally stable and highly accurate, allowing a relatively large time step length Δs. This pseudospectral method can be easily immigrated to our problems.
D operators to qB(r,u,s) numerically. In the pseudospectral algorithm developed by Rasmussen and Kalosakas44 for solving eqn (8), the operator exp(−0.5Δsw(r)) is applied in real space and exp(Δs∇r2) is applied to q(r,s) in Fourier space separately. This method is known to be unconditionally stable and highly accurate, allowing a relatively large time step length Δs. This pseudospectral method can be easily immigrated to our problems. ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) C and
C and ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) D are diagonals in Fourier representation and spherical harmonic representation respectively, thus eqn (12) can be solved by the following 5 steps:
D are diagonals in Fourier representation and spherical harmonic representation respectively, thus eqn (12) can be solved by the following 5 steps:![[script L]](https://www.rsc.org/images/entities/char_e144.gif) W)qBn
W)qBn![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) −1[(cos(0.5Δsβu·ik) + isin(0.5Δsβu·ik))
−1[(cos(0.5Δsβu·ik) + isin(0.5Δsβu·ik))![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) (qBn+1/5)]
(qBn+1/5)]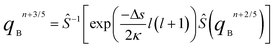
![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) −1[(cos(0.5Δsβu·ik) + isin(0.5Δsβu·ik))
−1[(cos(0.5Δsβu·ik) + isin(0.5Δsβu·ik))![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) (qBn+3/5)]
(qBn+3/5)]![[script L]](https://www.rsc.org/images/entities/char_e144.gif) W)qBn+4/5
W)qBn+4/5![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) denotes the Fourier forward transform converting a function in spatial (real space r) description into associated Fourier space k and
denotes the Fourier forward transform converting a function in spatial (real space r) description into associated Fourier space k and ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) −1 denotes the corresponding inverse Fourier transform turning a function in the Fourier space k into real space r. Similarly, Ŝ and Ŝ−1 denote spherical harmonic analysis and synthesis for a function in the real space u(θ,φ) and its associated spherical harmonic space lm.
−1 denotes the corresponding inverse Fourier transform turning a function in the Fourier space k into real space r. Similarly, Ŝ and Ŝ−1 denote spherical harmonic analysis and synthesis for a function in the real space u(θ,φ) and its associated spherical harmonic space lm.
![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) 2,v(r) characterizing the orientational structure:
2,v(r) characterizing the orientational structure: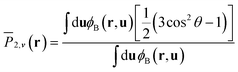
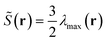 to quantify the overall degree of orientational order, where λmax(r) is the maximum eigenvalue corresponding to eigenvector vmax(r) (denoting the orientational direction) of the orientation tensor S(r)/ϕB(r).
to quantify the overall degree of orientational order, where λmax(r) is the maximum eigenvalue corresponding to eigenvector vmax(r) (denoting the orientational direction) of the orientation tensor S(r)/ϕB(r). ![[S with combining tilde]](https://www.rsc.org/images/entities/b_char_0053_0303.gif) (r) varies from 0 indicating perpendicular orientation to 1 indicating completely ordered alignment and 0 indicating free of orientation. To further illustrate the detailed structure of LC phases, the density distribution for the segment at s along the chain, in terms of the spatial position r, irrespective of the orientation of the segment u, φ(r,s) is given as:
(r) varies from 0 indicating perpendicular orientation to 1 indicating completely ordered alignment and 0 indicating free of orientation. To further illustrate the detailed structure of LC phases, the density distribution for the segment at s along the chain, in terms of the spatial position r, irrespective of the orientation of the segment u, φ(r,s) is given as: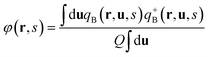
![[S with combining tilde]](https://www.rsc.org/images/entities/b_char_0053_0303.gif) (r) in Fig. 1b exhibits a quite strong orientation degree in semiflexible block domains, indicating that the semiflexible blocks are highly orientated along the nematic director n. Therefore, another question is raised: is it possible for semiflexible blocks with high chain rigidity ordering to form an almost circular shape without suffering expensive bending energy?
(r) in Fig. 1b exhibits a quite strong orientation degree in semiflexible block domains, indicating that the semiflexible blocks are highly orientated along the nematic director n. Therefore, another question is raised: is it possible for semiflexible blocks with high chain rigidity ordering to form an almost circular shape without suffering expensive bending energy?
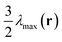 . (c) Visualization of tensor field S(r) by plotting the Gaussian ellipsoids.55 The orientation of the ellipsoid is determined by the eigenvectors of the two-order tensor and the magnitude of the three axes of each ellipsoid is controlled by the eigenvalues. (d) Orientation degree of the semiflexible blocks,
. (c) Visualization of tensor field S(r) by plotting the Gaussian ellipsoids.55 The orientation of the ellipsoid is determined by the eigenvectors of the two-order tensor and the magnitude of the three axes of each ellipsoid is controlled by the eigenvalues. (d) Orientation degree of the semiflexible blocks, ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) 2,vmax(rα)(r), which counted along major eigenvector at point α; (e)
2,vmax(rα)(r), which counted along major eigenvector at point α; (e) ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) 2,vmax(rβ)(r) counted along major eigenvector at point β. (f) Segment density distributions at the semiflexible terminal φ(r,s = 1) and (g) at the coil–semiflexible junction φ(r,s = fA). The area shown in (b–f) corresponds to that inside the red dashed square in (a).
2,vmax(rβ)(r) counted along major eigenvector at point β. (f) Segment density distributions at the semiflexible terminal φ(r,s = 1) and (g) at the coil–semiflexible junction φ(r,s = fA). The area shown in (b–f) corresponds to that inside the red dashed square in (a).![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) 2,v(r) counted along nα and nβ according to eqn (18) is shown in Fig. 1d and e. From these figures, we could see that the highly orientated area in Fig. 1d is slimmer than that in Fig. 1b and two crescent areas with high orientational degree occur in Fig. 1e, which is complementary to Fig. 1d. This result is consistent with Fig. 1c. Furthermore, the segment density of the semiflexible block terminal, φ(r,s = 1), has a peak in the center of the puck, as shown in Fig. 1f, and the coil–semiflexible conjunction points, φ(r,s = fA) are mainly aggregated in the poles of the shuttle as shown in Fig. 1g, further confirming the above mentioned structure of semiflexible blocks in the puck.
2,v(r) counted along nα and nβ according to eqn (18) is shown in Fig. 1d and e. From these figures, we could see that the highly orientated area in Fig. 1d is slimmer than that in Fig. 1b and two crescent areas with high orientational degree occur in Fig. 1e, which is complementary to Fig. 1d. This result is consistent with Fig. 1c. Furthermore, the segment density of the semiflexible block terminal, φ(r,s = 1), has a peak in the center of the puck, as shown in Fig. 1f, and the coil–semiflexible conjunction points, φ(r,s = fA) are mainly aggregated in the poles of the shuttle as shown in Fig. 1g, further confirming the above mentioned structure of semiflexible blocks in the puck.
![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) 2,v(r) in (a) on the left and right side are counted in directions nα and nβ, respectively. Line A is the projection of nα on the yz plane, which is recognized as the nematic direction of the puck and also the major axis of the ellipse, and line B is perpendicular to A. (c) Schematic representation of segments arrangement in a single puck domain (marked as a blue circle) suggested by Fig. 1c–g.
2,v(r) in (a) on the left and right side are counted in directions nα and nβ, respectively. Line A is the projection of nα on the yz plane, which is recognized as the nematic direction of the puck and also the major axis of the ellipse, and line B is perpendicular to A. (c) Schematic representation of segments arrangement in a single puck domain (marked as a blue circle) suggested by Fig. 1c–g.![[S with combining tilde]](https://www.rsc.org/images/entities/b_char_0053_0303.gif) (r). It is clear that the major axes of two nearest neighbor pucks are perpendicular to each other. It should also be noticed that the long-range packing structure of R90P is not hexagonal, instead with a rhombic packing structure of the P2gg group in a centered rectangular lattice. Thus we name this phase as rhombic puck (R90P), and the principle of this change will be discussed as follows. The segment alignment of semiflexible blocks in R90P is also in agreement with that in Fig. 2e. Similar phenomena were also observed for flexible block copolymers by Li and coworkers who discussed the interaction between chiral helixes with different rotation degrees in the double helices-on-cylinder (H2C) phase formed by ABC triblock copolymers.51 The interplay between helixes induced by chain frustration is similar to the current case, and from their work, we see that the free energy of Ha2C phases with different rotations of the hexagonal helical supercylinders is different. The stability comparison between HP and R90P phases will be shown later and we also calculated the phase diagram region they occupied in Section B.
(r). It is clear that the major axes of two nearest neighbor pucks are perpendicular to each other. It should also be noticed that the long-range packing structure of R90P is not hexagonal, instead with a rhombic packing structure of the P2gg group in a centered rectangular lattice. Thus we name this phase as rhombic puck (R90P), and the principle of this change will be discussed as follows. The segment alignment of semiflexible blocks in R90P is also in agreement with that in Fig. 2e. Similar phenomena were also observed for flexible block copolymers by Li and coworkers who discussed the interaction between chiral helixes with different rotation degrees in the double helices-on-cylinder (H2C) phase formed by ABC triblock copolymers.51 The interplay between helixes induced by chain frustration is similar to the current case, and from their work, we see that the free energy of Ha2C phases with different rotations of the hexagonal helical supercylinders is different. The stability comparison between HP and R90P phases will be shown later and we also calculated the phase diagram region they occupied in Section B.




