Graphenylene, a unique two-dimensional carbon network with nondelocalized cyclohexatriene units

Abstract

Over many years chemists have established the general principle that two-dimensional chemical structures constructed with pure sp²-carbon atoms will definitely form an aromatic system with delocalized electron density. However, based on a recently proposed chemical structure, graphenylene, this rule may finally be broken. Herein, we predict the properties of a new two-dimensional sp²-carbon network known as graphenylene, which is the first example of a non-delocalized sp²-carbon structure composed of cyclohexatriene units with two quite distinct C–C bonds within a C6 ring. In addition, theoretical calculations demonstrate that graphenylene has periodic pores of 3.2 Å in diameter and is a semiconductor with a narrow direct band gap, making it promising for various applications, such as electronic devices and efficient hydrogen separation. This study provides a new perspective on carbon allotropes, leading to a better understanding of [N] phenylene based organic frameworks, as well as clarifying the relationship between benzene and cyclohexatriene.

---

Introduction

Besides graphite and diamond, which have already been known for thousands of years, the family of carbon allotropes has suddenly undergone a rapid expansion in recent decades, particularly with the addition of forms such as fullerenes,¹ carbon nanotubes² and graphene.³ With its unique chemical character, carbon can bind with itself or other elements to generate not only countless organic compounds, but also new carbon allotropes. The combination of sp-, sp²- and sp³-hybridized carbon atoms leads to many possible carbon allotropes^4–6 with different dimensionalities.^7–13 Of all of these experimentally obtained or theoretically predicted materials, the family of sp²-carbon allotropes, which include fullerenes, nanotubes and graphene, is the most fascinating and has recently attracted considerable attention owing to their remarkable properties and potential applications in many emerging technologies. However, it is worth noting that fullerene, nanotubes and graphene all possess delocalized π-conjugated bonding such that they have relatively uniform bond lengths and electron distributions. Graphene can be considered as a building unit that can be wrapped up into fullerenes, rolled into carbon nanotubes or stacked into graphite.¹⁴ From a theoretical point of view, all of them are similar carbon networks with the same structural unit. One interesting and scientifically important question is whether sp²-carbon can form alternative networks with a structural unit distinct from that of graphene? To the best of our knowledge, this possibility has been rarely contemplated.

Result and discussion

In the present study, we explore the hypothetical two dimensional sp²-carbon structure dubbed graphenylene, through the use of computational methods based on first-principles density functional theory (DFT, GGA-PBEsol unless stated otherwise). Graphenylene is a two dimensional sp²-carbon network formed by the fusion of hexatomic rings and tetratomic rings. Concurrently with the present work, the structure of graphenylene was proposed in the literature by Balaban and Vollhardt¹⁵ and some properties have been investigated.^16–21 Graphenylene can be obtained by substituting each benzenoid C–C bond and connected two carbon atoms with a biphenylene unit, forming a two dimensional carbon honeycomb network that possesses the same point group, D_6h, as graphene (Fig. 1a and b). The optimized structure of graphenylene in a 2 × 2 supercell is presented in Fig. 1c. After being fully optimized, the lattice parameters of graphenylene are a = b = 6.76 Å and just as for other honeycomb structures, this value is also the distance between the two neighbouring pores. The unit cell of graphenylene contains 12 sp²-hybridized carbon atoms and three different kinds of carbon bonds (Fig. 1c). The most surprising feature is that two bonds in the hexatomic ring have totally different lengths, which are 1.366 and 1.467 Å, respectively. Compared with benzene and graphene, this difference is strong evidence of the presence of alternating single and double bonds, and undoubtedly all hexatomic rings are non-delocalized (i.e. maximally localized) cyclohexatriene units, which is totally different from the bonding characteristics of any other sp²-carbon network reported so far.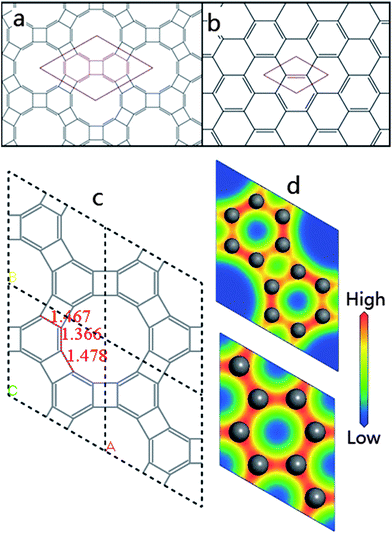

Fig. 1 The two-dimensional structures of (a) graphenylene and (b) graphene are shown. They are both honeycomb structures composed of sp²-carbon networks with the D_6h point group. (c) The 2 × 2 supercell of graphenylene. (d) The electron density in a unit cell of graphenylene and a 2 × 2 supercell of graphene. The electron density is colour coded from red to blue for high to low densities, respectively.

Cyclohexatriene is a commonly used example introduced as the hypothetical model for a bond-fixed benzene ring. Most people consider it as a strictly theoretical model and one that hardly exists in practice. However, in 1986, K. Peter C. Vollhardt reported a new organic compound, the triangular [4] phenylene, which has a completely bond-fixed cyclohexatriene ring at the centre.²² This discovery rectified a misunderstanding of the relationship between benzene and cyclohexatriene. It is confusing because often benzene is drawn as cyclohexatriene although they have totally different structures. Cyclohexatriene is a hexatomic non-aromatic structure with the D_3h point group, while benzene is the archetypal aromatic ring with the D_6h point group. While free-standing cyclohexatriene is unstable, cyclohexatriene units can exist in certain special circumstances, such as when fused with tetratomic rings²³ (ESI, Fig. S2†). The primary differences between cyclohexatriene and benzene are the bond lengths and the electron density. With alternating single and double bonds, cyclohexatriene should exhibit a heterogeneous electron density around its ring. In graphene, the electrons of C–C bonds are distributed equally amongst each of the carbon atoms, such that there are no distinct single or double bonds but instead a delocalized π-bond. This is clearly borne out by the computed electron densities from first-principles calculations, as shown in Fig. 1d. The electron density distribution in graphenylene is indeed totally different from that in graphene, in that there is a clear alternation between adjacent bonds. Clearly, localized double bonds exist in graphenylene, which is evidence that the hexatomic rings are cyclohexatriene units.

In order to examine the stability of graphenylene, the relative total energies per atom of various carbon allotropes have been calculated (Table 1). Here, several different density functionals have been employed in order to examine the sensitivity to this factor. Specifically, we have examined the local density approximation (LDA), the Perdew–Burke–Ernzerhof²⁴ (PBE) generalized gradient approximation (GGA) and its variant parameterized for solids, PBEsol.²⁵ There has already been extensive discussion of the performance of different functionals for the structure, thermodynamics and curvature related properties of diamond and graphite elsewhere.²⁶ Here we avoid the issue of van der Waals interactions by taking graphene as the reference point instead of graphite. Given that theoretical and experimental estimates of the interlayer binding energy in graphite vary from 0.02 to 0.07 eV per atom,²⁷ this is a small correction on the scale of the energy differences between allotropes other than graphite to diamond. Although there are small quantitative variations according to the functional chosen, the trends across the allotropes are unambiguous. Graphenylene is found to be energetically less favourable than graphite, diamond, SWNT[5,5] and C₆₀, but more thermodynamically stable than other predicted carbon allotropes, such as graphyne and carbyne. Furthermore, the phonon dispersion curves for graphenylene (Fig. S1†) demonstrate the absence of any imaginary frequencies, and therefore the structure is a genuine local minimum on the potential energy surface. Given that graphenylene is locally stable and that the degree of thermodynamic instability relative to graphene is only twice that of fullerenes, it is proposed that graphenylene is a novel carbon allotrope that is capable of existing in reality.

Table 1 Total energies per atom relative to graphene for a range of carbon allotropes, as computed with three different density functionals

Relative total energy per atom/eV	Graphene	Diamond	SWNT[5,5]tinm	C60	Graphenylene	Graphyne	Carbyne
LDA	0	−0.02	0.17	0.41	0.69	0.73	1.21
PBE	0	0.14	0.19	0.39	0.64	0.65	1.01
PBEsol	0	0.02	0.17	0.38	0.66	0.70	1.13

---

As a full sp²-carbon structure, graphenylene is expected to have unique electronic properties. Calculations on graphenylene predict a direct and narrow band gap (0.025 eV) with the valence band maximum (VBM) and conduction band minimum (CBM) both located at the K point, as shown in Fig. 2b. Although Kohn–Sham density functional theory calculations usually underestimate the band gap due to self-interaction, and thus the real band gap is almost certainly larger, it remains reasonable to conclude that graphenylene is a semiconductor with a direct band gap. It is well known that graphene is a semi-metal with zero band gap, which hinders its practical application in many important areas.²⁸ On the contrary, graphenylene, with a narrow direct band gap, may be suitable for use in various semiconductor-based devices. In addition, the band gap of graphenylene can also be adjusted in the same manner as for graphene.²⁹ In particular, the edge structure and the width of graphenylene nanoribbons influence its electronic properties significantly. Theoretical calculations demonstrate that the decrease of the width of graphenylene nanoribbons leads to a significant increase of its direct band gap. Compared with an infinite 2-D graphenylene sheet (0.025 eV), the narrowest nanoribbons have a much wider direct band gap approaching 1 eV (Fig. 2c and d). The edge effect is also obvious for the narrowest graphenylene nanoribbons, which show totally different band structures for armchair and zigzag edges (Fig. 2).

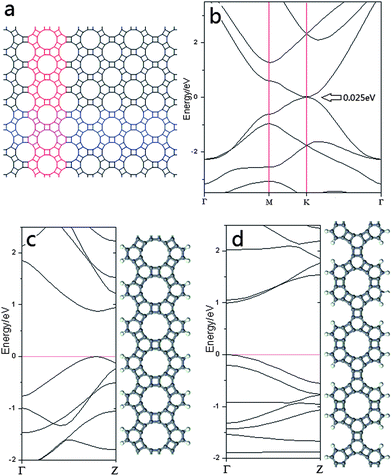Fig. 2 The band structures of graphenylene (b), narrow graphenylene nanoribbons with zigzag edge (c) and armchair edge (d) are shown. The white spheres indicate hydrogen atoms and the grey spheres represent carbon atoms. The Fermi level is assigned as 0 eV. The relationship of the nanoribbons to the periodic graphenylene structure is shown in (a) in which the zigzag and armchair edged ribbons are highlighted in red and blue, respectively.

Interestingly, the specific organization of sp²-carbon atoms makes graphenylene a two-dimensional mesh with periodically distributed pores of 3.2 Å in diameter. This unique structure may render graphenylene as a 2D molecular sieve for gas separation, just like AFI and SSZ-33 (Fig. S3†) and porous graphene.^30,31 Gas separation, especially hydrogen separation, is of particular importance for clean fuel production and usage. Surprisingly, graphenylene may be one of the best candidates for separating H₂ from many other gas molecules, including CO, N₂, CO₂ and CH₄. The pore diameter of 3.2 Å of graphenylene is, in principle, larger than the kinetic diameter of H₂, but smaller than all of the kinetic diameters of CO, N₂, CO₂ and CH₄, which makes the diffusion of these molecules dynamically unfavourable, except for H₂. Calculations demonstrate that H₂ can easily diffuse through graphenylene under experimental conditions with an approximate energy barrier of only 0.20 eV, while other molecules exhibit much larger activation energies for diffusion of 0.99, 1.01, 1.05 and 2.28 eV for CO, N₂, CO₂ and CH₄, respectively. It is possible to estimate the selectivity of graphenylene for gas separation according to the Arrhenius equation (ESI, Table S2†). Compared with traditional gas separation membranes, the selectivity of graphenylene is remarkably high even at room temperature (T = 300 K). For instance, the selectivity for hydrogen separation over methane (H₂/CH₄) can reach 10³⁴. A relatively high selectivity for hydrogen over other gases is also predicted; H₂/CO (10¹²), H₂/CO₂ (10¹³) and H₂/N₂ (10¹⁴) (Table 2). The unique structure and small pore dimensions make graphenylene promising for many other applications, such as highly sensitive gas and ion sensors.

Table 2 Kinetic diameter, diffusion barrier and separation selectivity for different gas molecules

	H2	CO	N2	CO2	CH4
Kinetic diameter/Å	2.89	3.76	3.65	3.30	3.80
Diffusion barrier/eV	0.20	0.99	1.01	1.05	2.28
Separation selectivity at 300 K (H2/G)	1	10^12	10^13	10^14	10^34

---

Conclusions

In summary, graphenylene is a new sp²-carbon network whose properties have been predicted by first-principles calculation. The maximally localized electron density and the direct band gap make graphenylene unique relative to other known sp²-carbon structures. Highly attractive physical and chemical properties are therefore expected. Beside its well-defined pore structure, which is interesting for hydrogen separation and storage, many significant properties may also arise from its electronic behaviour.

Acknowledgements

The authors would like to thank Ali Wang, Yuying Jia and Long Hao for their help and discussions, as well as acknowledging financial support from the National Natural Science Foundation of China (Grant no. 20973044, 21173057), the Ministry of Science and Technology of China (no. 2009DPF41220, no. 2012CB933400, no. 2012CB933403) and the Chinese Academy of Sciences (no. KJCX2-YW-H21). JDG thanks the Australian Research Council for a Professorial Fellowship.

Notes and references

1. H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163.
2. S. Iijima, Nature, 1991, 354, 56–58.
3. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666.
4. H. R. Karfunkel and T. Dressler, J. Am. Chem. Soc., 1992, 114, 2285–2288.
5. F. Diederich and Y. Rubin, Angew. Chem., Int. Ed. Engl., 1992, 31, 1101–1123.
6. A. Hirsch, Nat. Mater., 2010, 9, 868–871.
7. Y. P. Kudryavtsev, R. Heimann and S. Evsyukov, J. Mater. Sci., 1996, 31, 5557–5571.
8. F. Diederich and M. Kivala, Adv. Mater., 2010, 22, 803–812.
9. R. Baughman, J. Chem. Phys., 1987, 87, 6687.
10. G. Li, Y. Li, H. Liu, Y. Guo and D. Zhu, Chem. Commun., 2010, 46, 3256–3258.
11. J. A. Marsden and M. M. Haley, J. Org. Chem., 2005, 70, 10213–10226.
12. X. L. Sheng, Q. B. Yan, F. Ye, Q. R. Zheng and G. Su, Phys. Rev. Lett., 2011, 106, 155703.
13. Q. Li, Y. Ma, A. R. Oganov, H. Wang, Y. Xu, T. Cui, H. K. Mao and G. Zou, Phys. Rev. Lett., 2009, 102, 175506.
14. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191.
15. A. T. Balaban and K. P. C. Vollhardt, Open Org. Chem. J., 2011, 5, 117–126.
16. A. T. Balaban, C. C. Rentea and E. Ciupitu, Rev. Roum. Chim., 1968, 13, 231–247.
17. A. T. Balaban, Comput. Math. Appl., 1989, 17, 397–416.
18. A. T. Balaban, D. J. Klein and C. A. Folden, Chem. Phys. Lett., 1994, 217, 266–270.
19. H. Zhu, A. T. Balaban, D. J. Klein and T. P. Živković, J. Chem. Phys., 1994, 101, 5281–5292.
20. D. J. Klein and A. T. Balaban, Open Org. Chem. J., 2011, 5(1), 27–61.
21. K. M. Merz Jr, R. Hoffmann and A. T. Balaban, J. Am. Chem. Soc., 1987, 109, 6742–6751.
22. R. Diercks and K. P. C. Vollhardt, J. Am. Chem. Soc., 1986, 108, 3150–3152.
23. H. B. Bürgi, K. K. Baldridge, K. Hardcastle, N. L. Frank, P. Gantzel, J. S. Siegel and J. Ziller, Angew. Chem., Int. Ed. Engl., 1995, 34, 1454–1456.
24. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
25. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 2008, 100, 136406.
26. N. Mounet and N. Marzari, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 205214.
27. Y. J. Dappe, M. A. Basanta, F. Flores and J. Ortega, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 205434.
28. S. Park and R. S. Ruoff, Nat. Nanotechnol., 2009, 4, 217–224.
29. J. M. Cai, P. Ruffieux, R. Jaafar, M. Bieri, T. Braun, S. Blankenburg, M. Muoth, A. Seitsonen, M. Saleh, X. L. Feng, K. Müllen and R. Fasel, Nature, 2010, 466, 470–473.
30. Y. Li, Z. Zhou, P. Shen and Z. Chen, Chem. Commun., 2010, 46, 3672–3674.
31. D. Jiang, V. R. Cooper and S. Dai, Nano Lett., 2009, 9, 4019–4024.

---

Footnote

† Electronic supplementary information (ESI) available: Computational details, additional figures and data. See DOI: 10.1039/c2tc00006g

---