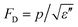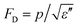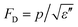Pyroelectric and electrocaloric materials
Xinyu
Li
a,
Sheng-Guo
Lu
a,
Xiang-Zhong
Chen
ab,
Haiming
Gu
a,
Xiao-shi
Qian
a and
Q. M.
Zhang
*a
aDepartment of Electrical Engineering and Materials Research Institute, The Pennsylvania State University, University Park, PA 16802, USA. E-mail: qxz1@psu.edu
bDepartment of Polymer Science & Engineering and Key Laboratory of Mesoscopic Chemistry of MOE, School of Chemistry & Chemical Engineering, Nanjing University, Nanjing 210093, China
First published on 23rd October 2012
Abstract
Both the pyroelectric and electrocaloric effects originate from the cross-coupling between polarization and temperature in insulating dielectrics. Although both effects have been studied for many decades for various applications and large pyroelectric effect has been observed in many polar-dielectrics, it is only very recently that a large electrocaloric effect (ECE) was obtained in ferroelectric ceramic thin films and polymers, which revives the interest in the ECE. This review will summarize typical properties of pyroelectric and electrocaloric materials, present figures of merit for both phenomena, examine the relationship between the pyroelectric and electrocaloric effect. Moreover, we will also present theoretical works, experimental results, and material modifications to achieve large responses in electrocaloric materials.
 Xinyu Li | Xinyu Li is a Ph.D. candidate in the Electrical Engineering Department of The Pennsylvania State University. He obtained his B.E. degree in Department of Materials Science and Engineering, Tsinghua University, Beijing, China. His current research focuses on the development of the electrocaloric effect in organic materials, as well as the design of solid-state cooling devices based on the phenomenon. |
 Sheng-Guo Lu | Sheng-Guo (David) Lu is currently a senior research scientist consultant at Strategic Polymer Sciences and an adjunct senior research associate at The Pennsylvania State University. Dr Lu's interest includes functional inorganic materials, electroactive polymers, composites, and applications as sensors, actuators, and electrocaloric refrigerators. He is a senior member of IEEE and has over 100 publications. |
 Xiang-Zhong Chen | Xiang-Zhong Chen received his bachelor degree (2007) in Polymer Materials and Engineering. He is pursuing his PhD degree in Polymer Chemistry and Physics from Nanjing University. Currently, he is visiting Prof. Qiming Zhang's group at The Pennsylvania State University. His research focuses on energy storage and conversion properties of PVDF-based electroactive polymers. |
 Haiming Gu | Haiming Gu received his B.S. and M.S. degree from Department of Electronics Engineering and Institute of Microelectronics, Tsinghua University, Beijing China. Currently, he is a Ph.D. candidate at The Pennsylvania State University. His research topics focus on modeling and fabrication of compact-size/micro-size solid-state cooling devices based on electrocaloric effect. |
 Xiao-shi Qian | Xiao-shi Qian studied materials science and engineering at Nanjing University, China, and received his masters degree in 2010. He is pursuing his Ph.D. degree in electric engineering department and Dr Qiming Zhang's lab. He is conducting research on the electrocaloric effect in dielectric fluids and ferroelectric polymers, and cooling devices using electrocaloric effect materials as refrigerant. |
 Q. M. Zhang | Dr Qiming Zhang is Distinguished Professor of Electrical Engineering and Materials Science and Engineering of Penn State University. His research area is in novel electronic materials, especially soft electronic materials and ferroelectric based materials, covering a broad range of applications of solid state electronic materials such as electromechanical, dielectric, photonic and electro-optic, and pyroelectric applications. |
1. Introduction
The pyroelectric and electrocaloric effects originate from the cross-coupling between polarization and temperature in certain classes of insulating dielectrics. In simple terms, the pyroelectric effect refers to the polarization change caused by temperature change, while the electrocaloric effect is the reversed process, i.e., a temperature change will be generated when there is a polarization change. These effects can be related by the Maxwell relations.1Pyroelectricity was first observed more than 2400 years ago,2 and has been studied for a long time.3–6 Pyroelectric materials have found a wide range of applications,7 such as thermal imaging, laser detectors, radiometers, infrared sensors, pollution monitor and tools for gas analysis, fire alarms, and intruder alarms.
Although the study on the electrocaloric effect (ECE) can be dated back to 1930, when a very weak ECE was measured in Rochelle salt,8 it was not until the 1960s that more studies on the electrocaloric materials were carried out. However, the small ECE observed in the second half of 20th century, where the adiabatic temperature change ΔT was less than 2 °C, makes it not attractive for practical applications. The field has been revived since 2006, when Mischenko et al. reported a giant ECE in ceramic thin films in which ΔT of 12 °C was observed at 226 °C,9 and Neese et al. discovered a giant ECE near room temperature in a class of ferroelectric polymer, which exhibits both a large ΔT (>12 °C) and isothermal entropy change ΔS (>50 J kg−1 K−1).10 Electrocaloric materials with large ECE are promising to realize compact cooling devices for next-generation refrigeration, temperature regulation and air-conditioning, with high efficiency and environmentally friendliness.
This review will summarize main properties of typical pyroelectric and electrocaloric materials, including figures of merit for both effects. In contrast to the study of pyroelectric materials and their device applications, which is a relatively mature field, the understanding of electrocaloric materials is still at an early stage. Hence, this review will devote most of the volume to covering theoretical works and experimental results related to the ECE. The relationship between the pyroelectric and electrocaloric effect will be discussed, and more importantly, considerations for material modifications to achieve large ECE (with an emphasis on electrocaloric polymers) will be presented.
2. Pyroelectricity and pyroelectric materials
2.1 Pyroelectricity
Pyroelectricity is the electrical response of an insulating dielectric to a change in temperature. In most experimental studies, the pyroelectric coefficient p is,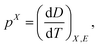 | (1) |
Pyroelectric materials are usually polar materials in which the lattice is non-centrosymmetrical. Among the 32 point group symmetries of crystals, only 10 belong to the polar point group, i.e., noncentrosymmetrical. They are: triclinic, 1 (C1); monoclinic, m and 2 (C2); orthorhombic, 2 mm (C2V); trigonal, 3 (C3) and 3 m (C3V); tetragonal, 4 (C4) and 4 mm (C4V); hexagonal, 6 (C6) and 6 mm (C6V). In addition, pyroelectricity is allowed in the two limiting Curie groups ∞ (C∞) and ∞mm (C∞V), which represent symmetry of a textured material (e.g., fabric structure) and that of an electrically poled polycrystalline material, respectively.
Pyroelectricity was first observed more than 2400 years ago by the Greek philosopher Theophrastus,2 and has been studied for a long time.3–6 To date, a large number of pyroelectric materials have been reported.7,11–15 Examples include barium strontium titanate (BST), triglycinesulphate (TGS), lithium niobate (LNB), lead zirconatetitanate (PZT), lead magnesium niobate-lead titanate (PMN-PT), strontium barium niobate (SBN), and polyvinylidene fluoride (PVDF).
2.2 Figure of merit (FOM) for pyroelectric materials
Pyroelectric materials have found a number of applications in areas such as thermal imaging, laser detectors, radiometers, infrared sensors, pollution monitoring and gas analysis, fire alarms, and intruder alarms.7 For these devices, three figures of merit are usually employed to evaluate a pyroelectric material and its interface with the electronic readout circuit, which can be a charge sensitive circuit or a voltage sensitivity circuit. They are current response FOM Fi = p for the charge sensitive readout, voltage response FOM FV = p/ε′ for the readout circuit in voltage mode, and for detectors, the signal to noise ratio (SNR) is a critical parameter and FOM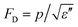 measures the SNR of the sensor. Here, ε′ and ε′′ are the real and imaginary parts of permittivity, respectively. Some examples of these FOM will be presented in the next section.
measures the SNR of the sensor. Here, ε′ and ε′′ are the real and imaginary parts of permittivity, respectively. Some examples of these FOM will be presented in the next section.
2.3 Secondary pyroelectric effect
The primary pyroelectric coefficient is defined as the pyroelectric coefficient measured in a clamped condition px (strain x = constant). As has been observed, pyroelectricity measured in a clamped condition can be quite different from that measured under stress free conditions (X = constant) because of the piezoelectric contribution caused by the thermal expansion of the material. The pyroelectric coefficient caused by the thermal expansion is termed as the secondary pyroelectric coefficient. The total pyroelectric coefficient measured at constant stress pX can be expressed as16,17| pXi = pxi + dXijkcX,EjklmαElm, | (2) |
| Materials | Primary coefficient (μC m−2 K−1) | Secondary coefficient (μC m−2 K−1) | Measured coefficient (μC m−2 K−1) |
|---|---|---|---|
| (A) Nonferroelectrics | |||
| CdS (6 mm) | −3.0 | −1.0 | −4.0 |
| CdSe (6 mm) | −2.94 | −0.56 | −3.50 |
| ZnO (6 mm) | −6.9 | −2.5 | −9.4 |
| BeO (6 mm) | −3.39 | −0.01 | −3.40 |
| Tourmaline (3 m) | −0.48 | −3.52 | −4.0 |
| Li2SO4·2H2O (2) | +60.2 | +20.1 | +80.3 |
| (B) Ferroelectrics | |||
| LiNbO3 (3m) | −95.9 | +12.9 | −83 |
| LiTaO3 (3m) | −178 | +2.0 | −176 |
| NaNO2 (2 mm) | −135 | −5.0 | −140 |
| Pb5Ge3O11 (3) | −110.5 | +15.5 | −95 |
| Sr0.5Ba0.5Nb2O6 (4 mm) | −529 | −21 | −550 |
| Ba2NaNb5O15 (2 mm) | −141.8 | +41.8 | −100 |
| TGS (2) | −330 | +60 | −270 |
| PVDF (2 mm) | −14 | −13 | −27 |
| BaTiO3 (∞m) | −260 | +60 | −200 |
| Pb(Zr0.95Ti0.05)O3(∞m) | −305.7 | +37.7 | −268 |
| Pb(Zr0.52Ti0.48)O3(∞m) | −110 | +60 | −50 |
2.4 Pyroelectric materials
Large numbers of ferroelectrics have been investigated for pyroelectric applications, which involve organic and inorganic materials. On the organic material side, PVDF based polymers, and side-chain liquid crystal polymers have been studied. On the inorganic material side, single crystals, poled polycrystalline ceramics, and ceramic thin films have been explored. Near a continuous ferroelectric–paraelectric (FE–PE) phase transition, an extremely large pyroelectric coefficient may be obtained when under a DC bias electric field. In addition, a hybrid approach, ceramic–polymer composites, has also been studied.PVDF as well as many PVDF based copolymers and terpolymers possess ferroelectricity. In most cases, these are semi-crystalline polymers and the crystalline phase is in a lamellar form. Polarization is the long range ordering of the dipoles formed from the C–H/C–F bonds, which are perpendicular to the backbone chains.18 PVDF does not show a FE–PE phase transition before melting (∼180 °C).19 The copolymers of PVDF with trifluoroethylene (TrFE >20 mol%) display FE–PE phase transition before melting and hence at room temperature show stronger pyroelectric coefficient.20Table 2 lists the pyroelectric coefficients of the P(VDF-TrFE) copolymers at different compositions at room temperature.21,22
| Materials | F i = p (μC m−2 K−1) | ε′ | F V = p/ε′ (μC m−2 K−1) |
|
|---|---|---|---|---|
| P(VDF-TrFE) 50/50 | 40 | 18 | 2 | 5.06 |
| P(VDF-TrFE) 56/44 | 38 | 12 | 3 | 70 |
| P(VDF-TrFE) 70/30 | 55 | 8 | 6.8 | 200 |
| P(VDF-TrFE) 75/25 | 33 | 7.4 | 4 | 94 |
| P(VDF-TrFE) 80/20 | 31 | 7 | 4.4 | 91 |
| PVDF | 27 | 11 | 2.46 | 33.24 |
| LCP | 0.98 | 6.7 | 0.15 | 3.46 |
Liquid crystal side-chain polymers (LCP), where the polymer architecture consists of a polymer backbone, flexible spacers, and mesogenic groups based on a cyanobiphenyl moiety, also exhibit some pyroelectric response.23 One example is the polymethacrylates separated with alkyl chains of five to seven methylene groups from 4′-cyano-4-biphenyl mesogenic moieties.
There are many reports on the pyroelectric coefficients for bulk single crystals and ceramics, especially the Pb(Mg1/3Nb2/3)O3–0.26PbTiO3(PMN-PT) and Pb(In1/2Nb1/2)O3–Pb(Mg1/3Nb2/3)O3–PbTiO3(PIMNT) relaxor ferroelectric single crystals and SrBaNb2O6(SBN) ceramics synthesized by the hot forging method.24−34 Single crystals demonstrate large pyroelectric coefficients and FOMs as listed in Table 3.24–34
| Materials | F i = p (μC m−2 K−1) | ε′ | F V = p/ε′ (μC m−2 K−1) |
|
|---|---|---|---|---|
| a ⊥: parallel to pressing axis; ‖: perpendicular to pressing axis. | ||||
| PMN-0.13PT 〈111〉 poled | 3260 | 3107 | 1.0 | 1018 |
| PMN-0.21PT 〈111〉 poled | 1790 | 961 | 1.8 | 1059 |
| Fe doped PMN-0.38PT | 568 | 310 | 1.8 | 394 |
| PMN-0.29PT | 1280 | 515 | 2.4 | 710 |
| Mn doped PMN-0.38PT | 1620 | 688 | 2.3 | 2790 |
| Mn doped PMN-0.26PT | 1720 | 660 | 2.6 | 2994 |
| PIMNT (42/30/28) | 900 | 702 | 1.28 | 760 |
| SBN53/47 HF (⊥)a | 510 | 980 | 0.52 | 120 |
| SBN53/47 HF (‖)a | 400 | 468 | 0.85 | 263 |
Thin films are attractive for pyroelectric applications because they can form texture or epitaxial structure, leading to properties approaching that of single crystals. Thin film devices are also more compatible with the semiconductor fabrication process, since many thin films can be integrated on Si substrates at temperatures as low as 600°C. In addition, it was also observed that the relaxor ferroelectric thin films exhibit much larger pyroelectric coefficients than conventional perovskite structured thin films.15Table 4 presents pyroelectric coefficients and FOMs of several thin films.35–45
| Materials | F i = p (μC m−2 K−1) | ε′ | F V = p/ε′ (μC m−2 K−1) |
|
|---|---|---|---|---|
| PbTiO3/Pt/Si | 130–145 | 180–260 | 0.50–0.81 | 43–91 |
| PZT 15/85/Pt/Si | 160–220 | 200–230 | 0.70–1.10 | 86–156 |
| PLT10-20/Pt/Si | 200–576 | 153–550 | 2.3 | 55–466 |
| Porous PLT/Pt/Si | 220 | 90 | 2.4 | 232 |
| LiNbO3 (006)/Pt/Si | 71 | (30) | 2.4 | 130 |
| PLT5-15/Pt/MgO | 400–1300 | 100–350 | 1.1–13 | 214–1678 |
| PLZT 7.5/8/92-20/80 | 360–820 | 193–260 | 1.4–4.2 | 171–518 |
| PbSc1/2Ta1/2O3/sapphire | 6000 | 6500 | 0.92 | 430 |
| K0.89Na0.11Ta0.55Nb0.45O3/KTaO3 | 5200 | 12000 | 0.43 | 336 |
The ceramic–polymer composites combine polymeric properties such as mechanical flexibility, formability, and low cost with the ceramic properties such as large p and excellent mechanical strength. These hybrids exhibit better pyroelectric properties over the individual constituent phase while possessing excellent mechanical strength, formability, and robustness of the polymer, which may someday be useful for IR detectors without supporting substrates. Table 5 lists pyroelectric coefficients and FOMs of several ceramic–polymer composites.46–52
| Materials | F i = p (μC m−2 K−1) | ε′ | F V = p/ε′ (μC m−2 K−1) |
|
|---|---|---|---|---|
| TGS-PVDF | 90 | 27.3 | 3.3 | — |
| PT-P(VDF-TrFE) | 40.7 | 57.3 | 0.71 | 28 |
| PCLT-P(VDF-TrFE) | 56.5 | 15.1 | 3.74 | 113 |
| PZT-PU | 90 | 24 | 3.75 | 22 |
| PZT-P(VDF-TrFE) | 92 | 29 | 3.2 | 93 |
| LiTaO3/P(VDF-TrFE) @70°C | 137.5 | 20.7 | 6.6 | 67 |
3. Electrocaloric effect and electrocaloric materials
3.1 General consideration of the electrocaloric effect
| G = U − TS − Xixi − EjDj, | (3) |
| dG = −SdT − xidXi − DjdEj, | (4) |
Hence the entropy S and electric displacement Dj are,
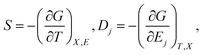 | (5) |
Eqn (5) leads to the Maxwell relation, linking the electrocaloric effect to the pyroelectric effect for a thermodynamically reversible system,1
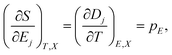 | (6) |
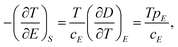 | (7) |
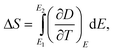 | (8) |
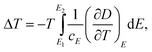 | (9) |
Eqn (6) through eqn (9) indicate that in order to achieve a large ΔS and ΔT, the dielectric materials should possess a large pyroelectric coefficient over a broad electric field range. For ferroelectric materials, a large pyroelectric effect exists near the FE–PE phase transition. It is also noted that a large ΔT may be achieved even if ΔS is small when cE of a dielectric material is small. However, for practical refrigeration applications, an ECE material should possess both a large ΔS and ΔT.53
It is noted that in the temperature region including a first-order FE–PE transition, eqn (8) should be modified to take into account the discontinuous change of the polarization ΔP (and ΔD) at the transition temperature, i.e.,
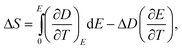 | (10) |
It should be emphasized that one should be cautious in using the Maxwell relation to deduce the ECE near first order FE–PE transitions. The hysteresis associated with first order FE–PE transition means the process is not thermodynamically reversible and the Maxwell relation is derived based on reversible thermodynamic process.
Although a few studies on the ECE were conducted in which direct measurement of ΔT and/or ΔS was made,54,55 most experimental studies were based on the Maxwell relation where the electric displacement D versus temperature T under different electric fields was characterized. ΔS and ΔT were deduced from eqn (8) and (9).
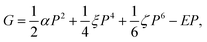 | (11) |
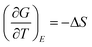 and at temperatures above FE–PE transition where a single P value exists under an applied field E, one obtains,
and at temperatures above FE–PE transition where a single P value exists under an applied field E, one obtains,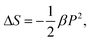 | (12) |
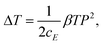 | (13) |
Eqn (12) indicates that the entropy will be reduced when the material increases its polarization or changes to a polar state from a non-polar state when an external action, e.g. temperature, electric field or stress, is applied. The entropy change and temperature change are associated with the phenomenological coefficient β and polarization, viz. proportional to β and P2. Both parameters will affect the ECE values of the materials. A material with a large β and a large P will generate a large ECE entropy change and temperature change near the FE–PE phase transition temperature.
As an example, the L–D phenomenological theory predicts large ECE values in ferroelectric P(VDF-TrFE) polymers. P(VDF-TrFE) 65/35 mol% copolymer, with β = 3.5 × 107 J m C−2 K−1 and D = 0.08 Cm−2,56 will exhibit a ΔS = 62 J kg−1 K−1. Making use of its specific heat capacity cE = 1.4 × 103 J kg−1 K−1,57 and Curie temperature Tc = 102 °C,56 yields a ΔT = 16.6 °C. The large ΔS and ΔT values suggest that a large ECE may be achieved in ferroelectric P(VDF-TrFE) copolymers.
In addition, the heat of FE–PE phase transition can also be used to assess the ECE (Q = TΔS) in a ferroelectric material at temperatures above the FE–PE transition. For example, P(VDF-TrFE) 68/32 mol% copolymer shows a heat of FE–PE transition larger than 2.1 × 104 J kg−1 (or ΔS ≈ 56.0 J kg−1 K−1), which is consistent with the prediction based on the phenomenological theory that a large ECE can be obtained in P(VDF-TrFE) ferroelectric polymers.10,58,59
| dG = −SdT − R·dF − QdV, | (14) |
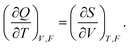 | (15) |
When the dimensional change is small, eqn (15) is reduced to eqn (6).
Assuming the ECE film has a volume Ω, an area Az in XY plane (perpendicular to the film thickness and the applied electric field), the electric field is along the z direction, and let D = P for ferroelectric polymers, then dQ should be written as
| dQ = AzdP + PdAz, | (16) |
So the unit volume entropy Δs = ΔS/Ω is
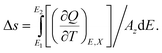 | (17) |
On the device side, the total dipole moment M of the sample is related to the measured charge Q and polarization P as60,61
| Q = AP = M/d. | (18) |
Making use of 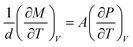 and eqn (6), we have
and eqn (6), we have
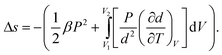 | (19) |
For freestanding films, the mechanical boundary conditions are Xi = 0 (I = 1, 2, and 3). Then the entropy change per unit volume Δs in eqn (19) has the form62
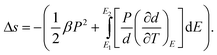 | (20) |
Using (∂d/d)/∂T = α and equation (E = β(T − Tc)P + γP3 for a 2nd order phase transition), Δs becomes
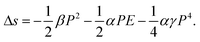 | (21) |
Taking the typical data of β = 2.4 × 107 J m C−2 K−1,58,63α = 2 × 10−3 K−1 (in the phase transition regime),64 and γ = 8.3 × 1011 J m5 C−4,65 for a P(VDF-TrFE)55/45 mol% copolymer, it can be estimated that 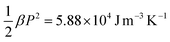 , the sum of the last two terms on the right side of eqn (21) is 2.05 × 104 J m−3 K−1, where P = 0.07 Cm−2 and E = 150 MV m−1 are used. The contribution of secondary pyroelectricity to the ECE is 26%. The results indicate that for polymers, the thermal expansion has a significant impact on the ECE entropy change through the interaction among the thermal expansion, electric field, and polarization.
, the sum of the last two terms on the right side of eqn (21) is 2.05 × 104 J m−3 K−1, where P = 0.07 Cm−2 and E = 150 MV m−1 are used. The contribution of secondary pyroelectricity to the ECE is 26%. The results indicate that for polymers, the thermal expansion has a significant impact on the ECE entropy change through the interaction among the thermal expansion, electric field, and polarization.
Now if the polymer films are fixed to an inorganic substrate, the boundary conditions become α1 = α2, x1 = x2 = 0, X1 = X2 ≠ 0 (the film surface is along the XY plane and Z is the film thickness direction). Using the electrostriction instead of piezoelectricity,66–68 near the phase transition temperature, the elastic Gibbs free energy can be written as
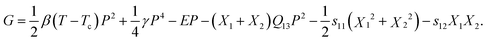 | (22) |
The equations of state could be expressed as11
| dx1 = dx2 = (sE,T11 + sE,T12)dX1 + 2QX,T13P3dP3 = 0, | (23) |
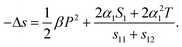 | (24) |
Eqn (24) indicates that the clamping effect of the substrate can change the ECE of polymer films. Since for P(VDF-TrFE) based polymers, the strain S1 = Q13P2 > 0,69 the second term of the right hand side of eqn (24) will enhance the ECE entropy change in the clamped situation in addition to the contribution of the field induced phase transition.70
3.2 ECE measurement methods
Generally, ECE measurement methods can be categorized into two groups: the indirect method, where entropy change ΔS and temperature change ΔT are deduced using Maxwell's relation; and the direct method, where ΔS and/or ΔT are acquired from specially designed calorimeters.The indirect method is based on the Maxwell relation, shown in eqn (6), from which the ΔS and ΔT of the ECE as the electric field changes from E1 to E2 can be deduced, i.e., eqn (8) and (9). The indirect method has been widely used to characterize the ECE since the 1960s,71 due to the fact that the apparatus measuring the polarization as a function of temperature is quite universal and relatively convenient to use. However, it should be noted that since the Maxwell relation is derived for ergodic systems, one needs to be cautious when using the indirect method to deducing the ECE in material systems that are not thermodynamically reversible such as the relaxor ferroelectric polymers.72
The direct method (measuring entropy change (extensive) or temperature change (intensive)) can thus be divided into two subgroups. Since there is no standard commercial equipment for measuring the ECE, various calorimeters have been developed by several research groups to measure the electrocaloric effect under different electric fields over a wide temperature range. The commercial DSC system can be modified so that electric fields can be applied to the sample, and the heat absorbed or ejected by the sample is simultaneously recorded.28 A calorimeter using a heat flux sensor was developed by Zhang's group at Penn State,73 as shown in Fig. 1, where the heat generated by the ECE of the sample is calibrated using the heat generated by a standard reference resistor R, from which ΔS is determined. By substituting the heat flux sensor with an infrared sensor or thermal couple, the adiabatic temperature change can be obtained using the same calorimeter.63 A high resolution calorimeter using a miniature thermistor and weak thermal link to the thermal bath was also developed for direct ECE measurement in thin films.63 Additionally, other apparatuses using multiple thermometers to measure the temperature difference between the sample and background were also reported.55,74 Factors that may influence the accuracy of a direct ECE measurement over a certain temperature range include the sensitivity, signal-to-noise ratio and response time of the thermal sensor, the stability of temperature controller, and the ability of the system to provide good thermal contact during the measurement.
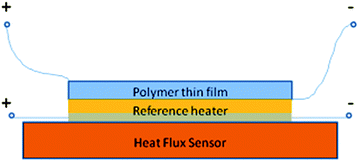 | ||
| Fig. 1 Schematic configuration of direct ECE measurement setup with heat flux sensor. | ||
3.3 Electrocaloric polymers
Very large ECE has been observed in PVDF-based polymers. These materials can also be fabricated into thin films (to operate the cooling device in voltages normally used in commercial cooling devices) and large size devices, these polymers are probably the most likely ECE materials to be developed into commercial applications. This section will summarize the main advancements achieved in this field.In PVDF based polymers, it has been reported that there exist five crystalline phases. The most interesting one is the ferroelectric β phase, in which, polymer chains adopt all-trans (TTTT) conformation, where all the fluorine atoms are on one side of the chain, forming dipoles perpendicular to the chain direction, as illustrated in Fig. 2.18,75,76 The ferroelectric β phase will undergo a phase transition and turn into a paraelectric phase, a phase consisting of a random sequence of trans-gauche (TG) bonds, such as TGTG′, and T3GT3G′ isomers. Correspondingly, the dipoles in the crystallites also change from an ordered state to a disordered state. Additionally, with defect modification such as high energy irradiation or copolymerizing with a third bulky monomer, the normal ferroelectric polymers can be converted into relaxor ferroelectrics, in which randomly distributed nano-polar regions are embedded in a non-polar matrix. When an external electric field is applied, the random dipoles in either the paraelectric phase of normal ferroelectric polymers or in the relaxor ferroelectrics, will reorient along the electric field direction, causing a structure change in the polymer as well as a temperature change as compensation for the entropy change.
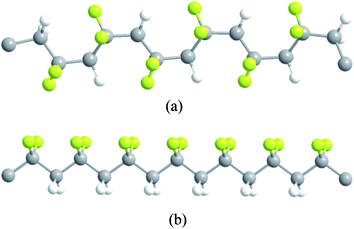 | ||
| Fig. 2 Schematic illustration of the two most common crystalline chain conformations in PVDF (a) tg+tg− conformation and (b) all-trans conformation. | ||
The PVDF-based polymers that have been studied include P(VDF-TrFE) copolymers, high-energy-electron-irradiated P(VDF-TrFE) copolymers, (P(VDF-TrFE-CFE)) terpolymers (CFE: chlorofluoroethylene), and P(VDF-TrFE) copolymer/P(VDF-TrFE-CFE) terpolymer blends.
Fig. 3 presents ΔS and ΔT at several electric field levels deduced by indirect measurement.10 As can be seen, the copolymer exhibits a ΔS of more than 55 J kg−1 K−1 and ΔT of more than 12 °C under an electric field of 209 MV m−1 and at temperatures around 80 °C, which are the first experimental result demonstrating a giant ECE in polymers. Fig. 4 presents ΔS and ΔT as a function of temperature measured under several electric fields in P(VDF-TrFE) 55/45 mol% copolymer using the direct method as well as the comparison between the ECE results directly measured and calculated from the indirect method.62 The data show that the ECE reaches a maximum at the FE–PE transition, where a ΔT = 12 °C can be induced under a 120 MV m−1 electric field. At temperatures away from the FE–PE transition, ΔT drops rapidly, which is a characteristic feature for normal ferroelectric materials. The comparison result reveals that within the experimental error, the ECE deduced from the Maxwell relation is consistent with that directly measured, and also indicates that for a ferroelectric material at temperatures above FE–PE transition, the Maxwell relation is valid for deducing ECE.
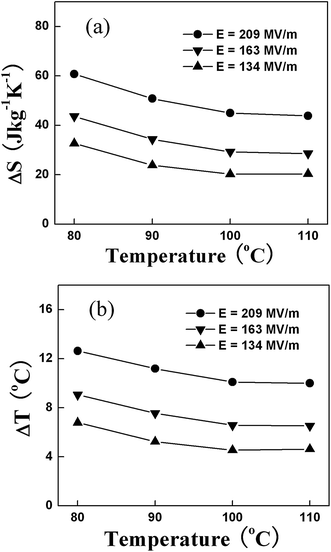 | ||
| Fig. 3 (a) Isothermal entropy change ΔS and (b) adiabatic temperature change ΔT, measured by indirect method, as a function of ambient temperature at different electric fields for P(VDF-TrFE) 55/45 copolymer. | ||
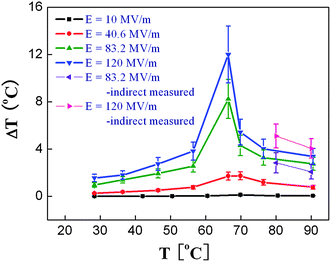 | ||
| Fig. 4 Directly measured ΔT as a function of temperature under several electric fields for non-stretched P(VDF-TrFE) 55/45 mol% copolymers and comparison with that indirectly measured. | ||
The ECE in a dielectric is determined by the dipolar entropy change ΔSp between polar and non-polar states, as shown in eqn (25) and (26),
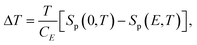 | (25) |
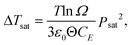 | (26) |
3.3.2.1 Giant electrocaloric effect in the irradiated P(VDF-TrFE) relaxor copolymers. It has been shown that by employing high energy electron irradiation, the normal ferroelectric P(VDF-TrFE) copolymer can be converted to a relaxor ferroelectric polymer which displays high dielectric constant (∼50 at 1 kHz), large reversible polarization change, and high electrostriction at room temperature.66Fig. 5(a) presents the dielectric constant of a high energy electron irradiated P(VDF-TrFE) 68/32 mol% copolymer, which has a broad dielectric constant peak around room temperature and that peak position moves progressively toward higher temperatures with frequency, a characteristic feature of relaxor ferroelectrics. The high energy electron irradiation breaks up long range polar-correlation in the polymer, which stabilizes dipolar disordered states around room temperature and generates local polar-states that may enhance the ECE, as discussed earlier. The ECE of the irradiated P(VDF-TrFE) 68/32 mol% copolymer measured near the broad dielectric peak (33 °C) as a function of electric field is presented in Fig. 5(b).63 Under a field of 160 MV m−1, an adiabatic temperature change ΔT = 20 °C and isothermal entropy change ΔS = 95 J kg−1 K−1 can be obtained. Such a large ECE response shows promise for compact cooling applications with high efficiency and cooling power, and may open up a new direction for electrocaloric materials research.
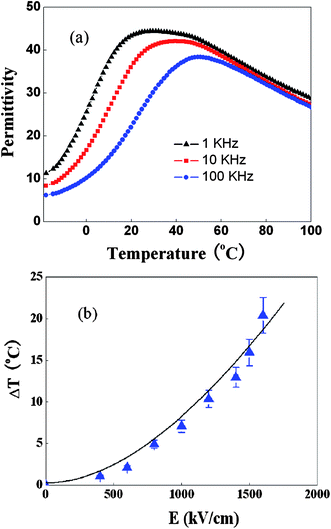 | ||
| Fig. 5 (a) Dielectric constant vs. temperature measured at different frequencies (b) directly measured ECE for the high energy electron irradiated P(VDF-TrFE) 68/32% relaxor copolymer. | ||
3.3.2.2 ECE in relaxor ferroelectric P(VDF-TrFE-CFE) terpolymers. In the P(VDF-TrFE-CFE) relaxor ferroelectric polymers, large ECE has also been observed. ECE of the P(VDF-TrFE-CFE) 59.2/33.6/7.2 mol% terpolymer directly measured at 30 °C, as presented in Fig. 6(a), showing a very large ΔT ∼ 16 °C induced under 160 MV m−1 electric field; besides the large ECE, several relaxor ferroelectric polymers also display a nearly temperature independent ECE as presented in Fig. 6(b).73 For a P(VDF-TrFE-CFE) 59.2/33.6/7.2 mol% relaxor ferroelectric terpolymer, the ECE response is nearly temperature independent from 0 °C to 45 °C, which is in sharp contrast to that in normal ferroelectrics where the ECE peaks at the FE-PE transition and displays strong temperature dependence. Such a temperature independent ECE over a broad range is attractive for practical cooling device applications, especially for those requiring large temperature spans between cold and hot ends. These results also reveal the intricate roles played by the defects in tailoring the ferroelectric response and its polar nano-structures to generate a large ECE and its temperature response behavior. As has been shown here, the temperature dependence of the ECE of the terpolymer films depends critically on the film preparation conditions, while the uniaxially stretched terpolymer films show a pronounced temperature dependence on the ECE, the non-stretched films exhibit a nearly temperature independent ECE from 5 °C to 45 °C. At 5 °C and 55 °C, the ΔT of the uniaxially stretched films is more than 15% smaller, compared with that of the non-stretched films. Such a difference is likely to be caused by the changes in possible polar states and polar-correlation length due to film stretching.
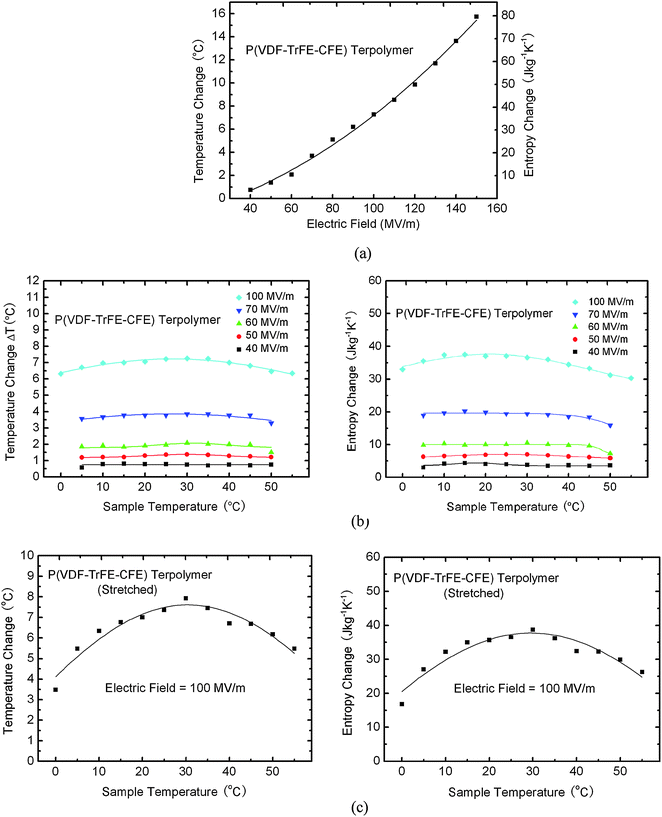 | ||
| Fig. 6 Directly measured ECE in non-stretched P(VDF-TrFE-CFE) 59.2/33.6/7.2 mol% terpolymer (a) adiabatic temperature change ΔT vs. applied electric field at 30 °C and (b) adiabatic temperature change ΔT and isothermal entropy change ΔS vs. sample temperature under different applied fields, (c) adiabatic temperature change ΔT and isothermal entropy change ΔS vs. sample temperature under different applied fields in stretched P(VDF-TrFE-CFE) terpolymer under a constant electric field of 100 MV m−1. | ||
It has also been observed that the ECE acquired in terpolymer by direct and indirect methods are very different, as presented in Fig. 7. The directly measured ECE from the relaxor terpolymer is much larger than that deduced from the Maxwell relation. Moreover, the directly measured ECE displays a much weaker temperature dependence at E < 70 MV m−1. The results indicate that the Maxwell relation is not suitable to deduce ECE for the relaxor ferroelectric polymers even at temperatures above the broad dielectric constant maximum, since the Maxwell relations are valid only for systems in thermodynamic equilibrium (ergodic systems), while the relaxor ferroelectric polymers are non-ergodic systems even at temperatures above the dielectric constant maximum.72
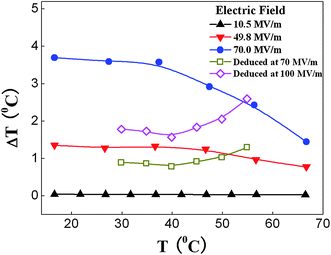 | ||
| Fig. 7 Temperature dependences of the directly measured ΔT of the terpolymer under different measuring electric fields. | ||
3.3.2.3 ECE in the relaxor ferroelectric P(VDF-TrFE-CFE) terpolymers/P(VDF-TrFE) copolymer blends. It is well known that nano-composites such as polymer blends, which exploit the merits of both the base polymer and the additive polymer, offer a great opportunity to enhance and tailor the material properties.19,79–81 It has been recently reported that the blends of P(VDF-TrFE-CFE) relaxor terpolymer with 10 wt% of P(VDF-TrFE) exhibit a 30% increase in the adiabatic temperature change compared with that of pure terpolymer, as shown in Fig. 8.82 Both increased crystallinity in the blends and conversion of the copolymer from a normal ferroelectric to a relaxor lead to an increased relaxor polarization response and an enhanced ECE. Another advantage of the blends over pure terpolymer is that the Young's modulus of the blends is improved compared to the pure terpolymer.
3.4 Electrocaloric ceramic materials
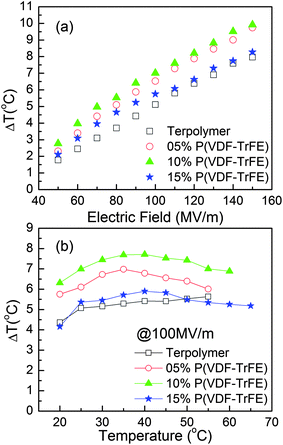 | ||
| Fig. 8 (a) Adiabatic temperature change as a function of electric field at room temperature (b) Adiabatic temperature changes as a function of sample temperature at fixed electric field of 100 MV m−1. | ||
After 1960s, the ECE in many perovskite ceramics were studied. It is well known that the properties of these ceramics can be tuned by doping, through which normal ferroelectrics (FE), anti-ferroelectrics (AFE), and ferroelectric relaxors can be obtained, providing very good models to understand the key factors that may influence the ECE.
Substitution of B-cations in PZT by Sn (PSZT) allows tuning of the temperature and composition ranges of the ferroelectric and antiferroelectric phases.71,87,88 The largest ECE (i.e., the change of entropy at the phase transition) appears in compositions where the both the AFE and FE reach their stability limit at high temperature and a first order transition from a PE to FE can be induced electrically. On the other hand, in compositions where an electric field-induced AFE to FE transition is observed, the ECE is much smaller and changes slowly in a wide range of temperature.89 The largest electrocaloric effect in bulk ceramics (2.6 °C) was measured for PSZT annealed at high temperature. The magnitude of this effect strongly depends on microstructure. Large grain ceramics with small temperature and field ranges of AFE phase stability yield the largest electrocaloric effect.90 La doped PZT thick films were also examined and a maximum temperature change of 8.5 °C was observed under a field of 7.5 MV m−1.91
In normal ferroelectrics, the sharp FE–PE transition usually leads to a narrow temperature range in which a large ECE exists. However, the ECE can be found in a wider temperature range in ferroelectric relaxors. For example, PMN (Pb(MgNb)TiO3) exhibits a diffused dielectric phase transition around −13 °C, which leads to a relatively large ECE near room temperature, i.e., maintaining a ΔT ∼ 2.5 °C in temperature range from 16 °C to 67 °C under an electric field of 9 MV m−1.92 PMN-PT (PbTiO3) with different compositions were also investigated in both ceramics and single crystals.93–98
In lead scandium niobate (PSN) and its solid solution with lead scandium tantalate (PST), the ordering of perovskite heterovalent ions in sublattice B can be tailored either by substitution or thermal treatment.99,100 A high degree of long-range order leads to a high ECE maximum (ΔT = 1.7 °C) as well as a high phase transition temperature, while a decreased order causes a lower ECE (which occurs over a broader temperature range) and diffuse phase transitions.
Some lead-free ceramics such as Ba0.73Sr0.27TiO3, Na0.5Bi0.5TiO3, and Ba0.3Na0.7Ti0.3Nb0.7O3 are also investigated for their ECE.101–103 Although ECE is small, lead-free materials are attractive because of their environmentally friendliness.
The ECE reported in all the bulk ceramic samples is below 3 °C, which makes them unimpressive for practical applications. The main reason is the low dielectric strength of bulk ceramics and the difficult in fabricating bulk ceramic to thin thickness (below 50 μm). By fabricating thick films using an interdigitated multilayer geometry, the film thickness of each layer can be reduced to ∼10 μm, which allows for application of high electric fields. Multilayered PbSc0.5Ta0.5O3,104 BaTiO3105–108 were also studied.
Mischenko et al.9 first reported a temperature change of 12 °C in 350 nm PbZr0.95Ti0.05O3 thin film near Curie temperature of 222 °C. A temperature change of about 11 °C was also observed in a 700 nm PbZrO3 thin film near its phase transition temperature at 235 °C.109 However, the phase transitions in these thin films are first-order transitions and the high ECE can only exist in a narrow temperature range. Additionally, the phase transition temperature is too high for applications near room temperature. To obtain a large ECE at a wide range of temperature near room temperature, La doped PZT thin films were explored and a ΔT ∼ 40 °C was reported under the electric field of 120 MV m−1 at 45 °C.63
A ΔT of 9 K under 72.3 MV m−1 in 0.93PMN-0.07PT thin films was observed at depolarizing temperature 18 °C instead of the temperature of 35 °C, where the dielectric constant peak appeared, suggesting a dipolar glass-relaxor phase transition in this system.110 For 0.9PMN-0.1PT, the maximum ΔT of 5 °C was observed at 75 °C, where a pseudocubic relaxor ferroelectric transforms to a cubic paraelectric phase.111 The PMN-PT with 30%–35% PT are extremely interesting, because of the morphotropic phase boundary (MPB) can contribute additionally to the ECE.112–115
Other thin films such as PbSc0.5Ta0.5O3 relaxor with a wide temperature range of ECE were also investigated. A ΔT = 6.2 °C at 77.4 MV m−1 was reported.116 SrBiTa2O9,117 a lead-free perovskite–type bismuth layered oxide, was investigated where a ΔT of 4.93 °C at around 290 °C was reported.
Table 6 summarizes the ECE properties for organic and inorganic materials. For comparison, selected ECE results reported in the literature on inorganic materials, especially inorganic ferroelectric thin films where very high voltage can be applied, are also included. As can be seen, the relaxor ferroelectric polymers, because of their large ΔT and ΔS, broad operation temperature range and easy scaling up for various sized cooling devices, offer the most attractive ECE properties for practical cooling device applications.
| Material | Form | Experiment temp. (°C) | ΔT (K) | ΔS (J kg−1 K−1) | ΔTΔS (J kg−1) | E (MV m−1) | Measurement method |
|---|---|---|---|---|---|---|---|
| P(VDF-TrFE) 55/45 (ref. 10) | Films | 80 | 12.6 | 62 | 781.2 | 209 | Indirect |
| P(VDF-TrFE) 55/45 (ref. 72) | Films | 67 | 12 | 120 | Direct | ||
| P(VDF-TrFE) 70/30 (ref. 118) | Films | 117 | 21 | 300 | Indirect | ||
| Irradiated P(VDF-TrFE) 68/32 (ref. 63) | Films | 33 | 20 | 95 | 1900 | 160 | Direct |
| P(VDF-TrFE-CFE) 59.2/33.6/7.2 (ref. 73) | Films | 30 | 15.7 | 80 | 1256 | 150 | Direct |
| SrTiO3 (ref. 84) | Ceramics | −256 | 0.06 | 0.8 | Direct | ||
| SrTiO3 (ref. 85) | Single crystal | −262 | 0.3 | 0.7 | Direct | ||
| KTaO3 (ref. 86) | Single crystal | −260 | 0.25 | 1.56 | Direct | ||
| PbZr0.455Sn0.455Ti0.0903 (ref. 71) | Ceramics | 44–55 | ∼1.4 | 3 | Direct | ||
| PbZr0.75Sn0.20Ti0.05O3 (ref. 90) | Ceramics | 161 | 2.6 | 3 | Direct | ||
| Pb0.97La0.02(Zr0.95Ti0.05)O3 (ref. 91) | Thick film | 1.7 | 8.5 | 112(75) | Indirect | ||
| PMN (ref. 92) | Ceramics | 16–67 | ∼2.5 | 2.5 | 6.25 | 9 | Direct |
| 0.9PMN-0.1PT (ref. 93) | Ceramics | 50 | 0.55 | 2.91 | Direct | ||
| 0.75PMN-0.25PT (ref. 94) | Ceramics | 120–130 | ∼0.5 | 1.35 | DSC | ||
| 0.87PMN-0.13PT (ref. 98) | Ceramics | 18 | ∼0.5 | 2 | Direct | ||
| Pb(Sc0.5Nb0.5)O3 (ref. 99) | Ceramics | 92 | 0.9 | 2 | Direct | ||
| Pb(Sc0.5Ta0.5)O3–Pb(Sc0.5Nb0.5)O3 (ref. 100) | Ceramics | −2 ∼ 10 | 1–1.7 | 2.5 | Direct | ||
| Pb(Mg0.5W0.5)0.5Ti0.5O3 (ref. 119) | Ceramics | 139 | 0.4 | 2.3 | Indirect | ||
| Na0.5Bi0.5TiO3 (ref. 102) | Ceramics | 140 | 0.33 | 0.45 | 0.1485 | 5 | Indirect |
| Ba0.73Sr0.27TiO3 (ref. 101) | Ceramics | 25 | ∼1 | 2.4 | DSC | ||
| Ba0.3Na0.7Ti0.3Nb0.7O3 (ref. 103) | Ceramics | −13 | 0.026 | 1.5 | DSC | ||
| PST(PbSc0.5Ta0.5O3) (ref. 104) | Multilayer | 2.4 (3.5) | 1.38 | Direct | |||
| BaTiO3 (commercial) (ref. 74) | Multilayer | 80 | 0.55 | 30 | Direct | ||
| PbZr0.95Ti0.05O3 (ref. 9) | Thin films | 226 | 12 | 7.9 | 94.8 | 77.6(50) | Indirect |
| Pb0.88La0.08Zr0.65Ti0.35O3 (ref. 63) | Thin films | 45 | 40 | 50 | 2000 | 120 | Direct |
| PbZr0.52Ti0.48O3 (ref. 120) | Thin films | 387 | 11.1 | 6.17 | 68.49 | 57.7 | Indirect |
| PbZrO3 (ref. 109) | Thin films | 235 | 11.4 | 51(40) | Indirect | ||
| 0.9 PMN-0.1 PT (ref. 111) | Thin films | 60 | 5 | 89.5 | Indirect | ||
| 0.93 PMN-0.07 PT (ref. 110) | Thin films | 25 | 9 | 72.3 | Indirect | ||
| 0.67 PMN-0.33 PT (ref. 112) | Thin films | 152 | 14.5 | 60 | Indirect | ||
| 0.65 PMN-0.35 PT (ref. 114) | Thin films | 140 | 31 | 74.7 | Indirect | ||
| SrBiTa2O9 (ref. 117) | Thin films | 288 | 4.93 | 60 | Indirect | ||
| PbSc0.5Ta0.5O3 (ref. 116) | Thin films | 68 | 6.2 | 6.3 | 39.06 | 77.4 | Indirect |
4. Concluding remarks
Pyroelectric effects in major polar materials are summarized, including the effects in polymers, single crystals, ceramics, thin films, and liquid crystalline polymers. It is shown that the pyroelectric effect experimentally measured often includes both the primary effect and the secondary effect (dimensional effect). Three figures of merit are usually used to evaluate the properties of the pyroelectric materials, which are necessary since besides the material, a sensor system also consists of an electronic readout circuit, which can be in either the charge detection mode (FOM Fi = p) or voltage detection mode (FOM FV = p/ε′). Also the signal-to-noise ratio is important in sensor designs which is related to the FOM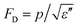 .
.
Compared with the pyroelectric materials, the study of ECE is still in its early stage. We note that in general the ECE and pyroelectric effect can be related through the Maxwell relation, and hence most ECE studies have been based on this relation (the indirect method). Since the Maxwell relation is valid only for systems and processes which are thermodynamically reversible and many ECE are studied near first order phase transitions, one should be cautious when using the indirect method to deduce ECE and interpret the experimental results.
Based on general thermodynamic considerations, a polar-material with a large polarization change and short polar-correlation length (and hence a small Curie constant (or a large β coefficient) in the L–D theory) will exhibit a large ECE. In ferroelectrics, the large polarization change occurs near a FE–PE transition and hence the largest ECE in the material will occur near the FE-PE transition. Moreover, since the dipolar entropy is basically directly related to the degree of dipolar disorder, by increasing the number of polar-states in the disordered phase can lead to a larger ECE. These considerations suggest that relaxor ferroelectrics may exhibit larger ECE than the normal ferroelectrics. Working with dielectrics near morphotropic phase boundary may also lead to higher ECE. All of these have indeed been experimentally observed. The advantage of working with the relaxor ferroelectrics is that the large ECE can occur over a broad temperature range compared with the normal ferroelectric in which the large ECE occurs over a narrower temperature range about the ferroelectric transition. Analogous to the pyroelectric effect, the secondary effect (the dimensional change of the EC material) can also play an important role.
The reports of large ECE in several materials systems create great opportunity to exploit these materials for solid-state cooling applications such as cooling of electronic components and on-chip cooling, refrigeration and air-conditioning. Compared with ceramic thin films which are supported by a substrate and in which large ECEs are obtained, polymer thin films with large ECE are more attractive for practical cooling device applications since they can be fabricated into large size devices with high breakdown field. Moreover, polymer/nano-particle composites can be very promising for device applications, due to the enhancement in both ECE and thermal conductivity, which are equally important from cooling device application point of view. In developing materials with large ECE, one should also pay special attention to the possibility of these materials and phenomena for practical applications. With the advancement of fundamental understanding of ECE in insulating dielectrics, further experimental studies of ECE materials, as well as cooling device studies exploiting these ECE materials, we expect that ECE materials possessing better properties will be developed.
Acknowledgements
Xinyu Li, Xiao-shi Qian, Q. M. Zhang were supported by the US DoE, Office of Basic Energy Sciences, Division of Materials Science and Engineering under Award no. DE-FG02-07ER46410. Sheng-Guo Lu and Xiang-Zhong Chen were supported by the Army Research Office under Grant no. W911NF-11-1-0534. Haiming Gu was supported by DOE SBIR Phase II, Contract no. DE-SC0003340 (subcontract from Strategic Polymers, Inc.) We thank Quinn Burlingame and Shan Wu for assistance in preparing the manuscript.References
- M. E. Lines and A. M. Glass, Principles and Applications of Ferroelectrics and Related Materials, Clarendon Press, Oxford Eng., 1977 Search PubMed.
- S. B. Lang, Phys. Today, 2005, 58, 31–36 CrossRef CAS.
- R. W. Whatmore and R. Watton, in Infrared Detectors and Emitters: Materials and Devices, ed. P. Capper and C. T. Elliott, Kluwer Academic, Boston, 2001 Search PubMed.
- S. B. Lang and D. K. Das-Gupta, Ferroelectr. Rev., 2000, 2, 217–354 CAS.
- P. Muralt, Rep. Prog. Phys., 2001, 64, 1339–1388 CrossRef CAS.
- S. B. Lang and A. S. Bhalla, Ferroelectrics, 1991, 118, R4–R5 CrossRef.
- R. W. Whatmore, Rep. Prog. Phys., 1986, 49, 1335–1386 CrossRef CAS.
- P. Kobeko and J. Kurtschatov, Z. Phys. A: Hadrons Nucl., 1930, 66, 192–205 CAS.
- A. S. Mischenko, Q. Zhang, J. F. Scott, R. W. Whatmore and N. D. Mathur, Science, 2006, 311, 1270–1271 CrossRef CAS.
- B. Neese, B. J. Chu, S. G. Lu, Y. Wang, E. Furman and Q. M. Zhang, Science, 2008, 321, 821–823 CrossRef CAS.
- S. T. Liu and D. Long, Proc. IEEE, 1978, 66, 14–26 CrossRef CAS.
- B. M. Kulwicki, A. Amin, H. R. Beratan and C. M. Hanson, ISAF 92: Proceedings of the Eighth IEEE International Symposium on Applications of Ferroelectrics, 1992, pp. 1–10 Search PubMed.
- M. H. Lee, R. Guo and A. S. Bhalla, J. Electroceram., 1998, 2, 229–242 CrossRef CAS.
- S. I. Raevskaya, Y. N. Zakharov, A. G. Lutokhin, A. S. Emelyanov, I. P. Raevski, M. S. Panchelyuga, V. V. Titov and S. A. Prosandeev, Appl. Phys. Lett., 2008, 93, 042903 CrossRef.
- M. Alguero, M. Stewart, M. G. Cain, P. Ramos, J. Ricote and M. L. Calzada, J. Phys. D: Appl. Phys., 2010, 43, 205401 CrossRef.
- J. F. Nye, Physical Properties of Crystals, Their Representation by Tensors and Matrices, Clarendon Press, Oxford, 1957 Search PubMed.
- R. E. Newnham, Properties of Materials: Anisotropy, Symmetry, Structure, Oxford University Press, Oxford, New York, 2005 Search PubMed.
- A. J. Lovinger, Science, 1983, 220, 1115–1121 CAS.
- H. S. Nalwa, Ferroelectric Polymers: Chemistry, Physics, and Applications, Marcel Dekker, New York, 1995 Search PubMed.
- Q. M. Zhang, C. Huang, F. Xia and J. Su, in Electroactive Polymer (EAP) Actuators as Artificial Muscles: Reality, Potential, and Challenges, ed. Y. Bar-Cohen, SPIE Press, Bellingham, 2004, pp. 95–148 Search PubMed.
- B. Ploss and S. Bauer, Sens. Actuators, A, 1991, 26, 407–411 CrossRef.
- J. H. Kim, T. K. Park, H. Lee and D. J. Lee, Korea Polym. J., 1995, 3, 101–105 CAS.
- G. H. Mehl, I. Nordmann, D. Lacey, J. W. Goodby, J. H. C. Hogg and D. K. DasGupta, Polym. Eng. Sci., 1996, 36, 1032–1037 CAS.
- Y. X. Tang, L. H. Luo, Y. M. Jia, H. S. Luo, X. Y. Zhao, H. Q. Xu, D. Lin, J. L. Sun, X. J. Meng, J. H. Zhu and M. Es-Souni, Appl. Phys. Lett., 2006, 89, 162906 CrossRef.
- X. M. Wan, X. G. Tang, J. Wang, H. L. W. Chan, C. L. Choy and H. S. Luo, Appl. Phys. Lett., 2004, 84, 4711–4713 CrossRef CAS.
- P. Kumar, S. Sharma, O. P. Thakur, C. Prakash and T. C. Goel, Ceram. Int., 2004, 30, 585–589 CrossRef CAS.
- M. Davis, D. Damjanovic and N. Setter, J. Appl. Phys., 2004, 96, 2811–2815 CrossRef CAS.
- G. Sebald, L. Seveyrat, D. Guyomar, L. Lebrun, B. Guiffard and S. Pruvost, J. Appl. Phys., 2006, 100, 124112 CrossRef.
- Y. X. Tang, X. M. Wan, X. Y. Zhao, X. M. Pan, D. Lin, H. S. Luo, J. L. Sun, X. J. Meng and J. H. Zhu, J. Appl. Phys., 2005, 98, 084104 CrossRef.
- J. T. Wang and C. Zhang, J. Appl. Phys., 2005, 98, 054103 CrossRef.
- Y. X. Tang, X. Y. Zhao, X. M. Wan, X. Q. Feng, W. Q. Jin and H. S. Luo, Mater. Sci. Eng., B, 2005, 119, 71–74 CrossRef.
- M. Venet, I. A. Santos, J. A. Eiras and D. Garcia, Solid State Ionics, 2006, 177, 589–593 CrossRef CAS.
- S. E. Aleksandrov, G. A. Gavrilov, A. A. Kapralov, E. P. Smirnova, G. Y. Sotnikova and A. V. Sotnikov, Tech. Phys., 2004, 49, 1176–1180 CrossRef CAS.
- L. H. Liu, X. A. Wu, X. Y. Zhao, X. Q. Feng, W. P. Jing and H. S. Luo, IEEE Trans. Ultrason. Ferroelectr. Freq. Control, 2010, 57, 2154–2158 CrossRef.
- A. Seifert, P. Muralt and N. Setter, Appl. Phys. Lett., 1998, 72, 2409–2411 CrossRef CAS.
- A. R. Zomorrodian, H. Lin, N. J. Wu, T. Q. Huang, D. Liu and A. Ignatiev, Appl. Phys. Lett., 1996, 69, 1789–1791 CrossRef CAS.
- Z. Sitar, R. Gutmann, H. Pierhofer and P. Gunter, Mater. Res. Soc. Symp. Proc., 1995, 361, 589–594 CrossRef CAS.
- M. Kohli and P. Muralt, Ferroelectrics, 1999, 225, 155–162 CrossRef.
- R. Watton and M. A. Todd, Ferroelectrics, 1991, 118, 279–295 CrossRef CAS.
- T. Gebre, A. K. Batra, P. Guggilla, M. D. Aggarwal and R. B. Lal, Ferroelectr., Lett. Sect., 2004, 31, 131–139 CrossRef CAS.
- A. Bell, Y. Huang, O. Paul, Y. Nemirovsky and N. Setter, Integr. Ferroelectr., 1995, 6, 231–240 CrossRef CAS.
- M. Kobune, S. Fujii, R. Takayama and A. Tomozawa, Jpn. J. Appl. Phys., 1996, 35, 4980–4983 CrossRef CAS.
- M. Kobune, H. Ishito, A. Mineshige, S. Fujii, R. Takayama and A. Tomozawa, Jpn. J. Appl. Phys., 1998, 37, 5154–5157 CrossRef CAS.
- K. Iijima, Y. Tomita, R. Takayama and I. Ueda, J. Appl. Phys., 1986, 60, 361–367 CrossRef CAS.
- D. H. Liu and D. A. Payne, J. Appl. Phys., 1995, 77, 3361–3364 CrossRef CAS.
- M. Wang, C. S. Fang and H. S. Zhou, Ferroelectrics, 1991, 118, 191–197 CrossRef CAS.
- H. L. W. Chan, W. K. Chan, Y. Zhang and C. L. Choy, IEEE Trans. Dielectr. Electr. Insul., 1998, 5, 505–512 CrossRef CAS.
- M. Dietze, J. Krause, C. H. Solterbeck and M. Es-Souni, J. Appl. Phys., 2007, 101, 054113 CrossRef.
- K. S. Lam, Y. W. Wong, L. S. Tai, Y. M. Poon and F. G. Shin, J. Appl. Phys., 2004, 96, 3896–3899 CrossRef CAS.
- C. S. Fang, Q. W. Wang, H. S. Zhuo, P. L. Zhang and W. L. Zhong, J. Korean Phys. Soc., 1998, 32, S1843–S1844 CAS.
- A. K. Batra, J. Corda, P. Guggilla, M. D. Aggarwal and M. E. Edwards, P. Soc. Photo-opt. Ins., 2009, 7213, 721313 Search PubMed.
- J. H. Li, N. G. Yuan and H. L. W. Chan, Sens. Actuators, A, 2002, 100, 231–235 CrossRef.
- M. E. Wood and W. H. Potter, Cryogenics, 1985, 25, 667–683 CrossRef CAS.
- Y. V. Sinyavsky, N. D. Pashkov, Y. M. Gorovoy and G. E. Lugansky, Ferroelectrics, 1989, 90, 213–217 CrossRef.
- D. Q. Xiao, Y. C. Wang, R. L. Zhang, S. Q. Peng, J. G. Zhu and B. Yang, Mater. Chem. Phys., 1998, 57, 182–185 CrossRef CAS.
- T. Furukawa, Ferroelectrics, 1984, 57, 63–72 CrossRef CAS.
- T. Furukawa, T. Nakajima and Y. Takahashi, IEEE Trans. Dielectr. Electr. Insul., 2006, 13, 1120–1131 CAS.
- S. G. Lu and Q. M. Zhang, Adv. Mater., 2009, 21, 1983–1987 CrossRef CAS.
- B. Neese, S. G. Lu, B. J. Chu and Q. M. Zhang, Appl. Phys. Lett., 2009, 94, 042910 CrossRef.
- H. Dveyaharon and P. L. Taylor, Ferroelectrics, 1981, 33, 103–110 CrossRef CAS.
- E. L. Nix, J. Nanayakkara, G. R. Davies and I. M. Ward, J. Polym. Sci., Part B: Polym. Phys., 1988, 26, 127–140 CrossRef CAS.
- S. G. Lu, B. Rozic, Q. M. Zhang, Z. Kutnjak and B. Neese, Appl. Phys. Lett., 2011, 98, 122906 CrossRef.
- S. G. Lu, B. Rozic, Q. M. Zhang, Z. Kutnjak, X. Y. Li, E. Furman, L. J. Gorny, M. R. Lin, B. Malic, M. Kosec, R. Blinc and R. Pirc, Appl. Phys. Lett., 2010, 97, 162904 CrossRef.
- K. Tashiro, S. Nishimura and M. Kobayashi, Macromolecules, 1990, 23, 2802–2806 CrossRef CAS.
- T. Furukawa, G. E. Johnson, H. E. Bair, Y. Tajitsu, A. Chiba and E. Fukada, Ferroelectrics, 1981, 32, 61–67 CrossRef CAS.
- Q. M. Zhang, V. Bharti and X. Zhao, Science, 1998, 280, 2101–2104 CrossRef CAS.
- Z. Y. Cheng, V. Bharti, T. B. Xu, S. X. Wang, Q. M. Zhang, T. Ramotowski, F. Tito and R. Ting, J. Appl. Phys., 1999, 86, 2208–2214 CrossRef CAS.
- Y. Tajitsu, A. Chiba, T. Furukawa, M. Date and E. Fukada, Appl. Phys. Lett., 1980, 36, 286–288 CrossRef CAS.
- Z. Y. Cheng, T. B. Xu, V. Bharti, S. X. Wang and Q. M. Zhang, Appl. Phys. Lett., 1999, 74, 1901–1903 CrossRef CAS.
- S. Lu, B. Rozic, Q. Zhang, Z. Kutnjak and R. Pirc, Appl. Phys. A: Mater. Sci. Process., 2012, 107, 559–566 CrossRef CAS.
- P. D. Thacher, J. Appl. Phys., 1968, 39, 1996–2002 CrossRef CAS.
- S. G. Lu, B. Rozic, Q. M. Zhang, Z. Kutnjak, R. Pirc, M. R. Lin, X. Y. Li and L. Gorny, Appl. Phys. Lett., 2010, 97, 202901 CrossRef.
- X. Y. Li, X. S. Qian, S. G. Lu, J. P. Cheng, Z. Fang and Q. M. Zhang, Appl. Phys. Lett., 2011, 99, 052907 CrossRef.
- S. Kar-Narayan and N. D. Mathur, J. Phys. D: Appl. Phys., 2010, 43, 032002 CrossRef.
- R. Hasegawa, Y. Takahash, H. Tadokoro and Y. Chatani, Polym. J., 1972, 3, 600–610 CrossRef CAS.
- M. A. Bachmann and J. B. Lando, Macromolecules, 1981, 14, 40–46 CrossRef CAS.
- F. Xia, Z. Y. Cheng, H. S. Xu, H. F. Li, Q. M. Zhang, G. J. Kavarnos, R. Y. Ting, G. Abdul-Sedat and K. D. Belfield, Adv. Mater., 2002, 14, 1574–1577 CrossRef CAS.
- R. Pirc, Z. Kutnjak, R. Blinc and Q. M. Zhang, Appl. Phys. Lett., 2011, 98, 021909 CrossRef.
- B. J. Chu, M. R. Lin, B. Neese, X. Zhou, Q. Chen and Q. M. Zhang, Appl. Phys. Lett., 2007, 91, 122909 CrossRef.
- J. J. Li, S. I. Seok, B. J. Chu, F. Dogan, Q. M. Zhang and Q. Wang, Adv. Mater., 2009, 21, 217–221 CrossRef CAS.
- B. J. Chu, B. Neese, M. R. Lin, S. G. Lu and Q. M. Zhang, Appl. Phys. Lett., 2008, 93, 152903 CrossRef.
- X. Z. Chen, X. S. Qian, X. Y. Li, S. G. Lu, H. M. Gu, M. R. Lin, Q. D. Shen and Q. M. Zhang, Appl. Phys. Lett., 2012, 100, 222902 CrossRef.
- R. Radebaugh, W. N. Lawless, J. D. Siegwarth and A. J. Morrow, Cryogenics, 1979, 19, 187–208 CrossRef CAS.
- E. Hegenbarth, Cryogenics, 1961, 1, 242–243 CrossRef.
- A. Kikuchi and E. Sawaguchi, J. Phys. Soc. Jpn., 1964, 19, 1497–1498 CrossRef CAS.
- W. N. Lawless, Phys. Rev. B: Solid State, 1977, 16, 433–439 CrossRef CAS.
- V. V. Shvartsman, S. E. Aksenov and E. D. Politova, Ferroelectrics, 2001, 258, 13–20 CrossRef CAS.
- R. B. Olsen, W. F. Butler, D. A. Payne, B. A. Tuttle and P. C. Held, Phys. Rev. Lett., 1980, 45, 1436–1438 CrossRef CAS.
- A. Sternberg, E. Birks, L. Shebanovs, E. Klotins, M. Ozolinsh, M. Tyunina, V. Zauls and M. Kundzinsh, Ferroelectrics, 1999, 226, 217–241 CrossRef CAS.
- B. A. Tuttle and D. A. Payne, Ferroelectrics, 1981, 37, 603–606 CrossRef CAS.
- X. H. Hao, Z. X. Yue, J. B. Xu, S. L. An and C. W. Nan, J. Appl. Phys., 2011, 110, 064109 CrossRef.
- B. Rozic, B. Malic, H. Ursic, J. Holc, M. Kosec and Z. Kutnjak, Ferroelectrics, 2011, 421, 103–107 CrossRef CAS.
- A. Sternberg, L. Shebanovs, V. Zauls and K. Kundzins, Ferroelectrics, 2003, 286, 1049–1056 CrossRef.
- D. Guyomar, G. Sebald, B. Guiffard and L. Seveyrat, J. Phys. D: Appl. Phys., 2006, 39, 4491–4496 CrossRef CAS.
- G. Sebald, S. Pruvost, L. Seveyrat, L. Lebrun, D. Guyomar and B. Guiffard, J. Eur. Ceram. Soc., 2007, 27, 4021–4024 CrossRef CAS.
- G. Sebald, B. Guiffard, L. Seveyrat, A. Benayad, L. Lebrun, S. Pruvost, D. Guyomar and Ieee, in 2006 15th IEEE International Symposium on Applications of Ferroelectrics, Ieee, New York, 2007, pp. 190–193 Search PubMed.
- D. Guyomar and G. Sebald, Int. J. Appl. Electrom., 2009, 31, 41–46 Search PubMed.
- J. Hagberg, A. Uusimaki and H. Jantunen, Appl. Phys. Lett., 2008, 92, 132909 CrossRef.
- E. H. Birks, Phys. Status Solidi A, 1986, 94, 523–527 CrossRef CAS.
- L. A. Shebanov, E. H. Birks and K. J. Borman, Ferroelectrics, 1989, 90, 165–172 CrossRef CAS.
- G. C. Lin, X. M. Xiong, J. X. Zhang and Q. Wei, J. Therm. Anal. Calorim., 2005, 81, 41–44 CrossRef CAS.
- Y. Bai, G. P. Zheng and S. Q. Shi, Mater. Res. Bull., 2011, 46, 1866–1869 CrossRef CAS.
- R. B. Zampiere, G. S. Dias, L. F. Cotica and I. A. Santos, Scr. Mater., 2012, 66, 542–545 CrossRef CAS.
- L. Shebanovs, K. Borman, W. N. Lawless and A. Kalvane, Ferroelectrics, 2002, 273, 137–142 CrossRef CAS.
- S. F. Karmanenko, O. V. Pakhomov, A. M. Prudan, A. S. Starkov and A. Eskov, J. Eur. Ceram. Soc., 2007, 27, 3109–3112 CrossRef CAS.
- Y. Bai, G. P. Zheng and S. Q. Shi, J. Appl. Phys., 2010, 108, 104102 CrossRef.
- Y. Bai, G. P. Zheng and S. Q. Shi, Appl. Phys. Lett., 2010, 96, 192902 CrossRef.
- Y. Bai, G. P. Zheng, K. Ding, L. J. Qiao, S. Q. Shi and D. Guo, J. Appl. Phys., 2011, 110, 094103 CrossRef.
- J. Parui and S. B. Krupanidhi, Phys. Status Solidi A, 2008, 2, 230–232 CrossRef CAS.
- T. M. Correia, J. S. Young, R. W. Whatmore, J. F. Scott, N. D. Mathur and Q. Zhang, Appl. Phys. Lett., 2009, 95, 182904 CrossRef.
- A. S. Mischenko, Q. Zhang, R. W. Whatmore, J. F. Scott and N. D. Mathur, Appl. Phys. Lett., 2006, 89, 242912 CrossRef.
- Z. Y. Feng, D. Q. Shi and S. X. Dou, Solid State Commun., 2011, 151, 123–126 CrossRef CAS.
- Z. Y. Feng, D. Q. Shi, R. Zeng and S. X. Dou, Thin Solid Films, 2011, 519, 5433–5436 CrossRef CAS.
- D. Saranya, A. R. Chaudhuri, J. Parui and S. B. Krupanidhi, Bull. Mater. Sci., 2009, 32, 259–262 CrossRef CAS.
- Y. He, X. M. Li, X. D. Gao, X. Leng and W. Wang, Funct. Mater. Lett., 2011, 4, 45–48 CrossRef CAS.
- T. M. Correia, S. Kar-Narayan, J. S. Young, J. F. Scott, N. D. Mathur, R. W. Whatmore and Q. Zhang, J. Phys. D: Appl. Phys., 2011, 44, 165407 CrossRef.
- H. Chen, T. L. Ren, X. M. Wu, Y. Yang and L. T. Liu, Appl. Phys. Lett., 2009, 94, 182902 CrossRef.
- P. F. Liu, J. L. Wang, X. J. Meng, J. Yang, B. Dkhil and J. H. Chu, New J. Phys., 2010, 12, 023035 CrossRef.
- V. V. Shvartsman and E. D. Politova, Ferroelectrics, 2001, 257, 75–84 CrossRef CAS.
- R. Chukka, J. W. Cheah, Z. Chen, P. Yang, S. Shannigrahi, J. Wang and L. Chen, Appl. Phys. Lett., 2011, 98, 242902 CrossRef.
| This journal is © The Royal Society of Chemistry 2013 |