A coarse-grained simulation to study the digestion and bioaccessibility of lipophilic nutrients and micronutrients in emulsion
Sébastien
Marze
*
UR1268 Biopolymères Interactions Assemblages, INRA, F-44300 Nantes, France. E-mail: sebastien.marze@nantes.inra.fr
First published on 11th November 2013
Abstract
The digestion of lipophilic nutrients and micronutrients requires numerous and simultaneous processes of chemical, physical and biological nature. Studying these processes experimentally is challenging, explaining why there is only little information about the mechanisms and interactions involved. Nevertheless, the bioaccessibility of lipophilic micronutrients is poorly understood so new investigation approaches are needed, all the more when digestion of lipophilic nutrients is also involved. In this article, the development of a coarse-grained simulation with no adjustable parameter is reported, enabling the study of the chemical and physical processes controlling bioaccessibility in such systems. The intestinal digestion of a droplet of a pure triglyceride containing a lipophilic vitamin was simulated to obtain their bioaccessibility kinetics (via lipolysis and/or solubilization in bile salt). The parameters examined here were the type of triglyceride, the type of vitamin, the digestive fluid amount, the droplet size, and different digestion conditions reflecting the in vitro or in vivo cases. Among these structure and composition parameters, the type of triglyceride and the digestion conditions had the greatest effects on bioaccessibility. An interplay between triglyceride digestion and micronutrient bioaccessibility kinetics was evidenced, highlighting the roles of the different parameters, in agreement with the experimental literature. This new approach is shown to be relevant to both nutrition and pharmacology.
1. Introduction
Because the digestion of nutrients and micronutrients consists of complex interdependent processes, its parameters and mechanisms are not well known, all the more since they are of several natures, essentially chemical, physical and biological. The study of the whole digestion of a (micro)nutrient requires these three sciences, as the endpoint is generally the bioavailability, that is the proportion used by the tissues as delivered by the systemic circulation.1 In practice, there are so many processes from the ingestion to the use that only biological aspects are classically studied. However, the chemical and physical processes in the digestive tube constitute the first step, shown to be critical for many food structures and formulations.2,3 The endpoint of this first step is called bioaccessibility and is the proportion of a (micro)nutrient transformed in its absorbable form. This is equivalent to the proportion of drug released in pharmacology. In both domains, the molecule has to be liberated from its matrix and prepared for absorption. To do so, chemical processes such as hydrolysis and physical aspects such as structural evolution and molecular diffusion act simultaneously. So such processes have to be studied simultaneously in order to identify their parameters and interactions. This is experimentally challenging to achieve, and requires a simplification to model foods, such as emulsions. Such model foods may also be simulated, giving the opportunity to understand the mechanisms involved for their digestion. Generic simulations exist mostly for bioavailability of drugs4–10 or hydrolysis of nutrients11–14 and only a few establish a kinetic relationship between one of these aspects and the matrix structural parameters.15,16 Promising methods enabling the simulation of such dynamic complex systems consist in working at a coarse-grained scale, where the fine molecular structure is not taken into account, the smallest element being either a functional group of the molecule, the molecule itself, or an assembly of molecules. This allows an expansion of the simulated space and time scales, making the link between microscopic and mesoscopic levels possible.17In this article, a model is built to study by coarse-grained simulation the role of the parameters influencing the bioaccessibility kinetics of lipophilic nutrients and micronutrients in emulsion during intestinal digestion. The effect of each parameter is studied independently, with an emphasis on the interactions between lipophilic nutrients and micronutrients, poorly known in the literature. All processes, including the main ones, lipolysis and solubilization in bile salt, are simulated from molecular knowledge, using no adjustable parameter. The results are interpreted in order to reveal the interplay between lipolysis and solubilization of glycerides and solubilization of micronutrients.
2. Simulation methods
NetLogo 4.1.3 was used to build the simulation. It is an agent-based modeling software using the Logo programming language. It is able to operate multiple agents independently and works in both 2D and 3D.182.a. Geometry
The model simulates a single lipid droplet stabilized by an interfacial layer and dispersed in an intestinal digestive fluid (IDF). It is built in 2 dimensions (2D). A square is used to represent the droplet in order to simplify the control of the interfacial layer particles during the digestion. This does not affect the specific interfacial length as the perimeter to surface area ratio is the same for a square and a circle. A square simulation box is defined, with a length of 316 patches and periodic boundary conditions. The droplet is set so that its equivalent volume ranges from 0.4 to 3% of the total simulation box equivalent volume, thus representing a dilute emulsion. The droplet length d ranges from 100 to 50 patches. The dimensions were chosen in order to limit the total number of particles in the simulation. The initial number of triglycerides (TGs) is set to (d − 1)2/3, so that the number of final digestion products, that are fatty acids (FAs) and monoglycerides (MGs), (FA + MG = 3TG) equals the initial number of patches inside the droplet. The initial number of lipophilic micronutrients (MNs) is set to 0.2% of the number of FA + MG. The density of the droplet is assumed to remain constant during digestion.2.b. Particles
Each type of molecule is defined as an agent, drawn as a specific round particle. For each type of molecule, a single particle represents a mass unity. Each simulation box patch can only be occupied by one particle at a time. Initially, TG and MN particles are set at random positions inside the droplet (lipid phase) whereas IDF particles are set at random positions outside the droplet (aqueous phase). The bile salt and lipase are not distinguished in this simulation so each IDF particle is actually defined as a bile/lipase complex, which was demonstrated to be the active form at the oil/water interface of emulsion.19 The concentration is such that lipase is in excess and bile salt is above its critical micelle concentration, so each IDF particle is actually a micelle. The interfacial layer is represented by particles situated on the patches delimiting the droplet perimeter. Using a random walk scheme, each particle is free to diffuse in its environment delimited by the interfacial layer particles, the latter being immobile. The step lengths of the walk scheme for the lipid particles are set relatively to each other as a ratio between the square root of their diffusion coefficients determined from the Stokes–Einstein equation according to the molar mass and the local viscosity.20 The MNs are assumed to have the same solubility in each glyceride class (some literature studies report an increased solubility in the digestion products21–24), so the step length of their walk is set for an averaged lipid phase viscosity, according to their molar mass. At each computation time step, the IDF particles are displaced to random positions outside the droplet, reflecting much higher diffusion coefficient for these particles compared to the lipid ones, and also possible convection of the whole droplet relative to the aqueous phase.2.c. Digestion
The simulated digestion consists of lipolysis with specific lipolysis rates (LRs) and solubilization of the digestion products and MNs in the digestive micelles with specific solubilization ratios (SRs, mass of solubilizate/mass of bile salt). Table 1 reports some literature experimental values for LR and SR. The lipolysis reactions, 1TG → 1DG + 1FA and 1DG → 1MG + 1FA where DGs are the diglycerides, are used to generate the digestion products, eventually resulting in a MG![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) FA molecular ratio of 1
FA molecular ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
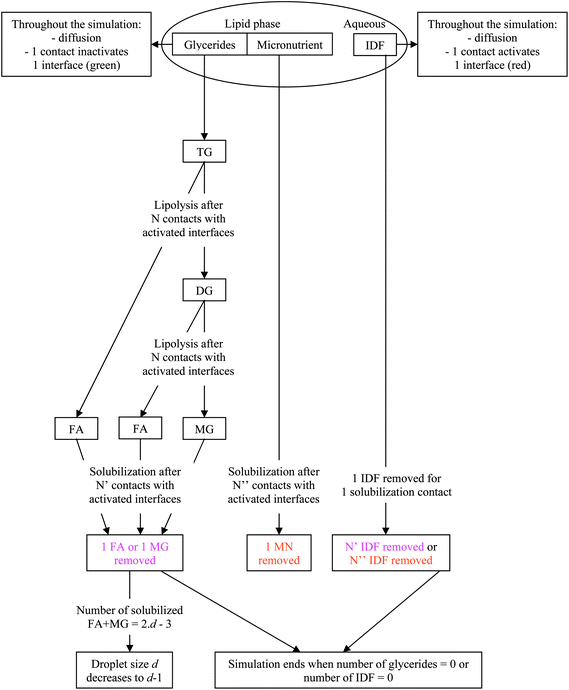
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. The difference due to the mass basis of the calculations was neglected as it is small but would imply different fractional reactions depending on the TG used. In practice, the interfacial layer particles are initially set to green. During the simulation, each time an IDF particle is on a patch in contact with an interfacial layer particle, the latter becomes red to signify an IDF particle adsorption. A reaction occurs when a TG or a DG particle is in contact with a red interfacial layer particle, the latter becoming green again to signify IDF particle inactivation. Depending on the lipolysis rate, which is assumed to be the same for TG and DG,38 the reaction is complete after a given number of contacts, inversely proportional to the LR. Similarly, partial solubilization occurs when a MG, a FA or a MN particle is in contact with a red interfacial layer particle, the latter becoming green again to signify bile solubilization. Depending on the solubilization ratio, the complete solubilization occurs after a given number of contacts, inversely proportional to the SR. In a simulation reflecting in vitro conditions where digestive micelles are assumed to saturate with solubilizates, the number of IDF particles is decreased in proportion to the number of contacts needed to solubilize the digestion products and MNs. In a simulation reflecting in vivo conditions where digestive micelles are assumed to empty during lipid absorption and recycle for other solubilizates,39,40 the number of IDF particles is set constant. In all cases, lipolysis reactions do not reduce the number of IDF particles. To conserve the density, the perimeter of the droplet is decreased as particles leave the lipid phase. All particles are counted at each computation time step and the result is expressed either as relative proportions of different particles or as bioaccessibility. The latter is expressed for FAs, MGs and MNs as the proportion of particles solubilized in bile salt relative to the amount of particles initially inside the droplet (2TG for FA and 1TG for MG). The digestion products are counted once they are solubilized in bile salt, not when they are still inside the droplet after lipolysis. The kinetics of bioaccessibility is characterized by the half life, that is the time (given as the number of computation time steps, CTS) at which half of the final bioaccessibility is reached. This enables a direct comparison of the effect of each parameter that does not require the fitting with a specific model. In summary, Fig. 1 presents a diagram illustrating the model used for the simulation.
2. The difference due to the mass basis of the calculations was neglected as it is small but would imply different fractional reactions depending on the TG used. In practice, the interfacial layer particles are initially set to green. During the simulation, each time an IDF particle is on a patch in contact with an interfacial layer particle, the latter becomes red to signify an IDF particle adsorption. A reaction occurs when a TG or a DG particle is in contact with a red interfacial layer particle, the latter becoming green again to signify IDF particle inactivation. Depending on the lipolysis rate, which is assumed to be the same for TG and DG,38 the reaction is complete after a given number of contacts, inversely proportional to the LR. Similarly, partial solubilization occurs when a MG, a FA or a MN particle is in contact with a red interfacial layer particle, the latter becoming green again to signify bile solubilization. Depending on the solubilization ratio, the complete solubilization occurs after a given number of contacts, inversely proportional to the SR. In a simulation reflecting in vitro conditions where digestive micelles are assumed to saturate with solubilizates, the number of IDF particles is decreased in proportion to the number of contacts needed to solubilize the digestion products and MNs. In a simulation reflecting in vivo conditions where digestive micelles are assumed to empty during lipid absorption and recycle for other solubilizates,39,40 the number of IDF particles is set constant. In all cases, lipolysis reactions do not reduce the number of IDF particles. To conserve the density, the perimeter of the droplet is decreased as particles leave the lipid phase. All particles are counted at each computation time step and the result is expressed either as relative proportions of different particles or as bioaccessibility. The latter is expressed for FAs, MGs and MNs as the proportion of particles solubilized in bile salt relative to the amount of particles initially inside the droplet (2TG for FA and 1TG for MG). The digestion products are counted once they are solubilized in bile salt, not when they are still inside the droplet after lipolysis. The kinetics of bioaccessibility is characterized by the half life, that is the time (given as the number of computation time steps, CTS) at which half of the final bioaccessibility is reached. This enables a direct comparison of the effect of each parameter that does not require the fitting with a specific model. In summary, Fig. 1 presents a diagram illustrating the model used for the simulation.
| Molecules | n | LR | SR (FA) | SR (MG) |
|---|---|---|---|---|
| Caprylic glycerides | 8 | 2.06 ± 0.97 | 3.5 | |
| Capric glycerides | 10 | 1.56 ± 0.62 | 0.88 | |
| Lauric glycerides | 12 | 1.06 ± 0.34 | 0.78 | 0.58 |
| Myristic glycerides | 14 | 0.596 ± 0.336 | 0.16 | |
| Palmitic glycerides | 16 | 0.362 ± 0.245 | 0.086 | 0.053 |
| Stearic glycerides | 18 | 0.283 ± 0.283 | 0.042 | |
| Oleic glycerides | 18* | 1 | 0.62 | 0.52 |
| Linoleic glycerides | 18* | 0.48 | ||
| Eicosapentaenoic glycerides | 20* | 0.162 ± 0.027 | ||
| Docosahexaenoic glycerides | 22* | 0.158 ± 0.071 | ||
| Retinol (vitA) | 0.0043 | |||
| α-Tocopherol (vitE) | 0.12 ± 0.06 |
2.d. Systems under study
The systems were chosen on the basis of the availability of digestion data in the literature, where mostly MCT oils (usually composed of caprylic and capric acids) and LCT vegetable oils (usually rich in oleic and linoleic acids) are represented. Thus, the digestion of tricaprylin (TC) and triolein (TO) was investigated, as well as a model long chain n-3 triglyceride interpolated from trieicosapentaenoin and tridocosahexaenoin (TEP–DH). To model integer data, the LR values of Table 1 were rounded to 2, 1 and 1/6 respectively, and the SR values for digestion products (considering that FAs and MGs have the same SRs) were rounded to 3.5, 0.5 and 0.1 respectively. The latter was extrapolated by noticing that ln(SR) as a function of the number of carbons in the aliphatic chain n follows a linear law of the form (−0.5n + b) for saturated MGs and FAs. For unsaturated glycerides, data are available only for oleic acid, monoolein and linoleic acid, with a common SR value around 0.5. An extrapolation from this value to n = 21 using a linear law with the same slope gives a SR of approximately 0.1 for TEP–DH digestion products. The SR of lipophilic MNs is not well documented, in contrast to lipophilic drugs.41 Nevertheless, some SRs were measured for a few vitamins and sterols. Vitamins A and E (retinol abbr. vitA and α-tocopherol abbr. vitE) were chosen because they present a low and a high SR respectively. Again, the SR values were rounded, to 0.005 and 0.1 respectively. The initial number of IDF particles was set as a ratio of the expected number of particles of digestion products (3TG), of 0.5, 1 or 2, which is in the typical range for the bile salt/(FA + MG) ratio evaluated from in vivo studies.42–44In summary, the parameters that were varied in the present simulation were the IDF particle conditions (saturated or recycled, IDF/(FA + MG) ratio), the types of triglycerides and of micronutrients, and the size of the droplet (square of length of 50, 75 or 100). The number of particles treated simultaneously during the simulation ranged typically between 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 30
000 and 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. Several simulations could be run simultaneously on a dedicated normal PC, with a duration ranging typically between 0.5 and 5 h.
000. Several simulations could be run simultaneously on a dedicated normal PC, with a duration ranging typically between 0.5 and 5 h.
All simulations were run in triplicate and the results are given as averages and standard deviations.
3. Results
First, control simulations with no MNs were run to define the contact rules needed to reproduce the relative LR between the three TGs under various conditions. In these simulations, only lipolysis was taken into account and no solubilization was permitted, therefore the droplet size and the number of IDF particles remained constant. When the relative LRs were recovered, simulations with solubilization and no MNs were run to quantify the contribution of the solubilization of the lipolysis products under the same conditions. For TC, the half life was not affected within 10% whereas for TO and TEP–DH, it was increased by a factor 2.3 ± 0.3 and 1.7 ± 0.1 respectively. This shows that the limiting process is lipolysis for TC and solubilization for TO and TEP–DH.Then, full simulations with MNs were run. Tables 2–5 report the final bioaccessibility and half life of FAs and MNs for all conditions described in the Simulation methods section. First, FA final bioaccessibility and FA half life do not significantly differ depending on the MNs, and are also similar for the simulations with no MN (results not shown). Then, FA final bioaccessibility ranges from 4.5% to 100% and FA half life may differ by a factor of more than 60 depending on the conditions, the greatest effect being due to the TG chain length. Similarly, MN final bioaccessibility ranges from 2.5% to 100% and MN half life may differ by a factor of more than 60 depending on the conditions, the greatest effect being due to the bile conditions (saturated or recycled). These results will be commented upon in the Discussion section.
| IDF/(FA + MG) mass ratio | TC + vitA | TO + vitA | TEP–DH + vitA | TC + vitE | TO + vitE | TEP–DH + vitE |
|---|---|---|---|---|---|---|
| Bile is saturated | ||||||
| 0.5 | 100.0 ± 0.0 | 23.7 ± 0.1 | 4.4 ± 0.2 | 100.0 ± 0.0 | 24.2 ± 0.1 | 4.5 ± 0.1 |
| 144 ± 7 | 185 ± 1 | 335 ± 11 | 146 ± 2 | 186 ± 18 | 324 ± 1 | |
| 1 | 100.0 ± 0.0 | 47.2 ± 0.2 | 9.6 ± 0.2 | 100.0 ± 0.0 | 48.1 ± 0.1 | 9.6 ± 0.2 |
| 89 ± 1 | 229 ± 14 | 321 ± 13 | 85 ± 4 | 225 ± 13 | 301 ± 24 | |
| 2 | 100.0 ± 0.0 | 93.1 ± 0.9 | 20.0 ± 0.2 | 100.0 ± 0.0 | 96.9 ± 0.3 | 20.1 ± 0.2 |
| 61 ± 9 | 308 ± 7 | 365 ± 8 | 59 ± 5 | 331 ± 19 | 359 ± 12 | |
| Bile is recycled | ||||||
| 0.5 | 128 ± 1 | 675 ± 64 | 3636 ± 125 | 131 ± 7 | 684 ± 25 | 3704 ± 44 |
| 1 | 84 ± 6 | 439 ± 29 | 2386 ± 96 | 89 ± 3 | 444 ± 33 | 2334 ± 71 |
| 2 | 62 ± 1 | 297 ± 1 | 1546 ± 95 | 66 ± 7 | 287 ± 40 | 1552 ± 90 |
| IDF/(FA + MG) mass ratio | TC + vitA | TO + vitA | TEP–DH + vitA | TC + vitE | TO + vitE | TEP–DH + vitE |
|---|---|---|---|---|---|---|
| Bile is saturated | ||||||
| 0.5 | 9.2 ± 1.2 | 2.6 ± 0.2 | 3.6 ± 1.0 | 97.2 ± 2.5 | 26.2 ± 10.6 | 26.0 ± 2.6 |
| 450 ± 21 | 246 ± 33 | 268 ± 86 | 313 ± 34 | 274 ± 77 | 216 ± 48 | |
| 1 | 12.6 ± 2.2 | 8.0 ± 1.5 | 4.3 ± 1.8 | 97.0 ± 2.6 | 64.3 ± 6.1 | 24.8 ± 0.3 |
| 264 ± 42 | 285 ± 71 | 314 ± 128 | 146 ± 15 | 300 ± 48 | 226 ± 73 | |
| 2 | 11.8 ± 0.7 | 24.5 ± 5.7 | 8.5 ± 1.3 | 98.7 ± 2.3 | 97.3 ± 0.6 | 40.7 ± 10.3 |
| 149 ± 23 | 597 ± 43 | 482 ± 80 | 97 ± 12 | 150 ± 16 | 263 ± 66 | |
| Bile is recycled | ||||||
| 0.5 | 9.5 ± 1.4 | 35.2 ± 4.4 | 86.2 ± 1.9 | 98.0 ± 1.7 | 100.0 ± 0.0 | 100.0 ± 0.0 |
| 306 ± 10 | 1312 ± 150 | 6238 ± 853 | 209 ± 24 | 752 ± 48 | 2367 ± 488 | |
| 1 | 11.0 ± 1.1 | 38.8 ± 3.8 | 91.6 ± 2.7 | 97.8 ± 2.6 | 100.0 ± 0.0 | 100.0 ± 0.0 |
| 213 ± 19 | 837 ± 94 | 3739 ± 568 | 161 ± 51 | 557 ± 79 | 1572 ± 149 | |
| 2 | 14.2 ± 1.4 | 43.9 ± 3.2 | 95.2 ± 3.1 | 97.7 ± 1.9 | 100.0 ± 0.0 | 100.0 ± 0.0 |
| 146 ± 14 | 556 ± 37 | 2147 ± 300 | 102 ± 16 | 285 ± 21 | 1212 ± 206 | |
| Length | TC + vitA | TO + vitA | TEP–DH + vitA | TC + vitE | TO + vitE | TEP–DH + vitE |
|---|---|---|---|---|---|---|
| Bile is saturated | ||||||
| 50 | 100.0 ± 0.0 | 48.0 ± 0.2 | 8.8 ± 0.4 | 100.0 ± 0.0 | 48.2 ± 0.2 | 8.4 ± 0.4 |
| 122 ± 10 | 324 ± 8 | 687 ± 30 | 130 ± 14 | 353 ± 2 | 647 ± 21 | |
| 75 | 100.0 ± 0.0 | 47.8 ± 0.3 | 9.3 ± 0.2 | 100.0 ± 0.0 | 47.9 ± 0.2 | 9.3 ± 0.1 |
| 96 ± 4 | 253 ± 3 | 417 ± 17 | 98 ± 2 | 272 ± 9 | 426 ± 27 | |
| 100 | 100.0 ± 0.0 | 47.2 ± 0.2 | 9.6 ± 0.2 | 100.0 ± 0.0 | 48.1 ± 0.1 | 9.6 ± 0.2 |
| 89 ± 1 | 229 ± 14 | 321 ± 13 | 85 ± 4 | 225 ± 13 | 301 ± 24 | |
| Bile is recycled | ||||||
| 50 | 111 ± 6 | 592 ± 15 | 3116 ± 55 | 114 ± 8 | 598 ± 41 | 3100 ± 64 |
| 75 | 93 ± 3 | 476 ± 24 | 2600 ± 47 | 93 ± 6 | 474 ± 11 | 2650 ± 19 |
| 100 | 84 ± 6 | 439 ± 29 | 2386 ± 96 | 89 ± 3 | 444 ± 33 | 2334 ± 71 |
| Length | TC + vitA | TO + vitA | TEP–DH + vitA | TC + vitE | TO + vitE | TEP–DH + vitE |
|---|---|---|---|---|---|---|
| Bile is saturated | ||||||
| 50 | 6.6 ± 1.8 | 3.9 ± 0.2 | 2.5 ± 0.8 | 100.0 ± 0.0 | 68.7 ± 1.2 | 47.3 ± 2.3 |
| 347 ± 50 | 362 ± 170 | 244 ± 73 | 267 ± 62 | 309 ± 166 | 356 ± 128 | |
| 75 | 9.5 ± 1.8 | 4.3 ± 1.2 | 3.3 ± 0.4 | 99.1 ± 1.6 | 60.9 ± 10.3 | 22.7 ± 5.1 |
| 221 ± 24 | 347 ± 150 | 398 ± 20 | 195 ± 33 | 199 ± 19 | 369 ± 135 | |
| 100 | 12.6 ± 2.2 | 8.0 ± 1.5 | 4.3 ± 1.8 | 97.0 ± 2.6 | 64.3 ± 6.1 | 24.8 ± 0.3 |
| 264 ± 42 | 285 ± 71 | 314 ± 128 | 146 ± 15 | 300 ± 48 | 226 ± 73 | |
| Bile is recycled | ||||||
| 50 | 9.6 ± 1.7 | 20.3 ± 5.5 | 65.1 ± 8.4 | 98.0 ± 2.0 | 100.0 ± 0.0 | 100.0 ± 0.0 |
| 316 ± 41 | 1080 ± 96 | 5234 ± 359 | 183 ± 14 | 614 ± 165 | 1855 ± 195 | |
| 75 | 8.9 ± 0.7 | 33.0 ± 4.0 | 90.1 ± 0.5 | 96.7 ± 3.7 | 100.0 ± 0.0 | 100.0 ± 0.0 |
| 222 ± 24 | 1006 ± 56 | 3807 ± 339 | 142 ± 48 | 461 ± 122 | 1468 ± 28 | |
| 100 | 11.0 ± 1.1 | 38.8 ± 3.8 | 91.6 ± 2.7 | 97.8 ± 2.6 | 100.0 ± 0.0 | 100.0 ± 0.0 |
| 213 ± 19 | 837 ± 94 | 3739 ± 568 | 161 ± 51 | 557 ± 79 | 1572 ± 149 | |
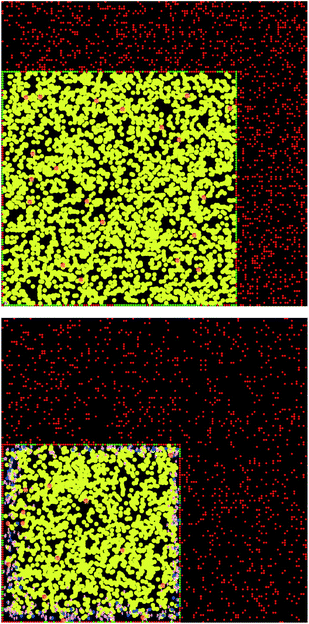
Here, a few representative results are presented starting in Fig. 2 with pictures from a simulation in a case where bile is saturated. Different types of particles are visible, from pure TG/MN to mixed TG/DG/MG/FA/MN inside the droplet. Obviously, the number of IDF particles decreases. Note that the digestion products are mainly located near the interface before solubilization (afterwards, they are removed from the simulation together with the IDF particles). The relative percentages of each glyceride are given in Fig. 3 in another case where bile is saturated, showing an incomplete digestion due to a limiting number of bile salt. These relative percentages should not be confused with bioaccessibility, the maximum for the digestion products being 66.7% for FAs and 33.3% for MGs. For the same conditions, those values are indeed reached in the case where bile is recycled, providing bile salt in excess hence a complete digestion (Fig. 4). Note that all glycerides except DG display sublinear kinetics.
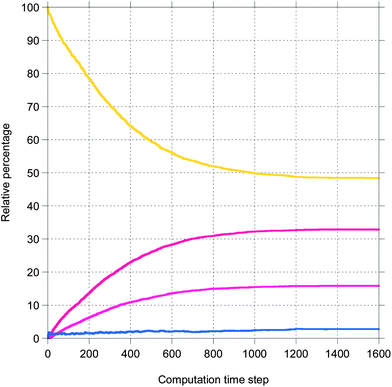 | ||
| Fig. 3 Representative result for the relative percentage of glycerides from a simulation of the digestion of TO + vitA with a droplet length of 100 and an IDF/(FA + MG) mass ratio of 1 (bile is saturated). The same colors as Fig. 2. | ||
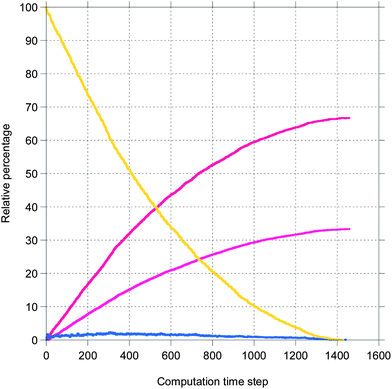 | ||
| Fig. 4 The same as Fig. 3 except that bile is recycled. | ||
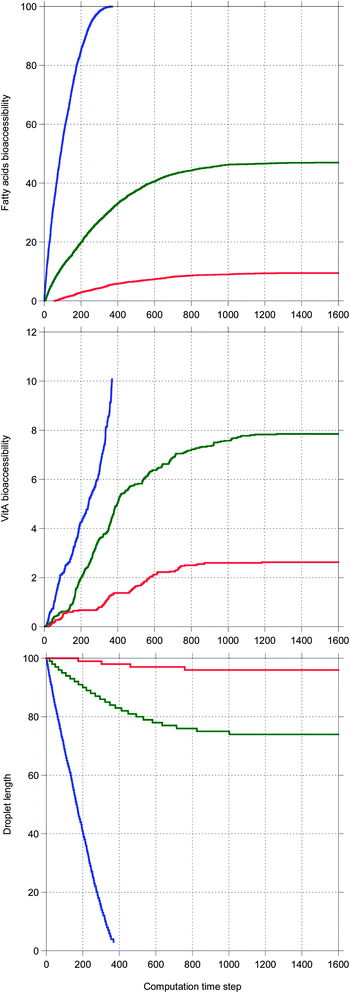
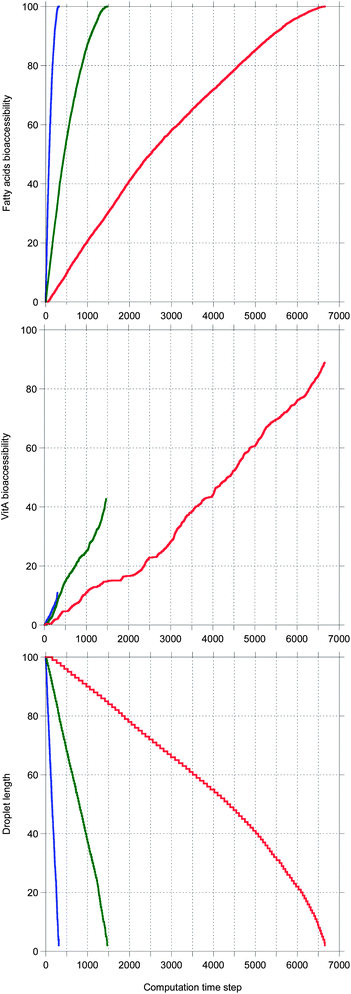
Fig. 5 shows the main results allowing a comparison between the digestion of the three TG + vitA systems in a case where bile is saturated. Very different kinetics are obtained, only TC being completely digested, as illustrated by the 100% bioaccessibility of its fatty acids. This is reflected in the decrease of the droplet length which is complete for TC, only partial for TO and very limited for TEP–DH. In contrast, the vitA bioaccessibility is low in all systems, although the same ordering is recovered. Note that all kinetics are sublinear except for vitA in TC being superlinear.
In Fig. 6, the same systems are compared in a case where bile is recycled. Again the kinetics are very different depending on the system, but here all TG digestions are complete. The ordering for all quantities is the same as in Fig. 5, but here all vitA kinetics are superlinear and higher values are reached for TO and TEP–DH.
 | ||
| Fig. 6 The same as Fig. 5 except that bile is recycled. | ||
Note that all sublinear bioaccessibility curves actually display the typical shape associated with lipid digestion kinetics. In contrast, the shape of the superlinear bioaccessibility curves was unexpected.
4. Discussion
In this section, the results in the tables are described in terms of trends which are compared to experimental data from the literature. All the trends are statistically significant except when mentioned. Then, the simulation is discussed in the context of available models and simulations of the literature.4.a. Effect of the triglyceride
Except when bile is recycled where final FA bioaccessibility is always 100%, tables show that final FA bioaccessibility decreases and FA half life increases with the chain length of TGs. This is an expected result due to both LR and SR decreasing as a function of the chain length of TGs (see Table 1 and ref. 3).When bile is saturated, final MN bioaccessibility decreases with the chain length of TGs and MN half life is not significantly affected. When bile is recycled, final MN bioaccessibility increases and MN half life increases with the chain length of TGs. This contradiction is reflected in the literature. Most authors reported an increase of MN bioaccessibility with the chain length of TGs in vitro45–53 and in vivo.54–61 Nevertheless, some authors reported a decrease of MN bioaccessibility with the chain length of TGs (ref. 52 and 53 for fish oil, and ref. 62–66) or no clear effect of the chain length of TGs (ref. 46 for lutein, and ref. 23, 24, 67 and 68).
The present simulation when bile is recycled shows that increasing the chain length of TG results in longer digestion, giving more time for MNs to solubilize in bile salt, hence a higher MN bioaccessibility. Thus, an interplay is evidenced between the duration of the TG digestion and the MN bioaccessibility. In fact, the same would be true if bile was in excess in the cases where bile is saturated, as proven by Fig. 7 showing that MN bioaccessibility as a function of FA bioaccessibility is almost not affected by the bile conditions. Fig. 7 also suggests that the relationship between these bioaccessibilities is not strictly linear as postulated by several authors,69,70 but might rather be superlinear with seemingly linear parts. This superlinearity could be due to the evolution of the droplet length, decreasing towards the molecular diffusion length as digestion progresses.
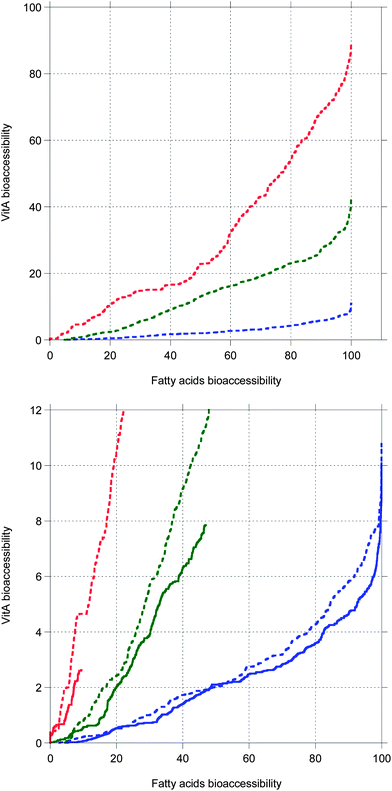 | ||
| Fig. 7 VitA bioaccessibility as a function of fatty acids bioaccessibility. Top: data from Fig. 6. Bottom: close-up to compare data from Fig. 6 (dashed lines, bile is recycled) and data from Fig. 5 (full lines, bile is saturated). | ||
4.b. Effect of the micronutrient
Whatever the other conditions are, vitE always shows a higher final MN bioaccessibility and shorter MN half life than vitA. No data are available to check this prediction and the in vivo data of absorption are highly variable, typically from 50 to 90%,71 making a direct comparison difficult.The type of MNs does not significantly affect final FA bioaccessibility and FA half life, which is an expected result as the concentration of MNs in TGs is very low.
4.c. Effect of the IDF/(FA + MG) ratio
When bile is saturated, final bioaccessibility increases and half life increases with the IDF/(FA + MG) ratio, except for TC where final bioaccessibility is not significantly affected and half life decreases with the IDF/(FA + MG) ratio, showing that bioaccessibility is more efficient at high IDF/(FA + MG) ratios. For TEP–DH, even though the mean half life increases with the IDF/(FA + MG) ratio, the difference is not always significant taking the standard deviation into account. For TO + vitE, the trend of the MN half life is uncertain.When bile is recycled, whatever the other conditions are, final bioaccessibility is not significantly affected and half life decreases with the IDF/(FA + MG) ratio.
The literature shows that when the concentration of IDF increases at constant glyceride concentration (as in the present simulation), the lipolysis and bioaccessibility of glycerides72–75 and the bioaccessibility of lipophilic MNs75–78 follow non-monotonic curves with a maximum plateau at intermediate concentrations. Reciprocally, when the concentration of glycerides increases at constant IDF concentration, the same non-monotonic trends are reported for lipolysis and bioaccessibility of glycerides48,50,73,74 and the bioaccessibility of lipophilic MNs.46,48,50,52,59,61,79
The present simulation recovers these results, what may again be understood as an interplay between the duration of the TG digestion and the MN bioaccessibility. When bile is saturated (equivalent to high TG or low IDF concentrations), the digestion duration decreases with decreasing IDF/(FA + MG) ratio (increasing TG concentration), giving less time for the MNs to solubilize hence a lower MN bioaccessibility. When bile is recycled (equivalent to intermediate TG or IDF concentrations), the digestion duration increases with decreasing IDF/(FA + MG) ratio (increasing TG concentration), giving more time for the MNs to solubilize, but resulting in a MN bioaccessibility plateau because the duration of the MN solubilization also increases.
4.d. Effect of the droplet size
Whatever the other conditions are, final FA bioaccessibility is not significantly affected and FA half life decreases with the droplet length. This is a known effect of the specific interfacial area (increasing with the droplet length in this single droplet simulation), of which the increase results in faster glyceride digestion and bioaccessibility (see ref. 3). This should not be confused with the effect of the droplet size in emulsion where the number of droplets and the dispersed volume fraction may also vary, making the specific interfacial area and the droplet size inversely proportional.20For the vitA systems, final MN bioaccessibility increases with the droplet length and MN half life is not significantly affected, except for TC where the MN half life decreases with the droplet length. For TC + vitA when bile is recycled, the trend of the final MN bioaccessibility is uncertain. For the vitE systems, final MN bioaccessibility and MN half life are not significantly affected by the droplet length. The same effect of the specific interfacial area explains these results, but vitE is less affected because it is always solubilized faster and to a higher extent. In the literature, recent articles reported an increasing MN bioaccessibility with decreasing particle size,78,80–83 or increasing specific interfacial area, thus in agreement with the present simulation results.
4.e. Effect of the bile conditions
When bile is recycled, final FA bioaccessibility is always 100% because this is the endpoint of the simulation. So it is always equal to or higher than when bile is saturated. At a comparable final FA bioaccessibility of 100% (for TC systems), FA half life is not significantly affected by the bile conditions.Final MN bioaccessibility and MN half life are always greater when bile is recycled than when bile is saturated, except for TC systems where the differences are not statistically significant.
These results may explain the high variability of bioaccessibility and bioavailability data found in the literature,3,71 especially when in vitro and in vivo data are compared. The absorption of EPA and DHA was indeed found to be higher than 98% in vivo,84 whereas the bioaccessibility was about 50% in a static in vitro study.85 The present simulation shows that in most static in vitro cases, bile salt is in lower total concentration than in vivo, limiting glycerides and lipophilic MN solubilization. However, Fig. 7 suggests that in the excess presence of bile salt, the in vitro cases would follow the same MN bioaccessibility vs. FA bioaccessibility curve as the in vivo cases. Nevertheless, it is known that a high bile salt concentration inhibits lipolysis,72,74 so using dynamic in vitro methods is preferable.86
4.f. Comparison to other simulations
With a similar aim in mind, that is studying digestion and/or bioavailability, hydrolysis modeling by enzymologists11–14 or generic dissolution/absorption simulations by pharmacologists4–10 treated one part of the present problem, and did not consider the detailed matrix structural parameters (only size is included in the dissolution number by pharmacologists). When hydrolysis and solubilization both affect the structure, only a few attempts exist in the literature by food scientists.15,16,87 Nevertheless, none of these are completely satisfactory, because these do not include MNs and either treat hydrolysis and solubilization with a single parameter,15,16 or neglect the matrix structural details.87 Moreover, all communities use adjustable parameters, which are not always linked to experimentally measurable quantities.The present bioaccessibility simulation is able to take all these aspects into account (not including absorption) with no adjustable parameter, the required molecular properties coming from experimentally measurable quantities of the literature. It recovers the typical lipolysis profiles modeled by enzymologists11–14 (Fig. 3). It confirms the roles of the formulation and structural parameters at different scales from microscopic (interface) to mesoscopic (droplet size) found for TG digestion,15,16 and extends those to lipophilic MN bioaccessibility. It thus precises the parameters that could be used by pharmacologists to specifically design emulsion-based drug dosage formulations.
5. Conclusion
To highlight the results, first the coarse-grained simulation presented here is only based on experimentally measurable quantities, using no adjustable parameter. Then, although it is a single droplet model, it features the same parameters as for emulsion, and enables the study of their effects independently. Applied to lipophilic (micro)nutrients digestion and bioaccessibility, it was able to identify the limiting processes as well as the mechanisms responsible for the effects of each parameter. This new approach is thus promising to formulate emulsion-based foods or drugs. The present simulation constitutes a fundamental starting point, but is flexible so independent particles could be used for bile and lipase, or the role of calcium on the formation of salts of saturated fatty acids could be integrated, for instance. It will be refined to gain realism by using e.g. triglyceride mixtures, different emulsifiers and their competition or inhibition at the interface, a gastric step, multiple nutrients and associated hydrolases (mainly proteases), other lipophilic micronutrients, mixed micelles structure, micronutrient solubility in digestion products. Another improvement will be to make the time step explicit in order to be fully quantitative. To validate the effects of these parameters, a dynamic experimental setup is currently designed to reproduce the conditions of a single droplet digestion, and overcome the limitations of static in vitro methods.Abbreviations
| IDF | Intestinal digestive fluid |
| TG | Triglyceride |
| DG | Diglyceride |
| MG | Monoglyceride |
| FA | Fatty acid |
| MN | Micronutrient |
| LR | Lipolysis rate |
| SR | Solubilization ratio |
| CTS | Computation time step |
| MCT | Medium chain triglyceride |
| LCT | Long chain triglyceride |
| TC | Tricaprylin |
| TO | Triolein |
| TEP–DH | Trieicosapentaenoin and tridocosahexaenoin |
| EPA | Eicosapentaenoic acid |
| DHA | Docosahexaenoic acid |
| vitA | Vitamin A |
| vitE | Vitamin E. |
Acknowledgements
The author acknowledges the ISC-PIF (Paris Île-de-France Complex Systems Institute) for the IDEAS workshop (Ideas for Design, knowledge Engineering Applied to living complex Systems), Olivier Vitrac (INRA Île-de-France) for his introduction to coarse-grained simulation, and the Carnot Institute Qualiment for financial support.References
- S. J. Fairweather-Tait and S. Southon, in Encyclopedia of Food Sciences and Nutrition, ed. B. Caballero, L. Trugo and P. Finglas, Academic Press, London, 2003, pp. 478–484 Search PubMed.
- J. Parada and J. M. Aguilera, J. Food Sci., 2007, 72, R21–R32 CrossRef CAS PubMed.
- S. Marze, Crit. Rev. Food Sci. Nutr., 2013, 53, 76–108 CrossRef CAS PubMed.
- G. L. Amidon, H. Lennernäs, V. P. Shah and J. R. Crison, Pharm. Res., 1995, 12, 413–420 CrossRef CAS.
- L. X. Yu, E. Lipka, J. R. Crison and G. L. Amidon, Adv. Drug Delivery Rev., 1996, 19, 359–376 CrossRef CAS.
- M. N. Martinez and G. L. Amidon, J. Clin. Pharmacol., 2002, 42, 620–643 CrossRef CAS PubMed.
- K. S. Pang, Drug Metab. Dispos., 2003, 31, 1507–1519 CrossRef CAS PubMed.
- S. Willmann, W. Schmitt, J. Keldenich, J. Lippert and J. B. Dressman, Med. Chem., 2004, 47, 4022–4031 CrossRef CAS PubMed.
- K. Sugano, Chem. Biodiversity, 2009, 6, 2014–2029 CAS.
- K. Sugano, Int. J. Pharm., 2010, 398, 73–82 CrossRef CAS PubMed.
- C. S. Wang, J. A. Hartsuck and D. Downs, Biochemistry, 1988, 27, 4834–4840 CrossRef CAS.
- H. Hermansyah, M. Kubo, N. Shibasaki-Kitakawa and T. Yonemoto, Biochem. Eng. J., 2006, 31, 125–132 CrossRef CAS PubMed.
- H. Hermansyah, A. Wijanarko, M. Kubo, N. Shibasaki-Kitakawa and T. Yonemoto, Bioprocess Biosyst. Eng., 2010, 33, 787–796 CrossRef CAS PubMed.
- D. A. Mitchell, J. A. Rodriguez, F. Carrière, J. Baratti and N. Krieger, J. Biotechnol., 2008, 133, 343–350 CrossRef CAS PubMed.
- Y. Li and D. J. McClements, J. Agric. Food Chem., 2010, 58, 8085–8092 CrossRef CAS PubMed.
- S. Marze and M. Choimet, Soft Matter, 2012, 8, 10982–10993 RSC.
- Model Reduction and Coarse-Graining Approaches for Multiscale Phenomena, ed. A. N. Gorban, N. K. Kazantzis, I. G. Kevrekidis, H. C. Öttinger and C. Theodoropoulos, Springer Berlin Heidelberg, New York, 2006 Search PubMed.
- U. Wilensky, NetLogo, http://ccl.northwestern.edu/netlogo/, Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL, 1999.
- D. Lairon, G. Nalbone, H. Lafont, J. Leonardi, J. L. Vigne, C. Chabert, J. C. Hauton and R. Verger, Biochim. Biophys. Acta, 1980, 618, 119–128 CrossRef CAS.
- S. Marze, M. Choimet and L. Foucat, Soft Matter, 2012, 8, 10994–11004 RSC.
- D. J. W. Grant and I. K. A. Abougela, Int. J. Pharm., 1983, 17, 77–89 CrossRef CAS.
- S. Meguro, K. Higashi, T. Hase, Y. Honda, A. Otsuka, I. Tokimitsu and H. Itakura, Eur. J. Clin. Nutr., 2001, 55, 513–517 CrossRef CAS PubMed.
- G. A. Kossena, B. J. Boyd, C. J. H. Porter and W. N. Charman, J. Pharm. Sci., 2003, 92, 634–648 CrossRef CAS PubMed.
- G. A. Kossena, W. N. Charman, B. J. Boyd, D. E. Dunstan and C. J. H. Porter, J. Pharm. Sci., 2004, 93, 332–348 CrossRef CAS PubMed.
- B. Entressangles, L. Paséro, P. Savary, L. Sarda and P. Desnuelle, Bull. Soc. Chim. Biol., 1961, 43, 581–591 CAS.
- R. G. Jensen, J. Sampugna, R. M. Parry Jr, K. M. Shahani and R. C. Chandan, J. Dairy Sci., 1962, 45, 1527–1529 CrossRef CAS.
- B. M. Laws and J. H. Moore, Biochem. J., 1963, 87, 632–638 CAS.
- Y. K. Yip, S. Ramachandran and S. R. Wagle, Proc. Soc. Exp. Biol. Med., 1975, 149, 683–687 CrossRef CAS.
- C. S. Wang, A. Kuksis and F. Manganaro, Lipids, 1982, 17, 278–284 CrossRef CAS.
- L. Y. Yang, A. Kuksis and J. J. Myher, J. Lipid Res., 1990, 31, 137–147 CAS.
- I. Ikeda, E. Sasaki, H. Yasunami, S. Nomiyama, M. Nakayama, M. Sugano, K. Imaizumi and K. Yazawa, Biochim. Biophys. Acta, 1995, 1259, 297–304 CrossRef.
- Y. Yang and M. E. Lowe, J. Lipid Res., 2000, 41, 48–57 CAS.
- A. F. Hofmann, Biochim. Biophys. Acta, 1963, 70, 306–316 CrossRef CAS.
- C. P. Freeman, Br. J. Nutr., 1969, 23, 249–263 CrossRef CAS.
- M. El-Gorab and B. A. Underwood, Biochim. Biophys. Acta, 1973, 306, 58–66 CrossRef CAS.
- J. Imai, M. Hayashi, S. Awazu and M. Hanano, Chem. Pharm. Bull., 1983, 31, 4077–4082 CrossRef CAS.
- P. B. Nielsen, A. Müllertz, T. Norling and H. G. Kristensen, Int. J. Pharm., 2001, 222, 217–224 CrossRef CAS.
- J. A. Rodriguez, Y. Ben Ali, S. Abdelkafi;, L. D. Mendoza, J. Leclaire, F. Fotiadu, G. Buono, F. Carrière and A. Abousalham, Biochim. Biophys. Acta, 2010, 1801, 77–83 CrossRef CAS PubMed.
- J. M. Dietschy, J. Lipid Res., 1968, 9, 297–309 CAS.
- C. T. Phan and P. Tso, Front. Biosci., 2001, 6, 299–319 CrossRef PubMed.
- T. S. Wiedmann and L. Kamel, J. Pharm. Sci., 2002, 91, 1743–1764 CrossRef CAS PubMed.
- B. Borgström, A. Dahlqvist, G. Lundh and J. Sjövall, J. Clin. Invest., 1957, 36, 1521–1536 CrossRef PubMed.
- M. Rautureau and J. C. Rambaud, Gut, 1981, 22, 393–397 CrossRef CAS.
- P. L. Zentler-Munro, D. R. Fine, W. J. F. Fitzpatrick and T. C. Northfield, Gut, 1984, 25, 491–499 CrossRef CAS.
- A. von Bonsdorff-Nikander, L. Christiansen, L. Huikko, A. M. Lampi, V. Piironen, J. Yliruusi and A. M. Kaukonen, Lipids, 2005, 40, 181–190 CrossRef CAS PubMed.
- T. Huo, M. G. Ferruzzi, S. J. Schwartz and M. L. Failla, J. Agric. Food Chem., 2007, 55, 8950–8957 CrossRef CAS PubMed.
- B. Nidhi and V. Baskaran, J. Am. Oil Chem. Soc., 2011, 88, 367–372 CrossRef CAS PubMed.
- K. Ahmed, Y. Li, D. J. McClements and H. Xiao, Food Chem., 2012, 132, 799–807 CrossRef CAS PubMed.
- C. Qian, E. A. Decker, H. Xiao and D. J. McClements, Food Chem., 2012, 135, 1440–1447 CrossRef CAS PubMed.
- L. Salvia-Trujillo, C. Qian, O. Martín-Belloso and D. J. McClements, Food Chem., 2013, 139, 878–884 CrossRef CAS PubMed.
- Y. Yang and D. J. McClements, Food Chem., 2013, 141, 473–481 CrossRef CAS PubMed.
- I. J. P. Colle, S. van Buggenhout, L. Lemmens, A. M. van Loey and M. E. Hendrickx, Food Res. Int., 2012, 45, 250–255 CrossRef CAS PubMed.
- I. J. P. Colle, L. Lemmens, S. van Buggenhout, K. Met, A. M. van Loey and M. E. Hendrickx, Food Res. Int., 2013, 51, 32–38 CrossRef CAS PubMed.
- C. Sylvén and B. Borgström, J. Lipid Res., 1969, 10, 351–355 Search PubMed.
- I. Holmberg, L. Aksnes, T. Berlin, B. Lindbäck, J. Zemgals and B. Lindeke, Biopharm. Drug Dispos., 1990, 11, 807–815 CrossRef CAS.
- D. Behrens, R. Fricker, A. Bodoky, J. Drewe, F. Harder and M. Heberer, J. Pharm. Sci., 1996, 85, 666–668 CrossRef CAS PubMed.
- P. Borel, V. Tyssandier, N. Mekki, P. Grolier, Y. Rochette, M. C. Alexandre-Gouabau, D. Lairon and V. Azaïs-Braesco, J. Nutr., 1998, 128, 1361–1367 CAS.
- S. M. Caliph, W. N. Charman and C. J. H. Porter, J. Pharm. Sci., 2000, 89, 1073–1084 CrossRef CAS.
- C. J. H. Porter, A. M. Kaukonen, A. Taillardat-Bertschinger, B. J. Boyd, J. M. O'Connor, G. A. Edwards and W. N. Charman, J. Pharm. Sci., 2004, 93, 1110–1121 CrossRef CAS PubMed.
- C. J. H. Porter, A. M. Kaukonen, B. J. Boyd, G. A. Edwards and W. N. Charman, Pharm. Res., 2004, 21, 1405–1412 CrossRef CAS.
- K. W. Y. Lee, C. J. H. Porter and B. J. Boyd, J. Pharm. Sci., 2013, 102, 565–578 CrossRef CAS PubMed.
- A. M. Kaukonen, B. J. Boyd, C. J. H. Porter and W. N. Charman, Pharm. Res., 2004, 21, 245–253 CrossRef CAS.
- A. M. Kaukonen, B. J. Boyd, W. N. Charman and C. J. H. Porter, Pharm. Res., 2004, 21, 254–260 CrossRef CAS.
- A. Dahan and A. Hoffman, Pharm. Res., 2006, 23, 2165–2174 CrossRef CAS PubMed.
- A. Dahan and A. Hoffman, Eur. J. Pharm. Biopharm., 2007, 67, 96–105 CrossRef CAS PubMed.
- H. Yu, K. Shi, D. Liu and Q. Huang, Food Chem., 2012, 131, 48–54 CrossRef CAS PubMed.
- G. A. Kossena, W. N. Charman, B. J. Boyd and C. J. H. Porter, J. Pharm. Sci., 2005, 94, 481–492 CrossRef CAS PubMed.
- M. Grove, G. P. Pedersen, J. L. Nielsen and A. Müllertz, J. Pharm. Sci., 2005, 94, 1830–1838 CrossRef CAS PubMed.
- P. Borel, P. Grolier, M. Armand, A. Partier, H. Lafont, D. Lairon and V. Azais-Braesco, J. Lipid Res., 1996, 37, 250–261 CAS.
- A. Malaki-Nik, M. Corredig and A. J. Wright, Mol. Nutr. Food Res., 2011, 55, S278–S289 Search PubMed.
- G. F. M. Ball, Vitamins in foods: analysis, bioavailability, and stability, CRC Press, Boca Raton, FL, 2006 Search PubMed.
- B. Borgström and C. Erlanson, Eur. J. Biochem., 1973, 37, 60–68 CrossRef.
- F. J. Alvarez and V. J. Stella, Pharm. Res., 1989, 6, 449–457 CrossRef CAS.
- Y. Li, M. Hu and D. J. McClements, Food Chem., 2011, 126, 498–505 CrossRef CAS PubMed.
- R. Devraj, H. D. Williams, D. B. Warren, A. Müllertz, C. J. H. Porter and C. W. Pouton, Int. J. Pharm., 2013, 441, 323–333 CrossRef CAS PubMed.
- G. T. Rich, R. M. Faulks, M. S. J. Wickham and A. Fillery-Travis, Lipids, 2003, 38, 947–956 CrossRef CAS.
- A. J. Wright, C. Pietrangelo and A. MacNaughton, Food Chem., 2008, 107, 1253–1260 CAS.
- P. Wang, H. J. Liu, X. Y. Mei, M. Nakajima and L. J. Yin, Food Hydrocolloids, 2012, 26, 427–433 CrossRef CAS PubMed.
- T. Sanz and H. Luyten, Food Hydrocolloids, 2007, 21, 203–211 CrossRef CAS PubMed.
- E. Acosta, Curr. Opin. Colloid Interface Sci., 2009, 14, 3–15 CrossRef CAS PubMed.
- M. M. R. M. M. Affandi, T. Julianto and A. B. A. Majeed, Food Sci. Technol. Res., 2012, 18, 549–554 CrossRef CAS.
- K. R. N. Moelants, L. Lemmens, M. Vandebroeck, S. van Buggenhout, A. M. van Loey and M. E. Hendrickx, J. Agric. Food Chem., 2012, 60, 11995–12003 CrossRef CAS PubMed.
- L. Salvia-Trujillo, C. Qian, O. Martín-Belloso and D. J. McClements, Food Chem., 2013, 141, 1472–1480 CrossRef CAS PubMed.
- L. Sanguansri, Z. Shen, R. Weerakkody, M. Barnes, T. Lockett and M. A. Augustin, Food Funct., 2013, 4, 74–82 CAS.
- S. Marze, A. Meynier and M. Anton, Food Funct., 2013, 4, 231–239 CAS.
- A. Guerra, L. Etienne-Mesmin, V. Livrelli, S. Denis, S. Blanquet-Diot and M. Alric, Trends Biotechnol., 2012, 30, 591–600 CrossRef CAS PubMed.
- M. Taghipoor, P. Lescoat, J. R. Licois, C. Georgelin and G. Barles, J. Theor. Biol., 2012, 294, 114–121 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2014 |