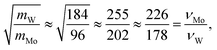First-principles investigation on dimerization of metal-encapsulated gold nanoclusters
Sora
Park
a,
Gunn
Kim
*b and
Young-Kyun
Kwon
*a
aDepartment of Physics and Research Institue for Basic Sciences, Kyung Hee University, Seoul 130-701, Korea. E-mail: ykkwon@khu.ac.kr
bDepartment of Physics and Graphene Research Institute, Sejong University, Seoul 143-747, Korea. E-mail: gunnkim@sejong.ac.kr
First published on 5th November 2013
Abstract
Density functional theory is used to study dimerization of metal-encapsulated gold nanoclusters M@Au12 (M = W, Mo) with Ih or Oh symmetry, and their structural and electronic properties. To determine the most stable dimer structure in each case, various configurations are considered. We find that during dimerization, gold atoms near the interface tend to form inter-cluster triangular bonds, which stabilize two monomer clusters by about 3.3–3.5 eV. The dimerization along a specific axis selected as the z axis causes the symmetry reduction of each M@Au12 cluster resulting in the modification of electronic structures. It is found that all the stable dimers exhibit a much smaller HOMO–LUMO gap than those of their comprising monomers. Such a gap decrease is mainly attributed to the dz2 orbital splitting of the central atoms owing to dimerization. We also calculate the vibrational modes and the corresponding IR-active spectra, which are distinguishable for different dimer configurations. In addition, we find that the IR-active modes of the Oh-based dimer structures appear to be red-shifted in comparison to those of Ih-based ones. Thus, the IR spectra may be utilized experimentally to discriminate dimer configurations with different central metal atoms and/or dissimilar structural symmetries.
1. Introduction
Nanoclusters have become very attractive in science and technology, since not only do they have intriguing physical and chemical properties, but they are also expected to be the building blocks of cluster-assembled materials to be used in future nanotechnology.1,2 For instance, during the last quarter of a century, various carbon nanoclusters based on C60 fullerenes have been reported.3–8 C60 fullerenes form not only a bulk structure with face-centred cubic symmetry, but also a variety of nanostructures under high pressure or specific light conditions.9–12 It was intriguingly observed that C60 molecules can be encapsulated into a carbon nanotube (CNT) to form a nanopeapod structure.13–16 Even more interestingly, when the nanopeapod structures are heated to 1100 °C, the encapsulated buckyballs are dimerized and further fused into “peanut-shaped” or nanocapsule structures inside their host CNTs.17–19Similar to carbon fullerene molecules, stable gold nanoclusters have received considerable attention of researchers in many fields. It has been reported that, because of the nanosize effect, they exhibit interesting optical, magnetic, and even catalytic properties20–31 that are not seen with bulk crystalline gold. In 2002, a new form of stable gold clusters with icosahedral symmetry (Ih) were proposed by Pyykkö and colleagues.32 The proposed gold cluster comprises twelve gold atoms with a transition metal atom enclosed at the centre to form M@Au12 (M = W, Mo, Ta+), and are stabilized by the aurophilic attractions, the relativistic effects, and the perfect 18-electron rule.33–36 Especially, W@Au12 and Mo@Au12 with several different symmetries such as Ih, Oh, and D5h were experimentally observed.33,34,36
Because of their structural similarity to C60, M@Au12 nanoclusters may also function as basic building units for constructing nanostructures fused through the dimerization and further polymerization process. The topic of such dimerization and polymerization is very important for identifying the growth pattern or characterizing the core structure of gold nanoclusters. Previous studies showed that small closed shell bimetallic magic clusters MAu4 (M = Ti, Zr, and Hf) are strongly stabilized by dimerization.37–40 Here, we propose dimerization of M@Au12 (M = W, Mo) nanostructures with either Ih or Oh symmetry analogous to dimerization of fullerene molecules, based on the first-principles study. Unlike their fullerene counterparts, these gold clusters have different encapsulated metal atoms and dissimilar structural symmetries, and therefore our proposed dimers could be extended to various nanostructures. In addition, we investigate the infrared (IR) active vibrational modes of stable dimer configurations to further understand the structural distinctions.
2. Computational details
To investigate the geometrical and electronic structures of dimerized gold nanoclusters, we performed density functional theory (DFT) calculations using the Vienna Ab-initio Simulation Package (VASP).41,42 Projector augmented wave potentials43 and the generalized gradient approximation (GGA)44 with the Perdew–Burke–Ernzerhof (PBE) functional45 were employed to describe the valence electrons and exchange-correlation (XC) energy, respectively. Moreover, since three elements (Au, W, and Mo) considered in this study are heavy, the scalar relativistic effect and the spin-orbit (SO) coupling were taken into account. The cutoff energy was 450 eV for the plane wave basis set. The energies were converged within 10−5 eV, and the geometrical relaxations were continued until the residual forces on all atoms became smaller than 0.02 eV Å−1. A cubic supercell with an edge length of 15 Å was used.To explore the IR-active vibrational spectra, we repeated our calculations using another DFT package, DMol3, which can deal with isolated molecules without considering periodic supercell configurations by utilizing a localized orbital basis set.46,47 We used GGA with the PBE XC functional, as in the calculations using VASP. Double numerical with polarization (DNP) and all-electron scalar relativistic potential48 were adopted. The optimized configurations obtained using both packages were almost identical. The force constant matrix and the derivation of the electric dipole moment were calculated to obtain the IR-active modes and intensities of M@Au12 and their dimers.49,50 However, the SO effects on the electronic structures cannot be considered using the DMol3 code. Therefore, we made use of the VASP package to obtain the optimized geometries and electronic structures, considering the SO effects, and then we calculated the vibrational modes with the DMol3 for the geometries from VASP.
3. Results and discussion
3.1. Structural properties
As the first step, we performed geometrical relaxation to obtain the equilibrium structures of four different monomer units distinguished by enclosed metal elements and symmetries. Fig. 1 depicts the typical structures of optimized M@Au12 (M = W or Mo) clusters with Ih and Oh symmetries. They are just different in the surface bonding and the ligand symmetry of the central atom. In both cases, the central M atom makes 12 equivalent radial bonds with the surface Au atoms. In addition to these radial bonds, the Ih M@Au12 cluster has 30 identical surface Au–Au bonds, which are ∼2.88 Å and ∼5% longer than the radial M–Au bonds, forming an icosahedron. On the other hand, in the Oh M@Au12 cluster, there are 36 equidistant bonds consisting of 12 radial M–Au bonds and 24 surface Au–Au bonds forming a cuboctahedron, which has 6 squares and 8 equilateral triangles. Our calculations show that the bonds in the latter cluster are ≤0.1 Å shorter than the surface bonds in the former one in good agreement with a previous study.33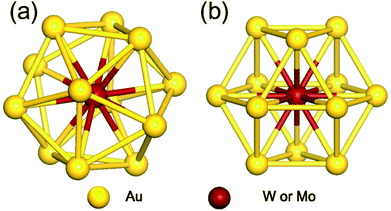 | ||
| Fig. 1 Optimized structures of M@Au12 (M = W, Mo) nanoclusters with (a) icosahedral (Ih) and (b) cuboctahedral (Oh) symmetries. | ||
Based on the equilibrium structures, we evaluated the relative stability between Ih and Oh clusters and found that Ih M@Au12 clusters are more stable than their Oh counterparts by ∼0.18 eV and ∼0.09 eV for M = W and Mo, respectively, consistent with a previous report.33 However, Ih and Oh M@Au12 clusters may coexist even at moderate temperature because their energy difference is quite small. To investigate the stability of dimer structures, we prepared more than 60 probable dimer configurations forming from any two monomer clusters to calculate their dimerization or formation energies, Ef defined by
| Ef = EM1@Au12 + EM2@Au12 − EM1@Au12−M2@Au12. |
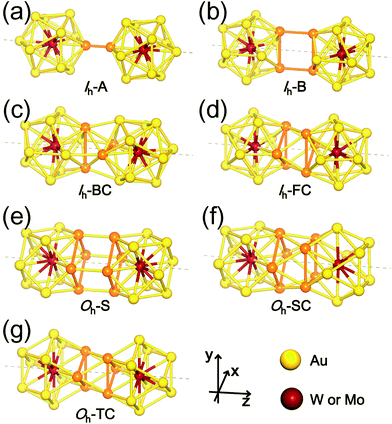
The first four configurations displayed in Fig. 2(a)–(d) are denoted as follows: (a) Ih-A (A stands for “Atom”) represents a dimer of two Ih monomers connected through a bond formed by two Au atoms from the respective monomers; (b) Ih–B (B for “Bond”) connected by two parallel Au–Au bonds, each from each monomers; (c) Ih-BC (BC for “Bond Cross”) combined through two perpendicular or crossed Au–Au bonds; and (d) Ih-FC (FC for “Face Cross”) combined through two crossed triangular faces forming a hexagram in the axial view. The latter three dimer configurations shown in Fig. 2(e)–(g) are denoted by Oh-S (S for “Square”), Oh-SC (SC for “Square Cross”), and Oh-TC (TC for “Triangle Cross”), respectively: (e) Oh-S and (f) Oh-SC are dimers connected by two square faces, one from each Oh monomer, facing each other in parallel and with a relative rotation of 45° forming an octagram along the axial direction, respectively; and (g) Oh-TC combined by two crossed triangular faces forming a hexagram similar to Ih-FC. There are, of course, “hybrid” dimer configurations composed of Ih and Oh monomers, but our calculations show that initially-prepared hybrid dimers are transformed into “pure” dimers (Ih–Ih and Oh–Oh) after full relaxation. Therefore, here we do not present such hybrid dimer configurations.
The formation energy of each dimer configuration depends strongly on the bonding structures formed at the interface between two monomers. As indicated with the orange colour in Fig. 2, the bonding structure at the interface, which is evidently different from each other, is determined by the number of interacting Au atoms and their relative positions. Our calculations show that among the selected Ih-based dimer configurations, Ih-B is the least stable one due to the unfavourable bonding configuration. Even Ih-A, which has only a single bond connection between two participating monomers, is about 1 eV more stable.
The other two dimer configurations Ih-BC and Ih-FC are at least 2 eV more stable than the least stable one. We found that they have not only shorter inter-cluster distances, but also triangular bonding structures at their interfaces. Similarly, Oh-SC and Oh-TC, both of which have shorter inter-cluster distances and triangular bonding structures, are more stable than Oh-S. From these results, we conclude that the triangular bonding formation preferred by Au atoms enhances the dimer stability.
From now on, we will focus on these four (Ih-BC, Ih-FC, Oh-SC, and Oh-TC) stable dimer configurations. In Table 1, we summarized our results on the structural properties of the four stable dimer configurations including their formation energies, Ef, the distances between M1 and M2, dM1−M2, as well as an average distances between Mi (i = 1, 2) and surface Au atoms, dMi−Au. For each dimer configuration, we considered two homogeneous (W–W and Mo–Mo) dimers and a heterogeneous W–Mo dimer. As is evident from Table 1, the Mo–Mo homogeneous dimer has the largest formation energy and the shortest M1–M2 distance for any given dimer configuration, but the formation energies of the other two dimer cases (W–W and W–Mo) are almost as large as the Mo–Mo dimer. It is also found that Ih-BC dimers are about 0.3 eV more stable than Ih-FC, so the former dimers would be abundant, whereas Oh-SC dimers are more stable than Oh-TC by 0.5–0.6 eV, so the former dimers are more likely to be observed. Nevertheless, we expect that various dimer configurations would form under different dimensional constraint.
| Configurations | I h-BC | I h-FC | O h-SC | O h-TC | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M1–M2 | W–W | Mo–Mo | W–Mo | W–W | Mo–Mo | W–Mo | W–W | Mo–Mo | W–Mo | W–W | Mo–Mo | W–Mo |
| E f (eV) | 3.364 | 3.481 | 3.422 | 3.048 | 3.214 | 3.114 | 3.354 | 3.472 | 3.403 | 2.843 | 2.857 | 2.845 |
| d M1–M2 (Å) | 6.467 | 6.398 | 6.433 | 6.500 | 6.334 | 6.473 | 6.475 | 6.433 | 6.458 | 6.826 | 6.820 | 6.819 |
| d M1–Au (Å) | 2.754 | 2.760 | 2.753 | 2.753 | 2.761 | 2.753 | 2.806 | 2.811 | 2.806 | 2.797 | 2.804 | 2.798 |
| d M2–Au (Å) | 2.754 | 2.760 | 2.758 | 2.753 | 2.761 | 2.759 | 2.805 | 2.811 | 2.812 | 2.797 | 2.804 | 2.805 |
| E gap (eV) | 0.812 | 0.732 | 0.757 | 0.497 | 0.404 | 0.459 | 0.440 | 0.385 | 0.401 | 0.659 | 0.564 | 0.594 |
3.2. Electronic properties
Any M@Au12 monomer cluster with either Ih or Oh symmetry is highly symmetric. Hence dimerization of any two monomers may reduce their symmetries and thus modify their electronic properties. We found that such modification appears to occur mainly on the d states of the central metal atom and the s states of the surface Au atoms. It was also found that as long as the comprising monomer clusters keep their symmetries in their dimer configuration, the electronic structure modification remains similar regardless of two comprising central metal atoms. Therefore, in this section we describe the electronic structures of the most stable homogeneous W–W dimers, Ih-BC and Oh-SC, as well as those of their corresponding respective constituent W@Au12 monomers.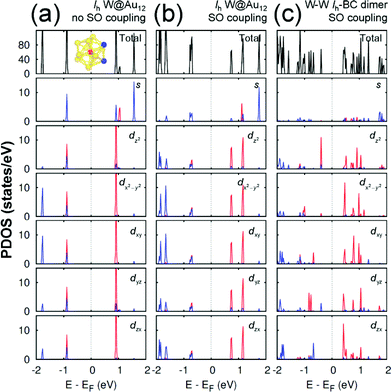 | ||
| Fig. 3 The PDOS of Ih W@Au12 cluster without the SO coupling effect (a), with the SO coupling effect (b), and of Ih-BC dimer (c). In the PDOS for each orbital, the red (blue) line is used for the W atom (Au atoms), which is (are) marked with the same colour in the inset of (a). The same coordinates system is used as shown in Fig. 2. | ||
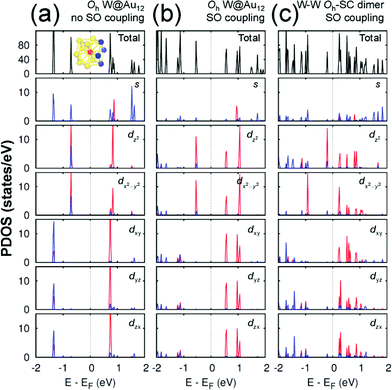 | ||
| Fig. 4 The PDOS of Oh W@Au12 cluster without the SO coupling effect (a), with the SO coupling effect (b), and of Oh-SC dimer (c). In the PDOS for each orbital, the red (blue) line is used for the W atom (Au atoms), which is (are) marked with the same colour in the inset of (a). The same coordinates system is used as shown in Fig. 2. | ||
In an Ih W@Au12 cluster, its twelve 6s orbitals of Au12 span the irreducible representations of ag + t1u + hg + t2u. At the same time, the first three representations are spanned respectively by the s, p, and d atomic orbitals of the central atom.32 As a result, the major orbital interactions in W@Au12 occur mainly between Au12 ligand group orbitals and the 5d orbitals of the W atom resulting in the highest occupied molecular orbital (HOMO) with the bonding hg and the lowest unoccupied molecular orbital (LUMO) with the antibonding h*g.
As shown in Fig. 3(a), the HOMO level of Ih W@Au12 is composed of the degenerate 5d orbitals of the central W atom and 6s and 5d orbitals of the surface Au atoms, while its LUMO level is mainly comprised of the degenerate 5d orbitals of the W atom. The SO coupling splits each 5d state of the W atom at the LUMO level significantly into two states separated by ∼0.44 eV, whereas its counter state at the HOMO splits only by ∼0.03 eV as shown in Fig. 3(b). It is also shown in Fig. 3(b) that the occupied states of the surface gold atoms, which have been located quite below the HOMO level without SO coupling, tend to shift towards the HOMO level due to the SO splitting. Some of the results are in close agreement with a previous report.33
On the other hand, the Oh W@Au12 cluster is affected by the crystal field effect of the Oh ligand on the central metal atom W. The 5d orbitals of the central atom, which have been degenerate in the Ih cluster, are split into two distinct states. One is the higher energy state of eg comprising dz2 and dx2−y2, and the other is the lower energy state of t2g composed of dxy, dyz, and dzx as seen in Fig. 4(a). As a result, the eg state becomes the HOMO level of the Oh cluster. To the empty molecular orbitals, in contrast, such a crystal field effect appears less significant resulting in small splitting, and the t*2g state becomes the LUMO level.
As shown in Fig. 4(b), the SO coupling effect on the Oh cluster is similar to on the Ih one: further splitting of the occupied and unoccupied molecular orbitals by about 0.01 and 0.4 eV, respectively. These two effects of the level splitting reduce the HOMO–LUMO energy gap of the Oh cluster to Egap ≈ 1.115 eV compared to Egap ≈ 1.437 eV of the Ih cluster. Similar tendencies were found for Mo@Au12 clusters with both Ih and Oh Mo@Au12 symmetries. Their respective energy gaps were calculated to be 1.343 eV and 1.088 eV.
Since the z axis was selected as the dimerization axis, we found in both Ih-BC and Oh-SC that the most remarkable changes take place at the occupied dz2 orbital. The symmetry breaking due to dimerization pushes up the occupied dz2 of the central W atom close to the Fermi level being the HOMO of each dimer. The W HOMO level of Ih-BC appears to be hybridized with Au dyz as shown in Fig. 3(c), which is contributed from two Au atoms coloured in blue shown in the inset of Fig. 3(a). In contrast for Oh-SC as shown in Fig. 4(c), the W HOMO level seems to interact weakly with Au dx2−y2, dyz, and dzx, which are from those four Au atoms marked in blue in the inset of Fig. 4(a). For both dimers, the dx2−y2 orbital split much less, because dimerization left this orbital still intact. The unoccupied states are mainly comprised of W 5d orbitals, which are split into many states resulting in the lowest level of each d orbital pushed down toward the Fermi level.
As a result, dimerization gives rise to a significant decrease in Egap, as shown in Fig. 3(c) and 4(c). Such a significant reduction in Egap was observed in all dimer configurations, not only Ih-BC and Oh-SC described above, but also Ih-FC and Oh-TC, with any combinations of central metal atoms (W–W, Mo–Mo, or W–Mo). We further found that the dimer configurations with the same symmetry have similar Egap values within less than 0.1 eV difference, regardless of the central metal compositions. We also observed another trend independent of dimer symmetries. For each given dimer configuration, the W–W dimer has the largest Egap; the Mo–Mo dimer has the smallest; and Egap of the W–Mo heterogeneous dimer is in between, as listed in Table 1. All dimer configurations reveal different Egap from one another, and smaller gap than their respective monomer clusters. Among all these dimers, the Oh-SC dimer reveals the smallest Egap. Due to such difference and reduction in Egap, the electronic property of each dimer may be different from each other, and distinguishable from the monomers. Our study will be extended further to investigate the electronic structures of M@Au12 based nanowires.
3.3. IR spectra
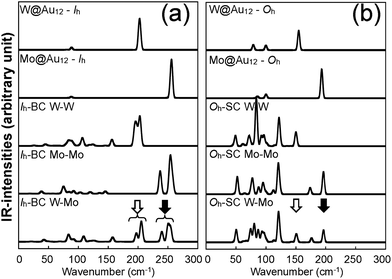
To further understand the structural distinctions, we investigated the IR-active spectra for various dimer configurations. The vibrational modes were calculated from the force constant matrix obtained by displacing each atom in the cluster in all directions. Fig. 5(a) and (b) show the calculated IR-active modes of the dimers M1@Au12–M2@Au12 (Mi = W, Mo) with Ih and Oh symmetries, respectively, as well as of respective corresponding clusters for comparison. Due to different atomic mass of W and Mo, W@Au12 and Mo@Au12 clusters show IR peaks at different frequencies. In Fig. 5(a), the intense IR peaks at 201–204 cm−1 for Ih W@Au12 and 254–256 cm−1 for Ih Mo@Au12 represent the vibrational modes of the central atoms, whereas those at 178 cm−1 and 226 cm−1 in Fig. 5(b) correspond to those of the Oh clusters. It is obvious that the IR-active modes of the central metal atoms of the Oh clusters are red-shifted, as compared with those of the Ih clusters. This red-shift is attributed to shallow interaction in the Oh cluster due to its longer M–Au bond length than that of the Ih cluster. It is clear that the vibrational frequency, ν, is inversely proportional to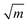 , that is,
, that is,where mW (≈184) and mMo (≈96) are atomic masses of W and Mo. Other IR-active vibrational modes of the surface Au atoms, forming a spherical cage structure, were found near ∼100 cm−1 in both cases of Ih and Oh clusters. For the Oh M@Au12 clusters, there were also low intensity peaks at ∼70 cm−1 and ∼86 cm−1 corresponding to other vibrational modes of the central metal atom and the surface Au atoms. Since the vibrational modes of the M atom were separate from those of Au atoms and distinguishable between the W and Mo atoms, we expect that the dimers with different configurations and compositions could be identified using IR spectra.
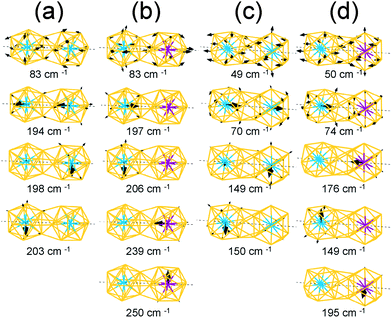
For the homogeneous M–M Ih-BC dimer, the intense peaks at 198–203 cm−1 and 253–257 cm−1 appearing for M = W and Mo, respectively, correspond to the vibrational modes of the central atom along the x and y axes; the intense peaks at 194 cm−1 and 237 cm−1 in Fig. 5(a) correspond to those along the z axis with in-phase modes.
The vectors of these separate and in-phase modes of the W and Mo atoms are presented in Fig. 6(a) and they clearly show the direction of the vibrations at given frequencies. Moreover, because the symmetry is broken owing to dimerization, the vibrational modes of the Au atoms split into various modes including in-plane stretching modes, radial modes for each cluster, and stretching modes of the bonds between two clusters. Among these various modes from the Au atoms, we present the vector of the in-plane stretching modes in Fig. 6(a).
For the heterogeneous W–Mo Ih-BC dimer, the IR spectrum (Fig. 5(a), bottom) shows intense peaks at 197–206 cm−1 and 239–254 cm−1 corresponding to the vibrations along the x, y, and z axes of the central W and Mo atoms, respectively. Their corresponding vector representations are shown in Fig. 6(b). The modes of the surface Au atoms are still active at almost the same frequency as those of the homogeneous dimers. Interestingly, the in-phase vibrational modes of the W and Mo atoms along the z axis disappeared while the separate modes at a similar frequency to those of homogeneous W–W and Mo–Mo Ih-BC.
We also performed the same calculations for Oh-SC dimers. The IR-active spectra and the vector representation of modes are presented in Fig. 5(b) and 6(c)–(d), respectively. The IR spectra are different from those of Ih-BC because of the different symmetries. It turned out that the vibrational modes of the Au atoms are more intense than their monomer counterparts. This may be due to mixing of the vibrational modes of the central atom and the surface Au atoms in the Oh clusters, as mentioned above. The intense peaks at ∼150 cm−1 and 195–197 cm−1 correspond to the vibrational modes of the central atom in the xy-plane, which becomes clear in the vector representation at given frequencies in Fig. 6(c).
We found the drastic difference in the frequency and behaviour of in-phase mode of the two W atoms along the z axis. This mode appeared at much lower frequency ∼70 cm−1, as shown in the 3rd graph of Fig. 5(b) and also in the vector representation of Fig. 6(c), than in W–W Ih-BC. However, the overall tendency of changes in the IR spectra owing to the different central atoms is practically the same as for Ih dimers. Similar to that of Ih-BC dimer, the heterogeneous W–Mo Oh-SC exhibits the vibrational modes of the Au atoms, and the W and Mo atoms at nearly the same frequencies as in two homogeneous Oh-SC dimers. From our investigation of IR spectra, we propose that the symmetries, configurations, and impurity compositions of various M1Au12–M2Au12 dimers can be identified through the IR spectroscopy experiment.
4. Conclusions
Using density functional theory, we studied the dimerization of metal-encapsulated Au12 nanoclusters (M@Au12, M = W, Mo) with either Ih or Oh symmetry. The most stable dimer structure in each case was determined among a variety of candidate dimer configurations. It was found that Au atoms from one monomer cluster located near the interface tend to form extra triangular bonds with Au atoms nearby from the other cluster during dimerization, which stabilizes the monomer clusters by about 3.3–3.5 eV. The dimerization along a specific axis selected as the z axis causes the symmetry reduction of each M@Au12 cluster resulting in the modification of electronic structures. We found that all the stable dimers exhibit much smaller HOMO–LUMO gap Egap mainly determined by the dz2 orbitals of the central atoms split owing to dimerization than those of their comprising monomers. We also investigated the vibrational modes and IR-active spectra for various dimers. The IR-active spectra were calculated to be significantly varied for different dimer configurations. In addition, we found that the IR-active modes of the Oh-based dimer structures appear to be red-shifted in comparison to those of Ih-based ones. Thus the IR spectra may be utilized experimentally to distinguish dimer configurations with different central metal atoms and/or different structural symmetries.Acknowledgements
We gratefully acknowledge financial support from the Korean government through National Research Foundation (NRF-2011-0016188, 2010-0020207 and 2013R1A1A2009131). Some portion of our computational work was done using the resources of the KISTI Supercomputing Center (KSC-2012-C2-72 and KSC-2013-C2-024).References
- S. A. Claridge, A. W. Castleman, Jr, S. N. Khanna, C. B. Murray, A. Sen and P. S. Weiss, ACS Nano, 2009, 3, 244 CrossRef CAS PubMed.
- M. Qian, A. C. Reber, A. Ugrinov, N. K. Chaki, S. Mandal, H. M. Saavedra, S. N. Khanna, A. Sen and P. S. Weiss, ACS Nano, 2010, 4, 235 CrossRef CAS PubMed.
- H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162 CrossRef CAS.
- W. Kratschmer, L. D. Lamb, K. Fostiropoulos and D. R. Huffman, Nature, 1990, 347, 354 CrossRef.
- M. S. Dresselhaus and G. Dresselhaus, Nanostruct. Mater., 1997, 9, 33 CrossRef CAS.
- A. M. Cassell, C. L. Asplund and J. M. Tour, Angew. Chem., Int. Ed., 1999, 38, 2403 CrossRef CAS.
- H. Hirai, K. Kondo, N. Yoshizawa and M. Shiraishi, Appl. Phys. Lett., 1994, 64, 1797 CrossRef CAS.
- M. Prato, J. Mater. Chem., 1997, 7, 1097 RSC.
- A. M. Rao, P. C. Eklund, J. L. Hodeau, L. Marques and M. Nunez-Regueiro, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 4766 CrossRef CAS.
- A. Takashima, J. Onoe and T. Nishii, J. Appl. Phys., 2010, 108, 033514 CrossRef.
- K. P. Meletov, S. Assimopoulos, I. Tsilika, G. A. Kourouklis, J. Arvanitidis, S. Ves, B. Sundqvist and T. Wagberg, Chem. Phys. Lett., 2001, 341, 435 CrossRef CAS.
- V. D. Blank, S. G. Buga, N. R. Serebryanaya, V. N. Denisov, G. A. Dubitsky, A. N. Ivlev, B. N. Mavrin and M. Y. Popov, Phys. Lett. A, 1995, 205, 208 CrossRef CAS.
- B. W. Smith, M. Monthioux and D. E. Luzzi, Nature, 1998, 396, 323 CrossRef CAS PubMed.
- B. W. Smith, M. Monthioux and D. E. Luzzi, Chem. Phys. Lett., 1999, 315, 31 CrossRef CAS.
- S. Berber, Y.-K. Kwon and D. Tománek, Phys. Rev. Lett., 2002, 88, 185502 CrossRef.
- Y. Cho, S. Han, G. Kim, H. Lee and J. Ihm, Phys. Rev. Lett., 2003, 90, 106402 CrossRef.
- B. W. Smith and D. E. Luzzi, Chem. Phys. Lett., 2000, 321, 169 CrossRef CAS.
- S. Bandow, M. Takizawa, K. Hirahara, M. Yudasaka and S. Iijima, Chem. Phys. Lett., 2001, 337, 48 CrossRef CAS.
- S. Han, M. Yoon, S. Berber, N. Park, E. Osawa, J. Ihm and D. Tománek, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 113402 CrossRef.
- M. Brust, J. Fink, D. Bethell, D. J. Schiffrin and C. Kiely, J. Chem. Soc., Chem. Commun., 1995, 1655 RSC.
- A. Sanchez, S. Abbet, U. Heiz, W. D. Schneider, H. Hakkinen, R. N. Barnett and U. Landman, J. Phys. Chem. A, 1999, 103, 9573 CrossRef CAS.
- P. Schwerdtfeger, Angew. Chem., Int. Ed., 2003, 42, 1892 CrossRef CAS PubMed.
- J. Zhao, J. Yang and J. G. Hou, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 085404 CrossRef.
- M.-C. Daniel and D. Astruc, Chem. Rev., 2003, 104, 293 CrossRef PubMed.
- M. Turner, V. B. Golovko, O. P. H. Vaughan, P. Abdulkin, A. Berenguer-Murcia, M. S. Tikhov, B. F. G. Johnson and R. M. Lambert, Nature, 2008, 454, 981 CrossRef CAS PubMed.
- B. Palpant, B. Prével, J. Lermé, E. Cottancin, M. Pellarin, M. Treilleux, A. Perez, J. L. Vialle and M. Broyer, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1963 CrossRef CAS.
- N. Lopez and J. K. Norskov, J. Am. Chem. Soc., 2002, 124, 11262 CrossRef CAS PubMed.
- T. V. Choudhary and D. W. Goodman, Top. Catal., 2002, 21, 25 CrossRef CAS.
- Y. Yamamoto, T. Miura, M. Suzuki, N. Kawamura, H. Miyagawa, T. Nakamura, K. Kobayashi, T. Teranishi and H. Hori, Phys. Rev. Lett., 2004, 93, 116801 CrossRef CAS.
- G. Kim, S.-H. Kang, C.-Y. Lim and Y.-K. Kwon, Chem. Phys. Lett., 2012, 545, 83 CrossRef CAS PubMed.
- S.-H. Kang, G. Kim and Y.-K. Kwon, J. Phys.: Condens. Matter, 2011, 23, 505301 CrossRef PubMed.
- P. Pyykkö and N. Runeberg, Angew. Chem., 2002, 114, 2278 CrossRef.
- X. Li, B. Kiran, J. Li, H. J. Zhai and L. S. Wang, Angew. Chem., Int. Ed., 2002, 41, 4786 CrossRef CAS PubMed.
- J. Long, Y.-X. Qiu, X.-Y. Chen and S.-G. Wang, J. Phys. Chem. C, 2008, 112, 12646 CAS.
- P. Pyykkö, J. Organomet. Chem., 2006, 691, 4336 CrossRef PubMed.
- Y.-X. Qiu, S.-G. Wang and W. H. E. Schwarz, Chem. Phys. Lett., 2004, 397, 374 CrossRef CAS PubMed.
- Y.-K. Han, J. C. Kim, J. Jung and U. Yu, Bull. Korean Chem. Soc., 2008, 29, 305 CrossRef CAS.
- M.-X. Chen and X. H. Yan, J. Chem. Phys., 2008, 128, 174305 CrossRef PubMed.
- T. K. Ghanty, K. R. S. Chandrakumar and S. K. Ghosh, J. Chem. Phys., 2004, 120, 11363 CrossRef CAS PubMed.
- J. Jung, H. Kim, J. C. Kim, M. H. Park and Y.-K. Han, Chem.–Asian J., 2011, 6, 868 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- J. P. Perdew and W. Yue, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8800 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- B. Delley, J. Chem. Phys., 2000, 113, 7756 CrossRef CAS.
- B. Delley, J. Chem. Phys., 1990, 92, 508 CrossRef CAS.
- D. D. Koelling and B. N. Harmon, J. Phys. C: Solid State Phys., 1977, 10, 3107 CrossRef CAS.
- G. Herzberg and B. L. Crawford, J. Phys. Chem., 1946, 50, 288 CrossRef.
- J. E. B. Wilson, J. G. Decius, P. G. Cross and R. T. Lagemann, Am. J. Phys., 1955, 23, 550 CrossRef.
| This journal is © The Royal Society of Chemistry 2014 |