The reorganization energy of intermolecular hole hopping between dyes anchored to surfaces†
Davide
Moia
*a,
Valérie
Vaissier
a,
Ismael
López-Duarte
b,
Tomás
Torres
bc,
Mohammad K.
Nazeeruddin
d,
Brian C.
O'Regan
e,
Jenny
Nelson
a and
Piers R. F.
Barnes
*a
aDepartment of Physics, Imperial College London, SW7 2AZ, UK. E-mail: davide.moia11@imperial.ac.uk; piers.barnes@imperial.ac.uk
bDepartamento de Química Orgánica, Facultad de Ciencias, Universidad Autónoma de Madrid, E-28049 Madrid, Spain
cIMDEA-Nanociencia, c/Faraday, 9, Campus de Cantoblanco, E-28049 Madrid, Spain
dLaboratory of Photonics and Interfaces, Department of Chemistry and Chemical Engineering, Swiss Federal Institute of Technology, Station 6, CH-1015 Lausanne, Switzerland
eDepartment of Chemistry, Imperial College London, SW7 2AZ, UK
First published on 18th October 2013
Abstract
We measured the rate of hole hopping between dye molecules on titanium dioxide nanocrystals using cyclic voltammetry. Dyes commonly used in the field of dye sensitized solar cells exhibited efficient intermolecular charge transport, showing apparent diffusion coefficient values between 10−8 up to over 10−7 cm2 s−1 at room temperature. From temperature dependent measurements, we observed that hole transport across dye monolayers is a thermally activated process with Arrhenius activation energies between about 170 and 370 meV depending on the dye. Analysis of the data in terms of non-adiabatic Marcus theory of charge transfer enabled the estimation of the reorganization energy (740–1540 meV) and of an effective electronic coupling for the different systems. The measured reorganization energies show reasonable agreement with values obtained from density functional theory based calculations, validating our computational approach. Finally, we interpret the experimental and calculated data with reference to the chemical structure of the dyes and to the packing of the dyes on the surface of the TiO2 and suggest that delocalization of the HOMO and rigidity of the conjugated molecular structure result respectively in lower outer and inner sphere reorganization energies.
Introduction
Understanding the nature of charge transfer between dye molecules on a surface at the microscopic scale could open new possibilities in the design of optoelectronic and electrochemical devices. Conjugated dye molecules have the capacity to act as both light absorbing species as well as centers for redox reactions. Sensitizing a surface with a monolayer of dye molecules is an effective approach to modify its physical properties. Sensitization has been applied in fields such as colour photography,1 sensors,2,3 modification of electrodes' properties4 and photovoltaics.5,6 For example, in dye sensitized solar cells (DSSCs) electrons are injected into a transparent semiconducting substrate from photoexcited dye molecules. The resulting ‘hole’ remaining on the oxidized dye must then be regenerated by electron transfer from a surrounding hole transporting medium (HTM) in order to collect the energetic charge from the device. Studies on solid state and liquid based DSSCs suggested that charge transfer may also occur laterally between neighbouring dye molecules to transport the charge at the interface between the semiconductor and the HTM.7,8 Molecules designed to enhance this process could improve the performance of solid state DSSCs by increasing the localized charge collection efficiency. Such molecules might also find applications in molecular transistors, solar fuel photoelectrodes and batteries.9–11 In this work we present measurements to determine the diffusion coefficient and the thermal activation energy required for hole transport through monolayers of dyes. The technique can be extended to any redox active molecules able to attach to surfaces. The measurements show agreement with our quantum chemical calculations of the reorganization energy and indicate that the process is sufficiently well understood for new hole transport materials to be designed.The first demonstration of lateral conduction in a monolayer of dye molecules in a DSSC configuration was shown by Bonhôte et al.12 and was followed by several pieces of work where either hole or electron hopping was demonstrated for several classes of molecules.10,13–20 In these studies, electrochemical, spectroelectrochemical and transient absorption anisotropy measurements were used to assess the diffusion of the charges across the dye sensitized surface, and the observations were discussed in relation to the chemical structure of the molecules and the kinetics of the charge transfer step.
Non-adiabatic Marcus theory is commonly used to express the charge transfer rate, Γ, between a weakly coupled electron donor and electron acceptor as a function of the electronic coupling, J, the reorganization energy, λ, and the difference in free energy between the equilibrium states of products and reactants, ΔG0 = Gproducts − Greactants:21
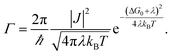 | (1a) |
In the particular case of a self exchange reaction, such as hole hopping between two identical dye molecules anchored to a surface, we can set ΔG0 = 0, if we assume negligible energetic disorder in the system (eqn (1b)). Then
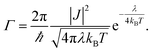 | (1b) |
The reorganization energy λ is a measure of the energetic cost of rearranging the molecules' conformation and the surrounding medium upon the charge transfer step. Electrochemistry as well as transient absorption spectroscopy and Raman spectroscopy have been employed to experimentally determine λ for non-adiabatic charge transfer processes referring to eqn (1a) and (1b).22–26 In these studies, heterogeneous charge transfer between an electrode and molecules either in solution or anchored to the electrode surface and homogeneous charge transfer reactions between molecules in solution have been considered. To our knowledge, no measurement of λ for charge transfer between dyes anchored to a surface has previously been reported.
In the case of transport between dyes anchored to a surface, the rate of intermolecular charge transfer between dyes (Γ) is expected to be related to the apparent diffusion coefficient of holes hopping across the surface of a dye sensitized film (Dapp). Dapp can be obtained from electrochemical measurements such as cyclic voltammetry of the films (see Fig. 1a–d).16 Thus, by examining the dependence of Dapp on temperature for a monolayer of dyes, we can use eqn (1b) to derive estimates for λ for thermally activated diffusion of holes across monolayers (Fig. 1e and f). The values of λ can then be compared to those that we obtain using a computational method recently proposed by our group.27
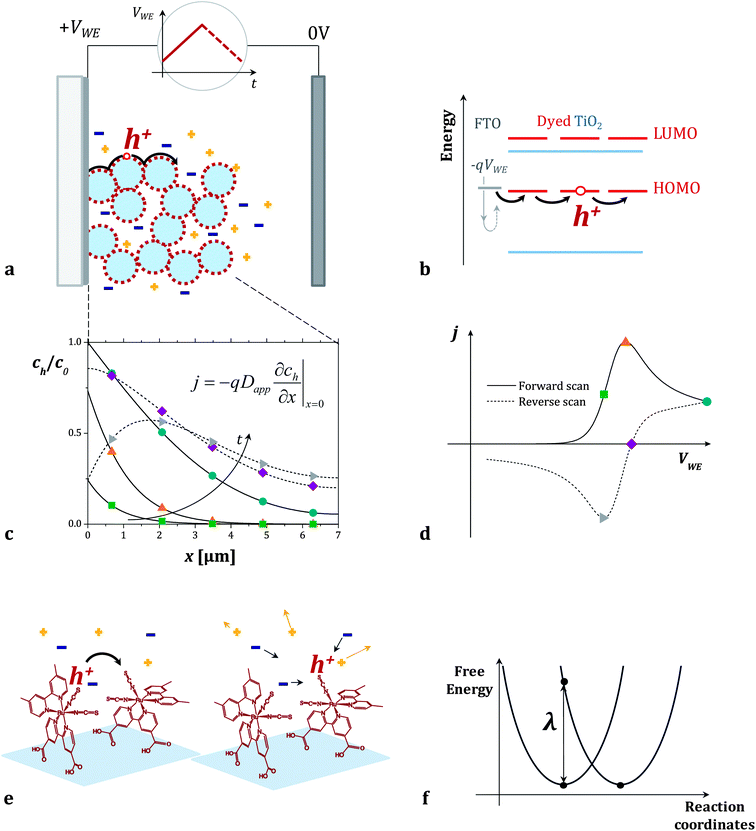 | ||
| Fig. 1 (a and b) Cyclic voltammetry measurement of dye sensitized titanium dioxide mesoporous films on FTO in an inert electrolyte. When the positive voltage ramp (VWE) is applied to the sample (working electrode of the electrochemical cell), holes injected from the FTO electrode in the HOMO level of the dyes travel across the dye sensitized surface. (c) Fraction of oxidized dyes in the film (concentration of holes, ch, divided by the total concentration of dyes, c0) as a function of position x in the film. The curves are calculated at different points of the cyclic voltammogram using the model described in the Section 2.1 of the ESI.†ch varies throughout the forward (solid lines) and the reverse (dashed lines) voltage scans following Fick's diffusion equation. The boundary conditions are set by the potential VWE at the FTO electrode (x = 0) and the finite thickness of the film. (d) The calculated current density j flowing across the dyes during the cyclic voltammogram is related to the gradient of ch at the FTO/dyed-TiO2 interface. (e and f) We describe the individual charge transfer process with non-adiabatic Marcus theory and estimate the value of the reorganization energy λ which refers to the energetic cost of rearranging the dye molecules' conformation and the surrounding electrolyte. | ||
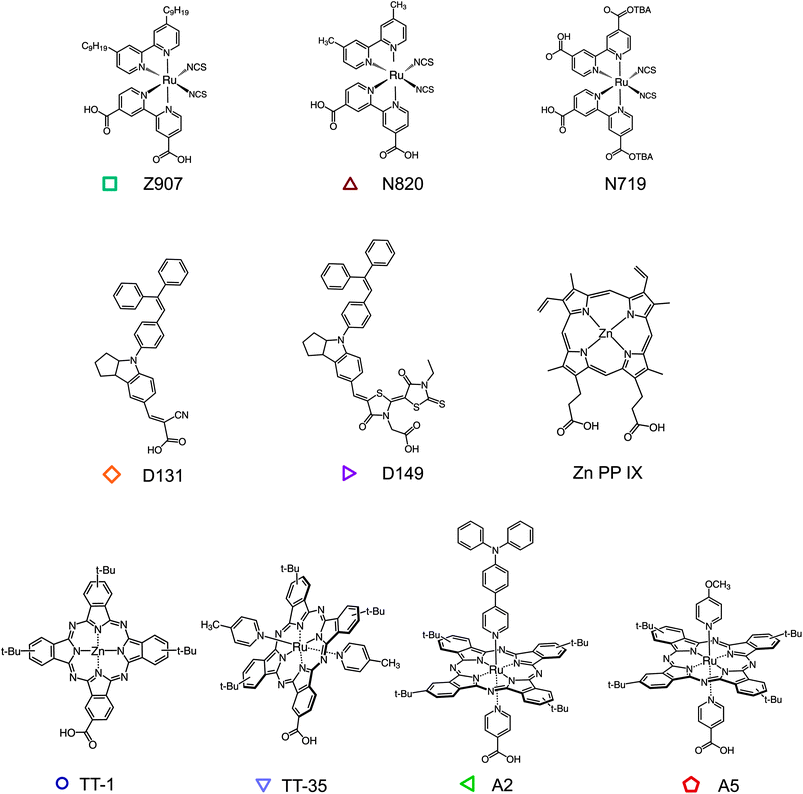
The method that we present can be applied to any redox active molecule, whose oxidized state is stable within the timescale of the measurement. The molecule also needs to be able to chemically anchor to a surface. Herein, we examine dye molecules, widely applied in DSSCs, that present a diverse range of chemical structures (Fig. 2) sensitizing films of TiO2 nanoparticles. TiO2 is a convenient scaffold for the formation of dye monolayers and does not participate in the hole hopping process. Note that other inert insulating materials can be used.9,12 The ruthenium bipirydine complexes Z907, N719 were chosen since they represent reference dyes in the field of DSSCs. The dye N820 was also considered to compare the effect of removing the long alkyl chains from the structure of Z907. Organic indoline dyes D131 and D149 have been successfully employed as sensitizers in DSSCs, especially in thinner film devices, on account of their high extinction coefficient. Phthalocyanines (Pc) represent another important family of organic semiconductors, used as sensitizers but also as absorbers and hole transport materials in organic electronic devices.28–33 A series of zinc (TT-1) and ruthenium (TT-35, A2 and A5) phthalocyanines were investigated. TT-1 (ref. 34) and TT-35 (ref. 35) complexes share the same peripheral substitution pattern based on the presence of tert-butyl groups and the carboxy anchoring group directly attached to the Pc ring. In the case of ruthenium phthalocyanines A2 and A5,36 the anchoring group is on one of the axial pyridine ligands and is therefore orthogonal to the Pc plane. The other axial pyridine ligand bears an electron-donor group, namely triphenylamine (A2) and methoxy (A5). The dye zinc protoporphyrin(IX) (ZnPP) was also tested since interest in porphyrin sensitizers has been increasing after high efficiency values for liquid DSSCs were achieved using a molecule from this class.37 Some of these molecules have been already studied as efficient hole transporters in dye sensitized systems.16,17,20,38
Method
Mesoporous TiO2 films were fabricated via doctor blading (thickness ∼7 μm, particle size ∼20 nm) on conducting glass substrates (Fluorine doped Tin Oxide, FTO). The films were immersed in dye solution for 3.5 hours for the indoline organic dyes, and for 20 hours in the case of all the other molecules. The samples were then rinsed in acetonitrile for 1 up to 5 minutes. Cyclic voltammetry (CV) measurements were performed using a three-electrode cell with the FTO/dyed-TiO2 films as the working electrode, a silver wire as the quasi reference electrode and a platinum counter electrode. A fresh sample was used for each (CV) scan to avoid uncertainty due to the degradation of films between scans. The electrolyte composition was 0.1 molar tetrabutylammonium perchlorate (TBAP) dissolved in acetonitrile and it was bubbled with nitrogen gas for 20 minutes before the experiment. The electrochemical cell was immersed in an acetone bath where dry ice was added to vary its temperature between 230 K and 300 K. The temperature inside the cell was measured by means of a thermocouple dipped in the electrolyte solution. More detailed experimental information is given in the ESI,† including the substrate preparation and dyeing procedure, the method for estimating the dye loading on the TiO2 film and discussion of the electrochemical reversibility of the dyes during the measurement.The reorganization energy of charge transfer between dyes was calculated using a standard method39 which was modified to incorporate the effect of a solvent.27 First, the geometry of both the hole donor (oxidized dye) and acceptor (unoxidized dye) were optimized with acetonitrile as the surrounding medium using DFT coupled with a polarizable continuum model (PCM). The cavity used in the PCM is made of interlocking spheres centered on each atom, offering a specific mapping of each molecule.40 In the PCM used to calculate these equilibrium geometries, the solvent was characterized by its static dielectric constant which we modified to account for the presence of electrolyte ions. The energy of the molecule in its surrounding medium was calculated under four conditions. The first pair of calculations give the equilibrium energy of the system: the energy of the unoxidized and oxidized states with their surrounding medium in the equilibrium geometries, as described above. Then the energies of the oxidized state in the unoxidized equilibrium geometry and unoxidized state in the oxidized equilibrium geometry were calculated. This second pair of calculations represent the energy of the system under non-equilibrium conditions immediately after the moment of charge transfer. For these non-equilibrium conditions the solvent in the PCM model was described using its optical dielectric constant. The reorganization energy is then calculated by subtracting the energy of the equilibrium states from the non-equilibrium states. This easily accessible method, which uses the Gaussian09 software package,41 accounts for the effects of the surrounding electrolyte (solvent and ions) on the reorganization energy. By repeating the calculations in a vacuum, we can discriminate between the inner sphere reorganization energy (λi), due to the rearrangement of the dyes upon hole transfer, from the outer sphere component (λo), related to the electrolyte.
Results
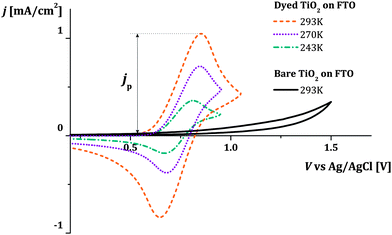
Fig. 3 shows examples of cyclic voltammograms performed on dye sensitized TiO2 films at different temperatures. A corresponding voltammogram of an unsensitized TiO2 film is also shown. The voltage range spanned by the scan lies within the band gap of TiO2, well below its conduction band. Under these conditions the unsensitized TiO2 behaves like an insulator. The low current density that is observed may be related to the oxidation of impurities at the FTO electrolyte interface. Conversely, with dye molecules anchored to the TiO2 film's surface, we record a significant redox response. The value of the integrated current density from the beginning of the scan up to the positive peak is in the order of 1 mC cm−2 (in this case at 0.1 V s−1 scan rate). Considering the dye loading and the thickness of the film (respectively about 7 × 1019 cm−3 and 7 μm), this suggests that the oxidation extends to about 10% of the molecules in the film when the current peak is reached. We conclude that holes are hopping from dye to dye, screened by the counter-ions in the electrolyte so that the surface of the TiO2 nanocrystals is charged and discharged by the diffusion of holes from and to the FTO substrate. The increase in the magnitude of the current density with increasing temperature suggests that the hole diffusion is thermally activated.We consider cases where the penetration depth of the holes into the film is sufficiently short relative to the film thickness at the time corresponding to the oxidation peak. If this condition is valid, the apparent diffusion coefficient of the holes, Dapp [cm2 s−1], can be determined from the peak current density of the cyclic voltammogram, jp [A cm−2], using the following relationship:
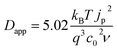 | (2) |
The Arrhenius plots in Fig. 4a–c show the values of Dapp for different dyes plotted as a function of temperature. They also show lines corresponding to the least square fits of the expression of a thermally activated process to the experimental data. The data quality is sufficient to discern differences in the values of the activation energy (Eact) between some of the systems (Table 1). Fig. 4d shows the values of reorganization energy estimated from these data as described in the following paragraphs where it will be discussed further.
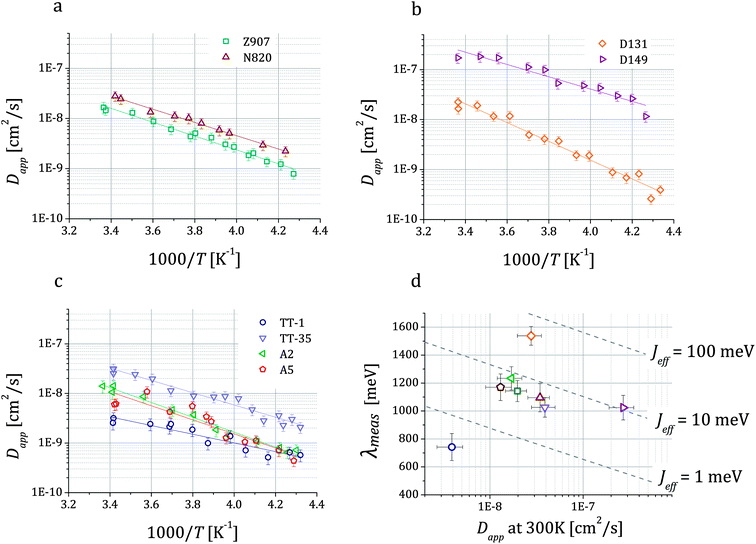 | ||
Fig. 4 Temperature dependent values of the hole apparent diffusion coefficient (Dapp) extracted from cyclic voltammetry performed on dye sensitized TiO2 films on FTO in 0.1 M TBAP in acetonitrile. For each dye, we show the fitting of the expression of a thermally activated process Dapp = D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Eact/kBT) to the data, which enables the estimation of the activation energy Eact related to the charge transfer between dyes. Three classes of dyes were examined: ruthenium bipyridine complexes (a), indoline dyes (b) and phthalocyanines (c). In (d) we show the values of the reorganization energy λmeas that we obtained by fitting the data using eqn (1b) and (3) plotted against Dapp at room temperature for all the dyes. Dashed lines represent the relation between λ and Dapp for different values of the effective electronic coupling Jeff and for a value of the mean intermolecular distance R of 1.35 nm (average over all the dyes considered). exp(−Eact/kBT) to the data, which enables the estimation of the activation energy Eact related to the charge transfer between dyes. Three classes of dyes were examined: ruthenium bipyridine complexes (a), indoline dyes (b) and phthalocyanines (c). In (d) we show the values of the reorganization energy λmeas that we obtained by fitting the data using eqn (1b) and (3) plotted against Dapp at room temperature for all the dyes. Dashed lines represent the relation between λ and Dapp for different values of the effective electronic coupling Jeff and for a value of the mean intermolecular distance R of 1.35 nm (average over all the dyes considered). | ||
| Dye | c 0 [1019 cm−3] | D app at 300 K [10−8 cm2 s−1] | E act [meV] |
J
eff [meV]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
λ meas [meV] | λ calc [meV] |
|---|---|---|---|---|---|---|
| a ×/ Expresses the geometric error. | ||||||
| Z907 | 9.1 ± 1.4 | 2.0 ± 0.5 | 274 ± 19 | 6.0 ×/1.5 | 1143 ± 76 | 976 |
| N820 | 9.6 ± 1.5 | 3.5 ± 0.9 | 262 ± 25 | 6.4 ×/1.7 | 1095 ± 101 | 979 |
| N719 | 6.6 ± 1.2 | — | — | — | — | — |
| D131 | 8.8 ± 1.4 | 2.8 ± 0.8 | 373 ± 17 | 51 ×/1.5 | 1538 ± 67 | 1062 |
| D149 | 6.6 ± 1.0 | 27 ± 8 | 244 ± 22 | 10 ×/1.6 | 1023 ± 88 | 914 |
| ZnPP | 4.2 ± 0.7 | — | — | — | — | — |
| TT-1 | 13 ± 2 | 0.39 ± 0.12 | 174 ± 24 | 0.40 ×/1.7 | 742 ± 97 | 710 |
| TT-35 | 4.4 ± 0.7 | 3.9 ± 1.1 | 245 ± 18 | 3.2 ×/1.5 | 1026 ± 70 | 680 |
| A2 | 7.0 ± 1.1 | 1.7 ± 0.5 | 297 ± 21 | 7.6 ×/1.6 | 1234 ± 83 | 666 |
| A5 | 2.7 ± 0.4 | 1.3 ± 0.4 | 281 ± 24 | 3.1 ×/1.7 | 1170 ± 95 | 669 |
Assuming that the temperature dependence of Dapp has the same functional form as the expression of the charge transfer rate shown in eqn (1b), then we are able to determine the reorganization energy describing the charge transfer reaction between the dye molecules anchored on the TiO2 surface. Moreover, considering the simple case of an isotropic arrangement of the dyes on the surface of the TiO2 with constant intermolecular distance R, the relationship describing Dapp can be expressed as:27
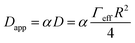 | (3) |
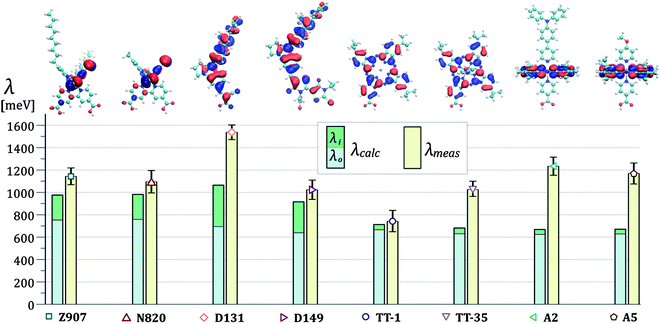
The results of the fits of eqn (1b) for the values of the effective electronic coupling, Jeff, and of the reorganization energy, λmeas, are shown in Table 1. The values of λmeas are also displayed in Fig. 4d, where they are plotted against the corresponding dye's apparent diffusion coefficient at room temperature. Lines representing the relation between the two quantities according to eqn (1b) and (3) are shown for different values of the effective electronic coupling using the average value of R over the dyes considered of 1.35 nm. Table 1 also shows the estimation of the activation energy, Eact (determined from the Arrhenius equation), the apparent diffusion coefficient at room temperature (Dapp) and the measured dye loading (c0) used for the estimation of Jeff. The measured values of reorganization energy (λmeas) are compared to values calculated via quantum chemical modelling (λcalc) using the method described in ref. 27 for the case of 0.1 molar concentration of ions in acetonitrile as surrounding dielectric medium.
In Fig. 5 we show this comparison between theory and experiments and we display values of λcalc as the sum of the inner sphere reorganization energy components (λi) and the outer sphere ones (λo). The dyes N719 and ZnPP showed highly irreversible behaviour. For these molecules, we did not apply the analysis in terms of hole diffusion. Further details can be found in Section 1.2 of the ESI.†
In the next section we discuss the results in Table 1 and describe the behavior of the dyes in terms of hole diffusion in relation to their chemical structure. We consider the HOMO delocalization, the rigidity and conjugation of the dyes, the presence of specific side groups or ligands, the anchoring mechanism and the configuration of the monolayer to interpret the calculated and measured reorganization energies and effective electronic couplings.
Discussion
Chemical structure and calculated reorganization energy
From our calculations, the outer sphere component of the reorganization energy represents the main contribution to the overall value of the reorganization energy for all the dyes investigated in this study. In the column chart in Fig. 5, λo is between 65 and 95% of the total λcalc depending on the dye. This is due to the highly polarizable surrounding medium used.27 The spatial location of the HOMOs is displayed in Fig. 5 where the volume enclosed within the isosurface corresponding to the isovalues ±0.02 electrons1/2a0−3/2 is shown for the different structures. We observe that the value of the calculated outer sphere reorganization energy is inversely correlated to the ‘size’ of the HOMO. Greater delocalization of the HOMO results in lower values of λo. The ruthenium bipyridine complexes Z907 and N820 show the highest λo. For these two dyes the HOMO is localized on the two NCS ligands (see structures and column chart in Fig. 5). λo is instead lower for the dye D131 and even lower for D149. For both these dyes, the HOMO is more evenly distributed on the whole molecular structure, which is slightly bigger in the case of D149. λo is also low for the phthalocyanine dyes, where the HOMO extends on the phthalocyanine ring. Another observation is that λo is not directly affected by the size of the molecule. For example, the HOMO of Z907 does not expand into the non-conjugated alkyl chains, which significantly increase the overall size of the molecule when comparing it to N820. However, the values of λo for Z907 and N820 are almost identical. Similarly, we observe only slight variation in λo when comparing the phthalocyanine dyes, where the HOMO localization is essentially unaffected by the presence of the axial ligands or change in the core atom.Regarding the calculated inner sphere reorganization energy, we report almost identical values for the ruthenium dyes Z907 and N820. This suggests that the alkyl chains play a negligible role in the rearrangement of the molecular conformation of Z907 upon charge transfer. For the indoline dyes, D131 shows higher λi than D149, possibly due to the reduced size of the conjugated structure. Finally, we observe that the phthalocyanine dyes show very low values of λi. We ascribe this result to the rigidity of the phthalocyanine ring, where the HOMO is mainly located (almost all atoms are braced by bonds to neighboring atoms, see Fig. 2), which constrains the unoxidized and the oxidized conformations to be similar. The planarity of the structure ensures high level of conjugation across the ring that provides easier accommodation for the hole.
Comparing measured and calculated reorganization energies
The experimental values of reorganization energy find good agreement with the calculations for the case of the ruthenium bipyridine complexes where λmeas is very similar for Z907 and N820 and only slightly higher than the relative values of λcalc. For the indoline dyes, we record higher value of reorganization energy for the D131 dye than for D149, confirming the trend observed in the numerical simulation. However, the mismatch between calculation and experiment is significant for the case of D131 and the difference in reorganization energy between the two dyes is higher for the measured values than for the calculated ones. In the case of the phthalocyanine dyes, the measured value of the reorganization energy of TT-1 matches the calculated value within experimental error, whereas for the ruthenium phthalocyanines TT-35, A2 and A5, we measure much higher reorganization energies than the ones predicted by our calculations. The substitution of the zinc core atom with ruthenium and/or the presence of the axial ligands may underlie the observed increase in λmeas. The exchange of the TPA group with the methoxy in the axial ligands of the dyes A2 and A5 seems not to affect λmeas. Finally, λmeas is lower for TT-35, where the anchoring group is on the periphery of the phthalocyanine ring, than for A2 and A5, where the anchoring group is located on one of the axial ligands. This change in reorganization energy may be related to the differences in the molecular conformation and in the interaction with the TiO2 surface deriving from the change in the anchoring group's position.Our analysis of the thermally activated charge transfer process with the non-adiabatic Marcus equation is based on reactions between redox sites of identical energy (see eqn (1b)). In reality, we expect that variations in the TiO2 surface, in the configuration of the dyes on the surface and in the dielectric and electrostatic environment result in variations in site energy (energetic disorder). This introduces additional temperature dependence in the charge diffusion process and a distribution of values for the activation energy. If these effects are significant, they could lead to an overestimate of λ in our experimental analysis. This could explain the mismatch between our experiments and calculations.
Hole diffusion: effect of chemical structure, monolayer configuration and relevance to organic thin films
We observe a slight decrease in apparent diffusion coefficient for Z907 when compared to N820. In this case, the presence of the alkyl chains results in molecular configurations that still allow relatively effective hole transfer between neighboring dyes. This is consistent with the similar values of the dye loading measured for the two systems. Larger differences in the Dapp resulting from the presence of alkyl chains were observed previously and may relate to a more significant impact of the chains on dye loading.16 The presence of non conjugated side groups can affect the packing density as well as the relative arrangement of the dyes sensitizing the surface. This may limit the overlap of the HOMO of neighboring molecules and reduce the charge transfer rate.The close packing of dyes on the TiO2 surface is expected to increase the coupling between molecules and result in faster charge transport. The enhancement of hole diffusion for indoline dyes due to J-aggregation has already been discussed by Fattori et al.17 Moreover, it has been shown that the preferential adsorption mechanism of D149 on the TiO2 surface occurs with lower packing and reduced interaction than for another indoline dye, D102, due to steric effects.44 In our experiments, D131 shows higher packing than D149 (see values of the dye loading c0 in Table 1), and probably adopts out of plane configurations, similar to what has been presented for the indoline dye D102. The difference in packing results in different effective electronic coupling, which is higher in this case for D131 than D149 (see Jeff in Table 1). The faster diffusion that we measure for D149 at room temperature compared to D131 must therefore be due to the difference in reorganization energy.
The phthalocyanine dye TT-1 adsorbs onto the TiO2 with very high packing density. Its slow hole diffusion at room temperature can be ascribed to the presence of the tert-butyl groups or to unfavorable relative orientations of neighboring dyes. The ruthenium phthalocyanines show significantly lower dye loading than TT-1 due to the presence of axial ligands, in the case of TT-35, and to the different anchoring scheme, for A2 and A5, (c0 is particularly low for A5, which we are not able to explain on the basis of the dye's chemical structure). For these dyes, we record apparent diffusion coefficients at room temperature above 10−8 cm2 s−1. All the phthalocyanine dyes investigated here are particularly interesting given the high degree of reversibility we observe when performing multiple CV measurements on the same sample.
The corresponding value of mobility that can be calculated from the measurement of Dapp at room temperature for the dyes investigated in this study ranges between 10−7 and 10−5 cm2 V−1 s−1. These values are lower than the mobilities recorded for solution processable amorphous organic semiconductors (up to 10−2 cm2 V−1 s−1). This may be because of the different dimensionality of a dye monolayer on a mesoporous structure compared to the bulk of a thin film. Mobility greater than 10−2 cm2 V−1 s−1 was reported using solution processable oligothiophenes in self assembled monolayer field effect transistors (SAMFETs), suggesting a potential improvement for the case of dyes that are able to order when sensitizing a surface.11,45 Organic semiconductor monolayers can occupy only about 10% volume fraction of a mesoporous film, and can revolutionize the provision/extraction of charge carriers in the bulk of a film. 2D transport across a semiconductor (Perovskite) sensitized nanocrystal was recently observed by Lee et al. and enabled the fabrication of high efficiency solid state solar cells.46,47
The method that we present has potential application beyond the field of DSSCs for the characterization of charge transport between semiconducting molecules. Traditionally, it has been difficult to resolve the contributions from energetic disorder and reorganization energy from observed temperature dependence of transport in these materials.48 Indeed, there is, as yet, no straightforward technique to determine λ experimentally. The experimental and theoretical methods used here could be applied to organic semiconducting moieties when attached to the surface of a supporting scaffold and used to study the reorganization energy in different dielectric environments. In the surface attached configuration we may expect a lower degree of disorder than in a three-dimensional solid film. However, as mentioned previously in this discussion, variations in the surface and in the configuration of the molecules could still make a significant contribution to the temperature dependence of hole diffusion.
Conclusion
We propose a method to estimate the value of the reorganization energy for the transport of holes across monolayers of dyes anchored to nanocrystalline surfaces via temperature dependent cyclic voltammetry. We analyzed materials that belong to different classes of dyes and discussed the influence of their chemical structure on their conduction properties. The results suggested that low values for the reorganization energy are achieved when dyes present a rigid structure, extended conjugation and when the HOMO is delocalized over a large volume. The presence of non conjugated side groups potentially have a detrimental effect on the rate of charge transfer between molecules, as high packing densities are desirable to enhance the hole diffusion. This method offers a robust approach to design chemical structures for the optimization of the charge transfer properties of dyes. Beside the analysis of the hole hopping for molecules anchored to a surface, measuring the reorganization energy and estimating the effective electronic coupling is of high importance in the general study of charge transport in organic semiconductors.Acknowledgements
We thank Dr Xiaoe Li, Dr Jarvist Frost, Dr Tim Albrecht, Prof. Dago de Leeuw, Prof. Michael Grätzel, Prof. Quing Wang, Prof. Alessandro Troisi for the useful and insightful discussions. DM and PB were supported by EPSRC Grant No EP/J002305/1. VV was supported through a studentship in the Centre for Doctoral Training on Theory and Simulation of Materials at Imperial College funded by EPSRC under grant number EP/G036888/1. JN acknowledges support from the Royal Society through an Industry Fellowship and from EPSRC through the Supergen programme. This work has been supported by the Spanish MICINN and MEC (CTQ2011-24187/BQU and CONSOLIDER INGENIO 2010, CSD2007-00010 Nanociencia Molecular), and the Comunidad de Madrid (MADRISOLAR-2, S2009/PPQ/1533). TT and MKN thank the European Community's Seventh Framework Programme (FP7/2007–2013) under Grant no. 287818 of the X10D project and Grant no. 309194 project title GLOBASOL for financial support.References
- C. Jones, Nature, 1904, 70, 553–555 CrossRef.
- E. Palomares, R. Vilar and J. R. Durrant, Chem. Commun., 2004, 362–363 RSC.
- K. Eaton, Sens. Actuators, B, 2002, 85, 42–51 CrossRef CAS.
- P. Ravirajan, A. M. Peiro, M. K. Nazeeruddin, M. Grätzel, D. D. C. Bradley, J. R. Durrant and J. Nelson, J. Phys. Chem. B, 2006, 110, 7635–7639 CrossRef CAS PubMed.
- B. C. O'Regan and M. Grätzel, Nature, 1991, 353, 737 CrossRef CAS.
- J. E. Moser and J. Salbeck, Nature, 1998, 395, 583–585 CrossRef PubMed.
- L. Yang, U. B. Cappel, E. L. Unger, M. Karlsson, K. M. Karlsson, E. Gabrielsson, L. Sun, G. Boschloo, A. Hagfeldt and E. M. J. Johansson, Phys. Chem. Chem. Phys., 2012, 14, 779–789 RSC.
- A. Fillinger and B. A. Parkinson, J. Electrochem. Soc., 1999, 146, 4559–4564 CrossRef CAS PubMed.
- Q. Wang, N. Evans, S. M. Zakeeruddin, I. Exnar and M. Grätzel, J. Am. Chem. Soc., 2007, 129, 3163–3167 CrossRef CAS PubMed.
- S. Ardo and G. J. Meyer, J. Am. Chem. Soc., 2011, 133, 15384–15396 CrossRef CAS PubMed.
- S. G. J. Mathijssen, E. C. P. Smits, P. a. van Hal, H. J. Wondergem, S. A. Ponomarenko, A. Moser, R. Resel, P. A. Bobbert, M. Kemerink, R. A. J. Janssen and D. M. de Leeuw, Nat. Nanotechnol., 2009, 4, 674–680 CrossRef CAS PubMed.
- P. Bonhôte, E. Gogniat, S. Tingry, C. Barbe, N. Vlachopoulos, F. Lenzmann, P. Comte and M. Grätzel, J. Phys. Chem. B, 1998, 5647, 1498–1507 CrossRef.
- S. A. Trammell and T. J. Meyer, J. Phys. Chem. B, 1999, 103, 104–107 CrossRef CAS.
- X. Li, M. K. Nazeeruddin, M. Thelakkat, P. R. F. Barnes, R. Vilar and J. R. Durrant, Phys. Chem. Chem. Phys., 2011, 13, 1575–1584 RSC.
- N. Papageorgiou, M. Grätzel, O. Enger, D. Bonifazi and F. Diederich, J. Phys. Chem. B, 2002, 106, 3813–3822 CrossRef CAS.
- Q. Wang, S. M. Zakeeruddin, M. K. Nakeeruddin, R. Humphry-Baker and M. Grätzel, J. Am. Chem. Soc., 2006, 128, 4446–4452 CrossRef CAS PubMed.
- A. Fattori, L. M. Peter, H. Wang, H. Miura and F. Marken, J. Phys. Chem. C, 2010, 205, 11822–11828 Search PubMed.
- S. Ardo and G. J. Meyer, J. Am. Chem. Soc., 2010, 132, 9283–9285 CrossRef CAS PubMed.
- L. Won-Yong, M. Marcin, G. Brezesinski, M. Wittek and D. Moebius, J. Phys. Chem. B, 1999, 103, 6950–6956 Search PubMed.
- A. Fattori, L. M. Peter, K. L. McCall, N. Robertson and F. Marken, J. Solid State Electrochem., 2010, 14, 1929–1936 CrossRef CAS PubMed.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, 1985, 811, 265–322 CrossRef CAS.
- Y. Tachibana, S. A. Haque, I. P. Mercer, J. E. Moser, D. R. Klug and J. R. Durrant, J. Phys. Chem. B, 2001, 105, 7424–7431 CrossRef CAS.
- J. F. Smalley, H. O. Finklea, C. E. D. Chidsey, M. R. Linford, S. E. Creager, J. P. Ferraris, K. Chalfant, T. Zawodzinsk, S. W. Feldberg and M. D. Newton, J. Am. Chem. Soc., 2003, 125, 2004–2013 CrossRef CAS PubMed.
- A. D. Abhayawardhana and T. C. Sutherland, J. Phys. Chem. C, 2009, 113, 4915–4924 CAS.
- H. O. Finklea and N. Madhiri, J. Electroanal. Chem., 2008, 621, 129–133 CrossRef CAS PubMed.
- A. B. Myers, Chem. Rev., 1996, 96, 911–926 CrossRef CAS PubMed.
- V. Vaissier, P. R. F. Barnes, J. Kirkpatrick and J. Nelson, Phys. Chem. Chem. Phys., 2013, 15, 4804–4814 RSC.
- M. G. Walter, A. B. Rudine and C. C. Wamser, J. Porphyrins Phthalocyanines, 2010, 14, 759–792 CrossRef CAS.
- M. V. Martínez-Díaz, M. Ince and T. Torres, Monatsh. Chem., 2011, 142, 699–707 CrossRef.
- C. G. Claessens, U. Hahn and T. Torres, Chem. Rec., 2008, 8, 75–97 CrossRef CAS PubMed.
- T. T. G. de La Torre and C. G. Claessens, Chem. Commun., 2007, 2000–2015 RSC.
- T. T. M. V. Martínez-Díaz and G. de La Torre, Chem. Commun., 2010, 46, 7090–7108 RSC.
- C. C. W. M. G. Walter and A. B. Rudine, in Handbook of Porphyrin Science, ed. R. G. K. M. Kadish and K. M. Smith, World Scientific, Singapore, 2010, vol. 10, pp. 141–181 Search PubMed.
- J.-J. Cid, J.-H. Yum, S.-R. Jang, M. K. Nazeeruddin, E. Martínez-Ferrero, E. Palomares, J. Ko, M. Grätzel and T. Torres, Angew. Chem., Int. Ed., 2007, 46, 8358–8362 CrossRef CAS PubMed.
- I. Lopez-Duarte, Ph.D. thesis, University Autonoma of Madrid, 2010.
- A. Morandeira, I. Lopez-Duarte, B. C. O'Regan, M. V. Martínez-Díaz, A. Forneli, E. Palomares, T. Torres and J. R. Durrant, J. Mater. Chem., 2009, 19, 5016–5026 RSC.
- A. Yella, H.-W. Lee, H. N. Tsao, C. Yi, A. K. Chandiran, M. K. Nazeeruddin, E. W.-G. Diau, C.-Y. Yeh, S. M. Zakeeruddin and M. Grätzel, Science, 2011, 334, 629–635 CrossRef CAS PubMed.
- A. Fattori, L. M. Peter, S. R. Belding, R. G. Compton and F. Marken, J. Electroanal. Chem., 2010, 640, 61–67 CrossRef CAS PubMed.
- K. Sakanoue, M. Motoda, M. Sugimoto and S. Sakaki, J. Phys. Chem. A, 1999, 103, 5551–5556 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- D. J. Frisch, M. J. Trucks, G. W. Schlegel, H. B. Scuseria, G. E. Robb, M. A. Cheeseman, J. R. Scalmani, G. Barone, V. Mennucci, B. Petersson, G. A. Nakatsuji, H. Caricato, M. Li, X. Hratchian, H. P. Izmaylov, A. F. Bloino, J. Zheng and G. Sonnenb, Gaussian 09, Revision A.1, 2009 Search PubMed.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods, 2nd edn, 2001 Search PubMed.
- D. W. Oscarson, Clays Clay Miner., 1994, 42, 534–543 CAS.
- M. Pastore and F. De Angelis, ACS Nano, 2010, 4, 556–562 CrossRef CAS PubMed.
- M. Defaux, F. Gholamrezaie, J. Wang, A. Kreyes, U. Ziener, D. V. Anokhin, D. A. Ivanov, A. Moser, A. Neuhold, I. Salzmann, R. Resel, D. M. de Leeuw, S. C. J. Meskers, M. Moeller and A. Mourran, Adv. Mater., 2012, 24, 973–978 CrossRef CAS PubMed.
- M. M. Lee, J. Teuscher, T. Miyasaka, T. N. Murakami and H. J. Snaith, Science, 2012, 338, 643–647 CrossRef CAS PubMed.
- J. Burschka, N. Pellet, S.-J. Moon, R. Humphry-Baker, P. Gao, M. K. Nazeeruddin and M. Grätzel, Nature, 2013, 499, 316–319 CrossRef CAS PubMed.
- H. Bässler and A. Köhler, in Unimolecular and Supramolecular Electronics I, ed. R. M. Metzger, Springer Berlin, Heidelberg, 2012, vol. 312, pp. 1–65 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3sc52359d |
| This journal is © The Royal Society of Chemistry 2014 |