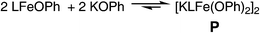Multimetallic cooperativity in activation of dinitrogen at iron–potassium sites†
Karen P.
Chiang
,
Sarina M.
Bellows
,
William W.
Brennessel
and
Patrick L.
Holland‡
*
Department of Chemistry, University of Rochester, Rochester, New York 14627, USA
First published on 15th October 2013
Abstract
The reaction of soluble iron–oxygen–potassium assemblies with N2 gives insight into the mechanisms of multimetallic N2 coordination. We report a series of very electron-rich three-coordinate, β-diketiminate-supported iron(I) phenoxide complexes, which are metastable but have been characterized under Ar by both crystallography and solution methods. Both monomeric and dimeric Fe–OPh–K compounds have been characterized, and their iron environments are very similar in the solid and solution states. In the dimer, potassium ions hold together the phenoxide oxygens and aryl rings of the two halves, to give a flexible diiron core. The reactions of the monomeric and dimeric iron(I) compounds with N2 are surprisingly different: the mononuclear iron(I) complexes give no reaction with N2, but the dimeric Fe2K2 complex reacts rapidly to give a diiron-N2 product. Computational studies show that the key to the rapid N2 reaction of the dimer is the preorganization of the two iron atoms. Thus, cooperation between Fe (which weakens the N–N bond) and K (which orients the Fe atoms) can be used to create a low-energy pathway for N2 reactions.
Introduction
Multimetallic complexes offer the opportunity for metals to cooperate in small-molecule activation.1–4 There has been a resurgence in the design of architectures for holding two or more redox-active metals in close proximity for multimetallic reactivity.5–11 This strategy is particularly compelling for the reactions of N2 with transition metals (nitrogen fixation).12Part of the motivation for multimetallic N2 fixation is that the Haber–Bosch process takes place at metal surfaces.13,14 Several zerovalent transition metals catalyze N2 reduction,13 but the most common catalyst comes from reduction of iron oxide that contains potassium oxide promoters.14–16 The highest-activity zerovalent iron surfaces have subsurface “C7 sites” at which N2 is surrounded by multiple Fe atoms.17 Steps on Fe(110) surfaces have also been implicated as reactive sites.18 This experimental work has been complemented by computations on possible structures for N2 adducts on single-crystal iron.19 However, these models for M-N2 surface structures do not yet incorporate potassium promoters that improve activity.16,20–23
A multi-iron coordination site for N2 is also implicated in nitrogenases, the enzymes that perform natural N2 reduction.24–26 The active-site cluster of molybdenum-dependent nitrogenase (FeMoco) has seven iron atoms and one molybdenum in a cage.27,28 The reactivity patterns of nitrogenase variants with changes in the amino acids near the FeMoco imply that N2 binds to one or more of the iron atoms on a four-iron face of the FeMoco.29,30 It is notable that multimetallic iron sites are important in both natural and industrial N2 fixation.
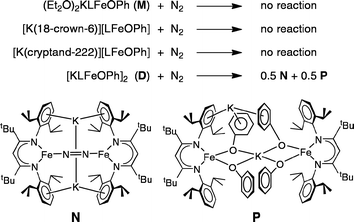
We have studied a number of iron/potassium complexes in an effort to elucidate the fundamental factors underlying N2 fixation at multimetallic sites.31–33 The most common way for transition and alkali metals to cooperate in N2 coordination is for N2 to bind end-on to the transition metal and side-on to the alkali metal.34,35 Precedents for this binding mode go back to the work of Jonas in the 1970's,36,37 and in the case of iron include recent examples from Gambarotta and Peters.38,39 We have reported reduced iron compounds in which the β-diketiminate aryl substituents interact with alkali metals,32,40–42 and related cobalt and nickel compounds have been reported by us and by Limberg.43–48 However, it is still not clear why heterobimetallic cooperation is so beneficial in terms of specific interactions between N2 and the multimetallic precursors.49,50 We know of only one study that directly quantitates the differences in N2 complexing ability between analogous monometallic and multimetallic species.51
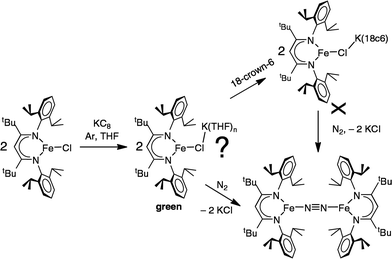
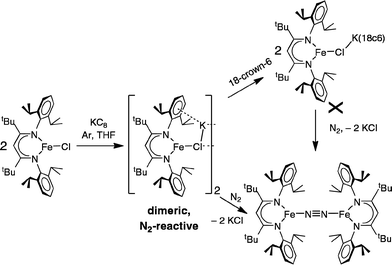
In an earlier report,32 we described the KC8 reduction of a diketiminate-supported iron(II) chloride precursor under argon to give a transient green iron(I) intermediate that is capable of coordinating N2 (Scheme 1). It was assigned as “LFe(μ-Cl)K(THF)n” based on the fact that addition of 18-crown-6 gave the crystallographically characterized green LFe(μ-Cl)K(18-crown-6). However, the isolated 18-crown-6 complex did not react with N2. Our inability to determine the structural difference between the two iron–potassium species prevented us from explaining the surprising difference in reactivity between (presumably) similar species.
Here, we report the characterization and reactivity of analogous complexes that have aryloxides in place of the chlorides in the earlier work. This substitution has enabled us to characterize the intermediate iron(I) species in more detail, and to elucidate the mechanism of N2 fixation. The results teach a general lesson about the kinetic and thermodynamic factors that can control N2 reactivity in multimetallic complexes, which may assist in the future design of multimetallic complexes for N2 reduction.
Results and discussion
Synthesis and properties of iron(I) phenoxide complexes
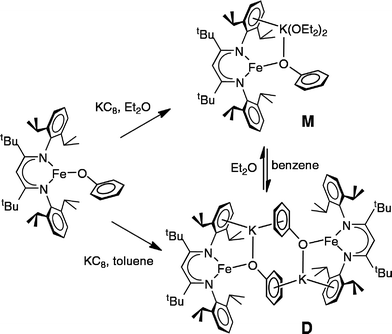
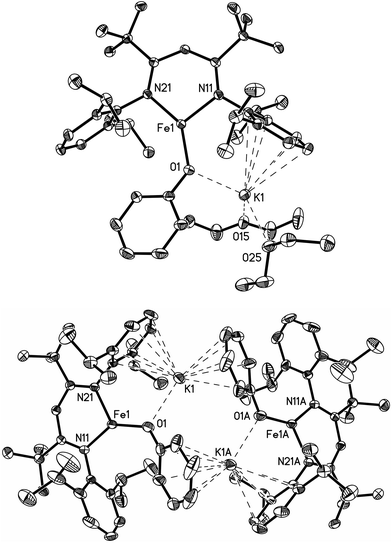
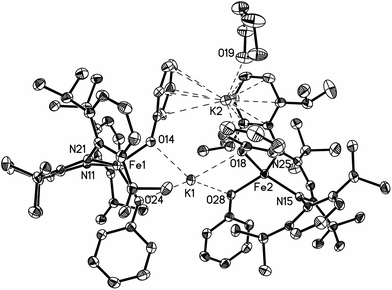
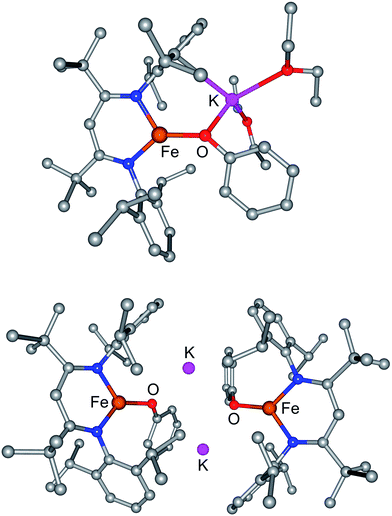
The monomeric three-coordinate iron(II) phenoxide complex LFeOPh (L = 2,2,6,6-tetramethyl-3,5-bis(2,6-diisopropylphenylimido)heptyl; Ph = phenyl) was previously reported.52 This iron(II) complex reacts rapidly with a slight excess of potassium graphite (KC8) under argon to reduce the iron(II) complex to an iron(I) product (Scheme 2). Interestingly, the iron(I) products have a different form depending on the solvents used during the synthesis and crystallization. When the reaction is performed in toluene and the product is crystallized from pentane, the dimeric (D) product [KLFeOPh]2 is isolated in 63% yield. If the reduction and crystallization are done in diethyl ether (Et2O), then monomeric (M) (Et2O)2KLFeOPh is isolated in 92% yield.X-ray crystallography (Fig. 1) shows that M and D have the same coordination at each iron, with two diketiminate N and a phenoxide O in a planar geometry. Charge counting shows that the iron centers in both complexes are iron(I). The Fe–O distances of 1.92–1.93 Å in these iron(I) compounds are about 0.1 Å longer than the analogous distances in the iron(II) phenoxide complex LFeOTol (Table 1).52 On the other hand, the Fe–N distances are shorter in the reduced iron(I) complexes, which can be attributed to π-backbonding from iron into the diketiminate π-system. The backbonding also explains the slightly longer N–C distances within the diketiminate backbone for the iron(I) complexes. Iron(I) backbonding into diketiminates has been supported by computations in related hydride and sulfide complexes.41,42
| M | D | LFeOTol | |
|---|---|---|---|
| Fe–O (Å) | 1.9220(9) | 1.929(2) | 1.833(2) |
| Fe–N (Å) | 1.913(1), 1.926(1) | 1.926(2), 1.936(2) | 1.965(2), 1.972(2) |
| N–C (Å) | 1.356(2), 1.368(2) | 1.344(3), 1.352(2) | 1.342(3), 1.335(3) |
| K–OAr (Å) | 2.609(1) | 2.586(2) | |
| K–OEt2 (Å) | 2.726(1), 2.753(1) | ||
| N–Fe–N (°) | 100.92(4) | 98.09(9) | 94.76(8) |
| N–Fe–O (°) | 142.28(4), 116.80(4) | 139.61(8), 122.28(8) | 140.20(8), 125.01(9) |
| Fe–O–C (°) | 133.13(8) | 132.5(2) | 138.8(2) |
In both M and D, the potassium cations interact with the phenoxide oxygen atom, and also engage in a cation–π interaction with one of the aromatic rings of the β-diketiminate supporting ligand. In dimeric D, the potassium coordination is completed by a second cation–π interaction with the phenyl group of the opposing phenoxide, whereas in monomeric M the potassium binds to two molecules of diethyl ether to complete its coordination.
Thus, the iron coordination is the same in M and D, and the differences only pertain to the potassium coordination. Since D does not have diethyl ether to complete its K coordination, the second cation–π interaction gives a dimeric structure with bridging to another Fe–OPh–K unit. The FeNN planes are not parallel; rather they are at an angle of 112.38(7)° to give a “bowl” with exposed Fe and K ions on the inside face (Fig. 2).
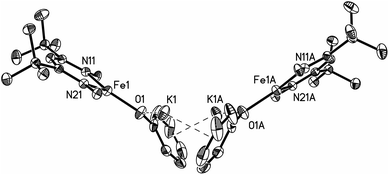 | ||
| Fig. 2 Thermal ellipsoid plot showing only the core of D; 2,6-diisopropylphenyl groups are omitted in order to reveal the core of the molecule. | ||
The solution magnetic moment of M is 4.1(2) μB, and for D is 6.5(3) μB (per dimer). Each value is consistent with high-spin (S = 3/2) iron(I) ions, as found in other three-coordinate iron(I) diketiminate complexes.32,41,42 The paramagnetically shifted 1H NMR spectra of D under argon in C6D6, C6D12, Et2O, and THF-d8 (Fig. S2†) give peak integrations consistent with local C2v symmetry around each iron atom. This indicates that the core of D is fluxional, though the high solubility suggests that the potassium ions remain surrounded by bound arenes. Dissolving crystals of M in C6D6 under an Ar atmosphere gives a 1H NMR spectrum identical to D (Fig. 3 and S2†), except for the observation of free Et2O in the solution from M. This indicates that the Et2O molecules are lost from M in benzene solution; the fact that the compound remains soluble suggests that the potassium ions are still part of the structure, and presumably the predominant solution structure in benzene is related to the crystallographic structure of D. Attempts to measure the solution molecular weight through cryoscopy gave irreproducible results (likely because of the extreme sensitivity of the compound to slight traces of moisture). However, as shown below, the reactivity ofM(in Et2O or THF) andD(in C6D6or C6D12) toward N2are very different (see below), indicating that their solution structures are different. The most reasonable model is thus that M (in Et2O or THF) and D (in C6D6 or C6D12) each have solution structures much like their crystallographic structures. The core of D must be highly flexible (consistent with computations below), but remains dimerized because of the inability to lose K+ into the nonpolar solvent.
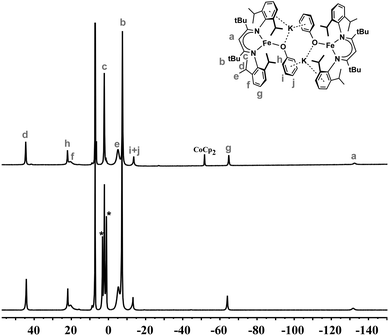 | ||
| Fig. 3 1H NMR spectra of D in C6D6 (top) and M dissolved in C6D6 to give D (bottom); asterisks (*) indicate peaks from released Et2O. | ||
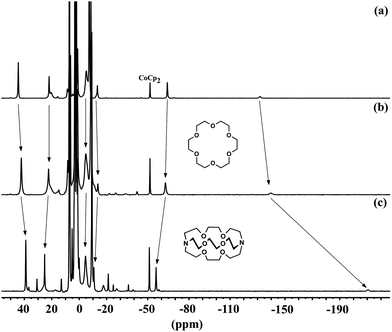
The most significant shift in the 1H NMR spectrum when changing the solvent from C6D6 (D) to Et2O (M) is that the most upfield peak shifts further upfield by about 10 ppm (Fig. S2†). Addition of 18-crown-6 or cryptand-222 to D in C6D6 gives larger upfield shifts of the same resonance, as shown in Fig. 4. This indicates the formation of ionic compounds (denoted M-18C6 and M-crypt, respectively) in which the potassium ions are increasingly separated from the iron–phenoxide. It has not been possible to isolate the chelate compounds in pure form, because of their exceptionally high sensitivity to trace air or moisture. We note that the related iron(I) hydride complex, K2[LFeH]2, can similarly be broken up into monomers with potassium chelating agents.41 In the hydride system, breaking up the dimer gave upfield shifts in the same resonance of the supporting ligand, with the amount of shift increasing from 18-crown-6 to cryptand-222.
Differential reactivity of iron(I) phenoxides with N2
Exposing solutions of the four iron(I) compounds D (in C6D6), M (in Et2O), M-18C6, and M-crypt to an atmosphere of purified dinitrogen (N2) at room temperature provides a direct comparison of their solution reactivity toward N2. Out of the four species, onlyDreacts with N2 (Scheme 3, top). In contrast, the electronically similar complexes M, M-18C6 and M-crypt each remain unchanged under N2 after 1 h. Though a solution of M in Et2O does not react, when the Et2O is evaporated from this solution and C6D6 is added to convert it into D, the reaction with N2 occurs, again showing that M and D have different behaviors in solution as well as the solid state.The reaction of N2 with a C6D6 solution of D is complete within 2 minutes at room temperature, as evidenced by complete disappearance of the 1H NMR peaks for D and the growth of new paramagnetically shifted peaks. The 1H NMR spectrum of the product shows that it is a roughly 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of the formally diiron(0) nitrogen (N) complex K2[LFeNNFeL] and the new iron(II) phenoxide (P) complex [KLFe(OPh)2]2 (Scheme 3, bottom). An internal integration standard shows that these two products account for 91% of the iron introduced into the reaction as D, indicating the iron stoichiometry in Scheme 3. Note that this reaction formally represents a disproportionation of iron(I) into equal amounts of iron(0) and iron(II).
1 mixture of the formally diiron(0) nitrogen (N) complex K2[LFeNNFeL] and the new iron(II) phenoxide (P) complex [KLFe(OPh)2]2 (Scheme 3, bottom). An internal integration standard shows that these two products account for 91% of the iron introduced into the reaction as D, indicating the iron stoichiometry in Scheme 3. Note that this reaction formally represents a disproportionation of iron(I) into equal amounts of iron(0) and iron(II).
Compound N was characterized previously, using crystallography, solution magnetism, NMR spectroscopy, resonance Raman spectroscopy, and elemental analysis.53 Its 1H NMR spectrum serves as the clearest identifying feature in mixtures of N and P, because it has seven distinct resonances of known chemical shifts. In N, N2 is surrounded by two Fe bound end-on and two K bound side-on. The N–N bond in N is substantially lengthened (1.23 Å) and weakened (stretching frequency 1589 cm−1) relative to that in N2 (1.11 Å and 2331 cm−1).32,35 Therefore, it is reasonable to consider the bridging ligand as N22−, in analogy to its neutral analogue LFeNNFeL that has been extensively characterized using variable-field Mössbauer spectroscopy and computations.54 Thus the reaction of D with N2 leads to significant structural activation of the N–N bond.
The iron(II) bis-phenoxide complex [KLFe(OPh)2]2 (P) can be synthesized independently by adding one equivalent of KOPh to a solution of LFeOPh in THF. Phenoxide P may be crystallized in 81% yield by vapor diffusion of Et2O into a toluene solution of P. The X-ray crystal structure of P (Fig. 5) shows a dimeric species with two pseudotetrahedral iron centers. The two halves of this molecule are not related by symmetry. One K cation lies near the centroid of the four phenoxide oxygen atoms with K–O distances of 2.657(2), 2.674(3), 2.677(2), and 2.818(2) Å (Table S1†). The second K cation associates with the aryl rings of a β-diketiminate ligand, one O atom of a phenoxide ligand, and is also coordinated to a THF solvent molecule. Other crystallographic details may be found in the ESI.†
While the solid-state structure of P shows no symmetry elements, the 1H NMR spectrum of P in C6D6 (Fig. S1†) contains eleven signals suggesting averaged D2h or D2d symmetry from a rapid fluxional process. Nine of the signals are assigned to the product (one of the aryl peaks integrating to 8 H is presumed to be underneath the solvent peak) based on integrations. Two of the peaks (δ 42 ppm and −29 ppm) belong to the starting material, LFeOPh, which exists in equilibrium with the product as shown in Scheme 4. This equilibrium prevents detailed solution characterization and thorough purification. It is not possible to drive the equilibrium all the way to P using an excess of KOPh, presumably due to the poor solubility of KOPh in THF. Despite these difficulties, the amassed spectroscopic and crystallographic characterization clearly establish the identity of P, and the observation of the same 1H NMR signals during the reaction of D with N2 shows that it is the product of this reaction.
Proposed mechanism for formation of N and P from D
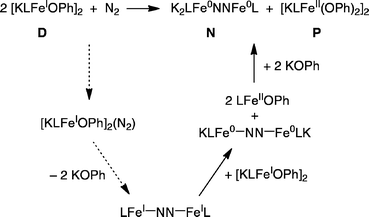
We suggest the mechanism in Scheme 5 to account for the formation of N and P from the reaction of D with N2. The first step in this mechanism is the reaction of N2 with one equivalent of D to form a complex; the possible geometry of this complex will be discussed below. Loss of two equivalents of KOPh would give the known N2 complex LFeNNFeL. This in turn could be reduced by the second equivalent of D to give the observed product N and the known iron(II) phenoxide complex LFeOPh. This is a net disproportionation of iron(I) to iron(0) (in N) and iron(II) (in LFeOPh). Finally, the iron(II) product LFeOPh could react with KOPh (released in the earlier step) to give the observed product P.This mechanism is supported by the independent experimental study of several of the steps; these are indicated by solid lines in Scheme 5. LFeNNFeL (the bottom compound in Scheme 5) has been characterized previously.32,53,54 Reaction of independently synthesized LFeNNFeL with a stoichiometric amount of D indeed gives N and LFeOPh in the expected 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 stoichiometry in 83% yield, as judged by 1H NMR integrations. As illustrated in Scheme 4, reaction of LFeOPh with KOPh gives P, verifying the feasibility of the final step. The steps indicated with dotted lines are too rapid to study using kinetics. Thus, we use computations to evaluate mechanistic possibilities for the early steps in the reaction.
2 stoichiometry in 83% yield, as judged by 1H NMR integrations. As illustrated in Scheme 4, reaction of LFeOPh with KOPh gives P, verifying the feasibility of the final step. The steps indicated with dotted lines are too rapid to study using kinetics. Thus, we use computations to evaluate mechanistic possibilities for the early steps in the reaction.
The greater reactivity of D results from a low-energy bimetallic pathway for N2 activation
We envisioned two hypotheses for explaining the difference in reaction rates between M and D. In hypothesis 1, N2 binds cooperatively to Fe and K, and backbonding into N2 is enhanced by the positive charge on the potassium cation(s). In this hypothesis, N2 would bind more strongly to D because there are two K+ in the bowl-shaped cavity of D (Fig. 2), but only one nearby K+ in M. In hypothesis 2, both M and D initially form Fe–N2 adducts, but the N2 adduct of D is more rapidly trapped by N2 coordination to the second iron atom, leading ultimately to the final products.In order to evaluate the unobserved, transient reactions of M and D with N2, we used density-functional theory (DFT) calculations performed with the ORCA computational package, using the BP86 functional and the def2-SVP basis set; computational details are described in the ESI.† In order to provide reasonable starting points, we optimized the geometries of M and of D starting from the crystallographic coordinates (Fig. 6), using a high-spin (quartet) electronic configuration at each iron atom.
The optimized geometry of M agrees well with the crystallographic structure (Table 2). For D, the optimized geometry has very similar Fe–N and Fe–O distances and an similar overall geometry. However, the geometry optimization gives a significant contraction of the molecular core (O⋯O calcd. 4.15 Å; obs. 5.01 Å) and lengthening of the K–O interactions (calcd. 2.68, 2.74 Å; obs. 2.586(2) Å) relative to the crystallographic structure. In an effort to gauge the importance of this core distortion, the computation was repeated on a model in which the Fe⋯Fe distance was constrained to the crystallographic distance of 8.17 Å. This shortens the K–O distances to be closer to the experimentally observed values (2.65, 2.68 Å), and gives an electronic energy that is the same as the unconstrained model within 1 kcal mol−1. This suggests that the potential energy surface for distortion of the potassium interactions with the arenes and oxygens is quite flat, indicating flexibility in the core of the molecule consistent with the NMR studies above. It also suggests that the energy of the molecule is not significantly influenced by the precise geometry of the K–arene and K–O interactions.
| M | D | |
|---|---|---|
| Fe–N (Å) | 1.904, 1.915 (1.913, 1.926) | 1.915–1.944 (1.926, 1.936) |
| Fe–O (Å) | 1.915 (1.922) | 1.938, 1.951 (1.929) |
| K⋯OAr (Å) | 2.636 (2.609) | 2.684, 2.742 (2.586) |
| K⋯OEt2 (Å) | 2.74, 2.754 (2.726, 2.753) |
The calculations also predict that reaction of D with four molecules of Et2O to split the dimer and form two molecules of M has ΔG° of only 2 kcal mol−1, which is indistinguishable from zero within the expected accuracy of the computations. This agrees with the experimental observations of the ability of D to transform into M in pure diethyl ether, and the ability to return M to D by evaporation of diethyl ether. The similar energies of M and D indicate that the difference in N2 reactivity betweenMandDis not due toDhaving a greater thermodynamic driving force to give the productsNandP.
Next, we introduced N2 to the computational models of M and of D, trying several potential binding modes on each side of the iron coordination plane, and both iron atoms of D. The lowest-energy N2 adducts of M-N2 and of D-N2 are shown in Fig. 7, and no stable isomers were observed with significant K–N2interactions. In both M-N2 and D-N2, the N2 molecule binds end-on and the N–N bond is slightly lengthened, to 1.155 Å in M-N2 and to 1.166 Å in D-N2. The lengthening comes from π-backbonding from the iron center into the π* orbital of N2, as shown by the somewhat shorter Fe–N(N2) distance in D-N2 (1.772 Å) than in M-N2 (1.797 Å) and from the occupation of frontier molecular orbitals with π bonding interactions between Fe and N and π* interactions between the two N atoms (see ESI†). The extent of backbonding into N2 is somewhat greater in D-N2, which might be explained by the approach of the terminal N atom of the N2 to the two K+ ions (K–N = 2.79 and 2.88 Å). However, the binding energy of N2is similar for bothM-N2andD-N2 (Table 3), with enthalpies and free energies for binding that are indistinguishable within the expected accuracy of DFT calculations. These observations argue against hypothesis 1.
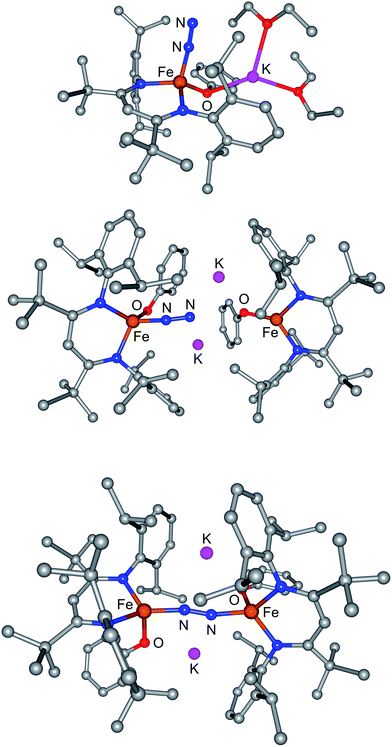 | ||
| Fig. 7 Computational models of (top) M-N2, (middle) D-N2 with terminal N2, and (bottom) D-N2 with bridging N2. | ||
| Reactants | Products | ΔH° (kcal mol−1) | ΔG°(kcal mol−1) |
|---|---|---|---|
| M + N2 | M-N2 | −17 | −5 |
| D + N2 | D-N2 | −19 | −6 |
| D-N2 | D-N2-bridge | −20 | −22 |
| D + N2 | D-N2-bridge | −39 | −28 |
If D does not bind N2 more tightly than M in an intermediate, why does it specifically give a net reaction with N2? Further computational exploration of geometries for D-N2 revealed a second isomer (D-N2-bridge), which has N2 bridging between the two iron atoms (Fig. 7, bottom). In D-N2-bridge, the N–N bond is weakened more significantly, with an N–N distance of 1.204 Å, due to backbonding from both iron atoms. The free energy of D-N2-bridge is 22 kcal mol−1lower than the initially studied D-N2 isomer that had N2 bound to only one iron atom. Therefore, bimetallic D-N2 is special because it can relax into a much more stable isomer with bridging N2. The ability to form a lower-energy isomer would provide a significant driving force for N2 reaction with D (Fig. 8), and clearly implicates the preorganization of the two Fe ions (hypothesis 2) as the key enabling factor for the rapid reaction of N2 with D. On the other hand, M does not benefit from the ability to form a stable FeNNFe unit, and does not show an overall reaction with N2.
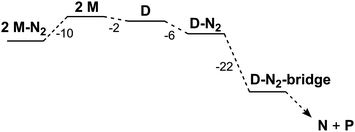 | ||
| Fig. 8 Relative free energies for computed species in kcal mol−1; free diethyl ether and N2 molecules were included in the thermodynamic calculations, but are not shown for clarity. | ||
The calculated structure of D-N2-bridge (Fig. 7, bottom) has K–O interactions that presage the loss of KOPh, as proposed in Scheme 5. Consistent with this idea, optimization of some geometries near D-N2-bridge led to spontaneous loss of KOPh molecules and contraction of the FeNNFe core (see ESI†). Exoergic addition of KOPh to LFeOPh could subsequently drive the reaction through formation of P. Overall, the computational results support the feasibility of the proposed mechanism in Scheme 5, and shed light upon key interactions in the proposed reaction intermediates.
Conclusions and implications
Mononuclear K[LFeOPh] (M) and dinuclear K2[L2Fe2(OPh)2] (D) have iron atoms with the same oxidation state, the same coordinating donors, and the same coordination geometry. Despite these similarities, and the fact that M and D are nearly isoenergetic, they react at very different rates with N2. No reaction is observed from M (in Et2O or THF) within 1 h, while D (in benzene or cyclohexane) reacts with N2 within 2 min to give a formally diiron(0) N2 complex (N). The product K2LFeNNFeL (N) has an N–N bond that is significantly stretched and weakened compared to that in free N2.32,35 Therefore, the formation of multimetallic intermediates can play a key role in trapping N2 and weakening its N–N bond.This work shows the detailed structures through which multiple iron atoms react with N2. In D, oxygen bridges between the iron and potassium play a key role in holding the iron and potassium ions in place, which may mimic the oxygen bridges between iron and potassium in the widely used Mittasch catalyst for the Haber–Bosch process. Therefore, these solution studies suggest that oxygen-bridged iron/potassium sites could be N2 binding locations on iron-based Haber–Bosch catalysts. In addition, the N2-binding ability of multiiron assemblies may be relevant to the mechanism of nitrogenase enzymes, which use iron clusters as their active sites.55,56
These studies also address the green intermediate in potassium reduction of diketiminate-bound iron(II) chloride complexes to give N2 complexes.32 The green iron(I) species in the phenoxide reaction have been crystallographically characterized, leading to valuable structural information. By analogy, we suggest that a dimeric Fe2K2Cl2 assembly would be very reactive toward N2 (Scheme 6). This hypothesis explains why the N2-binding ability of the iron(I) chloride species was lessened in the presence of 18-crown-6 in the earlier studies: the chelating agent broke up the N2-reactive bimetallic complex.
We have reported that electronically similar iron complexes with smaller diketiminate ligands can break the triple bond of N2.40 The N2-cleaving species in that system is also generated by KC8 reduction of an iron(II) chloride complex. Though its structure is not yet known, some possible structures were proposed through computations.57 The compounds described in the current study may serve as isolable mimics of the fleeting intermediates in N2-cleaving reactions of diketiminate-iron clusters. Further studies will take advantage of the stabilizing power of phenoxides, which can bind K+ through both the O atom and the phenyl group, to trap key intermediates in N2-activating reactions.
Acknowledgements
This research was supported by the National Institutes of Health (Grant no. GM065313). We thank the Fulbright Foundation and Frank Neese for making available computational resources during and after a sabbatical at the Max Planck Institute for Chemical Energy Conversion (Mülheim an der Ruhr, Germany).Notes and references
- V. Ritleng and M. J. Chetcuti, Chem. Rev., 2007, 107, 797 CrossRef CAS PubMed.
- M. E. Broussard, B. Juma, S. G. Train, W. J. Peng, S. A. Laneman and G. G. Stanley, Science, 1993, 260, 1784 CAS.
- M. Tachikawa and E. L. Muetterties, Prog. Inorg. Chem., 1981, 28, 203 CrossRef CAS.
- R. D. Adams, B. Captain and L. Zhu, J. Am. Chem. Soc., 2006, 128, 13672 CrossRef CAS PubMed.
- A. L. Gavrilova and B. Bosnich, Chem. Rev., 2004, 104, 349 CrossRef CAS PubMed.
- R. Tan and D. Song, Dalton Trans., 2009, 9892 RSC.
- I. Siewert, C. Limberg, S. Demeshko and E. Hoppe, Chem.–Eur. J., 2008, 14, 9377 CrossRef CAS PubMed.
- T. D. Harris and T. A. Betley, J. Am. Chem. Soc., 2011, 133, 13852 CrossRef CAS PubMed.
- S. L. Marquard, M. W. Bezpalko, B. M. Foxman and C. M. Thomas, J. Am. Chem. Soc., 2013, 135, 6018 CrossRef CAS PubMed.
- D. Lionetti, M. W. Day and T. Agapie, Chem. Sci., 2013, 4, 785 RSC.
- G. L. Guillet, F. T. Sloane, D. M. Ermert, M. W. Calkins, M. K. Peprah, E. S. Knowles, E. Cizmar, K. A. Abboud, M. W. Meisel and L. J. Murray, Chem. Commun., 2013, 49, 6635 RSC.
- V. Smil, Sci. Am., 1997, 277, 76 CrossRef CAS.
- R. Schlögl, Angew. Chem., Int. Ed., 2003, 42, 2004 CrossRef PubMed.
- R. Schlögl, in Handbook of Heterogeneous Catalysis, Wiley-VCH, Weinheim, 2nd edn, 2008, p. 2501 Search PubMed.
- A. Mittasch, Geschichte der Ammoniaksynthese, Verlag Chemie, Weinheim, 1951 Search PubMed.
- P. Iyngaran, D. C. Madden, S. J. Jenkins and D. A. King, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 925 CrossRef CAS PubMed.
- L. M. Falicov and G. A. Somorjai, Proc. Natl. Acad. Sci. U. S. A., 1985, 82, 2207 CrossRef CAS.
- R. C. Egeberg, S. Dahl, A. Logadottir, J. H. Larsen, J. K. Nørskov and I. Chorkendorff, Surf. Sci., 2001, 491, 183 CrossRef CAS.
- J. J. Mortensen, L. B. Hansen, B. Hammer and J. K. Nørskov, J. Catal., 1999, 182, 479 CrossRef CAS.
- S. R. Bare, D. R. Strongin and G. A. Somorjai, J. Phys. Chem., 1986, 90, 4726 CrossRef CAS.
- D. R. Strongin and G. A. Somorjai, Catal. Lett., 1988, 1, 61 CrossRef CAS.
- D. R. Strongin and G. A. Somorjai, J. Catal., 1988, 109, 51 CrossRef CAS.
- D. R. Strongin and G. A. Somorjai, J. Catal., 1989, 118, 99 CrossRef CAS.
- P. M. C. Benton, M. Laryukhin, S. M. Mayer, B. M. Hoffman, D. R. Dean and L. C. Seefeldt, Biochemistry, 2003, 42, 9102 CrossRef CAS PubMed.
- P. C. Dos Santos, R. Y. Igarashi, H.-I. Lee, B. M. Hoffman, L. C. Seefeldt and D. R. Dean, Acc. Chem. Res., 2005, 38, 208 CrossRef CAS PubMed.
- P. L. Holland, in Comprehensive Coordination Chemistry II, ed. J. McCleverty and T. J. Meyer, Elsevier, Oxford, 2004, p. 569 Search PubMed.
- O. Einsle, F. A. Tezcan, S. L. A. Andrade, B. Schmid, M. Yoshida, J. B. Howard and D. C. Rees, Science, 2002, 297, 1696 CrossRef CAS PubMed.
- T. Spatzal, M. Aksoyoglu, L. Zhang, S. L. A. Andrade, E. Schleicher, S. Weber, D. C. Rees and O. Einsle, Science, 2011, 334, 940 CrossRef CAS PubMed.
- J. Christiansen, J. M. Chan, L. C. Seefeldt and D. R. Dean, Prokaryotic Nitrogen Fixation, 2000, 101 CAS.
- B. M. Barney, R. Y. Igarashi, P. C. Dos Santos, D. R. Dean and L. C. Seefeldt, J. Biol. Chem., 2004, 279, 53621 CrossRef CAS PubMed.
- P. L. Holland, Can. J. Chem., 2005, 83, 296 CrossRef CAS.
- J. M. Smith, A. R. Sadique, T. R. Cundari, K. R. Rodgers, G. Lukat-Rodgers, R. J. Lachicotte, C. J. Flaschenriem, J. Vela and P. L. Holland, J. Am. Chem. Soc., 2006, 128, 756 CrossRef CAS PubMed.
- P. L. Holland, Acc. Chem. Res., 2008, 41, 905 CrossRef CAS PubMed.
- E. A. MacLachlan and M. D. Fryzuk, Organometallics, 2006, 25, 1530 CrossRef CAS.
- P. L. Holland, Dalton Trans., 2010, 39, 5415 RSC.
- K. Jonas, Angew. Chem., 1973, 85, 1050 CrossRef CAS.
- K. Jonas, D. J. Brauer, C. Krueger, P. J. Roberts and Y. H. Tsay, J. Am. Chem. Soc., 1976, 98, 74 CrossRef CAS.
- J. Scott, I. Vidyaratne, I. Korobkov, S. Gambarotta and P. H. M. Budzelaar, Inorg. Chem., 2008, 47, 896 CrossRef CAS PubMed.
- M.-E. Moret and J. C. Peters, J. Am. Chem. Soc., 2011, 133, 18118 CrossRef CAS PubMed.
- M. M. Rodriguez, E. Bill, W. W. Brennessel and P. L. Holland, Science, 2011, 334, 780 CrossRef CAS PubMed.
- K. P. Chiang, C. C. Scarborough, M. Horitani, N. S. Lees, K. Ding, T. R. Dugan, W. W. Brennessel, E. Bill, B. M. Hoffman and P. L. Holland, Angew. Chem., Int. Ed., 2012, 51, 3658 CrossRef CAS PubMed.
- M. M. Rodriguez, B. D. Stubbert, C. C. Scarborough, W. W. Brennessel, E. Bill and P. L. Holland, Angew. Chem., Int. Ed., 2012, 51, 8247 CrossRef CAS PubMed.
- K. Ding, W. W. Brennessel and P. L. Holland, J. Am. Chem. Soc., 2009, 131, 10804 CrossRef CAS PubMed.
- K. Ding, A. W. Pierpont, W. W. Brennessel, G. Lukat-Rodgers, K. R. Rodgers, T. R. Cundari, E. Bill and P. L. Holland, J. Am. Chem. Soc., 2009, 131, 9471 CrossRef CAS PubMed.
- S. Pfirrmann, C. Limberg, C. Herwig, R. Stoesser and B. Ziemer, Angew. Chem., Int. Ed., 2009, 48, 3357 CrossRef CAS PubMed.
- S. Pfirrmann, C. Limberg, C. Herwig, C. Knispel, B. Braun, E. Bill and R. Stoesser, J. Am. Chem. Soc., 2010, 132, 13684 CrossRef CAS PubMed.
- B. Horn, S. Pfirrmann, C. Limberg, C. Herwig, B. Braun, S. Mebs and R. Metzinger, Z. Anorg. Allg. Chem., 2011, 637, 1169 CrossRef CAS.
- B. Horn, C. Limberg, C. Herwig, M. Feist and S. Mebs, Chem. Commun., 2012, 48, 8243 RSC.
- S. Gambarotta and J. Scott, Angew. Chem., Int. Ed., 2004, 43, 5298 CrossRef CAS PubMed.
- T. Dube, S. Conochi, S. Gambarotta, G. P. A. Yap and G. Vasapollo, Angew. Chem., Int. Ed., 1999, 38, 3657 CrossRef CAS.
- J. P. Collman, J. E. Hutchison, M. A. Lopez and R. Guilard, J. Am. Chem. Soc., 1992, 114, 8066 CrossRef CAS.
- K. P. Chiang, P. M. Barrett, F. Ding, J. M. Smith, S. Kingsley, W. W. Brennessel, M. M. Clark, R. J. Lachicotte and P. L. Holland, Inorg. Chem., 2009, 48, 5106 CrossRef CAS PubMed.
- J. M. Smith, R. J. Lachicotte, K. A. Pittard, T. R. Cundari, G. Lukat-Rodgers, K. R. Rodgers and P. L. Holland, J. Am. Chem. Soc., 2001, 123, 9222 CrossRef CAS PubMed.
- S. A. Stoian, J. Vela, J. M. Smith, A. R. Sadique, P. L. Holland, E. Münck and E. L. Bominaar, J. Am. Chem. Soc., 2006, 128, 10181 CrossRef CAS PubMed.
- P. C. Dos Santos, D. R. Dean, Y. Hu and M. W. Ribbe, Chem. Rev., 2004, 104, 1159 CrossRef CAS PubMed.
- B. M. Hoffman, D. Lukoyanov, D. R. Dean and L. C. Seefeldt, Acc. Chem. Res., 2013, 46, 587 CrossRef CAS PubMed.
- T. M. Figg, P. L. Holland and T. R. Cundari, Inorg. Chem., 2012, 51, 7546 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthetic, crystallographic, and computational details. CCDC 936166–936168. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c3sc52487f |
| ‡ Current address: Department of Chemistry, Yale University, New Haven, Connecticut 06511, USA. E-mail: E-mail: patrick.holland@yale.edu. |
| This journal is © The Royal Society of Chemistry 2014 |