Full kinetic analysis of a rhodium-catalyzed hydroformylation: beyond the rate-limiting step picture

Abstract

A complete dynamic kinetic analysis beyond the steady state approximation of the rhodium-catalyzed hydroformylation with the 6-DPPon ligand is presented. The energy profile was calculated using a CCSD(T):B3LYP scheme. The results are compatible with the experimental trends for this system with regard to the activity, the selectivity and the substrate dependencies. In contrast to the classical understanding of the kinetics, not one rate-limiting step or energetic span governs the catalytic reaction. Conversely, the kinetic analysis shows that several intermediates and transition states control the reaction rate and the selectivity.

---

Introduction

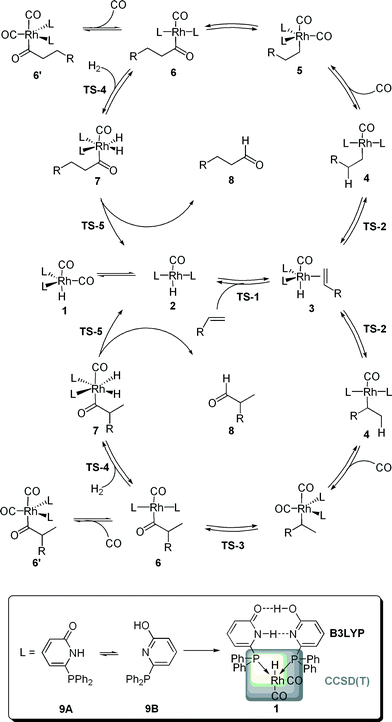
Rhodium catalyzed hydroformylation, i.e. the formation of aldehydes upon the addition of CO and H₂ to an olefin, is one of the most relevant homogeneous catalyzed processes in industry.¹ In particular, terminal alkenes are important substrates with linear aldehydes as the most desired products. Hence, beside the activity, the selectivity of the catalytic process is of importance.^2,3 Numerous experimental and computational studies on the mechanism of this process were reported.⁴ The current generally-accepted, dissociative mechanism is depicted in Scheme 1. A [HRh(L)₂(CO)₂] complex is formed in situ and dissociates in a [HRh(L)₂(CO)] complex and CO, the former compound being able to coordinate an olefin via the transition state TS-1. The alkene complex 3 can undergo hydrometallation towards the branched or linear alkyl complex 4. A subsequent CO insertion leads to the 16 valence electron complex [(Acyl)Rh(L)₂(CO)] 5. This intermediate can coordinate a second CO molecule to form the saturated acyl complex 5′, in previous studies detected by NMR and in situ IR,⁵ or undergoes oxidative addition of H₂ to yield the octahedral complex 6. Finally, a reductive elimination via TS-5 generates the aldehyde 8 under concomitant formation of the hydride complex 2. Classically, two types of kinetics are discussed. Within the so-called “type I” kinetic, 1 represents the “resting state” of the catalytic transformation and the “rate determining transition state” is either TS-1 or TS-2. A first order dependence of the reaction rate on the olefin concentration and an inverse first order with regard to the CO partial pressure are characteristic for this type of kinetics. The “type II” kinetics shows a first order dependence on the H₂ concentration, which is interpreted by assuming that 6′ is the “resting state” of the catalytic transformation and that TS-4 is the “rate determining transition state”.⁴

Scheme 1 The generally accepted mechanism of the rhodium-catalyzed hydroformylation leading to the linear (top cycle) or the branched aldehyde (bottom cycle). The 6-DPPon ligand 9 is able to form hydrogen bond networks in the coordination sphere of a late transition metal. Furthermore, a schematic representation of the two layer IMOMO scheme is given at the example of the hydridodicarbonyl complex 1 is presented: the grey box indicates atoms described at the CCSD(T) level, whereas all other atoms are described at the B3LYP level.

Model and numerical results

In order to gain a more profound understanding of the kinetics, especially with regard to the role of the individual intermediates and transition states for the activity and selectivity, we performed a detailed dynamic kinetic analysis of this process. As a case study we selected the rhodium catalyzed hydroformylation with the self-assembling 6-diphenylphosphinopyridone (6-DPPon, 9) ligand, since many experimental data, including kinetic studies as well as in situ IR and NMR investigations, are available for this system. Furthermore, due to its unique ability to form hydrogen bonds between two tautomeric forms in the coordination sphere of a transition metal, 9 is highly active and achieves selectivities comparable to those obtained with tailor-made bidentate ligands in the hydroformylation of terminal alkenes.⁶ In our work, quantum mechanical methods are used to model the energy profiles of the probranched and prolinear reaction path shown in Scheme 1. The experimentally used 1-octene was replaced by propene. Since the dynamic kinetic analysis presented herein requires accurate free energies for every elemental step of the catalytic process, methods beyond DFT are necessary.⁷ Following earlier work of Morokuma and co-workers, we decided to use a two-layer integrated molecular orbital – molecular orbital (IMOMO) scheme to allow for an accurate description of the energetics of all elementary steps of the catalytic transformation.⁸ The idea of an IMOMO calculation is to split the investigated system into two layers, which are treated by different methods and basis sets. An IMOMO method can be regarded as a special case of an ONIOM method, which usually combines DFT or ab initio methods with molecular mechanics. A model complex with PH₃ ligands serves as high layer and is treated with a high-level ab initio method [here a CCSD(T)/MP2 compound method on a BP86/aug-cc-pVTZ optimized structure], whereas the actual molecule of interest, treated at the DFT level (B3LYP/6-31G(d,p)), can be regarded as the low layer. The partitioning scheme is illustrated in Scheme 1. Hydrogen atoms were used to link the two layers. The free energy values obtained at this level of theory for the probranched and the prolinear pathways of the rhodium-catalyzed hydroformylation with 9 are summarized in Table 1. Gas phase translational contributions to the entropy have been corrected to take into account the reduced mobility of ions and complexes in solution.⁹ A recent theoretical study of a ruthenium-catalyzed metathesis suggests the necessity of this approach.¹⁰

Table 1 Free enthalpy values of the intermediates and transition states of the rhodium catalyzed hydroformylation with 9 in kcal mol⁻¹ (with respect to 1 and the sum of the substrate enthalpies)

	ΔGprolinear	ΔGprobranched
a IRC calculations confirmed that the lowest energy pathways for the prolinear and probranched hydroformylation involve different conformers of TS-1 and 3.
1	0	0
2	14.84	14.84
TS-1^a	22.37	20.97
3 ^a	14.35	14.05
TS-2	24.81	26.02
4	14.79	23.43
5	5.32	10.27
TS-3	18.04	19.95
6	8.61	11.54
TS-4	12.47	15.14
7	8.00	9.74
TS-5	15.99	16.79
8	0.48	−0.71
6′	−2.22	1.12

---

The kinetics of the catalytic cycle presented in Scheme 1 is approached with the help of first-order differential equations. Changes of concentrations of the species i with time are expressed by standard kinetic equations, such as

dc₄/dt = − (k_4,TS‐2 + k_4,5[CO])c₄ + k_TS‐2,4c_TS‐2 + k_5,4c5 (1)

for the rhodium-alkyl complex 4. The rate coefficients k_ij refer to reactions of species i to species j, they are usually asymmetric (k_ij ≠ k_ji) and are equal to zero if i and j are not connected by a chemical reaction, as indicated by an arrow in Scheme 1. For constant alkene, product, CO and H₂ concentrations, these equations are of (pseudo-)first order. In practice, the concentrations of CO and H₂ in solution are fixed via Henry's law by applying a constant pressure of these gases to the system, and the alkene concentration changes little with time in the early stages of the reaction, as the concentration of catalytically active species is always considerably smaller than the starting material concentration. The catalytic cycle can be closed by taking the formation of the product as irreversible. This approximation holds if the product formation is strongly exergonic or the product concentration is small, which is again valid in the early stages of the catalytic reaction. In this manner, the total reaction enthalpy is stored in the product rather than in the catalytic cycle, and the sum of the concentrations of the species within the cycle is constant, i.e. stoichiometry is obeyed. At stationarity, dc_i/dt = 0 holds for all species, and equations of the type 1 can be combined to a linear system of equations,¹¹from which the unknown concentrations, , can be computed. The elements of the matrix K are the reaction coefficients, multiplied by the constant concentrations of the starting materials, if applicable.

Shaik and coworkers have described a particularly interesting solution of eqn (2) that permits an approximation that leads to the computation of the steady-state concentrations and the catalytic activity of a cycle in terms of a simple quantity, the so-called energetic span.¹² From , it is possible to identify the most abundant species within the cycle, the resting state. Catalytic activity is described by the turnover frequency, here given by TOF = k_TS-5,2c_TS5/c_Rh. As an alternative to just looking at the stationary state, we suggest to investigate the complete dynamics of the system by substituting , reducing the quasi-first-order differential equations akin to eqn (1) to an eigenvalue problem independent of time. It reads

This problem has eigenvalues λ₁ = 0 and λ₂⋯λ_n > 0, and eigenvectors , from which the temporal evolution of the concentrations can be computed as

The coefficients that weight the partial solutions, A_μ, can be computed from the initial conditions. This approach has been used frequently in charge or energy transfer kinetics.¹³ With the help of eqn (4), a semi-analytical expression for the concentration of the catalytic species at any time is given, hence avoiding the tedious numerical integration of stiff kinetic equations. This approach can not only be used to compute a typical initialization time of the cycle, but in addition leads to a full description of the kinetics including varying alkene and product concentrations. Proceeding a small time step Δt, the product concentration can be computed, e.g. for the left cycle in Scheme 1, via an integration such as

c_p(Δt) = K_TS‐5,2∫^Δt₀c_TS‐5(t) dt. (5)

Again, it is possible to make use of eqn (4) for the computation of the reductive elimination transition state concentration, c_TS-5, and for an analytical representation of the integral. The alkene concentration at the end of this time step is given by a simple argument of stoichiometry as c_E(Δt) = c_E(0) − c_P(Δt) − Σ_ic_i(Δt), where the sum is only taken over those rhodium complexes within the catalytic cycle ligated by the alkene. Replacing the initial conditions by and c_E(Δt), the calculation can now be performed repeatedly, until the starting material has all but vanished. In practice, Δt is chosen to meet a small decline in the alkene concentration, Δc_E = c_E(t = 0) × 10⁻⁴, at each time step. From this integration, further characteristic times such as the starting material half life can be accessed.

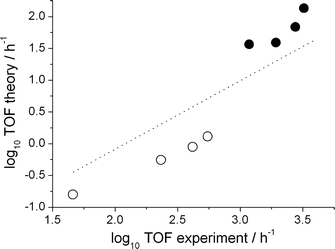
First, however, the reliability of the kinetic model has to be demonstrated. For this purpose, we compare the calculated turn over frequency and the selectivity to those obtained experimentally (Table 2). Keeping in mind the notoriously high error propagation associated with taking the exponential of a free energy to obtain a reaction coefficient (an error of 1.8 kcal mol⁻¹ in ΔG propagates to an order of magnitude in the TOF), the agreement between the experiment and the kinetic model is good with regard to both the catalyst activity and the regioselectivity. To further validate the kinetic analysis approach we benchmarked it against a series of experiments with varied 1-octene concentration and CO partial pressure. Both experimental trends in the TOFs, namely a decrease with increasing CO concentration and an increase with increasing alkene concentration, are reproduced by the numerical approach. All results are displayed in Fig. 1 as a double logarithmic plot of the theoretical versus the experimental TOFs.

Table 2 Experimental selectivity and activity of the rhodium catalysed hydroformylation with 9 compared to the results of the kinetic analysis

	Exp.^a	Calculated
a Conditions: Rh/9/substrate = 1 : 20 : 7500, 353.15 K, 10 bar, toluene.
TOF [h^−1]	3250	425
Selectivity linear : branched	96 : 4	87 : 13

---

Fig. 1 Decadic logarithm of the computed vs. the experimental turnover frequency. Open symbols: olefin concentration series (from left to right: 1.21, 3.63, 6.07 and 8.63 mmol l⁻¹). Closed symbols: CO partial pressure series (from left to right 20, 15, 10 and 5 bar). The dotted line has a slope of unity, it serves as a guide to the eye.

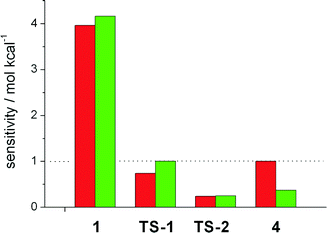
We then focussed on the question which intermediates and transition states are responsible for the activity and selectivity. To study the influence of the free enthalpy of states within the catalytic cycles, the ΔG value of each state has been varied by a small amount, resulting in a change in the turnover frequency. This procedure is equivalent to computing the derivative S_i = TOF⁻¹(∂TOF/∂G_i) and extrapolating to a change in ΔG_i of one kcal mol⁻¹. The results are depicted in Fig. 2. Here, a value of S_i > 1 implies a speedup of the reaction, for S_i < 1 the reaction slows down, and ΔG_i has no impact on the reaction if S_i equals unity. The TOF of the linear hydroformylation is particularly sensitive to changes in the enthalpy of the hydrometallation transition state TS-2 and the hydridocarbonyl complex 1 (red bars). In case of the probranched hydroformylation (green bars), the hydridocarbonly complex 1 together with the alkyl complex 4 and the transition state for the hydrometallation TS-2 have the strongest influence on the TOF (Fig. 3).

Fig. 2 Sensitivity of the turnover frequency w.r.t. a change in the free energy of a reaction intermediate or transition state. The colours indicate the formation of a linear product (red) and a branched product (green). Other states do not show a significant deviation from unity at any reaction condition.

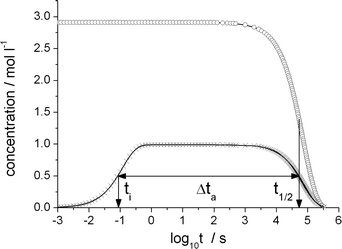Fig. 3 Olefin (circles) and product-generating transition state TS-5 (crosses) concentration as a function of the decadic logarithm of time reaction conditions as in Table 2. The TS-5 concentration has been divided by its static limit. Characteristic time scales: initialization time t_i, olefin half life t_1/2 and time during which the catalytic cycle is active, Δt_a.

Increasing the enthalpy of 4 results in a decrease of the activity, an interesting finding as deuterium labelling experiments demonstrated that the probranched hydrometallation is reversible. Notably, our results show that not one rate determining step or energetic span accounts for the activity. Therefore the ΔΔG^TS between two transition states neither accounts for the selectivity of the catalytic process! This finding is in stark contrast to the conclusions usually derived from static steady state interpretations of catalytic transformations.

The kinetic analysis predicts that the hydridodicarbonyl complex 1 and at high alkene concentrations is the most abundant species. This is in agreement with previous experimental studies where 1 was detected by in situ IR at low alkene concentrations.⁷

An approach complementary to our mathematical description of catalytic cycles has been presented by Reek and co-workers.¹⁴ By varying the starting material concentrations, these authors have been able to directly access selected reaction rates and integrate them into a kinetic scheme. This approach is feasible once the reaction setup permits such a variation, the number of relevant species participating in the catalytic cycle is comparable to the number of variations that are possible, and if the starting materials participate in only one relevant reaction. Unfortunately, none of these conditions are met by the experimental setup and reaction scheme used in our work. In the most extended scheme, we make use of two coupled catalytic cycles containing 24 species, with CO participating in five of them. Furthermore, our analysis relies on a constant concentration of CO and H₂via Henry's law, permitting the application of a (quasi)first order scheme.

Conclusions

In summary, we have developed a method enabling the dynamic kinetic analysis of catalytic transformations and successfully tested it for the rhodium-catalyzed hydroformylation with the 6-DPPon ligand 9.‡ The results show that several intermediates and transition states contribute to the activity and selectivity of the catalytic transformation. This finding is in contrast to common interpretations of the kinetics of catalytic transformations and has to be taken into account when efforts are made towards the in silico design of new catalysts.

Acknowledgements

This work was supported by the DFG, the International Research Training Group “Catalysts and Catalytic Reactions for Organic Synthesis” (IRTG 1038). Experimental and computational support by Dr. S. Diezel and M. Kähny is gratefully acknowledged.

Notes and references

1. K. Weissermel and H.-J. Arpe, Industrial Organic Chemistry, Wiley-VCH, Weinheim, 2003, pp. 127–144; K. D. Wiese and D. Obst, Top. Organomet. Chem., 2006, 18, 1–33.
2. B. Breit and L. Diab, in Comprehensive Organic Synthesis, ed. Gary A. Molander and Paul Knochel, Elsevier, Oxford, 2nd edn, 2014, vol. 4, pp. 995–105; B. Breit, Top. Curr. Chem., 2008, 279, 139–172; B. Breit and W. Seiche, Synthesis, 2001, 1–36.
3. T. J. Devon, G. W. Philips, T. A. Puckette, J. L. Stavinoha and J. J. Vanderbilt, US Pat., 4 694 109, 1987; C. P. Casey, G. T. Whiteker, M. G. Melville, L. M. Petrovich, J. A. Gavey and D. R. Powell, J. Am. Chem. Soc., 1992, 114, 10680–10680; E. Billig, A. G. Abatjoglou and D. R. Bryant, US Pat., 4 769 498, 1988; G. D. Cunny and S. L. Buchwald, J. Am. Chem. Soc., 1993, 115, 2066–2068; M. Kranenburg, Y. E. M. v. d. Burgt, P. C. J. Kamer, P. W. N. M. v. Leeuwen, K. Goubitz and J. Fraanje, Organometallics, 1995, 14, 3081–3089.
4. See for example P.W.N.M. van Leeuwen in Rhodium Catalyzed Hydroformylation, ed. P.W.N.M. van Leeuwen and C. Claver, Kluwer Academic Publishers, Dordrecht, 2000; T. Matsubara, N. Koga, Y. Ding, D. G. Musaev and K. Morokuma, Organometallics, 1997, 16, 1065–1078; C. R. Landis and J. Uddin, J. Chem. Soc., Dalton Trans., 2002, 729–742; M. Sparta, K. J. Børve and V. Jensen, J. Am. Chem. Soc., 2007, 129, 8487–8499; J. J. Carbo, F. Maseras, C. Bo and P. W. N. M. van Leeuwen, J. Am. Chem. Soc., 2001, 123, 7630–7637; A. L. Watkins and C. R. Landis, J. Am. Chem. Soc., 2010, 132, 10306; E. Zuidema, L. Escorihuela, T. Eichelsheim, J. J. Carbo, C. Bo, P. C. J. Kamer and P. W. N. M. van Leeuwen, Chem. – Eur. J., 2008, 14, 1843–1853 and the references cited therein. For a recent study on the computational kinetics of the cobalt catalyzed hydroformyation see: L. E. Rush, P. G. Pringle and J. N. Harvey, Angew. Chem., Int. Ed., 2014, 53, 8672–8676.
5. A. G. Kent and J. M. Brown, J. Chem. Soc., Perkin Trans. 2, 1988, 1587–1607; S. C. van der Slot, P. C. J. Kamer, P. W. N. M. van Leuween, J. A. Iggo and B. T. Heaton, Organometallics, 2001, 20, 430–441; U. Gellrich, W. Seiche, M. Keller and B. Breit, Angew. Chem., 2012, 124, 11195 ( Angew. Chem., Int. Ed. , 2012 , 51 , 11038 ).
6. B. Breit and W. Seiche, J. Am. Chem. Soc., 2003, 125, 6608–6609; U. Gellrich, J. Huang, W. Seiche, M. Keller, M. Meuwly and B. Breit, J. Am. Chem. Soc., 2011, 122, 964–975; J. Huang, D. Häussinger, U. Gellrich, W. Seiche, B. Breit and M. Meuwly, J. Phys. Chem. B, 2012, 116, 14406–14415.
7. U. Gellrich, D. Himmel, M. Meuwly and B. Breit, Chem. – Eur. J., 2013, 19, 16272–16281.
8. M. Svensson, S. Humbel, R. D. J. Froese, T. Matsubara, S. Sieber and K. Morokuma, J. Phys. Chem., 1996, 100, 19357; S. Humbel, S. Sieber and K. Morokuma, J. Chem. Phys., 1996, 105, 1959; T. Vreven and K. Morokuma, J. Chem. Theory Comput., 2000, 21, 1419; V. P. Ananikov, D. G. Musaev and K. Morokuma, J. Mol. Catal. A: Chem., 2010, 324, 104; A. Anoop, W. Thiel and F. Neese, J. Chem. Theory Comput., 2010, 6, 3137.
9. R. L. Martin, P. J. Hay and L. R. Pratt, J. Phys. Chem. A, 1998, 102, 3565–3573; D. Huang, O. V. Makhlynets, L. L. Tan, S. C. Lee, E. V. Rybak-Akimova and R. H. Holm, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 1222–1227; D. Huang, O. V. Makhlynets, L. L. Tan, S. C. Lee, E. V. Rybak-Akimova and R. H. Holm, Inorg. Chem., 2011, 50, 10070–10081; Y. Liang, S. Liu, Y. Xia, Y. Li and Z.-X. Yu, Chem. – Eur. J., 2008, 14, 4361–4373; Y. Chen, S. Ye, L. Jiao, Y. Liang, S.-D. K. Mahapatra, J. W. Herndon and Z.-X. Yu, J. Am. Chem. Soc., 2007, 129, 10773–10784; Z. X. Yu and K. N. Houk, J. Am. Chem. Soc., 2003, 125, 13825–13830; M. Wen, F. Huang, G. Lu and Z.-X. Wang, Inorg. Chem., 2013, 52, 12098.
10. A. Poater, E. Pump, S. V. C. Vummaleti and L. Cavallo, J. Chem. Theory Comput., 2014, 10, 4442–4448.
11. J. Christiansen, Adv. Catal., 1953, 5, 311–353.
12. S. Kozuch and S. Shaik, J. Am. Chem. Soc., 2006, 128, 3355–3365; S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101–110.
13. T. Cramer, A. Volta, A. Blumen and T. Koslowski, J. Phys. Chem. B, 2004, 108, 16586–16592 , and references therein.
14. V. Bocokić, A. Kalkan, M. Lutz, A. L. Spek, D. T. Gryko and J. N. H. Reek, Nat. Commun., 2013, 4, 2670.

---

Footnotes

† Electronic supplementary information (ESI) available: quantum chemistry input geometries, experimental details, sample kinetic analysis input and output files. See DOI: 10.1039/c4cy01209g

‡ For non-commercial applications, the code written for the full kinetic analysis is available on request free of charge from the authors.

---