Equilibrium voltage and overpotential variation of nonaqueous Li–O2 batteries using the galvanostatic intermittent titration technique†
Z. H.
Cui
a,
X. X.
Guo
*a and
H.
Li
b
aState Key Laboratory of High Performance Ceramics and Superfine Microstructure, Shanghai Institute of Ceramics, Chinese Academy of Sciences, Shanghai 200050, China. E-mail: xxguo@mail.sic.ac.cn
bInstitute of Physics, Chinese Academy of Sciences, Zhongguancun South 3rd Street No. 8, Beijing 100190, China
First published on 4th September 2014
Abstract
The Li–air (or Li–O2) battery has attracted wide attention, since it has the highest theoretical specific gravimetric energy density. In spite of the rapid progress made on improving its cyclic performance and reducing its voltage polarization, many key issues on thermodynamics and kinetics in nonaqueous Li–O2 batteries are still unresolved. In this study, by using the galvanostatic intermittent titration technique, several novel phenomena have been observed, such as zero voltage gap for the open circuit voltage (OCV) between charging and discharging, asymmetrical polarization behaviours at different current densities and temperatures, a continuous increase of overpotential during charging, and a negative temperature coefficient of the cell's thermodynamic equilibrium voltage. These results could inspire other researchers to comprehensively investigate the complicated reaction mechanisms, thermodynamics, and kinetic properties of the Li–air battery, as well as other advanced batteries.
The Li–air (or Li–O2) battery offers great potential for achieving much higher specific gravimetric energy density than state-of-the-art Li-ion batteries. It has become the focus of much scientific research, especially in the past few years.1–6 By virtue of material design of the air cathodes, the introduction of a redox mediator, optimization of the operation protocols, and by adding a soluble catalyst in the electrolyte many reports have shown that Li–O2 batteries could be run for hundreds or even thousands of cycles, while delivering considerably large specific capacities.7–16 In spite of the rapid progress made on improving their cyclic performance and reducing their voltage polarization, many issues on thermodynamics and kinetics in non-aqueous Li–O2 batteries are still unresolved.
The forward discharging reaction and backward charging reaction of lithium and oxygen in the air cathode can be written as the following:
| 2Li+ + 2e− + O2 ↔ Li2O2 | (1) |
According to the formation energies of the reactants and products at 25 °C under ambient conditions, the thermodynamic equilibrium voltage (emf) for reaction (1) in aprotic electrolyte is 2.959 V vs. Li+/Li.1,17 Based on the surface enhanced Raman spectroscopy and differential electrochemical mass spectroscopy (DEMS) investigations,18 it has been suggested that LiO2 exists as an intermediate phase and then disproportionates to Li2O2, as described by eqn (2) and (3):
| Li+ + e− + O2 → LiO2 | (2) |
| 2LiO2 → Li2O2 + O2 | (3) |
The emf value for reaction (2) is 3.0 V.19 The single electron reaction path (2) during discharging was argued by a combination of experimental cyclic voltammetry and DEMS.20
During charging, the Li2O2 is oxidized directly in a one-step reaction, without passing via the decomposition of LiO2.20 Kang et al. agreed that the direct decomposition of Li2O2 is a thermodynamic equilibrium reaction path, but the formation of a series of off-stoichiometric Li2−xO2 compounds is favourable for decreasing the overpotential.21 The above arguments could be clarified by showing the open circuit voltage (OCV) profiles. However, experimentally, the thermodynamic equilibrium voltages of Li–O2 batteries during discharging and charging have rarely been measured.
The high overpotential of discharging (oxygen reduction reaction: ORR) and charging (oxygen evolution reaction: OER), is actually the most challenging problem for Li–O2 batteries, and leads to a low round-trip electrical energy efficiency, typically less than 70%.2 In the best case,16 the difference in the charge and discharge voltage is approximately 0.50–0.75 V. This leads to an electrical energy efficiency of ∼75–85%, which is below the value of 90% required by most practical applications.2 Whether this voltage gap can be ultimately eliminated or significantly reduced requires a deep understanding of its thermodynamic and kinetic features.
Taking into account the electrochemical reactions occurring at the cathode, there should be many factors affecting the cathode reaction rate as well as the overpotential, at the very least: the Li+ and O2 transfer at the gas/electrolyte and electrolyte/cathode interfaces; Li+, e−, and O2− transport in the lattice of Li2O2; nucleation; the growth and decomposition of Li2O2; and other chemical reactions related to the electrolyte. All these factors contribute to the discharge or charge overpotentials, which can be experimentally determined according to the equation:
| η = Umeas − Ueq | (4) |
The galvanostatic intermittent titration technique (GITT), which combines transient and steady-state measurements, is a widely used tool to determine the Ueq and η values.23 In this work, we carried out studies into the OCV and overpotential issues of Li–O2 batteries with intentionally selected N-methyl-N-propylpiperidinium bis(trifluoromethanesulfonyl)imide (PP13TFSI) as the electrolyte solvent. By taking advantage of the relatively good chemical and electrochemical stability of this electrolyte at elevated temperatures,24 the values of Ueq, the discharge overpotential (ηdis = Udis − Ueq), and the charge overpotential (ηchg = Uch − Ueq) measured with different current densities, as well as at different temperatures, were determined. The mechanisms underlying the electrochemical reactions during the cell operations are discussed accordingly.
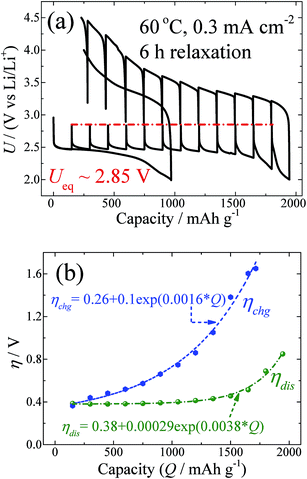
GITT measurements of the Swagelok-type Li–O2 batteries with PP13TFSI:LiClO4 as the electrolytes and with vertically aligned carbon nanotubes (VACNTs) as the cathodes were carried out. Fig. 1a shows the GITT curves for the battery voltage as a function of specific capacity measured at 60 °C and at a fixed current density of 0.3 mA cm−2 during galvanostatic discharge/charge, with a relaxation time of 6 h. Correspondingly, Fig. 1b shows ηdis, as well as ηchg, as a function of capacity (Q). From the figures, four points are worth noting.
First, the discharge capacity under the GITT condition is nearly a factor of two larger than that for the continuous galvanostatic discharge (Fig. 1a). A scanning electron microscopy (SEM) measurement reveals that the Li2O2 grows like the abacus balls around the carbon nanotubes at the current density of 0.3 mA cm−2 under either GITT or the continuous condition (Fig. S1†). Nevertheless, the particles in the GITT case are smaller in size (∼100 nm) but larger in density than those in the continuous galvanostatic discharge case. The increased density of the Li2O2 particles indicates that the GITT condition promotes the usage of the carbon-nanotube surfaces, leading to the increased discharge capacity. This phenomenon has also been noted by Zhu et al.25 In their results, they found that discharging at 120 minute intervals at a current density of 0.25 mA cm−2 can increase the capacity to 1250 mA h g−1, compared to 750 mA h g−1 for the continuous galvanostatic discharge.
Second, in the process of discharging (Fig. 1a), nearly all the OCVs reach the same Ueq of 2.85 V after 6 h relaxation. Actually, as shown by the GITT curves in Fig. S2,† the OCVs during the whole process reach the same value of 2.85 V after 24 h relaxation. The equilibrium voltage of an electrochemical reaction is determined by the formation energy difference of the reactants and products, as shown in the Nernst eqn (5):26
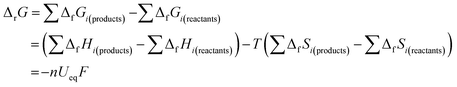 | (5) |
According to the results shown in Fig. S3,† the simulated Ueq at 25 °C is 2.861 V. It is interesting to note that this value is 0.098 V smaller than the theoretical value 2.959 V of reaction (1). X-ray diffraction (XRD) scans reveal that Li2O2 is the only detectable crystalline product in both the discharge and charge processes (Fig. S4†). Under standard conditions, the emf of reaction (1) should be constant, where this value is 2.959 V if the formation energy value from the bulk Li2O2 and lithium, and an oxygen partial pressure of 1 atm are used. In real situations, the formed Li2O2 could include two parts: the defective Li2O2 nanoparticle and solvated Li2O2 in solvents. The solubility of Li2O2 in the current electrolyte is not clear. It should be a low value. If the Li2O2 is saturated soon after discharging, then variations of the concentration of Li2O2 could be negligible. However, the observed emf value is constant in most of the discharge and charge range, indicating that the solubility of Li2O2 should be very small, and hence, the concentration of solvated Li2O2 in the solvents does not change immediately after discharging. Currently, it is not clear quantitatively whether the solvated Li2O2 in the solvents is one of the reasons for the change in emf value from 2.959 V to 2.85 V. Previous reports indicate that Li2O2 crystals with various orientations and different surface energies might be formed.22,28 It is known that the variation of the surface energy during discharge and charge may influence emf for the conversion reaction.27 The theoretical emf of 2.959 V is calculated based on the thermodynamic data of the homogenous bulk Li2O2. Therefore, it is not difficult to understand why the emf in the experiments is smaller, considering the specific orientations of the Li2O2 crystals formed during the cell operation, as well as due to the existence of a small amount of solvated Li2O2 in the solvents. Actually, an OCV of 2.85 V has also been reported in a Li–O2 battery using LiTFSI-DME electrolyte at room temperature by Viswanathan et al.22 It is reasonable then that the real emf value for each Li–O2 battery could deviate from the ideal value of 2.959 V due to the above two possibilities.
Third, Fig. 1a shows a zero OCV hysteresis between the equilibrium voltage of the discharge and charge. At first glance, this is surprising, since the reaction paths have been regarded as asymmetry in previous papers.18 Our results reveal that the product at the equilibrium state during the discharge and charge is dominated by crystalline Li2O2, and that unstable intermediate phases formed during the reaction of Li and O2 do not exist in the equilibrium states. This result also means that the voltage gap during the galvanostatic discharge and charge or cyclic voltammogram only originates from the kinetics, not from the asymmetrical thermodynamic reaction path, which is different from that which occurs with conversion reactions, such as in MnO anodes and FeF3 cathode.29,30
Fourth, since Ueq is determined unambiguously, the overpotential during discharge and charge can be calculated from the GITT results. From the beginning to the specific capacity of ∼1000 mA h g−1, as shown in Fig. 1a, the discharge overpotential does not increase too much, but as the capacity increases further up to the end of discharge, the overpotential increases exponentially as shown in Fig. 1b. This relationship is consistent with a diffusion controlled process. It is natural to presume that the size enlargement of the Li2O2 particles, as indicated by the SEM results (Fig. S1†), leads to an increase in the transport resistance of Li+ and O2−. Upon charging, ηchg also shows an exponential increase as a function of Q, as shown in Fig. 1b. This indicates that the mass transport during charging also plays a key role in the rate determining step. The detailed decomposition process of Li2O2 at the atomic level is still not clear. It has been reported that Li2O2 will decompose either at the contact site with the carbon nanotube31 or at the edge site of Li2O2, based on in situ SEM and TEM investigations.32 In each case, there is no doubt that the particle size of Li2O2 decreases gradually during charging. Therefore, it is not reasonable that the diffusion resistance of Li+ and O2− in Li2O2 particles will increase during charging. The electronic contact of Li2O2 particles with the electrical conducting medium will gradually become worse with charging; however, that will lead to the ohmic rule. Therefore, the exponential increase of the overpotential during charging could be caused by other factors related to the mass transport. It has been known that side products, such as carbonate species (mostly Li2CO3), at the electrolyte/Li2O2 interfaces will be formed during charging.13,15 It is therefore plausible to suggest that the coverage and formation of the side products on Li2O2 could be the reason for the diffusion controlled behaviour as shown in Fig. 1b.
As shown in Fig. 1a, the OCVs during charging reach the same value (Ueq ∼ 2.85 V) when the charge voltage is smaller than 4.0 V. Above 4.0 V, the OCVs cannot return 2.85 V after 6 h relaxation, but can reach the equilibrium value of ∼2.85 V after 24 h relaxation (Fig. S2†). Our previous study revealed that most Li2O2 particles could be decomposed at a charge voltage above 4.0 V.24b Above this value, carbonate species become detectable, owing to the side reactions.24b This result further implies that the formation of side products leads to a longer relaxation period for the battery in order to reach equilibrium.
Fig. 2a shows the GITT curve measured at 0.1 mA cm−2 with the same relaxation time (i.e. 6 h) as that shown in Fig. 1a. Clearly, with a relaxation time of 6 h, the equilibrium voltages for discharge and charge cannot reach the same value. Fig. 2b shows the GITT curve measured at 0.1 mA cm−2 with a prolonged relaxation time (i.e. 12 h), in contrast to Fig. 2a. It can be seen that in the case of 0.1 mA cm−2, the Ueq can also be relaxed to 2.85 V by prolongation of the relaxation time. It is known that different current densities lead to Li–O products with different morphologies, as well as crystallinities,33 which is also confirmed by the SEM results, as shown in Fig. S5.† This may lead to different relaxation kinetics in the processes of Li2O2 growth and decomposition. The fact that the Ueq is not significantly dependent on the current density after a sufficient relaxation is further supported by investigations of the GITT curves measured at other current densities, as shown in Fig. S6.† These results clearly indicate that Li2O2 crystals with the same surface energy can be eventually formed with approximately the same values of Ueq.
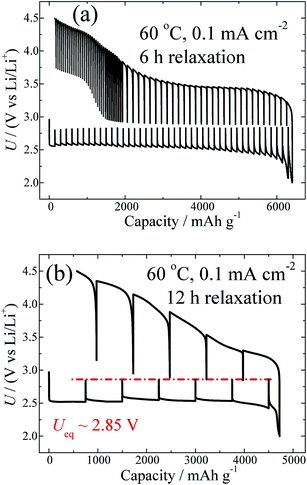 | ||
| Fig. 2 GITT curves measured at 60 °C and at a fixed current density of 0.1 mA cm−2, with a relaxation time of 6 h (a) and 12 h (b). | ||
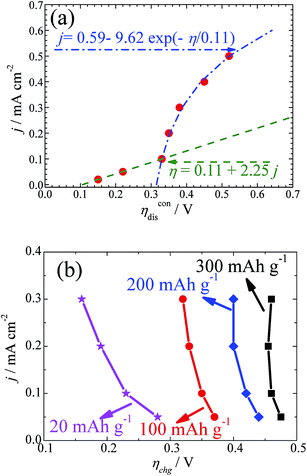
As Ueq is known accurately from the GITT curves measured at the different current densities, the values of the discharge and charge overpotentials and the relationship between the overpotential and applied current density can be obtained accordingly. Fig. 3a shows the dependence of ηdis on the current density j. It can be seen that the results obey the linear ohmic law when the current density is less than 0.1 mA cm−2. This is consistent with the fact that the transport of electrons in the electrode and ions in the electrolyte control the reactions. Then, an exponential relationship can be seen when the current density is above 0.1 mA cm−2. This is in agreement with a typical diffusion-limited charge-transfer polarization behaviour. Both behaviours can be well simulated, as shown in Fig. 3a. At a high current density, it is reasonable to believe that the diffusion of oxygen will become the rate determining step. It is interesting to find that the transition from ohmic polarization to the diffusion limited charge transfer polarization at the current density of 0.1 mA cm−2 seems to be the first-order transition in our battery. The reason behind this is not clear, but might be related to the variation of the particle size or morphology when the current density changes, as discussed above. This needs further clarification.
As shown in Fig. 1 and 2, the overpotential increases continuously upon charging. The analysis of ηchg cannot be done in a similar way to that of ηdis. Therefore, the overpotential values at a certain charging depth but different current densities are compared and drawn in Fig. 3b. It is worth noting that ηchg decreases with increasing j in the measured current density range. In the case of the small charge capacity (e.g. 20 mA h g−1), the decreasing amplitude is much larger than that in the case of a large charge capacity (e.g. 200 or 300 mA h g−1). This abnormal relationship means that the status of the cathode can be subject to a significant variation during charging. Since the overpotential for charging shows a diffusion controlled behaviour, it is plausible that the morphology and particle size of Li2O2 and the side products are influenced by the current density.13,34
Normally, the overpotential should increase when the current density increases. Two issues should be mentioned here. First, in the case of Li–O2 batteries, as shown in our GITT results as well as in other galvanostatic experiments, the overpotential increases during charging, although Li2O2 decomposes gradually. As explained above, the formation of another high resistive species accompanies the decomposition of Li2O2, leading to an increase of the overpotential during charging. In addition, we notice that the overpotentials for the GITT measurements at the smaller current densities are higher than those measured at the larger current densities. It is reasonable then that the morphology of Li2O2 is influenced by the current densities. At larger current densities, as shown in Fig. S5,† the particle size of Li2O2 is smaller. Due to the particle size effect of Li2O2 and the formation of high resistive unidentified species (most probably Li2CO3), the overpotential shows abnormal behaviours, as shown in Fig. 3b.
Temperature is another factor that can influence the thermodynamics and kinetic properties. GITT measurements at different temperatures, including 60 °C, 80 °C, 100 °C, and 120 °C, were carried out at the same current density of 0.3 mA cm−2, and with the same relaxation time of 6 h. The GITT curves for 60 °C and 120 °C are shown in Fig. 1a and 4, respectively. Those for the two other temperatures are shown in Fig. S7.† On the basis of these curves, the values of Ueq, ηdis, and ηchg (100 mA h g−1) are calculated and are summarized in Table 1. As clearly shown in Fig. S3,† this battery shows a negative temperature coefficient of −62.6 J mol−1 K−1.
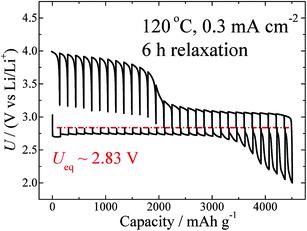 | ||
| Fig. 4 GITT curves measured at 120 °C and at a fixed current density of 0.3 mA cm−2, with a relaxation time of 6 h. | ||
| T (°C) | U eq (V) | η dis (V) | η chg (V) at 100 mA h g−1 |
|---|---|---|---|
| 60 | 2.850 | 0.390 | 0.320 |
| 80 | 2.842 | 0.218 | 0.309 |
| 100 | 2.835 | 0.142 | 0.255 |
| 120 | 2.830 | 0.100 | 0.170 |
The elevated temperature greatly decreases the overpotential for both the discharge and charge. At 120 °C, the ηdis and ηchg (100 mA h g−1) are 0.10 V and 0.17 V, respectively, compared to 0.39 V and 0.32 V at 60 °C. This result indicates that the increase of temperature is an effective means to reduce the battery overpotential.
According to ref. 22, the current density as a function of the overpotential for discharge or charge can be written as
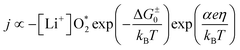 | (6) |
As shown in Fig. 4, a semi-plateau of charge voltage appears around 4.0 V. In comparison to Fig. 1, it seems that the temperature increase from 60 °C to 120 °C makes this plateau behaviour even more obvious. As discussed above, this region corresponds to the side-product reaction, which is enhanced by the elevated temperature. This information is consistent with that reported for MPP-TFSI-based cells,35 the details of which will be presented in a forthcoming paper.
Conclusions
GITT measurements have been carried out on Li–O2 batteries at different current densities, as well as at different temperatures. Several conclusions can be drawn:(1) The OCV of the Li–O2 battery at 60 °C is 2.850 V in the observed cell.
(2) The Li–O2 battery shows a negative temperature coefficient of −62.6(−3.25 × 10−4nF, with n = 2) J mol−1 K−1, and, accordingly, the emf of the Li–O2 battery at 25 °C should be 2.861 V.
(3) The thermodynamic equilibrium voltage gap between charging and discharging is zero.
(4) The overpotential increases exponentially during discharging under a constant current density, where the relationship between the overpotential and the current density obeys the linear ohmic law when the current density is smaller than 0.1 mA cm−2 and an exponential relationship when the current density is above 0.1 mA cm−2.
(5) During charging at the fixed current density (i.e. galvanostatic charging), the size effect of Li2O2 and the formation of high resistive unidentified species (most probably Li2CO3) might be responsible for the anomalous relationship between the overpotential and the current density.
(6) Elevating the temperature from 60 °C to 120 °C can decrease the voltage gap from 0.71 V to 0.27 V.
Overall, herein, a number of issues related to the thermodynamics and kinetic behaviours, as aforementioned, have been raised by the GITT technique. For a greater and deeper understanding, investigations based on GITT in combination with other techniques such as electrochemical impedance spectroscopy (EIS), the potentiostatic intermittent titration technique (PITT), and in situ X-ray absorption spectroscopy (XAS) are currently underway in our laboratory.
Acknowledgements
The authors would thank the financial supports from the National Key Basic Research Program of China 2014CB921004, Key Project of the Chinese Academy of Sciences under Grant no. KGZD-EW-202-2, NSFC (51325206) and the Science Foundation for Youth Scholar of State Key Laboratory of High Performance Ceramics and Superfine Microstructures (SKL201303).Notes and references
- K. M. Abraham and Z. Jiang, J. Electrochem. Soc., 1996, 143, 1 CrossRef CAS PubMed.
- G. Girishkumar, B. McCloskey, A. C. Luntz, S. Swanson and W. Wilcke, J. Phys. Chem. Lett., 2010, 1, 2193 CrossRef CAS.
- P. G. Bruce, S. A. Freunberger, L. J. Hardwick and J. M. Tarascon, Nat. Mater., 2012, 11, 19 CrossRef CAS PubMed.
- Y. Y. Shao, F. Ding, J. Xiao, J. Zhang, W. Xu, S. Park, J.-G. Zhang, Y. Wang and J. Liu, Adv. Funct. Mater., 2013, 23, 987 CrossRef CAS.
- Y. C. Lu, D. G. Kwabi, K. P. C. Yao, J. R. Harding, J. Zhou, L. Zuin and Y. Shao-Horn, Energy Environ. Sci., 2011, 4, 2999 CAS.
- R. Black, B. Adams and L. F. Nazar, Adv. Energy Mater., 2012, 2, 801 CrossRef CAS.
- H. G. Jung, J. Hassoun, J. B. Park, Y. K. Sun and B. Scrosati, Nat. Chem., 2012, 4, 579 CrossRef CAS PubMed.
- Z. Peng, S. A. Freunberger, Y. Chen and P. G. Bruce, Science, 2012, 337, 563 CrossRef CAS PubMed.
- J. Lu, Y. Lei, K. C. Lau, X. Luo, P. Du, J. Wen, R. S. Assary, U. Das, D. J. Miller, J. W. Elam, H. M. Albishri, D. A. El-Hady, Y.-K. Sun, L. A. Curtiss and K. Amine, Nat. Commun., 2013, 4, 2383 Search PubMed.
- J. J. Xu, Z. L. Wang, D. Xu, L. L. Zhang and X. B. Zhang, Nat. Commun., 2013, 4, 2438 Search PubMed.
- H.-D. Lim, K.-Y. Park, H. Song, E. Y. Jang, H. Gwon, J. Kim, Y. H. Kim, M. D. Lima, R. O. Robles, X. Lepró, R. H. Baughman and K. Kang, Adv. Mater., 2013, 25, 1348 CrossRef CAS PubMed.
- K. Takechi, S. Higashi, F. Mizuno, H. Nishikoori, H. Iba and T. Shiga, ECS Electrochem. Lett., 2013, 1, A27 CrossRef PubMed.
- R. Black, J.-H. Lee, B. Adams, C. A. Mims and L. F. Nazar, Angew. Chem., Int. Ed., 2013, 52, 392 CrossRef CAS PubMed.
- Z. Jian, P. Liu, F. Li, P. He, X. Guo, M. Chen and H. Zhou, Angew. Chem., Int. Ed., 2014, 53, 442 CrossRef CAS PubMed.
- (a) X. X. Guo and N. Zhao, Adv. Energy Mater., 2013, 3, 1413 CrossRef CAS; (b) N. Zhao, C. L. Li and X. X. Guo, Energy Technol., 2014, 2, 317 CrossRef CAS.
- H.-D. Lim, H. Song, J. Kim, H. Gwon, Y. Bae, K.-Y. Park, J. Hong, H. Kim, T. Kim, Y. H. Kim, X. Lepró, R. Ovalle-Robles, H. B. Ray and K. Kang, Angew. Chem., Int. Ed., 2014, 126, 4007 CrossRef.
- I. Kowalczk, J. Read and M. Salomon, Pure Appl. Chem., 2007, 79, 851 CrossRef CAS.
- Z. Peng, S. A. Freunberger, L. J. Hardwick, Y. Chen, V. Giordani, F. Barde, P. Novak, D. Graham, J.-M. Tarascon and P. G. Bruce, Angew. Chem., Int. Ed., 2011, 50, 6351 CrossRef CAS PubMed.
- C. O. Laoire, S. Mukerjee, K. M. Abraham, E. J. Plichta and M. A. Hendrickson, J. Phys. Chem. C, 2010, 114, 9178 CAS.
- B. D. McCloskey, R. Scheffler, A. Speidel, G. Girishkumar and A. C. Luntz, J. Phys. Chem. C, 2012, 116, 23897 CAS.
- S. Y. Kang, Y. Mo, S. P. Ong and G. Ceder, Chem. Mater., 2013, 25, 3328 CrossRef CAS.
- V. Viswanathan, J. K. Nørskov, A. Speidel, R. Scheffler, S. Gowda and A. C. Luntz, J. Phys. Chem. Lett., 2013, 4, 556 CrossRef CAS.
- (a) W. Weppner and R. A. Huggins, J. Electrochem. Soc., 1977, 124, 1569 CrossRef CAS PubMed; (b) P. L. Taberna, S. Mitra, P. Poizot, P. Simon and J.-M. Tarascon, Nat. Mater., 2006, 5, 567 CrossRef CAS PubMed.
- (a) F. Mizuno, K. Takechi, S. Higashi, T. Shiga, T. Shiotsuki, N. Takazawa, Y. Sakurabayashi, S. Okazaki, I. Nitta, T. Kodama, H. Nakamoto, H. Nishikoori, S. Nakanishi, Y. Kotani and H. Iba, J. Power Sources, 2013, 228, 47 CrossRef CAS PubMed; (b) Z. H. Cui, W. G. Fan and X. X. Guo, J. Power Sources, 2013, 235, 251 CrossRef CAS PubMed.
- D. Zhu, L. Zhang, M. Song, X. Wang, R. Mi, H. Liu, J. Mei, L. W. M. Lau and Y. Chen, J. Solid State Electrochem., 2013, 17, 2539 CrossRef CAS PubMed.
- C. X. Zu and H. Li, Energy Environ. Sci., 2011, 4, 2614 CAS.
- M. Binnewies and E. Mike, Thermochemical Data of Elements and Compounds, Wiley-VCH, Weinheim, second, revised and extended edn, 2002 Search PubMed.
- Y. Mo, S. P. Ong and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 205446 CrossRef.
- (a) O. Delmer, P. Balaya, L. Kienle and J. Maier, Adv. Mater., 2008, 20, 501 CrossRef CAS; (b) K. Zhong, B. Zhang, S. Luo, W. Wen, H. Li, X. Huang and L. Chen, J. Power Sources, 2011, 196, 6802 CrossRef CAS PubMed.
- (a) Z. H. Cui, X. X. Guo and H. Li, Electrochim. Acta, 2013, 89, 229 CrossRef CAS PubMed; (b) R. E. Doe, K. A. Persson, Y. S. Meng and G. Ceder, Chem. Mater., 2008, 20, 5274 CrossRef CAS.
- L. Zhong, R. R. Mitchell, Y. Liu, B. M. Gallant, C. V. Thompson, J. Y. Huang, S. X. Mao and Y. Shao-Horn, Nano Lett., 2013, 13, 2209 CrossRef CAS PubMed.
- H. Zheng, D. Xiao, X. Li, Y. Liu, Y. Wu, J. Wang, K. Jiang, C. Che, L. Gu, X. Wei, Y.-S. Hu, Q. Chen and H. Li, Nano Lett., 2014, 14, 4245 CrossRef CAS PubMed.
- B. D. Adams, C. Radtke, R. Black, M. Trudeau, K. Zaghib and L. F. Nazar, Energy Environ. Sci., 2013, 6, 1772 CAS.
- B. M. Gallant, R. R. Mitchell, D. G. Kwabi, J. Zhou, L. Zuin, C. V. Thompson and Y. Shao-Horn, J. Phys. Chem. C, 2012, 116, 20800 CAS.
- B. D. McCloskey, D. S. Bethune, R. M. Shelby, T. Mori, R. Scheffler, A. Speidel, M. Sherwood and A. C. Luntz, J. Phys. Chem. Lett., 2012, 3, 3043 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental methods and Fig. S1 to S7 are given. See DOI: 10.1039/c4ee01777c |
| This journal is © The Royal Society of Chemistry 2015 |