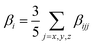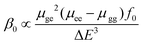Theoretical studies on tricarbonyl metal derivatives of Lindqvist-type polyoxometalate complexes: electronic structures and nonlinear optical properties
Ting
Zhang
,
Wei
Guan
,
Tengying
Ma
,
Yan
Lin
,
Likai
Yan
* and
Zhongmin
Su
*
Institute of Functional Material Chemistry, Key Laboratory of Polyoxometalate Science of Ministry of Education, Faculty of Chemistry, Northeast Normal University, Changchun 130024, P. R. China. E-mail: yanlk924@nenu.edu.cn; zmsu@nenu.edu.cn; Fax: +86-431-5684009
First published on 8th April 2015
Abstract
The density functional theory (DFT) method and natural bond orbital (NBO) analysis have been employed to investigate the electronic structures and second-order nonlinear optical (NLO) properties for tricarbonyl metal derivatives of a Lindqvist-type polyoxometalate, [Nb2W4O19M(CO)3]3−/2− (M = MnI, TcI, ReI, FeII, RuII and OsII). The position of the tricarbonyl metal ligand and the substitution of different metal atoms M have an influence on the electronic absorption spectra and NLO responses of all complexes. Among the three isomers of [Nb2W4O19Mn(CO)3]3−, the β0 value of isomer 1a is the largest, which is 1.4 times and 2.3 times larger than those of isomers 1b and 1c, respectively. The β0 value also depends on the tricarbonyl metal M, the β0 value decreases in the order M = Ru > Re > Fe > Os > Mn > Tc. In addition, the analysis of the main transition orbitals shows that the tricarbonyl metal ligand acts as an electron donor in [Nb2W4O19M(CO)3]3−/2− (M = MnI, TcI, ReI, RuII and OsII), while the [Fe(CO)3]2+ ligand acts as an electron acceptor in [Nb2W4O19Fe(CO)3]2−.
Introduction
Polyoxometalate (POM)-supported metal carbonyl derivatives as a peculiar class of organometallic oxides have attracted increasing attention owing to their unique structures, potential catalytic properties, photochemical properties and potential applications in solar energy production.1–10 This kind of complex can be regarded as a subcategory of functionalized POMs, which can be prepared by step-wise and controlled methods. Most of these complexes contain Lindqvist-type,1–4 lacunary Keggin-type9 and lacunary Dawson-type POMs.10 All these POM-supported metal carbonyl complexes contain a fac-{M(CO)3}+, d6 low-spin metal (MnI, ReI) carbonyl fragment.1–10In 1980, Besecker and co-workers synthesized [Nb2W4O19M(CO)3]3− (M = Mn, Re) complexes in which [Nb2W4O19]4− is coordinated to a tricarbonyl Mn/Re unit by a triangle of three adjacent bridging oxygens (Ob).1,2 Interestingly, 17O NMR spectroscopy provides conclusive evidence for the presence of all three [Nb2W4O19M(CO)3]3− isomers. The studies of POM-supported metal carbonyl derivatives have been in progress all the time.3–10 Recently, Hill and co-workers have synthesized [P4W35O124{Re(CO)3}]16− and [X2W20O70{M(CO)3}2]12− (X = Sb, Bi; M = Mn, Re) complexes, and density functional theory (DFT) calculations show that these complexes exhibit an intense Re-to-POM charge-transfer (CT) transition, an example of a potentially general transition, called metal-to-POM (MP)CT.9,10 The chromophoric and catalytic properties, and photoactivities of these CT complexes are under investigation.
Nonlinear optical (NLO) materials have received tremendous attention owing to their unique applications in optical fibers, data storage, optical limiting, computing and switching. Among these NLO materials, the donor–acceptor (D–A) model has been widely used. POM complexes with the electron storage ability can be designed as a good electron-acceptor group.11–13 So the POM-based complexes with good thermal and photochemical stability as well as redox switching ability are potential NLO materials. Theoretical studies would be helpful in rationalization of the observed properties and design of novel POM-based hybrid materials with excellent properties. Previous studies on related POMs show that DFT calculations give a satisfactory description of the geometrical structures, bonding character, redox properties, charge-transfer and NLO properties.14–17
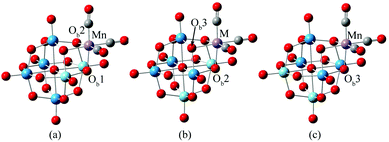
Obviously, POM-supported metal carbonyl derivatives are potential NLO materials, while studies on second-order NLO properties and electronic structures of tricarbonyl metal polyanions are rare. In the present work, DFT calculations were performed to investigate the electronic structures and nonlinear optical properties of tricarbonyl metal derivatives of the Lindqvist-type POM. The calculation models of complexes are shown in Fig. 1. In cis-[Nb2W4O19]4−, there are three different types of bridging oxygen atoms, which bond to two niobiums (Ob1), one niobium and one tungsten (Ob2), or two tungstens (Ob3). The experimental spectra2 provide conclusive evidence for the presence of all three isomers. In isomer a, the M(CO)3 binding site is formed by one ONb2 oxygen and two ONbW oxygens. In isomer b, two ONbW oxygens and one OW2 oxygen are involved, and in isomer c, three OW2 oxygens form the binding site. The complex [Nb2W4O19Mn(CO)3]3− was taken as an example to investigate the difference in geometrical and electronic structures among the three isomers. In order to investigate the effect of the tricarbonyl center metal M on NLO properties of [Nb2W4O19M(CO)3]3−/2−, Mn or Re was substituted by other d6 metals (TcI, FeII, RuII, and OsII).
Computational details
The quantum chemical calculations were carried out using the GAUSSIAN 09W program package.18 The ground states of all the studied complexes were closed-shell singlet states and the geometries were optimized at the BP86/6-31G(d) level. This functional has given good insight into the structure. Considering the relativistic effects for transition-metal atoms, the LANL2DZ basis set was applied for metal atoms in this work. The static first hyperpolarizabilities (β0) were calculated by using analytical third energy derivatives, which are more efficient and less expensive than numerical derivatives19 and with the pure functional MPWPW91*20 and the long-range corrected CAM-B3LYP functional21 to examine the reliability of the calculated results. The static first hyperpolarizability is termed as the zero-frequency hyperpolarizability and is an estimate of the intrinsic molecular hyperpolarizability in the absence of any resonance effects. Thus, β0 is defined as| β0 = (βx2 + βy2 + βz2)1/2 |
In order to obtain a more intuitive description of the second-order NLO behavior of the studied complexes, time-dependent DFT (TDDFT) methods were used to simulate the molecular electronic spectra at the PBE1PBE/6-31+G(d) level (LANL2DZ basis set for metal atoms). PBE1PBE, also known as PBE0, is obtained by casting the function and correlation of Perdew, Burke and Erzenrhof in the hybrid HF/DFT scheme with a fixed 1/4 ratio.22 This functional has been shown to improve the accuracy of excitation energies and CT bands in metal complexes for solvation calculations.
All the calculations were performed in acetonitrile solvent. The solvent effect was considered using the polarizable continuum model (PCM)23 using the integral equation formalism variant. The Wiberg bond index (WBI) was computed by natural bond orbital (NBO) calculations at the same level with the geometrical optimization.
Results and discussion
Ground-state structures
In this study, all complexes have similar structures which contain one identical cis-[Nb2W4O19]4− unit joined by one fac-{M(CO)3}+/2+ moiety, M = Mn (1), Tc (2), Re (3), Fe (4), Ru (5), and Os (6). It exhibits slight differences in bond distances of MO3C3 coordinated octahedra with different M centres. In all complexes, a tricarbonyl metal unit bonds to a triangle bridging oxygen on the surface of a [Nb2W4O19]4− anion. We take 1 as an example to discuss the difference in structural parameters of the three isomers (1a, 1b, 1c) in detail. 1a and 1c contain a mirror plane, and possess Cs symmetry, while 1b has no symmetry. The calculations indicate that 1a is the most stable isomer with energies of 0.8 and 0.9 kcal mol−1, which are lower than 1b and 1c, respectively. The small energy differences are compatible with the existence of the three isomers in solution (Table 1).| Bond length | |||
|---|---|---|---|
| C–O | M–C | M–Ob | |
| 1a | 1.173 | 1.780 | 2.087 |
| 1b | 1.173 | 1.781 | 2.079 |
| 1c | 1.174 | 1.781 | 2.071 |
| Exp | 1.144 | 1.843 | 2.001 |
| 2 | 1.175 | 1.909 | 2.213 |
| 3 | 1.180 | 1.908 | 2.200 |
| 4 | 1.156 | 1.800 | 1.987 |
| 5 | 1.158 | 1.923 | 2.121 |
| 6 | 1.163 | 1.913 | 2.122 |
Among 1a, 1b and 1c, the calculated average bond length of C–O is 1.17 Å, which is in good agreement with the experimental results 1.14 Å. It suggests that the functional and basis sets that we adopted are reliable for the studied complexes. In 1a, 1b and 1c, the difference in Mn–C and C–O bond lengths is about 0.001 Å, illustrating that the structure of the tricarbonyl metal ligand in the three isomers is basically consistent. The Mn–Ob bond length is 2.087 Å for 1a, 2.079 Å for 1b, and 2.071 Å for 1c, showing that the position of the tricarbonyl metal ligand slightly affects the Mn–Ob bond length.
The experimental results confirmed that isomer b predominates in solution. For 2–6, the isomer b was investigated. The M–Ob bond length increases in the order 1b (2.079) < 2 (2.213) ≈ 3 (2.200); 4 (1.987) < 5 (2.121) ≈ 6 (2.122), which is consistent with the radii of the metal atom. The M–Ob bond length decreases in the order: 4 < 1b, 5 < 2, 6<3, indicating that the interactions between the metal M (M = Fe, Ru and Os) and Ob are stronger than those of Mn, Tc and Re.
NBO analysis
The experimental X-ray diffraction study confirms that Mn(CO)3+ bonds to three adjacent bridging oxygen atoms (Ob) of [Nb2W4O19]4−. However, the interaction between metal M and bridge-oxygen Ob has never been reported. In order to investigate the bonding interaction between metal M and bridge-oxygen Ob in the [Nb2W4O19M(CO)3]3− anion, WBI was computed using NBO theory and the results are listed in Table 2.| Bond | 1a (M = Mn) | 1b (M = Mn) | 1c (M = Mn) | 2 (M = Fe) |
|---|---|---|---|---|
| M–C1 | 1.169 | 1.182 | 1.180 | 1.290 |
| M–Ob1 | 0.386 | 0.384 | 0.389 | 0.379 |
| M–Ob2 | 0.386 | 0.399 | 0.389 | 0.390 |
| M–Ob3 | 0.399 | 0.393 | 0.404 | 0.383 |
| Bond | 3 (M = Re) | 4 (M = Fe) | 5 (M = Ru) | 6 (M = Os) |
|---|---|---|---|---|
| M–C1 | 1.365 | 0.962 | 1.059 | 1.195 |
| M–Ob1 | 0.398 | 0.483 | 0.466 | 0.490 |
| M–Ob2 | 0.410 | 0.498 | 0.482 | 0.505 |
| M–Ob3 | 0.401 | 0.494 | 0.473 | 0.494 |
The Mn–C bonds in three isomers (1a–1c) are very similar with obvious single-bond nature as indicated by the calculated WBI of 1.169–1.182. However, with different metals, M = Mn (1), Tc (2), Re (3), Fe (4), Ru (5), Os (6), the interaction between M and C is slightly different, 3 (1.365) > 6 (1.195); 2 (1.290) > 5 (1.059); 1b (1.182) > 4 (0.962), which is consistent with the M–C bond length, 3 (1.908) < 6 (1.913); 2 (1.909) < 5 (1.923); 1b (1.781) < 4 (1.800). It indicates that the interactions between M and C in [Nb2W4O19M(CO)3]3− (M = Mn, Tc and Re) are stronger than those of [Nb2W4O19M(CO)3]2− (M = Fe, Ru and Os). The WBI of Mn–Ob for the three isomers (0.384–0.404) shows weak interactions between Mn and bridging oxygen Ob. Compared with 1 and 3, the M–Ob1 bond orders of 4, 5 and 6 are larger, 6 (0.490) > 4 (0.483) > 5 (0.466) > 3 (0.398) > 1b (0.384) > 2 (0.379), which are consistent with the M–Ob bond lengths.
Electronic spectrum
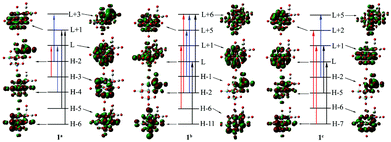
Based on the BP86 optimized structures of tricarbonyl metal Lindqvist-type polyoxometalate complexes [Nb2W4O19M(CO)3]3−/2− (M = MnI, TcI, ReI, FeII, RuII and OsII), TDDFT was used to calculate the excited-state properties of complexes. The calculated absorption wavelengths, oscillator strength (f0) and major transition states for the studied complexes are summarized in Table 3. The absorption UV-Vis spectra of all complexes are illustrated in Fig. 2. As shown in Fig. 2(a), the UV-vis absorption spectra of 1a–1c display one intense absorption (λmax) in the range of 260–270 nm, which follows the order: 1a (270 nm) > 1b (264 nm) > 1c (260 nm). It also can be seen that the absorption bands of 1a–1c undergo a slight shift from 270 nm to 260 nm. The frontier molecular orbitals involved in the dominant electronic transitions in 1a–1c are shown in Fig. 3. The charge transition characteristics of 1a, 1b and 1c are similar and the transition molecular orbitals of 1b are taken as representatives, so the charge transition characteristic 1b is analyzed. In 1b, the H−2 → L+6 and H−1 → L+5 transitions can be assigned to the CT from the p orbitals of Ob atoms in POM and the tricarbonyl metal ligand to Nb/W atoms. The H−6 → L+1 and H−11 → L transitions occur between Nb/W atoms and O atoms in POM. The [Nb2W4] acts as an electron acceptor and the tricarbonyl metal ligand acts as an electron donor. The charge transition characteristics of 1a, 1b and 1c show that the position of the tricarbonyl metal ligand has a slight influence on the orbital transition.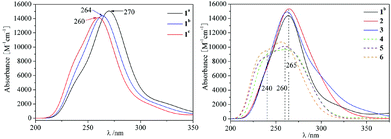 | ||
| Fig. 2 (a) The absorption UV-Vis spectra of three isomers 1a–1c; (b) the absorption UV-Vis spectra of systems 1b–6. | ||
| λ | ΔE | f 0 | Major contribution | |
|---|---|---|---|---|
| 1a | 276.3 | 4.49 | 0.0400 | H−3 → L (19%) |
| 275.1 | 4.51 | 0.0342 | H−4 → L (40%) | |
| H−2 → L+3 (20%) | ||||
| 268.8 | 4.61 | 0.0954 | H−5 → L+1 (33%) | |
| H−6 → L+1 (17%) | ||||
| 1b | 265.0 | 4.68 | 0.0392 | H−2 → L+6 (17%) |
| H−6 → L+1 (13%) | ||||
| 264.7 | 4.69 | 0.0194 | H−2 → L+6 (16%) | |
| H−11 → L (12%) | ||||
| 262.7 | 4.72 | 0.0199 | H−1 → L+5 (17%) | |
| H−2 → L+6 (14%) | ||||
| 1c | 263.0 | 4.71 | 0.0212 | H−2 → L+5 (42%) |
| 260.7 | 4.76 | 0.0760 | H−5 → L+1 (34%) | |
| H−7 → L+1 (22%) | ||||
| 254.3 | 4.88 | 0.0151 | H−6 → L+2 (58%) | |
| 2 | 267.0 | 4.64 | 0.0152 | H−5 → L+1 (33%) |
| 264.6 | 4.69 | 0.0195 | H−6 → L+1 (11%) | |
| 263.9 | 4.70 | 0.0661 | H−5 → L+1 (17%) | |
| 3 | 263.7 | 4.70 | 0.0283 | H−6 → L+2 (11%) |
| 262.6 | 4.72 | 0.0426 | H−8 → L (14%) | |
| 261.0 | 4.76 | 0.0215 | H−2 → L+9 (16%) | |
| 4 | 268.8 | 4.61 | 0.0525 | H−6 → L+1 (39%) |
| 253.3 | 4.89 | 0.0158 | H−8 → L+2 (7%) | |
| H → L+4 (6%) | ||||
| 251.9 | 4.92 | 0.0140 | H → L+4 (14%) | |
| 5 | 261.4 | 4.74 | 0.0264 | H−9 → L (8%) |
| 261.0 | 4.75 | 0.0429 | H−4 → L+2 (19%) | |
| H−7 → L+1 (18%) | ||||
| 253.8 | 4.88 | 0.0199 | H−5 → L+2 (16%) | |
| 6 | 262.9 | 4.71 | 0.0130 | H−4 → L+2 (16%) |
| 257.0 | 4.82 | 0.0222 | H−7 → L+1 (21%) | |
| 252.3 | 4.91 | 0.0156 | H−9 → L (16%) |
As shown in Fig. 2(b), 1b, 2 and 3 show an intense absorption at around 265 nm, 4–6 show a broad band at 240–260 nm. The spectra of 2 and 3 have similar transition features to 1b. The blue shifts of the absorption are observed in 4–6 compared with 1b, 2 and 3. It indicates that the more positive charge of [M(CO)3] (FeII, RuII and OsII) units causes the blue shifted absorption peak. In order to concisely describe the transition character, the electron density differences between the ground state and the dominant excited state were also plotted using GaussSum2.2 (Fig. 4). For 2, 3, 5 and 6, the decreasing electron density mainly localizes on the tricarbonyl segment and oxygen atoms of POM, while the increasing electron density mainly localizes on the Nb/W atoms. The tricarbonyl ligand acts as an electron acceptor and the POM acts as an electron donor, which is consistent with MPCT. It can be seen that the increasing electron density in 4 mainly localizes on the tricarbonyl segment and oxygen atoms of POM, while the decreasing electron density mainly localizes on the Nb/W atoms. We infer that the large electronegativity of FeII (4) has an important influence, which leads to the tricarbonyl ligand acting as an electron acceptor.
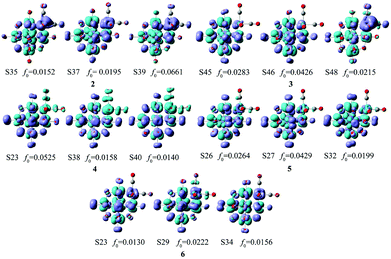 | ||
| Fig. 4 The electron density difference maps (EDDM) of systems 2–6 between the ground state and the dominant electronic transitions with an isodensity surface of 0.001 au. | ||
Static second-order polarizability
The β0 values computed by MPWMPW91* and CAM-B3LYP functionals are listed in Table 4. The functional CAM-B3LYP results are larger than that of the MPWMPW91* functional. For 1a–1c, 2, 4 and 6, two functionals yield the same order of β0 values: 4 > 6 > 1a > 1b > 1c > 2. The β0 values of 3 and 5 are calculated to be 11.325 and 11.221 × 10−30 esu by the CAM-B3LYP functional, the little difference may be in the range of calculation errors. Therefore, the MPWMPW91* functional was used to compute the second-order polarizabilities. The β0 value of 1a is about 1.5 times as large as that of 1b, which is about 1.6 times as large as that of 1c. It indicates that the orientation of the tricarbonyl metal ligand affects the β0 values of 1a–1c. For all complexes, the tricarbonyl ligand locates the y-axis direction. The larger βy component indicates that the CT between the tricarbonyl ligand and POM is decisive for 1a and 1b.| Δμ | Function | β x | β y | β z | β 0 | |
|---|---|---|---|---|---|---|
| 1a | 3.27 | MPWPW91* | 3.28 | 8.22 | −0.16 | 8.85 |
| CAM-B3LYP | 3.80 | 8.25 | −0.16 | 9.08 | ||
| 1b | 7.05 | MPWPW91* | −0.19 | 2.97 | 5.54 | 6.29 |
| CAM-B3LYP | −0.19 | 2.41 | 6.33 | 6.77 | ||
| 1c | 9.12 | MPWPW91* | −3.52 | −1.73 | −0.00 | 3.92 |
| CAM-B3LYP | −3.98 | −2.81 | 0.00 | 4.87 | ||
| 2 | 7.23 | MPWPW91* | −0.41 | −0.46 | 5.42 | 5.46 |
| CAM-B3LYP | −0.38 | −0.91 | 6.24 | 6.32 | ||
| 3 | 6.43 | MPWPW91* | −0.41 | −9.60 | 5.39 | 11.02 |
| CAM-B3LYP | −0.38 | −9.45 | 6.23 | 11.33 | ||
| 4 | 15.92 | MPWPW91* | −0.76 | 9.74 | 4.62 | 10.81 |
| CAM-B3LYP | −0.80 | 8.95 | 5.39 | 10.48 | ||
| 5 | 17.06 | MPWPW91* | −0.36 | 11.285 | 5.26 | 12.46 |
| CAM-B3LYP | −0.38 | 9.46 | 6.03 | 11.22 | ||
| 6 | 14.22 | MPWPW91* | −0.49 | 4.88 | 4.92 | 6.95 |
| CAM-B3LYP | −0.52 | 3.43 | 5.76 | 6.72 |
When M is Mn, Tc and Re, the β0 values present the order: β0 (3) > β0 (1b) > β0 (2); when M is Fe, Ru and Os, the β0 values present the order: β0 (5) > β0 (4) > β0 (6). Among all complexes, 5 shows the largest β0 value, 12.456 × 10−30 esu according to the MPWPW91* calculations. Compared with those of 1b and 2 (6.287 and 5.455 × 10−30 esu), 4 and 5 have larger β0 values, 10.807 and 12.456 × 10−30 esu, respectively. Furthermore, for all complexes except for 2βy tensor components are small; the large βy tensor components of complexes indicate that the charge transfer in the y direction plays an important role.
In order to elucidate the origin of second-order nonlinear responses of all complexes, we took a further step to analyse the main excited states that contribute to the β value. From the two-level model
Conclusions
We report a theoretical study on the first hyperpolarizabilities, electronic transitions, and charge transfer involved in the second-order nonlinear optical response of tricarbonyl metal derivatives of a Lindqvist-type polyoxometalate [Nb2W4O19M(CO)3]3−/2− (M = MnI, TcI, ReI, FeII, RuII and OsII). The relative energy analysis suggests that the isomer 1a is the most stable among the three isomers, 1a, 1b, 1c. The calculations show that the nonlinear optical response coefficient of the isomer 1a is the largest among the three isomers. Interestingly, among metal-substituted complexes, [Nb2W4O19Ru(CO)3]2− has the largest β0 value. The analysis of the molecular orbital indicates that [Nb2W4O19]4− acts as an electron acceptor and the tricarbonyl metal ligand acts as an electron donor in all complexes except for [Nb2W4O19Fe(CO)3]2−. In [Nb2W4O19Fe(CO)3]2−, the tricarbonyl metal ligand [Fe(CO)3]2+ displays the electron acceptor character.Acknowledgements
The authors gratefully acknowledge financial support by NSFC (21131001), the Program for New Century Excellent Talents in University (NCET-10-318), the Doctoral Fund of Ministry of Education of China (20100043120007), and the Science and Technology Development Planning of Jilin Province (20100104, 20100320).Notes and references
- C. J. Besecker and W. G. Klemperer, J. Am. Chem. Soc., 1980, 102, 7598 CrossRef CAS.
- C. J. Besecker, V. W. Day and W. G. Klemperer, Inorg. Chem., 1985, 24, 44 CrossRef CAS.
- W. G. Klemperer and D. J. Main, Inorg. Chem., 1990, 29, 2355 CrossRef CAS.
- W. G. Klemperer and B. X. Zhong, Inorg. Chem., 1993, 32, 5821 CrossRef CAS.
- T. Nagata, M. Pohl, H. Weiner and R. G. Finke, Inorg. Chem., 1997, 36, 1366 CrossRef CAS PubMed.
- A. V. Besserguenev, M. H. Dickman and M. T. Pope, Inorg. Chem., 2001, 40, 2582 CrossRef CAS PubMed.
- C. C. Zhao, Z. Huang, C. W. Rodríguez, C. S. Kambara, K. P. O'Halloran, K. I. Hardcastle, D. G. Musaev, T. Lian and C. L. Hill, J. Am. Chem. Soc., 2011, 133, 20134 CrossRef CAS PubMed.
- J. Y. Niu, L. P. Yang, J. W. Zhao, P. T. Ma and J. P. Wang, Dalton Trans., 2011, 40, 8298 RSC.
- H. Wang, S. Hamanaka and Y. Nishimoto, J. Am. Chem. Soc., 2012, 134, 4918 CrossRef CAS PubMed.
- C. C. Zhao, C. S. Kambara, Y. Yang, A. L. Kaledin, D. G. Musaev, T. Lian and C. L. Hill, Inorg. Chem., 2013, 52, 671 CrossRef CAS PubMed.
- D. L. Long, E. Burkholder and L. Cronin, Chem. Soc. Rev., 2007, 36, 105 RSC.
- D. L. Long, R. Tsunashima and L. Cronin, Angew. Chem., Int. Ed., 2010, 49, 1736 CrossRef CAS PubMed.
- H. Wang, S. Hamanaka, Y. Nishimoto, S. Irle, T. Yokoyama, H. Yoshikawa and K. Awaga, J. Am. Chem. Soc., 2012, 134, 4918 CrossRef CAS PubMed.
- T. Zhang, L. K. Yan, S. Cong, W. Guan and Z. M. Su, Inorg. Chem. Front., 2014, 1, 65 RSC.
- T. Zhang, N. N. Ma, L. K. Yan, T. Y. Ma and Z. M. Su, Dyes Pigm., 2014, 106, 105 CrossRef CAS PubMed.
- C. G. Liu, Z. M. Su, W. Guan and L. K. Yan, Inorg. Chem., 2009, 48, 541 CrossRef CAS PubMed.
- C. G. Liu, W. Guan, L. K. Yan, Z. M. Su, P. Song and E. B. Wang, J. Phys. Chem. C, 2009, 113, 19672 CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, GAUSSIAN 09 (Revision A.2), Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- P. Chopra, L. Carlacci, H. F. King and P. N. Prasad, J. Phys. Chem., 1989, 93, 7120 CrossRef CAS.
- (a) J. Lin, K. C. Wu and M. K. Zhang, J. Comput. Chem., 2009, 30, 2056 CrossRef CAS PubMed; (b) According to the parameter in ref. 20a, we worked out the iops keywords: Iop(3/76 = 1000004000), Iop(3/77 = 0600006000), Iop(3/78 = 1000010000).
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999 CrossRef CAS PubMed.
| This journal is © the Partner Organisations 2015 |