In situ formation of polypropylene (PP) fibrils in the olefinic block copolymer (OBC): effect of viscosity ratio and OBC block architecture†
Zhen Li,
Chengxiao Sun,
Xiaoyu Li,
Qin Zhang and
Qiang Fu*
College of Polymer Science and Engineering, State Key Laboratory of Polymer Materials Engineering, Sichuan University, Chengdu 610065, P. R. China. E-mail: qiangfu@scu.edu.cn; Fax: +86 28 8546 1795; Tel: +86 28 8546 1795
First published on 2nd October 2015
Abstract
Microfibrillar composites (MFCs) can be created when the viscosity ratio of polypropylene (PP) and olefinic block copolymer (OBC) is well controlled. PP can be easily deformed into well-refined microfibrils in OBC with different architectures. The mechanical properties of the obtained MFCs are prominently improved.
A new concept for creating polymeric composites, microfibrillar composites (MFCs), is increasingly attracting interest in the last few decades. The critical steps of MFC preparation are as follows: (a) the components are blended and extrude, (b) hot or cold drawing of the extrudates, (c) molding at temperatures between the melting temperature of the lower melting component and the higher melting one.1 Because MFCs are reinforced by bundles of fibrils developed in situ during the drawing processing, MFCs avoid dispersal of the agglomerated reinforcing components when compared with nanocomposites.2–5 Another prominent advantage of MFC is the easy processing and complete recycling, making it possible to large scale preparation polymeric composites. MFC concept has been applied in reinforcing polyolefinic materials and the composites included PC/HDPE,6,7 PET/HDPE,8 PA/HDPE,9 PET/PP10,11 and PA/PP.12
As one innovative elastomer developed by Dow Chemical Company, olefin block copolymers (OBCs) bring new application opportunities in hoses, tubes, profile extruded products, gaskets, foams, etc. and mechanical-reinforced OBCs are needed in some areas. Traditionally, organic fibres and inorganic fillers are used to improve the physical properties.13–16 But it always compromises of flexibility and it is difficult to recycle the waste blends due to the intrinsic nature of the second components differ a lot from the elastomers. To overcome the shortcomings via utilizing the MFC concept, we are trying to prepare “homogeneous” composites by blending OBC with PP, both of which belong to polyolefin family.
In our previous study, we have successfully created micro and nano fibrillar reinforced elastomer composites based on polypropylene (PP)/olefinic block copolymer (OBC).17 Unlike the mentioned MFCs, both of which are rigid plastics and their structures differ a lot from each other, OBC and PP have familiar structures, which would guarantee a good reinforcing effect and also good recycling. It was the first time that the MFCs concept was used in elastomer/plastic composites. In the previous work, we mainly focused on how the external process parameters affect PP fiber morphology and the mechanical performance of the composites. It is shown that once the continuous PP fibrils network are established, the property of OBC could be remarkably improved.
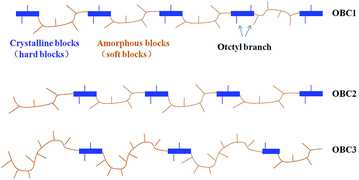
However, from the engineering point of view, the universality of using MFC concept to modify OBC elastomers should be further proved since OBC has plenty of architectures. As illustrated in Fig. 1, the chain structure of OBC can be tuned by the comonomer content, the length, content of hard segment etc. Thus the properties of OBCs vary a lot based on different block architectures.18–21 One may wonder whether or not microfibrillar composites could be produced for OBC with highly variable structures and properties. In addition, numerous grades of PP exist in the market and would they all be proper to form elaborate microfibrils inside the OBC matrix? This two questions need to be well resolved before the large-scale production OBC/PP microfibrillar composites. This is the main goal of the present work.
In the current study, the intrinsic characters of the two materials like the viscosity of PP and block architecture of OBC are investigated how they affect PP morphology and the final properties of the composites. Three OBCs (ranked by hard segment content OBC1 > OBC2 > OBC3) and three PP (ranked by viscosity PP1 > PP2 > PP3) are used as matrix and potential microfibril-forming materials, respectively.
The in situ OBC/PP fibrillar blends were fabricated through a single-screw extruder equipped with a take-up device with two pinching rolls. The weight ratios of OBC/PP were fixed at 90/10. The extrudates were compression molding at 140 °C, which is for rheological analysis. The specimens injection molded at 140 °C were used for tensile test. Both in the tensile and rheological, the temperature is controlled at 140 °C to preserve the original fibrillar structure of PP in the blends. To investigate how the OBC block architecture and PP viscosity affect the final morphologies of PP and the properties of the composites, five groups of samples are prepared: OBC1-10PP1, OBC1-10PP2, OBC1-10PP3, OBC2-10PP2 and OBC3-10PP2 (ESI†).
Fig. 2 shows high resolution SEM images of PP component after OBC was removed by xylene. It can be observed that the dispersed PP2 phase formed well-defined microfibrils in three OBCs (first row). The diameters of PP2 seem to increase from 243 nm to 274 nm as the hard segment decrease in OBC matrix. This discrepancy is within the margin of error when taken into account the uncertainties, e.g. the fluctuation of post draw process, when preparing the fibrillar composites. The photograph below displays how the PP viscosities affect final morphologies. Combined with OBC1-10PP2, the three PP have obviously different appearances. For OBC1-10PP1, PP particles are only deformed into ellipsoids even without being elongated. As PP viscosity decreases, uniform distributions of PP fibrils with high aspect ratios are obtained and the average diameters of the fibrils are 243 nm and 169 nm for OBC1-10PP2 and OBC-10PP3, respectively.
To analyze how PP melt drops deform and break up in OBC matrix, Taylor's theory was used here. According to the theory, the formation of microfibrils in polymer blends is driven by two counteracting forces: normal stress (δPn see eqn (1)) difference across the drop/matrix interface dispersing and elongating the minor component, and interfacial capillary stress (δPt see eqn (2)) acting against the breakup between melt components.22,23
| δPn = −4(Gηm/F0)sin(2φ) | (1) |
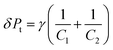 | (2) |
| −δPn > δPt | (3) |
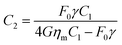 | (4) |
F0 is a function the viscosity ratio, p, i.e.,
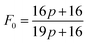 | (5) |
G is the effective shear rate and for simplicity, its value is reflected by apparent shear rate (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) in the die:
) in the die:
G ≈ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 4Q/πr3 = 4Q/πr3
| (6) |
When δPn is balanced by δPt, smallest diameters of the microfibrils can be obtained (see eqn (3) and (4)).
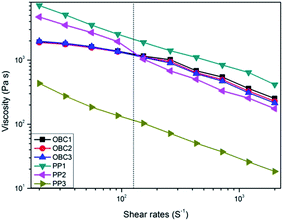
Firstly, we began the discussion of δPt, which is mainly dominated by γ (the interfacial tension of polymers). For OBC1-10PP2, OBC2-10PP2 and OBC3-10PP2, the three OBCs nearly share the same apparent viscosities from Fig. 3. Thus in the molten state, only γ is left that might affect the fibril forming result. The block architecture of the OBCs is illustrated in Fig. 1. For OBC1 to OBC3, the hard segment content decreases, accompanied by increased octene comonomers and decreased crystallinity. According to the literature, the higher octene content is expected to give the soft block segments better miscibility to PP. Thus it leads to higher adhesion to PP,25,26 implying a smaller γ and δPt. Thus the diameters of PP fibrils are supposed to decrease. Surprisingly, for the three composites, the PP diameters almost keep constant. The possible explanation is that when PP is melt blended with OBC, the interfacial interactions between the two materials display no essential differences. This discrepancy could be neglected under the complicated processing flow field. For OBC1 with lower octene content, the interfacial interaction is already strong enough to propel PP to form impeccable fibrillar structure. Still, the result proves that delicate PP fibrils can be created in OBCs matrix with a wide range of block architectures.
Another force controlling the formation of the microfibrils is δPt, which is a function of viscosity ratio (p) of thermoplastic and matrix polymers. Based on Fig. 3, the calculated p for OBC1-10PP1, OBC1-10PP2 and OBC1-10PP3 is 1.75, 1.10 and 0.09 respectively (the used ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is 131 s−1, seen ESI†). Based on Taylor's theory, the following equation was derived by Wu:27
is 131 s−1, seen ESI†). Based on Taylor's theory, the following equation was derived by Wu:27
| Gηman/γ = 4p0.84 | (7) |
From eqn (7), as the viscosity ratio of dispersed phase (PP) and matrix phase (OBC) decreases, PP can easily be dispersed and elongated into microfibrils with smaller diameters (an). An intuitive explanation is also suggested: with smaller viscosity of dispersed phase, the shear stress transferred from the matrix to the dispersed phase becomes more efficient, accelerating the breakup of the droplets. Also, the coalescence of broken PP particles is restrained more efficiently for PP with smaller viscosity in the matrix. Therefore the diameter of droplets is smaller and more uniform in low viscosity ratio system.
The rheological characterizations of OBC/PP composites in terms of storage modulus (G′) and loss modulus (G′′) as function of frequency is presented in Fig. 4. Fig. 4(a) shows an increase in both storage modulus and loss modulus by the incorporation of microfibrillar PP into three neat OBCs matrix. The dynamic modulus is enhanced significantly at low frequencies regime in particular. The PP fibrils result in rising G′ of three OBCs by factor around 4 at frequency 0.0628 rad s−1. The increase origins from the formation of physical network-like structure constructed by polymer chains and PP fibrils. Therefore the molecular mobility of the OBC chains became more restricted, resulting in a higher modulus value.
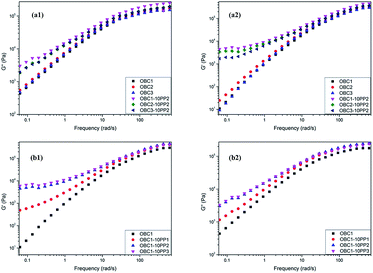 | ||
| Fig. 4 Storage modulus (a1) and loss modulus (a2) of three OBCs reinforced by PP2, storage modulus (b1) and loss modulus (b2) of OBC1 reinforced by PP1, PP2 and PP3. | ||
In Fig. 4(b), the incorporation of different PP also caused increase of both G′ and G′′. A prominent difference is observed that for OBC1-10PP1, the enhancement is weaker compared with the other two counterparts and no obvious low-frequency modulus plateau is observed. It indicates the ellipsoidal and spherical PP particle failed to form the network-like structure. Although the diameter of PP3 fibrils in the matrix is smaller than that of PP2, the enhancement extent of dynamic modulus is almost kept constant. It may imply that once the well-refined microfibrils with diameters at a considerable scope are formed in the matrix, the variation of fibril diameters exerts little influence on the rheological properties.
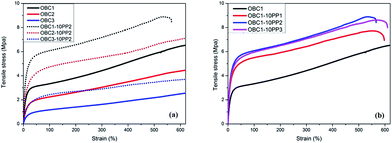
Fig. 5 displays the stress–strain curves of the OBC/PP composites and the corresponding mechanical properties are summarized in Table 1. From Fig. 5(a), the fibrillar-reinforced elastomeric composites display superior mechanical properties compared with the neat OBCs. Except for OBC1-10PP2, the composites show a strain over 600% (reaching the measurement range), implying the elasticity of the composites is also kept. Due to the more rigid nature of OBC1, the strain of its microfibrillar composites decreased to 500% which is also acceptable in some engineering applications. The mechanical strength and modulus are highly promoted. However the enhancement amplitude for OBC3-10PP2 is smaller than OBC2-10PP2 and OBC1-10PP2. That may be caused by the different block architectures of the OBCs. In our previous work,28 epitaxial crystallization of OBC on the surface of PP fibers are observed and the transcrystalline (TC) structures may be responsible for realizing effective interfacial adhesion.29–31 In OBC3, the hard segment content is only 12% and the crystallinity is only 10.4%. It may be difficult for PP fibrils to induce TC structures onto the surface due to the lower crystallization capacity, resulting in a weaker interfacial interaction. Yet more evidence needs to be obtained for the TC morphology.
| Sample | Tensile strength MPa | Tensile modulus MPa | Elongation at break % |
|---|---|---|---|
| OBC1 | 6.9 ± 0.12 | 41.2 ± 3.10 | Unbreak (626) |
| OBC2 | 4.5 ± 0.36 | 16.2 ± 2.07 | Unbreak (626) |
| OBC3 | 2.4 ± 0.17 | 6.1 ± 1.41 | Unbreak (626) |
| OBC1-10PP1 | 7.9 ± 0.20 | 86.6 ± 1.79 | 578.7 ± 18.08 |
| OBC1-10PP2 | 9.0 ± 0.23 | 102.8 ± 3.67 | 512.9 ± 41.38 |
| OBC1-10PP3 | 8.6 ± 0.09 | 90.1 ± 2.95 | 614.1 ± 10.06 |
| OBC2-10PP2 | 7.1 ± 0.31 | 30.2 ± 1.98 | Unbreak (626) |
| OBC3-10PP2 | 3.5 ± 0.21 | 19.7 ± 2.08 | Unbreak (626) |
Fig. 5(b) compares the mechanical performances of OBC1 reinforced by different PP. When the extrudates did not form the fibrils in OBC1-10PP1, the reinforcing result is unsatisfactory. The results proved that only when PP was turned into fibrils with large aspect ratio, the performance of the composites could be substantially improved. Although PP3 formed fibrils with smaller diameters, the mechanical properties of OBC1-10PP3 are a little lower than OBC1-10PP2. It is suggested when the diameters are in a considerable range the reinforcing equilibrium would be achieved which is similar to the rheological result. The final properties would be affected by the intrinsic strength of PP in the composites with fibrillar PP network inside.
In conclusion, we have demonstrated that the MFC concept is successfully applied to reinforce OBC elastomers. It shows great universality for OBC with different block architectures. PP with proper viscosity can be easily deformed into refined micro and nano fibrils in the three investigated OBCs. Especially, OBC with higher hard segment are reinforced more effectively may be due to the enhanced interfacial interaction brought by transcrystalline structures in injection molding process. Besides we also proved that viscosity ratio is the critically controlling factor determining the final PP morphologies. When the viscosity is around or less than 1, delicate fibrils can be created and the composites shows well improved mechanical properties. However in the future study, a series of PP with multiple viscosities are needed to be investigated to figure out whether the morphology of PP would experience gradual change or sudden change as the viscosity of PP increases.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (grant no. 51210005 and grant no. 51421061) and the Special Funds for Major State Basic Research Projects of China (2011CB606006).Notes and references
- S. Fakirov, Macromol. Mater. Eng., 2013, 298, 9–32 CrossRef CAS PubMed.
- X. Yi, L. Xu, Y.-L. Wang, G.-J. Zhong, X. Ji and Z.-M. Li, Eur. Polym. J., 2010, 46, 719–730 CrossRef CAS PubMed.
- W. Liu, M. Nie and Q. Wang, RSC Adv., 2014, 4, 47793–47796 RSC.
- V. Jašo, M. V. Rodić and Z. S. Petrović, Eur. Polym. J., 2015, 63, 20–28 CrossRef PubMed.
- X.-C. Xia, W. Yang, Q.-P. Zhang, L. Wang, S. He and M.-B. Yang, Polymer, 2014, 55, 6399–6408 CrossRef CAS PubMed.
- X.-C. Xia, Q.-P. Zhang, L. Wang, J.-M. Feng and M.-B. Yang, Macromol. Chem. Phys., 2014, 215, 1146–1151 CrossRef CAS PubMed.
- H.-S. Xu, Z.-M. Li, S. Y. Yang, J.-L. Pan, W. Yang and M.-B. Yang, Polym. Eng. Sci., 2005, 45, 1231–1238 CAS.
- C.-H. Jiang, X.-B. Xu and Z.-M. Li, J. Macromol. Sci., Part B: Phys., 2008, 47, 10–25 CrossRef CAS PubMed.
- N. Dencheva, T. Nunes, M. J. Oliveira and Z. Denchev, Polymer, 2005, 46, 887–901 CrossRef CAS PubMed.
- F. K. P. Leung, W. L. Cheung, X. D. Lin, D. Jia and C. Y. Chung, J. Appl. Polym. Sci., 2007, 104, 137–146 CrossRef CAS PubMed.
- R. J. Shields, D. Bhattacharyya and S. Fakirov, Composites, Part A, 2008, 39, 940–949 CrossRef PubMed.
- H. Garmabi and S. Naficy, J. Appl. Polym. Sci., 2007, 106, 3461–3467 CrossRef CAS PubMed.
- I. Mora-Barrantes, A. Rodríguez, L. Ibarra, L. González and J. L. Valentín, J. Mater. Chem., 2011, 21, 7381 RSC.
- F. Goharpey, A. Mirzadeh, A. Sheikh, H. Nazockdast and A. A. Katbab, Polym. Compos., 2009, 30, 182–187 CrossRef CAS PubMed.
- I. Kang, M. A. Khaleque, Y. Yoo, P. J. Yoon, S.-Y. Kim and K. T. Lim, Composites, Part A, 2011, 42, 623–630 CrossRef PubMed.
- I. Mora-Barrantes, L. Ibarra, A. Rodríguez, L. González and J. L. Valentín, J. Mater. Chem., 2011, 21, 17526 RSC.
- Z. Li, Y.-J. Shi, C.-X. Sun, Q. Zhang and Q. Fu, Compos. Sci. Technol., 2015, 115, 34–42 CrossRef CAS PubMed.
- F. Zuo, Y. Mao, X. Li, C. Burger, B. S. Hsiao, H. Chen and G. R. Marchand, Macromolecules, 2011, 44, 3670–3673 CrossRef CAS.
- F. Zuo, C. Burger, X. Chen, Y. Mao, B. S. Hsiao, H. Chen, G. R. Marchand, S.-Y. Lai and D. Chiu, Macromolecules, 2010, 43, 1922–1929 CrossRef CAS.
- G. Liu, Y. Guan, T. Wen, X. Wang, X. Zhang, D. Wang, X. Li, J. Loos, H. Chen, K. Walton and G. Marchand, Polymer, 2011, 52, 5221–5230 CrossRef CAS PubMed.
- J. Jin, J. Du, Q. Xia, Y. Liang and C. C. Han, Macromolecules, 2010, 43, 10554–10559 CrossRef CAS.
- G. I. Taylor, Proc. R. Soc. London, Ser. A, 1934, 858, 501–523 CrossRef.
- D. Wang, G. Sun and B.-S. Chiou, Macromol. Mater. Eng., 2007, 292, 407–414 CrossRef CAS PubMed.
- S. Mohanty and S. K. Nayak, Polym. Eng. Sci., 2007, 47, 1634–1642 CAS.
- Y. Lin, G. R. Marchand, A. Hiltner and E. Baer, Polymer, 2011, 52, 1635–1644 CrossRef CAS PubMed.
- A. R. Kamdar, R. K. Ayyer, B. C. Poon, G. R. Marchand, A. Hiltner and E. Baer, Polymer, 2009, 50, 3319–3328 CrossRef CAS PubMed.
- S. Wu, Polym. Eng. Sci., 1987, 27, 335–343 CAS.
- Z. Li, Y. Shi, H. Liu, F. Chen, Q. Zhang, K. Wang and Q. Fu, RSC Adv., 2014, 4, 45234–45243 RSC.
- R. Su, Z. Li, H. Bai, K. Wang, Q. Zhang, Q. Fu, Z. Zhang and Y. Men, Polymer, 2011, 52, 3655–3660 CrossRef CAS PubMed.
- T. Wen, Y. Zhou, G. Liu, F. Wang, X. Zhang, D. Wang, H. Chen, K. Walton, G. Marchand and J. Loos, Polymer, 2012, 53, 529–535 CrossRef CAS PubMed.
- T. Wen, G. Liu, Y. Zhou, X. Zhang, F. Wang, H. Chen, J. Loos and D. Wang, Macromolecules, 2012, 45, 5979–5985 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details for the materials, sample preparation and characterization. See DOI: 10.1039/c5ra15358a |
| This journal is © The Royal Society of Chemistry 2015 |