The gold(I)⋯lead(II) interaction: a relativistic connection

Abstract

The crystal structure of complex [Pb{HB(pz)₃}Au(C₆Cl₅)₂] 1 displays an unsupported Au(I)⋯Pb(II) interaction. This complex emits at 480 nm in the solid state due to an aurate(I) to lead(II) charge transfer, in which the existence of a metallophilic interaction is a pre-requisite. Ab initio calculations show a very strong Au(I)⋯Pb(II) closed-shell interaction of −390 kJ mol⁻¹, which has an ionic plus a dispersive (van der Waals) nature strengthened by large relativistic effects (>17%).

---

Introduction

Relativistic effects are particularly important in elements having fast-moving electrons. The main consequence for inner s and p electrons is a mass increase and, consequently, a smaller Bohr radius, yielding a contraction and stabilization of these orbitals and a concomitant expansion of d and f ones. Nevertheless, an exact solution of the Dirac equation for hydrogen-like atoms shows that the higher s and p states are relatively as strongly relativistic as their inner counterparts. Therefore, these relativistic effects should also be important in s and p valence shells of heavy metals.¹

Indeed, through the analysis of Pyykkö and Desclaux² on the radial contraction (relativistic radius/nonrelativistic radius) for a 6s orbital, they found that period 6 had minima for groups 1 (Cs) and 18 (Rn) and a pronounced maximum in group 11 (Au), being in the neighborhood of other metals such as platinum, mercury, thallium or lead, which should present, in principle, strong relativistic effects.

Traditionally, the best-known example of the implication that these effects have in many chemical or physical properties of the heavier elements is gold. For instance, its yellow color, lowest electrochemical potential or the obstinate tendency to aggregate gold centers at short distances (less than 3.80 Å) within a given molecule or between different molecules, among others, are widely recognized as caused or strongly influenced by the relativistic effects. In fact, from a synthetic viewpoint, the so-called aurophilicity has been employed as an imaginative tool to prepare gold compounds with a wide complexity of structures and stoichiometries with evident consequences for their physical properties.³

On the other hand, these relativistic effects have been invoked to play an important role in very active research fields, such as catalysis and photoluminescence, as occurs in gold or platinum chemistry.^4–7 In other metals, such as lead and mercury, the relativistic effects have been thought to explain the behaviour of the lead and mercury batteries, where 80 and 30% of their electromotive forces, respectively, arise from relativistic effects.^8,9 These facts prompted many groups to investigate more closely other closed-shell heavy metal complexes, or even heterometallic gold-containing ones with identical d¹⁰ or different (s², d⁸) configurations.¹⁰ Theoretical studies that often accompany these syntheses have confirmed that a more general term was needed: metallophilicity. These studies conclude that the interactions between the metals arise, among others, from dispersion forces reinforced in different percentages by relativistic effects.¹¹ In addition, as we have previously reported, the presence of gold in the complexes increases the relativistic effects in the heterometals, therefore strengthening the metal–metal interaction.¹²

Following different strategies, our group succeeded in preparing heterometallic gold-containing complexes with different period 6 heavy metals. Thus, by means of acid–base reactions we prepared a number of Au(I)⋯Tl(I) complexes;¹³ by a transmetallation reaction we prepared the only known example of a complex displaying a Au(I)⋯Bi(III) interaction;¹⁴ or, recently, making use of the isolobal principle, we succeeded in synthesizing the first complex displaying an unsupported Au(I)⋯Hg(II) interaction.¹⁵

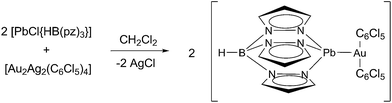
Thus, pursuing our continuous efforts in the synthesis of this type of heterometallic gold-containing complexes, and to gain insight into the relativity present in period 6 heavy metals, in this paper we describe the synthesis of the first Au(I)/Pb(II) complex displaying an unsupported metallophilic interaction. At this point, it is worth mentioning that Fackler and coworkers had previously reported the only example of a complex showing a Au(I)⋯Pb(II) contact although in that case a sulfur-coordinated ligand acted as a bridge between the metal centers.¹⁶ Therefore, in our case, the absence of additional structural factors that favour the approach between the metals permits the study of the pure metallophilic attraction.

Thus, in this paper we report the synthesis of the complex [Pb{HB(pz)₃}Au(C₆Cl₅)₂] (1), in which an unsupported Au(I)⋯Pb(II) interaction is observed in the solid state. Here we describe its crystal structure, photophysical properties, and a thorough study of the nature of the interaction between both metals and the influence of relativistic effects in the interaction.

Following a synthetic route consisting of a transmetallation reaction between [Au₂Ag₂(C₆Cl₅)₄] and [PbCl{HB(pz)₃}] in a 1 : 2 molar ratio, complex [Pb{HB(pz)₃}Au(C₆Cl₅)₂] (1) was obtained (Scheme 1). Its ¹H NMR spectrum shows the characteristic resonances of pyrazolyl groups (see ESI†). The IR spectrum of complex 1 shows the bands attributed to the presence of C₆Cl₅ rings bonded to Au(I) at 835(s) and 618(s) cm⁻¹, as well as the ν(B–N) and ν(B–H) stretching vibration absorptions at 2509(s) cm⁻¹ and at 1497(s) and 1400(s) cm⁻¹, respectively, arising from the HB(pz)₃ ligand. The base peak in the MALDI(+) mass spectrum of 1 is that corresponding to the cation [Pb{HB(pz)₃}]⁺ (m/z = 421), while in its MALDI(−) mass spectrum the peak corresponding to [Au(C₆Cl₅)₂]⁻ appears at m/z = 695, also as the base peak. This behaviour might suggest a fragmentation of the complex in solution. Indeed, the molar conductivity measurements in acetone gives a value of 127 Ω⁻¹ cm² mol⁻¹, which is in accordance with a 1 : 1 electrolyte.

Scheme 1 Synthesis of complex [Pb{HB(pz)₃}Au(C₆Cl₅)₂] (1).

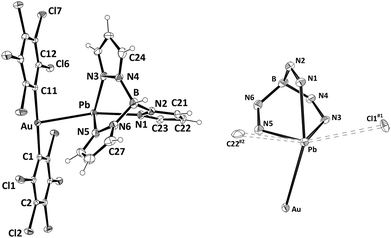
Upon slow evaporation of a diethyl ether solution of 1 single-crystals suitable for X-ray crystallography were obtained and the crystal structure of this new complex was determined. Its molecular structure contains a cationic [Pb{HB(pz)₃}]⁺ unit and a linear anionic [Au(C₆Cl₅)₂]⁻ fragment held together through an unprecedented non-assisted Au(I)⋯Pb(II) interaction of 3.0494(4) Å (Fig. 1, left). This Au–Pb distance is longer than those observed in Au₂Pb(CH₂P(S)Ph₂)₄ (2.896(1) and 2.963(2) Å),¹⁶ the unique species previously reported displaying Au⋯Pb contacts, although in such a case these interactions are supported by the P,S-donor bridging ligands, which allow the metal centers to get closer than in complex 1. The [Au(C₆Cl₅)₂]⁻ fragment displays a nearly linear coordination sphere for gold(I) with typical Au–C bond lengths, while the lead(II) atom shows an hemidirected geometry leaving a void that is occupied by the stereochemically active electron pair (see Fig. 1, right). The lead(II) center binds the tridentate chelate HB(pz)₃ ligand through the three endodentate nitrogen atoms, with asymmetric Pb–N bond distances ranging from 2.364(5) to 2.513(5) Å, which fall in the usual range for hemidirected lead(II) complexes containing pyrazolyl-type ligands (2.37–2.56 Å).¹⁷ The mentioned metallophilic interaction, as well as additional contacts between lead(II) and a chlorine atom of an adjacent molecule and a carbon atom of a different neighboring molecule gives rise to a coordination number of six, which increases to seven when the active lone pair is considered. The geometry around lead(II) is best described as distorted pentagonal bipyramidal with the gold atom and N1 at the apical positions (Au–Pb–N1 159.60(12)°) and the active lone pair occupying one of the equatorial positions (Fig. 1, right). Finally, the Pb⋯Cl1#1 and Pb⋯C22#2 weak interactions cited above give rise to a polymeric chain that runs parallel to the crystallographic a axis, and additional Cl⋯Cl (3.4070(24)–3.4764(25) Å) as well as C⋯Cl (3.4113(59) Å) contacts between pentachlorophenyl rings of neighboring chains afford a 3-D polymer (see ESI†).

Fig. 1 ORTEP-style diagram of the molecular structure of complex 1 (30% probability) (left). Coordination environment of Pb(II) (right). Selected bond distances [Å] and angles [°]: Au–Pb 3.0494(4), Au–C1 2.059(6), Au–C11 2.041(16), Pb–N1 2.513(5), Pb–N3 2.395(6), Pb–N5 2.364(5), Pb–Cl1#1 3.436(2), Pb–C22#2 3.518(9), C1–Au–C11 178.9(2), Au–Pb–N1 159.60(12). Symmetry transformations used to generate equivalent atoms: (#1) x − 1, y, z; (#2) −x + 1, −y, −z + 1.

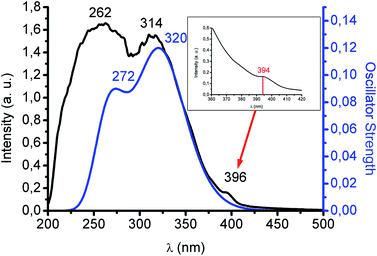
Colourless complex 1, not unexpectedly, is highly luminescent in the solid state with a blue emission at 480 nm upon excitation at 370 nm both at room temperature and at 77 K. This interesting rigidochromism can be related to the short Au–Pb interaction (3.05 Å), much shorter than the sum of their van der Waals radii (3.62 Å), which inhibits the thermal contraction with decreasing temperature. The lifetime of the emission at room temperature is 0.35 μs, a value that does not allow us to suggest with certainty whether it is a fluorescent or a phosphorescent process, especially when a very strong spin–orbit coupling is anticipated in this complex. The involvement of the metallophilic interaction in the excited state properties of this species can be deduced from its behaviour in solution, since it does not emit in THF solution, recovering its emissive properties when the solvent is evaporated, and without degradation of the product after several dissolution/evaporation cycles. This is interpreted in terms of a rupture of the metallophilic interaction by the presence of the donor THF molecules. In addition, the UV-Vis spectrum in THF displays two absorptions at 251 (ε = 16 262) and 295 nm (ε = 5392 M⁻¹ cm⁻¹) corresponding to internal π–π* transitions located in the pentachlorophenyl groups and in the tris(pirazolate) ligand (see ESI†). By contrast, interestingly, the solid UV-Vis spectrum shows two intense bands at 262 and 314 nm and an additional shoulder at 396 nm (see Fig. 2). The first two absorptions can be assigned to a charge transfer transition between the anionic [Au(C₆Cl₅)₂]⁻ and cationic [Pb{HB(pz)₃}]⁺ counterparts and a metal-perturbed intraligand (C₆Cl₅) transition, respectively. This assignment is based on the theoretical UV-Vis spectrum, obtained at TD-DFT level, whose singlet–singlet electronic excitations match the experimental absorption (see Fig. 2 and ESI†). In the case of the shoulder that appears at lower energy, its intensity could be related to a forbidden transition. In this sense, as we have mentioned, the excitation maximum in the solid state appears roughly at similar energy and far from the energies of the most intense absorption bands suggesting its forbidden character. The singlet to triplet theoretical excitation calculated at the TD-DFT level appears at 394 nm (exp. 396 nm), which confirms the phosphorescent nature of the emission in this case. The most important contribution to this singlet–triplet excitation arises from the HOMO, which is mostly located at the [Au(C₆Cl₅)₂]⁻ unit, to the LUMO, which is mainly placed at the Pb(II) center, with a small contribution from the aurate unit or, to a minor extent, to the LUMO + 2, which is located at the aurate unit (see ESI†). Therefore, the blue emissive behaviour of 1 can be ascribed to a metal–ligand (aurate) to metal (Pb) charge transfer transition, with a minor contribution from internal transitions in the aurate unit.

Fig. 2 Absorption spectrum of complex 1 in solid state (black) and TD-DFT theoretical absorption spectrum (blue) based on singlet–singlet excitations. Inset: TD-DFT lowest singlet–triplet excitation (red).

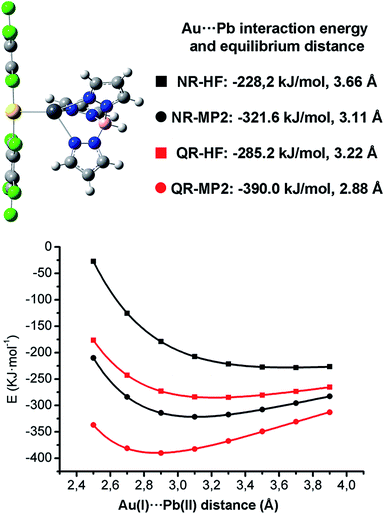
The presence of this unprecedented Au(I)⋯Pb(II) unsupported interaction prompted us to study its nature in detail. We have carried out DFT, HF and MP2 calculations on the dinuclear model system [Pb{HB(pz)₃}Au(C₆Cl₅)₂] 1A (see Fig. 3), which is not simplified with respect to the experimentally characterized X-ray structure and displays an unsupported metallophilic interaction. All computational methods are described in the ESI.†

Fig. 3 DFT-optimized model system [Pb{HB(pz)₃}Au(C₆Cl₅)₂] 1A (top-left); interaction energies and equilibrium distances (top-right) and corresponding interaction energy curves (bottom) at HF and MP2 levels using non-relativistic (NR) and quasirelativistic (QR) ECPs for the metal centers.

The full optimization of model [Pb{HB(pz)₃}Au(C₆Cl₅)₂] 1A at the DFT/B3LYP level in the gas phase leads to an attractive interaction between the ionic units with an Au(I)⋯Pb(II) distance 3.04 Å, which is very similar to the experimental one of 3.05 Å found for complex 1 in the solid state structure. The rest of calculated structural parameters agree well with the experimental ones (see ESI†).

When non-relativistic (NR) ECPs are used, the MP2 curve is strongly attractive, displaying a minimum corresponding to a Au(I)⋯Pb(II) equilibrium distance of 3.11 Å, which is slightly larger than the one obtained when QR ECPs are used, showing the positive influence of the relativistic effects in the metallophilic Au(I)⋯Pb(II) interaction strength. Indeed, a very large decrease of the MP2 interaction energy from −390.0 kJ mol⁻¹ (QR ECPs) to −321.6 kJ mol⁻¹ (NR ECPs) is obtained. This trend would be in agreement with a very important contribution of the relativistic effects of 17% to the Au(I)⋯Pb(II) interaction energy. The fact that the non-relativistic HF minimum is obtained at a very large distance of 3.66 Å (3.22 Å in the relativistic case) strongly suggests that the relativistic effects exert an important influence both in the coulombic and dispersive components of the Au(I)⋯Pb(II) metallophilic interactions.

The 17% of relativistic effect contribution to the Au(I)⋯Pb(II) interaction obtained at QR-MP2 level is slightly smaller than the Au(I)⋯Hg(II) (21%)¹⁵ or the Au(I)⋯Au(I) (27%)¹¹ ones. The most interesting issue here is that this relativistic effect contribution follows a very similar trend to the relativistic vs. non-relativistic 6s shell radial contraction already analyzed by Pyykkö and Desclaux² in which the relativistic 6s shell contraction for Pb, Hg and Au is ca. 12, 14 and 17%, respectively. This permits to state that the study of the nature of the metallophilic Au(I)⋯M interaction would also serve as a tool to classify the role of relativity in heavy metal atoms. Nevertheless, as is well known, the MP2 level gives an overestimation of the metallophilicity, thus more accurate CCSD and CCSD(T) calculations on simplified model systems are needed.

The analysis of the NBO fragment charges also supports the important role played by the relativistic and correlations effects in the metallophilic Au(I)⋯Pb(II) interaction. We have compared the overall fragment charges for [Au(C₆Cl₅)₂]⁻ and [Pb{HB(pz)₃}]⁺ both isolated (−1 and +1, respectively) or when they interact each other. Table 1 depicts the fragment charges at HF and MP2 levels of theory using QR and NR ECPs. As can be observed, the net charge at [Au(C₆Cl₅)₂]⁻ is less negative at QR-MP2 level (−0.767) than at NR-MP2 level (−0.826), leading to less positive charge in the lead(II) fragment at the QR-MP2 level (+0.767) than in the NR-MP2 case (+0.826). This trend would be in agreement with a less pronounced acid–base character of the interaction when relativistic effects are included in the calculation. Moreover, when the same charges are analyzed at QR-HF level (+0.856 for gold and −0.856 for lead) and at NR-HF level (+0.923 for gold and −0.923 for lead) and they are compared with the MP2 level ones, the results show that the inclusion of correlation effects (dispersive forces) also leads to a less pronounced ionic character of the Au(I)⋯Pb(II) interaction.

Table 1 NBO charges for the ionic counterparts in model [Pb{HB(pz)₃}Au(C₆Cl₅)₂] 1A at HF and MP2 level using QR and NR ECPs for the metals

	QR ECPs	NR ECPs
[Au(C6Cl5)2]^− (MP2)	−0.767	−0.826
[Pb{HB(pz)3}]^+ (MP2)	0.767	0.826
[Au(C6Cl5)2]^− (HF)	−0.856	−0.923
[Pb{HB(pz)3}]^+ (HF)	0.856	0.923

---

Another interesting parameter that can be computed using QR and NR ECPs is the p-character of the Pb(II) lone pair. As has been observed experimentally the lone pair is stereochemically active, and therefore, it should not be involved in the metallophilic Au(I)⋯Pb(II) interaction, which displays an ionic plus dispersive origin. We have compared the Pb lone pair s- and p-character for the free [Pb{HB(pz)₃}]⁺ fragment and for the same fragment when the Au(I)⋯Pb(II) interaction is taken into account. In the case of the free Pb(II) fragment, when relativistic effects are considered (QR ECP for Pb), a larger s-character (92.5% s vs. 7.5% p) is achieved if compared to the non-relativistic case (NR ECP for Pb), for which a larger p-character of the lone pair is observed (86.8% s vs. 13.2% p). This trend is in agreement with the marked relativistic stabilization of the 6s level of Pb with respect to the 6p one. In fact, one could expect that the Pb 6s shell radii would enter via the changed Pauli repulsion between the filled cores. The most interesting feature here is that if we make the same comparison between the QR and NR character of the Pb lone pair in the model [Pb{HB(pz)₃}Au(C₆Cl₅)₂] 1A, an even larger stabilization of the 6s level is achieved if compared to the free Pb(II) fragment. Thus, when relativistic ECPs are considered for the metals the s-character is 96.1% (3.9% p), whereas the non-relativistic case (NR EPC for Au and Pb) displays a 90.6% of s-character (9.4% p). In view of this analysis we can state that the presence of a metallophilic Au(I)⋯Pb(II) interaction strengthens the relativistic effects for Pb(II).

Conclusions

In conclusion, this unprecedented unsupported metallophilic Au(I)⋯Pb(II) interaction displays an important contribution from ionic, correlation and relativistic effects, the latter being 17% of the interaction, in agreement with the large relativistic effects expected for these two metal centers. Future ligand variations, more accurate calculations and study of the interesting photoluminescent properties observed for these systems are now under progress.

Acknowledgements

This work was supported by the DGI Project MINECO/FEDER (CTQ2013-48635-C2-2-P). R. E. thanks the MINECO for a FPI grant. The Centro de Supercomputación de Galicia (CESGA) is acknowledged for computational resources. Prof. Pekka Pyykkö is acknowledged for fruitful discussions.

Notes and references

1. P. Pyykkö, Annu. Rev. Phys. Chem., 2012, 63, 45–64.
2. P. Pyykkö and J. P. Desclaux, Acc. Chem. Res., 1979, 12, 276–281.
3. H. Schmidbaur and A. Schier, Chem. Soc. Rev., 2012, 41, 370–412.
4. D. J. Gorin and F. D. Toste, Nature, 2007, 446, 395–403.
5. A. Leyva-Pérez and A. Corma, Angew. Chem., Int. Ed., 2012, 51, 614–635.
6. Optoelectronic Properties of Inorganic Compounds, ed. D. M. Roundhill and J. P. Fackler Jr, Plenum, New York, 1999, pp. 195–226.
7. V. W. W. Yam and E. C. C. Cheng, Top. Curr. Chem., 2007, 281, 269–309.
8. R. Ahuja, A. Blomqvist, P. Larsson, P. Pyykkö and P. Zaleski-Ejgierd, Phys. Rev. Lett., 2011, 106, 018301.
9. P. Zaleski-Ejgierd and P. Pyykkö, Phys. Chem. Chem. Phys., 2011, 13, 16510–16512.
10. C. Silvestru, in Modern Supramolecular Gold Chemistry, ed. A. Laguna, Wiley-VCH, Weinheim, 2008, pp. 181–293.
11. P. Pyykkö, N. Runeberg and F. Mendizabal, Chem.–Eur. J., 1997, 3, 1451–1457.
12. E. J. Fernández, J. M. López-de-Luzuriaga, M. Monge, M. A. Rodríguez, O. Crespo, M. C. Gimeno, A. Laguna and P. G. Jones, Chem.–Eur. J., 2000, 6, 636–644.
13. See for example: (a) A. J. Blake, R. Donamaría, E. J. Fernández, T. Lasanta, V. Lippolis, J. M. López-de-Luzuriaga, E. Manso, M. Monge and M. E. Olmos, Dalton Trans., 2013, 42, 11559–11570; (b) E. J. Fernández, A. Garau, A. Laguna, T. Lasanta, V. Lippolis, J. M. López-de-Luzuriaga, M. Montiel and M. E. Olmos, Organometallics, 2010, 29, 2951–2959; (c) E. J. Fernández, A. Laguna, T. Lasanta, J. M. López-de-Luzuriaga, M. Montiel and M. E. Olmos, Inorg. Chim. Acta, 2010, 363, 1965–1969; (d) E. J. Fernández, P. G. Jones, A. Laguna, J. M. López-de-Luzuriaga, M. Monge, J. Pérez and M. E. Olmos, Inorg. Chem., 2002, 41, 1056–1063; (e) E. J. Fernández, P. G. Jones, A. Laguna, J. M. López-de-Luzuriaga, M. Monge, M. Montiel, M. E. Olmos and J. Pérez, Z. Naturforsch., B: J. Chem. Sci., 2004, 59, 1379–1386; (f) E. J. Fernández, A. Laguna, J. M. López-de-Luzuriaga, M. Montiel, M. E. Olmos and J. Pérez, Organometallics, 2005, 24, 1631–1637; (g) E. J. Fernández, A. Laguna, J. M. López-de-Luzuriaga, F. Mendizabal, M. Monge, M. E. Olmos and J. Pérez, Chem.–Eur. J., 2003, 9, 456–465.
14. E. J. Fernández, A. Laguna, J. M. López-de-Luzuriaga, M. Monge, M. Nema, M. E. Olmos, J. Pérez and C. Silvestru, Chem. Commun., 2007, 571–573.
15. J. M. López-de-Luzuriaga, M. Monge, M. E. Olmos, D. Pascual and T. Lasanta, Chem. Commun., 2011, 47, 6795–6797.
16. S. Wang, G. Garzon, C. King, J. C. Wang and J. P. Fackler Jr, Inorg. Chem., 1989, 28, 4623–4629.
17. R. D. Hancock, S. M. Shaikjee, S. M. Dobson and J. C. A. Boeyens, Inorg. Chim. Acta, 1988, 154, 229–238.

---

Footnote

† Electronic supplementary information (ESI) available: X-ray crystallographic data in CIF format and plots of the polymeric crystal structure of 1, experimental and theoretical details. CCDC 1033939. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4sc03680h

---