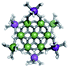
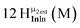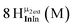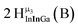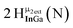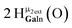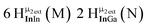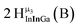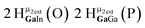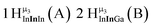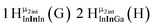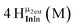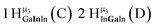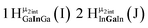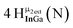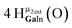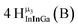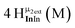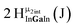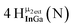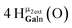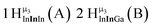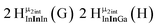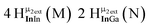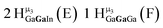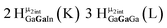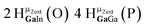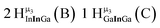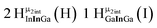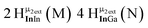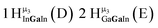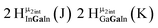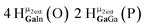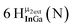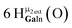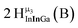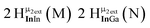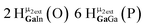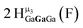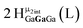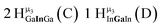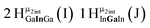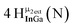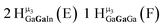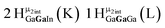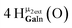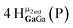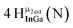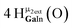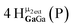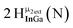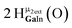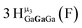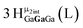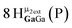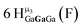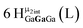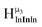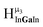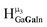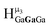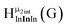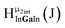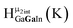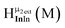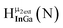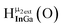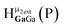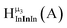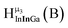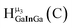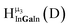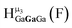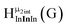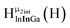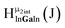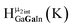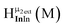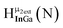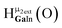Open Access Article
Open Access ArticleSolution structural characterization of an array of nanoscale aqueous inorganic Ga13−xInx (0 ≤ x ≤ 6) clusters by 1H-NMR and QM computations†
Anna F.
Oliveri
a,
Lindsay A.
Wills
b,
Caitlyn R.
Hazlett
a,
Matthew E.
Carnes
a,
I-Ya
Chang
b,
Paul
Ha-Yeon Cheong
*b and
Darren W.
Johnson
*a
aDepartment of Chemistry & Biochemistry and Materials Science Institute, University of Oregon, Eugene, Oregon 97403-1253, USA. E-mail: dwj@uoregon.edu
bDepartment of Chemistry, Oregon State University, 153 Gilbert Hall, Corvallis, Oregon 97331-4003, USA. E-mail: paulc@science.oregonstate.edu; Web: http://sustainablematerialschemistry.org
First published on 28th April 2015
Abstract
NMR spectroscopy is the go-to technique for determining the solution structures of organic, organometallic, and even macromolecular species. However, structure determination of nanoscale aqueous inorganic clusters by NMR spectroscopy remains an unexplored territory. The few hydroxo-bridged inorganic species well characterized by 1H Nuclear Magnetic Resonance spectroscopy (1H-NMR) do not provide enough information for signal assignment and prediction of new samples. 1H-NMR and quantum mechanical (QM) computations were used to characterize the NMR spectra of the entire array of inorganic flat-Ga13−xInx (0 ≤ x ≤ 6) nanoscale clusters in solution. A brief review of the known signals for μ2-OH and μ3-OH bridges gives expected ranges for certain types of protons, but does not give enough information for exact peak assignment. Integration values and NOESY data were used to assign the peaks of several cluster species with simple 1H-NMR spectra. Computations agree with these hydroxide signal assignments and allow for assignment of the complex spectra arising from the remaining cluster species. This work shows that 1H-NMR spectroscopy provides a variety of information about the solution behavior of inorganic species previously thought to be inaccessible by NMR due to fast ligand and/or proton exchange in wet solvents.
Introduction
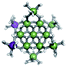
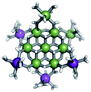
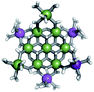
Proton Nuclear Magnetic Resonance spectroscopy (1H-NMR) is an important tool heavily utilized by chemists and biochemists since its discovery in 1945.1 Unfortunately, it is often not a viable technique for characterizing purely inorganic clusters due to the fast exchange of protons and/or ligands in aqueous coordination clusters dissolved in wet/polar solvents. The reliable trends and generalizations in 1H-NMR shifts tabulated for numerous carbon-containing molecules do not translate to this purely inorganic world. The focus of this manuscript is to correlate the 1H-NMR spectral shifts of nanoscale aqueous clusters dissolved in wet solvents to their hydroxo ligands to substantiate cluster characterization and speciation in solution. The 1H-NMR spectrum of [Ga13(μ3-OH)6(μ2-OH)18(H2O)24]-(NO3)15 (Ga13) in wet d6-DMSO is known.2 Due to the spectral complexity, no peaks were assigned to specific hydroxo and aquo protons in the structure at that time. Further analysis coupled with computations of the complete series of [Ga13−xInx(μ3-OH)6(μ2-OH)18(H2O)24]-(NO3)15 clusters (1 ≤ x ≤ 6: Ga12In1, Ga11In2, Ga10In3, Ga9In4, Ga8In5, Ga7In6) provides trends and clarity, allowing partial 1H signal assignment and complete assignment of all hydroxo bridges in the “mother clusters” (i.e., clusters entirely capped with water molecules that potentially undergo exchange with coordinating solvents, Fig. 1).1H-NMR spectroscopy is the first characterization technique used in modern organic, organometallic, and coordination chemistry, yet such data are only sporadically reported for aqueous inorganic clusters. We have found that under the right conditions such clusters often exhibit rich 1H-NMR spectra that enable characterization by 2D NMR techniques as well.2 A bottleneck in determining solution structure by NMR spectroscopy has been the lack of tabulated data for such clusters and predictive methods for peak assignment. For instance, there is no known way for predicting where M − H2O or M–(μ2-OH)–M 1H-NMR signals should resonate like there is for organic compounds. In this manuscript we provide a literature survey of 1H-NMR spectroscopic resonances reported for known hydroxo- and aquo-coordinated metal complexes. To the best of our knowledge, such data have not been aggregated in one location. We then use this information and complementary quantum mechanical (QM) computations to provide the complete solution structure and peak assignment for a series of clusters.
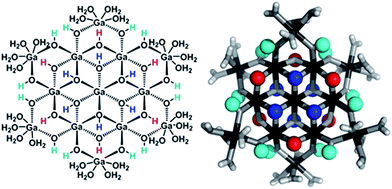
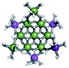
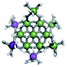
The Ga13−xInx clusters in this work are completely inorganic. Clusters of this type are often more difficult to isolate and challenging to characterize13 than organic ligand-supported versions, because the ligands lower the cluster charge and can increase stability.14 However, the lack of organic ligands makes these species attractive candidates as precursors (inks) for metal oxide films, as the lack of organic additives that must be “burned” off during film formation/condensation leads to fewer defects and increases density of thin films. These clusters also serve as excellent inks/precursors due to their high solubility in aqueous and alcoholic solutions, which eliminates toxic solvents often used in thin film production. Minimizing the organic ligands for such applications has produced superior precursors,13 but the lack of spectroscopic handles has limited the complete understanding of the solution behavior of these species.
Previously, single crystal X-ray diffraction (XRD) and elemental analysis were the techniques used to differentiate the seven known flat-Ga13−xInx clusters.15 These techniques suggest that multiple cluster species might co-crystallize during isolation (for example, Ga10.2In2.8 has been isolated, which could be an 80/20 mixture of Ga10In3 and Ga11In2 or some other such combination). Ga13 has been recently characterized in solution using NMR, Small Angle X-ray Scattering (SAXS), and Raman.2,16 Although single crystal XRD can provide excellent solid-state data, it cannot answer pressing current questions. Does Ga10In3 even exist or are all of the mixed clusters simply various ratios of Ga13 and Ga7In6? Do all of the possible isomers in the Ga9In4–Ga11In2 clusters (Fig. 1) co-crystallize or are certain ones thermodynamically favored? Is there a way to determine the ratio of isomers present in a sample? Using 1H-NMR, we have established a quick technique for characterizing samples that could address these questions and will accelerate the synthesis and identification of cluster species in solution.
1H-NMR spectra of hydroxo/aquo bridged coordination compounds
Only a limited number of reports of completely inorganic, hydroxo bridged species have been studied via1H-NMR spectroscopy. However, the moderate chemical shift library of hydroxo protons identified in ligand-supported metal complexes and coordinated water allows for some comparison. The typical chemical shifts of coordinated water ligands are generally downfield (Table 1). Typically hexaaquo species have proton signals in the range of 8.3 to 11.3 ppm, while water ligands on metal oligomers tend to appear slightly upfield between 6.3 and 10 ppm.| Metal | Type of complex | Chem. shift (ppm) | NMR conditions | Ref. |
|---|---|---|---|---|
| AlIII | Hexaaquo | 10.2 | d 6-Acetone; 400 MHz | 3 |
| GaIII | Hexaaquo | 8.3 | d 6-Acetone; −50 °C; 500 Hz | 4 |
| RhIII | Hexaaquo | 9.0–9.2 | d 6-Acetone; −83 °C; 400 MHz | 5 |
| SnIV | Hexaaquo | 10.1–11.3 | d 6-Acetone; −100 °C; 60 MHz | 6 |
| AlIII | Oligomer (Al13-Keggin) | 7.5 | d 6-Acetone; −30 °C; 400 MHz | 7 |
| AlIII | Oligomer (Al13-Keggin) | 6.3 | d 3-Acetonitrile; 400 MHz | 7 |
| AlIII | Oligomer (Al13-Keggin) | 8.0 | H2O/d6-Acetone (2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); −20.6 to −5.2 °C; 500 MHz 1); −20.6 to −5.2 °C; 500 MHz |
8 |
| AlIII | Oligomers | 7–10 | d 6-Acetone; 400 MHz | 3 |
| AlIII | Oligomers | 8–9.5 | — | 5, 7 |
| RhIII | Oligomers | 8.4, 8.7 | d 6-Acetone; −83 °C; 400 MHz | 5 |
Little is known about the potential trends for these hydroxide bridges in inorganic species, although it appears that the metal atom and its coordination number are main contributors to the chemical shift of these hydroxo protons. The collected chemical shifts have been tabulated and discussed for the readers benefit (Tables 2–5). For diamagnetic complexes, μ2-OH protons fall between −4.5 and 7 ppm; while μ3-OH proton signals occur from −1.05 to 6.79 ppm (Fig. 2). The observation of these 1H-NMR signals at lower chemical shifts than that of the hexaaquo species and the free hydroxide ions is caused by the increased electron density around the proton in the bridge.5 These are fairly large regions that are not distinguishable from one another, but can be differentiated from water ligands. By looking more closely at specific metals, coordination environments, and groups on the periodic table, refined assignments of chemical shift regions and apparent trends emerge.
| Metal | Molecular geometry of MX+ | μ2-OH Chem. shift (ppm) | NMR conditions | Ref. |
|---|---|---|---|---|
| AlIII | Octahedral (Al13-Keggin) | 3.8, 3.9 | d 6-Acetone; −30 °C; 400 MHz | 7 |
| AlIII | Octahedral (Al13-Keggin) | 2.8, 3.0 | d 3-Acetonitrile; 400 MHz | 7 |
| AlIII | Octahedral (Al13-Keggin) | 3.8, 4.5 | H2O/d6-Acetone (2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); −20.6 to −5.2 °C; 500 MHz 1); −20.6 to −5.2 °C; 500 MHz |
8 |
| AlIII | Octahedral (Al13-Keggin) | 3.8 | H2O/d6-DMSO (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); 3.7 to 95.2 °C; 500 MHz 1); 3.7 to 95.2 °C; 500 MHz |
8 |
| AlIII | Octahedral | 4.8 | — | 5 |
| GaIII | Octahedral | 2.03 | d 6-DMSO; 400 MHz | 9 |
| GaIII | Octahedral | 4.2 | d 3-Acetonitrile/D2O; 250 MHz | 10 |
| IrIII | Distorted octahedral | 1.6 | d-Chloroform; 25 °C; 270 MHz | 11 |
| RhIII | Octahedral (di/trimer) | 3.7, 4.3 | d 6-Acetone; −83 °C; 400 MHz | 5 |
| WIII | Octahedral | 2.05 | d-Chloroform; 19 and 55 °C; 400 MHz | 12 |
| Metal | Molecular geometry of MX+ | μ2-OH Chem. shift (ppm) | NMR conditions | Ref. |
|---|---|---|---|---|
| a No indication of molecular geometry. b Distorted geometry. c Six or more proton signals in this range. | ||||
| BeII | Tetrahedral | 4.3 | −55 °C; 220 MHz | 22 |
| MgII | Trigonal bipyramidal | 3.99 | d 8-THF; 25 °C; 300 MHz | 44 |
| MoII | Square pyramidalb | 2.44 | — | 45 |
| MoII | Pentagonal bipyramidal | 1.24 | d 2-Dichloromethane; −78 °C; 400 MHz | 46 |
| RuII | Five coordinatea | 3.00, 2.94 | d 6-Acetone; 60 & 220 MHz | 47 |
| SnIV | Trigonal bipyramidal | 2.61, 3.85, 2.3 | d-Chloroform; 360 & 400 MHz | 36–38 |
| WII | Pentagonal bipyramidal | 1.7 | d 2-Dichloromethane; −78 °C; 400 MHz | 46 |
| ZnII | Trigonal bipyramidal | 4.16 | d 3-Acetonitrile; 270 MHz | 41 |
| ZnII | Octahedral | 2.08 | d 6-DMSO | 43 |
| ZrIV | Pentagonal bipyramidal | 3.8 | d 8-THF; 200 MHz | 48 |
| ZrIV | Octahedralb | 1.39–1.57c | d 6-DMSO; 400 MHz | 49 |
| CdII | Trigonal bipyramidal | −2.43 | d 3-Acetonitrile; 20 °C; 400 MHz | 42 |
| CoIII | Octahedral | −2 | d 6-DMSO | 17 |
| CoIII | Octahedral | 0.63 | d 3-Acetonitrile; 250 MHz | 18 |
| CoIII | Octahedral | −4.18 | d 6-DMSO | 19 |
| CoIII | Octahedral | −0.15, −2.56, −4.95 | d 6-DMSO; 20 °C; 300 MHz | 21 |
| CoIII | Octahedral | −1.195, 1.397 | d 6-DMSO; 25 °C; 600 MHz | 20 |
| CoIII | Octahedral | −0.702, −0.670 | D2O; 4 °C; 600 MHz | 20 |
| GaIII | Tetrahedral | 0.14 | d 6-Benzene; 300 MHz | 50 |
| InI | Square pyramidal | 0.93 | d 6-Benzene; 400 MHz | 51 |
| Os0/II | Six/seven coordinatea | −2.8 | d 2-Dichloromethane; 400 MHz | 24 |
| Os0/II | Octahedral | −1.98 to −0.44c | d-Chloroform; 200 MHz | 25 |
| PdII | Square planar | −1.58, −1.66, −2.96, −3.09 | — | 26 |
| PdII | Square planar | −2.84, −1.53, −1.67 | d-Chloroform; 200 MHz | 27 |
| PdII | Square planar | −1.01, −1.17, −1.25 | d 6-Acetone; 200 and 300 MHz | 28 |
| PdII | Square planar | −0.9, −1.0 | d-Chloroform; −3 and 27 °C; 600 MHz | 29 |
| PdII | Square planar | −0.85 | d-Chloroform; 200 MHz | 30 |
| PtII | Square planar | −0.14 | d 2-Dichloromethane; 200 MHz | 31 |
| PtII | Square planar | −2.04, −1.22, −1.03, −0.56 | d-Chloroform; 25 °C; 80 MHz | 32 |
| PtII | Square planar | 1.9, −0.8, −0.46 | d-Chloroform; 80 and 200 MHz | 34 |
| PtII | Square planar | 2.0, −0.9, −0.45 | d 2-Dichloromethane; 80 and 200 MHz | 34 |
| PtII | Square planar | 2.12 | d-Chloroform; 300 MHz | 33 |
| SnIV | Octahedral | 7.33 | d 6-DMSO; 300 MHz | 39 |
| SnIV | Octahedral | 7.02 | d 2-Dichloromethane; 300 MHz | 39 |
| YIII | Eight coordinatea | 6.4, 5.45 | d 3-Acetonitrile; 300 MHz | 40 |
| YIII | Dodecahedralb | 5.4 | d 3-Acetonitrile; 300 MHz | 40 |
| YIII | Bicapped trig. prismatic | 5.23, 5.35 | d 3-Acetonitrile; 300 MHz | 40 |
| YIII | Square antiprismaticb | 6.2 | d 2-Dichloromethane; 300 MHz | 40 |
| ZnII | Trigonal bipyramidalb | −1.15, −0.66 | d 3-Acetonitrile; 20 °C; 300 & 400 MHz | 42 |
| Metals | Molecular geometry of MX+ | μ2-OH Chem. shift (ppm) | NMR conditions | Ref. |
|---|---|---|---|---|
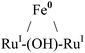
|
Octahedral | −2.16, −1.78, −1.75 | d-Chloroform | 52 |
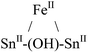
|
Tetrahedral | 1.7 | d 6-Benzene; 27 °C; 300 and 500 MHz | 35 |
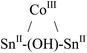
|
Tetrahedral | 1.63 | d 6-Benzene; 27 °C; 300 and 500 MHz | 35 |
| GaIII–(OH)–CaII | Octahedral (Ga) | 4.73 | d-Chloroform; 25 °C; 500 MHz | 53 |
| GaIII–(OH)–SrII | Octahedral (Ga) | 4.49 | d-Chloroform; 25 °C; 500 MHz | 53 |
| Metal | Molecular geometry of MX+ | μ3-OH Chem. shift (ppm) | NMR conditions | Ref. |
|---|---|---|---|---|
| a No indication of molecular geometry. b Distorted geometry. c Associated CuI32−. | ||||
| CaII | Octahedral | 1.32, 2.77, 4.57 | d 6-Benzene; 25 °C; 300 MHz | 44 |
| RhI | Six coordinatea | −1.05 | d 4-Methanol; 300 MHz | 54 |
| RhI | Six coordinatea | −0.61, −0.48, −0.02 | d 2-Dichloromethane; 300 MHz | 54 |
| SnIV | Trigonal bipyramidal | 3.219, 3.221 | d-Chloroform; 500 MHz | 55 |
| ThIV | Square pyramidalb | 5.97, 6.16, 6.79 | d 6-DMSO; 500 MHz | 56 |
| YIII | Dodecahedralc | 2.93, 3.1 | d 3-Acetonitrile; 300 MHz | 57 |
| YIII | Dodecahedral | 6.05 | d 3-Acetonitrile | 58 |
| ZnII | Trig. bipyramidal/octahedral | 5.4 | d-Chloroform; 25 °C; 300 MHz | 59 |
Octahedral M(III) ions (M = Al, Ga, Ir, Rh, and W), the most relevant for this work, tend to produce signals for μ2-OH protons that range from 1.5–5.0 ppm, although this does not hold true for Co(III).17–21 Geometries, chemical shift data, and available NMR conditions for these metal complexes are shown in Table 2. The majority of this data was referenced to TMS or residual protic peaks described in the primary papers. Solvent and temperature do not appear to significantly affect the chemical shifts.12
The top section of Table 3 indicates some metal complexes with different oxidation states and/or non-octahedral geometries exhibit resonance for hydroxide bridges similar to the ranges observed for “trivalent octahedral” metal complexes. In addition to experimental data, computational data is occasionally found for bridging hydroxides. For instance, computed 1H-NMR shifts during the oligomerization of Be(II) species mirrors the experimental measurement of 4.3 ppm.22,23 Like the trivalent octahedral complexes listed above, certain metals have distinct areas within the bigger region were the 1H-NMR signals of μ2-OH bridges appear. The data presented in the bottom section of Table 3 reveals these ranges. As previously mentioned, octahedral Co(III) complexes differ from the other trivalent octahedral complexes with signals appearing between −4.5 and 0.5 ppm.17–21 Mixed valence Os(0/II) compounds tend to have bridges in the −2.8 to −0.44 ppm range.24,25 Square planar Pd(II) and Pt(II) complexes have μ2-OH bridges that range from −3 to 2 ppm.26–34 Sn has the largest range producing signals anywhere from 1.63 to 7.33 ppm.35–39 Yttrium hydroxo bridges tend to have chemical shift values downfield ranging from 5.2 to 6.4 ppm.40 Zn(II) bridges fall into the −1.15 to 4.16 range.41–43 The proton signal for the only example of a Cd–(μ2-OH)–Cd bridge appeared at −2.43 ppm.42 The typical ranges of these metal hydroxo bridges have been plotted in Fig. 3 to allow for easy comparison.
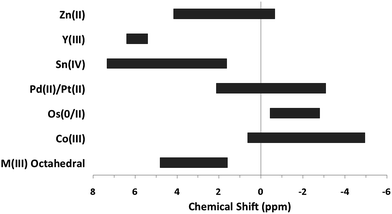 | ||
| Fig. 3 General 1H-NMR signal regions for homometallic μ2-OH bridges in a variety of metal complexes. | ||
Data from the literature for heterometallic complexes was also analysed because the present work focuses on heterometallic Ga/In clusters as well. Not all of the heterometallic complexes in Table 4 feature bridging hydroxides between two different metal atoms, but for completeness they were included.
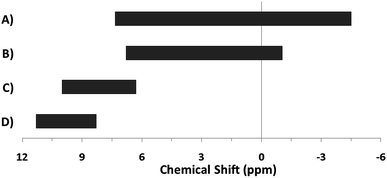
The hydroxo bridges in trivalent Group 13 octahedral metal complexes are the most relevant for this report. Akitt and colleagues suggests a range of 3 to 6 ppm for Al3+ μ2-OH bridges.3 However, the data listed above suggests these resonances should fall within the 2.0 to 4.8 ppm region. The heterometallic octahedral Ga–(μ2-OH)–M (M ≠ Ga) bridges have very similar chemical shifts to the homometallic hydroxo bridges listed in Table 2. This indicates that Ga–(μ2-OH)–Ga bridges may not easily be distinguished from Ga–(μ2-OH)–In bridges. Fig. 4 illustrates the regions where μ2-OH bridges and capping water ligands on the Ga13−xInx clusters most likely will resonate.
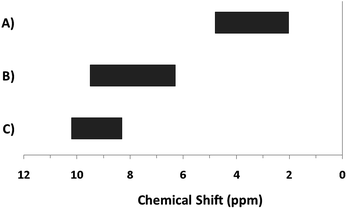 | ||
| Fig. 4 General 1H-NMR signal regions for hydroxo bridges and aquo ligands on Group 13 metals. (A) μ2-OH ligands; (B) aquo ligands in multimetallic complexes; (C) hexaaquo metal complexes. | ||
One trend that stood out in the general data was that hydroxide bridges shift downfield with increased coordination number of the metal. This trend is visible with metals such as Sn, Ga, and Zr (Fig. 5). These were the only metals that had data from several independent sources allowing reasonable conclusions to be made. This trend holds true for all of Group 13, not just gallium (Fig. 6). Tetrahedral gallium has a Ga–(μ2-OH)–Ga bridge at 0.14 ppm,50 Square pyramidal gallium and indium have peaks in the 1 to 1.5 ppm range,51,60 and as stated above octahedral aluminium and gallium produce signals between 2 and 5 ppm.
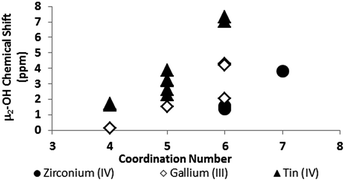 | ||
| Fig. 5 As the coordination number of a cation increases, the 1H-NMR signals shift downfield (Tables 2 and 3). | ||
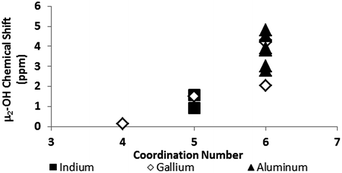 | ||
| Fig. 6 As the coordination number in Group 13 increases, the 1H-NMR signals shift downfield (Tables 2 and 3). | ||
1H-NMR data reported for μ3-OH protons are even scarcer. As previously stated, these signals appear from −1.05 to 6.79 ppm. The proton chemical shifts in these complexes are listed in Table 5. No examples of Group 13 metals with μ3-OH ligands were found. The most relevant is the trivalent yttrium complex with a proton signal at 6.05 ppm.58 Related hydroxide ligands in Th(IV) and Zn(II) compounds also resonate in this region.56,59 Unfortunately, there are not enough examples of μ3-OH protons to suggest any trends or regions for specific metals or coordination geometries.
This brief literature survey will not only help the structural study and assignments presented herein, but we hope this serves as a useful resource for others seeking to assign aquo and bridging hydroxo ligands in inorganic clusters and related compounds. This survey highlights some of the challenges in interpreting even the most basic NMR signals. For example, when two distinct μ2-OH signals arise in the same 1H-NMR spectrum, it can be difficult to tell them apart. Two examples of this from above are the Al–(μ2-OH)–Al bridges of Elders and colleagues' Keggin cluster,7 and the hexanuclear yttrium species by Hubert-Pfalzgraf and coworkers.57
These data can also help with identifying possibly mis-assigned signals. For instance, in [Al(μ-OH)(hbo)2]2 (hbo: 2-(2′-hydroxphenyl)-2-benzoxazole) a peak at 11.47 ppm observed in CDCl3 is proposed to be the bridging hydroxo ligands.61 Is it possible that this is really a small amount of an aquo–Al(III) complex or some other aquo ligand-containing species? The data reported herein and our literature survey suggest that resonances this far downfield are typically due to aquo ligands; however, there are very few examples of NMR data reported for such species in CDCl3, so much remains to be learned. Similarly, are the peaks assigned to aquo ligands in the spectra of Al(III) and Ga(III) porphyrins containing Ga–(μ2-OH)–Ga and In–(μ2-OH)–In bridges at 1.5 and 1.56 ppm, respectively, actually the hydroxide bridges?60 Hopefully, these tabulated data can be helpful for the future assignment of μ2-OH and μ3-OH bridges in related compounds and help begin to develop a reliable database of such peak assignments.
Experimental section
Chemicals were purchased from Sigma-Aldrich, TCI America, and STREM, and were used as received without further purification. The Ga13−xInx clusters were synthesized using previously published methods.13,15,621H-NMR experiments were conducted at 25 °C in 5 mm tubes on a 500 MHz Varian spectrometer. Data were collected using Varian Software, referenced to TMS, and processed using MestReNova. The DOSY experiments were performed using the gradient stimulated echo with spin-lock and convection compensation (DgsteSL_cc) pulse sequences. All Varian software standard default settings were kept for DOSY unless otherwise stated. The diffusion delay was increased to 200 ms, the number of increments was increased to 20, and the highest gradient value was set to 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. The alternate gradient sign on odd scans and lock gating during gradient portions were also selected. All Varian software standard default settings were kept for NOESY unless otherwise stated. The NOESY experiment was performed after setting the 90° pulse-width to 13.0 ms, d scale increment to 700 ms, and the t1 increment to 256. To acquire quality resolution, 16 scans were performed.
000. The alternate gradient sign on odd scans and lock gating during gradient portions were also selected. All Varian software standard default settings were kept for NOESY unless otherwise stated. The NOESY experiment was performed after setting the 90° pulse-width to 13.0 ms, d scale increment to 700 ms, and the t1 increment to 256. To acquire quality resolution, 16 scans were performed.
Quantum mechanical computations were used to predict the chemical shifts of each hydroxo proton in the clusters. The geometries of all of the clusters were obtained from the crystal structures, including the counterions. The NMR chemical shifts were computed using gauge-independent atomic orbital (GIAO) method in B3LYP/def2-SVP level of theory in the gas-phase, all as implemented in Gaussian03.63 Since the position of the counterions was not perfectly symmetric, we computed the chemical shifts for multiple counterion positions for each cluster structure, in order to eliminate the effects of static, individual counterion positions on the proton shifts. For example, for Ga8In5, with one external gallium, we computed the chemical shifts of 6 geometries of this cluster, one for each position the gallium could occupy relative to the counterion positions. Each computed shift for each type of proton was averaged across clusters of the same geometry discounting counterions, and the shifts were scaled using constant factors for each type.16
This particular method and procedure were chosen because exclusion of the counterions yielded incorrect ordering of the external and internal μ2-OH protons, regardless of geometry of the protons at any level of theory attempted by our hands. Initially, we fully optimized the entire cluster species, including the proton positions. However, the resulting structures deviated largely from the known symmetry of these structures as determined by NMR, yielding wildly varying values for the chemical shifts of identical proton types. In addition, it is important to note that the theoretical predictions of the proton spectra appeared uncannily consistent with experimental spectra, even with accounting for all peaks. However, upon deeper examination of the experimental spectra of the clusters, we have discovered that the internal and external μ2-OH signals were switched (see ESI†). Therefore, these were not used, and crystallographically determined positions were used instead. Bond lengths for the oxygen hydrogen bonds determined from crystallography may often be 0.2–0.3 Å short; however, we found that experimentally consistent and useful computed shift values could still be obtained in comparison to experiments, in contrast to results from DFT geometry optimizations.
Results and discussion
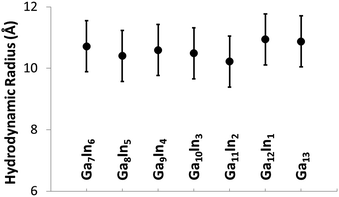
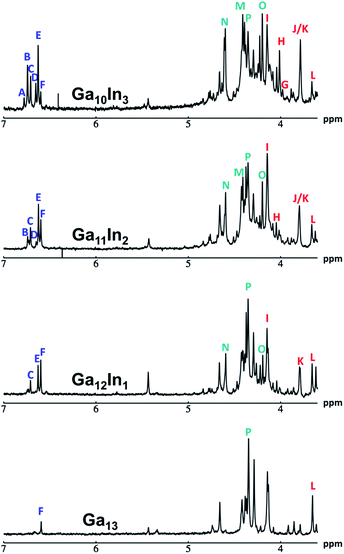
The mixed Ga13−xInx clusters each yield a unique 1H-NMR spectrum after one day in d6-DMSO solution (Fig. 7).64 The clusters were crystallographically resolved prior to 1H-NMR analysis to determine the stoichiometric ratio of the metal atoms. Diffusion Ordered Spectroscopy (DOSY) was used to verify the presence and integrity of clusters in solution (see ESI Fig. SI1–7†). The hydrodynamic radius of each heterometallic cluster matches that of Ga13 (Fig. 8), which was previously characterized using complementary techniques.2,65 The combination of consistent hydrodynamic radii and the absence of any other proton signals (other than solvent) suggest that the spectra of the clusters consist of bridging hydroxide and/or capping water ligand signals. The distinct combinations of resonances observed in each spectrum confirm that the heterometallic clusters exist as distinct species.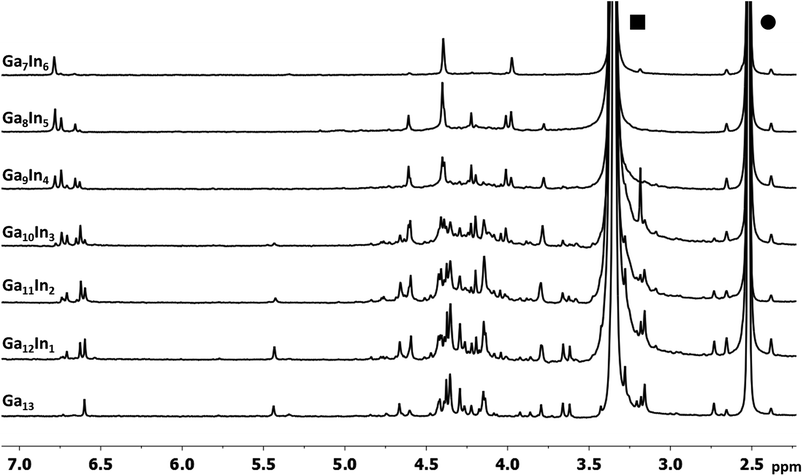 | ||
| Fig. 7 1H-NMR spectra of 2 mM clusters in d6-DMSO one day after dissolution. H2O peak (■) and DMSO peak (●). | ||
Understanding the symmetry of these Ga13−xInx clusters is essential for analyzing and assigning the proton shifts from NMR. The symmetry of each cluster dictates the number of expected signals that the cluster will have from the hydroxyl protons and aquo ligands. For example, the Ga7In6 and Ga13 clusters have identical symmetry, and therefore should only ideally yield three total signals from hydroxyl protons. Table 6 lists the symmetry of all Ga13−xInx clusters studied herein.
Water ligands coordinated to multimetallic Group 13 complexes are known to produce signals from 7–10 ppm.3 The Ga13−xInx clusters contain signals between 2.5 and 7 ppm, which falls into the range expected for μ2-OH and μ3-OH bridges. The spectrum of Ga7In6 is much simpler than that of the Ga13 cluster.2 We suspect this is due to the fact that the 1st order rate constant of water exchange for In(III) is 100× faster than for Ga(III) (4 × 104 s−1 and 4 × 102 s−1, respectively).66 The lack of peaks in the 7–10 ppm region indicates that the exchange rate of the outer water ligands is too fast to observe on the NMR time scale.2 The rapid aquo ligand exchange of the In(III) ions allows us to observe only the protons associated with the central 7-atom Ga(III) core of Ga7In6 leading to 3 signals (μ3-OH, μ2-OHext, and μ2-OHint) are observable. This aquo ligand exchange process happens much slower with gallium; therefore, the symmetry within the core of Ga13 is not retained and results in a complex spectrum containing more proton signals.
1. Ga7In6 peak assignments: establishing a basis for comparison
Ga7In6 is a great test case to understand the more complicated clusters where gallium occupies one or more of the peripheral metal sites. The simplicity of the experimental data and the high symmetry of this cluster makes this cluster ideal for the purpose of assigning regions of the spectrum to particular types of protons, which in turn may be used to assign shifts for the other clusters. This assignment was in turn used to determine an appropriate computational method for predicting the proton shifts of the remaining clusters. The computations resulted in subtle differences in the positions of the signals from different types of hydroxo bridges in the clusters, in particular, the μ2-OH region, which shows strong overlap of the two types of signals (Fig. 7). The μ3-OH proton signals are observed between 6.5 and 7.0 ppm. The remaining μ2-OHint and μ2-OHext proton signals are found between 3.5 and 5.0 ppm.
Ga7In6
1H-NMR spectra reveal 3 signals, which can be assigned to the three types of bridging hydroxides (Fig. 9). These three signals integrate to a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, matching the number of protons on specific hydroxide bridges within the 7-atom cluster core (μ3-OH
1 ratio, matching the number of protons on specific hydroxide bridges within the 7-atom cluster core (μ3-OH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μ2-OHext
μ2-OHext![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μ2-OHint ratio = 6
μ2-OHint ratio = 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6) (Fig. 1, Table 6). This suggests that the peak at 4.4 ppm corresponds to the μ2-OHext, which bridge between the 7-atom gallium core and the exterior indiums ions. Other examples of mixed metal Ga–(μ2-OH)–M bridges corroborate this assignment (Ga–(μ2-OH)–Ca and Ga–(μ2-OH)–Sr; 4.73 ppm and 4.49 ppm respectively).53 As stated above, the signal furthest downfield (∼6.8 ppm) corresponds to the protons of the μ3-OH, similar to the chemical shift of the μ3-OH bridge in the octahedral Y3+ complex.58 The final peak at 4.0 ppm represents the μ2-OHint protons. This assignment is in agreement with M–(μ2-OH)–M bridges reported for other Group 13 complexes.5,7–10
6) (Fig. 1, Table 6). This suggests that the peak at 4.4 ppm corresponds to the μ2-OHext, which bridge between the 7-atom gallium core and the exterior indiums ions. Other examples of mixed metal Ga–(μ2-OH)–M bridges corroborate this assignment (Ga–(μ2-OH)–Ca and Ga–(μ2-OH)–Sr; 4.73 ppm and 4.49 ppm respectively).53 As stated above, the signal furthest downfield (∼6.8 ppm) corresponds to the protons of the μ3-OH, similar to the chemical shift of the μ3-OH bridge in the octahedral Y3+ complex.58 The final peak at 4.0 ppm represents the μ2-OHint protons. This assignment is in agreement with M–(μ2-OH)–M bridges reported for other Group 13 complexes.5,7–10
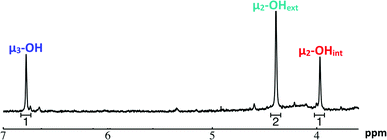 | ||
| Fig. 9 1H-NMR spectra of 2 mM Ga7In6 cluster in d6-DMSO one day after dissolution: the visible signals correspond to the 3 types of bridging hydroxides. | ||
Due to the simplicity of Ga7In6, the spectra and analysis for this cluster make a good basis for determining a suitable theoretical method for computational elucidation of the μ2-OH signals. Most importantly, computations performed without explicit counterions in the structure predict the exact opposite ordering of the internal and external μ2-OH signals. This was so, regardless of the theoretical methods (HF, B3LYP), basis sets (6-31G*67,68/LANL2DZ,69,70 def2-SVP,71 def2-TZVP,71 def2-QZVP,71etc.), or solvation methods (gas, COSMO,72 PCM,73 and CPCM74) employed. From our observations, improvements in levels of theory are unlikely to address the discrepancy. However, when counterions are included, correct ordering is obtained, namely that the μ2-OHext signals are downfield from the μ2-OHint protons (Fig. 9). These results indicate that the presence, location, and identity of the counterions is immensely important for determining even the qualitative assignments of 1H-NMR chemical shifts of aqueous metal clusters. The ordering or the μ2-OHint and μ2-OHext protons is more difficult to see for the remainder of the clusters due to significant overlap of μ2-OH signals, and computations were diagnostic in discriminating these convoluted overlapping signals in all the clusters.
2. Hydroxo ligand naming convention
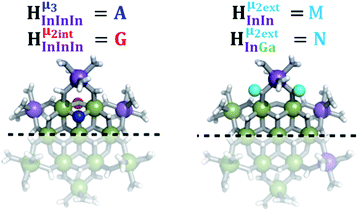
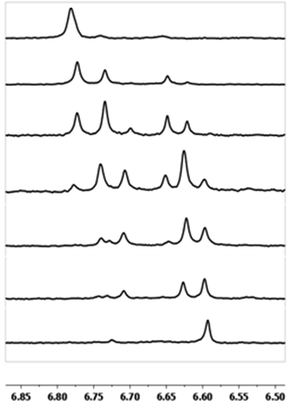
As gallium is substituted for indium in the exterior positions of the cluster, a greater number of proton types emerge (Fig. 6). There are 16 unique types of protons in the clusters based on idealized symmetry: 6 μ3-OH, 6 μ2-OHint, and 4 types of μ2-OHext (Table 6). The environments of these protons were determined by the identity of the nearest external metal ion and its two nearest neighbors (i.e., Ga or In). For example, proton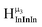 is a μ3-OH proton in a section of the cluster with an exterior indium ion directly outside (always indicated in bold) possessing two additional exterior indium atoms on either side (Fig. 10). Proton
is a μ3-OH proton in a section of the cluster with an exterior indium ion directly outside (always indicated in bold) possessing two additional exterior indium atoms on either side (Fig. 10). Proton  corresponds to the symmetry-equivalent μ2-OHint proton bridging the same metals as proton
corresponds to the symmetry-equivalent μ2-OHint proton bridging the same metals as proton 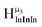 (Fig. 10). The μ2-OHext protons are described in a similar manner. Proton
(Fig. 10). The μ2-OHext protons are described in a similar manner. Proton  corresponds to the μ2-OHext proton connected to an indium ion (indicated in bold) and positioned facing towards a second indium. This naming system is comprehensively represented by Table 6.
corresponds to the μ2-OHext proton connected to an indium ion (indicated in bold) and positioned facing towards a second indium. This naming system is comprehensively represented by Table 6.
3. μ3-OH peak assignments
The peak in the 6.55–6.85 ppm region of the Ga7In6 spectrum corresponds to the μ3-OH protons. This region contains the simplest set of signals in all the mixed clusters. We suspect that this is because the μ3-OH protons are the farthest away from, and therefore, the least affected by the bound DMSO. Each peak in this region for the 7 NMR spectra is corresponds to one of the 6 types of μ3-OH protons (Table 7). Proximity to the indium ion causes downfield shifting in the proton signal. This is best shown in Ga7In6, which has one type of proton , and exhibits the farthest downfield signal. Ga13 also has only one type of μ3-OH proton
, and exhibits the farthest downfield signal. Ga13 also has only one type of μ3-OH proton 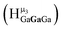 ; however, the lack of indium atoms in the structure leads to the farthest upfield μ3-OH signal. Ga8In5 and Ga12In1 each possess one isomer and 3 unique μ3-OH proton types (
; however, the lack of indium atoms in the structure leads to the farthest upfield μ3-OH signal. Ga8In5 and Ga12In1 each possess one isomer and 3 unique μ3-OH proton types (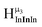 ,
,  ,
, 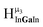 and
and 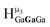 ,
, 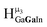 ,
,  , respectively) in 3
, respectively) in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratios. This is mirrored in the NMR spectra facilitating the assignment of each proton type to a peak (Table 7). Ga9In4, Ga10In3, and Ga11In2 are slightly more complicated because each has 3 possible isomers (Table 6), but each predicted μ3-OH peak is observed. The
1 ratios. This is mirrored in the NMR spectra facilitating the assignment of each proton type to a peak (Table 7). Ga9In4, Ga10In3, and Ga11In2 are slightly more complicated because each has 3 possible isomers (Table 6), but each predicted μ3-OH peak is observed. The 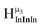 type protons are shifted farthest downfield, while the
type protons are shifted farthest downfield, while the 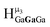 type protons are shifted the farthest upfield, for an overall ranking from highest to lowest ppm of
type protons are shifted the farthest upfield, for an overall ranking from highest to lowest ppm of 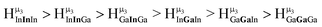 (Table 7). Computations support that these signals are produced by μ3-OH protons and that the
(Table 7). Computations support that these signals are produced by μ3-OH protons and that the 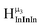 ,
,  , and
, and  protons should be more deshielded than the
protons should be more deshielded than the 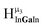 ,
, 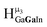 , and
, and 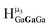 protons. The calculations cannot corroborate or contradict the relative rankings within those two sets (Table 7).
protons. The calculations cannot corroborate or contradict the relative rankings within those two sets (Table 7).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 isomeric ratio)
1 isomeric ratio)
In the case of clusters with multiple isomers, the peak integrations of the μ3-OH protons in the NMRs can provide information about the ratio of each isomer present in the sample. The statistical probability of each isomer, along with the calculated % present in solution, is shown in Table 8. Similarities in the structures of Ga9In4 and Ga11In2 allow for comparisons.75 The NMR data remarkably show a strong correlation to the statistical ratio of isomeric heterometallic clusters. This data indicates that no specific substitution pattern of indium in the outer shell of the clusters is kinetically favorable.
4. μ2-OH peak assignments
The μ2-OH regions of the NMR spectra are not as easily deconvoluted. Based on the Ga7In6 spectrum, the upfield peaks correspond to μ2-OH bridges, but as more gallium atoms are introduced into the outermost shell and exchange between the coordinating water ligands and DMSO slows, symmetry is broken, and complexity increases. We now propose to assign these peaks as well. As with the μ3-OH protons, computations were used to establish the range in which the μ2-OH protons should be found.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio
1 ratio  . The μ2-OHext appear in an 8
. The μ2-OHext appear in an 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio
2 ratio  , making it difficult to differentiate between protons
, making it difficult to differentiate between protons  and
and  . However, Nuclear Overhauser Effect Spectroscopy (NOESY) correlates protons that are near each other through space. The μ3-OH protons are 3.34 Å and 3.24 Å away from the neighboring μ2-OHext bridges in the solid state. Since the μ3-OH and μ2-OHext bridges are significantly less than 5 Å,76 they exhibit strong through-space interactions allowing
. However, Nuclear Overhauser Effect Spectroscopy (NOESY) correlates protons that are near each other through space. The μ3-OH protons are 3.34 Å and 3.24 Å away from the neighboring μ2-OHext bridges in the solid state. Since the μ3-OH and μ2-OHext bridges are significantly less than 5 Å,76 they exhibit strong through-space interactions allowing  and
and  to be assigned using NOESY (Fig. 12).
to be assigned using NOESY (Fig. 12).
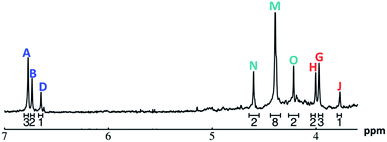 | ||
Fig. 11 The 1H-NMR of 2 mM Ga8In5 in d6-DMSO 1 day after dissolution with peak assignment. 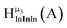 , , 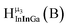 , , 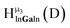 , , 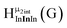 , , 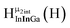 , , 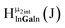 , , 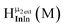 , ,  , ,  . . | ||
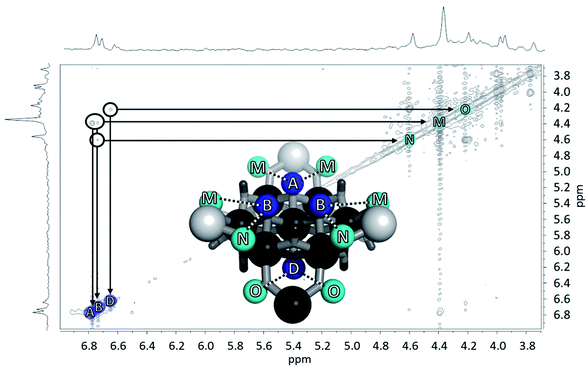 | ||
Fig. 12 The NOESY of Ga8In5 indicating the proper peak assignment of the  , , 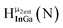 , and , and 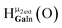 protons. Water ligands have been omitted from the structure for clarity. ● Gallium, ○ indium, protons. Water ligands have been omitted from the structure for clarity. ● Gallium, ○ indium, 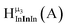 , , 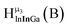 , , 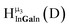 . . | ||
The use of these experimental results allowed for additional verification of quantum mechanical methods. The assignments based on integration values and the NOESY spectra established a basis of comparison for determining the most accurate computational method. Using the average computed NMR shifts from the structures with counterions for each proton type, the computed results were compared to the experimentally determined proton shifts for several basis sets, as mentioned previously. The def2-SVP basis set was found to provide the optimal combination of accuracy and computational time, as the computed proton rankings were an exact match with experimental results. Therefore, we know this computational method can be used to assign the protons in the more complicated spectra with a larger number of isomers and an increasing number of gallium centers.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. This means that the protons in Ga9In4 integrate to the ratios shown in Table 8. Based on these integrations, peaks have been experimentally assigned to the Ga9In4 spectrum (Fig. 13). Peaks
1 ratio. This means that the protons in Ga9In4 integrate to the ratios shown in Table 8. Based on these integrations, peaks have been experimentally assigned to the Ga9In4 spectrum (Fig. 13). Peaks  ,
,  , and
, and  are the same as for Ga8In5. Proton
are the same as for Ga8In5. Proton  which integrates to 1 is too small to identify in the baseline noise between 3.7 and 4.8 ppm. The peak for proton
which integrates to 1 is too small to identify in the baseline noise between 3.7 and 4.8 ppm. The peak for proton  overlaps with
overlaps with  giving an integration of 5 for the combined signal. There should still be a strong signal at 4.4 ppm from
giving an integration of 5 for the combined signal. There should still be a strong signal at 4.4 ppm from  for Ga9In4; however, an integration of 14 suggests that proton
for Ga9In4; however, an integration of 14 suggests that proton 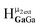 also appears at this chemical shift. Interestingly, the signal for proton
also appears at this chemical shift. Interestingly, the signal for proton  seems to have split into two peaks at ∼4.2 ppm. This is most likely due to the slower exchange rate of the outer water ligands on gallium. Because
seems to have split into two peaks at ∼4.2 ppm. This is most likely due to the slower exchange rate of the outer water ligands on gallium. Because  is bridging an outer gallium atom this may be the first sign of the complex spectrum we see for Ga13. This may also explain the small shoulder/splitting of peak
is bridging an outer gallium atom this may be the first sign of the complex spectrum we see for Ga13. This may also explain the small shoulder/splitting of peak  and
and 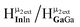 .
.
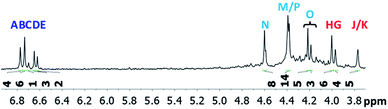 | ||
Fig. 13 The 1H-NMR of 2 mM Ga9In4 in d6-DMSO 1 day after dissolution with experimental peak assignment. 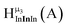 , , 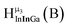 , , 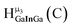 , , 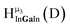 , ,  , , 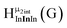 , , 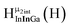 , , 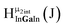 , , 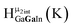 , , 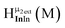 , , 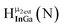 , , 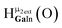 , , 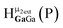 . . | ||
Computations are particularly useful for corroborating the assignments in the spectra of Ga9In4. Because many of the peaks overlap with others, the integrations are no longer solely reliable for making full assignments. Therefore, the relative values of the computed NMR shifts were used alongside the known assignments from Ga7In6 and Ga8In5 for the most precise results. This allowed for the  and
and 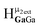 peaks to be distinguished, as well as the
peaks to be distinguished, as well as the  and
and  peaks (Fig. 14). For the
peaks (Fig. 14). For the  and
and 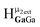 peaks, computations showed that the
peaks, computations showed that the  peak should have a slightly downfield chemical shift compared to
peak should have a slightly downfield chemical shift compared to 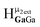 . Likewise, the computed shift for the
. Likewise, the computed shift for the  was compared to the signals from the other internal and external μ2-OH protons. This analysis showed that I should have the farthest downfield shift of the internal μ2-OH protons, but should not be higher than any of the external μ2-OH protons. After determining the identity of the peaks in the Ga9In4 spectrum, this method was used to further assign the peaks in the spectra of the clusters with increasing gallium content.
was compared to the signals from the other internal and external μ2-OH protons. This analysis showed that I should have the farthest downfield shift of the internal μ2-OH protons, but should not be higher than any of the external μ2-OH protons. After determining the identity of the peaks in the Ga9In4 spectrum, this method was used to further assign the peaks in the spectra of the clusters with increasing gallium content.
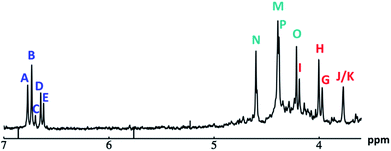 | ||
Fig. 14 The 1H-NMR of 2 mM Ga9In4 in d6-DMSO 1 day after dissolution with computed peak assignment. 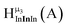 , , 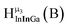 , , 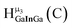 , , 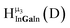 , ,  , , 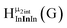 , , 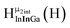 , ,  , , 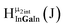 , , 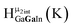 , , 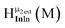 , , 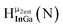 , , 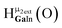 , , 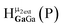 . . | ||
While these computations were successful in reproducing the relative ordering of proton signals, the present method is not sufficient to quantitatively reproduce the exact proton shifts. This is because this method does not rely on quantum mechanically determined positions of the counterions with respect to the clusters. Quantitative predictions will necessitate a more rigorous method for determining the cluster–counterion complex. We suspect that the success of our method in being able to reproduce qualitative ordering of the proton peaks suggests that the counterions are loosely coordinated around the cluster and is dynamically equilibrating among the different sites in the NMR time scale. Work is continuing in this area to produce quantitative predictions from ab initio molecular dynamics simulations with explicit counterions and solvents.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio leading to the peak integrations listed in Table 8. Unfortunately, the complexity caused by the increasing number of exterior gallium atoms and the isomers does not allow these signals to be assigned experimentally. Similar issues arise for Ga11In2 to Ga13. Given the complexity of the signals arising from the protons in these clusters, computations are particularly useful for peak assignment.
1 ratio leading to the peak integrations listed in Table 8. Unfortunately, the complexity caused by the increasing number of exterior gallium atoms and the isomers does not allow these signals to be assigned experimentally. Similar issues arise for Ga11In2 to Ga13. Given the complexity of the signals arising from the protons in these clusters, computations are particularly useful for peak assignment.
Computed shifts were used to assign the remaining types of protons for each of these clusters (Fig. 15). Unfortunately, we are unable to compute the changes based on coordinated DMSO breaking the symmetry; therefore, only the peaks of the “mother cluster” (fully H2O ligated) can be assigned in these spectra. Primarily, this involved computing the position of 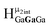 , which represents the protons in a section of the cluster with three external gallium ions next to each other. Computed results suggest that
, which represents the protons in a section of the cluster with three external gallium ions next to each other. Computed results suggest that 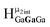 should have the lowest shift of all of the internal μ2-OH protons, which is the lowest ppm value for all of the computed signals.
should have the lowest shift of all of the internal μ2-OH protons, which is the lowest ppm value for all of the computed signals.
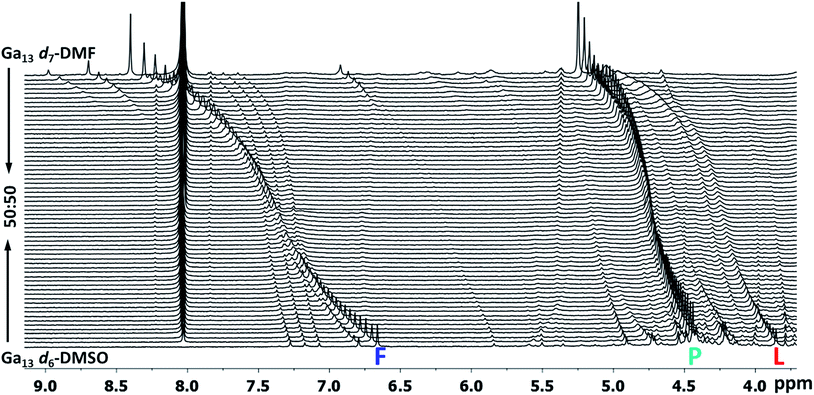 | ||
Fig. 16 Stacked titration data indicating that only the 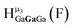 , ,  , and , and 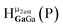 protons translate from the 100% d6-DMSO to the 100% d7-DMF spectrum. The triplet that persists in the 7.0 to 7.5 ppm region is attributed to ammonia in the sample.77 protons translate from the 100% d6-DMSO to the 100% d7-DMF spectrum. The triplet that persists in the 7.0 to 7.5 ppm region is attributed to ammonia in the sample.77 | ||
The Ga13 mother cluster peaks 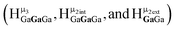 assigned via computations were thereafter confirmed experimentally. By plotting the 1H-NMR spectra of Ga13 dissolved in a variety of ratios of d6-DMSO and d7-DMF, it is clearly visible that only 3 peaks persist from 100% d6-DMSO to 100% d7-DMF (Fig. 16). The other peaks visible in the spectra are caused by “daughter clusters” substituted with either DMSO or DMF ligands at the aquo sites; therefore, the only shared species must be the mother cluster.
assigned via computations were thereafter confirmed experimentally. By plotting the 1H-NMR spectra of Ga13 dissolved in a variety of ratios of d6-DMSO and d7-DMF, it is clearly visible that only 3 peaks persist from 100% d6-DMSO to 100% d7-DMF (Fig. 16). The other peaks visible in the spectra are caused by “daughter clusters” substituted with either DMSO or DMF ligands at the aquo sites; therefore, the only shared species must be the mother cluster.
Conclusion
This research has led to quick and cost effective differentiation and structural characterization of the Ga13−xInx clusters in solution via1H-NMR spectrscopy.77 We have shown that each mixed Ga13−xInx cluster does independently exist in solution and that there are no kinetically or enthalpically favored isomers (i.e., only the expected statistical ratios of the various isomers were observed). These isomers exist in statistical ratios determined by probability of formation. In general, this study provides a complete method for experimentally and computationally predicting proton shifts for inorganic μ3-OH and μ2-OH signals in gallium and indium species, as well as, a literature review of hydroxide bridges for all diamagnetic metals available in the literature to the best of our knowledge. This knowledge will initiate the study of cluster dynamics in solution, allowing for better control and manipulation of precursor clusters. The solution behavior of clusters condensing into films is a primary interest of this research; however, inorganic cluster species are not only relevant to the thin film and electronics markets. Many small clusters, including the Ga13−xIn13 clusters have structures much like fragment of minerals. The reverse process, bulk material breaking down into smaller components (i.e. minerals dissolving in acid rain) is a promising environment for locating dynamic clusters. It is possible that a plethora of clusters form naturally as minerals dissolve, but we have had no way of detecting these intermediate molecules. Geoscience may be greatly affected by the use of 1H-NMR for the observation of inorganic –OH bridges. Al13 Keggin and calcium carbonate clusters have both been detected in nature.78,79 It would be beneficial for the geoscience community to investigate water samples from streams, caves, hot springs, geysers, and ocean vents for the presence of these observable hydroxo bridges. 1H-NMR research on completely inorganic systems is limited, but this study shows that it can lead to a variety of information previously thought to be inaccessible.Acknowledgements
This work was generously supported by the NSF Center for Sustainable Materials Chemistry (CHE-1102637). University of Oregon NMR facilities are supported by NSF CHE-0923589. DWJ is a Scialog Fellow of Research Corporation for Science Advancement and gratefully acknowledges additional support provided to assist this project. PHYC is the Vicki & Patrick F. Stone Scholar of Oregon State University and gratefully acknowledges financial support.Notes and references
- R. J. Abraham, J. Fisher and P. Loftus, Introduction to NMR Spectroscopy, John Wiley & Sons Ltd, New York, 1988 Search PubMed.
- A. F. Oliveri, M. E. Carnes, M. M. Baseman, E. K. Richman, J. E. Hutchison and D. W. Johnson, Angew. Chem., Int. Ed., 2012, 51, 10992–10996 CrossRef CAS PubMed.
- J. W. Akitt, J. E. Elders, X. L. R. Fontaine and A. K. J. Kundu, J. Chem. Soc., Dalton Trans., 1989, 1889–1895 RSC.
- B. Y. A. Fratiello, R. E. Lee and R. E. Schuster, Inorg. Chem., 1969, 82–85 Search PubMed.
- M. C. Read, J. Glaser, M. Sandstrom and I. Toth, Inorg. Chem., 1992, 31, 4155–4159 CrossRef CAS.
- A. Fratiello, S. Peak, R. Schuster and D. J. Davis, J. Phys. Chem., 1970, 74, 3730–3734 CrossRef CAS.
- J. W. Akitt and J. M. J. Elders, J. Chem. Soc., Dalton Trans., 1988, 1347–1355 RSC.
- J. R. Houston, B. L. Phillips and W. H. Casey, Geochim. Cosmochim. Acta, 2006, 70, 1636–1643 CrossRef CAS PubMed.
- G. S. Papaefstathiou, A. Sofetis, C. P. Raptopoulou, A. Terzis, G. Spyroulias and T. F. J. Zafiropoulos, J. Mol. Struct., 2007, 837, 5–14 CrossRef CAS PubMed.
- P. Hodge and B. Piggott, Chem. Commun., 1998, 4, 1933–1934 RSC.
- S. Ogo, N. Makihara and Y. Watanabe, Organometallics, 1999, 18, 5470–5474 CrossRef CAS.
- K. M. Carlson-Day, J. L. Eglin, L. T. Smith and R. J. Staples, Inorg. Chem., 1999, 38, 2216–2220 CrossRef CAS PubMed.
- Z. L. Mensinger, J. T. Gatlin, S. T. Meyers, L. N. Zakharov, D. A. Keszler and D. W. Johnson, Angew. Chem., Int. Ed., 2008, 47, 9484–9486 CrossRef CAS PubMed.
- Z. L. Mensinger, W. Wang, D. A. Keszler and D. W. Johnson, Chem. Soc. Rev., 2012, 41, 1019–1030 RSC.
- M. K. Kamunde-Devonish, M. N. Jackson, Z. L. Mensinger, L. N. Zakharov and D. W. Johnson, Inorg. Chem., 2014, 53, 7101–7105 CrossRef CAS PubMed.
- M. N. Jackson, L. A. Wills, I.-Y. Chang, M. E. Carnes, L. F. Scatena, P. H.-Y. Cheong and D. W. Johnson, Inorg. Chem., 2013, 52, 6187–6192 CrossRef CAS PubMed.
- W. G. Jackson, J. A. McKeon, M. Zehnder, M. Neuberger and S. Fallab, Chem. Commun., 2004, 6, 2322–2323 RSC.
- D. Schweinfurth, J. Klein, S. Hohloch, S. Dechert, S. Demeshko, F. Meyer and B. Sarkar, Dalton Trans., 2013, 42, 6944–6952 RSC.
- I. Bernal, J. Cetrullo and S. J. Berhane, Coord. Chem., 2000, 52, 185–205 CrossRef CAS PubMed.
- N. Juranic and S. Macura, Inorg. Chim. Acta, 2000, 298, 103–106 CrossRef CAS.
- P. Angus, D. Fairlie, R. Gunasingam, Z. Tao and W. G. Jackson, Inorg. Chim. Acta, 1993, 209, 123–127 CrossRef CAS.
- J. W. Akitt and R. H. J. Duncan, J. Chem. Soc., Faraday Trans. 1, 1980, 76, 2212 RSC.
- J. a. Tossell, J. Magn. Reson., 1998, 135, 203–207 CrossRef CAS PubMed.
- J. P. Canal, M. Jennings, G. P. A. Yap and R. K. Pomeroy, Dalton Trans., 2008, 1375–1382 RSC.
- S. M. T. Abedin, K. A. Azam, M. B. Hursthouse, S. E. Kabir, K. M. A. Malik, R. Miah and H. J. Vahrenkamp, Organomet. Chem., 1998, 564, 133–141 CrossRef.
- J. Ruiz, C. Vicente, J. Marti, N. Cutillas, G. Garcia and G. J. Lopez, Organomet. Chem., 1993, 460, 241–248 CrossRef CAS.
- G. Lopez, J. Ruiz, G. Garcia, C. Vicente, J. Casab, E. Molins and C. Miravitlles, Inorg. Chem., 1991, 30, 2605–2610 CrossRef CAS.
- G. Sanchez, J. Serrano, J. Garcia, G. Lopez, J. Perez and E. Molins, Inorg. Chim. Acta, 1999, 287, 37–46 CrossRef CAS.
- V. M. Nosova, Y. A. Ustynyuk, L. G. Bruk, O. N. Temkin, A. V. Kisin and P. A. Storozhenko, Inorg. Chem., 2011, 50, 9300–9310 CrossRef CAS PubMed.
- J. L. Serrano, I. J. S. Fairlamb, G. Sánchez, L. García, J. Pérez, J. Vives, G. López, C. M. Crawforth and R. J. K. Taylor, Eur. J. Inorg. Chem., 2004, 2706–2715 CrossRef CAS PubMed.
- A. Bandini, G. Banditelli, M. A. Cinellu, G. Sanna, G. Minghetti, F. Demartin and M. Manassero, Inorg. Chem., 1989, 28, 404–410 CrossRef CAS.
- P. Bergamini, S. Sostero, O. Traverso, T. J. Kemp and P. G. J. Pringle, J. Chem. Soc., Dalton Trans., 1989, 2017–2021 RSC.
- B. Longato, D. Montagner, G. Bandoli and E. Zangrando, Inorg. Chem., 2006, 45, 1805–1814 CrossRef CAS PubMed.
- A. Bandini, G. Banditelli, F. Demartin, M. Manassero and G. Minghetti, Gazz. Chim. Ital., 1993, 123, 417–423 CAS.
- J. Schneider, J. Hagen, N. Czap, C. Kruger, S. Mason, R. Bau, J. Ensling, P. Gutlich and B. Wrackmeyer, Chem.–Eur. J., 2000, 6, 625–635 CrossRef CAS.
- L. Dostál, J. Taraba and R. J. Jambor, Organomet. Chem., 2009, 694, 1251–1253 CrossRef PubMed.
- R. Zhang, Q. Zhang, Y. Shi and C. J. Ma, Organomet. Chem., 2006, 691, 1668–1672 CrossRef CAS PubMed.
- C. Ma, J. Li, R. Zhang and L. J. Qiu, J. Mol. Struct., 2007, 830, 1–7 CrossRef CAS PubMed.
- C. Eychenne-Baron, F. Ribot, S. Nathalie and C. Sanchez, Organometallics, 2000, 19, 1940–1949 CrossRef CAS.
- S. Mishra, S. Daniele, L. G. Hubert-Pfalzgraf and E. Jeanneau, Eur. J. Inorg. Chem., 2007, 15, 2208–2215 CrossRef PubMed.
- E. Asato, H. Furutachi, T. Kawahashib and M. J. Mikuriyab, J. Chem. Soc., Dalton Trans., 1995, 3897–3904 RSC.
- D. L. Reger, A. E. Pascui, P. J. Pellechia and M. D. Smith, Inorg. Chem., 2013, 52, 11638–11649 CrossRef CAS PubMed.
- A. Tarushi, F. Kastanias, V. Psycharis, C. P. Raptopoulou, G. Psomas and D. P. Kessissoglou, Inorg. Chem., 2012, 51, 7460–7462 CrossRef CAS PubMed.
- W. Teng, M. Guino-o, J. Hitzbleck, U. Englich and K. Ruhlandt-Senge, Inorg. Chem., 2006, 45, 9531–9539 CrossRef CAS PubMed.
- F. A. Cotton, L. M. Daniels, G. T. Jordan, C. Lin and C. A. Murillo, Inorg. Chem. Commun., 1998, 1, 109–110 CrossRef CAS.
- P. Rosendorfer and W. Beck, Chem. Ber., 1995, 128, 729–734 CrossRef CAS PubMed.
- J. Cook, J. Hamilin, A. Nutton and P. M. J. Maitlis, J. Chem. Soc., Dalton Trans., 1981, 2342–2352 RSC.
- D. Walther, B. Ritter, H. Gorls and G. Z. Zahn, Z. Anorg. Allg. Chem., 1997, 623, 1125–1130 CrossRef CAS PubMed.
- R. Zhang, C. Li, Q. Wang and M. Chunlin, Struct. Chem., 2010, 21, 745–753 CrossRef CAS.
- R. J. Wehmschulte, J. M. Steele and M. A. Khan, Organometallics, 2003, 22, 4678–4684 CrossRef CAS.
- M. Stender and P. P. Power, Polyhedron, 2002, 21, 525–529 CrossRef CAS.
- D. F. Jones, P. H. Dixneuf, A. Benoit and J. Le Marouille, Inorg. Chem., 1983, 22, 29–33 CrossRef CAS.
- Y. J. Park, S. A. Cook, N. S. Sickerman, Y. Sano, J. W. Ziller and A. S. Borovik, Chem. Sci., 2013, 4, 717–726 RSC.
- A. Preetz, W. Baumann, H.-J. Drexler, C. Fischer, J. Sun, A. Spannenberg, O. Zimmer, W. Hell and D. Heller, Chem.–Asian J., 2008, 3, 1979–1982 CrossRef CAS PubMed.
- L. Wang, T. Sheng, J. Zhang, S. Hu, R. Fu, X. Wu, Y. Li, X. Huang and S. Xiang, Polyhedron, 2007, 26, 1098–1104 CrossRef CAS PubMed.
- M. Vasiliu, K. E. Knope, L. Soderholm and D. A. J. Dixon, J. Phys. Chem. A, 2012, 116, 6917–6926 CrossRef CAS PubMed.
- S. Mishra, E. Jeanneau, S. Daniele and L. G. Hubert-Pfalzgraf, CrystEngComm, 2008, 10, 814–816 RSC.
- S. Mishra, L. G. Hubert-Pfalzgraf, S. Daniele, M. Rolland, E. Jeanneau and B. Jouguet, Inorg. Chem. Commun., 2009, 12, 97–100 CrossRef CAS PubMed.
- J. Martinez, I. Aiello, A. Bellusci, A. Crispini and M. Ghedini, Inorg. Chim. Acta, 2008, 361, 2677–2682 CrossRef CAS PubMed.
- P. G. Parzuchowski, J. W. Kampf, E. Roźniecka, Y. Kondratenko, E. Malinowska and M. E. Meyerhoff, Inorg. Chim. Acta, 2003, 355, 302–313 CrossRef CAS.
- H. Hoveyda, S. Rettig and C. Orvig, Inorg. Chem., 1993, 32, 4909–4913 CrossRef CAS.
- W. Wang, K. M. Wentz, S. E. Hayes, D. W. Johnson and D. A. Keszler, Inorg. Chem., 2011, 50, 4683–4685 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez, and J. A. Pople. Gaussian, 2004 Search PubMed.
- Data is shown for clusters in solution one day after dissolution because this is the relative amount of time it takes for the outer ligand shell to equilibrate with incoming DMSO ligands of solvation at room temperature.
- A. F. Oliveri, E. W. Elliott, M. E. Carnes, J. E. Hutchison and D. W. Johnson, ChemPhysChem, 2013, 14, 2655–2661 CrossRef CAS PubMed.
- The Group 13 Metals Aluminium, Gallium, Indium, and Thallium: Chemical Patterns and Peculiarities, ed. AldridgeS. and DownsA. J., A John Wiley and Sons, Ltd., Chichester, 2011, pp. 52–55 Search PubMed.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS PubMed.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS PubMed.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 1, 1993, 2, 799–805 RSC.
- B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 106, 5151–5158 CrossRef CAS PubMed.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- Due to a small impurity in Ga11In2, the spectra could not accurately be integrated; therefore, the experimental percentages were not calculated.
- T. D. W. Claridge, High-Resolution NMR Techniques in Organic Chemistry, Elsevier, Oxford, 2nd edn, 2009, pp. 303–334 Search PubMed.
- M. E. Carnes, C. C. Knutson, A. Nadarajah, M. N. Jackson, A. F. Oliveri, K. M. Norelli, B. M. Crockett, S. R. Bauers, H. A. Moreno-Luna, B. N. Taber, D. J. Pacheco, J. Z. Olson, K. R. Brevick, C. E. Sheehan, D. W. Johnson and S. W. Boettcher, J. Mater. Chem. C, 2014, 2, 8492–8496 RSC.
- G. Furrer, B. L. Phillips, K.-U. Ulrich, R. Pöthig and W. H. Casey, Science, 2002, 297, 2245–2247 CrossRef CAS PubMed.
- D. Gebauer, A. Völkel and H. Cölfen, Science, 2008, 322, 1819–1822 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sc00776c |
| This journal is © The Royal Society of Chemistry 2015 |