Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A multiscale approach to the adsorption of core–shell nanoparticles at fluid interfaces
Adrienne
Nelson
a,
Dapeng
Wang†
b,
Kaloian
Koynov
b and
Lucio
Isa
*a
aDepartment of Materials, ETH Zürich, Zürich, Switzerland. E-mail: lucio.isa@mat.ethz.ch; Fax: +41 44 633 10 27; Tel: +41 44 633 63 76
bMax Planck Institute for Polymer Research, Ackermannweg 10, D-55128 Mainz, Germany
First published on 27th October 2014
Abstract
Self-assembly of colloidal particles at liquid–liquid interfaces is a process with great potential for the creation of controlled structures, due to the trapping of the particles in the plane of the interface combined with their lateral mobility. Here we present a multiscale characterisation of the adsorption and interfacial behaviour of core–shell iron oxide–poly(ethylene glycol) nanoparticles at a water–n-decane interface using three complementary, in situ, methods, which span many different length scales. First, dynamic interfacial measurements are taken to follow the adsorption of particles from the bulk aqueous phase to the interface. The mechanical properties of the interface are then probed using micron-sized tracers in probe-particle tracking and nano-tracers in fluorescence correlation spectroscopy. The results show that the rate of particle adsorption to the interface scales with the square of bulk concentration, as predicted by a recent model. In addition, we show that despite full monolayers of nanoparticles forming, the interface remains unexpectedly fluid, with only a slowing of tracer particle mobility but no evidence of interface jamming as seen for hard nanoparticles. Our results illustrate that nanoparticles stabilised by soft, extended polymeric shells, display distinct features at fluid interfaces that can be harnessed for the fabrication of functional materials.
1 Introduction
Nanoparticle monolayers at the interface between two fluids are materials with high potential in a vast range of technologies. Their use has been demonstrated in the production of functional membranes and capsules1–5 and in surface patterning applications,6 as well as in the stabilisation of foams and emulsions.7,8 Functional nanoparticle building blocks can impart novel properties to the final nanostructured materials, and are of interest in fields such as tailored magnetic materials,9 plasmonics,10,11 optical materials (e.g. mirrors with tunable surface plasmon resonance and electrical conductance12 and moth-eye anti-reflection structures13), biosensing,6 electronic memory,14 photonics15 and oil recovery.16Interfacial nanoparticle monolayers can be obtained using two main strategies. The first, leading to so-called Langmuir monolayers, consists of directly depositing a particle film onto the interface with the aid of a spreading solvent, which is either immiscible and volatile for liquid–gas interfaces (e.g. hexane or chloroform for air–water interfaces), or highly miscible with the liquids for the liquid–liquid case (e.g. alcohols). The main advantage of preparing Langmuir monolayers is that a controlled number of particles can in principle be inserted at the interface, making it possible to have a system with externally controlled surface concentration and thereby suited for well-defined mechanical and thermodynamic characterisation (e.g. compression isotherms in a Langmuir trough).
In practice however, this relies on the assumption that all of the injected particles are effectively trapped at the interface during spreading. While this is true for insoluble monolayers, e.g. hydrophobic NPs spread at an air–water interface, partial solubility in the subphases or weak binding to the interface may ultimately lead to reduced control of the surface concentration and thus limited reproducibility. Moreover, the use of spreading solvents has been demonstrated to alter the wetting properties (i.e. contact angle) of particles at fluid interfaces17,18 and the preparation of Langmuir monolayers is not feasible in many relevant practical situations, e.g. in the case of foams and emulsions.
The alternative strategy, the creation of so-called Gibbs monolayers, goes instead via the spontaneous adsorption to the interface of nanoparticles initially dispersed in one of the bulk fluid phases. The main advantages of this approach are common to all self-assembly processes: the process is parallel, spontaneous and driven by thermodynamics and thus, at least in theory, facile and reproducible. Spontaneous adsorption is therefore the preferred option in many cases, including the fabrication of capsules and particle-stabilised emulsions using microfluidics.19–21
In spite of the ideal simplicity, spontaneous adsorption of interfacial monolayers with controlled microstructure can in reality be far from trivial. As pointed out in detail in a recent review article by Garbin and coworkers,22 spontaneous adsorption can only take place under specific circumstances. First and foremost, adsorption has to be energetically favourable; when a nanoparticle adsorbs at a fluid interface, the free energy of the particle in one bulk phase combined with that of the pure interface needs to be compared to the free energy of the particle at the interface, exposing part of its surface to the second fluid and “cutting a hole”23 in the pure interface. Given the typical high energies associated with fluid interfaces, the balance is often tipped towards adsorption.
Even if energetically favourable, adsorption can be complicated by kinetic effects. In fact barriers to adsorption can be present, due to electrostatic, solvation and steric effects.22 Regarding the latter, further adsorption at the interface can be hindered or slowed down by the presence of other particles already adsorbed at the interface. In this case, new particles can adsorb only if large enough spaces are available at the interface and the time scale for adsorption becomes then coupled to the timescale for the creation of these voids, i.e. to the dynamics of the particles already at the interface.24
In order to obtain an interface with a desired microstructure, the interactions between the nanoparticles at the interface need to be controlled. Using small nanoparticles capped with functional ligands (surfactants, polymers or bio-molecules) gives one great flexibility to tailor the final structure and material properties. For instance, magnetic particles with hydrophobic coatings of the right length can be embedded in lipid vesicles for triggered release9,25,26 or silica particles stabilised by different amounts of cationic surfactants can be used to invert oil-in-water emulsions.27
Using stabilisers to tune particle adsorption and interactions has, on the contrary, the drawback of significantly complicating the thermodynamic description of particle adsorption. If the length scale of the stabilisers is comparable to the particle size, the details of the interaction of the ligands with the interface and with the two fluid phases, i.e. the core–shell nature of the NPs, can no longer be ignored. Various numerical simulations and experimental studies have shown that, if the stabilising shell is deformable and surface-active, this causes an accumulation of the ligands at the interface and deformation of the shell.28 In this situation, even the notion of the wetting or contact angle of the particle becomes ill-defined and the composite, core–shell nature of the particle plays a key role.
For solid spherical particles, neglecting gravity and line tension effects, the trapping energy of a single particle at a fluid interface, i.e. the energy, ΔE, required to remove the particle from the interface into the bulk oil phase (positive sign in brackets) or into the aqueous phase (negative sign) is given by:
ΔE = πR2γow(1 ± cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)2 θ)2 | (1) |
Du and co-workers verified the R2 scaling of the adsorption energy of polystyrene NPs, measuring the steady state value of the apparent interfacial tension of particle-laden interfaces, assuming particle size and hexagonal close-packing at the interface.30 Recent modelling work, has instead shown that for core–shell particles, the scaling of eqn (1) breaks down and the particle size is substituted by an effective size depending on the full details of the polymer solubility into the two phases.31 For this reason, the development of alternative methods where ΔE can be directly measured, without any assumptions, is a continuing and highly important pursuit.32,33
The directed formation of controlled Gibbs monolayers using core–shell NPs therefore requires a thorough investigation of the kinetics and energetics of NP adsorption. In addition, another fundamental, but mostly neglected, aspect in determining the structural evolution of interfacial NP assemblies is the characterisation of their rheological and mechanical properties. One of the features that makes particle self-assembly at fluid interfaces such an attractive process is that despite the trapping in the direction perpendicular to the plane of the interface, the NPs retain lateral mobility within the interface plane, as opposed to binding at solid–liquid interfaces. This allows the NPs to move, release internal strains and gradients and evolve towards equilibrium microstructures. The absence of lateral mobility, stemming from attractive interactions, clustering or steric effects can on the other hand freeze the interface into non-equilibrium structures, such as 2D gels34 or glasses35,36 with very different viscoelastic properties.
In this paper we perform a thorough characterisation of the adsorption and mechanical properties of Gibbs monolayers of composite, core–shell iron oxide–poly(ethylene glycol) (PEG) NPs at a water–n-decane interface using three complementary experimental techniques that bridge from the millimeter scale of a droplet used for dynamic interfacial tension measurements, through the micron scale of probe-particle tracking, to the nanometer scale of fluorescence correlation spectroscopy used to measure nanoparticle mobility at the interface.
2 Experimental
2.1 Nanoparticles
Nanoparticles were produced in house,37 consisting of an 8.4 ± 1.4 nm diameter superparamagnetic iron oxide core surrounded by a PEG shell of varying thickness and architecture. Here we focus on three particle batches: two sets of linear PEG with molecular weights of 2737 and 5557 g mol−1 (named L2.5 and L5, respectively) and a second generation dendritic PEG with molecular weight 2477 g mol−1 (termed D2.5). In previous work using X-ray reflectivity, we have directly demonstrated that these nanoparticles spontaneously adsorb at a water–n-decane interface with a small, but detectable protrusion into the oil phase.382.2 Pendant drop tensiometry
PDT experiments were performed with a drop shape analysis system (DSA100, Krüss, Germany). 30 μl droplets of the aqueous NP suspension (in MilliQ water, R = 18.2 Ω, TAC ≤ 6 ppb) were produced directly inside n-decane (99%, Sigma-Aldrich). The n-decane was cleaned before use to remove surface-active impurities. The n-decane was passed five times through a basic alumina column39 and the purity confirmed by measuring the dynamic interfacial tension of a pure water–decane interface over a period of 15 hours, with a reduction of γ of less than 5% being termed clean. During each experiment, several aqueous droplets were passed through the oil phase to sequester any remaining impurities and the measurements were started only when the values of γ were within a 0.5 mN m−1 tolerance over a 3 min time window. Both the short- and longtime measurements were repeated for consistency and to detect any presence of drift due to contamination.The droplets were produced at the tip of a stainless steel needle (diameter 1.80 mm) at a rate of 200 μl min−1, at room temperature and imaged with a CCD camera as a function of time. At such formation rates in n-decane, inertia effects do not play a significant role; i.e. oscillations and drift in the droplet profile are absent. The droplet profile was detected automatically with an analysis software (DSA3, Krüss) and fitted with the Laplace–Young equation40 to obtain the interfacial tension (γ) as a function of time; the accuracy in determining γ from each image is 0.1 mN m−1. Experiments were completed on all samples at three frame rates (12.5 Hz, 0.25 Hz and 0.025 Hz) over different time scales (3 minutes, 3 hours and 15 hours, respectively). In some cases measurements were performed additionally at lower frequencies over time scales up to 48 hours. In this way both the fast initial adsorption dynamics and the long-time evolution were captured.
2.3 Probe-particle tracking
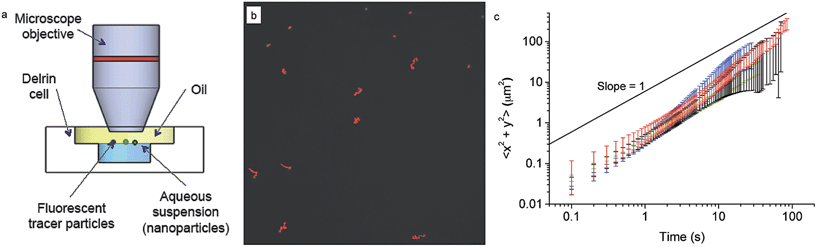
The rheological properties of the interface on the microscale were investigated by tracking the motion of monodisperse polystyrene fluorescent tracers (diameter 2.8 ± 0.2 μm, labelled with FITC, PS-Fluo Particles, Microparticles GmbH, Germany) at the interface in a custom-designed cell using an upright microscope and a 40× immersion lens, as shown in Section 3.2.The sample cell is made of Delrin with a chamber of diameter 5 mm and depth 5 mm. The cell was placed within a glass crystallisation dish and the chamber filled with the NP in milliQ suspension. Purified decane (as above) was gently poured over the cell to create an interface, while filling the surrounding dish and covering the cell to a depth of approximately 4 mm. The interface between the NP-containing aqueous suspension and n-decane was made first and then 5 μl of the 0.25% w/v tracers was injected directly at the interface, to ensure sufficient tracers were present at the interface. The tracers were repeatedly washed in MilliQ water to ensure that no surface-active impurities were present. Trapping of the tracers at the interface is confirmed by the fact that they only move visibly within the interface plane, without going out of focus. This finding has also been confirmed by freeze-fracture cryo-scanning electron microscopy imaging, which unequivocally shows tracers trapped at the interface. We waited a sufficient amount of time to ensure that a full monolayer of core–shell NPs adsorbed at the interface from the bulk and then started tracking the motion of the fluorescent tracers.
A typical image from within a measurement is shown in Section 3.2, as an illustration of ideal tracer particle density, so that there are enough for statistical analysis and removal of drift, while they are sufficiently far apart to avoid interactions with each other. The red lines indicate the trajectories followed by each particle during a 500 frame video.
Videos of the tracers at the interface were analysed using the IDL particle tracking code of Crocker and Grier41 available on the internet42 to track the tracer particles over time. Drift in the videos was removed from the tracking, along with any tracer aggregates. From the particle tracks, their mean squared displacements were calculated and subsequently D‖, the value of the tracers in-plane diffusion coefficient at the interface in the presence of NPs, was calculated using the equation below:
| 〈x2 + y2〉 = 4D‖t | (2) |
Data sets generally contained 5–10 particles and were 200–1000 frames long, with frame rates varying between 20 fps and 0.5 fps, to cover short and long time behaviour. We emphasise here that these microscopy measurements are only able to measure D‖ and not the diffusion coefficients of the tracers in the direction transverse to the interface. Previous studies have demonstrated that the two can differ significantly when a particle crosses a fluid interface.43 In any case, given the high interfacial adsorption energies of the tracers, we expect them to be trapped in a deep potential well transverse to the interface, and thus to only exhibit limited motion in that direction.44
2.4 FCS
Water-soluble quantum dots (QDot®585 ITK™Carboxyl Quantum Dots) with a diameter of 10.8 ± 1.0 nm purchased from Invitrogen were used as tracer nanoparticles. Their surface is modified with carboxyl-derivatised amphiphilic molecules.The experiments were performed following a procedure described in detail in ref. 45. Briefly, the water–n-decane interfaces were prepared in an Attofluor cell chamber (Invitrogen, Leiden, Netherlands) with a thin microscope cover glass base. An aluminum foil O-ring with inner diameter of 5 mm and thickness of approximately 0.3 mm was fixed on the cover glass to restrict the sample volume and surface. This O-ring was first filled with a PEG-ylated nanoparticle solution (which contained also tracer QDs with a concentration of roughly 10−10 M) to a height of approximately 100 μm. Then, the n-decane phase (100 μL) was carefully added on top of the aqueous phase. The QDs adsorbed to the interface with a typical surface coverage of 0.1–1.0 μm2 per particle. The QDs were used at a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-fold dilution compared to the initial stock solution, so that the effect of any residual surface-active impurity from synthesis is negligible.
000-fold dilution compared to the initial stock solution, so that the effect of any residual surface-active impurity from synthesis is negligible.
Fluorescence Correlation Spectroscopy (FCS) measurements were carried out using a commercial setup (Carl Zeiss, Germany) comprising the module ConfoCor2 and an inverted microscope Axiovert 200. The fluorescent particles were excited by a HeNe laser (543 nm) focused at the interface (Fig. 5a) by a water-immersion microscope objective, C-Apochromat 40×, NA 1.2 (Carl Zeiss, Germany). The fluorescent light was collected by the same objective, passed through a confocal pinhole and a LP585 long-pass emission filter, and finally directed to an avalanche photodiode detector that enabled single-photon counting. This arrangement results in the formation of a confocal detection volume Vd around the laser focus. The detection volume has a 3D Gaussian shape and typical dimension of approximately 300 nm in the radial direction and 1.5 μm in the normal direction46 Only the fluorescence originating from species within Vd can be delivered to and detected by the avalanche photodiode detector.
The confocal detection volume was scanned through the interface (in 200 nm steps) by moving the microscope objective mounted on a high-precision electromechanical stage. No fluorescence could be detected if Vd was moved away from the interface (Fig. 5b), which indicates that there were negligibly few QDs diffusing in the bulk aqueous or n-decane phases. In previous work it was also demonstrated that the diffusion coefficient of the QD tracers at different interfaces scales with the viscosity of both the aqueous and the oil phases, giving a clear evidence that the tracers are trapped at the interface and are immersed in both liquids.45 As a next step, Vd was positioned exactly at the interface, i.e. at the height of maximum fluorescence intensity. The fluctuations δF(t) = F(t) − 〈F(t)〉 of the fluorescence intensity F(t) caused by the interfacial diffusion of the tracer QDs through the confocal detection volume were recorded and evaluated in terms of an autocorrelation function G(t) = 〈δF(t′)δF(t′ + t)〉/〈δF(t′)〉2 (Fig. 5c). For each data point, the autocorrelation curves were recorded for 60 seconds; data sets influenced by occasional large aggregates were excluded. The experiments were repeated on different days with freshly prepared samples.
For the case of two-dimensional Brownian diffusion considered here the FCS autocorrelation function has the form:46
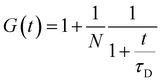 | (3) |
3 Results and discussion
3.1 Pendant drop tensiometry
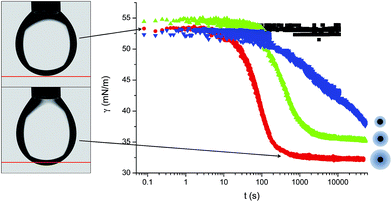
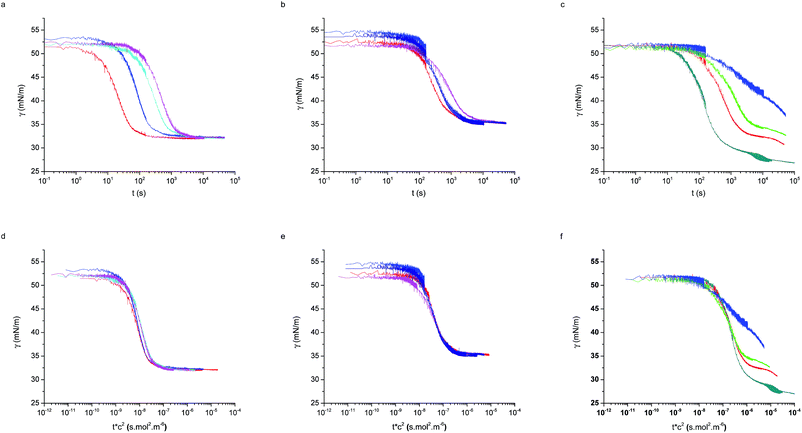
The macroscopic adsorption behaviour of the particles was investigated by measuring the apparent interfacial tension, γ, of a droplet of an aqueous suspension of the NPs in n-decane, using a pendant drop tensiometer. As NPs diffuse from the bulk of the droplet and adsorb at the interface, they effectively reduce γ resulting in a modification of the droplet profile. Therefore, by fitting the droplet profile with the Laplace–Young equation as a function time, we can follow the kinetics of NP adsorption. Fig. 1 shows the characteristic behaviour previously reported for those particles.31 At short times γ decreases relatively slowly due to the adsorption of single NPs onto a pristine interface (akin to the low surface pressure rise in the gas phase of a compression isotherm). When the surface concentration of NPs increases, the apparent interfacial tension drops more rapidly (linked to the steeper increase of surface pressure in a liquid phase), followed by a slow adsorption phase, corresponding to very high surface coverage, approaching saturation. In the absence of NPs in the bulk, the interfacial tension of the pure liquids remains constant over time. As indicated by Fig. 1, the time scales for the different adsorption regimes depend on the nature of the polymer shell stabilising the NPs. In particular, we observed that for a concentration of 1 × 10−5 mol m−3 the particles stabilised by the dendrimers do not reach steady state. Multiple concentrations were therefore investigated for all three NP types to monitor adsorption over different timescales and elucidate the effects of bulk concentration on the adsorption kinetics.Fig. 2 shows the adsorption curves for the three particle types and for varying bulk concentrations. Fig. 2a–c report the raw data, while the Fig. 2d–f show that a master curve can be obtained for each particle type, by appropriately normalising the adsorption time with a characteristic, concentration-dependent time scale. The characteristic time is found to scale quadratically with the concentration.
In order to understand where such dependence originates from, we investigated in detail the kinetics of particle adsorption following a recent model proposed by Bizmark et al.48 These authors identified a model for NP adsorption that is based on previous results for surface-active molecules49–51 or nanoparticles,52 but that explicitly takes into account the fact that NPs can show irreversible binding at interfaces, with trapping energies easily exceeding 102–103kBT. In particular, two limiting adsorption regimes exist, at short and long times. At short times, t → 0, an individual NP adsorbing to the interface sees no other particles there, rather experiencing a pristine interface. Assuming that there is no barrier to adsorption at the interface, the adsorption is Fickian, i.e. the rate of diffusion of the particles through the bulk is the rate-limiting factor. In this regime, the time dependence of the apparent interfacial tension obeys the following equation:
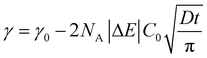 | (4) |
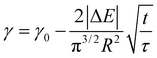 | (5) |
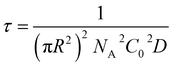 | (6) |
From this we can observe that indeed the characteristic time scale for interfacial tension reduction scales with the square of the concentration. We note here that particle diffusion close to the interface may be different to bulk diffusion due to wall effects.53 Such deviations are expected to appear at distances from the interface comparable to the particle radius, but the presence of a solvated polymer shell around the particle complicates the hydrodynamics of the problem, making it difficult to estimate accurately this effect. For simplicity's sake, we neglect the occurrence of such effects; in any case, they will have the effect of rescaling the characteristic time scale for particle adsorption.
On the other hand, at long times t → ∞, adsorbing NPs experience an already crowded interface. In order to allow the adsorption of an additional particle, those already residing at the interface must rearrange to make space. The rate of this rearrangement is determined by the mobility of the particles within the interface, i.e. the diffusion coefficient at the interface, rather than in bulk as in the case of eqn (5). Previous reports for NPs stabilised by rigid, short and hydrophobic ligands have demonstrated that interface diffusion coefficients can drop to between 10 and 104 times the bulk values (in water or oil as appropriate),45,54,55 when the viscosities of the two phases are similar. However, data presented later in the FCS results for our soft, hydrophilic, core–shell NPs show that diffusion at a crowded interface drops to, at the minimum, 30% of the bulk value and to approximately 40% of the value at a pristine interface.
The slowing of adsorption can effectively be accounted for by introducing a blocking function (as described by Adamczyk56). The blocking function can be combined with existing equations to give the following description of long-time behaviour:48
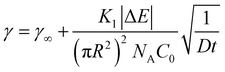 | (7) |
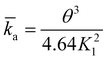 | (8) |
![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) a the dimensionless adsorption constant. Even though the time dependence of γ has changed, the characteristic time scale can still be rescaled by C02.
a the dimensionless adsorption constant. Even though the time dependence of γ has changed, the characteristic time scale can still be rescaled by C02.
Again, this can be rearranged with the same τ as above to give:
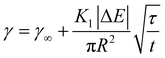 | (9) |
ka = ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) aDNAC0πR2 aDNAC0πR2 | (10) |
As seen in Fig. 2 the two linear-PEG-coated particle batches display analogous behaviour, also consistent with those measured by Bizmark et al.48 for other particle types. The dendritic-coated particles follow instead a more complex behaviour, which will be described later. First we will consider the particles of type L5 and L2.5 and use the previously described models to characterise the adsorption parameters.
Fig. 3, shows that the short-time and the long-time values of γ follow the 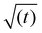 and
and 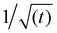 dependencies predicted by eqn (5) and (9), respectively. This behaviour has also been confirmed by interfacial tension measurements carried out by microfluidics, in addition to conventional pendant drop tensiometry.57 We emphasise again the fact that analytical expressions for the time evolution of the interfacial tensions exist only in these two limiting cases; the rest of the adsorption curves cannot be fitted by the functions introduced above.
dependencies predicted by eqn (5) and (9), respectively. This behaviour has also been confirmed by interfacial tension measurements carried out by microfluidics, in addition to conventional pendant drop tensiometry.57 We emphasise again the fact that analytical expressions for the time evolution of the interfacial tensions exist only in these two limiting cases; the rest of the adsorption curves cannot be fitted by the functions introduced above.
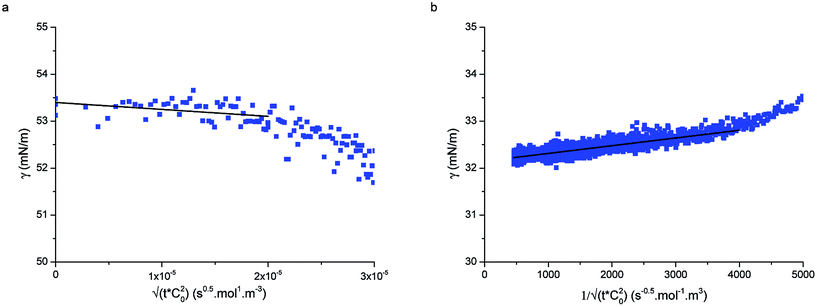 | ||
| Fig. 3 (a) Short-time and (b) long-time fitting of adsorption curves using eqn (5) and (9), respectively for particle type L5 at concentration 1 × 10−5 mol m−3. | ||
Fig. 3a displays an example of the short-time adsorption curve, here for particles L5 at concentration 1 × 10−5 mol m−3 after the shift onto the master curve. The values of the bulk diffusion coefficient in Table 1 were calculated from the Stokes–Einstein relation for the previously measured hydrodynamic radii of the particles in water38 and the viscosity of water at room temperature. Using these values we were able to fit the data in Fig. 3a and extract the adsorption energies of the particles to the interface. Given that all other prefactors in eqn (5) are known, ΔE is the only fitting parameter (since the fits are done on the shifted curves, the bulk concentration does not enter the fit). Table 1 reports the values of the adsorption energies and of the diffusion coefficients for particle types L5 and L2.5 and compares them with literature values measured by an independent technique.33 The measured values here are in close agreement with the values reported by Zell et al. and are of the order of 1000kBT, reinforcing our view that these particles adsorb irreversibly at the interface (unless mechanically forced out). Possible sources of the discrepancies with the surface pressure measurements of Zell et al. may be stemming from errors in determining precisely the hydrodynamic radius of our core–shell particles or from inaccuracies in determining the surface concentration in ref. 33.
| D (m2 s−1) | ΔE (microtensiometer) | ΔE (PDT) | |
|---|---|---|---|
| L5 | 1.45 × 10−11 | 1930 ± 250kBT | 1230 ± 120kBT |
| L2.5 | 1.90 × 10−11 | 1160 ± 110kBT | 860 ± 160kBT |
| D2.5 | 2.57 × 10−11 | — | 790 ± 130kBT |
Fig. 3b shows the long-time adsorption curve for the same sample as in Fig. 3a. Using the results of the previous fit and the known inputs, here the only fitting parameter is the dimensionless reaction coefficient K1. From eqn (8), assuming a saturation interface packing of 91% (close-packed), we can calculate the kinetic constant ka.
Using the following relation, it was possible to calculate an approximate value for the interaction energy or adsorption barrier, ϕb, between the pristine interface and an individual particle adsorbing:58
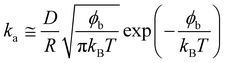 | (11) |
The values of ϕb in Table 2 are very small, of the order of 10kBT compared to adsorption energies of approximately 1000kBT, indicating that the assumption made at small times, that the adsorption is barrier-free, is valid.
| K 1 (—) | k a (m s−1) | ϕ b (kBT) | |
|---|---|---|---|
| L5 | 0.049 ± 0.009 | 7.9 × 10−6 ± 3.8 × 10−6 | 5.6 ± 0.5 |
| L2.5 | 0.08 ± 0.03 | 1.5 × 10−6 ± 0.4 × 10−6 | 7.6 ± 0.4 |
| D2.5 | 0.387 | 1.5 × 10−7 | 10.6 |
We remark here that the assumption of 0.91 as the final interface coverage is strongly dependent on the particle size distribution and adsorption kinetics. Nevertheless, recent computer simulations24 demonstrated that the overall adsorption mechanism is very robust, regardless of the details of the particles used. Therefore, we expect that, even if the absolute values of the reaction constants are slightly different, our result effectively captures the two different adsorption regimes, as well as the dependence on bulk concentration.
After discussing the details of the linear PEG-stabilised NPs, we turn our attention again to the dendrimer-stabilised NPs. The D2.5 particles show a more complex behaviour, presenting a shoulder in the adsorption curve. Previously the presence of such shoulders has been attributed to the occurrence of collective rearrangements that enable further adsorption to an interface that is jammed at short times due to rapid adsorption.24 In this case, the height of the intermediate adsorption plateau was only a very weak function of the bulk concentration.31
The difference with the D2.5 particles may be ascribed to the presence of a small, but non-negligible charge on the particle surface of −9.8 mV compared to −1.4 mV and −3.2 mV for L5 and L2.5 respectively.37 The greater surface charge compared to the L2.5 particles stems from lesser shielding of the core surface charge by the shorter and stiffer dendritic PEG molecules, compared to the linear PEG of a similar molecular weight. At longer times, the presence of a charged interfacial layer of already adsorbed D2.5 NPs may act as an additional adsorption barrier. Nevertheless, at short times, when these collective particle–particle interaction effects are absent, the adsorption curves can be effectively rescaled and eqn (5) used to estimate the single-particle adsorption energy, which had not been previously possible using other methods.
Using the results of the short time fit, we also calculated the reaction constants for the data set using the long time fit. As only one of the pendant drop curves seemed to approach the final plateau, calculations were made using the data set with concentration 4 × 10−5 mol m−3. The fitting parameters were used to calculate ka, K1 and ϕb as shown in Table 2. The values for ϕb are in good agreement with those from the linear-PEG coated particles, indicating that the interaction between these particles and the pure interface is analogous to that described previously.
3.2 Probe-particle tracking
After investigating the details of the adsorption kinetics, we focus our attention on the rheological characterisation of the interfacial assemblies. As previously mentioned, the mechanical properties of the interface are crucial for a range of applications, and therefore many different methods have been devised to carry out such measurements.59 The mechanical properties of the interfacial NP monolayers were here initially studied by means of passive microrheology/probe-particle tracking.60 The details of the procedure are given in the materials and methods section, but briefly, the method consists of extracting the viscoelastic properties of the nanoparticle-laden interface by following the motion of micron-sized fluorescent tracer particles (see Fig. 4a and b). The method presents marked advantages compared to standard rheological approaches, in that it is very sensitive to low interfacial viscosities and that the properties of the interface are measured at a local level, which is very important in the presence of heterogeneous interfaces.61,62Fig. 4c shows the mean square displacement of the tracer particles as a function of time for tracers at the pristine water–n-decane interface as well as at oil–water interfaces with a saturated NP monolayer for all the three particle types. The saturation of the interface was ensured by waiting times significantly longer than the characteristic times found in the adsorption curves in Fig. 2. The linear behaviour with a slope of unity, in a log–log plot, indicates purely diffusive tracer behaviour, with a diffusion coefficient that can be extracted using eqn (2). The tracers exhibited purely diffusive motion both at the pure oil–water interface and in the presence of a NP monolayer, excluding the presence of any detectable interface elasticity.
Moreover, the mean squared displacements did not seem to depend significantly on the type of particles composing the interfacial monolayer or even on whether the particles were present at all. All the data are basically overlapping within errors (please note that at higher times the error bars increase due to lower statistics) meaning that tracer diffusivity at the interface is not affected by the presence of a NP monolayer. The measured values of the diffusion coefficient were 1.2 ± 0.2 × 10−9 cm2 s−1 in comparison with the calculated Stokes–Einstein bulk diffusion coefficient of 1.7 × 10−9 cm2 s−1. Previous studies have demonstrated that at low surface coverage, if the tracers are not interacting and are trapped at the interface, they undergo two-dimensional Brownian diffusion.63 The ratio between the bulk and the interface diffusion coefficients that we measured is indeed indicating that the prefactor in the diffusion coefficient goes from 6 to 4, as the particles effectively diffuse in two dimensions and no longer in three. Previous theoretical work has predicted that the presence of a free interface, and thus of a significant viscosity difference between the two phases, can significantly slow the in-plane particle diffusion; in our case, since the difference in viscosity between water and n-decane is lower than 5%, the particle practically sees a uniform environment, and thus does not experience the increased flow resistence.43 Therefore, tracers could only be slowed down by the presence of a full core–shell NPs monolayer surrounding them, but the technique is not sensitive enough to detect it. The main reason for this lack of sensitivity is probably to be found in the fact that the tracers may be too large for the presence of a weak particle monolayer to affect their motion. For this reason we moved to a different technique, using tracers on the same scale as the adsorbing NPs, as described in the following section.
3.3 FCS
Using fluorescence correlation spectroscopy (FCS) we measured the diffusion coefficient of small fluorescent tracers at the oil–water interface during the adsorption of our core–shell nanoparticles. As tracers we used carboxyl quantum dots (QDs) with diameter of approximately 10 nm purchased from Invitrogen (see Experimental section for details). As previously shown and evidenced in Fig. 5b, when dispersed at very low concentrations in the water phase these QDs adsorb and accumulate at the water–n-decane interface. During an FCS experiment one measures the fluorescence intensity fluctuations resulting from the thermal motion of the fluorescent tracers through a small observation volume formed around the focus of a confocal microscope.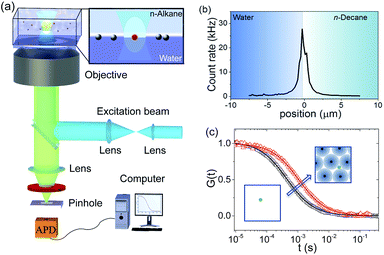 | ||
| Fig. 5 (a) Schematic of the FCS setup. (b) A fluorescence intensity scan through a water–n-decane interface on which QDs are adsorbed. Scanning was carried out by moving the focus from water into the n-decane phase in steps of 200 nm. The position of the maximum identifies the position of the interface. (c) Typical FCS autocorrelation curves at the interface and their fits (solid lines) following eqn (3) for QDs diffusing at a pristine water–decane (black squares) and a water–decane interface with a monolayer of L5 NPs adsorbed suspension of concentration 2 × 10−5 mol m−3 (red triangles). | ||
Akin to a dynamic light scattering experiment, these fluctuations are evaluated in the form of an autocorrelation curve that has a characteristic decay time directly related to the diffusivity of the tracers.46,64 As depicted in Fig. 5, here the method was specifically applied to measure the lateral diffusion coefficient of the QD tracers at the n-decane–water interface.45,65 The adsorption of the core–shell iron oxide–PEG particles from the bulk is followed indirectly by monitoring the change of the QD tracers' diffusivity at the interface as a function of time and thus the interfacial concentration of the core–shell iron oxide–PEG particles.
Typical examples of FCS autocorrelation curves measured at the interface at different adsorption times are shown in Fig. 5c. These curves can be fitted well (solid lines, Fig. 5c) with eqn (3) (Experimental section), indicating single-component Brownian diffusion of the QD probes. From the fits, the corresponding values of the tracers' diffusion coefficient were obtained. As opposed to the previous probe-particle tracking measurements, FCS has sufficient sensitivity to capture the change of the tracers' diffusivity as a function of NP content at the interface, for all NP types.
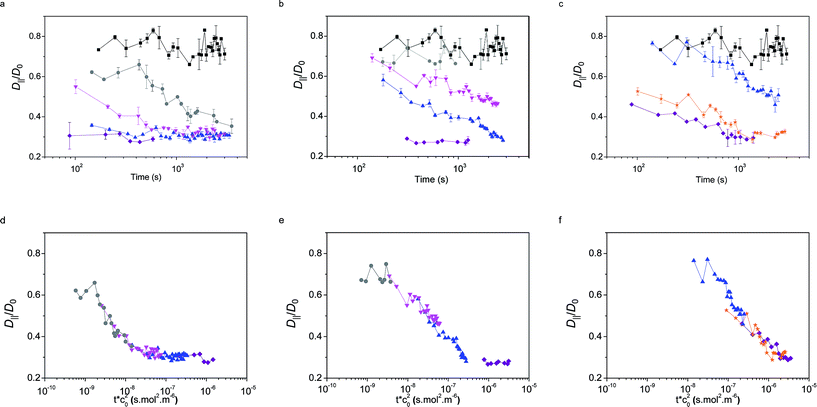
The values of the QDs' interfacial diffusion coefficients D‖, normalised by their bulk diffusion coefficient (D0 = 4.2 × 1011 m2 s−1 as measured independently by FCS in bulk water), as a function of time are plotted in Fig. 6a–c. The black data points represent the case of the pristine oil–water interface; it can be seen that these values are time-independent, and smaller than 1, indicating that the diffusion of the QDs is slower at the interface than in the bulk, despite the viscosity of the decane and water being very similar. This is consistent with previous observations.45
The coloured symbols give the values of D‖/D0 as a function of time for varying initial bulk concentrations of core–shell NPs for the three particle types L5, L2.5 and D2.5.
The general observed trend was that D‖ decreased as a function of time with the adsorption of NPs; this change was more pronounced at higher concentrations, up to a point where a plateau was reached and D‖ did not reduce further (saturation may not be reached for the D2.5 particles within experimental timescales). This corresponds to the point at which a full monolayer is formed, no further NPs adsorb to the interface and the diffusivity of the tracers reaches a steady state.
Several observations can be made from this data. Firstly, in all cases, the fitting of the autocorrelation curve indicates that tracers' mobility remains purely diffusive at all times and concentrations, including in the presence of a full monolayer. This result coincides with the findings of the probe-particle tracking experiments, albeit on a much smaller length scale. This has the surprising consequence that the interface remains liquid-like, without showing any sign of elasticity characteristic of a glassy or crystalline structure.36,66–68
The second remarkable fact emerging from the data is that the values of the tracer diffusivity at full coverage are only 30% of the diffusivity in the bulk and approximately 40% of the tracer diffusivity on the pristine interface. This result is in stark contrast with the findings of particle diffusivity in dense interfacial monolayers of hydrophobic NPs stabilised by short and rigid ligands.55 In the latter case, reductions up to four orders of magnitude were found. The main difference may arise from the loss of colloidal stability and aggregation of the particles with short ligands at the interface.
In fact, as previously discussed, the requirements for colloidal stability in the bulk and at the interface can be different, with the latter typically being more stringent.22 Cryo-TEM images of the adsorption of the above-mentioned hydrophobic NPs at various stages, indeed show that the realisation of an interfacial monolayer proceeds via the formation of NPs clusters that subsequently merge to form a gel-like spanning network.69 This implies NP aggregation at interfaces and the formation of an elastic, arrested interface. In the case of our hydrophilic core–shell NPs, previous measurements have demonstrated that even at saturation, the vast majority of the interface is covered by PEG chains, leaving highly spaced iron oxide cores at the interface,38 as depicted in the sketch in Fig. 5. Moreover, measurements of the desorption energy of PEG chains from an air–water interface, showed that each single ethylene glycol (EG) unit is bound with an energy of 0.15kBT and that whole chains as well as whole particles can be desorbed upon compression.33 Similar values are expected at the water–n-decane interface. It is therefore possible that the local fluctuations in the compressive state of the particle shells coming from the thermal motion of QDs, or even more pronounced from that of the micron-sized tracers, are sufficient to push some PEG sections of the polymer shell into the bulk water. As a result, the fluidity of the interface is retained and the tracers can diffuse freely, albeit more slowly, in the presence of NPs at the interface. Therefore, the softness of the polymer shell and its solubility in the bulk play a crucial role in defining the mechanical properties of the particle-laden interface.
The time and concentration dependence of D‖ in Fig. 6 for the three particle types suggests that concentration-independent master curves can be drawn as a function of an effective time for each particle type. Using the adsorption model and the scaling previously described for the dynamic interfacial tension data, we obtain that the tracer diffusivity at the interface can also be rescaled by the bulk concentration squared, as observed in Fig. 6d–f. This finding further confirms the adsorption model for the adsorption kinetics.
4 Conclusions
In this paper we have demonstrated a comprehensive approach to investigate the formation and the mechanical properties of monolayers composed of hydrophilic core–shell iron oxide–polymer NPs at fluid interfaces. Our experiments span length scales over several orders of magnitude. We first elicited the adsorption kinetics and measured the adsorption energy of single NPs via monitoring the dynamic interfacial tension of macroscopic droplets. We emphasise that the latter quantity is measured directly, without any assumption of particle size or coverage at the interface, from the early stages of diffusion-dominated particle adsorption and that this matches values previously and independently found. From the analysis of the pendant drop tensiometry data, we could also extract additional information on the adsorption constants and barriers, shedding additional light on the mechanisms of interface formation. We then moved to the mechanical characterisation of the particle-laden interfaces using both tracers which are much larger than the adsorbed NPs and other tracers in the same size range as the NPs. Through FCS measurements we could follow in real time the modification of the particle diffusivity at the interface as a function of NP adsorption and we verified that the scaling of the adsorption kinetics measured by macroscopic interfacial tension is matched by the nanoscale dynamic characterisation of interface mechanics.Our findings also highlighted that our interfaces remain fluid, even at full NP coverage, which is a result strikingly different to the behaviour of interfaces covered by proteins70 or, as previously discussed, hydrophobic NPs capped by short ligands, and which has a direct impact on tuning the mechanical properties of such interfaces. The outcome of the probe-particle tracking and of the FCS measurements indeed unexpectedly indicates that the interfaces always show a fully viscous response. Translating probe particle diffusivity into surface viscosities has been investigated theoretically,71 but still presents significant open experimental challenges and orders of magnitude differences may be found between macro and microrheological characterisations of complex fluid interfaces.72,73 There is still open debate on the true origins of this discrepancies; among the different factors, theoretical predictions for instance make the assumption that the interface is incompressible, while recent measurements on the NPs used in this study show that interfacial monolayers can be compressed to varying extents and that compression can also cause the NPs to desorb.33 The fluidity of the monolayers may be directly related to the soft nature of the polymer shell surrounding the particles; the polymer layer provides sufficient steric stabilisation so that the particles do not aggregate at the interface74 and are able to move as single objects rather than clusters. Furthermore, the softness of the polymer chains may also make it possible that upon local compression, stemming from in-plane NP thermal motion, they can be partially and temporarily desorbed from the interface (single EG units have an adsorption energy comparable to thermal energy, while the NP as a whole stays bound with much higher energy), allowing more space for particles to “squeeze past each other”, even in crowded environments, such as full monolayers. This behaviour may be analogous to the one of soluble surfactants that, despite significantly lowering the interfacial tension, do not exhibit any measurable surface viscosity.75 It is worth emphasising that X-ray reflectivity data show that at saturation more than 90% of the interface is actually occupied by PEG chains for both the linear PEG-stabilised NPs.38 For the dendritic PEG particles, both the X-ray reflectivity and FCS measurements may have not reached full saturation in the experimental time window, and their adsorption behaviour is more complex, as evidenced by the pendant drop measurements. It would be extremely interesting for future studies to access systems where interface activity and softness can be varied over a large range, to detect the onset of deviations from purely viscous interfaces. Recent numerical simulations are indeed going into the direction of calculating explicit interaction potentials between soft particles at interfaces as a function of parameters such as chain length, grafting density and solvent quality.76
The use of soft, deformable nanoscale objects for interfacial self-assembly and stabilisation is rapidly growing. In addition to the above-mentioned properties, using polymer shells makes it also possible to encode different functions in the stabilising layer, e.g. for triggered response77 or multi-functional capping that adapts to local environments.78 Our results constitute a step further in the understanding of the complexity of interfacial adsorption and assembly of such versatile intriguing objects.
Acknowledgements
The authors thank Nicholas D. Spencer, Emanuela Del Gado, Konrad Schwenke and Erik Reimhult for stimulating discussions. LI acknowledges the SNSF grants PZ00P2_142532/1 and PP00P2_144646/1 for financial support. AN acknowledges financial support from ETH Zurich. KK acknowledges the financial support of DFG (SFB 1066, Q2).References
- F. Caruso, Science, 1998, 282, 1111–1114 CrossRef CAS.
- F. Tiarks, K. Landfester and M. Antonietti, Langmuir, 2001, 17, 908–918 CrossRef CAS.
- A. D. Dinsmore, M. F. Hsu, M. G. Nikolaides, M. Marquez, A. R. Bausch and D. A. Weitz, Science, 2002, 298, 1006–1009 CrossRef CAS PubMed.
- H. Xu and W. A. Goedel, Langmuir, 2002, 18, 2363–2367 CrossRef CAS.
- Y. Lin, H. Skaff, A. Böker, A. D. Dinsmore, T. Emrick and T. P. Russell, J. Am. Chem. Soc., 2003, 125, 12690–12691 CrossRef CAS PubMed.
- L. Isa, K. Kumar, M. Müller, J. Grolig, M. Textor and E. Reimhult, ACS Nano, 2010, 4, 5665–5670 CrossRef CAS PubMed.
- B. P. Binks and T. S. Horozov, Angew. Chem., Int. Ed., 2005, 44, 3722–3725 CrossRef CAS PubMed.
- A. R. Studart, A. Nelson, B. Iwanovsky, M. Kotyrba, A. A. Kündig, F. H. D. Torre, U. T. Gonzenbach, L. J. Gauckler and J. F. Löffler, J. Mater. Chem., 2011, 22, 820–823 RSC.
- E. Amstad, J. Kohlbrecher, E. Müller, T. Schweizer, M. Textor and E. Reimhult, Nano Lett., 2011, 11, 1664–1670 CrossRef CAS PubMed.
- M. Hojeij, N. Younan, L. Ribeaucourt and H. H. Girault, Nanoscale, 2010, 2, 1665–1669 RSC.
- V. A. Turek, M. P. Cecchini, J. Paget, A. R. Kucernak, A. A. Kornyshev and J. B. Edel, ACS Nano, 2012, 6, 7789–7799 CrossRef CAS PubMed.
- P.-P. Fang, S. Chen, H. Deng, M. D. Scanlon, F. Gumy, H. J. Lee, D. Momotenko, V. Amstutz, F. Cortés-Salazar, C. M. Pereira, Z. Yang and H. H. Girault, ACS Nano, 2013, 7, 9241–9248 CrossRef CAS PubMed.
- M. A. Ray, N. Shewmon, S. Bhawalkar, L. Jia, Y. Yang and E. S. Daniels, Langmuir, 2009, 25, 7265–7270 CrossRef CAS PubMed.
- S. Paul, C. Pearson, A. Molloy, M. A. Cousins, M. Green, S. Kolliopoulou, P. Dimitrakis, P. Normand, D. Tsoukalas and M. C. Petty, Nano Lett., 2003, 3, 533–536 CrossRef CAS.
- S. Xiong, X. Miao, J. Spencer, C. Khripin, T. S. Luk and C. J. Brinker, Small, 2010, 6, 2126–2129 CrossRef CAS PubMed.
- J. S. Huang and R. Varadaraj, Curr. Opin. Colloid Interface Sci., 1996, 1, 535–539 CrossRef CAS.
- A. Maestro, L. J. Bonales, H. Ritacco, R. G. Rubio and F. Ortega, Phys. Chem. Chem. Phys., 2010, 12, 14115–14120 RSC.
- M. A. Ray and L. Jia, Adv. Mater., 2007, 19, 2020–2022 CrossRef CAS.
- A. B. Subramaniam, M. Abkarian and H. A. Stone, Nat. Mater., 2005, 4, 553–556 CrossRef CAS PubMed.
- Z. Nie, J. I. Park, W. Li, S. A. F. Bon and E. Kumacheva, J. Am. Chem. Soc., 2008, 130, 16508–16509 CrossRef CAS PubMed.
- C. Priest, M. D. Reid and C. P. Whitby, J. Colloid Interface Sci., 2011, 363, 301–306 CrossRef CAS PubMed.
- V. Garbin, J. C. Crocker and K. J. Stebe, J. Colloid Interface Sci., 2012, 387, 1–11 CrossRef CAS PubMed.
- V. Garbin, Phys. Today, 2013, 66, 68–69 CrossRef CAS PubMed.
- K. Schwenke, L. Isa and E. Del Gado, Langmuir, 2014, 30, 3069–3074 CrossRef CAS PubMed.
- E. Amstad and E. Reimhult, Nanomedicine, 2012, 7, 145–164 CrossRef CAS PubMed.
- E. Amstad, S.-H. Kim and D. A. Weitz, Angew. Chem., Int. Ed., 2012, 51, 12499–12503 CrossRef CAS PubMed.
- B. P. Binks, L. Isa and A. T. Tyowua, Langmuir, 2013, 29, 4923–4927 CrossRef CAS PubMed.
- K. A. Tay and F. Bresme, J. Am. Chem. Soc., 2006, 128, 14166–14175 CrossRef CAS PubMed.
- P. Pieranski, Phys. Rev. Lett., 1980, 45, 569–572 CrossRef CAS.
- K. Du, E. Glogowski, T. Emrick, T. P. Russell and A. D. Dinsmore, Langmuir, 2010, 26, 12518–12522 CrossRef CAS PubMed.
- L. Isa, E. Amstad, K. Schwenke, E. Del Gado, P. Ilg, M. Kröger and E. Reimhult, Soft Matter, 2011, 7, 7663 RSC.
- V. Garbin, J. C. Crocker and K. J. Stebe, Langmuir, 2012, 28(3), 1663–1667 CrossRef PubMed.
- Z. A. Zell, L. Isa, P. Ilg, L. G. Leal and T. M. Squires, Langmuir, 2014, 30, 110–119 CrossRef CAS PubMed.
- S. Reynaert, P. Moldenaers and J. Vermant, Langmuir, 2006, 22, 4936–4945 CrossRef CAS PubMed.
- F. Ebert, G. Maret and P. Keim, Eur. Phys. J. E: Soft Matter Biol. Phys, 2009, 29, 311–318 CrossRef CAS PubMed.
- S. Mazoyer, F. Ebert, G. Maret and P. Keim, EPL, 2009, 88, 66004 CrossRef.
- T. Gillich, C. Acikgöz, L. Isa, A. D. Schlüter, N. D. Spencer and M. Textor, ACS Nano, 2013, 7, 316–329 CrossRef CAS PubMed.
- L. Isa, D. C. E. Calzolari, D. Pontoni, T. Gillich, A. Nelson, R. Zirbs, A. Sánchez-Ferrer, R. Mezzenga and E. Reimhult, Soft Matter, 2013, 9, 3789–3797 RSC.
- A. Goebel and K. Lunkenheimer, Langmuir, 1997, 13, 369–372 CrossRef CAS.
- Q. He, Y. Zhang, G. Lu, R. Miller, H. Möhwald and J. Li, Adv. Colloid Interface Sci., 2008, 140, 67–76 CrossRef CAS PubMed.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310 CrossRef CAS.
- Particle tracking using IDL, http://www.physics.emory.edu/faculty/weeks//idl/.
- M. E. O'Neill, K. B. Ranger and H. Brenner, Phys. Fluids, 1986, 29, 913–924 CrossRef PubMed.
- P. Pieranski, Phys. Rev. Lett., 1980, 45, 569–572 CrossRef CAS.
- D. Wang, S. Yordanov, H. M. Paroor, A. Mukhopadhyay, C. Y. Li, H.-J. Butt and K. Koynov, Small, 2011, 7, 3502–3507 CrossRef CAS PubMed.
- R. Rigler and E. Elson, Fluorescence Correlation Spectroscopy: Theory and Applications, Springer, 2001 Search PubMed.
- C. B. Müller, A. Loman, V. Pacheco, F. Koberling, D. Willbold, W. Richtering and J. Enderlein, EPL, 2008, 83, 46001 CrossRef.
- N. Bizmark, M. A. Ioannidis and D. E. Henneke, Langmuir, 2014, 30, 710–717 CrossRef CAS PubMed.
- A. F. H. Ward and L. Tordai, J. Chem. Phys., 1946, 14, 453–461 CrossRef CAS PubMed.
- J. Eastoe and J. S. Dalton, Adv. Colloid Interface Sci., 2000, 85, 103–144 CrossRef CAS.
- L. Liggieri, F. Ravera and A. Passerone, Colloids Surf., A, 1996, 114, 351–359 CrossRef CAS.
- S. Kutuzov, J. He, R. Tangirala, T. Emrick, T. P. Russell and A. Boker, Phys. Chem. Chem. Phys., 2007, 9, 6351–6358 RSC.
- H. Brenner, Chem. Eng. Sci., 1961, 16, 242–251 CrossRef CAS.
- A. Stocco, T. Mokhtari, G. Haseloff, A. Erbe and R. Sigel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 011601 CrossRef.
- Y. Lin, A. Böker, H. Skaff, D. Cookson, A. D. Dinsmore, T. Emrick and T. P. Russell, Langmuir, 2005, 21, 191–194 CrossRef CAS PubMed.
- Z. Adamczyk, J. Colloid Interface Sci., 2000, 229, 477–489 CrossRef CAS PubMed.
- Q. Brosseau, J. Vrignon and J.-C. Baret, Soft Matter, 2014, 10, 3066–3076 RSC.
- Z. Adamczyk, in Adsorption: Theory, Modeling, and Analysis, ed. J. Toth, CRC Press, 2002, vol. 107, pp. 251–374 Search PubMed.
- P. Erni, Soft Matter, 2011, 7, 7586–7600 RSC.
- T. G. Mason, K. Ganesan, J. H. van Zanten, D. Wirtz and S. C. Kuo, Phys. Rev. Lett., 1997, 79, 3282–3285 CrossRef CAS.
- L. Isa, J.-M. Jung and R. Mezzenga, Soft Matter, 2011, 7, 8127–8134 RSC.
- S. Jordens, L. Isa, I. Usov and R. Mezzenga, Nat. Commun., 2013, 4, 1917 CrossRef PubMed.
- Y. Peng, W. Chen, T. M. Fischer, D. A. Weitz and P. Tong, J. Fluid Mech., 2009, 618, 243–261 CrossRef CAS.
- D. Magde, E. Elson and W. W. Webb, Phys. Rev. Lett., 1972, 29, 705–708 CrossRef CAS.
- K. Koynov and H.-J. Butt, Curr. Opin. Colloid Interface Sci., 2012, 17, 377–387 CrossRef CAS PubMed.
- C. L. Klix, F. Ebert, F. Weysser, M. Fuchs, G. Maret and P. Keim, Phys. Rev. Lett., 2012, 109, 178301 CrossRef.
- B. Brugger, J. Vermant and W. Richtering, Phys. Chem. Chem. Phys., 2010, 12, 14573–14578 RSC.
- S. Reynaert, P. Moldenaers and J. Vermant, Phys. Chem. Chem. Phys., 2007, 9, 6463–6475 RSC.
- J. T. Russell, Y. Lin, A. Böker, L. Su, P. Carl, H. Zettl, J. He, K. Sill, R. Tangirala and T. Emrick, Angew. Chem., Int. Ed., 2005, 44, 2420–2426 CrossRef CAS PubMed.
- E. Dickinson, Colloids Surf., B, 1999, 15, 161–176 CrossRef CAS.
- T. M. Fischer, P. Dhar and P. Heinig, J. Fluid Mech., 2006, 558, 451–475 CrossRef.
- F. Ortega, H. Ritacco and R. G. Rubio, Curr. Opin. Colloid Interface Sci., 2010, 15, 237–245 CrossRef CAS PubMed.
- J. R. Samaniuk and J. Vermant, Soft Matter, 2014, 10, 7023–7033 RSC.
- L. Isa, E. Amstad, M. Textor and E. Reimhult, Chimia, 2010, 64, 145–149 CrossRef CAS.
- Z. A. Zell, A. Nowbahar, V. Mansard, L. G. Leal, S. S. Deshmukh, J. M. Mecca, C. J. Tucker and T. M. Squires, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 3677–3682 CrossRef CAS PubMed.
- K. Schwenke, L. Isa, D. L. Cheung and E. Del Gado, Langmuir, 2014, 30(42), 12578–12586 CrossRef PubMed.
- B. Brugger, S. Rütten, K.-H. Phan, M. Möller and W. Richtering, Angew. Chem., Int. Ed., 2009, 48, 3978–3981 CrossRef CAS PubMed.
- R. J. K. Udayana Ranatunga, R. J. B. Kalescky, C.-c. Chiu and S. O. Nielsen, J. Phys. Chem. C, 2010, 114, 12151–12157 CAS.
Footnote |
| † Present address: Department of Chemical and Biological Engineering, University of Colorado, Boulder, Colorado 80309, USA. |
| This journal is © The Royal Society of Chemistry 2015 |