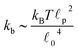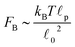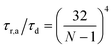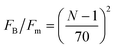The role of filament length, finite-extensibility and motor force dispersity in stress relaxation and buckling mechanisms in non-sarcomeric active gels
Andrés
Córdoba†
a,
Jay D.
Schieber†
*ab and
Tsutomu
Indei
a
aDepartment of Chemical and Biological Engineering and Center for Molecular Study of Condensed Soft Matter, Illinois Institute of Technology, 3440 S. Dearborn St, Chicago, Illinois 60616, USA. E-mail: schieber@iit.edu
bDepartment of Physics, Illinois Institute of Technology, 3101 S. Dearborn St., Chicago, Illinois 60616, USA
First published on 22nd October 2014
Abstract
After relaxing some assumptions we apply a single-chain mean-field mathematical model recently introduced [RSC Adv. (2014)] to describe the role of molecular motors in the mechanical properties of active gels. The model allows physics that are not available in models postulated on coarser levels of description. Moreover it proposes a level of description that allows the prediction of observables at time scales too difficult to achieve in multi-chain simulations for realistic filament lengths and densities. We model the semiflexible filaments that compose the active gel as bead-spring chains; molecular motors are accounted for by using a mean-field approach, in which filaments undergo transitions of one motor attachment state depending on the state of the probe filament. The level of description includes the end-to-end distance and attachment state of the filaments, and the motor-generated forces, as stochastic state variables which evolve according to a proposed differential Chapman–Kolmogorov equation. The motor-generated forces are drawn from a stationary distribution of motor stall forces. We consider bead-spring chains with multiple beads, explore the effect of finite-extensibility of the strands and incorporate into the model motor force distributions that have been measured experimentally. The model can no longer be solved analytically but is amenable to numerical simulation. This version of the model allows a more quantitative description of buckling dynamics [Lenz et. al. PRL, 2012, 108, 238107] and the dynamic modulus of active gels. The effect of finite extensibility of the filament strands on the dynamic modulus was also found to be in agreement with the microrheology experiments of Mizuno et. al., [Science, 2007, 315, 370–373].
I. Introduction
Active gels are networks of semiflexible polymer filaments driven by motor proteins that can convert chemical energy from the hydrolysis of adenosine triphosphate (ATP) to mechanical work and motion. Active gels perform essential functions in living tissue including motions, generation of forces and sensing of external forces. The cell cytoskeleton is an active gel composed of many different types of filaments and motors that performs most of the mechanical functions of cells. Moreover, active gels play a central role in driving cell division and cell motility.1–3 Active gels have also been successfully prepared in vitro to study their mechanical and rheological properties.4–6In active gels, molecular motors assemble into clusters with a rigid, roughly cylindrical, backbone and groups of binding heads on both ends that can attach to active sites along semiflexible filaments.7,8 These clusters of motor proteins constitute the active component of active gels. In the absence of ATP motor clusters act as passive cross-links between the semiflexible filaments. In the presence of ATP molecular motors can “walk” along the filaments. The direction in which motors move is determined by the filament structural polarity.9,10 A molecular motor starts “walking” when an ATP molecule attaches to a binding head domain of the motor protein, which causes it to detach from the filament. Using the chemical energy from the hydrolysis of ATP the detached motor head moves towards the next attachment site along the filament contour and reattaches, in a process known as the Lymn–Taylor cycle.11 Each motor has at least two clusters of binding heads performing this same process. However, both of them do not necessarily detach at the same time. When the binding heads on one end of the motor are detached and moving towards the next attachment site, the heads on the other end can be attached to a different filament. This filament will feel a force due to the motion of the motor. Therefore, in a network molecular motors can generate active, pair–wise interactions between filaments.
The forces generated by the motors when they move along the filament are a function of the chemical potential difference between ATP and its hydrolysis products. In vivo molecular motors operate far from equilibrium. In typical active gels found in living cells the difference in chemical potential between ATP and its hydrolysis products is on the order of 10kBT.10,12 Examples of molecular motors that have been extensively studied are myosin which moves along actin filaments; and kynesin and dynesin which move along microtubules. Each type of motor protein has particular characteristics that determine its function inside the cytoeskeleton. For instance the duty ratio of mysosin (ratio of attached to unattached time) increases with decreasing ATP concentration, when motor release induced by ATP binding becomes the rate-limiting step in the Lymn–Taylor cycle.6,11 Non-equilibrium motor activity appears when the motors switch from a non-processive mode, which cannot generate forces between filaments, to a processive tension-generating mode. In addition, the processing time of different myosin isoforms have different sensitivity to tension.13 It has been recently shown that Myo1b is very sensitive to tension, where forces >0.5 pN cause the motor to transform from a low-duty-ratio motor with attachment times <1 s to a high-duty-ratio motor with attachment times >50 s.14 On the other hand Myo1c is far less sensitive to force than Myo1b enabling it to power motility over a range of forces.
The semiflexible filaments that form active gels, such as actin and tubulin, are characterized by having a persistence length (length over which the tangent vectors to the contour of the filament remain correlated) that is much larger than the size of a monomer, and larger than the mesh size of the network, but typically smaller than the contour length of the filament. For instance, for filamentous actin (F-actin) the persistence length is around 10 μm, while the mesh size of actin networks is estimated to be approximately 1 μm.15–17 This sets them apart from flexible networks where the persistence length of the polymeric chains is much smaller than the mesh size of the networks formed by those chains. An important mechanical characteristic of semiflexible networks is that they exhibit significant strain hardening for modest strains. A tension of a few pN can increase the modulus of a semiflexible network by a factor of 100.15,16 This capacity of biological gels to stiffen as they are strained allows them to prevent large deformations that could threaten tissue integrity.
Recent advances in experimental techniques have allowed the characterization of mechanical and rheological properties of active gels. For instance an important mechanical feature of active gels that has been extensively studied experimentally, is their capacity of self-contraction and self-organization.1,18–21 These mechanical features of active gels play a central role in cell division and motion. For instance, a widely studied active gel is the actin cortex, which is a disordered network of F-actin decorated with myosin II motors. Changes in cell shape, as required for migration and division, are mediated by the cell cortex. Myosin II motors drive contractility of the cortical actin network, enabling shape change and cytoplasmic flows underlying important physiological processes such as cell division, migration and tissue morphogenesis.3
Several works have used a continuum-mechanics level of description to model self-organization22,23 and rheology24–26 of active gels and fluids. More microscopic models have described active gels using a master equation for interacting polar rods; Aranson and Tsimring23 presented analytic and numerical results for rigid rods, later Head, Gompper, and Briels27 presented more detailed numerical simulations that account for filament semiflexibility. These models have been very successful in describing large scale phenomena such as the formation and dynamics of cytoskeletal patterns (e.g.: asters, vortices). The latter work also investigated the effect of motor attachment/detachment rates on the predictions of the super-diffusive mass transport typical of active gels. However, the precise microscopic mechanisms underlying this process are still the subject of considerable experimental and theoretical investigation. Recently, a microscopic single-filament mean-field model to describe myosin-induced contraction of non-sarcomeric F-actin bundles was postulated by Lenz et al.18 However there are several issues in the level-of-description and mathematical formulation of Lenz et al.18 which we discussed in a previous manuscript.28
Rheological experiments in active polymeric networks have revealed fundamental differences from their passive counterparts. Some of the differences are not surprising given that these are materials in which molecular motors continuously convert chemical energy into mechanical work. Recent microrheology experiments4–6 on active gels have shown that the fluctuation–dissipation theorem (FDT) and the generalized Stokes–Einstein relation (GSER) are violated in active gels. The FDT is a central part of data analysis of passive microrheology experiments, where it is used to relate the position fluctuations of the probe bead to a frequency-dependent friction coefficient, from which, using a generalized Stokes relation, rheological properties can be extracted.29–31 The violation of FDT is observed as a frequency-dependent discrepancy between the material response function obtained from active and passive microrheology experiments. In the active experiments an external force is applied to the probe bead and the material response function is calculated from the bead position signal.31 In passive microrheology experiments, no external force is applied, and the material response function is calculated from the bead position autocorrelation function using the FDT.6 Other microrheology experiments in active gels also indicate that the activity of molecular motors can produce significant strain hardening of the active networks. For instance non-Gaussian statistics of the probe bead position have been observed4 in beads embedded in gels made to mimic the cytoskeleton. In other passive microrheology experiments a decrease in the overall magnitude of the probe-bead power-spectral density and a slow-down of stress relaxation was observed after addition of ATP6 to an actomyosin gel.
A considerable amount of work has been devoted to deriving simple generalizations or extensions of the FDT for out-of-equilibrium systems, such as active gels.32–34 In general, these extensions of FDT to out-of-equilibrium systems model the non-equilibrium forces as Brownian forces, but introduce an effective temperature,24,35–37 which is higher than the real temperature and is meant to account for the larger magnitude of the non-equilibrium fluctuations. This kind of approach can not explain the observations in the microrheology experiments in active gels6 since Brownian forces alone can not produce a frequency-dependent discrepancy between the material response obtained from the material's spontaneous stress fluctuations, and the material response obtained by applying a small external perturbation and observing the material response. Other works38,39 have modeled the attachment/detachment dynamics of motor forces as a stochastic jump process. This approach has been successful in describing some of the features observed in the microrheology experiments of active gels, such as diffusive and superdiffusive behavior of tracer beads at frequencies where storage modulus of the gel has plateau behavior. However these models assume that the motors do not interact through the strain field in the network and neglect strain hardening. Given the level of description of such models, removal of these assumptions is difficult; therefore more microscopic models seem necessary to elucidate the specific effect that these physical features have on the rheology of active gels.
In our previous manuscript “A Single-Chain Model for Active Gels I: Active dumbbell model”,28 referred through this text as Part I, we introduced a single-chain mean-field model for active gels. We proposed a level of description with the minimum set of components necessary to predict mechanical and rheological features that have been observed in active gels. In that work we considered dumbbells, meaning that we had only two beads per filament. The filaments were modeled as Fraenkel springs, and the motor force distribution was made a Dirac delta function centered around a mean motor stall force. Those assumptions allowed us to obtain analytical expressions for several observables of the model, such as relaxation modulus and fraction of buckled filaments.
The main objective of this manuscript is to relax some of the assumptions of the model presented in Part I. More specifically, we consider bead-spring chains with multiple beads, explore the effect of finite-extensibility of the filament segments and incorporate into the model motor force distributions that have been measured experimentally. In that form the model can no longer be solved analytically and we therefore use numerical simulations. In Section II we give a detailed description of the model, and discuss the main assumptions, and parameters. We generalize the proposed differential Chapman–Kolmogorov equation to the case of multiple beads and give the expressions for the finite-extensibility of the strands and the motor force distributions. We also discuss the numerical solution of the model and provide checks of the numerical algorithm used to solve the model against analytic solutions that can be obtained in special cases. In Section III we present predictions of the dynamic modulus of active gels using the active single-chain mean-filed model. The effect of multiple beads and finite extensibility of the strands in the relaxation spectrum of the active gel is discussed. We show that the model can predict the violation of the FDT observed in microrheology experiments of active gels.6 This is done by comparing the dynamic modulus of the gel obtained from the autocorrelation function of stress at the non-equilibrium steady state, with the modulus obtained from the stress response when a small perturbation is applied to the gel. In Section IV we discuss transport of filaments in an active gel using our model. We do this by following the mean-squared displacement of the probe filament center at the non-equilibrium steady-state. In Section V we illustrate the use of the model to describe the underlying mechanisms of self-contraction in active non-sarcomeric F-actin bundles. Here we specifically focus on the effect that the density of active crosslinks along the filament has on the fraction of buckled filaments and present predictions that show the relation between filament buckling and contraction of non-sarcomeric actomyosin bundles.
II. The active single-chain mean-field model
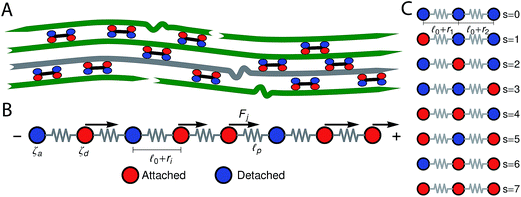
In this section we describe a single-chain mean-field model for an active bundle. Active networks are formed by semiflexible filaments and motor clusters (hereafter simply called motors) that form active cross-links between filaments (Fig. 1B). For instance myosin II thick filaments, which cross-link actin, are ∼1.5 μm in length and contain ∼400 attachment heads.3 In the presence of ATP, motors will go through detachment/attachment cycles11 in which they detach from one filament and take nanometer-sized steps towards a direction determined by the filament's structural polarity, therefore exerting a force on the filament to which they remain attached. Our model follows a single probe filament (illustrated in gray in Fig. 1B) and approximate its surroundings by an effective medium of motor clusters that attach and detach from specific sites along the probe filament. The motors are assumed to form pair–wise interactions between filaments. When a motor is attached to the probe filament it is detached and steps forward on another filament in the mean-field and therefore pulls/pushes on the probe filament. The formulation of temporary network models provides a very useful mathematical and conceptual framework to model these dynamics.40–42 In Fig. 1B a probe filament is shown in more detail, each bead represents a site along the filament where a motor can attach, and the springs represent the filament segments between this active sites. In this manuscript we consider the case of multiple beads. The motors create the type of pair–wise active interactions between the bead-spring chains described above. To model these interactions we use a mean-field approach, in which filaments have certain probabilities to undergo a transition from one attachment/detachment state into another depending on the state of the particular filament.It is convenient to represent the attachment state by a single number s; by allocating number 0 to free beads and 1 to beads attached to a motor. In the following, the number 0 or 1 assigned to bead j on the chain in an attachment state is denoted by nj(s). By definition, s takes one of the values 0, 1, …, 2N(=smax), where N is the number of beads. For example, s is equal to 0 for a chain whose beads are all free (i.e., nj(0) = 0 for all j) and s = smax for a chain whose all beads are attached (i.e., nj(smax) = 1 for all j). Fig. 1 illustrates the labeling of the attachment states for a chain with three beads.
We assume that before addition of ATP the distance between non-processive motors (acting as passive cross-links) is given by ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0. This is the rest length of the filament segments and therefore there is no tension in the filaments before addition of ATP. For instance, if an actin network is formed in the presence of high concentrations of myosin the resulting cross-link density is higher and
0. This is the rest length of the filament segments and therefore there is no tension in the filaments before addition of ATP. For instance, if an actin network is formed in the presence of high concentrations of myosin the resulting cross-link density is higher and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 smaller than in the same network formed under lower concentrations. In typical actin networks prepared in vitro
0 smaller than in the same network formed under lower concentrations. In typical actin networks prepared in vitro ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 is on the order of 1 μm.16,17 After addition of ATP the motors (cross-links) become active and start detaching from and reattaching to the beads. τd is the average time a motor spends attached to a bead before detaching from it, whereas the average time a motor spends detached before reattaching is given by the model parameter τa. The force generated by a motor attached to bead j will be denoted Fj. Molecular motors can only move in one direction along the filament, determined by the filament's polarity. Filaments are thus expected to move in the opposite direction. In this single-chain description we introduce this asymmetry by making all the forces Fj, that the motors exert on the beads of a given filament, have the same sign (either positive or negative). Another force acting on the filament is the viscous drag from the surrounding solvent (which is mainly water for biological networks). The frictional force from the surrounding solvent is characterized by a friction coefficient. Bulky motor cluster (i.e.: 1.5 μm for myosin II thick filaments) increase the friction coefficient of the filament when attached to an active site. Therefore this friction coefficient is allowed to take two different values: ζa when attached, and ζd < ζa if there is no motor attached to that bead. The change in the end-to-end length of a filament segment due to the action of the motors is denoted ri.
0 is on the order of 1 μm.16,17 After addition of ATP the motors (cross-links) become active and start detaching from and reattaching to the beads. τd is the average time a motor spends attached to a bead before detaching from it, whereas the average time a motor spends detached before reattaching is given by the model parameter τa. The force generated by a motor attached to bead j will be denoted Fj. Molecular motors can only move in one direction along the filament, determined by the filament's polarity. Filaments are thus expected to move in the opposite direction. In this single-chain description we introduce this asymmetry by making all the forces Fj, that the motors exert on the beads of a given filament, have the same sign (either positive or negative). Another force acting on the filament is the viscous drag from the surrounding solvent (which is mainly water for biological networks). The frictional force from the surrounding solvent is characterized by a friction coefficient. Bulky motor cluster (i.e.: 1.5 μm for myosin II thick filaments) increase the friction coefficient of the filament when attached to an active site. Therefore this friction coefficient is allowed to take two different values: ζa when attached, and ζd < ζa if there is no motor attached to that bead. The change in the end-to-end length of a filament segment due to the action of the motors is denoted ri.
The following state variables (level of description) are used to construct the model of the active chain Ω: {s,F,r}. Where F: = {F1,F2,Fj,…,FN} is a vector that contains the motor forces for all the beads and r: = {r1,r2,ri…rN−1} is a vector that contains the change from the rest length in the end-to end distance of all the strands due to motor forces. Now let ψ(Ω) be the distribution function describing the probability of finding an active filament in state s with strands with a change in their end-to-end distance r due to motor forces F at time t. The time evolution for ψ(Ω) is given by the following differential Chapman–Kolmogorov equation:
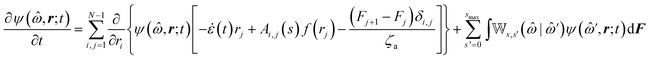 | (1) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) c) semiflexible filaments43 is given by
c) semiflexible filaments43 is given by 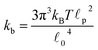 . The rest length
. The rest length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 is related to the contour length by
0 is related to the contour length by 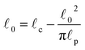 . For F-actin filaments, the persistence length,
. For F-actin filaments, the persistence length, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) p, is approximately 10 μm and
p, is approximately 10 μm and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 ∼ 1 μm and therefore kb is on the order of 1 μN m−1. However approximating the filament segments (strands) as Fraenkel springs is only expected to be valid for very small deviations from the relaxed length
0 ∼ 1 μm and therefore kb is on the order of 1 μN m−1. However approximating the filament segments (strands) as Fraenkel springs is only expected to be valid for very small deviations from the relaxed length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0. We discuss another, more accurate, expression for f (rj) below.
0. We discuss another, more accurate, expression for f (rj) below.
The matrix Ai,j(s), in eqn (1) gives the connectivity of the beads as a function of the motor-attachment state, s, and is defined as.
| Ai,j(s) = −ai(s)δi,j−1 + [ai(s) + bi(s)]δi,j − bi(s)δi,j+1 | (2) |
 | (3) |
As stated above, ζa is the friction coefficient of a bead when a motor is attached to it and ζd is the friction coefficient when there is no motor attached to it. For instance, several experimental measurements18,19 have shown that myosin II motors move along actin filaments at approximately 0.5–1 μm s−1, and have an average stall force of 1 pN; therefore ζa is estimated to be around 1 μN s m−1ζa is expected to be larger than ζd since the motor attachment heads increase the cross-sectional area of the actin filament when they attach to it. In addition to τa and τd it is convenient to label two additional time scales of the model τr,a = ζa/kb and τr,d = ζa/kb which are local relaxation times of the filament when a motor is attached to it, or is not, respectively. For myosin motors in actin gels τd is on the order of 100 ms while τa is usually between an order to two orders of magnitude smaller.18,38 Therefore in a typical active gel τa < τd ≲ τr,d < τr,a is expected.
In Part I we treated the strands between motors as linear springs to be able to obtain analytic solutions of the model. However semiflexible filaments are known to strain harden under a tension of a few pN, which motors are known to generate. The end-to-end, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , versus tension, f, behavior of semi-flexible filaments has been the subject of extensive theoretical and experimental study during the last four decades.15,43–45 Given the importance of such relations to accurately model biological networks the elasticity of semiflexible filaments is still the object of ongoing experimental and theoretical work. In bead-spring simulations an interpolation formula developed by Marko and Siggia15 that approximates the force–extension curve of inextensible (i.e.: fixed contour length
, versus tension, f, behavior of semi-flexible filaments has been the subject of extensive theoretical and experimental study during the last four decades.15,43–45 Given the importance of such relations to accurately model biological networks the elasticity of semiflexible filaments is still the object of ongoing experimental and theoretical work. In bead-spring simulations an interpolation formula developed by Marko and Siggia15 that approximates the force–extension curve of inextensible (i.e.: fixed contour length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) c) semiflexible filaments is commonly used,45,46
c) semiflexible filaments is commonly used,45,46
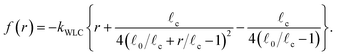 | (4) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 is the rest length and r is the deviation from
0 is the rest length and r is the deviation from ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0. The end-to-end length vs. tension curve given by eqn (4) displays a linear regime for small tensions f and in the limit of strong stretching approaches
0. The end-to-end length vs. tension curve given by eqn (4) displays a linear regime for small tensions f and in the limit of strong stretching approaches ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) c with a characteristic saturation ∼−f−1/2 (see Fig. 2). Polymeric filaments that display this characteristic behavior are usually referred to as wormlike chains15,43,44 (WLC). Note that since to linear order in reqn (4) must match the behavior of the Fraenkel springs kb and kWLC are related by
c with a characteristic saturation ∼−f−1/2 (see Fig. 2). Polymeric filaments that display this characteristic behavior are usually referred to as wormlike chains15,43,44 (WLC). Note that since to linear order in reqn (4) must match the behavior of the Fraenkel springs kb and kWLC are related by 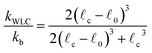 .
.
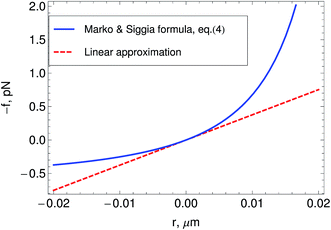 | ||
Fig. 2 Relation between tension f and the deviation r from the rest-length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 in a semiflexible filament as predicted by the wormlike chain model. The plot shows the linear approximation to it, and the Marko and Siggia15 formula, eqn (4). The plot is made for values of the parameters typical of actin filaments in a network 0 in a semiflexible filament as predicted by the wormlike chain model. The plot shows the linear approximation to it, and the Marko and Siggia15 formula, eqn (4). The plot is made for values of the parameters typical of actin filaments in a network ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , , ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) p = 10 μm p = 10 μm ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 = 1 μm. 0 = 1 μm. | ||
In our model, a filament of end-to-end length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) f is constructed by connecting N − 1 segments of rest length
f is constructed by connecting N − 1 segments of rest length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 through the connectivity matrix A (s). We assume a single value for
0 through the connectivity matrix A (s). We assume a single value for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0. In real systems a distribution of
0. In real systems a distribution of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 is expected, even if the strands have the same
0 is expected, even if the strands have the same ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) c. Initial cross-linking by non-processive motors of the thermally undulating filaments can create local pair–wise separations that differ from the zero-force end-to-end lengths of the filaments. Storm et al.17 have performed a detailed analysis of
c. Initial cross-linking by non-processive motors of the thermally undulating filaments can create local pair–wise separations that differ from the zero-force end-to-end lengths of the filaments. Storm et al.17 have performed a detailed analysis of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 distributions and their effect in the mechanical response of semiflexible networks. We also assume that the tension in each segment as a function of r is given by eqn (4), or its linearized version. This assumption implies that the end-to-end length vs. tension relation does not couple the strands (filament segments), the tension in each strand only depends in its own deviation from the relaxed length and not on the state of the other segments in the chain. However in the real WLC the tension in a particular strand depends on the orientation of the other segments in the chain.
0 distributions and their effect in the mechanical response of semiflexible networks. We also assume that the tension in each segment as a function of r is given by eqn (4), or its linearized version. This assumption implies that the end-to-end length vs. tension relation does not couple the strands (filament segments), the tension in each strand only depends in its own deviation from the relaxed length and not on the state of the other segments in the chain. However in the real WLC the tension in a particular strand depends on the orientation of the other segments in the chain.
A more accurate bead-spring chain discretization of the WLC would include bending potentials between the springs which introduce correlations between the strands' orientations. The approximation without bending potentials is expected to work best when the end-to-end length of the segment represented by a spring is larger than the persistence length of the filament.45 More accurate bead-spring chain descriptions of semiflexible filaments include, in addition to finite extensibility of the strands, bending potentials between the springs. Recently a theoretical framework that allows one to systematically obtain coarse-grained models for semiflexible filaments was proposed.47 This framework has been used to construct a bead-spring model for the WLC that incorporates quadratic penalties for stretch, shear, and bending deviations as well as coupling between the bend and shear degrees of freedom of the free energy of the chain.48 That model allows for discretization at any segment length while still remaining accurate at shorter length-scale.
The transition rate matrix ![[Doublestruck W]](https://www.rsc.org/images/entities/char_e17a.gif) (
(![[small omega, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b4.gif) ′|
′|![[small omega, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b4.gif) ) in eqn (1) contains the transition rates between attachment/detachment states. To construct
) in eqn (1) contains the transition rates between attachment/detachment states. To construct ![[Doublestruck W]](https://www.rsc.org/images/entities/char_e17a.gif) (
(![[small omega, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b4.gif) ′|
′|![[small omega, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b4.gif) ) a matrix
) a matrix ![[Doublestruck K]](https://www.rsc.org/images/entities/char_e16e.gif) (l) of dimensions 2l × 2l(l = 1, …, N) is first generated by the following iterative procedure:
(l) of dimensions 2l × 2l(l = 1, …, N) is first generated by the following iterative procedure:
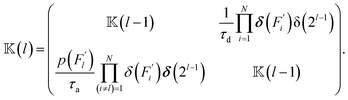 | (5) |
![[Doublestruck K]](https://www.rsc.org/images/entities/char_e16e.gif) (0) = 1, δ(…) is the Dirac delta function and δ(2l) is an identity matrix of dimensions 2l × 2l. Then
(0) = 1, δ(…) is the Dirac delta function and δ(2l) is an identity matrix of dimensions 2l × 2l. Then ![[Doublestruck W]](https://www.rsc.org/images/entities/char_e17a.gif) (
(![[small omega, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b4.gif) ′|
′|![[small omega, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b4.gif) ) is defined in terms of
) is defined in terms of ![[Doublestruck K]](https://www.rsc.org/images/entities/char_e16e.gif) (l) as,
(l) as,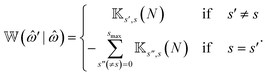 | (6) |
The block matrix at the upper-left or lower-right block element of ![[Doublestruck W]](https://www.rsc.org/images/entities/char_e17a.gif) (
(![[small omega, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b4.gif) ′|
′|![[small omega, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b4.gif) ) represents the transition rate matrix of a chain having N − 1 beads, whereas the upper right and lower left elements stand for the detachment and attachment rates of motors in the Nth bead, respectively.
) represents the transition rate matrix of a chain having N − 1 beads, whereas the upper right and lower left elements stand for the detachment and attachment rates of motors in the Nth bead, respectively.
The function p(F) is the probability density from which a motor force is drawn every time a motor attaches to a bead. In eqn (5) the subindex i indicates the bead to which the motor attaches. Motor force distributions have been measured experimentally in actomyosin bundles.18,19 In those systems, the dispersion in the motor-generated forces likely arises from the variation in the number of myosin attachment heads in the motor cluster. In Part I we assumed that the motor force distribution was given by a delta function centered around the mean-motor stall force that is p(F) = δ(F − Fm). where Fm is the mean motor-stall force. This assumption allowed us to proceed with the analytic solution of the model. However a more realistic shape of these motor force distributions can be incorporated into the model. Fig. 3 shows the cumulative probability function of myosin motors in an actin bundle.19 To incorporate this distribution in the model we fit the experimental data with either a triangular distribution (for fast, preliminary calculations) or with a gamma distribution (for final, quantitative calculations). The first moment of this distribution is approximately Fm = 0.7 nN and with standard-deviation, for the distribution shown in Fig. 3 of approximately δFm = 0.25 nN. We assume that the motor force distribution is independent of time, or that it is stationary, this is expected to be a good assumption as long as the kinetics of the ATP → work reaction in the motors are much faster than any of the time scales in the model. To summarize, we use a single-filament model of the active gel where binary active crosslinks with other filaments are accounted for by a mean-field of motors that undergo transitions between attachment states determined by the phenomenological parameters τa, τd and p(F) all found by independent experiments.
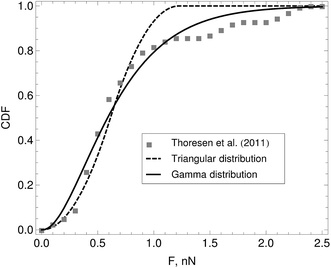 | ||
| Fig. 3 Cumulative distribution function (CDF) of myosin-generated forces in an actomyosin bundle. Symbols represent experimental data reported by Thoresen, Lenz, and Gardel.19 The lines are fits to the cumulative distribution function of analytic probability distributions used to incorporate p (F) in the model. From this distribution we find that the mean motor stall force for a myosin thick filament is approximately Fm = 0.7 nN with standard-deviation given by δFm = 25 nN. | ||
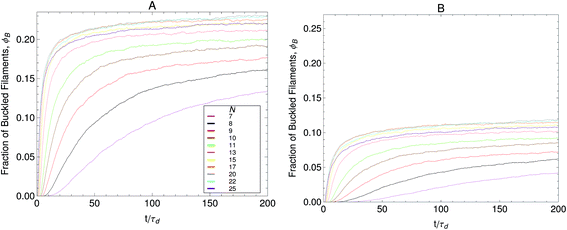
In this work a numerical algorithm derived from the proposed differential Chapman–Kolmogorov equation, eqn (1), is used to simulate an ensemble of filament trajectories40 from which moments of the probability density ψ(Ω) can be calculated. In Part I we presented analytic solutions for a dumbbell (two beads) version of the model with several simplifying assumptions. Even for chains with more than two beads the numerical solutions can be checked against analytic solutions that can be obtained in specific cases. For instance, Fig. 4A shows a comparison between the fraction of filaments in attachment state s (i.e., ∫ψ(Ω)dFdr) obtained from a simulation where all motor forces are turned off and the analytic solution that is obtained for that particular case. The calculations were performed for the three-beads chain (attachment states illustrated in Fig. 1C). Fig. 4B shows a check of the numerical algorithm in the other case where analytic solutions are attainable. That is, when the jumps between attachment states are turned off and the motor forces for all beads are made equal to Fm. In that case the model reduces to a system of deterministic ordinary differential equations. The two calculations shown in Fig. 4 confirm all terms in eqn (1) which is why these two particular checks were chosen. In general we find that to obtain convergence it is sufficient to set the value of the time step a factor of 10 times smaller than the smallest characteristic time scale of the system, taking relaxation times of the segments, attachment/detachment time scales into account.
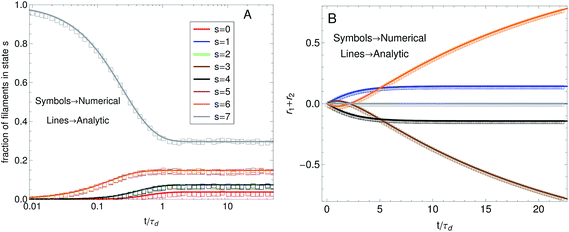 | ||
Fig. 4 Check of the numerical algorithm used to solve the model against analytical solutions in particular cases. The procedure is illustrated for a filament with three beads (attachment states illustrated in Fig. 1C). (A) Motor forces are turned off and the jump process between attachment states is checked against an analytic solution for the fraction of filaments in each attachment state. For the example shown the parameters were set to τa = 0.5, τd = 1. (B) The jump process between attachment states is turned off and predefined values for the motor forces are specified. The numerical solution for 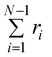 is checked against the analytic solution of the resulting deterministic equation for each attachment state. For the example shown the parameters were set to τr,a = 20, τr,d = 2, F = {1,2,1}, kb = 1. is checked against the analytic solution of the resulting deterministic equation for each attachment state. For the example shown the parameters were set to τr,a = 20, τr,d = 2, F = {1,2,1}, kb = 1. | ||
Note that in the model presented here p(F) is bead independent in contrast to the model by Lenz et al.18 In that model the motor force distribution depends on the position along the filament of the bead to which the motor is attached. In other words in that model the underlying mechanism for buckling is postulated to be a spatial gradient of the motor stall forces. Physically this assumption can be interpreted as the motors having spatial memory and being able to identify the particular position along the filament to which they are attaching. Presumably this pre-averaging and its related assumptions are done to simplify the mathematics; however this leads to several issues in the solution and interpretation of the model predictions that have not been clearly resolved. We do not make such assumptions. Instead F is kept as a stochastic state variable, p(F) is the same for all motors, and the transition rates depend on this motor force distribution. In other words, our model exists at a more detailed level of description than the model of Lenz et al.18 In Section V we discuss the implications that these conceptual differences between the two models have in the explanation of the mechanisms underlying buckling and self-contraction in active gels. In Sections III and IV we use the active single-chain mean-field model to describe some of the rheological and mass transport properties that have been observed in active gels.
III. Dynamic modulus of active gels
A. Introduction
To test the validity of FDT in active gels, Mizuno et al.6 compared the complex compliance of actin–myosin networks measured with active and passive microrheology. In the active experiment they used an optical trap to apply a small-amplitude oscillatory force to the bead, ftrap = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωtδx, where A is the amplitude, ω is the frequency and δx is the unit vector in the direction of the applied force. The complex compliance, α(ω), is obtained form the relation 〈rb(ω)〉 = α(ω) ftrap. Where rb(ω) is the measured probe bead position, which can also be written as 〈rb(ω)〉 = A[α′ (ω)cos
ωtδx, where A is the amplitude, ω is the frequency and δx is the unit vector in the direction of the applied force. The complex compliance, α(ω), is obtained form the relation 〈rb(ω)〉 = α(ω) ftrap. Where rb(ω) is the measured probe bead position, which can also be written as 〈rb(ω)〉 = A[α′ (ω)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωt + α′′(ω)sin
ωt + α′′(ω)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωt]δx. Where α′(ω) characterizes the elastic response of the medium, in phase with the applied force, and α′′(ω) characterizes the viscous response, out of phase with the applied force. In a passive microrheology experiment no external force is applied to the bead or a static harmonic trap is used to hold the bead near its equilibrium position and the imaginary part of α(ω) is obtained using the FDT,
ωt]δx. Where α′(ω) characterizes the elastic response of the medium, in phase with the applied force, and α′′(ω) characterizes the viscous response, out of phase with the applied force. In a passive microrheology experiment no external force is applied to the bead or a static harmonic trap is used to hold the bead near its equilibrium position and the imaginary part of α(ω) is obtained using the FDT, 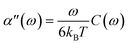 . Where
. Where 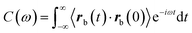 is the autocorrelation function of the bead position.29,30 Before addition of ATP the complex compliance of the actin–myosin network obtained with the passive and active techniques were identical. In gels activated with ATP a frequency-dependent discrepancy between the complex compliance obtained from the passive and active experiments appears at frequencies below 10 Hz. This discrepancy is due to a frequency-dependent increase in the magnitude of the bead fluctuations observed in the passive microrheology experiment, in the actin–mysosin gels activated with ATP. These increased fluctuations have been linked to motor activity.38,39,49 Since the FDT does not account for motor activity, the complex compliance calculated from these fluctuations using the FDT does not agree with the complex compliance obtained from the active experiment.
is the autocorrelation function of the bead position.29,30 Before addition of ATP the complex compliance of the actin–myosin network obtained with the passive and active techniques were identical. In gels activated with ATP a frequency-dependent discrepancy between the complex compliance obtained from the passive and active experiments appears at frequencies below 10 Hz. This discrepancy is due to a frequency-dependent increase in the magnitude of the bead fluctuations observed in the passive microrheology experiment, in the actin–mysosin gels activated with ATP. These increased fluctuations have been linked to motor activity.38,39,49 Since the FDT does not account for motor activity, the complex compliance calculated from these fluctuations using the FDT does not agree with the complex compliance obtained from the active experiment.
Fig. 5A shows the imaginary part of the complex compliance J′′(ω) = 6πRα′′(ω) of the actomyosin gel studied by Mizuno et al.6 The complex compliance, J*(ω), is related to the dynamic modulus, G*(ω), by J*(ω) G*(ω) = 1. The symbols are experimental data obtained using passive and active microrheology, while the lines are fits used to transform J*(ω) to G*(ω). The data were taken at steady state after addition of ATP to the actomyosin network. Part B of Fig. 5 shows the dynamic modulus obtained from the fits to J′′(ω) shown in Fig. 5A using standard procedures.39,50,51 The red lines represent the dynamic modulus obtained from the active microrheology experiment, where an external strain or force was applied using optical tweezers. The blue lines represent the modulus obtained from the passive microrheology technique without applying any external strain or force.
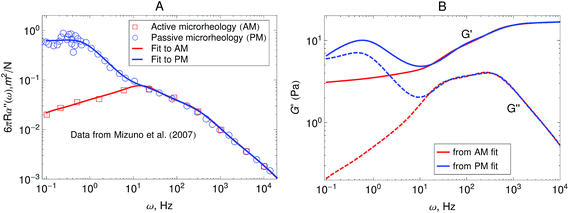 | ||
| Fig. 5 (A) Imaginary part of the creep compliance, J′′(ω) = 6πRα′′(ω), of an actomyosin gel measured using passive and active microrheology. The symbols are experimental results by Mizuno et al.6 and the lines are fits used to convert J* to G*. (B) Dynamic modulus obtained from the creep compliance shown in part A. | ||
In this section, we perform calculations with the active single-chain mean-field model that test the validity of FDT in active gels in a way similar to the microrheology experiments of Mizuno et al.6 We begin by calculating the relaxation modulus of the active gel from the autocorrelation function of stress at the non-equilibrium steady-state. That is, we apply the Green–Kubo formula, that relates the autocorrelation function of stress with the relaxation modulus of a material,52 to the active gel. In a second calculation we apply a small step-strain to the active gel and estimate the dynamic modulus from the stress relaxation curve. If the active single-chain mean-field model satisfies the FDT the dynamic modulus obtained from those two calculations should be the same, if it does not, a frequency-dependent discrepancy should appear. Similar calculations are often performed for single-chain models of not-active networks, to demonstrate FDT compliance.42,53
Other microrheology experiments in active gels4,6 have shown that motor-activity induces significant strain hardening of the semiflexible network. Mizuno et al.6 observed this effect in the power-spectral density of the probe bead in passive microrheology experiments. Their experimental results are shown in Fig. 6A. As can be observed the overall magnitude of the response function starts to decrease after the myosin motors switch from a nonprocessive mode to a processive tension-generating mode at approximately 2.5 hours after addition of ATP. The strain hardening can also be observed in the storage modulus obtained from this passive microrheology experiments shown in Fig. 6B. The stiffening of the filaments generated by the motors causes an overall decrease in the magnitude of stress fluctuations and therefore a decrease in the storage modulus obtained from passive microrheology experiments. A broadening in the relaxation spectrum of the gel which causes a slow-down in stress relaxation at frequencies around 102 Hz is also observed. For instance, the storage modulus obtained from passive microrheology goes from a ω0.67 behavior to ω0.5 when myosin motors become processive.
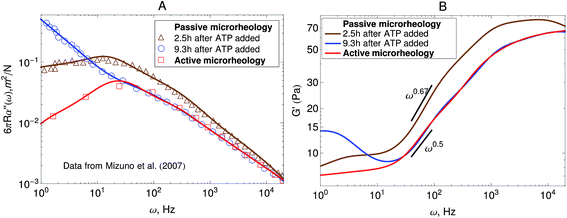 | ||
| Fig. 6 Strain hardening of the active gel due to motor activity with initial 3.5 mM ATP concentration. The response function is reduced after the myosin motors switch from a nonprocessive mode to a processive tension-generating mode at approximately 2.5 hours after addition of ATP. (A) Imaginary part of the creep compliance, J′′(ω) = 6πRα′′(ω), of an actomyosin gel measured using passive microrheology. The symbols are experimental results by Mizuno et al.6 and the lines are fits used to convert J* to G*. (B) Storage modulus obtained from the creep compliance shown in part A. | ||
B. Dynamic modulus of active gels from a Green–Kubo formula
For the derivation of the dynamic modulus we introduce the conditional probability ψst(![[small omega, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b4.gif) ,r;t|
,r;t|![[small omega, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b4.gif) 0,r0;0) (where
0,r0;0) (where ![[small omega, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b4.gif) :{s,F}) that an active filament at steady state is in attachment state s with strands that have a change in their end-to end distance r due to motor forces F at time t when it had the initial conformation r0 and the initial attachment state s0 at t = 0. The time-evolution of ψst(
:{s,F}) that an active filament at steady state is in attachment state s with strands that have a change in their end-to end distance r due to motor forces F at time t when it had the initial conformation r0 and the initial attachment state s0 at t = 0. The time-evolution of ψst(![[small omega, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b4.gif) ,r;t|s0,r0;0) obeys the same evolution equation as ψst(
,r;t|s0,r0;0) obeys the same evolution equation as ψst(![[small omega, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b4.gif) ,r;t), that is eqn (1), with initial condition given by ψst(ω,r;t = 0|
,r;t), that is eqn (1), with initial condition given by ψst(ω,r;t = 0|![[small omega, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b4.gif) 0,r0;0) = δ(r − r0)δs,s0.
0,r0;0) = δ(r − r0)δs,s0.
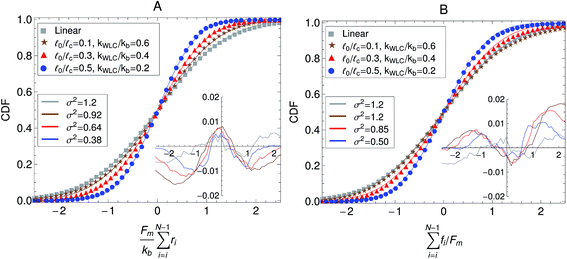
To obtain the relaxation modulus in a way similar to what is done in passive microrheology experiments, we use the Green–Kubo formula. This formula relates the relaxation modulus, G(t), of a material to the autocorrelation function of stress at equilibrium (see Appendix for derivation). We apply it at a non-equilibrium steady state without modification, in the same way the FDT is applied for the analysis of passive microrheology data in active gels. This requires the calculation of the autocorrelation function of stress at steady-state 〈σ(0)σ(t)〉st. Where σ is the normal stress in the direction of filament alignment in the bundle. For the mean-field single-chain model, such as the one under consideration, the macroscopic stress is related to the tension on the filaments by 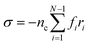 where fi is the tension on strand i and nc is the number of filaments per unit volume.40,41,54 For the calculations with linear springs σ simplifies to
where fi is the tension on strand i and nc is the number of filaments per unit volume.40,41,54 For the calculations with linear springs σ simplifies to 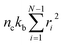 , whereas for WLC springs the tension fi is given by eqn (4). With these, the non-equilibrium steady-state relaxation modulus of the active gel is obtained from,
, whereas for WLC springs the tension fi is given by eqn (4). With these, the non-equilibrium steady-state relaxation modulus of the active gel is obtained from,
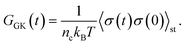 | (7) |
The Green–Kubo simulations start with an ensemble of filaments in which for all the filaments the beads have motors attached to them, and all the strands are relaxed (ri = 0 for all i) we let the ensemble of filaments reach steady state before calculating 〈σ(t) σ(0)〉st on the fly using the photon correlation spectroscopy algorithm.55,56
The relaxation modulus of the active single-chain mean-field model obtained from Green–Kubo simulations is shown in Fig. 7A. Where the symbols represent simulation results and the lines are fits used to carry the information to the frequency domain.50,57 By taking the one-sided Fourier transform of the relaxation modulus the non-equilibrium steady-state dynamic modulus of the active gel is obtained 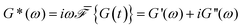 . Where
. Where 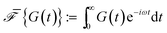 is the one-sided Fourier transform; G′GK(ω) is the storage modulus and G′′GK(ω) is the loss modulus. The storage modulus of the active bundle as predicted by our model is shown in Fig. 7B. A distinctive feature of this storage modulus is that it has a maximum. Extrema do not occur in the relaxation or storage modulus of passive networks, and therefore this is a specific feature of active gels. As we show in Section III.C this feature is essential to the violation of FDT observed in active gels. The storage modulus of the active single-chain mean-field model also has features in common with the storage modulus of passive temporary networks, such as the high frequency plateau in the storage modulus and the low frequency terminal zone in GGK′(ω) that goes as ω2.
is the one-sided Fourier transform; G′GK(ω) is the storage modulus and G′′GK(ω) is the loss modulus. The storage modulus of the active bundle as predicted by our model is shown in Fig. 7B. A distinctive feature of this storage modulus is that it has a maximum. Extrema do not occur in the relaxation or storage modulus of passive networks, and therefore this is a specific feature of active gels. As we show in Section III.C this feature is essential to the violation of FDT observed in active gels. The storage modulus of the active single-chain mean-field model also has features in common with the storage modulus of passive temporary networks, such as the high frequency plateau in the storage modulus and the low frequency terminal zone in GGK′(ω) that goes as ω2.
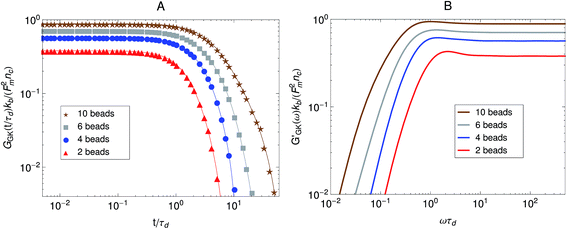 | ||
Fig. 7 Effect of the number of beads for a fixed strand rest length, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0, on the stress relaxation behavior of the active single-chain mean-field model with linear springs observed in a Green–Kubo simulation. Model parameters used were τa/τd = 0.005, τr,a/τd = 2, ζd/ζa = 0.1, and the Gamma motor force distribution shown in Fig. 3. (A) Relaxation modulus, symbols are simulation results and lines are fits used to transfer the information to the frequency domain. (B) Storage modulus obtained from the fits in part A. 0, on the stress relaxation behavior of the active single-chain mean-field model with linear springs observed in a Green–Kubo simulation. Model parameters used were τa/τd = 0.005, τr,a/τd = 2, ζd/ζa = 0.1, and the Gamma motor force distribution shown in Fig. 3. (A) Relaxation modulus, symbols are simulation results and lines are fits used to transfer the information to the frequency domain. (B) Storage modulus obtained from the fits in part A. | ||
In Part I we discussed how the shape of the dynamic modulus of the active network depends on the model parameters τa, τd and ζd, ζa. In general, we observe that as the values of τa/τd increase, G′′GK(ω) and the maximum in G′GK(ω) decrease slightly. The shape of the dynamic modulus does not depend strongly on the ratio τa/τd. On the other hand the position of the maxima in G′GK(ω) and G′′GK(ω) strongly depends on the ratio of friction coefficients ζa/ζd. When ζd is much smaller than ζa local relaxation of the filament upon motor detachment is faster than tension build-up when the motor is attached. Therefore stress relaxation in the gel occurs at shorter time scales (higher frequencies). Here we will focus on what changes when we relax some of the assumptions made in Part I.
First we consider the effect of the density of motor clusters in the dynamic modulus of active gels. In experiments the number of motors per filament is commonly used as a control parameter to study the effect of motor activity in the mechanical properties of active gels.3,19,58 For instance, rheological measurements in actomyosin gels58 have shown that varying the myosin concentration at fixed actin filament length has the same effect on the magnitude of the storage modulus of an actomyosin gel as varying the average actin filament length (with the capping protein gelsolin) for fixed myosin concentration. Therefore it has been suggested that the number of myosin thick filaments per actin filament is the relevant control parameter to study the effect of motors on the dynamic modulus of actomyosin gels. In the active single-chain mean-field model the number of motors per filament can be controlled by changing the number of beads, N, for a fixed rest length of the strands, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 and a fixed τa/τd ratio. Which is equivalent to varying the total rest length of the filaments,
0 and a fixed τa/τd ratio. Which is equivalent to varying the total rest length of the filaments, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) f = (N − 1)
f = (N − 1)![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0, for a fixed motor concentration. The average number density of active cross-links, at steady-state, is given by ncNτd/(τa + τd). Where nc is the number of filaments per unit volume and τd/(τa + τd) is the fraction of attached motors. If the motors are operating under strong attachment or high duty ratios, τa ≪ τd, such as the case under consideration, the average number density of active cross-links is approximately ncN.
0, for a fixed motor concentration. The average number density of active cross-links, at steady-state, is given by ncNτd/(τa + τd). Where nc is the number of filaments per unit volume and τd/(τa + τd) is the fraction of attached motors. If the motors are operating under strong attachment or high duty ratios, τa ≪ τd, such as the case under consideration, the average number density of active cross-links is approximately ncN.
The effect of increasing the number of motors per filament in the relaxation modulus of the active single-chain mean-field model is shown in Fig. 7A. We find that the magnitude of the relaxation modulus increases with increasing number of motors per filament. This tendency agrees with what is observed experimentally in actomyosin gels.58 In real systems however entanglements between myosin filaments contribute significantly to the modulus, especially in concentrated gels formed by long filaments.58 The results obtained with the single-chain mean-field model are also consistent with theoretical calculations in temporary networks formed by associating polymers,41,42 where the magnitude of the storage modulus also increases with increasing number of stickers per chain. Another effect of increasing the density of active cross-links is that the spectrum of relaxation times becomes broader making the longest relaxation time larger. The shape of the characteristic peak in G′GK(ω) also changes as the number of motors per filament is increased as can be observed in Fig. 7B. The peak is narrow and relatively high compared to the plateau for low motor densities. It becomes wider and relatively lower for larger motor densities, as τd and the longest relaxation time become more separated.
We previously considered only a linear version of our model, in which the strands were modeled by Fraenkel springs. However as has been shown on microrheology experiments in actomyosin gels6 (Fig. 6) molecular motors can cause strain hardening of the active gel. Therefore here we check for the effect of finite extensibility of the strands in the relaxation modulus observed in the Green–Kubo simulations. To perform a calculation similar to the experiments of Mizuno et al.6 we vary the initial stiffness of the strands by changing the ratio between the rest length of the strands, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0, and their contour length,
0, and their contour length, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) c. Strands for which
c. Strands for which ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 is closer to
0 is closer to ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) c can be thought of as being initially stiffer than strands for which the ratio
c can be thought of as being initially stiffer than strands for which the ratio ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0/
0/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) c is small. Fig. 8A shows the effect of finite-extensibility on the relaxation modulus obtained from Green–Kubo simulations. As the strands are made stiffer by making the ratio
c is small. Fig. 8A shows the effect of finite-extensibility on the relaxation modulus obtained from Green–Kubo simulations. As the strands are made stiffer by making the ratio ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0/
0/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) c larger there is an overall decrease in the magnitude of the relaxation modulus obtained from Green–Kubo simulations. The result for a chain with linear springs (i.e.,
c larger there is an overall decrease in the magnitude of the relaxation modulus obtained from Green–Kubo simulations. The result for a chain with linear springs (i.e., ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0/
0/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) c → 0) is shown as reference. The parameter kWLC for the non-linear springs is chosen such that their small-tension behavior matches the linear spring behavior. In addition to the overall decrease in magnitude, there is also a decrease in the slope of the relaxation modulus at long times, which means that the breadth of the spectrum of relaxation times of the active gel becomes larger as the strands are made stiffer. Fig. 8B shows the storage modulus obtained from the one-sided Fourier transform of the relaxation modulus shown in Fig. 8A. The same effects observed in the relaxation modulus can be seen here. For the linear springs the low-frequency behavior in G′GK(ω) is the ω2 typical of a terminal zone. On the other hand, at the same frequencies, the G′GK(ω) of the gel with the stiffer WLC springs considered displays a ω1.6 behavior and the terminal zone can not be observed in the calculated frequency window. This again indicates that the stiffer strands increase the breadth of the relaxation spectrum of the gel. These theoretical results agree qualitatively with the experimental observations of Mizuno et al.6 shown in Fig. 6 where stiffer filaments were also observed to produce a broader relaxation spectrum and an overall decrease in the modulus obtained from passive microrheology experiments in actomyosin gels.
c → 0) is shown as reference. The parameter kWLC for the non-linear springs is chosen such that their small-tension behavior matches the linear spring behavior. In addition to the overall decrease in magnitude, there is also a decrease in the slope of the relaxation modulus at long times, which means that the breadth of the spectrum of relaxation times of the active gel becomes larger as the strands are made stiffer. Fig. 8B shows the storage modulus obtained from the one-sided Fourier transform of the relaxation modulus shown in Fig. 8A. The same effects observed in the relaxation modulus can be seen here. For the linear springs the low-frequency behavior in G′GK(ω) is the ω2 typical of a terminal zone. On the other hand, at the same frequencies, the G′GK(ω) of the gel with the stiffer WLC springs considered displays a ω1.6 behavior and the terminal zone can not be observed in the calculated frequency window. This again indicates that the stiffer strands increase the breadth of the relaxation spectrum of the gel. These theoretical results agree qualitatively with the experimental observations of Mizuno et al.6 shown in Fig. 6 where stiffer filaments were also observed to produce a broader relaxation spectrum and an overall decrease in the modulus obtained from passive microrheology experiments in actomyosin gels.
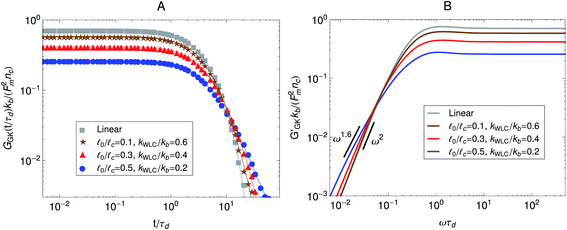 | ||
Fig. 8 Effect of strand stiffness on the stress relaxation behavior of the active single-chain mean-field model observed in a Green–Kubo simulation. Strands for which the ratio ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0/ 0/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) c is large can be considered more prestressed than strands for which the ratio c is large can be considered more prestressed than strands for which the ratio ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0/ 0/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) c is small. Model parameters used were τa/τd = 0.005, N = 6, τr,a/τd = 2, ζd/ζa = 0.1, and the Gamma motor force distribution shown in Fig. 3. Results shown are for a chain with six beads. kWLC for eqn (4) was chosen such that the small tension behavior matches the linear spring. (A) Relaxation modulus, symbols are simulation results and lines are fits used to transfer the information to the frequency domain. (B) Storage modulus obtained from the fits in part A. c is small. Model parameters used were τa/τd = 0.005, N = 6, τr,a/τd = 2, ζd/ζa = 0.1, and the Gamma motor force distribution shown in Fig. 3. Results shown are for a chain with six beads. kWLC for eqn (4) was chosen such that the small tension behavior matches the linear spring. (A) Relaxation modulus, symbols are simulation results and lines are fits used to transfer the information to the frequency domain. (B) Storage modulus obtained from the fits in part A. | ||
Other passive microrheology experiments in active gels have also shown that motor activity induces significant strain hardening of the semiflexible network. For instance, Stuhrmann et al.4 observed the statistics of the displacements of a tracer bead embedded in an in vitro cytoskeleton and found that the distribution of the bead position fluctuations becomes narrower with time due to motor activity. Moreover the position statistics develop non-Gaussian tails when the gels are activated with ATP. These observations have been attributed to the stiffening of the semiflexible filaments due to motor activity. The effect of molecular motors and strand semi-flexibility in the non-equilibrium statistics of the active single-chain mean-field model are shown in Fig. 9. The change in the total end-to-end length of the filaments, 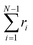 , is plotted in Fig. 9A and the non-equilibrium statistics of the total tension are shown in Fig. 9B. As the filaments are made stiffer by increasing the ratio
, is plotted in Fig. 9A and the non-equilibrium statistics of the total tension are shown in Fig. 9B. As the filaments are made stiffer by increasing the ratio ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0/
0/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) c these distributions become narrower (i.e., smaller variance). It can also be observed in the insets of Fig. 9 that the absolute residuals between the distributions obtained from the simulation and their best Gaussian fits are larger for the WLC filaments. This indicates that the molecular motors are indeed extending/compressing the filaments beyond the linear regime of the tension–extension relation. This explains why a tracer bead embedded in an active gel “feels” a non-harmonic potential. Note that there is a slight asymmetry in the absolute residuals between the distribution obtained from the simulation and their best Gaussian fit, this is due to the asymmetric character of the WLC tension–extension relation, eqn (4), where tension rises steeply for extensions but remains relatively flat for compressions. In real systems filaments actually buckle for small compressions, which leads to contraction of the entire gel. Buckling and contraction in active gels is discussed in Section V.
c these distributions become narrower (i.e., smaller variance). It can also be observed in the insets of Fig. 9 that the absolute residuals between the distributions obtained from the simulation and their best Gaussian fits are larger for the WLC filaments. This indicates that the molecular motors are indeed extending/compressing the filaments beyond the linear regime of the tension–extension relation. This explains why a tracer bead embedded in an active gel “feels” a non-harmonic potential. Note that there is a slight asymmetry in the absolute residuals between the distribution obtained from the simulation and their best Gaussian fit, this is due to the asymmetric character of the WLC tension–extension relation, eqn (4), where tension rises steeply for extensions but remains relatively flat for compressions. In real systems filaments actually buckle for small compressions, which leads to contraction of the entire gel. Buckling and contraction in active gels is discussed in Section V.
 | ||
| Fig. 9 Effect of the strand stiffness on the non-equilibrium steady state statistics of the active single-chain mean-field model. (A) Cumulative density function (CDF) of the change in the end-to-end length of the filaments due to motor activity. (B) CDF of the total tension on filaments due to motor activity. Model parameters used were τa/τd = 0.005, N = 6, τr,a/τd = 2, ζd/ζa = 0.1, and the Gamma motor force distribution shown in Fig. 3. Results shown are for a chain with six beads. kWLC for eqn (4) was chosen such that the small tension behavior matches the linear spring. Symbols are simulation results, the lines are fits to Gaussian CDFs. The lower legend shows the second moments of the fitted Gaussian curves and the insets show the absolute residuals between these fits and the simulation results. | ||
C. Dynamic modulus of active gels from a small step-strain calculation
To show that the active single-chain mean-field model violates FDT in the way active gels do,6 we calculate the dynamic modulus observed in the stress response to an externally applied small step-strain in the direction of filament orientation. We simulate an ensemble of chains with dynamics given by eqn (1), starting from an initial condition in which all the strands are relaxed (ri = 0 for all i) we let the ensemble of chains reach steady state before applying a small step-strain ε, at t = tst. We assume that on the time scale of interest for which G(t) is calculated the step-strain applied at the boundaries propagates instantaneously through the system. Therefore ri (t = tst+) = ri (t = tst−) + ε0ri (t = tst−) for i = 1, 2, 3, …, N − 1, where ε0 is the strain magnitude. Then the relaxation of stress back to its steady state value is followed. In this externally driven calculation the relaxation modulus is given by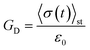 . The subscript D indicates that the modulus is obtained from an externally driven experiment (externally applied strain). To obtain the plots shown here we average over an ensemble of 3000 filaments.
. The subscript D indicates that the modulus is obtained from an externally driven experiment (externally applied strain). To obtain the plots shown here we average over an ensemble of 3000 filaments.
A plot of the relaxation modulus of the active single-chain mean-field model obtained from the step-strain calculation is shown in Fig. 10A. Similar to what is observed in the Green–Kubo calculations, the overall magnitude of the relaxation modulus increases with increasing density of motors, which is controlled by varying the number of beads, N, for a fixed rest length of the strands, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 and a fixed τa/τd ratio. Also, the breadth of the relaxation spectrum for the gel increases with increasing number of motors per filament. The storage moduli corresponding to the relaxation moduli shown in Fig. 10A are plotted in Fig. 10B. These results show a trend similar to what is observed in the rheological experiments of Koenderink et al.58 in actomyosin gels, who find that G′(ω) can be tuned over two orders of magnitude by controlling the number of myosin motors per actin filament. With increasing N, a behavior that goes as ∼ω0.5 appears at intermediate frequencies in the storage modulus obtained from the step-strain calculations. This viscoelastic relaxation behavior is of the Rouse type and does not appear in G′GK because in that case the characteristic peak appears instead. This type of relaxation behavior is also observed experimentally in the dynamic modulus of actomyosin gels measured using active microrheology (see Fig. 6). In the active single-chain mean-field model the Rouse behavior originates from the attachment/detachment of motors. However it does not become visible until the longest relaxation time becomes significantly larger and separated from τd. This type of low-frequency Rouse mode also appears in temporary networks formed by associating polymers,41,42 where it is called associative Rouse behavior, to distinguish it from another Rouse behavior observed at high frequencies in those type of systems. The frequency-dependent discrepancy between the modulus obtained from the Gree–Kubo formula and the one obtained from the step-strain calculation that appears at frequencies around 1/τd indicates a violation of the FDT.
0 and a fixed τa/τd ratio. Also, the breadth of the relaxation spectrum for the gel increases with increasing number of motors per filament. The storage moduli corresponding to the relaxation moduli shown in Fig. 10A are plotted in Fig. 10B. These results show a trend similar to what is observed in the rheological experiments of Koenderink et al.58 in actomyosin gels, who find that G′(ω) can be tuned over two orders of magnitude by controlling the number of myosin motors per actin filament. With increasing N, a behavior that goes as ∼ω0.5 appears at intermediate frequencies in the storage modulus obtained from the step-strain calculations. This viscoelastic relaxation behavior is of the Rouse type and does not appear in G′GK because in that case the characteristic peak appears instead. This type of relaxation behavior is also observed experimentally in the dynamic modulus of actomyosin gels measured using active microrheology (see Fig. 6). In the active single-chain mean-field model the Rouse behavior originates from the attachment/detachment of motors. However it does not become visible until the longest relaxation time becomes significantly larger and separated from τd. This type of low-frequency Rouse mode also appears in temporary networks formed by associating polymers,41,42 where it is called associative Rouse behavior, to distinguish it from another Rouse behavior observed at high frequencies in those type of systems. The frequency-dependent discrepancy between the modulus obtained from the Gree–Kubo formula and the one obtained from the step-strain calculation that appears at frequencies around 1/τd indicates a violation of the FDT.
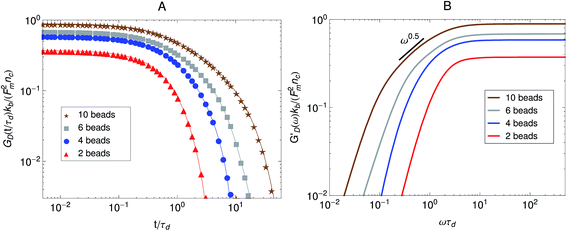 | ||
Fig. 10 Effect of the number of beads for a fixed strand rest length, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0, on the stress relaxation behavior of the active single-chain mean-field model with linear springs observed in a step-strain calculation. Model parameters used were τa/τd = 0.005, τr,a/τd = 2, ζd/ζa = 0.1, and the motor force distribution shown in Fig. 3. (A) Relaxation modulus, symbols are simulation results and lines are fits used to transfer the information to the frequency domain. (B) Storage modulus obtained from the fits in part A. 0, on the stress relaxation behavior of the active single-chain mean-field model with linear springs observed in a step-strain calculation. Model parameters used were τa/τd = 0.005, τr,a/τd = 2, ζd/ζa = 0.1, and the motor force distribution shown in Fig. 3. (A) Relaxation modulus, symbols are simulation results and lines are fits used to transfer the information to the frequency domain. (B) Storage modulus obtained from the fits in part A. | ||
D. FDT in active gels
By comparing the moduli obtained from the Green–Kubo simulations, shown in Fig. 7, with the moduli obtained from the step-strain simulations, shown in Fig. 10, it can now be checked if the active single-chain mean-field model describes the frequency-dependent violation of FDT observed in the microrheology of active gels. Fig. 11A shows a comparison between the relaxation modulus for a ten-bead chain with linear springs obtained from the Green–Kubo formula and the one obtained from the step-strain calculation. It can be observed that at high frequencies the two dynamic moduli are equal. At intermediate frequencies G′GK grows towards a maximum while G′D exhibits a Rouse relaxation behavior ∼ω0.5. Both G′GK and G′′D exhibit maxima but the maximum in G′′GK is larger than in G′′D. At lower frequencies, below the maximum, G′GK and G′D decrease as ω,2 while G′′GK and G′′D decrease as ω. The difference between G*GK and G*D persists as ω → 0.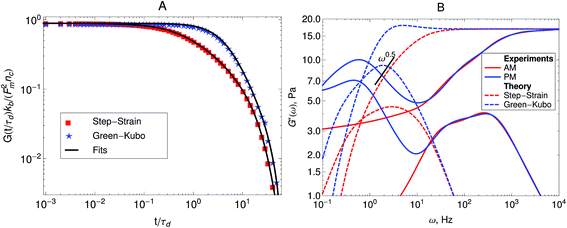 | ||
Fig. 11 Predictions of the active dumbbell model of the dynamic modulus of active gels. (A) Comparison between the modulus obtained from the Green–Kubo simulations and the modulus obtained from a step-strain simulation for a 10-beads chain. (B) Comparison of the dynamic modulus, G*(ω), predicted by the active single-chain mean-field model with the dynamic modulus determined from the passive (PM) and active (AM) microrheology experiments of Mizuno et al.6 The parameter values used in these figures are ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 = 1 μm, τa = 1 ms, τd = 200 ms, ζa = 0.8 μN s m−1ζa = 0.8 μN s m−1, ζd = 0.8 μN s m−1, N = 10, nc = 2.3 × 1013 filaments per m3 and the motor force distribution shown in Fig. 3. The parameter, ζa is fitted to the experimental data to match the time scale at which the moduli determined from passive and active microrheology start to diverge. 0 = 1 μm, τa = 1 ms, τd = 200 ms, ζa = 0.8 μN s m−1ζa = 0.8 μN s m−1, ζd = 0.8 μN s m−1, N = 10, nc = 2.3 × 1013 filaments per m3 and the motor force distribution shown in Fig. 3. The parameter, ζa is fitted to the experimental data to match the time scale at which the moduli determined from passive and active microrheology start to diverge. | ||
Fig. 11B presents a comparison between the dynamic moduli obtained from our theory and the microrheology experiments of Mizuno et al.6 in actomyosin gels. The parameters τa, τd, Fm and kb used for the prediction shown in Fig. 11B were determined from other experiments.18,19 Only ζa and ζd were fitted to the data of Mizuno et al.6 The frequency-dependent discrepancy between the response function of the active gel obtained from the step-strain and Green–Kubo calculations is in good qualitative agreement with the experimental observations of Mizuno et al.6 in microrheology experiments in actomyosin gels. The model also describes the characteristic maximum observed in the G′(ω) obtained from the passive microrheology technique, which causes G′GK to be larger than G′D at low frequencies. The frequency-dependent increase in the magnitude of the probe bead autocorrelation function observed in the passive microrheology of active gels is caused by the frequency-dependent stress fluctuations caused by motor activity. These fluctuations are therefore not related to the response function of the bead by the FDT. An additional, frequency-dependent term, is necessary to account for the magnitude and dynamics of motor activity. If such a modified FDT is used in the analysis of the passive microrheology data in active gels, it will account for a frequency-dependent increase in the magnitude of the probe bead autocorrelation, yielding the same dynamic modulus obtained from the active technique.38,39
The predictions shown in Fig. 11B are an improvement with respect to the ones presented in Part I, given the wider relaxation spectrum achieved by increasing the number of beads in the filaments from two beads to ten beads. However, there is still some discrepancy between the model predictions and the Experimental results. In the data, significant stress relaxation is occurring at frequencies between 101 to 103 Hz while in the model predictions most of the relaxation occurs at frequencies below 101 Hz. This could be due to a high polydispersity in the total lengths of actin filaments that form the gel, which can further increase the breadth of the relaxation spectrum of the gel. Accounting for polydispersity in the filament lengths is possible and straightforward to implement in the single-chain mean-field approach.59 However this will require experimental characterization of the molecular-weight distribution of actin filaments from which the active gel is formed. Accounting for dispersion17 in the rest length of the strands, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0, may also improve the predictions by increasing the breadth of the relaxation spectrum. However the model predictions are worst at the lower frequencies, where the experimental observations indicate that G′D(ω) goes to an elastic plateau, while the predictions present a terminal zone. The model also predicts a time scale for the maximum in G′GK(ω) that is about ten times shorter than the one observed experimentally. The two latter discrepancies are related to the fact that the actomyosin gels prepared by Mizuno et al.6 also contain biotin cross-links, while our model does not contain permanent passive cross-links, but only active cross-links (motors). When passive cross-linkers such as biotin or α-actinin are present in an actomyosin gel myosin contracts F-actin into dense foci around the passive cross-links. Once contracted, these aggregates can undergo further coalescence and may form larger length-scale structures such as asters or vortices.58 This in turn introduces longer time scales and length scales relevant for the dynamics of the active gel. The proposed single-chain mean-field framework does not yet seem appropriate for modeling those physics. Other descriptions such as multi-chain models27 or coarser levels of description22,23 have been used to describe such phenomena.
0, may also improve the predictions by increasing the breadth of the relaxation spectrum. However the model predictions are worst at the lower frequencies, where the experimental observations indicate that G′D(ω) goes to an elastic plateau, while the predictions present a terminal zone. The model also predicts a time scale for the maximum in G′GK(ω) that is about ten times shorter than the one observed experimentally. The two latter discrepancies are related to the fact that the actomyosin gels prepared by Mizuno et al.6 also contain biotin cross-links, while our model does not contain permanent passive cross-links, but only active cross-links (motors). When passive cross-linkers such as biotin or α-actinin are present in an actomyosin gel myosin contracts F-actin into dense foci around the passive cross-links. Once contracted, these aggregates can undergo further coalescence and may form larger length-scale structures such as asters or vortices.58 This in turn introduces longer time scales and length scales relevant for the dynamics of the active gel. The proposed single-chain mean-field framework does not yet seem appropriate for modeling those physics. Other descriptions such as multi-chain models27 or coarser levels of description22,23 have been used to describe such phenomena.
The deviation from the equilibrium FDT predicted by our model is additive and frequency-dependent and cannot, in general, be interpreted as an effective temperature. This result is in agreement with the conclusions of a recent and more general theoretical work by Ganguly and Chaudhuri34 in which an extension of the FDT for active systems was derived. In contrast to other models for active gels in which motor activity is accounted for by means of an effective temperature.24,35,36 These latter works can not, in general, predict the correct frequency-dependent violation of the FDT due to the use of an effective temperature to model motor activity. Other works38,39 have used an attachment/detachment jump process to model motor dynamics. However those models were postulated in a continuum level of description, where motors are treated as force dipoles embedded within a continuum. Those models have also been successful in describing some of the observations in the microrheology of active gels. However given their level of description, including physics such as finite extensibility of the network strands or realistic motor force distributions can be difficult.
IV. Super-diffusive mass transport
The “diffusion” of tracer beads or labeled filaments inside active gels has been extensively studied both experimentally and theoretically.38,39,49,60 In experiments, the mass transport of probe beads or filaments in active gels often exhibits super-diffusive behavior.49,60 This is different from passive networks where the mass transport of probe beads often exhibits sub-diffusive behavior due to the viscoelasticity of the medium. Head, Gompper, and Briels27 investigated the mass-transport of filaments in active gels using a multi-chain model. Their model also accounts for the elasticity of the filaments and for motor attachment/detachment dynamics. They find that filament translational motion ranges from diffusive to super-diffusive, depending on the ratio of attachment/detachment rates of the motors. And becomes sub-diffusive when motor forces are turned off.In our model mass transport can be quantified by the mean-squared displacement of the probe filament center, 〈ΔRc2(t)〉st. Fig. 12 shows 〈ΔRc2(t)〉st obtained from simulations of the active single-chain mean-field model for different values of the ratio of detachment and attachment rates. It can be observed that filament transport has behavior that ranges from diffusive 〈ΔRc2(t)〉st ∼ t to super-diffusive 〈ΔRc2(t)〉st ∼ tα with α as large as 2. It can be observed that for gels with weak motor attachment, large τa/τd ratio, filament translational motion of the filaments has two well-defined regions. At time scales shorter than τr,a the mean-squared displacement of filament centers goes roughly as t2 which is the characteristic ballistic behavior expected from a filament being pulled by motors. While for time scales larger than τr,a the behavior becomes diffusive. Note that we have not included Brownian forces in eqn (1) and therefore the apparent diffusive behavior that is observed in 〈ΔRc2(t)〉st at long times for large τa/τd ratios is not due to thermal motion of the filaments. In these weak attachment scenarios significant local relaxation occurs in the strands between motor attachment events. This causes the motion of the filament centers to become slower, since the filament has time to significantly retract between motor attachment events.
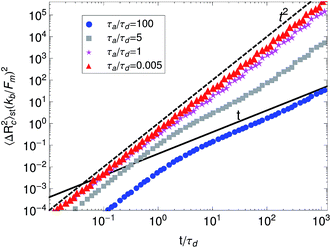 | ||
| Fig. 12 Mean-squared displacement of the probe filament center, 〈ΔRc2(t)〉st, of 3-beads filaments for different values of the ratio between detachment and attachment rates. For this simulations τr,a/τd = 2 and ζa/ζd = 0.1, we use the gamma motor force distribution shown in Fig. 3. The lines are given as reference for diffusive 〈ΔRc2(t)〉st ∼ t and super-diffusive behavior 〈ΔRc2(t)〉st ∼ tα, α > 0. | ||
In the strong motor attachment regime, achieved by making the ratio τa/τd smaller the two regions in 〈ΔRc2(t)〉st become less well-defined. For strong motor attachment the mean-squared displacement of filament centers deviates only slightly from the t2 behavior at long times. This is because in the strong attachment scenario almost no relaxation of the strands occurs between attachment events. This means that for the strong motor attachment mass-transport is mostly dominated by motor dynamics. The filament's and motor size (i.e.: friction coefficients) have a negligible effect in 〈ΔRc2(t)〉st in the strong motor attachment regime. These observations agree with what is observed in the simulations of Head, Gompper, and Briels27 who also find that in the strong motor attachment regime only slight deviations from super-diffusive behavior are observed in 〈ΔRc2(t)〉st. As discussed above, in the low and intermediate motor attachment regimes, they also observe sub-diffusion of the filaments at short time scales related to non-processive motors acting as passive cross-links which generate viscoelasticity of the aggregate structures that retards filament motion.61 Since our model does not account for permanent passive cross-links we do not observe this sub-diffusive behavior in the filaments' motion.
V. Buckling and contraction in active bundles
Recent experiments1,3,18 in actomyosin bundles without sarcomeric organization have shown that self-contraction, upon addition of ATP, is related to the buckling of individual F-actin filaments that form the bundle. In the experiments, individual bundles were observed and F-actin buckling was found coincident with contraction. Prior to ATP addition, compact bundles with aligned F-actin are observed. Upon ATP addition, the frequency of buckles increases rapidly during contraction, and then diminishes once contraction stops. These F-actin buckles are dynamic, with their amplitude, curvature, and location changing over time. Motor-induced buckling of actin filaments has been shown to be a ubiquitous process in the self-organization of the cellular cytoskeleton.1The main purpose of this Section is to expand the results presented in Part I by presenting more quantitative predictions of the buckling dynamics observed in active bundles. We also compare our model and results to the other single-chain mean-field description of active gels available in the literature.18 As pointed out in Section II, there are several differences in the level of description and mathematical formulation of the two models. Here we discuss in more detail how these differences reflect in a specific observable of the model. Using the model presented in Section II we calculate the fraction of buckled filament segments, ϕB, as a function of time after addition of ATP in the absence of externally applied strain. Before addition of ATP all the myosin motors are attached (as passive cross-links) and the strands between them have relaxed end-to-end length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0. Therefore a filament has total rest length
0. Therefore a filament has total rest length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) f = (N − 1)
f = (N − 1)![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0, where N is the number of myosin cross-links along the filament (beads). Upon addition of ATP, motor activity can change the end-to-end length of the strands by an amount r. This change can cause compression (r < 0) or extension (r > 0) of the strands. However F-actin filaments support large tensions but buckle easily under piconewton compressive loads.1,17 Therefore only strands under compression (r < 0) buckle. A compressed strand buckles when its tension f = −kbr reaches a buckling force threshold, FB. An estimation of this force threshold can be obtained by treating the filaments as thin elastic cylinders17,62
0, where N is the number of myosin cross-links along the filament (beads). Upon addition of ATP, motor activity can change the end-to-end length of the strands by an amount r. This change can cause compression (r < 0) or extension (r > 0) of the strands. However F-actin filaments support large tensions but buckle easily under piconewton compressive loads.1,17 Therefore only strands under compression (r < 0) buckle. A compressed strand buckles when its tension f = −kbr reaches a buckling force threshold, FB. An estimation of this force threshold can be obtained by treating the filaments as thin elastic cylinders17,62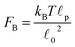 . For a typical F-actin filament, using the values presented in Section II, FB ∼ 0.1 pN. We simulate an ensemble of filaments and keep track of the number of strands that buckle in each filament. We then average over the ensemble of filaments and divide by the total number of strands in the filament to obtain ϕB.
. For a typical F-actin filament, using the values presented in Section II, FB ∼ 0.1 pN. We simulate an ensemble of filaments and keep track of the number of strands that buckle in each filament. We then average over the ensemble of filaments and divide by the total number of strands in the filament to obtain ϕB.
In Part I we presented buckling predictions with the dumbbell version of the model (N = 2). The analytic results presented there revealed that in our model buckling arises because a fraction of the filaments in the bundle exist in a motor attachment state where contraction is favored. This is achieved by maintaining the motor forces as stochastic state variables instead of pre-averaging eqn (1) over them. The filaments on attachment states that undergo contraction buckle when the tension in them reaches FB. However the model presented in Part I did not allow us to make quantitative predictions of the buckling dynamics. Since the dumbbell version had only two beads along the filament, which is not a sufficiently accurate representation of real systems. Additionally in Part I we assumed p(F) = (F − Fm) and therefore the filament compression was possible only in one of the attachment states of the dumbbell. Here we consider the case of N beads in a filament of total rest length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) f, and use a motor force distribution shown in Fig. 3. In Fig. 13 the effect that the number of beads has on the fraction of buckled filaments is shown. In general, the fraction of buckled filaments increases with the number of beads until reaching a maximum. After this maximum the fraction of buckled filaments sharply decreases with increasing number of beads. The fraction of buckled filaments also depends strongly on the width of the motor force distribution. For the case with a wider motor force distribution shown in Fig. 13A compression of filaments in a given attachment state is more likely to occur and this results in more buckling. The fraction of buckled filaments is reduced significantly when the width of the motor force distribution is reduced from δFm/Fm = 0.5 to δFm/Fm = 0.3 as can be observed in Fig. 13B.
f, and use a motor force distribution shown in Fig. 3. In Fig. 13 the effect that the number of beads has on the fraction of buckled filaments is shown. In general, the fraction of buckled filaments increases with the number of beads until reaching a maximum. After this maximum the fraction of buckled filaments sharply decreases with increasing number of beads. The fraction of buckled filaments also depends strongly on the width of the motor force distribution. For the case with a wider motor force distribution shown in Fig. 13A compression of filaments in a given attachment state is more likely to occur and this results in more buckling. The fraction of buckled filaments is reduced significantly when the width of the motor force distribution is reduced from δFm/Fm = 0.5 to δFm/Fm = 0.3 as can be observed in Fig. 13B.
We showed previously with the analytic solutions obtained in Part I that the steady state value of the fraction of buckled filaments depends strongly on the ratios ζa/ζd and τa/τd. For a given set of friction coefficients there is a critical value of τa/τd at which buckling occurs. If, the detachment rate of the motors becomes comparable to, or larger than the attachment rate then motor activity can not produce buckling of the filaments. Fig. 14 shows a more systematic exploration of the parameter space of the model with regards to buckling predictions. Note that we consider only the strong-attachment case (i.e.: τa/τd < 1) since this is the relevant case for the actomyosin bundles to which we compare our predictions. In Fig. 14A the effect of the density of beads along the filaments is shown. It can be observed that independently of the width of the motor force distribution and the ratio of friction coefficients the steady-state fraction of buckled filaments goes as 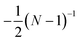 until it reaches a maximum around N = 17. For the number of beads larger than the location of this maximum, ϕB decreases in a way that also appears to be independent of the width of the motor force distribution and the ratio of friction coefficients. For the part of these curves that lies on the right side of the maximum the observed behavior can be interpreted as being due to the increase in the number of attachment states where compression of strands occurs caused by the higher density of active cross-links. However increasing the number of beads for a constant filament length
until it reaches a maximum around N = 17. For the number of beads larger than the location of this maximum, ϕB decreases in a way that also appears to be independent of the width of the motor force distribution and the ratio of friction coefficients. For the part of these curves that lies on the right side of the maximum the observed behavior can be interpreted as being due to the increase in the number of attachment states where compression of strands occurs caused by the higher density of active cross-links. However increasing the number of beads for a constant filament length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) f also makes the strands between beads shorter (i.e.:
f also makes the strands between beads shorter (i.e.: ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 =
0 = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) f/(N − 1)) and therefore stiffer since
f/(N − 1)) and therefore stiffer since 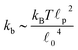 . When the curves in Fig. 14A reach their maxima it is because the latter effect becomes predominant over the former effect. This indicates that there exists a critical value for the number of beads in the filament for which buckling is maximized. For values of N larger than this critical value the stiffening of the strands dominates and ϕB drops sharply. In that regime the translational motion of the filaments is expected to be more relevant than the buckling dynamics. In Fig. 14B it can be observed that for values of N below the location of the maximum observed in Fig. 14B the curves of ϕBvs. t can be collapsed into a single master curve. The time shift factor goes with the number of beads in the filament as (N − 1)3.3 and is independent of δFm and ζd/ζa. For values of N larger than the critical value the buckling dynamics appear to be independent of the number of beads along the filament. This again indicates that below a critical number of beads (around N = 17), increasing the density of active cross-links along the filament can increase how fast contraction occurs in non-sarcomeric bundles, while for N larger than that critical value contraction dynamics are dominated by the stiffness of the strands and increasing the density of active cross-links has no effect.
. When the curves in Fig. 14A reach their maxima it is because the latter effect becomes predominant over the former effect. This indicates that there exists a critical value for the number of beads in the filament for which buckling is maximized. For values of N larger than this critical value the stiffening of the strands dominates and ϕB drops sharply. In that regime the translational motion of the filaments is expected to be more relevant than the buckling dynamics. In Fig. 14B it can be observed that for values of N below the location of the maximum observed in Fig. 14B the curves of ϕBvs. t can be collapsed into a single master curve. The time shift factor goes with the number of beads in the filament as (N − 1)3.3 and is independent of δFm and ζd/ζa. For values of N larger than the critical value the buckling dynamics appear to be independent of the number of beads along the filament. This again indicates that below a critical number of beads (around N = 17), increasing the density of active cross-links along the filament can increase how fast contraction occurs in non-sarcomeric bundles, while for N larger than that critical value contraction dynamics are dominated by the stiffness of the strands and increasing the density of active cross-links has no effect.
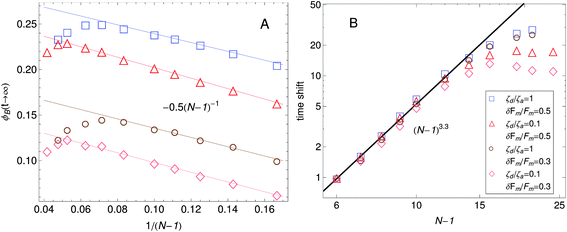 | ||
Fig. 14 Effect of the number of beads N, width of the motor for distribution, δFm, and ratio of detached to attached friction coefficients, ζa/ζd, on the fraction of buckled filaments. Simulations were performed with linear springs, with τa/τd set to 0.1. The total rest length of the filaments ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) f is held fixed, then the length of the strands is f is held fixed, then the length of the strands is ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 = 0 = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) f/(N − 1). Since f/(N − 1). Since 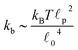 and and 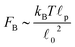 we make we make 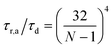 and and 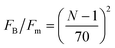 . (A) Steady state value of the fraction of buckled filaments. (B) Time shift required to collapse the different curves of ϕB such as the ones shown in Fig. 13 to a single master curve. . (A) Steady state value of the fraction of buckled filaments. (B) Time shift required to collapse the different curves of ϕB such as the ones shown in Fig. 13 to a single master curve. | ||
Fig. 15 shows a comparison between the fraction of buckled filaments predicted by the active single-chain mean-field model and contraction data for a non-sarcomeric actomyosin bundle reported by Lenz et al.18 The friction coefficients (i.e.: ζa and ζd) were used to fit the prediction to the data. The other parameters are known from independent measurements and were reported by Lenz et al.18 The values for the friction coefficients obtained from fitting the bundle contraction data are significantly larger than the ones obtained from the fits to the microrheology data of Mizuno et al.6 Although both experiments used actomyosin gels there were differences in their composition and ATP concentration. Moreover the gels prepared by Mizuno et al.6 also contained biotin—a passive cross-linker, while Lenz et al.18 used bundles in which the actin filaments are closely packed, which can translate into higher friction coefficients. The contour length of actin between myosin motors and the size of the myosin motor clusters can vary significantly depending on gel composition and preparation, which may explain the discrepancy in friction coefficients obtained from different experiments. The role of filament buckling as a mechanism in non-sarcomeric actomysosin bundle contraction has been observed experimentally.3,18 Network contraction has been observed to correspond exactly with the extent of individual F-actin shortening via buckling. Moreover in experiments19 it is observed that for low myosin density (N ≤ 2) bundle structure is weak and dissociation occurs upon addition of ATP. Intermediate myosin densities (N = 2 − 4) allow enough cross-linking within the bundles to maintain network integrity upon ATP addition, but contraction is not observed. For higher myosin densities (N > 4) myosin-generated forces lead to filament buckling and bundle contraction. We note that in its present form the active single-chain mean-field model can only describe contraction in active bundles containing myosin and actin alone. In these conditions, the length scale over which contraction occurs within the network is proportional to the F-actin length, consistent with poor network connectivity by myosin motors. Through the addition of permanent passive cross-linkers such as α-actinin the length of contraction can be increased to macroscopic length scales. This leads to the formation of structures such as asters and vortices that form due to clustering of actin filaments around the permanent cross-links.
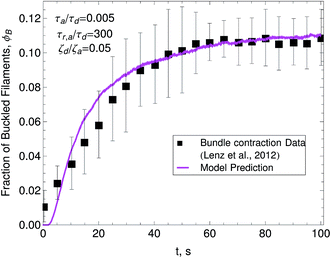 | ||
Fig. 15 Fraction of buckled filaments, ϕB, in a active bundle after addition of ATP as predicted by the active single-chain mean-field model. Predictions are compared to the contraction data of an actomyosin bundle reported by Lenz et al.18 ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 = 1 μm, τa = 1 ms, τd = 200 ms, ζa = 121 μN s m−1, ζd = 6.1 μN s m−1, N = 10, and the motor force distribution shown in Fig. 3. The only parameters fitted to the contraction data are the friction coefficients. 0 = 1 μm, τa = 1 ms, τd = 200 ms, ζa = 121 μN s m−1, ζd = 6.1 μN s m−1, N = 10, and the motor force distribution shown in Fig. 3. The only parameters fitted to the contraction data are the friction coefficients. | ||
Some previous attempts have also been made to use microscopic models to describe buckling of filaments in nonsarcomeric active bundles,18,63 however, to our knowledge, this is the first attempt to quantitatively describe the dynamics of buckling formation. For instance Lenz et al.18 proposed a single-chain bead-spring model to explain their bundle contraction data. They also investigated the effect of density of active crosslinks and found that there is a value for which contraction is maximized. They found that strong active cross-linking suppress buckling while filaments with very sparse motors do not buckle. Our results are apparently in agreement with their theoretical results. As discussed in Section II we assumed a single value for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0— in real systems a distribution of
0— in real systems a distribution of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 is expected. Lenz et al.18 studied the effect of a distribution of
0 is expected. Lenz et al.18 studied the effect of a distribution of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 by arbitrarily assuming a uniform distribution and found that it does not have a qualitative effect in their model predictions. However there is a fundamental difference on how the model presented in this paper and the model by Lenz et al.18 explain the mechanisms that cause buckling and self-contraction in active bundles as was discussed in Section II. In the model presented here buckling arises because a fraction of the filaments in the bundle exist in a motor attachment state where contraction is favored. In the model of Lenz et al.18 buckling arises due to a spatial gradient of the motor stall forces.
0 by arbitrarily assuming a uniform distribution and found that it does not have a qualitative effect in their model predictions. However there is a fundamental difference on how the model presented in this paper and the model by Lenz et al.18 explain the mechanisms that cause buckling and self-contraction in active bundles as was discussed in Section II. In the model presented here buckling arises because a fraction of the filaments in the bundle exist in a motor attachment state where contraction is favored. In the model of Lenz et al.18 buckling arises due to a spatial gradient of the motor stall forces.
VI. Conclusions
We presented a single-chain mean-field mathematical model for active gels that can describe several experimental observations. For instance, our model describes the dynamic modulus and the frequency-dependent violation of the fluctuation-dissipation theorem observed in active gels. It also describes the super-diffusion of filaments and the contraction mechanisms in non-sarcomeric active bundles. The model allows accounting for physics that are not available in models that have been postulated on coarser levels of description.18,38,39 Recently microscopic multi-chain models for describing the dynamics of active gels have also been proposed.27,61 However for realistic chain lengths and densities the numerical simulation of those models is notoriously expensive. This makes observables such as the relaxation modulus difficult to calculate for time-scales of practical interest. Here we have proposed a more coarse grained level of description that overcomes those limitations by using a mean-field approach. Although our framework can not yet account for the large length scale physics that arise when permanent cross-links are present, it provides important insight into the role of molecular motors in the mechanical properties of active gels.In Part I28 we made several assumptions to simplify the mathematics and with the aim of obtaining analytical results. In the present manuscript we discussed numerical simulations results for a more general version of the model and examined the effect of relaxing some of the aforementioned assumptions. We implemented experimentally measured motor force distributions into the model, generalized the differential Chapman–Kolmogorov equation to bead-spring chains made of multiple beads and examined the effect of finite extensibility of the filament segments. This allowed a more quantitative description of the role of molecular motors in the rheology and mechanical properties of active gels. For instance, we presented quantitative agreement of the predictions of buckling dynamics in non-sarcomeric actomyosin bundles with the contraction data of Lenz et al.18 We were also able to look at the effect of density of active cross-links along the filaments and find that there is a fairly universal density for which buckling is maximized. This universality arises from the competing effects of increased motor activity and strand stiffening as the density of active cross-links along the filament is increased.
By increasing the length of the filaments we were also able to increase the breadth of the relaxation spectrum of the gel which improved the agreement of the dynamic modulus predictions with the data of Mizuno et al.6 The effect of finite extensibility of the filament strands on the dynamic modulus obtained from the Green–Kubo formula was also found to be in agreement with the passive microrheology experiments of Mizuno et al.6 The strain hardening of the filaments causes an overall decrease in the response function observed in passive microrheology experiments as well as a slowdown of the stress relaxation processes in the gel. This is observed in our simulations as a decrease in the slope of the terminal zone of the storage modulus obtained from the Green–Kubo simulations. We also calculated the mass transport of filaments in the active gel using our model. We found that the mean-squared displacement of filament centers has a behavior that varies from diffusive to super-diffusive depending on the motor attachment and detachment rates. These results are in agreement with experimental results49,60 as well a observations in multi-chain simulations.27
By removing some assumptions we obtained certain improvements in the quality of the predictions of the active single-chain mean-field model for active gels. However, fully quantitative predictions will require a more accurate bead-spring description of the semiflexible filaments which includes, in addition to finite-extensibility, bending potentials between the springs.48 Polydispersity in the molecular weight of the filaments is also expected to be important in biological networks and could have an impact in the quality of the predictions. This will require characterization of the molecular weight distribution of the filaments forming the gel. Including specific details about the motor protein used to prepare the gel might also be necessary to have a fully quantitative description of the rheology of active gels. For instance, different myosin isoforms have been shown to have different sensitivity to tension.13 Including all these additional physics in the framework of our model is straightforward. However we note that this will introduce additional parameters into the model that must be determined either from experiments or independent theories.
We are grateful to the Army Research Office (grants W911NF-09-2-0071 and W911NF-09-1-0378) for financial support.
Appendix A: Derivation of the Green–Kubo formula
Consider a physical system described by the set of state variables Ω, which may be deterministic (e.g., position and momentum) or coarse-grained variables. Now let ψ(Ω; t) be the probability density describing the probability that the system is in state Ω at time t. The time evolution for ψ(Ω; t) is given by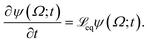 | (A1) |
The linear operator ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) eq may be the Liouville operator for atoms, or an infinitesimal generator for a Fokker–Planck or differential Chapman–Kolmogorov equation. Formally, we can write the solution of eqn (A1) as ψ(Ω;t)=e
eq may be the Liouville operator for atoms, or an infinitesimal generator for a Fokker–Planck or differential Chapman–Kolmogorov equation. Formally, we can write the solution of eqn (A1) as ψ(Ω;t)=e![[script L]](https://www.rsc.org/images/entities/char_e144.gif) eqtψ(Ω;0). The equilibrium probability density ψeq(Ω) is
eqtψ(Ω;0). The equilibrium probability density ψeq(Ω) is
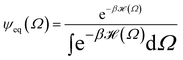 | (A2) |
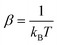 , and
, and ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (Ω) is the Hamiltonian for an atomistic level of description or the free energy for a single-chain level of description.
(Ω) is the Hamiltonian for an atomistic level of description or the free energy for a single-chain level of description.
Now consider that the system is in an initial equilibrium state denoted by Ω0. At t = 0 a small step-strain of magnitude ε0 is applied to the system. The subset of Ω that is changed by the external perturbation is denoted by x. The microscopic stress, ![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) (x) can be written in terms of
(x) can be written in terms of ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (Ω) using a virtual work argument,64
(Ω) using a virtual work argument,64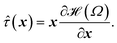
At this point it is useful to introduce the marginal probability density ϕ(x;t) = ∫ψ(Ω;t)d![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) where
where ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) is the subset of Ω not contained in x. Then ϕ(x;t) for t = 0 + is given by,
is the subset of Ω not contained in x. Then ϕ(x;t) for t = 0 + is given by,
| ϕ+(x;t) = ∫δ(x −[δ + γ]x0)ψeq(Ω0)dΩ0 | (A3) |
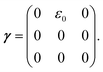 | (A4) |
We assume that the step-strain, applied at the boundaries, propagates instantaneously through the system, on the time scale of interest for which G(t) is calculated. eqn (A3) can be written in terms of ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (Ω) by making use of eqn (A2)
(Ω) by making use of eqn (A2)
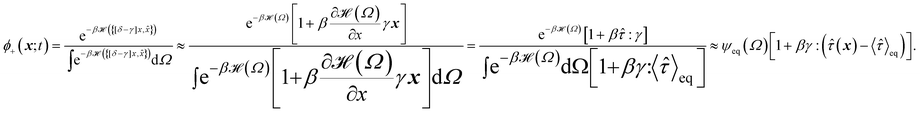 | (A5) |
![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) (x) given above.
(x) given above.
The macroscopic stress that is observed after applying the step strain, t ≥ 0, is
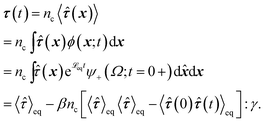 | (A6) |
![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) 〉eq = 〈
〉eq = 〈![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) (0)〉eq = 〈
(0)〉eq = 〈![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) (t)〉eq to obtain the last line. The relaxation modulus is obtained from,
(t)〉eq to obtain the last line. The relaxation modulus is obtained from,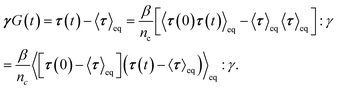 | (A7) |
![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) and eqn (A6) to obtain the first line. By defining δτ(t) = τ(t) − 〈τ〉eq we obtain the Green–Kubo formula for stress,
and eqn (A6) to obtain the first line. By defining δτ(t) = τ(t) − 〈τ〉eq we obtain the Green–Kubo formula for stress,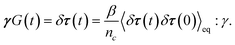 | (A8) |
In the main text we consider the case of a bundle of filaments aligned in the z direction to which a step-strain of magnitude ε0 is applied in the direction of filament orientation. Therefore γzz = ε0, and all the other components of γ are set equal to zero. The fluctuations of the zz component of stress, σ(t) = δτzz(t), are followed.
References
- M. S. e Silva, M. Depken, B. Stuhrmann, M. Korsten, F. C. MacKintosh and G. H. Koenderink, Active multistage coarsening of actin networks driven by myosin motors, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 9408–9413 CrossRef PubMed.
- T. Surrey, F. Nédélec, S. Leibler and E. Karsenti, Physical properties determining self-organization of motors and microtubules, Science, 2001, 292, 1167–1171 CrossRef CAS PubMed.
- M. P. Murrell and M. L. Gardel, F-actin buckling coordinates contractility and severing in a biomimetic actomyosin cortex, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 20820–20825 CrossRef CAS PubMed.
- B. Stuhrmann, M. S. e. Silva, M. Depken, F. C. MacKintosh and G. H. Koenderink, Nonequilibrium fluctuations of a remodeling in vitro cytoskeleton, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 020901 CrossRef.
- O. J. N. Bertrand, D. K. Fygenson and O. A. Saleh, Active, motor-driven mechanics in a DNA gel, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 17342–17347 CrossRef CAS PubMed.
- D. Mizuno, C. Tardin, C. F. Schmidt and F. C. MacKintosh, Nonequilibrium mechanics of active cytoskeletal networks, Science, 2007, 315, 370–373 CrossRef CAS PubMed.
- A. F. Huxley, Muscular contraction, J. Physiol., 1974, 243, 1 CAS.
- T. L. Hill, E. Eisenberg, Y. D. Chen and R. J. Podolsky, Some self-consistent two-state sliding filament models of muscle contraction, Biophys. J., 1975, 15, 335–372 CrossRef CAS.
- A. Yamada and T. Wakabayashi, Movement of actin away from the center of reconstituted rabbit myosin filament is slower than in the opposite direction, Biophys. J., 1993, 64, 565–569 CrossRef CAS.
- F. Jülicher and J. Prost, Cooperative molecular motors, Phys. Rev. Lett., 1995, 75, 2618–2621 CrossRef.
- R. W. Lymn and E. W. Taylor, Mechanism of adenosine triphosphate hydrolysis by actomyosin, Biochemistry, 1971, 10, 4617–4624 CrossRef CAS.
- F. Jülicher, A. Ajdari and J. Prost, Modeling molecular motors, Rev. Mod. Phys., 1997, 69, 1269 CrossRef.
- K. I. Morozov and L. M. Pismen, Strain dependence of cytoskeleton elasticity, Soft Matter, 2012, 8, 9193–9199 RSC.
- H. Shuman, M. J. Greenberg, A. Zwolak, T. Lin, C. V. Sindelar, R. Dominguez and E. M. Ostap, A vertebrate myosin-I structure reveals unique insights into myosin mechanochemical tuning, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(6), 2116–2121 CrossRef CAS PubMed.
- J. F. Marko and E. D. Siggia, Stretching DNA, Macromolecules, 1995, 28, 8759–8770 CrossRef CAS.
- F. Gittes and F. C. MacKintosh, Dynamic shear modulus of a semiflexible polymer network, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1998, 58, 1241–1244 CrossRef.
- C. Storm, J. J. Pastore, F. C. MacKintosh, T. C. Lubensky and P. A. Janmey, Nonlinear elasticity in biological gels, Nature, 2005, 435, 191–194 CrossRef CAS PubMed.
- M. Lenz, T. Thoresen, M. L. Gardel and A. R. Dinner, Contractile units in disordered actomyosin bundles arise from F-actin buckling, Phys. Rev. Lett., 2012, 108, 238107 CrossRef.
- T. Thoresen, M. Lenz and M. L. Gardel, Reconstitution of contractile actomyosin bundles, Biophys. J., 2011, 100, 2698–2705 CrossRef CAS PubMed.
- K. Kruse and K. Sekimoto, Growth of fingerlike protrusions driven by molecular motors, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 031904 CrossRef CAS.
- K. Kruse, J. Joanny, F. Jülicher, J. Prost and K. Sekimoto, Asters, vortices, and rotating spirals in active gels of polar filaments, Phys. Rev. Lett., 2004, 92, 78101 CrossRef CAS.
- K. Kruse and F. Jülicher, Self-organization and mechanical properties of active filament bundles, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 051913 CrossRef.
- I. S. Aranson and L. S. Tsimring, Pattern formation of microtubules and motors: inelastic interaction of polar rods, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 050901 CrossRef.
- T. B. Liverpool and M. C. Marchetti, Rheology of active filament solutions, Phys. Rev. Lett., 2006, 97, 268101 CrossRef CAS.
- M. E. Cates, S. M. Fielding, D. Marenduzzo, E. Orlandini and J. M. Yeomans, Shearing active gels close to the isotropic-nematic transition, Phys. Rev. Lett., 2008, 101, 068102 CrossRef CAS.
- L. Giomi, T. B. Liverpool and M. C. Marchetti, Sheared active fluids: Thickening, thinning, and vanishing viscosity, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 051908 CrossRef.
- D. A. Head, G. Gompper and W. Briels, Microscopic basis for pattern formation and anomalous transport in two-dimensional active gels, Soft Matter, 2011, 7, 3116–3126 RSC.
- A. Córdoba, J. D. Schieber and T. Indei, A single-chain model for active gels I: active dumbbell model, RSC Adv, 2014, 4, 17935–17949 RSC.
- T. Indei, J. D. Schieber and A. Córdoba, Competing effects of particle and medium inertia on particle diffusion in viscoelastic materials, and their ramifications for passive microrheology, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 041504 CrossRef.
- A. Córdoba, T. Indei and J. D. Schieber, The effects of compressibility, hydrodynamic interaction and inertia on two-point, passive microrheology of viscoelastic materials, Soft Matter, 2013, 9, 3521 RSC.
- J. D. Schieber, A. Córdoba and T. Indei, The analytic solution of Stokes for time-dependent creeping flow around a sphere: application to linear viscoelasticity as an ingredient for the Generalized Stokes-Einstein relation and microrheology analysis, J. Non-Newtonian Fluid Mech., 2013, 200, 3–8 CrossRef CAS PubMed.
- J. Prost, J.-F. Joanny and J. M. R. Parrondo, Generalized fluctuation-dissipation theorem for steady-state systems, Phys. Rev. Lett., 2009, 103, 090601 CrossRef CAS.
- P. Bohec, F. Gallet, C. Maes, S. Safaverdi, P. Visco and F. van Wijland, Probing active forces via a fluctuation-dissipation relation: Application to living cells, Europhys. Lett., 2013, 102, 50005 CrossRef.
- C. Ganguly and D. Chaudhuri, Stochastic thermodynamics of active brownian particles, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 032102 CrossRef.
- T. B. Liverpool, A. C. Maggs and A. Ajdari, Viscoelasticity of solutions of motile polymers, Phys. Rev. Lett., 2001, 86, 4171–4174 CrossRef CAS.
- T. B. Liverpool and M. C. Marchetti, Bridging the microscopic and the hydrodynamic in active filament solutions, Europhys. Lett., 2007, 69, 846 CrossRef.
- J. Palacci, C. Cottin-Bizonne, C. Ybert and L. Bocquet, Sedimentation and effective temperature of active colloidal suspensions, Phys. Rev. Lett., 2010, 105, 088304 CrossRef.
- A. J. Levine and F. C. MacKintosh, The mechanics and fluctuation spectrum of active gels, J. Phys. Chem. B, 2009, 113, 3820–3830 CrossRef CAS PubMed.
- D. A. Head and D. Mizuno, Nonlocal fluctuation correlations in active gels, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 041910 CrossRef CAS.
- J. G. Hernández Cifre, T. H. Barenbrug, J. D. Schieber and B. H. A. A. van den Brule, Brownian dynamics simulation of reversible polymer networks under shear using a non-interacting dumbbell model, J. Non-Newtonian Fluid Mech., 2003, 113, 73–96 CrossRef.
- T. Indei and J. Takimoto, Linear viscoelastic properties of transient networks formed by associating polymers with multiple stickers, J. Chem. Phys., 2010, 133, 194902 CrossRef PubMed.
- T. Indei, J. D. Schieber and J. Takimoto, Effects of fluctuations of cross-linking points on viscoelastic properties of associating polymer networks, Rheol. Acta, 2012, 51, 1021–1039 CrossRef CAS.
- F. C. MacKintosh, J. Käs and P. A. Janmey, Elasticity of semiflexible biopolymer networks, Phys. Rev. Lett., 1995, 75, 4425–4428 CrossRef CAS.
- M. Fixman and J. Kovac, Polymer conformational statistics. iii. Modified gaussian models of stiff chains, J. Chem. Phys., 1973, 58, 1564 CrossRef CAS PubMed.
- P. T. Underhill and P. S. Doyle, Alternative spring force law for bead-spring chain models of the worm-like chain, J. Rheol., 2006, 50, 513 CrossRef CAS.
- P. T. Underhill and P. S. Doyle, On the coarse-graining of polymers into bead-spring chains, J. Non-Newtonian Fluid Mech., 2004, 122, 3–31 CrossRef CAS PubMed.
- E. F. Koslover and A. J. Spakowitz, Systematic coarse-graining of microscale polymer models as effective elastic chains, Macromolecules, 2013, 46, 2003–2014 CrossRef CAS.
- E. F. Koslover and A. J. Spakowitz, Discretizing elastic chains for coarse-grained polymer models, Soft Matter, 2013, 9, 7016–7027 RSC.
- A. W. C. Lau, B. D. Hoffman, A. Davies, J. C. Crocker and T. C. Lubensky, Microrheology, stress fluctuations, and active behavior of living cells, Phys. Rev. Lett., 2003, 91, 198101 CrossRef CAS.
- M. Baumgaertel and H. H. Winter, Determination of discrete relaxation and retardation time spectra from dynamic mechanical data, Rheol. Acta, 1989, 28, 511–519 CrossRef CAS.
- F. C. MacKintosh and A. J. Levine, Nonequilibrium mechanics and dynamics of motoractivated gels, Phys. Rev. Lett., 2008, 100, 18104 CrossRef CAS.
- D. Chandler, Introduction to modern statistical mechanics, Oxford University Press, 1987, vol. 1 Search PubMed.
- J. D. Schieber and K. Horio, Fluctuation in entanglement positions via elastic slip-links, J. Chem. Phys., 2010, 132, 074905 CrossRef PubMed.
- R. B. Bird, C. F. Curtiss, R. C. Armstrong and O. Hassager, Dynamics of Polymeric Liquids, Wiley-Interscience, 1996, vol. 2 Search PubMed.
- D. Frenkel and B. Smit, Understanding molecular simulation: from algorithms to applications, Academic press, 2nd edn, 2001 Search PubMed.
- D. Magatti and F. Ferri, Fast multi-tau real-time software correlator for dynamic light scattering, Appl. Opt., 2001, 40, 4011–4021 CrossRef CAS.
- M. Baumgaertel and H. H. Winter, Interrelation between continuous and discrete relaxation time spectra, J. Non-Newtonian Fluid Mech., 1992, 44, 15–36 CrossRef CAS.
- G. H. Koenderink, Z. Dogic, F. Nakamura, P. M. Bendix, F. C. MacKintosh, J. H. Hartwig, T. P. Stossel and D. A. Weitz, An active biopolymer network controlled by molecular motors, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15192–15197 CrossRef CAS PubMed.
- M. Katzarova, M. Andreev, Y. R. Sliozberg, R. A. Mrozek, J. L. Lenhart, J. W. Andzelm and J. D. Schieber, Rheological predictions of network systems swollen with entangled solvent, AIChE Journal, 2014, 60, 1372–1380 CrossRef CAS.
- T. Sanchez, D. T. Chen, S. J. DeCamp, M. Heymann and Z. Dogic, Spontaneous motion in hierarchically assembled active matter, Nature, 2012, 491, 431–434 CrossRef CAS PubMed.
- D. A. Head, W. J. Briels and G. Gompper, Nonequilibrium structure and dynamics in a microscopic model of thin-film active gels, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 032705 CrossRef CAS.
- F. Gittes, B. Mickey, J. Nettleton and J. Howard, Flexural rigidity of microtubules and actin filaments measured from thermal fluctuations in shape, J. Cell Biol., 1993, 120, 923–934 CrossRef CAS.
- M. Lenz, M. L. Gardel and A. R. Dinner, Requirements for contractility in disordered cytoskeletal bundles, New J. Phys., 2012, 14, 033037 CrossRef PubMed.
- R. J. Steenbakkers and J. D. Schieber, Derivation of free energy expressions for tube models from coarse-grained slip-link models, J. Chem. Phys., 2012, 137, 034901 CrossRef PubMed.
Footnote |
| † Current address for Andrés Córdoba and Jay D. Schieber: Institute for Molecular Engineering, University of Chicago, 5747 South Ellis Avenue, Chicago, Illinois 60637, USA. |
| This journal is © The Royal Society of Chemistry 2015 |