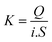Clayey–sand filter for the removal of pharmaceuticals from wastewater effluent: percolation experiments†
T.
Thiebault
*,
M.
Boussafir
,
R.
Guégan
,
C.
Le Milbeau
and
L.
Le Forestier
Institut des Sciences de la Terre d'Orléans, UMR 7327, Univ Orléans, CNRS, BRGM, 1A Rue de la Férollerie, 45071 Orléans, France. E-mail: thomas.thiebault@cnrs-orleans.fr
First published on 6th April 2016
Abstract
The objective of the study was to evaluate the sorption of a pool of pharmaceutically active compounds (PhACs) onto a clay–sand filter in a dynamic sorption experiment. The chosen adsorbent should have suitable chemical properties for the removal of the targeted PhACs and also a consistent hydrodynamic behavior regarding field application. In this aim, the impact of interfoliar cations (Ca2+ or Na+) intercalated into natural montmorillonite (Swy2) was tested by using different clay–sand ratios (from 0% to 100% of clay minerals). Only Ca-Swy2 showed a consistent hydraulic conductivity for field application with a value of 4.78 × 10−8 m s−1 for a 5%/95% clay–sand ratio. The sorption of PhACs onto this filter was investigated using œdometer cells by varying two parameters: the solution matrix (ultra-pure water or natural effluent) and the injection pressure (0.1 MPa and 0.2 MPa). The PhACs were effectively adsorbed onto the filter for each experiment at different levels. The drop in injection pressure was a favorable factor for sorption whatever the matrix was, with median global removal of ∼45% at 0.2 MPa and ∼75% at 0.1 MPa. The effect of the matrix exhibited two different trends as a function of the molecular charge of each PhAC. While cationic compounds were more effectively sorbed in the ultra-pure water matrix than in the effluent matrix, the sorption of anionic PhACs was more effective in the effluent matrix than in ultra-pure water. This indicates that the charge of the pollutant is a key parameter in controlling the efficiency of the adsorbent. Despite these removal variations, the filter exhibited a significant sorption capacity especially at 0.1 MPa. It can therefore be an efficient solution for the removal of PhACs by tertiary filtration.
Water impactThis work presents a new approach for the purification of pharmaceuticals by using a natural geosorbent (montmorillonite) in percolation experiment with a significant flow. The removal values, whatever the charge of the pollutant was, allowed us to think about the potential of this material at a larger scale. |
Introduction
Emerging Pollutants (EPs) represent a common form of pollution in numerous water compartments, from effluents to drinking water. Pharmaceutically Active Compounds (PhACs) account for more than 3000 compounds among the most concentrated and persistent ones in the environment.1,2 They constitute a representative part of EPs due to their wide variety of chemical properties.3,4Ever since the study by Richardson and Bowron highlighted the fate of pharmaceutical residues in the environment,5 several investigations have been conducted in this field over the last thirty years. Studies have focused on the removal of PhACs in Waste-Water Treatment Plants (WWTPs),6,7 and on improving the sensitivity of analytical methods in order to better characterize their occurrence in the environment.8,9
There are three main types of WWTPs: activated sludge treatment plants, phytoplanted filters or lagoon-based systems, but the removal of EPs remains insufficient for all of them.10–12 The main consequence of this lack of efficiency is the constant discharge of PhACs into the aquatic system. Even if PhACs are present in natural waters at relatively low concentrations, from several ng L−1 to μg L−1,4,13 their toxicity has been widely proved,14,15 particularly for endocrine disruptors.16,17 Moreover, some PhACs can be concentrated in natural beings,18 and contaminate the whole trophic chain including humans with poorly-known consequences.19 While this contamination goes beyond issues of human health, it raises awareness of the hazards generated by EPs and particularly PhACs.
Waste-water treatment is framed by two major factors: purification capacity and cost. Numerous innovative methods such as activated carbon or UV-oxidation exhibit excellent results for the removal of EPs but are often reserved for drinking water treatment due to prohibitive costs.20 In addition, oxidation creates metabolites,21 whose toxicity is still unknown today.
Ali et al. showed by a simple calculation between several removal techniques that adsorption mechanisms are the most appropriate and easiest way to remove both inorganic and organic micro-pollutants,22 since the adsorbent material has a large specific surface and a good affinity with the targeted micro-pollutants.23,24
Natural materials such as clays offer a good balance between reactivity and cost for the treatment of effluents.25 The efficiency of clays CEC (Cationic Exchange Capacity) in water is well documented.26–28 After all, numerous PhACs are not in cationic forms but in neutral or anionic forms under environmental conditions. Another key parameter is the influence of the solid–liquid ratio, which is often very remote from realistic applications.29,30 The latter two studies sought to gain a better understanding of the sorption mechanisms in which the starting concentrations are often largely overestimated compared to simulation approaching field conditions. To our knowledge, no study has investigated the sorption of PhACs at low starting concentrations (25 μg L−1) onto natural clays. However, sorption experiments with PhAC concentrations that are as close as possible to those found in natural environments and water purification plants are necessary in order to estimate the efficiency of sand and clay mixtures and the real affinities between the tested materials and the targeted pollutants.
A similar concern also frames the choice of the geosorbents and their characteristics as interlayer cations, which control the sorption capacity and hydrodynamic behavior.31,32
In view of the well-established capacity of clays to remove numerous compounds from water, the present study addressed three main issues: (i) the real capacity of slightly modified clay to treat a complex solution in pure water or effluent (ii) the impact of the kinetic transfer and the matrix effect on the sorption and (iii) the feasibility of a clay-based filter for the removal of PhACs.
Materials and methods
Filter: clay minerals and sand
The sand used was uniformly fine-grained Fontainebleau quartz sand (from the Paris basin, France) of analytical grade, and with a granulometry of 100–150 mesh.The clay mineral chosen was Swy2 Wyoming montmorillonite (Crook County Wyoming, United States), supplied by the Source Clays Repository of the Clay Minerals Society. After <2 μm fractionation by gravity sedimentation, the Swy2 sample was Na-exchanged by well-established procedures.33 This Na-Swy2 was the starting material for the production of Ca-Swy2 with the same procedure, by replacing NaCl with CaCl2. These two interlayer cations were chosen because of their predominance in the environment.
Different proportions of sand and clay were tested to estimate the hydrodynamic properties of the resulting mix, with clay percentages of 5%, 10%, 50% and 100% (i.e. pure clay) in the filter and with a constant total mass of 8.0 ± 0.4 g. For percolation tests with PhACs, a 5% clay filter was used.
PhACs and chemical reagents
The 14 PhAC standards (purity grade > 98%; see Table 1 for details) were obtained from Sigma-Aldrich for ATE, COD, DIA, DOX (Doxepin Hydrochloride), GEM, KET, MET (Metoprolol Tartrate salt), NAP, OXA, PRO, TRA (Tramadol Hydrochloride), TRI, and from Acros Organics for DCF (Diclofenac Sodium) and IBU.| Drug | Abbreviation | CAS-number | M w | pKa | log Kow | S w | Charge |
|---|---|---|---|---|---|---|---|
| Where Mw is the molecular weight in g mol−1, pKa the acid dissociation constant, log Kow the octanol/water partition coefficient, Sw the solubility in water at 25 °C in mg L−1 and charge, the dominant form at pH = 7. | |||||||
| Atenolol C14H22N2O3 | ATE | 29122-68-7 | 266.34 | 9.6 | 0.16 | 300 | + |
| Codeine C18H21NO3 | COD | 76-57-3 | 299.36 | 8.21 | 1.2 | 79 × 102 | + |
| Diazepam C16H13ClN2O | DIA | 439-14-5 | 284.74 | 3.4 | 2.82 | 50 | 0 |
| Diclofenac C14H11Cl2NO2 | DCF | 15307-79-6 | 296.15 | 4.15 | 4.06 | 50 × 103 | − |
| Doxepin C19H21NO | DOX | 1229-29-4 | 279.38 | 8.96 | 3.86 | 32 × 103 | + |
| Gemfibrozil C15H22O3 | GEM | 25812-30-0 | 250.33 | 4.8 | 4.33 | 4.97 | − |
| Ibuprofen C13H18O2 | IBU | 15687-27-1 | 206.28 | 4.91 | 3.72 | 21 | − |
| Ketoprofen C16H14O3 | KET | 22071-15-4 | 254.28 | 4.45 | 2.81 | 51 | − |
| Metoprolol C15H25NO3 | MET | 56392-17-7 | 267.36 | 9.6 | 1.79 | 47 × 102 | + |
| Naproxen C14H14O3 | NAP | 22204-53-1 | 230.26 | 4.15 | 3 | 15.9 | − |
| Oxazepam C15H11ClN2O2 | OXA | 604-75-1 | 286.97 | 1.7–11.6 | 2.31 | 20.71 | 0 |
| Progesterone C21H30O2 | PRO | 57-83-0 | 314.46 | — | 4.04 | 8.81 | 0 |
| Tramadol C16H25NO2 | TRA | 27203-92-5 | 263.37 | 9.41 | 2.51 | 75 × 103 | + |
| Trimethoprim C14H18N4O3 | TRI | 738-70-5 | 290.32 | 7.2 | 0.38 | 400 | 0 |
The chemical reagents of analytical grade, methanol (MeOH) and pyridine, were purchased from Fisher Scientific. N-tert-Butyldimethylsilyl-N-methyltrifluoroacetamide (MTBSTFA, >95%) was supplied by Sigma-Aldrich.
Percolation experiments
Percolation experiments were carried out in œdometer cells. This specific equipment was developed to understand the hydrodynamic behavior of a solid sample under different conditions.34The œdometer cell (internal diameter = 0.04 m) and the injection syringe were both connected to a distinct compressed-air system in order to apply the mechanical pressure on the sorbent material and the injection pressure on the leaching solution, respectively. The equipment scheme and further details are given in Fig. S1† and by Gautier et al.35
For each experiment, 8 g of material (clay–sand mix) was gradually compacted on the bottom side at up to 0.5 MPa, then totally unloaded, and compacted again at a mechanical pressure of 0.3 MPa. The solution was injected at the upper side into this compacted sample at a constant pressure during experiments. The injection pressure is the variable which controls the interaction kinetics between the solution and the material. Indeed, œdometer cells enable physical and hydraulic properties to be jointly controlled. Two different injection pressures were used in this study, 0.1 and 0.2 MPa.
In order to control the impact of the matrix on the adsorption of PhACs, two solutions were used in the experiments: (i) a mix, hereafter called S, of each of the 14 selected PhACs at concentrations around 25 μg L−1 in ultra-pure water, and (ii) a mix between the 14 PhACs and an effluent of a French rural WWTP, called N. Although PhACs were present in this effluent, their maximum concentration around 200 ng L−1 did not affect our results by modifying starting concentrations noticeably (Table S1 for details, and Table S2† for the chemical parameters of the chosen effluent).
The choice of the starting concentration at 25 μg L−1 for each PhAC corresponds to the maximum PhAC concentrations in some effluents.13
During percolation experiments, leachate samples were collected each time a volume of 100 mL solution passed through the filter. A total of 1 L (10 × 100 mL) was therefore used for each percolation experiment.
Leachate and clay analyses
PhAC extraction was carried out on a 6 mL glass cartridge filled with HR-X phase (Macherey-Nagel). Cartridges were conditioned with 5 mL of MeOH then with 5 mL of ultra-pure water. Columns were filled with 100 mL of sample and then rinsed with 5 mL of ultra-pure water before drying for 30 minutes under vacuum. Finally, elution was performed with 3 × 5 mL of MeOH. Thereafter, an internal standard was added to organic layers, which were evaporated under reduced pressure. Residues were derivatized with MTBSTFA according to Schummer et al.36
Analyses were performed on a Trace GC Ultra gas chromatograph (GC) coupled to a TSQ Quantum XLS mass spectrometer equipped with an AS 3000 autosampler (both from Thermo Scientific). The GC was fitted with a Thermo Trace Gold TG-5 MS capillary column (60 m, 0.25 mm i.d., 0.25 μm film thickness).
The temperature of the column was held at 50 °C for 3 min, increased from 50 to 120 °C at 30 °C min−1, and from 120 to 310 °C at 3 °C min−1 with a final isothermal hold at 310 °C for 21 min. 2 μL of the sample was injected in splitless mode at 280 °C. Helium was the carrier gas (1 mL min−1). The mass spectrometer was operated in EI mode at 70 eV, from m/z 50 to 500.
Fourier transform infrared (FTIR) measurements were recorded in the range 650–4000 cm−1, using a Thermo Nicolet 6700 FT spectrometer equipped with a Deuterated Triglycine Sulfate (DTGS) detector and a Nicolet Continuum microscope. The analyses were performed in transmission mode and each spectrum was the average of 256 scans collected at 2 cm−1 resolution.
Carbon and nitrogen analyses were performed on powdered samples by using a Thermo Scientific Flash 2000 organic analyzer assuming an analytical error of 0.05%.
Data analysis
To characterize the distribution of a compound between a potential sorbent and the dissolved phase, the log Kd parameter is often used.37 The computation corresponding to its calculation is expressed as follows: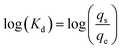 | (1) |
Statistical tests were performed to verify the significance of some hypothesis using the Student test with a chosen statistical threshold of 0.01 for the resulting p-values.
To estimate the link between time and sorption capacity and to describe the sorption dynamics, the first-order Lagergren equation, the second-order kinetics model and the Bangham equations are often used.38
These equations are expressed in a linear form by eqn (2)–(4) respectively:
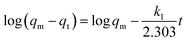 | (2) |
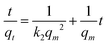 | (3) |
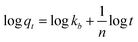 | (4) |
Each equation is based on different assumptions:
(i) the first-order Lagergren model considers that the quantity of unoccupied adsorption sites is proportional to the adsorption rate of adsorbate onto adsorption sites;
(ii) the second-order kinetics model assumes that the adsorption is chemically accomplished; and
(iii) the Bangham equation considers a fast velocity of adsorption and a slow attainment of sorption equilibrium.
These equations were applied to the experimental results.
Results and discussion
Hydrodynamic properties
Percolation experiments were first performed using a water solution in order to determine the hydraulic conductivity (K) of the different clay–sand materials. K, expressed in m s−1, was calculated from Darcy's law, using the expression developed for a saturated medium:39where Q is the measured volumetric flow rate (m3 s−1) at the steady state, i is the hydraulic gradient and S is the cross-sectional area of the œdometer cell (m2).
For a potential environmental application, the clay–sand filter should have hydrodynamic properties that correspond to the hydraulic conductivities operable in actual treatment installations, whereas clays are a natural barrier used, for example, to trap nuclear wastes.40
This specific application should find a good balance between high permeable Fontainebleau sand and Na- or Ca-Swy2 clay with a low permeability.
Different clay–sand ratios were tested for both Na- and Ca-Swy2 in order to simulate and calculate the maximum flow of solution that can pass through the filter.
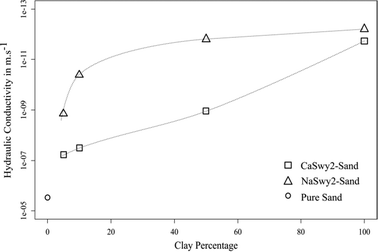
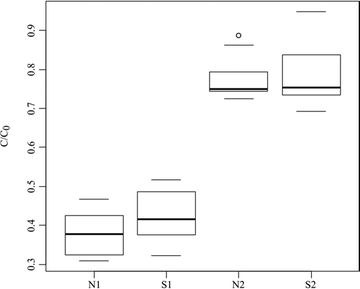
In accordance with the aim of this work, the ideal clay–sand ratio should include a low proportion of clay. As expected, the decrease in K was correlated with the finer texture related to the increase in clay percentage. Nevertheless, this evolution differed between the two clay materials tested (Fig. 1):
- the NaSwy2–sand mix can be considered as a waterproof material with K values between 1.35 e−9 m s−1 (5% clays) and 1.5 e−12 m s−1 (50% clays); and
- the CaSwy2-sand mix allowed a better percolation at a low clay proportion with K between 4.76e−8 m s−1 (5% clays) and 1.11 e−9 m s−1 (50% clays).
This permeability gap between the two materials can be explained by the differences in physico-chemical clay properties. Whereas the specific surface area and the cationic exchange capacity were similar for both Na- and Ca-Swy2 (Table 2), their macroscopic swelling performance varied greatly impacting their Θmax value. The maximum axial swelling strain εmax, deduced from the measured axial displacements of the piston, revealed a high degree of swelling for the Na-Swy2 smectite compared to Ca-Swy2, of 37% and 1.5%, respectively (Table 2).
| Clays | SSA | CEC | ε max | Θ max |
|---|---|---|---|---|
| Where SSA is the Specific Surface Area (m2 g−1); CEC, the Cationic Exchange Capacity (meq. 100 g−1 of clays); εmax, the maximum axial swelling strain for 100% clay sample; and Θmax, the maximum water content for 100% clay sample. a Ref. 33. b Ref. 41. | ||||
| Na-Swy2 | 45.4a | 85.0 ± 2.7a | 37%a | 75% |
| Ca-Swy2 | 46.0b | 85.1 ± 0.01b | 1.5% | 62% |
The high swelling capacity of Na-Swy2 influenced the decrease in K especially at a low clay percentage (5%). Conversely, the extremely low macroscopic swelling for Ca-Swy2 indicates a textural and crystalline swelling control on the decrease in K. 5% was the clay proportion selected for the percolation experiments with PhACs in solution.
Ca-Swy2 presents another advantage compared to Na-Swy2 for a field use: the high macroscopic swelling capacity of Na-Swy2 under wet conditions could damage installations which are subjected to dry/wet cycles. While the mechanical behavior of the Ca-Swy2 smectite in association with sand was very similar to non-swelling clay (such as kaolinites) with a low impact of dry/wet cycles, this adsorbent was characterized by a high specific surface area, making it suitable for interaction experiments with emerging organic pollutants.
In view of the very low permeability of the NaSwy2–sand mix, percolation experiments with the PhACs in solution were carried out only with CaSwy2–sand materials as filter. The experimental conditions for the percolation tests with a 5%/95% CaSwy2–sand mix are presented in Table 3.
| Injection pressure | 0.1 MPa | 0.2 MPa | ||
|---|---|---|---|---|
| Where S is the ultra-pure water matrix; N, the effluent matrix; Q, the flow in mL min−1 and pH of the initial solution. | ||||
| Matrix | S | N | S | N |
| Abbreviation | S1 | N1 | S2 | N2 |
| Q | 9 | 9.1 | 17.9 | 18 |
| Filter thickness (mm) | 4.39 | 4.24 | 4.05 | 3.95 |
| pH | 6.5 | 6.7 | 6.5 | 6.7 |
Drug removal
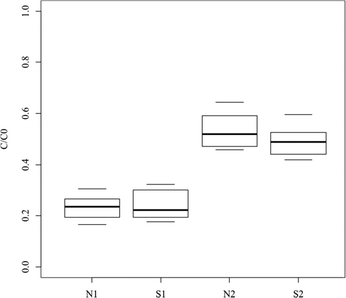
The global removal of the PhAC pool can be used to estimate the efficiency of the filter under different experimental conditions.The term C0 was calculated by the addition of the initial concentrations of the 14 PhACs and C corresponds to the addition of the 14 PhAC concentrations for one collected sample.
The spread of the ten values is around 10% of the total removal (Fig. 2) indicating a good regularity in the sorption capacity of the tested material. The adsorption capacity was significant (i.e. >40%) for all the experimental conditions and the total removal reached was between the extreme values of 35 and 85%. No significant differences in total C/C0 in the global removal were observed for the two matrices at the same pressure (p = .04 and .06 at 0.1 and 0.2 MPa, respectively). The median removal was around 75% at 0.1 MPa and 50% at 0.2 MPa whatever the matrix. The enrichment of the matrix with natural organic matter (NOM) and electrolytes (matrix N) appeared to have no impact on global removal whereas the drop in injection pressure significantly enhanced the removal (p < .01 between N1 and N2 and between S1 and S2).
Partition and removal efficiency of targeted PhACs
The solid–liquid distribution coefficient (Kd) is often used to determine the ability of a material to sorb compounds from a solution. This parameter was used to calculate the partition between the solution and the sorbent for each collected sample and estimate its variability between the ten samples for each percolation experiment. Unlike modeling equations of sorption kinetics, the Kd value does not directly depend on the duration of the experiment.Due to the chosen solid–liquid ratio, the PhACs were half-sorbed (50:50) if, log Kd = 3.40 L kg−1, and the starting concentration is precisely 25 μg L−1.
Cationic species
Two major trends emerged from the analysis of the total C/C0 values for the cationic species (Fig. 3).The decrease in the injection pressure, corresponding to a slowdown of the flux was a favorable factor for sorption. For all the compounds, the transition from S2 to S1 was accompanied by a significant increase in log Kd (p < .01 for the whole cationic compounds) together with an increase in the total removal (Fig. 3). For the S2 experiment, the log Kd values varied between ATE (3.43) and DOX (5.38), while the log Kd values were more homogeneous for the S1 experiment (Table 4).
| S1 | N1 | S2 | N2 | On sludge | |||||
|---|---|---|---|---|---|---|---|---|---|
| Log Kd | MRv | Log Kd | MRv | Log Kd | MRv | Log Kd | MRv | Log Kd | |
| Where log Kd is in L kg−1, MRv in %, relative standard deviation values equal to average/standard deviation for n = 8 (clipped for the two extreme samples). a Values on sludge from ref. 42. b Values on sludge from ref. 43. c Value on sludge from ref. 44. | |||||||||
| Cationic species | |||||||||
| ATE | 4.99 ± 0.03 | 97.0 ± 0.04 | 4.34 ± 0.04 | 87.6 ± 0.09 | 3.43 ± 0.05 | 46.2 ± 0.41 | 3.31 ± 0.04 | 37.2 ± 0.39 | 1.58a |
| COD | 4.74 ± 0.02 | 95.2 ± 0.03 | 4.31 ± 0.04 | 88.6 ± 0.11 | 4.03 ± 0.06 | 73.2 ± 0.24 | 4.26 ± 0.02 | 86.4 ± 0.09 | 1.15ab |
| DOX | 5.79 ± 0.01 | 99.6 ± 0.01 | 4.86 ± 0.02 | 96.2 ± 0.03 | 5.38 ± 0.01 | 98.9 ± 0.01 | 4.57 ± 0.02 | 93.2 ± 0.03 | 2.14b |
| MET | 5.09 ± 0.03 | 96.9 ± 0.03 | 4.34 ± 0.03 | 89.0 ± 0.08 | 4.01 ± 0.03 | 77.2 ± 0.16 | 3.96 ± 0.01 | 75.8 ± 0.12 | 1.81b |
| TRA | 4.63 ± 0.03 | 94.3 ± 0.04 | 3.96 ± 0.04 | 74.6 ± 0.24 | 3.94 ± 0.02 | 77.2 ± 0.14 | 3.65 ± 0.02 | 60.4 ± 0.19 | 1.67b |
| TRI | 4.76 ± 0.02 | 95.3 ± 0.06 | 4.90 ± 0.04 | 96.4 ± 0.03 | 4.87 ± 0.05 | 95.0 ± 0.04 | 4.36 ± 0.02 | 91.4 ± 0.07 | 1.15b |
| Neutral species | |||||||||
| DIA | 4.20 ± 0.03 | 86.5 ± 0.07 | 4.19 ± 0.03 | 86.1 ± 0.09 | 3.45 ± 0.04 | 44.4 ± 0.46 | 4.33 ± 0.04 | 90.1 ± 0.59 | 1.72b |
| OXA | 3.78 ± 0.01 | 71.6 ± 0.09 | 3.84 ± 0.01 | 74.4 ± 0.12 | 2.01 ± 0.13 | 2.0 ± 0.56 | 3.17 ± 0.01 | 34.4 ± 0.19 | 1.11b |
| PRO | 4.92 ± 0.01 | 97.4 ± 0.01 | 4.76 ± 0.02 | 96.1 ± 0.03 | 5.80 ± 0.03 | 99.5 ± 0.01 | 5.77 ± 0.03 | 99.6 ± 0.01 | 3.28a |
| Anionic species | |||||||||
| DCF | 3.45 ± 0.02 | 55.3 ± 0.12 | 3.60 ± 0.02 | 59.8 ± 0.19 | 2.99 ± 0.02 | 26.2 ± 0.35 | 3.01 ± 0.02 | 28.9 ± 0.36 | 1.2c |
| GEM | 3.76 ± 0.02 | 71.6 ± 0.09 | 3.72 ± 0.02 | 67.2 ± 0.18 | 2.71 ± 0.05 | 13.9 ± 0.72 | 3.48 ± 0.01 | 52.6 ± 0.16 | 0.95a |
| IBU | 3.07 ± 0.02 | 34.2 ± 0.35 | 3.35 ± 0.01 | 48.3 ± 0.22 | 2.08 ± 0.04 | 5.1 ± 0.58 | 2.61 ± 0.04 | 12.5 ± 0.93 | 2.23a |
| KET | 4.11 ± 0.04 | 81.9 ± 0.03 | 4.12 ± 0.02 | 84.5 ± 0.09 | 3.44 ± 0.04 | 40.0 ± 0.56 | 3.99 ± 0.01 | 79.8 ± 0.05 | — |
| NAP | 3.12 ± 0.02 | 40.4 ± 0.29 | 3.55 ± 0.02 | 53.7 ± 0.41 | 2.26 ± 0.12 | 6.1 ± 0.86 | 2.96 ± 0.01 | 24.5 ± 0.27 | 2.08a |
Whatever the injection pressure was, the retention of cationic PhACs was generally favored in the case of ultra-pure water (S), except for TRI at 0.1 MPa and COD at 0.2 MPa for which the opposite was recorded. The cationic PhACs were probably in competition with other components (organic or inorganic) contained in the wastewater effluent. As a result, the adsorption of cationic PhACs was lower in matrix N than in S (p < .01 for the two injection pressures).
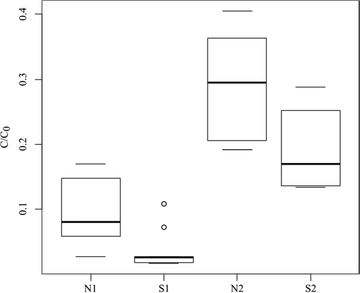
Anionic species
For anionic PhACs, the shift to a lower injection pressure was also favorable for sorption (Fig. 4), especially for IBU in ultra-pure water (S2 vs. S1) (Table 4). These results indicated that the interaction kinetics is an important component of the sorption, as for cationic PhACs.The complexation of the matrix, especially at 0.2 MPa, significantly increased the sorption of all the anionic PhACs (p < .01 at 0.1 and 0.2 MPa). Between S1 and N1, except for IBU, DCF and NAP (e.g. 3.10 to 3.54 respectively), the variations in the log Kd values were not statistically significant (p = .44 and 0.36 for GEM and KET respectively).
Neutral species
The solid–liquid distribution variations for the three neutral PhACs did not follow a trend. It was therefore difficult to evaluate the impact of the matrix or of the injection pressure. PRO was well sorbed whatever the experimental conditions were, whereas for DIA and OXA, variations in the log Kd values were closer to the behavior of anionic species (Table 4).Partition control factors
The effect of ionic strength or of the presence of organic matter in water, which can favor the sorption of anionic species, was confirmed by the experimental results as suggested in other studies.45 This assumption can be explained by the adsorption of organic compounds or electrolytes which could enhance the anionic sorption capacities of the clay material.46Kinetic transfer is the second major influence on the sorption capacity. The sorption improvement is particularly strong on anionic species, whose sorption kinetics is known to be slower in reaching equilibrium,47 compared to that of cationic species (Fig. 4).27
Measurements of log Kd values are generally performed on sludge to better understand the partition of PhACs during waste-water treatment.42–44 Thus, sorption on sludge can be considered as a removal despite the variable further use of sludge. If we compare the log Kd values onto secondary sludge in the literature for each compound (Table 4), there is no link between the charge of the pollutant and log Kd. IBU or NAP are well sorbed on sludge whereas other anionic compounds have a log Kd < 2. These compounds were also among the three anionic compounds that are significantly well sorbed in N matrix than in S (Table 4) at 0.1 MPa. The combination of these two factors demonstrated the NOM impact on the sorption of some anionic PhACs.
For cationic species, only one value (for DOX) exceeds 2 and only the neutral compound PRO is well sorbed by the sludge.
The affinity of our material with PhACs was far greater than that of the sludge, with log Kd values up to at least 3.0 for the N1 experiment, indicating that the chosen material has better trapping properties than the sludge.
The greater complexity of the sludge in terms of chemical reactivity results in a variable affinity with the targeted PhACs that do not depend only on the charge of the pollutants,48 whereas with clay material, the charge seems to play the most important role in the control of sorption.
Sorption kinetics modeling
Based on the obtained correlation coefficients of the three models tested that spread out from 0.90 to 0.999 (Tables S3, S4 and S5†), it appears that the experimental data are better adjusted with the Bangham equation (r2 comprised between 0.970 and 0.999). Nevertheless, the whole models used here provide similar trends. The efficiency of the adsorption is enhanced at a high pressure as shown by k1 constants (first-order Lagergren). Fig. 5 and 6 confirm and highlights that the sorption rate was higher at 0.2 MPa than at 0.1 MPa, indicating a better sorption efficiency at a higher kinetic percolation.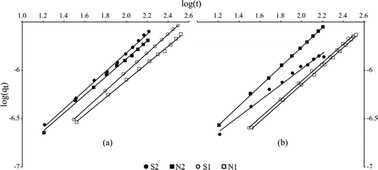 | ||
| Fig. 5 Bangham fits (solid lines) for (a) tramadol (cationic) and (b) ketoprofen (anionic) for each experiment. | ||
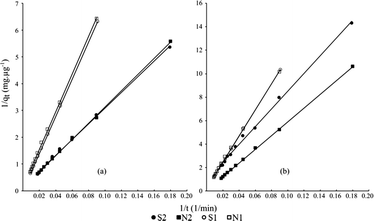 | ||
| Fig. 6 Pseudo second-order fits (solid lines) for (a) metoprolol (cationic) and (b) diazepam (neutral) for each experiment. | ||
The second-order Lagergren (Table S4†) and Bangham (Table S5†) equations suggested a good regularity of the removal quality of the material as log Kd standard deviation values expressed.
For the best sorbed compounds, DOX, PRO and TRI, the comparison of k2 and qm values indicated the same trends as those observed with the log Kd analysis on the matrix effect. An increase in log k2 corresponding with a drop in qm between S and N (for each injection pressure) indicated a matrix effect that was unfavorable for the adsorption of cationic compounds.
The exact opposite was observed for IBU, OXA and NAP, with a lower log k2 and a higher qm for N compared to S. For the other compounds, the data can be interpreted as shown in Fig. 6. For cationic species, there was a slight unfavorable effect of the N matrix whereas the opposite was observed for the anionic species.
Unlike the log Kd values, the modeling and resulting sorption efficiency values gave contrasting results. The main controlling factor for the sorption capacity of Ca-Swy2 towards PhACs is the chemical properties of the molecule. As this material has a greater cationic than anionic exchange capacity, the cationic compounds were strongly favored for sorption.
Otherwise, the sorption of anionic compounds was slightly better in effluent matrix than in ultra-pure water but it remained significantly lower than for cationic compounds. This enhancement of anionic species adsorption by the addition of NOM or electrolytes has already been reported for IBU alone onto montmorillonite, indicating that without a saturation effect, the behavior of a pool of PhACs with Ca-Swy2 is similar to that of a single PhAC.
Model fittings demonstrated that Ca-Swy2 has a large sorption capacity spectrum even if the molecular charge remained a key factor for the removal ratio.
While the better removal efficiency at a lower injection pressure seemed to improve sorption, modeling results showed that the sorption rate was higher for higher injection pressures. With a view to optimizing the kinetic transfer through the filter, further data need to be obtained to combine the best removal efficiency with the best sorption rate constant.
Clay characterization
Clays were separated from sand after the leachate test for further characterization. Two methods were applied to investigate the adsorbent reaction to the leachate, XRD and FTIR analysis.After the experiments, the XRD patterns and FTIR spectra exhibited no significant layer expansion or band stretching, respectively.
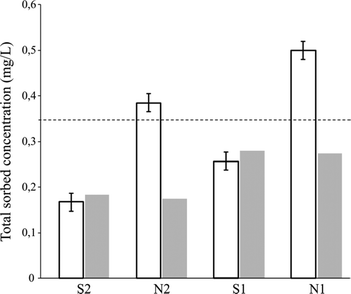
Elemental analyses were carried out on the clay minerals after the percolation of 1 liter in order to estimate the total sorbed concentration based on the carbon percentage of the clays (Fig. 7).
The comparison between elemental analyses on clays and leachate sample analyses exhibited similar results for the ultra-pure water matrix. This is consistent with the assumption that clays are responsible for most of the sorption in comparison with sand. Similar results between clays and water samples also indicated that PhACs are effectively adsorbed onto Ca-Swy2 and not degraded furthermore.
In accordance with previous results obtained from solution analyses, the total sorbed concentration was higher for S1 than for S2, with a total removal of 65.7% and 48.2%, respectively.
For N matrices, the elemental analysis results are significantly higher than those of the leachate samples. This indicates that the material adsorbed more PhACs from the effluent matrix. The additional organic compounds that were adsorbed may possibly explain the better sorption for anionic compounds in the effluents.49
Sorption mechanisms
Despite the excellent removal efficiency of the prepared mineral mixture in this study, sorbed PhACs amounts remain low due to the selected starting concentrations that were 25 μg L−1. Since the sorbed amounts for the whole PhACs were rather low, it was rather hard to probe any changes through the use of classical analytical techniques such as FTIR or XRD, which may give us information about the conformation of the molecules and their localization for a proper description of the adsorption processes.Nevertheless, it appears that the sorption of anionic PhACs is particularly enhanced for clay minerals with Ca2+ as compensating cations. Indeed, Ca2+ is divalent and it showed its ability to adsorb anionic species by cationic bridges.50 Here, the results suggest a better sorption efficiency of anionic species in contrast to previous studies using sodium exchanged Na-Swy2.49,51 However electrostatic interactions or even hydrogen bonds cannot be excluded, which may also play as the driving forces for the adsorption. Further experiments need to be carried out to better point out the sorption mechanisms.
Cationic species are usually adsorbed on clay minerals through cation exchanges and it may also the case for PhACs here. This mechanism is thermodynamically spontaneous,27 but only compensating cations on the external surfaces are involved since no changes in the diffraction patterns were observed.
Conclusions
From the results of this study, the following conclusions can be drawn:- Natural Ca-saturated smectite (Ca-Swy2) incorporated into a sand-filter allowed a flow consistent with in-situ applications whereas Na-saturated smectite (Na-Swy2) is a waterproof material that is not adapted to the sorption of pollutants in a simulation of dynamic sorption close to field reality.
- Ca-Swy2 exhibited a large adsorption capacity even for cationic, neutral and anionic PhACs at a similar wastewater pH. With the values of the relative standard deviation of samples, it seems that the sorption efficiency over time is steady. The sorption capacity is guided by two major parameters: infiltration kinetics and the composition of the matrix.
- The effluent matrix played a contrasting role on the sorption efficiency, depending on the molecular charge and the speciation at the tested pH: anionic species were favored by this complex matrix in contrast to cationic ones, for which the sorption efficiency was lower. Some NOM and/or electrolytes of the effluent were also adsorbed onto the filter and played a key role in the sorption of anionic compounds whereas they were in competition with cationic species. Further analyses need to be carried out to characterize them.
- The applied models fitted our data well, but due to the pseudo equilibrium that was reached, the calculated constants did not correspond to previous observations for all the models. However, even a low kinetics (0.1 MPa) favored the sorption processes, and at a higher injection pressure, the sorption processes were more efficient
- Natural Ca-smectite is a slightly modified material that could significantly improve the removal efficiency of current treatment chains, especially concerning the removal of PhACs.
- The key role played by the interlayer cation can direct the choice of geosorbent for further studies, using clay minerals that are naturally saturated by Ca2+, rather than by Na+.
- Implementation in the field of the tertiary treatment technique presented here requires further experiments. Nevertheless, this study stresses out the relevance of the material in a field application for a good removal efficiency especially in comparison with tertiary treatments using chemical products, which are potentially toxic for the environment. The main question now is the management costs induced by this technique, especially concerning the durability of the filter.
Acknowledgements
The work received financial support from the HArPE Project (2012-00073536) funded by the Région Centre-Val de Loire. The authors would also like to thank Fabrice Muller for XRD and FTIR analysis and Marielle Hatton for carbon analysis.Notes and references
- C. G. Daughton and T. A. Ternes, Environ. Health Perspect., 1999, 107, 907 CrossRef CAS PubMed.
- A. Masiá, J. Campo, P. Vázquez-Roig, C. Blasco and Y. Picó, J. Hazard. Mater., 2013, 263, Part 1, 95–104 CrossRef PubMed.
- T. Heberer, J. Hydrol., 2002, 266, 175–189 CrossRef CAS.
- R. Loos, B. M. Gawlik, G. Locoro, E. Rimaviciute, S. Contini and G. Bidoglio, Environ. Pollut., 2009, 157, 561–568 CrossRef CAS PubMed.
- M. L. Richardson and J. M. Bowron, J. Pharm. Pharmacol., 1985, 37, 1–12 CrossRef CAS PubMed.
- T. A. Ternes, Water Res., 1998, 32, 3245–3260 CrossRef CAS.
- T. Heberer, Toxicol. Lett., 2002, 131, 5–17 CrossRef CAS PubMed.
- B. F. da Silva, A. Jelic, R. López-Serna, A. A. Mozeto, M. Petrovic and D. Barceló, Chemosphere, 2011, 85, 1331–1339 CrossRef PubMed.
- P. Vazquez-Roig, V. Andreu, C. Blasco and Y. Picó, Sci. Total Environ., 2012, 440, 24–32 CrossRef CAS PubMed.
- M. S. Kostich, A. L. Batt and J. M. Lazorchak, Environ. Pollut., 2014, 184, 354–359 CrossRef CAS PubMed.
- P. Cardinal, J. C. Anderson, J. C. Carlson, J. E. Low, J. K. Challis, S. A. Beattie, C. N. Bartel, A. D. Elliott, O. F. Montero, S. Lokesh, A. Favreau, T. A. Kozlova, C. W. Knapp, M. L. Hanson and C. S. Wong, Sci. Total Environ., 2014, 482–483, 294–304 CrossRef CAS PubMed.
- X. Li, W. Zheng and W. R. Kelly, Sci. Total Environ., 2013, 445–446, 22–28 CrossRef CAS PubMed.
- R. Loos, R. Carvalho, D. C. António, S. Comero, G. Locoro, S. Tavazzi, B. Paracchini, M. Ghiani, T. Lettieri, L. Blaha, B. Jarosova, S. Voorspoels, K. Servaes, P. Haglund, J. Fick, R. H. Lindberg, D. Schwesig and B. M. Gawlik, Water Res., 2013, 47, 6475–6487 CrossRef CAS PubMed.
- K. Fent, A. A. Weston and D. Caminada, Aquat. Toxicol., 2006, 76, 122–159 CrossRef CAS PubMed.
- Â. Almeida, R. Freitas, V. Calisto, V. I. Esteves, R. J. Schneider, A. M. V. M. Soares and E. Figueira, Comp. Biochem. Physiol., Part C: Toxicol. Pharmacol., 2015, 172–173, 26–35 CrossRef PubMed.
- T. Brodin, J. Fick, M. Jonsson and J. Klaminder, Science, 2013, 339, 814–815 CrossRef CAS PubMed.
- N. Casatta, G. Mascolo, C. Roscioli and L. Viganò, Sci. Total Environ., 2015, 511, 214–222 CrossRef CAS PubMed.
- K. Grabicova, R. H. Lindberg, M. Östman, R. Grabic, T. Randak, D. G. Joakim Larsson and J. Fick, Sci. Total Environ., 2014, 488–489, 46–50 CrossRef CAS PubMed.
- C. M. de Jongh, P. J. F. Kooij, P. de Voogt and T. L. ter Laak, Sci. Total Environ., 2012, 427–428, 70–77 CrossRef CAS PubMed.
- J. Altmann, A. Sperlich and M. Jekel, Water Res., 2015, 84, 58–65 CrossRef CAS PubMed.
- M. Klavarioti, D. Mantzavinos and D. Kassinos, Environ. Int., 2009, 35, 402–417 CrossRef CAS PubMed.
- I. Ali, M. Asim and T. A. Khan, J. Environ. Manage., 2012, 113, 170–183 CrossRef CAS PubMed.
- S. M. Lee and D. Tiwari, Appl. Clay Sci., 2012, 59–60, 84–102 CrossRef CAS.
- R. Guégan, M. Giovanela, F. Warmont and M. Motelica-Heino, J. Colloid Interface Sci., 2015, 437, 71–79 CrossRef PubMed.
- G. Z. Kyzas, J. Fu, N. K. Lazaridis, D. N. Bikiaris and K. A. Matis, J. Mol. Liq., 2015, 209, 87–93 CrossRef CAS.
- T. Polubesova, D. Zadaka, L. Groisman and S. Nir, Water Res., 2006, 40, 2369–2374 CrossRef CAS PubMed.
- P.-H. Chang, W.-T. Jiang, Z. Li, C.-Y. Kuo, J.-S. Jean, W.-R. Chen and G. Lv, J. Hazard. Mater., 2014, 277, 44–52 CrossRef CAS PubMed.
- A. Mahamat Ahmat, M. Boussafir, C. Le Milbeau, R. Guegan, J. Valdès, M. Guiñez, A. Sifeddine and L. Le Forestier, Mar. Chem., 2016, 179, 23–33 CrossRef CAS.
- S. Zheng, Z. Sun, Y. Park, G. A. Ayoko and R. L. Frost, Chem. Eng. J., 2013, 234, 416–422 CrossRef CAS.
- T. Thiebault, R. Guégan and M. Boussafir, J. Colloid Interface Sci., 2015, 453, 1–8 CrossRef CAS PubMed.
- I. Aksu, E. Bazilevskaya and Z. T. Karpyn, GeoResJ, 2015, 7, 1–13 CrossRef.
- L. Wu, L. Liao and G. Lv, J. Colloid Interface Sci., 2015, 454, 1–7 CrossRef CAS PubMed.
- L. Le Forestier, F. Muller, F. Villieras and M. Pelletier, Appl. Clay Sci., 2010, 48, 18–25 CrossRef CAS.
- A. Jullien, C. Proust, L. Le Forestier and P. Baillif, Appl. Clay Sci., 2002, 21, 143–153 CrossRef CAS.
- M. Gautier, F. Muller, L. Le Forestier, J.-M. Beny and R. Guegan, Appl. Clay Sci., 2010, 49, 247–254 CrossRef CAS.
- C. Schummer, O. Delhomme, B. M. R. Appenzeller, R. Wennig and M. Millet, Talanta, 2009, 77, 1473–1482 CrossRef CAS PubMed.
- M. Carballa, G. Fink, F. Omil, J. M. Lema and T. Ternes, Water Res., 2008, 42, 287–295 CrossRef CAS PubMed.
- L. Yang, M. Jin, C. Tong and S. Xie, J. Hazard. Mater., 2013, 244–245, 77–85 CrossRef CAS PubMed.
- P. A. Domenico and F. W. Schwartz, Physical and chemical hydrogeology, Wiley, New York, NY, 2nd edn, 1998 Search PubMed.
- F. T. Madsen, Clay Miner., 1998, 33, 109–129 CrossRef CAS.
- M. Ghayaza, L. Le Forestier, F. Muller, C. Tournassat and J.-M. Beny, J. Colloid Interface Sci., 2011, 361, 238–246 CrossRef CAS PubMed.
- B. Blair, A. Nikolaus, C. Hedman, R. Klaper and T. Grundl, Chemosphere, 2015, 134, 395–401 CrossRef CAS PubMed.
- A. Wick, G. Fink, A. Joss, H. Siegrist and T. A. Ternes, Water Res., 2009, 43, 1060–1074 CrossRef CAS PubMed.
- T. A. Ternes, N. Herrmann, M. Bonerz, T. Knacker, H. Siegrist and A. Joss, Water Res., 2004, 38, 4075–4084 CrossRef CAS PubMed.
- T. X. Bui and H. Choi, Chemosphere, 2010, 80, 681–686 CrossRef CAS PubMed.
- H. Mansouri, R. J. Carmona, A. Gomis-Berenguer, S. Souissi-Najar, A. Ouederni and C. O. Ania, J. Colloid Interface Sci., 2015, 449, 252–260 CrossRef CAS PubMed.
- V. Calisto, C. I. A. Ferreira, J. A. B. P. Oliveira, M. Otero and V. I. Esteves, J. Environ. Manage., 2015, 152, 83–90 CrossRef CAS PubMed.
- M. Hörsing, A. Ledin, R. Grabic, J. Fick, M. Tysklind, J. la C. Jansen and H. R. Andersen, Water Res., 2011, 45, 4470–4482 CrossRef PubMed.
- S. K. Behera, S. Y. Oh and H. S. Park, Int. J. Environ. Sci. Technol., 2012, 9, 85–94 CrossRef CAS.
- E. Errais, J. Duplay, M. Elhabiri, M. Khodja, R. Ocampo, R. Baltenweck-Guyot and F. Darragi, Colloids Surf., A, 2012, 403, 69–78 CrossRef CAS.
- J. Gao and J. A. Pedersen, Environ. Sci. Technol., 2005, 39, 9509–9516 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ew00034g |
| This journal is © The Royal Society of Chemistry 2016 |