Open Access Article
Open Access ArticleUnderstanding the magnetism of {Fe2Ln} dimers, step-by-step†
S. G.
Baca
ab,
J.
van Leusen
b,
M.
Speldrich
b and
P.
Kögerler
 *bc
*bc
aInstitute of Applied Physics, Academy of Sciences of Moldova, 5 Academiei str., Chisinau, MD-2028, Moldova
bInstitute of Inorganic Chemistry, RWTH Aachen University, Landoltweg 1, D-52074 Aachen, Germany. E-mail: paul.koegerler@ac.rwth-aachen.de
cPeter Grünberg Institute, PGI-6, Research Centre Jülich, D-52425 Jülich, Germany
First published on 13th June 2016
Abstract
A magnetochemical comparison between the {FeIII4LnIII2}-type coordination clusters [Fe4M2(OH)2(N3)2(bdea)4(O2CCMe3)5(H2O)]NO3·2(EtOH) (M = Dy, Y) and [Fe4M2(OH)2(N3)2(bdea)4(O2CCMe3)4(NO3)2]·3(EtOH) (M = Gd, Eu; H2bdea = N-butyldiethanolamine), of which {Fe4Dy2} reveals slow molecular magnetization relaxation up to 6 K, allows assessment of the exchange coupling governing the clusters’ multiplet patterns.
Though research on single molecule magnets (SMMs) has reached its peak with most of the underlying spin physics now well understood,1 the investigation of heterometallic d/f-based SMMs remains a challenging and attractive goal. In lanthanide-containing SMMs exhibiting very large zero-field splitting of the ground state multiplets of the individual 4f ions, the relaxation mechanisms that effectively limit the threshold temperature for the detection of magnetization hysteresis – either of thermal or quantum tunneling origin – are still not completely understood, and these compounds exhibit a surprisingly wide range of relaxation phenomena.2 All this has prompted an extensive effort to assess the magnetism of polynuclear 4f but also heterometallic d/f coordination clusters,3 in order to gain a deeper insight into the relaxation pathways. Until now research on polyheterometallic 3d/4f SMMs was mainly focused on Mn/Ln, Co/Ln, and Ni/Ln heterometallic systems.4 Although some FeIII/LnIII heterometallic coordination clusters have also been reported,5 only a few of them exhibit slow magnetization relaxation in the absence of a static field, i.e. SMM characteristics.5c,g,i,j,l,n–p This surprisingly frequent absence of slow magnetization relaxation here might be caused by the stray fields produced by the FeIII spin centers, which apparently increases the probability of relaxation via quantum tunneling mechanisms.
At the same time, modeling the thermodynamic magnetic properties of more complex 3d/4f spin structures, such as the susceptibility, requires taking into account all microscopic aspects, in particular single ion effects and spin–spin interactions, which frequently lead to over-parameterization issues. In order to minimize the number of magnetically relevant independent fitting parameters, a comparison between nearly isostructural complexes of increasing magnetic complexity allows us to stepwise ascertain the ligand field parameters and exchange energies even of 3d/4f compounds comprising magnetically complex spin centers such as Dy(III).
In this context, we explored the potential of our strategy6 for using both structure-directing aminoalcohols and carboxylates for the synthesis of heterometallic coordination cluster families based on archetypal triangular (M/M′)3(μ3-O) fragments.7 Here we present the synthesis, structures and magnetic properties of four hexanuclear heterometallic cluster compounds: [Fe4Dy2(OH)2(N3)2(bdea)4(O2CCMe3)5(H2O)]NO3·2(EtOH) (1), which exhibits slow magnetization relaxation and non-zero out-of-phase ac susceptibility up to 6 K, and nearly identical analogues comprising diamagnetic YIII ions, [Fe4Y2(OH)2(N3)2(bdea)4(O2CCMe3)5(H2O)]NO3·2(EtOH) (2), or spin-only GdIII ions, [Fe4Gd2(OH)2(N3)2(bdea)4(O2CCMe3)4(NO3)2]·3(EtOH) (3). Another compound virtually isostructural to 3 but incorporating EuIII ions, [Fe4Eu2(OH)2(N3)2(bdea)4(O2CCMe3)4(NO3)2]·3(EtOH) (4), has also been prepared.
The reaction of the μ-oxo-centered trinuclear iron pivalate with sodium azide and lanthanide(III)/yttrium(III) nitrate in the presence of N-butyldiethanolamine (H2bdea) in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio in ethanol solution produced crystals of 1–4 in relatively high yields (53%, 21%, 40% and 46% based on Fe, respectively). All compounds remain thermally stable up to ca. 200 °C. Single-crystal X-ray diffraction analysis‡ reveals that all complexes crystallize in the space group P
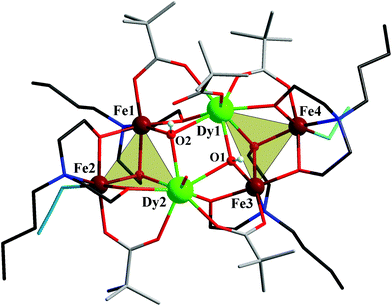
2 ratio in ethanol solution produced crystals of 1–4 in relatively high yields (53%, 21%, 40% and 46% based on Fe, respectively). All compounds remain thermally stable up to ca. 200 °C. Single-crystal X-ray diffraction analysis‡ reveals that all complexes crystallize in the space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) and feature the coordination cluster monocation [Fe4M2(OH)2(N3)2(bdea)4 (O2CCMe3)5(H2O)]+ (M = Dy, Y), a nitrate counteranion and two ethanol solvate molecules in 1 and 2, or the neutral [Fe4M2(OH)2(N3)2(bdea)4(O2CCMe3)4(NO3)2] (M = Gd, Eu) cluster and three ethanol solvates in 3 and 4. As complexes 1 and 2 as well as 3 and 4 are isostructural, we limit the structural description to 1 and 3. The cationic complex in 1 consists of a hexanuclear oxido-linked core fragment of four FeIII and two DyIII ions and can be regarded as two nearly identical Fe2Dy triangles condensed via two μ3-hydroxo groups (Fig. 1), with a Dy⋯Dy distance of 3.871(6) Å.
and feature the coordination cluster monocation [Fe4M2(OH)2(N3)2(bdea)4 (O2CCMe3)5(H2O)]+ (M = Dy, Y), a nitrate counteranion and two ethanol solvate molecules in 1 and 2, or the neutral [Fe4M2(OH)2(N3)2(bdea)4(O2CCMe3)4(NO3)2] (M = Gd, Eu) cluster and three ethanol solvates in 3 and 4. As complexes 1 and 2 as well as 3 and 4 are isostructural, we limit the structural description to 1 and 3. The cationic complex in 1 consists of a hexanuclear oxido-linked core fragment of four FeIII and two DyIII ions and can be regarded as two nearly identical Fe2Dy triangles condensed via two μ3-hydroxo groups (Fig. 1), with a Dy⋯Dy distance of 3.871(6) Å.
Four bridging pivalate groups and four doubly deprotonated N-butyldiethanolamine ligands additionally bridge the Fe2Dy triangles [Dy⋯Fe, 3.392(12) and 3.404(11) Å] and the metal sites within each triangle motif [Fe⋯Fe, 3.169(15)−3.172(17) Å; Fe⋯Dy, 3.450(12)–3.542(12) Å]. The central [Fe4Dy2(μ-O)10] fragment can alternatively be decomposed into four edge-sharing [M2M′(μ3-O)] triangles: Fe1Fe2Dy2, Dy1Dy2Fe1, Dy1Dy2Fe3, and Fe3Fe4Dy1. Two (end-on) azide ligands (to Fe2/Fe4), one monodentate carboxylate and a water molecule (to Dy1/Dy2) complete the metal coordination spheres. Each N-butyldiethanolamine group links two FeIII and two DyIII atoms: two polyalcohol residues act as hexadentate ligands via one N atom and μ3-O and μ2-O atoms and the remaining two bdea2− act as pentadentate ligands via one N atom and two μ2-O linkages. All Fe(III) ions adopt distorted octahedral environments: Fe1 and Fe3 are NO5 coordinated by a μ3-OH group [Fe−(μ3-O), 1.943(5)/1.969(5) Å], a carboxylate oxygen [Fe–Ocarb, 1.967(6)/1.953(6) Å] as well as three alkoxy oxygen atoms (one μ3-O and two μ2-O) from two bdea2− groups [Fe–Oalk, 1.968(5)–2.069(5) Å] and a nitrogen atom from one polyalcoholamine [Fe–N, 2.218(7)/2.196(7) Å]; Fe2 and Fe4 are N2O4 coordinated by a carboxylate oxygen atom [Fe–Ocarb, 2.027(6)/2.046(6) Å], three alkoxy oxygen atoms (one μ3-O, two μ2-O) of two bdea2− groups [Fe–Oalk, 1.949(5)–2.055(5) Å], a bdea2−-N atom [Fe–Nalk, 2.212(7)/2.215(6) Å] and an azide-N atom [Fe–Nazide, 1.992(8)/1.990(8) Å]. Both DyIII ions are eight-coordinated: two μ3-OH− groups, two oxygen atoms from two carboxylates, two alkoxy μ2-O and one μ3-O atoms from two bdea2−; Dy1 additionally binds to a monodentate pivalate, Dy2 to H2O [Dy–O, 2.304(5)−2.364(5) Å]. The coordinated water molecule and monodentate pivalate as well as the outer-sphere nitrate anion and two solvate ethanol molecules engage in extensive intra- and intermolecular hydrogen bonding in 1. In particular, one of the OH− groups forms a strong intramolecular O–H⋯O hydrogen bond [2.608(8) Å] with the uncoordinated carboxylate oxygen (O2⋯O4), whereas the second hydroxide forms an intermolecular O–H⋯O hydrogen bond [2.777(8) Å] with the nitrate anion (O1⋯O22, see Fig. S2†).
Very similar to 1, the charge-neutral coordination cluster in 3 also consists of a hexanuclear oxido-linked core fragment of four FeIII and two GdIII ions or two nearly identical Fe2Gd triangles bridged by two μ3-OH groups [Gd⋯Gd, 4.053(1) Å, Fig. S5†]. The difference stems from apical ligands coordinated to the two LnIII ions: in 3, these are two chelated NO3− anions vs. monodentate pivalic acid and H2O in 1. As a result, both GdIII sites are O9-coordinated (Fig. 2); Gd–O, 2.316(8)–2.650(8) Å. The coordination environment of the four FeIII atoms is similar to 1 [NO5 for Fe1 and Fe3, N2O4 for Fe2 and Fe4; Fe–O, 1.965(7)−2.079(7) Å; Fe–N, 1.993(8)–2.254(9) Å].
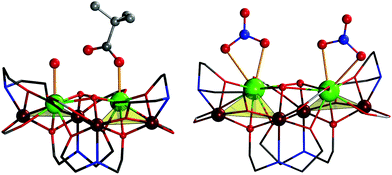 | ||
| Fig. 2 Comparison of the structure of the {Fe4Dy2} complex in 1 (left) and the {Fe4Gd2} complex in 3 (right), in an approx. perpendicular view to that in Fig. 1. Highlighted are the terminal ligands (H2O and monodentate pivalate in 1, nitrate in 3) resulting in eight- and nine-coordinated lanthanide centers. All terminal organic residues, azide and hydrogen omitted for clarity. | ||
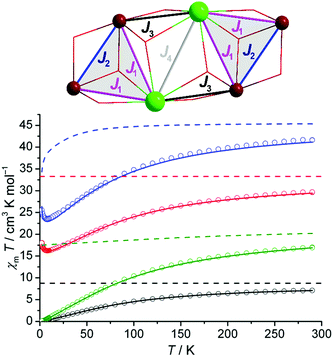
Magnetochemical analyses of 1–4 (Fig. 3) – with the ultimate goal of modeling the magnetically complex {Fe4Dy2} species 1 – employed the computational framework CONDON that implements a ‘full model’ Hamiltonian and thus accounts for all microscopic aspects necessary to model the complex 3d–4f spin structure,8 in particular the relevant single-ion effects and coupling interactions (see the ESI† for computational details). To quantify these effects, we analyzed the magnetic susceptibility data considering ligand-field effects, spin–orbit coupling, and external magnetic field. Standard values are employed for spectroscopic parameters (e.g. Racah energies B and C or spin–orbit coupling energies). CONDON alternatively implements an effective isotropic spin model that is used for comparison where applicable. Note that the presence of at least three different exchange pathways (all mediated by μ3-O bridges) precludes the unambiguous direct determination of their associated exchange energies (J1, J2, J3, J4, or the molecular field parameter λmf; see coupling scheme) based on χm(B,T) data. Furthermore, the computational requirements for a full model of the hexanuclear {Fe4Ln2} cluster mandate a simplification to the coupling scheme that is herein divided into two identical {Fe2Ln} triangles (see Fig. 1), the interaction of which is accounted for by a molecular field term. To address these issues the following strategy was employed: we start with the magnetically simplest system {Fe4Y2} containing diamagnetic YIII to extract the parameters of the FeIII centers which are adopted for all other systems. Next, {Fe4Gd2} is analyzed as a purely isotropic spin system; these results are compared to full-model calculations based on the two-triangle coupling scheme, in order to validate the latter. Finally, full-model calculations are applied to {Fe4Dy2}. {Fe4Eu2} serves as an additional reference point for this approach.
Given the nearly identical geometries, the nearest-neighbor Fe–Fe coupling (J2) is assumed to vary minimally between 1–4 and can be directly determined from the {Fe4Y2} species (2). Based on the angular overlap model, implemented and parameterized in the program wxJFinder,7b these variations should not exceed ±10% for the individual Fe–O(H)–Fe exchange pathway geometries in 1–4. Here, any inter-triangle Fe⋯Fe exchange coupling (which would involve extended –O–Y–O– exchange pathways) can be neglected and the Heisenberg-type intra-molecular exchange interaction pattern (Hex = –2J2S1·S2) is simplified to that of a spin dimer. The tetragonally distorted FeO6 coordination environments in 1–4 are best described as D4h symmetric; for this assumption the FeIII ligand field parameters derived from a least-squares fit for 2 are B20 = –3500 cm−1, B40 = 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, and B44 = 19
000 cm−1, and B44 = 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (in Wybourne notation) and J2 = –6.5 cm−1 (SQ = 1.0%; Fig. 3). These Bkq values are used as constants in the fitting procedures of 1, 3, and 4. As is evident from the susceptibility temperature dependence (at 0.1 Tesla; Fig. S9†) with a maximum at 55 K and a minimum at 5 K, a small paramagnetic impurity is present and it can also be quantified (ρ = 0.2%). Analyzing 2 as a purely isotropic spin system (geff = gS = 2.0) results in a slightly worse fit but yields the same J2 value of −6.5 cm−1 (SQ = 1.8%, ρ = 0.25%; Fig. S10†).
000 cm−1 (in Wybourne notation) and J2 = –6.5 cm−1 (SQ = 1.0%; Fig. 3). These Bkq values are used as constants in the fitting procedures of 1, 3, and 4. As is evident from the susceptibility temperature dependence (at 0.1 Tesla; Fig. S9†) with a maximum at 55 K and a minimum at 5 K, a small paramagnetic impurity is present and it can also be quantified (ρ = 0.2%). Analyzing 2 as a purely isotropic spin system (geff = gS = 2.0) results in a slightly worse fit but yields the same J2 value of −6.5 cm−1 (SQ = 1.8%, ρ = 0.25%; Fig. S10†).
Next, we swap diamagnetic YIII for spin-only GdIII centers, i.e. moving from 2 to 3. The low-field χT curve of 3 decreases from 29.6 cm3 K mol−1 and reaches a minimum of around 16.6 cm3 K mol−1 at 8.0 K. Approximating {Fe4Gd2} as an isotropic spin system, a least-squares fit to a Heisenberg-type Hamiltonian (see coupling scheme, Fig. 3) yields J1 = –(0.38 ± 0.12) cm−1, J2 = –(6.5 ± 0.1) cm−1, J3 = +(0.20 ± 0.06) cm−1 and J4 = +(0.03 ± 0.01) cm−1 (SQ = 1.2%; see the ESI† for correlation analysis). We note that the converged J2 value is identical to that for 2, as expected for the nearly identical exchange pathway geometries. The weak Gd⋯Gd contact (J4) is found to be approx. one order of magnitude smaller than the Gd⋯Fe contacts; weak ferromagnetic interactions are also documented for μ3-hydroxo-bridged Fe⋯Gd9a and Gd⋯Gd9b examples.
As mentioned above, modeling the FeIII and GdIII centers in {Fe4Gd2} with their full single-ion effects mandates restrictions to the exchange coupling scheme in the model Hamiltonian: the {Fe4Gd2} cluster is described as a dimer of triangles, where all inter-triangle exchange interactions are represented by the molecular field approximation χ−1 = χ′−1 − λmf, where χ′ represents the susceptibility contribution of the two uncoupled {Fe2Gd} triangles. This model then yields B20 = –200 cm−1, B40 = –1900 cm−1, and B60 = 205 cm−1 for Gd3+ and J1 = –0.42 cm−1, J2 = –6.5 cm−1 and λmf = +0.042 mol cm−3 (SQ = 1.9%). Both models for 3 are in excellent agreement, see Fig. S11,† with identical values for J2 and ferromagnetic inter-triangle coupling (i.e. λmf > 0).
The {Fe4Eu2} species (4) with its nearly temperature-independent paramagnetic EuIII centers (mj = 0, see Fig. S9†) further corroborates that the J2 value is nearly independent of the lanthanide in the {Fe4Ln2} family. The χ vs. T curve (0.1 Tesla) shows a maximum at 55 K and a minimum at 5 K, i.e. the same as those for 2. Thus, in a first-order approximation we adopted the coupling scheme for 2, augmented by the additive contributions of the two EuIII centers. A least-squares fit (SQ = 1.0%) then yields B20 = –150 cm−1, B40 = –1940 cm−1, B60 = 208 cm−1 (lf parameters for EuIII) and confirms J2 = –6.7 cm−1.
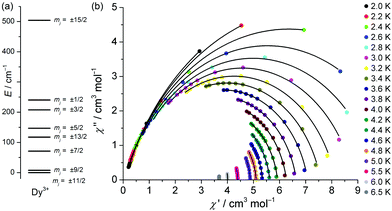
The magnetism of the {Fe4Dy2} species (1), with the DyIII ions in a non-cubic coordination environment, is strongly dependent on both the single-ion effects, in particular the thermal population of higher DyIII multiplet states, and the Fe⋯Fe and Fe⋯Dy interactions. The increase in χT with decreasing temperatures below 8 K that is also observed for 2 is caused by very weak ferromagnetic inter-triangle interactions. Akin to 2, the {Fe4Dy2} unit is modeled as a dimer of identical isosceles triangles, in order to allow the usage of the Russell–Saunders ground term for each DyIII ion and FeIII ion (note that the full {Fe4Dy2} system would require 3.2 TByte random access memory for matrix diagonalization). The assumption of D4d-symmetric DyIIIO8 environments in 1 was found to be an adequate approximation, a less-symmetric ligand field (correspondingly parameterized by a higher number of independent ligand field parameters) did not significantly increase the fitting quality. As for 2, intra-triangle exchange interactions are described by Heisenberg coupling; all inter-triangle interactions were modeled via the molecular field approximation. A least-squares fit (SQ = 1.6%) results in B20 = –300 cm−1, B40 = –1850 cm−1, and B60 = 210 cm−1 for DyIII and J1 = –0.48 cm−1, J2 = –6.7 cm−1, and λmf = +0.075 mol cm−3. Note that J2 converges very close to the corresponding values for 2–4 and that the Fe⋯Dy exchange energy (J1) as expected is very similar to the Fe⋯Gd exchange in 2. The derived lf parameters for DyIII correspond to a zero-field splitting of the free-ion j = 15/2 ground state multiplet into mj levels, where the lowest states with mj = ±11/2 are 7.9 cm−1 below the next-highest mj = ± 9/2 states (Fig. 4a). The energetic separation to the mj = ± 1/2 states, relevant for thermal magnetization relaxation processes, is 240.4 cm−1.
Therefore, alternating-current magnetic susceptibility measurements with no dc bias were analyzed in order to determine if these splitting patterns lead to an effective slowing-down of the relaxation of the magnetization upon an external field change. Frequency-dependent peaks are observed in the out-of-phase response and indicate that {Fe4Dy2} exhibits single-molecule characteristics up to 6 K, although this is close to the thermal quantum regime (Fig. S12 and S13†). The corresponding real (in-phase) χ′ and the imaginary (out-of-phase) components χ′′ were fitted to a Cole–Cole equation (Fig. 4b).9c The resulting average relaxation times of the magnetization, τ, allow the parameterization of common relaxation process types. The observed spread in α (0.03–0.24) indicates several relaxation pathways, and we determined that a combined Orbach–Raman relaxation, τ = 1/[τ0−1 exp(–ΔE/kBT) + CTn], allows for a more adequate determination of relaxation parameters (Fig. S14†). This results in an attempt time τ0 = (1.01 ± 0.89) × 10−7 s, an effective relaxation barrier ΔE = (18.4 ± 2.7) cm−1, i.e. less than a tenth of the mj = ±11/2⋯±1/2 splitting, and Raman parameters n = 6.6 ± 0.4 and C = (0.66 ± 0.23) K−n s−1. We note that the Orbach parameters are similar to previously reported {FeyDyz} species.5n,o The Raman parameter n is lower than 9, i.e. the value expected for Kramers ions, but such lower values (4–9) have been reported previously and may be due to e.g. optical phonons.9d
Conclusions
In conclusion, the four hydroxide-bridged {Fe2M} dimer complexes in 1–4 enable us to analyze their magnetic characteristics in a stepwise, comparative ansatz. In particular, the full magnetochemical analysis of the susceptibility data of the {Fe4Dy2} species requires exploiting the clusters’ close structural relationship in order to avoid over-parametrization issues. The {Fe4Dy2} compound (1) exhibits slow magnetization relaxation, i.e. SMM behavior, which we link to the zero-field splitting of the DyIII ground multiplet. Contrasting all previous work on FeIII/DyIII complexes, herein we were able to also model the Fe–Fe and Fe–Dy coupling energies: antiferromagnetic interactions are dominant, yet weaker inter-triangle interactions appear ferromagnetic. Finally, we cautiously note that our magnetochemical interpretation, based solely on susceptibility data derived from microcrystalline samples, only allows for an assessment within the limitations of the various employed models. Numerous attempts to isolate larger single crystal specimens for single-crystal anisotropy measurements unfortunately remained fruitless.Notes and references
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, New York, 2006 Search PubMed.
- (a) M.-E. Boulon, G. Cucinotta, J. Luzon, C. Degl'Innocenti, M. Perfetti, K. Bernot, G. Calvez, A. Caneschi and R. Sessoli, Angew. Chem., Int. Ed., 2013, 52, 350 CrossRef CAS PubMed; (b) F. Moro, D. P. Mills, S. T. Liddle and J. van Slageren, Angew. Chem., Int. Ed., 2013, 52, 3430 CrossRef CAS PubMed; (c) J. Luzon and R. Sessoli, Dalton Trans., 2012, 41, 13556 RSC; (d) F. Tuna, C. A. Smith, M. Bodensteiner, L. Ungur, L. F. Chibotaru, E. J. L. McInnes, R. E. P. Winpenny, D. Collison and R. A. Layfield, Angew. Chem., Int. Ed., 2012, 51, 6976 CrossRef CAS PubMed; (e) S.-Y. Lin, W. Wernsdorfer, L. Ungur, A. K. Powell, Y.-N. Guo, J. Tang, L. Zhao, L. F. Chibotaru and H.-J. Zhang, Angew. Chem., Int. Ed., 2012, 51, 12767 CrossRef CAS PubMed; (f) J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078 RSC; (g) N. Magnani, E. Colineau, R. Eloirdi, J.-C. Griveau, R. Caciuffo, S. M. Cornet, I. May, C. A. Sharrad, D. Collison and R. E. P. Winpenny, Phys. Rev. Lett., 2010, 104, 197202 CrossRef CAS PubMed.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110 CrossRef CAS PubMed.
- (a) K. C. Mondal, A. Sundt, Y. Lan, G. E. Kostakis, O. Waldmann, L. Ungur, L. F. Chibotaru, C. E. Anson and A. K. Powell, Angew. Chem., Int. Ed., 2012, 51, 7550 CrossRef CAS PubMed; (b) Y. Zheng, E. Moreno Pineda, M. Helliwell and R. E. P. Winpenny, Chem. – Eur. J., 2012, 18, 4161 CrossRef CAS PubMed; (c) S. K. Langley, L. Ungur, N. F. Chilton, B. Moubaraki, L. F. Chibotaru and K. S. Murray, Chem. – Eur. J., 2011, 17, 9209 CrossRef CAS PubMed; (d) J. Rinck, G. Novitchi, W. van den Heuvel, L. Ungur, Y. Lan, W. Wernsdorfer, C. E. Anson, L. F. Chibotaru and A. K. Powell, Angew. Chem., Int. Ed., 2010, 49, 7583 CrossRef CAS PubMed.
- (a) A. Baniodeh, Y. Lan, G. Novitchi, V. Mereacre, A. Sukhanov, M. Ferbinteanu, V. Voronkova, Ch. E. Anson and A. K. Powell, Dalton. Trans., 2013, 42, 8926 RSC; (b) Q. Zhou, F. Yang, D. Liu, Y. Peng, G. Li, Z. Shi and S. Feng, Dalton. Trans., 2013, 42, 1039 RSC; (c) S. Schmidt, D. Prodius, V. Mereacre, G. E. Kostakis and A. K. Powell, Chem. Commun., 2013, 49, 1696 RSC; (d) S. Schmidt, D. Prodius, G. Novitchi, V. Mereacre, G. E. Kostakis and A. K. Powell, Chem. Commun., 2012, 48, 9825 RSC; (e) A. Baniodeh, I. J. Hewitt, V. Mereacre, Y. Lan, G. Novitchi, C. E. Anson and A. K. Powell, Dalton Trans., 2011, 40, 4080 RSC; (f) V. Mereacre, D. Prodius, Y. Lan, K. Turta, C. E. Anson and A. K. Powell, Chem. – Eur. J., 2011, 17, 123 CrossRef CAS PubMed; (g) S. Nayak, O. Roubeau, S. J. Teat, C. M. Beavers, P. Gamez and J. Reedijk, Inorg. Chem., 2010, 49, 216 CrossRef CAS PubMed; (h) D. Schray, G. Abbas, Y. Lan, V. Mereacre, A. Sundt, J. Dreiser, O. Waldmann, G. E. Kostakis, C. E. Anson and A. K. Powell, Angew. Chem., Int. Ed., 2010, 49, 5185 CrossRef CAS PubMed; (i) Y.–F. Zeng, G.-C. Xu, X. Hu, Z. Chen, X.-H. Bu, S. Gao and E. C. Sanudo, Inorg. Chem., 2010, 49, 9734 CrossRef CAS PubMed; (j) G. Abbas, Y. Lan, V. Mereacre, W. Wernsdorfer, R. Clerac, G. Buth, M. T. Sougrati, F. Grandjean, G. J. Long, C. E. Anson and A. K. Powell, Inorg. Chem., 2009, 48, 9345 CrossRef CAS PubMed; (k) M. N. Akhtar, V. Mereacre, G. Novitchi, J. P. Tuchagues, C. E. Anson and A. K. Powell, Chem. – Eur. J., 2009, 15, 7278 CrossRef CAS PubMed; (l) J. Bartolome, G. Filoti, V. Kuncser, G. Schinteie, V. Mereacre, C. E. Anson, A. K. Powell, D. Prodius and C. Turta, Phys. Rev. B: Condens. Matter, 2009, 80, 014430 CrossRef; (m) F. Pointillart, K. Bernot, R. Sessoli and D. Gatteschi, Chem. – Eur. J., 2007, 13, 1602 CrossRef PubMed; (n) M. Ferbinteanu, T. Kajiwara, K. Y. Choi, H. Nojiri, A. Nakamoto, N. Kojima, F. Cimpoesu, Y. Fujimura, S. Takaishi and M. Yamashita, J. Am. Chem. Soc., 2006, 128, 9008 CrossRef CAS PubMed; (o) M. Murugesu, A. Mishra, W. Wernsdorfer, K. A. Abboud and G. Christou, Polyhedron, 2006, 25, 613 CrossRef CAS; (p) S. Chen, V. Mereacre, C. E. Anson and A. K. Powell, Dalton Trans., 2016, 45, 98 RSC.
- (a) I. L. Malaestean, M. Kutluca, M. Speldrich, A. Ellern and P. Kögerler, Inorg. Chim. Acta, 2012, 380, 72 CrossRef CAS; (b) I. L. Malaestean, M. Speldrich, A. Ellern, S. G. Baca and P. Kögerler, Dalton Trans., 2011, 40, 331 RSC; (c) I. L. Malaestean, M. Speldrich, A. Ellern, S. G. Baca and P. Kögerler, Polyhedron, 2010, 29, 1990 CrossRef CAS; (d) S. G. Baca, M. Speldrich, J. van Leusen, A. Ellern and P. Kögerler, Dalton Trans., 2015, 44, 7777 RSC.
- (a) G. M. Dulcevscaia, I. G. Filippova, M. Speldrich, J. Leusen, V. C. Kravtsov, S. G. Baca, P. Kögerler, S.-X. Liu and S. Decurtins, Inorg. Chem., 2012, 51, 5110 CrossRef CAS PubMed; (b) S. G. Baca, T. Secker, A. Mikosch, M. Speldrich, J. van Leusen, A. Ellern and P. Kögerler, Inorg. Chem., 2013, 52, 4154 CrossRef CAS PubMed.
- (a) M. Speldrich, H. Schilder, H. Lueken and P. Kögerler, Isr. J. Chem., 2011, 51, 215 CrossRef CAS; (b) J. van Leusen, M. Speldrich, H. Schilder and P. Kögerler, Coord. Chem. Rev., 2015, 289–290, 137 CrossRef CAS.
- (a) S. Mukherjee, M. R. Daniels, R. Bagai, K. A. Abboud, G. Christou and C. Lampropoulos, Polyhedron, 2010, 29, 54 CrossRef CAS; (b) T. S. Hatscher and W. Urland, Angew. Chem., Int. Ed., 2003, 42, 2862 CrossRef PubMed; (c) K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341 CrossRef CAS; (d) K. Shrivastava, Phys. Status Solidi B, 1983, 117, 437 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthesis, characterization, X-ray diffraction, magnetochemical analysis details, additional structural plots and thermal stability data. CCDC 937876, 959015–959017. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6qi00095a |
‡ Crystal data for 1: C61H129Dy2Fe4N11O26, Mr = 1981.15 g mol−1, triclinic, space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , a = 14.4435(9), b = 17.3551(11), c = 18.0251(12) Å, α = 92.765(2)°, β = 104.869(2)°, γ = 96.595(2)°, V = 4323.9(5) Å3, Z = 2, R1 = 0.0548 (I > 2σ(I)), wR2 = 0.1246 (for 14 , a = 14.4435(9), b = 17.3551(11), c = 18.0251(12) Å, α = 92.765(2)°, β = 104.869(2)°, γ = 96.595(2)°, V = 4323.9(5) Å3, Z = 2, R1 = 0.0548 (I > 2σ(I)), wR2 = 0.1246 (for 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 285 unique reflections and 1040 refined parameters). 2: C61H129Fe4N11O26Y2, Mr = 1833.97 g mol−1, triclinic, space group P 285 unique reflections and 1040 refined parameters). 2: C61H129Fe4N11O26Y2, Mr = 1833.97 g mol−1, triclinic, space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , a = 14.423(4), b = 17.383(5), c = 18.109(5) Å, α = 92.839(7)°, β = 104.682(7)°, γ = 96.704(7)°, V = 4347(2) Å3, Z = 2, R1 = 0.0766 (I > 2σ(I)), wR2 = 0.1859 (for 12 , a = 14.423(4), b = 17.383(5), c = 18.109(5) Å, α = 92.839(7)°, β = 104.682(7)°, γ = 96.704(7)°, V = 4347(2) Å3, Z = 2, R1 = 0.0766 (I > 2σ(I)), wR2 = 0.1859 (for 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 825 unique reflections and 886 refined parameters). 3: C61H129Fe4Gd2N11O26, Mr = 1833.97 g mol−1, triclinic, space group P 825 unique reflections and 886 refined parameters). 3: C61H129Fe4Gd2N11O26, Mr = 1833.97 g mol−1, triclinic, space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , a = 15.278(2), b = 16.228(3), c = 16.672(3) Å, α = 88.375(2)°, β = 89.375(2)°, γ = 82.960(2)°, V = 4100.6(11) Å3, Z = 2, R1 = 0.0654 (I > 2σ(I)), wR2 = 0.1652 (for 16 , a = 15.278(2), b = 16.228(3), c = 16.672(3) Å, α = 88.375(2)°, β = 89.375(2)°, γ = 82.960(2)°, V = 4100.6(11) Å3, Z = 2, R1 = 0.0654 (I > 2σ(I)), wR2 = 0.1652 (for 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 129 unique reflections and 930 refined parameters). 4: C61H129Eu2Fe4N11O26, Mr = 1949.01 g mol−1, triclinic, space group P 129 unique reflections and 930 refined parameters). 4: C61H129Eu2Fe4N11O26, Mr = 1949.01 g mol−1, triclinic, space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , a = 15.269(2), b = 16.216(2), c = 16.655(2) Å, α = 88.379(2)°, β = 89.398(2)°, γ = 82.993(2)°, V = 4091.3(9) Å3, Z = 2, R1 = 0.0461 (I > 2σ(I)), wR2 = 0.1096 (for 17 , a = 15.269(2), b = 16.216(2), c = 16.655(2) Å, α = 88.379(2)°, β = 89.398(2)°, γ = 82.993(2)°, V = 4091.3(9) Å3, Z = 2, R1 = 0.0461 (I > 2σ(I)), wR2 = 0.1096 (for 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570 unique reflections and 929 refined parameters). CCDC 937876 (1), 959015 (2), 959016 (3), and 959017 (4) contain the supplementary crystallographic data. 570 unique reflections and 929 refined parameters). CCDC 937876 (1), 959015 (2), 959016 (3), and 959017 (4) contain the supplementary crystallographic data. |
| This journal is © the Partner Organisations 2016 |