A mechanistic study on guanidine-catalyzed chemical fixation of CO2 with 2-aminobenzonitrile to quinazoline-2,4(1H,3H)-dione†
Weiyi
Li
*a,
Na
Yang
b and
Yajing
Lyu
a
aSchool of Science, Xihua University, Chengdu, 610039, Sichuan, P. R. China. E-mail: weiyili@mail.xhu.edu.cn; Fax: +86-028-87727663; Tel: +86-028-87727663
bInstitute of Nuclear Physics and Chemistry, China Academy of Engineering Physics, Mianyang, 621900, P. R. China
First published on 28th April 2016
Abstract
The organic base-catalyzed mechanism of chemical fixation of CO2 with 2-aminobenzonitrile to quinazoline-2,4-(1H,3H)-dione has been studied by means of density functional theory (DFT) calculations on such reactions in the presence of two typical organic guanidines: 1,1,3,3-tetramethylguanidine (TMG) and 1,5,7-triazabicyclo[4.4.0]dec-1-ene (TBD). The calculations reveal that the guanidine-catalyzed reaction prefers to proceed through a general base mechanism rather than the CO2 activation mechanism that involves the formation of guanidine–CO2 adducts. In the general base mechanism, the guanidine primarily plays a catalytic role as a strong base to promote the fixation of CO2 by the amino group of 2-aminobenzonitrile, leading to a carbamate intermediate. Meanwhile, the acidity of guanidinium and the synergistic catalysis from the amino group of 2-aminobenzonitrile are also found to be crucial for lowering energy barriers of intramolecular nucleophilic attack from the carbamate to the nitrile group and the isocyanate intermediate formation via the ring-opening step. In comparison with the TBD-catalyzed reaction, the catalytic advantage of TMG is exerted at the less H-bonding interaction between [TMGH]+ guanidinium and the carbamate anion, owing to its own acyclic framework.
1. Introduction
As the principal greenhouse gas, carbon dioxide (CO2) is likely associated with global warming due to the combustion of fossil fuels and deforestation in the past few decades. On the other hand, from a green synthetic point of view, CO2 is also considered as one of the most easily available renewable carbon resources, which has the advantages of being nontoxic, abundant, inexpensive and non-flammable when compared to the other C1 sources like toxic phosgene and CO employed by the chemical industry.1 Consequently, the catalytic fixation of CO2 into various useful chemicals has received considerable attention, and extensive efforts have been devoted to the development of more efficient catalysts to promote CO2 transformations under mild conditions.2,3 In this context, the chemical fixation of CO2 with 2-aminobenzonitriles to quinazoline-2,4(1H,3H)-diones is a promising synthetic strategy (Scheme 1), as the final product quinazoline-2,4(1H,3H)-diones and their derivatives are an important class of biological and pharmaceutical agents.4 Furthermore, as compared with the traditional synthetic methods that involved the use of anthranilic acid with urea, anthranilic acid with KCN, and anthranilamide with phosgene,5 this approach is greener with higher atom-economy.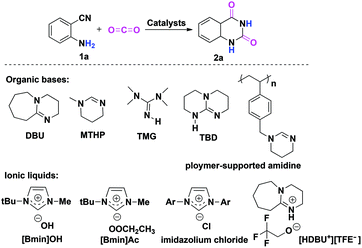 | ||
| Scheme 1 Chemical fixation of CO2 with 2-aminobenzonitrile 1a to quinazoline-2,4-(1H,3H)-dione 2a catalyzed by organic bases and ionic liquids. | ||
To date, organic bases6 and ionic liquids7 are two kinds of most widely used catalysts for chemical fixation of CO2 with 2-aminobenzonitrile 1a to quinazoline-2,4(1H,3H)-dione 2a. In most cases, the desired product 2a can be obtained with moderate to good yields. In addition, other catalytic systems, such as an inorganic base Cs2CO3,8a a solid base catalyst MgO/ZrO2,8b a monomeric tungstate (TBA2[WO4]),8c,d a series of magnesium containing mesoporous smectites with incorporation of alkali hydroxide,8e and an organic superbase-functionalized Fe3O4 (base@Fe3O4)8f are also found to be effective for this reaction. Indeed, it is very interesting to note that the reaction can proceed in water without any catalysts,9 although higher reaction temperatures and longer reaction time are required for acquiring a satisfactory yield of 2a.
Despite a number of impressive experimental research studies focused on increasing the yield of the target product and improving the reaction conditions, thorough mechanistic studies on the reported catalytic reactions are rather limited. In 2011, Wu and co-workers10a reported the first example of a theoretical study on the mechanism of the title reaction catalyzed by the [Bmim]OH ionic liquid. The DFT calculations at the B3PW91/6-311G(d, p) level of theory indicate that N-heterocyclic carbine (NHC) generated from the dehydration of the [Bmim]OH ionic liquid is the actual active species in the catalytic reaction. The catalytic cycle is composed of three elementary steps: (i) the formation of the NHC–CO2 complex, (ii) the attack of one oxygen atom of CO2 to the carbon atom of the cyano group of 1a, and (iii) the formation of the C–N bond from the carbon atom of CO2 and the nitrogen atom of the amino group. As the energy barrier of each step is comparable with one another (35.5, 35.5 and 36.0 kcal mol−1), the reaction rate is controlled by each of them. Subsequently, Mizuno and co-workers8d studied the catalytic mechanism of the monomeric tungstate (TBA2[WO4]) in the reaction. Their DFT calculations disclose that the monomeric tungstate works not only as a base to abstract the hydrogen of the carbamic acid intermediate, but also an acid to activate the cyano group. As a continuous work, Ma et al.10b also carried out a mechanistic study of the reaction in water. The DFT calculations at the M06-2X/aug-cc-PVDZ level show that carbonic acid (H2CO3) formed form CO2 and water is essential for the reaction to proceed in the absence of catalysts. With the weak acidity, H2CO3 can more easily react with the cyano group of 1a than CO2. Meanwhile, H2CO3 can act as a proton transfer reagent to promote the intramolecular dehydration step.
With respect to the organic base-catalyzed chemical fixation of CO2 with 1a, a hypothetic catalytic reaction mechanism involved in the formation of the carbamate and isocyanate intermediates was proposed by the related experimental research groups (Scheme 2).6 Cao and co-worker11 reported a mechanistic study of the base NHC-catalyzed chemical fixation of CO2 with the amine and silane to formamide, which concerns the analogous C–N bond formation, C–O bond formation/cleavage processes. However, there is no computational investigation aiming at the mechanism of the organic base-catalyzed chemical fixation of CO2 with 1a to 2a available in the literature so far. As organic guanidines are well established as one kind of powerful and promising organocatalyst for the catalytic transformation of CO2 molecules,12 the guanidine-based catalytic system, developed by He's group,6e was employed as a reaction model in our quantum chemical study on the mechanism of such a reaction. In the present work, the detailed reaction course in the presence of two commonly used guanidines (TMG and TBD) was explored by means of DFT calculations. Meanwhile, the catalytic role of organic guanidines, the similarities and differences of TMG and TBD, and the synergistic catalysis of substrate 1a were also disclosed and compared. This mechanistic study may help optimize/improve reaction conditions and develop more efficient catalytic systems for synthesis of quinazoline-2,4(1H,3H)-diones from chemical fixation of CO2 with 2-aminobenzonitriles.
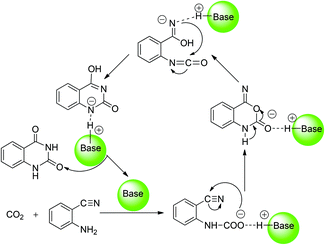 | ||
| Scheme 2 Proposed mechanism for organic base-catalyzed chemical fixation of CO2 with 2-aminobenzonitrile 1a to quinazoline-2,4-(1H,3H)-dione 2a. | ||
2. Computational details
For the present mechanistic study, all electronic structure calculations were carried out with the Gaussian 09 program.13 Zhao and Truhlar14 developed hybrid meta exchange–correlation functional M06-2X, with the 6-31+G(d) basis set15 was used for the geometry optimization of all reactants, products, intermediates (IMs) and transition states (TSs) involved in the reaction. The vibrational frequency calculations at the same level of theory were performed to verify that a local minimum has no imaginary frequency and each transition state has a unique imaginary frequency. In addition, intrinsic reaction coordinate (IRC16) scans were also conducted to confirm some key transition states that were hard to simply judge by their vectors of imaginary frequencies. To consider the solvent effect of this solvent-free reaction system, substrate 1a was employed as the reaction medium, as the reaction primarily took place in this rich phase. However, the accurate dielectric constant (ε) of 1a is not available in any handbooks or literature. Hence, the solvent radius (RSOLV = 4.01 Å) calculated for 1a with the dielectric constants reported for aniline (ε = 7.01) and benzonitrile (ε = 25.57)17 was respectively set as the major parameters for the approximate reaction media in the present theoretical simulation. For all of the optimized-structures in a gas phase, single-point energy calculations in the two approximate reaction media were performed by employing the continuum solvation model (SMD18) at the M06-2X/6-31++G(d, p) level, respectively. The relative Gibbs free energies (ΔGsol) were obtained by the combination of these single-point energies with the Gibbs free energy corrections in the gas phase. Nonetheless, it should be emphasized that such thermal corrections based on the ideal gas-phase model inevitably overestimate entropy contributions to free energies for reactions in solvent, in particular for reactions involving component changes, because the suppressing effect of the solvent on the rotational and transitional freedoms of the substrates is ignored.19 Accordingly, Martin et al.20 proposed an approximate entropy correction for ΔGsol. As many earlier theoretical studies did,21 a correction of 4.3 kcal mol−1 was applied for a reaction with per component change at 298 K and 1 atm [i.e., a reaction from m to n components has an additional correction of (n − m) × 4.3 kcal mol−1]. Since the relative Gibbs free energies (ΔGsol) obtained in the two reaction media are very close, the lower ones are used in the following discussion for brevity. In addition, the relative enthalpies (ΔHsol) are given in the ESI† as references.Furthermore, molecular electrostatic potential (MESP22) and atoms in molecules (AIM23) analysis were carried out to infer the existence, or otherwise, of a molecular interaction in some key intermediates with the Multiwfn24 and AIM 2000 program, respectively. In the AIM theory, the interaction between two atoms is revealed by the presence of a charge density in the interconnection space and this electron density is related to a bond critical point (BCP). If a (3, −1) BCP existed between any pair of nuclei, these nuclei were considered to be bonded to one another.
3. Results and discussion
3.1 Background reaction without a guanidine catalyst
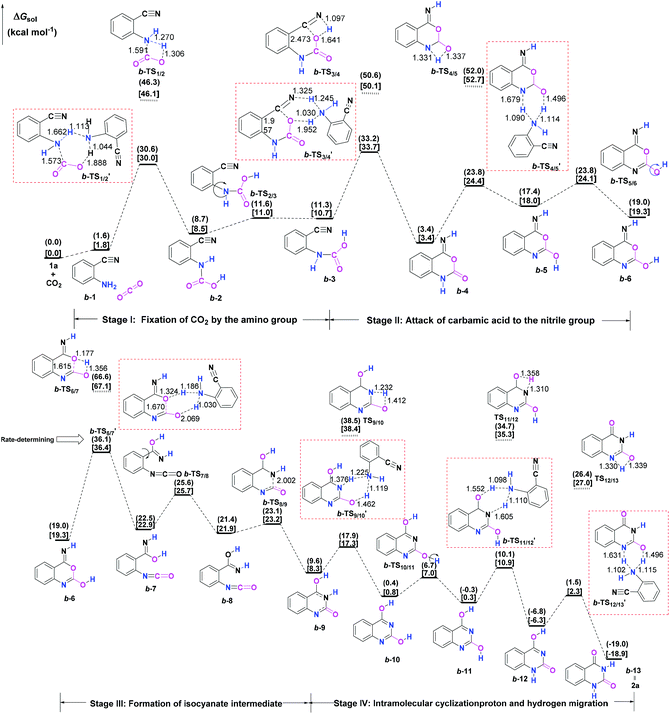
Initially, the reaction mechanism of 1a with CO2 in the absence of catalysts was examined as an ideal benchmark to discuss the catalytic role of guanidines. The calculated potential energy surface (PES) for the uncatalyzed reaction pathway is presented in Fig. 1, together with the schematic structures of all stationary points along the reaction pathway.From the viewpoint of the chemical bond construction, the synthesis of 2a from the reaction of 1a with CO2 concerns the split of one C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double bond of CO2 molecule, the formation of one C–O bond from one oxygen atom of CO2 with the carbon atom of the nitrile group of 1a, and two C–N bonds from the carbon atom of CO2 with the nitrogen atoms of the amino and nitrile groups, respectively. Accordingly, the multiple elementary steps along the whole uncatalyzed reaction pathway are classified as four major stages. Firstly, one of the C–N bonds is formed through the fixation of CO2 by the amino group of 1a over a 1a-assisted six-membered ring b-TS′1/2, leading to the carbamic acid IM b-2. Then, the isomer (b-3) of the carbamic acid IM b-2 is generated as a consequence of the rotation of the C–N bond via b-TS2/3. Secondly, the C–O bond is constructed through the attack of the carbamic acid moiety to the nitrile group through a 1a-assisted concerted b-TS′3/4, allowing the formation of a ring-closure IM b-4. The following tautomerization and isomerization steps of IM b-4 yield IM b-6. Thirdly, the cleavage of the C–O bond via a 1a-assisted ring-opening b-TS′6/7 yields the isocyanate IM b-7, which is followed by the isomerization step to give the isocyanate IM b-8. Lastly, the second C–N bond is constructed through the intramolecular cyclization addition b-TS8/9, leading to the ring-closure IM b-9. From IM b-9, the desired product 2a can be produced through a series of hydrogen migration steps. The present four stages are generally in line with the mechanism reported by Ma et al.10b for the uncatalyzed reaction of 1a and CO2 in aqueous solvent, which is energy-favourable than the one calculated in Wu's work.10a However, it should be emphasised that our calculations found the energy barriers of the steps that involve the hydrogen migration can be further dropped when an external molecule 1a is employed as a proton transfer reagent. The amino group of 1a can serve as the hydrogen shuttle in the relevant hydrogen migration step, which is analogous to the role of a water molecule reported in a number of organic reactions involved in the hydrogen transfer process.25 The remarkable decrease in relative energy barriers could be ascribed to two aspects: (i) the basicity of the amino group of 1a, and (ii) the alleviation of ring strain in the hydrogen migration steps upon changing from a four- to a six-membered ring transition state. Overall, the formation of the isocyanate IM b-7via b-TS′6/7 is the rate-determining step (RDS) for the uncatalyzed reaction pathway, which is analogous to the result reported by Ma et al.,10b but the calculated activation energy barrier of b-TS′6/7 (36.1 vs. 50.7 kcal mol−1) is much lower. Nevertheless, the activation free energy barriers of b-TS′1/2, b-TS′3/4 and b-TS′6/7 in the steps of the formation of the carbamic acid species, the nucleophilic attack of the carbamic acid species to the nitrile group of 1a and the formation of the isocyanate species all exceed over 30.0 kcal mol−1, meaning that the background reaction can hardly occur under mild conditions. Hence the screening of effective catalysts to overcome the energetic bottleneck in these three steps is crucial for the whole reaction.
O double bond of CO2 molecule, the formation of one C–O bond from one oxygen atom of CO2 with the carbon atom of the nitrile group of 1a, and two C–N bonds from the carbon atom of CO2 with the nitrogen atoms of the amino and nitrile groups, respectively. Accordingly, the multiple elementary steps along the whole uncatalyzed reaction pathway are classified as four major stages. Firstly, one of the C–N bonds is formed through the fixation of CO2 by the amino group of 1a over a 1a-assisted six-membered ring b-TS′1/2, leading to the carbamic acid IM b-2. Then, the isomer (b-3) of the carbamic acid IM b-2 is generated as a consequence of the rotation of the C–N bond via b-TS2/3. Secondly, the C–O bond is constructed through the attack of the carbamic acid moiety to the nitrile group through a 1a-assisted concerted b-TS′3/4, allowing the formation of a ring-closure IM b-4. The following tautomerization and isomerization steps of IM b-4 yield IM b-6. Thirdly, the cleavage of the C–O bond via a 1a-assisted ring-opening b-TS′6/7 yields the isocyanate IM b-7, which is followed by the isomerization step to give the isocyanate IM b-8. Lastly, the second C–N bond is constructed through the intramolecular cyclization addition b-TS8/9, leading to the ring-closure IM b-9. From IM b-9, the desired product 2a can be produced through a series of hydrogen migration steps. The present four stages are generally in line with the mechanism reported by Ma et al.10b for the uncatalyzed reaction of 1a and CO2 in aqueous solvent, which is energy-favourable than the one calculated in Wu's work.10a However, it should be emphasised that our calculations found the energy barriers of the steps that involve the hydrogen migration can be further dropped when an external molecule 1a is employed as a proton transfer reagent. The amino group of 1a can serve as the hydrogen shuttle in the relevant hydrogen migration step, which is analogous to the role of a water molecule reported in a number of organic reactions involved in the hydrogen transfer process.25 The remarkable decrease in relative energy barriers could be ascribed to two aspects: (i) the basicity of the amino group of 1a, and (ii) the alleviation of ring strain in the hydrogen migration steps upon changing from a four- to a six-membered ring transition state. Overall, the formation of the isocyanate IM b-7via b-TS′6/7 is the rate-determining step (RDS) for the uncatalyzed reaction pathway, which is analogous to the result reported by Ma et al.,10b but the calculated activation energy barrier of b-TS′6/7 (36.1 vs. 50.7 kcal mol−1) is much lower. Nevertheless, the activation free energy barriers of b-TS′1/2, b-TS′3/4 and b-TS′6/7 in the steps of the formation of the carbamic acid species, the nucleophilic attack of the carbamic acid species to the nitrile group of 1a and the formation of the isocyanate species all exceed over 30.0 kcal mol−1, meaning that the background reaction can hardly occur under mild conditions. Hence the screening of effective catalysts to overcome the energetic bottleneck in these three steps is crucial for the whole reaction.
3.2 Mechanisms of TMG-catalyzed reaction
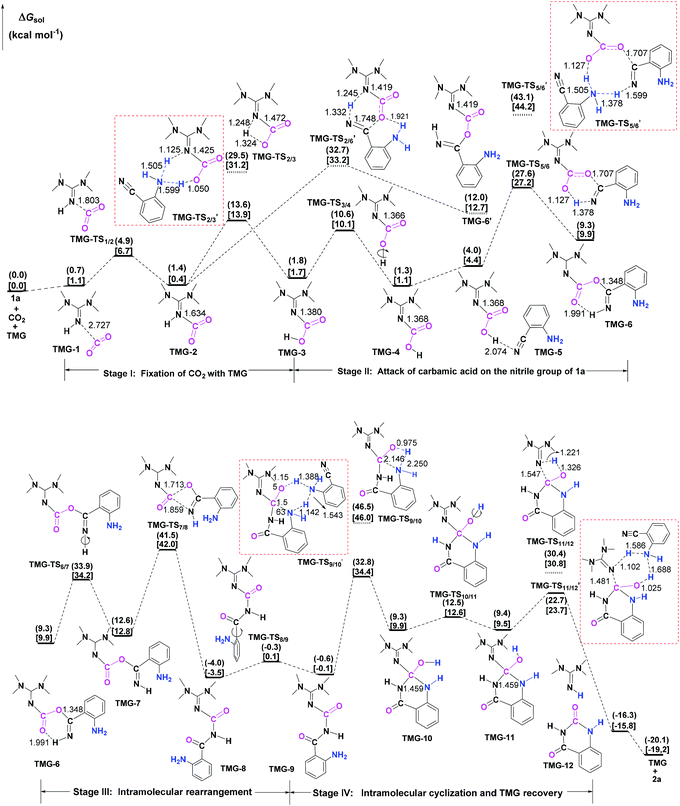
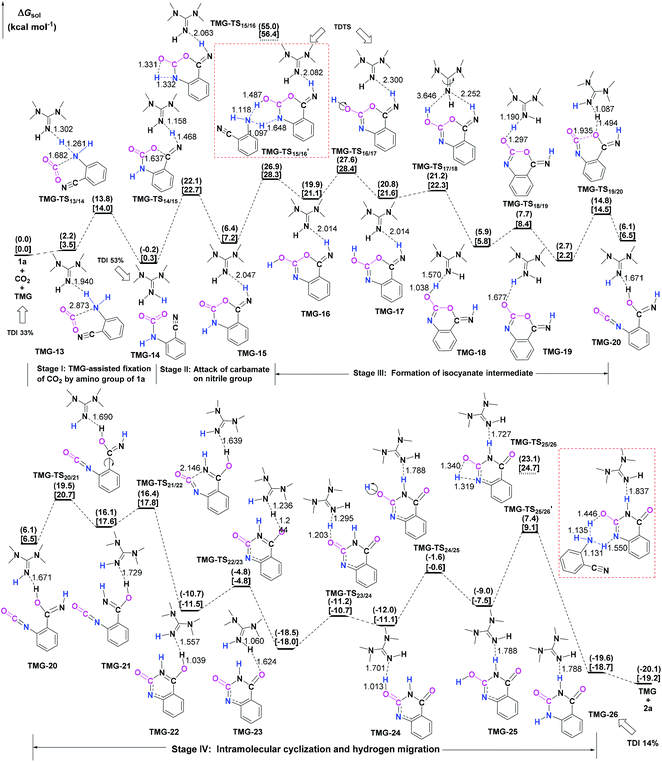
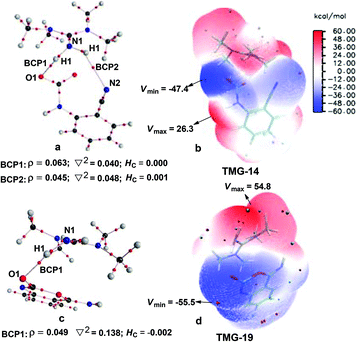
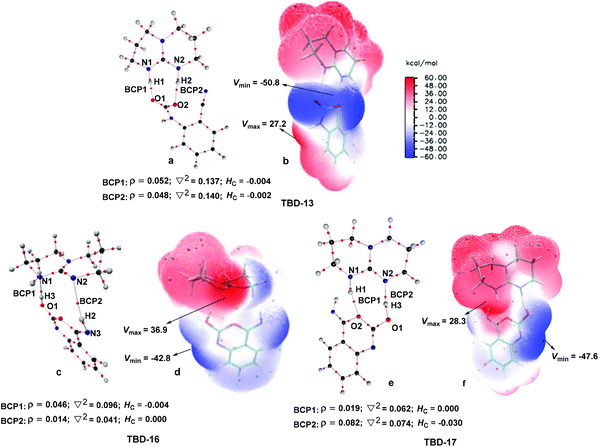
Next, the mechanisms of the reaction in the presence of TMG were investigated, as this simplest guanidine exhibited the highest catalytic activity among all the tested guanidines in He's experiment.6e In this section, two possible reaction pathways, differing in the catalytic role of TMG, were considered. One is through the CO2 activation mechanism (Pathway A) that involves the formation of the zwitterionic TMG–CO2 adduct. The other one is through the general base mechanism (Pathway B), in which TMG plays the role as a strong base to promote the fixation of CO2 with the amino group of 1a.Starting from the termolecular complex TMG-13, the fixation of CO2 by the amino group of 1a is through the TMG-assisted TMG-TS13/14, in which the nucleophilic attack from the amino nitrogen atom to the carbon atom of CO2 as well as the abstraction of the amino hydrogen atom by the nitrogen atom of TMG is concerted. With respect to the uncatalyzed process, the catalytic effect of TMG is significant, as the free energy barrier dramatically drops from 30.0 kcal mol−1 (b-TS′1/2) to 13.8 kcal mol−1 (TMG-TS13/14). This result indicates that TMG can act as a strong base to promote the incorporation of CO2 with the amino group of 1a. After the crosses TMG-TS13/14, the C–N bond is constructed in an ionic pair IM TMG-14. This ionic pair IM is slightly stable than the initial separated reactants and TMG by 0.2 kcal mol−1 in free energy. To gain further insight into the inherent stabilizing interactions in this ionic pair IM, AIM and MESP analyses were performed on TMG-14, respectively. In AIM theory, Laplacian of the charge density (∇2) on (3, −1) BCPs between the interacting hydrogen and hydrogen acceptor usually serves as a symbol of bond nature, viz., the shared electron (covalent) interactions (∇2 < 0) and closed-shell (electrostatic) interactions (∇2 > 0), while the charge density (ρ) and total electron density (Hc) on (3, −1) BCPs are used to quantify the strength of the H-bond.23Fig. 4a shows the result of AIM analysis on TMG-14 using the wave function generated at the M06-2X/6-31++G(d, p) level. The positive Laplacian values at the two BCPs indicate that two H-bonds are formed between the [TMGH]+ guanidinium and the [carbamate]− anion. According to the suggested classification for the H-bond,27 the N1–H1⋯O1 H-bond at BCP1 belongs to a strong H-bond (ρ > 0.05 a.u and Hc ≤ 0), while the N1–H2⋯N2 H-bond at BCP2 is a medium H-bond (0.02 a.u. < ρ < 0.05 a.u., Hc ≥ 0). Besides H-bonding interaction, electrostatic attraction is suggested as the other essential stabilizing interaction in ionic pair IM.27 As shown in Fig. 4b, the carboxyl oxygen atoms and nitrile groups of the carbamate moiety are negatively charged, while the rest of the region is positively charged. The region that connected the [TMGH]+ guanidinium and [carbamate]− anion has a zero MESP value, indicating that these two moieties are compactly in contact with electrostatic attraction. Additionally, the minimum MESP (Vmin = −47.4 kcal mol−1) appears at the region between the carbamate oxygen anion, suggesting this carbamate oxygen anion has high reactivity. Hence, TMG-14 can easily undergo an intramolecular nucleophilic attack from the carbamate oxygen atom to the carbon atom of the nitrile group via TMG-TS14/15, leading to a ring-closure in IM TMG-15 with the construction of the C–O bond. Relative to 1a-assisted b-TS′3/4, the free energy barrier of TMG-TS14/15 is lowered by 11.1 kcal mol−1, indicating that the [TMGH]+ guanidinium with enough acidity can accelerate this intramolecular cyclization. From TMG-15, the C–O bond cleavage with the generation of the isocyanate IM TMG-20 takes place through stage III, which is composed of tautomerization (TMG-15 → TMG-16), isomerization (TMG-16 → TMG-17 → TMG-18), hydrogen migration (TMG-18 → TMG-19), and ring-opening (TMG-19 → TMG-20) steps. For the tautomerization step, the synergistic catalysis from the amino group of an external 1a is significant, as the direct hydrogen migration from the imino atom to the carbonyl oxygen atom via a four-membered-ring TMG-TS15/16 requires a very high free energy barrier of 55.0 kcal mol−1. For 1a-assisted six-membered-ring TMG-TS′15/16, the free energy barrier is reduced to 26.9 kcal mol−1, meaning that this tautomerization can proceed under moderate conditions. Subsequently, the isomerization of TMG-16via the O–H bond rotation TS (TMG-TS16/17, 27.6 kcal mol−1) generates TMG-17. With less steric hindrance, TMG can further undergo a conformational rotation to TMG-TS17/18 (20.8 kcal mol−1), leading to a more stable IM TMG-18. In TMG-18, TMG is bonded with the benzo[1,3]oxazin moiety via a H-bond. Due to the strong basicity of TMG and its own acyclic framework,28a the hydroxyl hydrogen atom of the benzo[1,3]oxazin moiety can be snatched by the nitrogen center of TMG via TMG-TS18/19 (7.7 kcal mol−1), resulting in an ionic pair IM TMG-19. In this ionic pair IM, the [TMGH]+ guanidinium serves as a H-bond donor to interact with the carbonyl oxygen atom of the benzo[1,3]oxazin moiety, forming a medium to strong strengthened H-bond (Fig. 4c). Meanwhile, the [TMGH]+ guanidinium and benzo[1,3]oxazin anion interact with each other through electrostatic attractions (Fig. 4d). The MESP maximum (Vmax = 54.8 kcal mol−1) appears around the hydrogen atom of the [TMGH]+ guanidinium, implying this N–H bond has strong activity. Consequently, the following intramolecular ring-opening step via TMG-TS19/20 can be promoted by the hydrogen migration from the [TMGH]+ guanidinium to the lactone oxygen atom, resulting in the isocyanate IM TMG-20. The relative free energy of TMG-TS19/20 is predicted to be 14.5 kcal mol−1, lying 21.6 kcal mol−1 below 1a-assisted b-TS′6/7 (36.1 kcal mol−1). This result suggests that the [TMGH]+ guanidinium with enough acidity is also crucial for the generation of isocyanate IM. Once this isocyanate IM is generated, the desired product 2a can be easily formed through the intramolecular cyclization (TMG-20 → TMG-22) and hydrogen migration (TMG-22 → TMG-26) steps in stage IV. This stage is almost similar to the one in the absence of guanidines, but the relative free energy of each IM and TS involved is much lower. With regard to the whole PES, TMG-TS′15/16 and TMG-TS16/17 with the comparable overall free energies of 26.9 and 27.6 kcal mol−1 relative to the zero-point reference are both rate-determining in the general base mechanism. These overall free energies are lower than the one (TMG-TS7/8, 41.5 kcal mol−1) calculated in the CO2 activation mechanism and reasonable to account for the experimental conditions.6e Therefore, the chemical fixation of CO2 with 1a in the presence of TMG should adopt the general base mechanism. In comparison with the reported overall free energy barriers of 25.6 and 36.0 kcal mol−1 for the reaction catalyzed by the monomeric tungstate (TBA2[WO4])8d and [Bmim]OH ionic liquid,10a this simplest guanidine exhibits an equal or a better catalytic effect.
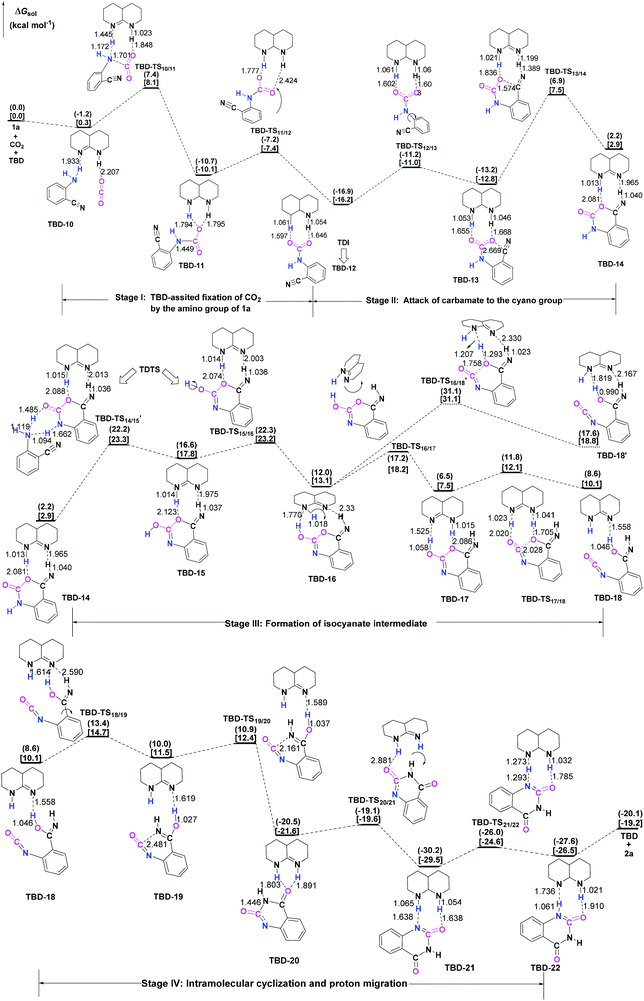
3.3 TBD-catalyzed reaction
To further elucidate the origin of the catalytic advance of TMG, the reaction under the catalysis of TBD was comparatively investigated, as this guanidine catalyst is also widely applied in a number of CO2 transformations. For the TBD-catalyzed reaction, both the CO2 activation mechanism and general base mechanism were located at the same level of theory, and the calculations indicate that the general base mechanism is also remarkably favourable over the CO2 activation mechanism (see Fig. S1 in the ESI†). As a result, the general base mechanism is emphatically discussed in what follows.In general, the TBD-catalyzed reaction of 1a with CO2 to 2a proceeds through an analogous reaction course as mentioned in the TMG-mediated base mechanism, but the detailed energetic property for each reaction stage is quite distinct (Fig. 5). In the first stage, TBD-assisted fixation of CO2 by the amino group of 1a (TBD-TS10/11, 7.4 kcal mol−1) is predicted to be kinetically more favourable than the TMG-catalyzed process. This result should be attributed to two advantages of TBD: (i) the basicity of TBD is stronger than TMG,28b,c making the hydrogen migration from the amino group to the basic nitrogen center more feasible; and (ii) the N–H bond beside the basic nitrogen center can act as a H-bond donor to interact with one oxygen atom of the CO2 molecule, which favours the negative charge delocalization on the CO2 moiety during the nucleophilic addition process. After crossing the first stage, [TBDH]+ guanidinium can combine with the carbamate cation to generate an ionic pair IM TBD-13. This process is exergonic by 16.9 kcal mol−1 in free energy. In this ionic pair IM, the dual H-bonds (N1–H1⋯O1 and N2–H2⋯O2) are formed between the [TBDH]+ guanidinium and the carbamate cation. According to the result of AIM analysis (Fig. 6a), the dual H-bonds can be regarded as strong H-bonds, and therefore TBD-13 is more stable than the analogous ionic pair IM TMG-14, in which only a single strong H-bond is formed between [TMGH]+ guanidinium and carbamate. Additionally, a more negative MESP minimum (−50.8 kcal mol−1) appears at the region between carbamate oxygen atoms (Fig. 6b), implying that the reactivity of the carbamate oxygen atom in TBD-13 is higher than that in TMG-14. Thus, the subsequent intramolecular nucleophilic attack from the carbamate oxygen atom to the carbon atom of the nitrile group can more facilely proceed through TBD-TS13/14, with a lower free energy barrier of 6.9 kcal mol−1 relative to TMG-TS14/15 (22.1 kcal mo−1). After TBD-TS13/14, the C–O bond is constructed in IM TBD-14, which is coupled with the other dual H-bonds formed between the benzo[1,3]oxazin moiety and TBD. In the third stage of the reaction, the dual H-bonds maintains well during the tautomerization (TBD-14 → TBD-15) and isomerization (TBD-15 → TBD-16) steps, and therefore the relative free energies of 1a-assisted hydrogen migration TBD-TS′14/15 and the O–H bond rotation TBD-TS15/16 are lower than the those of the analogous TMG-TS′15/16 and TMG-TS16/17. However, the dual H-bonds are reorganized in IM TBD-16. The original strong H-bond (N1–H1⋯O1) is destroyed by the repulsion from the hydroxyl hydrogen (H3) atom. Instead, the hydroxyl group can act as a H-bond donor to interact with the N1 atom from the backside of the N1–H1 bond, resulting in a medium strengthened H-bond (N1–H3⋯O1). This change also makes the strength of the H-bond (N2–H2⋯O2) become weak (Fig. 6c). From TBD-16, two possible scenarios for the subsequent ring-opening step leading to the isocyanate species were considered. One is through the direct C–O bond cleavage at TBD-TS′16/18. This ring-opening is associated with two successive hydrogen migrations: firstly, the H3 atom transfers from the hydroxyl oxygen atom to the N1 atom from the backside of the N1–H1 bond, forming an instantaneously unstable guanidinium with a positively charged N1 center, and then the H1 atom transfers from the N1 atom to the lactone oxygen atom, leading to the isocyanate IM TBD-18′ (see Fig. S2 in the ESI†). The calculation indicates that the free energy barrier of TBD-TS′16/18 is high up to 31.1 kcal mol−1, which is likely due to the weak proton affinity of the N1 atom and activity of the N1–H1 bond. On the other hand, the TBD moiety in IM TBD-16 might alternatively undergo a conformational flip over TBD-TS16/17 (17.2 kcal mol−1), which leads the basic N2 atom of the TBD moiety to face toward the hydroxyl group of the benzo[1,3]oxazin moiety and alters the H-bond arrangement between TBD and benzo[1,3]oxazin moieties simultaneously. In the resultant IM TBD-17, the N1–H1 bond serves as a H-bond donor to interact with the lactone oxygen atom with the formation of a weak to medium strengthened H-bond, while the basic N2 atom acts as the H-bond acceptor to interact with the H3 atom of the hydroxyl group with the formation of a strong H-bond (Fig. 6e). With this rearranged dual H-bond, the C–O bond cleavage can be more facile with the aid of the asynchronous hydrogen migrations: initially, the H3 atom transfers from the hydroxyl oxygen atom to the basic N2 atom, forming a guanidinium at TBD-TS17/18, and then the H1 atom transfers from the N1 atom to the lactone oxygen atom, resulting in the isocyanate IM TBD-18 (see Fig. S3 in the ESI†). The free energy barrier of TBD-TS17/18 is reduced to 11.8 kcal mol−1, which is somewhat analogous to the H-bonding pathway for the ring-opening of L-lactide in the presence of TBD.29 After the isocyanate IM TBD-18 is generated, the following intramolecular cyclization and hydrogen migration steps in the last stage can be experienced smoothly, as the free energy barrier of each elementary step is no more than 20.0 kcal mol−1. As compared with the TMG-catalyzed process, a notable difference is that the IM TBD-21 (−30.2 kcal mol−1) and the product–catalyst complex TBD-22 (−27.6 kcal mol−1) are thermodynamically more stable than the separated product 2a and TBD, owing to the dual H-bonds formed between TBD and the quinazoline moiety. On the whole, 1a-assisted hydrogen migration TBD-TS′14/15 and the O–H bond rotation TBD-TS15/16 with the overall free energy barrier of 22.2 and 22.3 kcal mol−1 are situated on the energy summit along the PES, which can be regarded as the rate-determining TSs for the TBD-catalyzed general base mechanism.
In comparison with overall free energy barriers (26.9 and 27.6 kcal mol−1) predicted for the TMG-catalyzed general base mechanism, it seems that the TBD-catalyzed chemical fixation of CO2 with 1a is kinetically favourable. However, as pointed out by Kozuch and Shaik,30 the efficiency of catalysts should be evaluated by using the global energetic span model (δE) in the whole catalytic cycle. Accordingly, the turnover frequency (TOF) analysis of the catalytic cycles in the presence of two guanidines was performed with the AUTOF program30c based on the computed potential profiles. The TOF-determining intermediate (TDI), TOF-determining transition state (TDTS), degree of TOF control, and TOF value of each catalytic cycle are listed in Table 1.
| Catalytic system | TDI | TDTS | TOF (h−1) |
|---|---|---|---|
| TMG | 0.33 (reactants + TMG) + 0.53 TMG-14 + 0.14 TMG-26 | 0.25 TMG-TS′15/16 + 0.75 TMG-TS16/17 | 3.34 × 10−5 |
| TBD | TBD-12 | 0.46 TBD-TS′14/15 + 0.54 TBD-TS15/16 | 2.23 × 10−13 |
For the TMG-mediated catalytic cycle, the TDI is shared with three local minima: the initial separated reactants and TMG, the guanidinium [TMGH]+[carbamate]− ionic pair IM TMG-14 and TMG-product complex TMG-26, in which IM TMG-14 possesses the maximum weight of 53%. The 1a-assisted hydrogen migration of TMG-TS′15/16 and O–H bond rotation of TMG-TS16/17 shape the TDTS, with 25% and 75% degree of TOF control, respectively. The theoretical TOF value of the catalytic cycle is predicted to be 3.34 × 10−5 h−1. On the other hand, the TDI is the analogous guanidinium [TBDH]+[carbamate]− ionic pair IM TBD-12 in the TBD-mediated catalytic cycle, and the TDTS is hydrogen migrated TBD-TS′14/15 and O–H bond rotated TBD-TS15/16 with a comparable degree of TOF control. Comparatively, although the relative free energies of TBD-TS′14/15 and TBD-TS15/16 are lower than those of TMG-TS′15/16 and TMG-TS16/17, the TOF value (2.23 × 10−13 h−1) of the TBD-mediated catalytic cycle is much smaller. This is because the TDI TBD-12 falls into the deeper potential well (−16.9 kcal mol−1), leading to a larger global energy span in the whole catalytic cycle. As a consequence, it can be judged that the catalytic efficiency of TBD is inferior to that of TMG in the chemical fixation of CO2 with 1a, which is consistent with the experimental observation.6e
From the above calculations, both TMG and TBD are predicted to be effective promoters for the chemical fixation of CO2 with 1a. With respect to the reaction without catalysts, the basicity of guanidines and the acidity of the conjugate guanidinium play an important role in lowering the energy barriers for the steps of CO2 fixation with the amino group, nucleophilic addition of carbamate to the cyano group and C–O bond cleavage with the formation of isocyanate species. Relative to TBD, the catalytic advantage of TMG is reflected in the relatively weak H-bonding interaction between the [TMGH]+ guanidinium and the carbamate anion, which makes the TDI not fall into the deeper potential well.
4. Conclusions
In this work, the mechanisms of chemical fixation of CO2 with 2-aminobenzonitrile to quinazoline-2,4-(1H,3H)-dione in the presence of two typical organic guanidines (TMG and TBD) were comprehensively studied by means of DFT calculations. The major conclusions are listed as below:(1) the calculations reveal that the guanidine-catalyzed chemical fixation of CO2 with 2-aminobenzonitrile prefers to proceed through a general base mechanism rather than the CO2 activation mechanism. The catalytic cycle of the general base mechanism is composed of four reaction stages: (I) guanidine-assisted fixation of CO2 by the amino group of 2-aminobenzonitrile, (II) intramolecular nucleophilic attack from the carbamate to the nitrile group, (III) formation of the isocyanate intermediate, and (IV) intramolecular cyclization and hydrogen migrations.
(2) In the catalytic reaction, guanidine primarily plays the catalytic role as a strong base to promote the fixation of CO2 with the amino group of 2-aminobenzonitrile. Meanwhile, the corresponding conjugate acid guanidinium and the synergistic catalysis from the amino group of 2-aminobenzonitrile are also essential for generating the isocyanate intermediate in the ring-opening and hydrogen migration steps.
(3) With respect to TBD, the catalytic advantages of TMG are mainly exerted at the relatively weak H-bonding interactions between [TMGH]+ guanidinium and the carbamate anion, due to its own acyclic structure fragment.
Acknowledgements
The authors are grateful for the financial support from the Scientific Research Fund of Education Department of Sichuan Province (No. 14ZB0131), National Natural Science Foundation of China (No. 21402158), Key Scientific Research Foundation of Xihua University (No. Z1313319) and Open Research Subject of Key Laboratory (Research center for advanced computation) of Xihua University (No. szjj2015-051).Notes and references
- (a) T. Sakakura, J. C. Choi and H. Yasuda, Chem. Rev., 2007, 107, 2365 CrossRef CAS PubMed; (b) M. Aresta and A. Dihenedetto, Dalton Trans., 2007, 39, 2975 RSC; (c) D. J. Darensbourg, Inorg. Chem., 2010, 49, 10765 CrossRef CAS PubMed; (d) I. Omae, Coord. Chem. Rev., 2012, 256, 1384 CrossRef CAS; (e) X. Han and M. Poliakoff, Chem. Soc. Rev., 2012, 41, 1428 RSC.
- (a) S. N. Riduan and Y. Zhang, Dalton Trans., 2010, 39, 3347 RSC; (b) M. B. Ansari and S.-E. Park, Energy Environ. Sci., 2012, 5, 9419 RSC; (c) Z.-Z. Yang, L.-N. He, J. Gao, A.-H. Lu and B. Yu, Energy Environ. Sci., 2012, 5, 6602 RSC; (d) L. Yang and H. Wang, ChemSusChem, 2014, 7, 962 CrossRef CAS PubMed; (e) B. Yu and L.-N. He, ChemSusChem, 2015, 8, 52 CrossRef CAS PubMed.
- (a) G. Fiorani, W. Guo and A. W. Kleij, Green Chem., 2015, 17, 1375 RSC; (b) S. Bontemps, Coord. Chem. Rev., 2016, 308, 117 CrossRef CAS; (c) M. Hollering, B. Dutta and F. E. Kühn, Chem. Rev., 2016, 309, 51 CAS.
- (a) T. P. Tran, E. L. Ellsworth, M. A. Stier, J. M. Domagala, H. D. H. Showalter, S. J. Gracheck, M. A. Shapiro, T. E. Joannides and R. Singh, Bioorg. Med. Chem. Lett., 2004, 14, 4405 CrossRef CAS PubMed; (b) M. B. Andrus, S. N. Mettath and C. Song, J. Org. Chem., 2002, 67, 8284 CrossRef CAS PubMed; (c) J. Wagner, P. von Matt, B. Faller, N. G. Cooke, R. Albert, R. Sedrani, H. Wiegand, C. Jean, C. Beerli, G. Weckbecker, J.-P. Evenou, G. Zenke and S. Cottens, J. Med. Chem., 2011, 54, 6028 CrossRef CAS PubMed; (d) P. A. Zunszain, C. Federico, M. Sechi, S. Al-Damluji and C. R. Ganellin, Bioorg. Med. Chem., 2005, 13, 3681 CrossRef CAS PubMed; (e) F. Russo, G. Romeo, S. Guccione and A. De Blasi, J. Med. Chem., 1991, 34, 1850 CrossRef CAS PubMed; (f) E. Mounetou, J. Legault, J. Lacroix and R. C. Gaudreault, J. Med. Chem., 2001, 44, 694 CrossRef CAS PubMed.
- (a) M. C. Willis, R. H. Snell, A. J. Fletcher and R. L. Woodward, Org. Lett., 2006, 8, 5089 CrossRef CAS PubMed; (b) L. N. Zhu, J. Jin, C. Liu, C. J. Zhang, Y. Sun, Y. S. Guo, D. C. Fu, X. G. Chen and B. L. Xu, Bioorg. Med. Chem., 2011, 19, 2797 CrossRef CAS PubMed; (c) D. Q. Shi, G. L. Dou, Z. Y. Li, S. N. Ni, X. Y. Li, X. S. Wang, H. Wu and S. J. Jia, Tetrahedron, 2007, 63, 9764 CrossRef CAS; (d) H. Vorbruggen and K. Krolikiewicz, Tetrahedron, 1994, 50, 6549 CrossRef CAS; (e) L. Jiarong, C. Xian, S. Daxin, M. Shuling, L. Qing, Z. Qi and T. Jianhong, Org. Lett., 2009, 11, 1193 CrossRef PubMed; (f) Z. G. Li, H. Huang, H. B. Sun, H. L. Jiang and H. Liu, J. Comb. Chem., 2008, 10, 484 CrossRef CAS PubMed; (g) M. Akazome, J. Yamamoto, T. Kondo and Y. Watanabe, J. Organomet. Chem., 1995, 494, 229 CrossRef CAS.
- (a) T. Mizuno and Y. Ishino, Tetrahedron, 2002, 58, 3155 CrossRef CAS; (b) T. Mizuno, T. Iwai and Y. Ishino, Tetrahedron Lett., 2004, 45, 7073 CrossRef CAS; (c) T. Mizuno, N. Okamoto, T. Ito and T. Miyata, Heteroat. Chem., 2000, 11, 428 CrossRef CAS; (d) T. Mizuno, M. Mihara, T. Nakai and T. Iwai, Synthesis, 2007, 2524 CrossRef CAS; (e) J. Gao, L.-N. He, C. X. Miao and S. Chanfreau, Tetrahedron, 2010, 66, 4063 CrossRef CAS; (f) D. Nagai and T. Endo, J. Polym. Sci., Part A: Polym. Chem., 2009, 47, 653 CrossRef CAS; (g) W. Lu, J. Ma, J. Hu, Z. Zhang, C. Wu and B. Han, RSC Adv., 2014, 4, 50993 RSC.
- (a) Y. P. Patil, P. J. Tambade, K. M. Deshmukh and B. M. Bhanage, Catal. Today, 2009, 148, 355 CrossRef CAS; (b) W. J. Lu, J. Ma, J. Y. Hu, J. L. Song, Z. F. Zhang, G. Y. Yang and B. X. Han, Green Chem., 2014, 16, 221 RSC; (c) Y. Xiao, X. Kong, Z. Xu, C. Cao, G. Pang and Y. Shi, RSC Adv., 2015, 5, 5032 RSC; (d) Y. Zhao, B. Yu, Z. Yang, H. Zhang, L. Hao, X. Gao and Z. Liu, Angew. Chem., Int. Ed., 2014, 53, 5922 CrossRef CAS PubMed.
- (a) Y. P. Patil, P. J. Tambade, S. R. Jagtap and B. M. Bhanage, Green Chem. Lett. Rev., 2008, 1, 127 CrossRef CAS; (b) Y. P. Patil, P. J. Tambade, K. D. Parghi, R. V. Jayaram and B. M. Bhanage, Catal. Lett., 2009, 133, 201 CrossRef CAS; (c) T. Kimura, K. Kamata and N. Mizuno, Angew. Chem., Int. Ed., 2012, 51, 6700 CrossRef CAS PubMed; (d) T. Kimura, H. Sunaba, K. Kamata and N. Mizuno, Inorg. Chem., 2012, 51, 13001 CrossRef CAS PubMed; (e) S. Fujita, M. Tanaka and M. Arai, Catal. Sci. Technol., 2014, 4, 1563 RSC; (f) Y.-N. Zhao, B. Yu, Z.-Z. Yang and L.-N. He, RSC Adv., 2014, 4, 28941 RSC.
- J. Ma, B. Han, J. Song, J. Hu, W. Lu, D. Yang, Z. Zhang, T. Jiang and M. Hou, Green Chem., 2013, 15, 1485 RSC.
- (a) Y. Ren, T.-T. Meng, J. Jia and H.-S. Wu, Comput. Theor. Chem., 2011, 978, 47 CrossRef CAS; (b) J. Ma, J. Hu, W. Lu, Z. Zhang and B. Han, Phys. Chem. Chem. Phys., 2013, 15, 17333 RSC.
- B. Wang and Z. Cao, RSC Adv., 2013, 3, 14007 RSC.
- (a) F. S. Pereira, E. R. deAzevedo, E. F. da Silva, T. J. Bonagamba, D. L. da Silva Agostíni, A. Magalhães, A. E. Job and E. R. Pérez González, Tetrahedron, 2008, 64, 10097 CrossRef CAS; (b) C. Villiers, J. P. Dognon, R. Pollet, P. Thuéry and M. Ephritikhine, Angew. Chem., Int. Ed., 2010, 49, 3465 CrossRef CAS PubMed; (c) R. Nicholls, S. Kaufhold and B. N. Nguygen, Catal. Sci. Technol., 2014, 4, 3458 RSC; (d) S. Zhang and L.-N. He, Aust. J. Chem., 2014, 67, 980 CrossRef CAS; (e) Z. Xin, C. Lescot, S. D. Früs, K. Daasbjerg and T. Skrydstrup, Angew. Chem., Int. Ed., 2015, 54, 6862 CrossRef CAS PubMed.
- M. J. Frisch, et al., Gaussian 09, Reversion A.02, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- (a) Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 CrossRef CAS; (b) Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157 CrossRef CAS PubMed.
- (a) R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724 CrossRef CAS; (b) W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257 CrossRef CAS; (c) P. C. Hariharan and J. A. Pople, Mol. Phys., 1974, 27, 209 CrossRef CAS; (d) M. S. Gordon, Chem. Phys. Lett., 1980, 76, 163 CrossRef CAS; (e) P. C. Hariharan and J. A. Pople, Theor. Chem. Acc., 1973, 28, 213 CrossRef CAS; (f) J. P. Blaudeau, M. P. McGrath, L. A. Curtiss and L. Radom, J. Chem. Phys., 1997, 107, 5016 CrossRef CAS; (g) M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654 CrossRef CAS; (h) R. C. Binning, Jr. and L. A. Curtiss, J. Comput. Chem., 1990, 11, 1206 CrossRef; (i) V. A. Rassolov, J. A. Pople, M. A. Ratner and T. L. Windus, J. Chem. Phys., 1998, 109, 1223 CrossRef CAS; (j) V. A. Rassolov, M. A. Ratner, J. A. Pople, P. C. Redfern and L. A. Curtiss, J. Comput. Chem., 2001, 22, 976 CrossRef CAS.
- (a) C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154 CrossRef CAS; (b) C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523 CrossRef CAS.
- W. Christian, Static Dielectric Constants of Pure Liquids and Binary Liquid Mixtures, Springer-Verlag, Berlin Heidelberg, 2008 Search PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378 CrossRef CAS PubMed.
- (a) C. Zhang, R. Zhang, Z. Wang, Z. Zhou, S. Zhang and Z. Chen, Chem. – Eur. J., 2009, 15, 5910 CrossRef CAS PubMed; (b) Y. Liang, S. Liu, Y. Xia, Y. Li and Z. Yu, Chem. – Eur. J., 2008, 14, 4361 CrossRef CAS PubMed; (c) Y. Chen, S. Ye, L. Jiao, Y. Liang, D. K. Sinha-Mahapatra, J. W. Herndon and Z. Yu, J. Am. Chem. Soc., 2007, 129, 10773 CrossRef CAS PubMed.
- R. L. Martin, P. J. Hay and L. R. Pratt, J. Phys. Chem. A, 1998, 102, 3565 CrossRef CAS.
- (a) F. Huang, C. Zhang, J. Jiang, Z. Wang and H. Guan, Inorg. Chem., 2011, 50, 3816 CrossRef CAS PubMed; (b) M. Wen, F. Huang, G. Lu and Z. Wang, Inorg. Chem., 2013, 52, 12098 CrossRef CAS PubMed; (c) W. Li, D. Huang and Y. Lv, RSC Adv., 2014, 4, 17236 RSC.
- (a) P. Politzer and D. G. Truhlar, Chemical applications of atomic and molecular electrostatic potentials: reactivity, structure, scattering, and energetics of organic, inorganic, and biological systems, Plenum Press, New York, 1981 Search PubMed; (b) S. R. Gadre and R. N. Shirsat, Electrostatics of Atoms and Molecules, Universities Press, Hyderabad, India, 2000 Search PubMed.
- R. F. W. Bader, Atoms in Molecular A Quantum Theory, Oxford University, Oxford, 1990 Search PubMed.
- (a) T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580 CrossRef CAS PubMed; (b) T. Lu and F. Chen, J. Mol. Graphics Modell., 2012, 38, 314 CrossRef CAS PubMed.
- (a) D. Roy and R. B. Sunoj, Org. Lett., 2007, 9, 4873 CrossRef CAS PubMed; (b) D. Roy and R. B. Sunoj, Chem. – Eur. J., 2008, 14, 10530 CrossRef CAS PubMed; (c) D. Roy, C. Patel and R. B. Sunoj, J. Org. Chem., 2009, 74, 6936 CrossRef CAS PubMed; (d) R. Robiette, V. K. Aggarwal and J. N. Harvey, J. Am. Chem. Soc., 2007, 129, 15513 CrossRef CAS PubMed; (e) L. Dong, S. Qin, Z. Su, H. Yang and C. Hu, Org. Biomol. Chem., 2010, 8, 3985 RSC; (f) Y. Zeng and Y. Ren, Int. J. Quantum Chem., 2007, 107, 247 CrossRef CAS; (g) Y. Zeng, Y. Xue and G. Yan, J. Phys. Chem. B, 2008, 112, 10659 CrossRef CAS PubMed; (h) Y. Zeng, Y. Xue and G. Yan, J. Phys. Chem. A, 2011, 115, 4995 CrossRef CAS PubMed.
- P. Jaramilio, L. R. Domingo, E. Chamorro and P. Pérez, THEOCHEM, 2008, 865, 68 CrossRef.
- P. A. Hunt, C. R. Ashworth and R. P. Matthews, Chem. Soc. Rev., 2015, 44, 1257 RSC.
- (a) M. P. Coles, Chem. Commun., 2009, 3659 RSC; (b) J. E. Taylor, S. D. Bull and J. M. J. Williams, Chem. Soc. Rev., 2012, 41, 2109 RSC; (c) C. Alonso-Moreno, A. Antiñolo, F. Carrillo-Hermosilla and A. Otero, Chem. Soc. Rev., 2014, 43, 3406 RSC.
- A. Chuma, H. W. Horn, W. C. Swope, R. C. Pratt, L. Zhang, B. G. G. Lohmeijer, C. G. Wade, R. M. Waymouth, J. L. Hedrick and J. E. Rice, J. Am. Chem. Soc., 2008, 130, 6749 CrossRef CAS PubMed.
- (a) S. Kozuch and S. Shaik, J. Am. Chem. Soc., 2006, 128, 3355 CrossRef CAS PubMed; (b) S. Kozuch and S. Shaik, J. Phys. Chem. A, 2008, 112, 6032 CrossRef CAS PubMed; (c) A. Uhe, S. Kozuch and S. Shaik, J. Comput. Chem., 2011, 32, 978 CrossRef CAS PubMed; (d) S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101 CrossRef CAS PubMed; (e) S. Kozuch and J. M. L. Martin, ACS Catal., 2012, 2, 2787 CrossRef CAS; (f) S. Kozuch, ACS Catal., 2015, 5, 5242 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Computational details, optimized geometries, calculated energies and the full citation of the Gaussian 09 program. See DOI: 10.1039/c6qo00085a |
| This journal is © the Partner Organisations 2016 |