Spin–orbit coupling analyses of phosphorescence: the effects of cyclometalated ligand replacement in fac-Ir(ppy)₃ with various bpy ligands on blue phosphorescence

Abstract

Multi-configuration self-consistent field (MCSCF) calculations followed by second-order configuration interaction (SOCI) and spin–orbit coupling (SOC) calculations were performed using one of the effective core potentials and its associated basis set, the Stevens–Basch–Krauss–Jasien–Cundari (SBKJC) basis set referred to here as SBKJC+p, in order to examine the effects of replacement of a methine group in each phenylpyridine (ppy) ligand of the facial (fac) isomer of tris(2-phenylpyridinato)iridium(III)[fac-Ir(ppy)₃] by a nitrogen atom for the purpose of obtaining deep blue phosphorescence. Only replacements of the methine group at the 3′ or 5′ site of each ppy ligand by nitrogen atoms were calculated to induce a spectral shift to the blue region. These results can be explained by the strong electronegativity of nitrogen atoms and by the magnitude of the electron density at the 2′ carbon atom of the ppy or bipyridine (bpy) ligands. Subsequently, the substituent effects in the fac isomer of tris(bipyridinato)iridium(III)[fac-Ir(bpy)₃] were investigated and found to be similar to those in fac-Ir(ppy)₃ as reported in our previous study (RSC Adv., 2015, 5, 35760–35772). Based on systematic calculations and theoretical consideration, the most effective modification for deep blue phosphorescence should be the introduction of a nitrogen atom into the 3′ or/and 5′ site of benzene rings of the ppy ligands in fac-Ir(ppy)₃ together with the combination of the substituents X = F, NR₂, or OR (R = alkyl group) and Y = CN or NO₂.

---

Introduction

The use of organic light-emitting diodes (OLEDs) as displays and room lights has recently become popular, but OLEDs use fluorescence emission and some OLEDs use the combination of blue fluorescence and green/red phosphorescence emissions.^1–60 On the basis of statistical consideration, it is known that phosphorescence emission provides much better efficiency of energy than does fluorescence emission. However, only bis[2-(4′,6′-difluorophenyl)pyridinato-N,C2′]iridium(III)[picolinato-N,O]FIrpic[Ir(4′,6′-dF-ppy)₂(pic)] is used as a tentative blue-color emitter in most research laboratories,^8,11 and the development of better blue-color materials for OLEDs is needed. Phosphorescence is caused by spin–orbit coupling (SOC) among the electronic states of different spin multiplicities and is part of the relativistic effects. Recently, much attention has been paid to relativistic effects in research fields of theoretical chemistry. In the recent series of our research projects, SOC effects in the main-group elements, the first-through third-row transition elements, and their hydrids, as well as typical iridium and platinum complexes including FIrpic, have been investigated^61–74 by using multi-configuration self-consistent field (MCSCF) method followed by second-order configuration interaction (SOCI) calculations, together with the Breit-Pauli Hamiltonian (BPH), instead of the popular density functional theory (DFT).^75,76 The MCSCF+SOCI+SOC method was proved to be useful and provided semi-quantitative predictions for the spectral peaks of phosphorescence.^55–60 These results have encouraged us to design new molecular complexes for appropriate blue-color phosphorescence emission by using these theoretical methods.

In our most recent study,⁵⁹ substituent effects were investigated in the facial (fac) isomer of tris(2-phenylpyridinato)iridium(III)[Ir(ppy)₃]. When fluorine or amino substituents were introduced into the 4′ and 6′ sites of the benzene ring in each ppy ligand and when a cyano or nitro group was introduced into the 5′ site of the benzene ring in each ppy ligand (Fig. 1), a large blue shift of phosphorescence was calculated to be obtained for the fac isomer of Ir(ppy)₃. However, the computational method was found to overestimate the magnitudes of spectral shifts of the phosphorescence caused by the introduction of substituents into the ligands and it is necessary to make more efforts to design new materials for deep blue phosphorescence. In the present study, the effects of replacement of a methine group (C–H moiety) in each ppy ligand by a nitrogen atom and the effects of replacement of the ppy ligands by phenyldiazine (pdz) or bipyridine (bpy) ligands as well as the substituent effects in the benzene ring of each bpy ligand provided by the replacement were theoretically investigated for the purpose of obtaining deep blue phosphorescence. Since the fac isomer of each complex IrL₃ (L = ligand) is more stable than the corresponding meridional (mer) isomer as shown in Table 1, only the fac isomers were considered in the present investigation as performed in our previous investigation (see Table S1†).⁵⁹

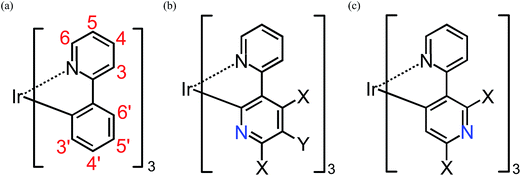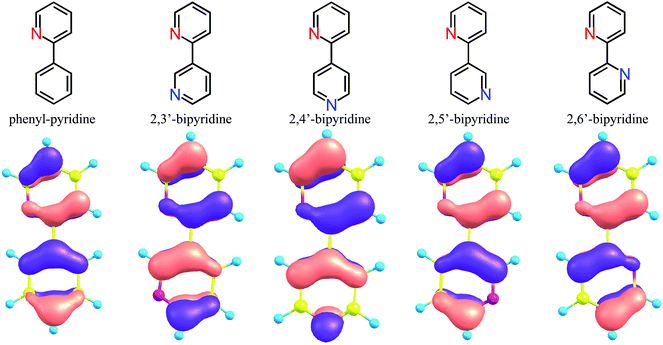
Fig. 1 Geometrical structures of substituted fac-Ir(ppy)₃, fac-Ir(2,3′-bpy)₃, and fac-Ir(2,5′-bpy)₃ (see Table S1†). X = H, F, NH₂, or OH. Y = H, CN, or NO₂. Note that the atom numbering for the ppy ligands is maintained after the replacement of a methane group by a nitrogen atom for simplicity.

Table 1 Energy differences (kcal mol⁻¹) between the facial (fac) and meridional (mer) isomers of Ir(ppy)₃, Ir(pdz)₃, and Ir(bpy)₃^a

Complex	DFT	MCSCF	+SOCI^b	+SOC^c	Ref.
a The positive values indicate that the fac isomer is lower than the corresponding mer isomer.b The MCSCF calculation followed by the SOCI calculation.c The MCSCF calculation followed by the SOCI and SOC calculations.
Ir(ppy)3	6.4	6.1	6.0	5.7	58
Ir(1,3-pdz)3	6.0	8.5	6.9	6.6
Ir(1,4-pdz)3	6.3	5.5	5.3	5.5
Ir(1,5-pdz)3	7.3	6.3	6.6	6.5
Ir(1,6-pdz)3	10.3	10.0	10.6	10.0
Ir(2,3′-bpy)3	3.6	2.3	1.3	1.4
Ir(2,4′-bpy)3	5.9	5.7	5.8	5.7
Ir(2,5′-bpy)3	7.1	6.6	6.4	6.5
Ir(2,6′-bpy)3	7.3	6.9	6.9	7.1

---

Methods of calculation

Although geometrical structures of the ground state and the lowest triplet state in the target complexes were optimized by using one of the popular density functional theory (DFT) methods together with the B3LYP functionals,^75,76 the multi-configuration self-consistent field (MCSCF) method⁷⁷ was employed to optimize molecular orbitals since strong configuration mixture occurs among the low-lying triplet states in IrL₃ as described in the next section. All of the calculations used one of relativistic effective core potentials, Stevens–Basch–Krauss–Jasien–Cundari (SBKJC) potentials,^78–80 and their associated basis sets augmented by one set of f functions for the iridium atom and one set of polarization functions for the other atoms. This basis set is referred to as SBKJC+p in this series of our research projects. Second-order configuration interaction (SOCI) wavefunctions⁸¹ were constructed by using the MCSCF-optimized orbitals and were used to calculate the spectral peaks of phosphorescence and their intensities.^55–60 SOCI is one of multi-reference singles and doubles configuration interaction (MR-CISD) approaches. All calculations were performed using the GAMESS suite of program codes.^82,83

Results and discussion

Brief review of the substituent effects

It is known that the transition from the lowest metal-ligand charge-transfer (MLCT) triplet state to the ground state provides effective phosphorescence in OLEDs because of the strong SOC effects originating from iridium atoms. Traditional molecular orbital theories suggest that the phosphorescent energy is roughly proportional to the energy difference between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO). Since the HOMO and LUMO consist mainly of the iridium's d orbitals and the ligand's π* orbitals, respectively (Fig. 2),⁵⁹ it can be said that if the energy of the LUMO is lifted by the introduction of substituents to the ligands or by the replacement of the ligands themselves, the phosphorescent spectra can be shifted to the blue region. However, since IrL₃ has the identical three ligands, the three lowest unoccupied orbitals are energetically close to each other and, as a result, strong configuration mixture occurs among these triplet states, as well as in the low-lying singlet states. This is the main reason that the MCSCF method, instead of DFT method, is used in the processes of orbital optimization in the series of our research projects.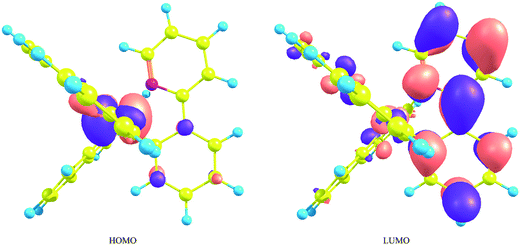

Fig. 2 The highest occupied molecular orbital and the lowest unoccupied molecular orbital of fac-Ir(ppy)₃. This figure is the same as Fig. 3 in ref. 59, but the value for the isosurface of electron density is 0.03 [e bohr⁻³].

Nevertheless, it is true that the energy difference between the HOMO and LUMO is related to that between the lowest triplet state and the ground state and can be used as one of criterions for estimating the spectral shift of phosphorescence, as well as fluorescence. For example, since the fac isomer of Ir(ppy)₃ has a geometrical structure largely displaced from C₃ symmetry, the degeneracy of the LUMO is broken by the geometrical deformation and the LUMO is energetically somewhat far from the other unoccupied orbitals.⁵⁸ As a result, the electronic wave function of the lowest triplet state is described mainly by the singly excited configuration from the HOMO to the LUMO. This indicates that the electronic transition between the ground state and the lowest excited triplet state can be approximately described by the single excitation from the HOMO to the LUMO. In fact, as described in our previous paper,⁵⁹ the spectral shifts calculated by the MCSCF+SOCI+SOC method were explained by the energetic shifts of the HOMO and LUMO when appropriate substituents were introduced into each ppy ligand (Fig. 3). It can be summarized briefly as follows: when a substituent has lone-pair electrons such as fluorine, amino, and hydroxy substituents, the introduction of these substituents to the 4′ and/or 6′ sites in the benzene ring of the ppy ligands (Fig. 1(a)) induces a large blue shift of phosphorescence because of energetic lifting of the LUMO by the substituents (Fig. 3(a)). When a substituent has low-lying π* orbitals such as cyano and nitro substituents, the introduction of these substituents to the 5′ site induces a strong blue shift of phosphorescence because of energetic lowering of the HOMO by the substituents (Fig. 3(b)). Note that the most important point is the fact that the orbital coefficients in the LUMO at the 5′ site of the complex are very small as shown in Fig. 2;⁵⁹ otherwise the strong π conjugation between the ligands and substituents makes the LUMO lower in energy. In the following sections, the effects of replacement of a methine group by a nitrogen atom on the phosphorescent peaks in Ir(ppy)₃ are discussed on the basis of the above considerations by using such sophisticated theoretical methods.

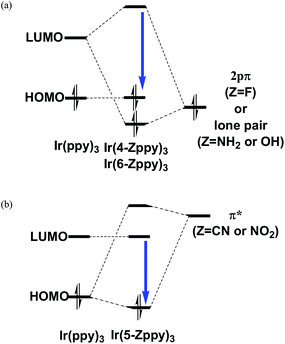Fig. 3 Schematic diagrams of the orbital interaction between a ppy ligand and a substituent in the facial (fac) isomer of IrL₃ (L = ligand). Also see Fig. 4 in ref. 59.

Another important factor for estimating the spectral peaks and their intensities of phosphorescence is the magnitude of the geometrical displacement between the lowest triplet state and the ground state. As discussed in our previous paper,⁵⁹ a large displacement (ΔQ_S0−T1 = 0.1611 Å; see Table 2) in the mer isomer of Ir(ppy)₃ should be one of the reasons why dark phosphorescence has been obtained for this isomer. The displacements in other complexes investigated in our previous study were smaller and were expected to have negligible effects on their phosphorescence. Fortunately, small geometrical displacements have also been obtained between the lowest triplet states and the ground states in the present complexes, where the amino substituents are somewhat largely rotated in Ir(4′,6′-dNH₂-2,3′-bpy)₃ and Ir(4′,6′-dNH₂-5′-CN-2,3′-bpy)₃ (Table 2 and S1; see the following discussion†), and therefore no discussion of the geometrical displacements will appear in the following sections.

Table 2 Geometrical displacements ΔQ_S0−T1 (Å) between the optimized geometries for the ground state and the lowest triplet state, wavelengths λ (nm) of spectral peaks, transition dipole moments (TDMs) (e bohr), weights (%) of the lowest triplet state and all singlet states in the spin-mixed (SM) states, and wavelengths λ_TDDFT of spectral peaks obtained by time-dependent density functional theory (TDDFT)

Complex^a	ΔQS0−T1^b (Å)	λ^c (nm)	Principal contribution^d	Wavelength^c (nm)	TDM (e bohr)	T1 (%)	Singlets (%)	HOMO^e	LUMO^e	λTDDFT^f (nm)	Expt.^g (nm)	Ref.
a The facial isomers were used except for Ir(ppy)3.b Averaged displacement of all atoms. See ref. 58.c Spectral peaks were calculated with the assumption of Lorentzian widths for all electronic transitions between the spin-mixed (SM) states. The values in parentheses are magnitudes of the spectral shifts when the peak wavelength in the parent complex 1 is taken as the origin. The negative and positive values indicate spectral shifts to blue and red regions, respectively.d Transition from this state to the ground state SM0. “SM3” and “SM4” indicate the third and fourth excited SM states.e The eigenvalues (hartree) obtained by the diagonalization of standard MCSCF Fock matrices. Although the words, HOMO and LUMO, are not appropriate in MCSCF calculations, those are used for simplicity of understanding (see ref. 59).f Time-dependent (TD) DFT calculations using the B3LYP functionals and the SBKJC+p basis sets at the geometries optimized for the lowest triplet state.g Temperature is shown in parenthesis. RT, DFT, and Dev indicate room temperature, the B3LYP/CEP-31G results (ref. 84), and the value measured as a device (ref. 84), respectively.h The DFT calculation was performed for dimethyl-amino substituents (ref. 84).i The DFT calculation was performed for methoxy substituents (ref. 84).j Only (π,π*) excited states are obtained as low-lying excited states.
fac-Ir(ppy)3	0.0557	491 (0)	SM3	501	0.299	13	43	−0.3409	0.0246	615		58
			SM4	491	0.890	55	17				510 (298 K)	6
											517 (298 K)	7
											509 (RT)	9
											515 (RT)	15
											494 (77 K)	42
mer-Ir(ppy)3	0.1611	530 (+39)	SM3	530	0.255	75	14	−0.3080	0.0243	698		58
		511 (+20)	SM4	512	1.156	9	66				512 (298 K)	6
Ir(1,3-pdz)3	0.0837	522 (+31)	SM3	522	0.369	19	41	−0.3538	0.0181	599
		509 (+18)	SM4	509	0.708	43	20
Ir(1,4-pdz)3	0.0778	506 (+15)	SM4	506	1.039	57	16	−0.3603	−0.0008	657
Ir(1,5-pdz)3	0.0669	508 (+17)	SM3	509	0.273	30	36	−0.3597	0.0069	588
		494 (+3)	SM4	493	0.970	34	24
Ir(1,6-pdz)3	0.0877	564 (+73)	SM3	564	0.115	55	25	−0.3349	0.0206	648
		529 (+38)	SM4	529	1.363	19	35
Ir(2,3′-bpy)3	0.0719	475 (−16)	SM4	474	0.802	52	19	−0.3490	0.0256	505	495 (DFT)	84
Ir(2,4′-bpy)3	0.0774	537 (+46)	SM3	537	0.334	37	33	−0.3504	0.0041	511
Ir(2,5′-bpy)3	0.0375	518 (+27)	SM4	518	0.940	31	25	−0.3709	0.0089	466	462 (DFT)	84
		448 (−43)	SM4	448	0.857	64	13				496 (Dev)	84
Ir(2,6′-bpy)3	0.0430	511 (+20)	SM3	512	0.340	27	36	−0.3529	0.0113	493
		499 (+8)	SM4	498	0.846	39	22
Ir(4′,6′-dF-2,5′-bpy)3	0.0333	396 (−95)	SM4	395	0.805	63	13	−0.4021	−0.0070	447	438 (RT)	16
											430 (77 K)	84
											437 (RT)	84
Ir(4′,6′-dNH2-2,5′-bpy)3	0.0883	399 (−92)	SM4	398	0.944	43	20	−0.3581	0.0407	491	511 (DFT)^h	84
Ir(4′,6′-dOH-2,5′-bpy)3	0.0338	390 (−101)	SM4	389	0.881	52	18	−0.3696	0.0294	458	464 (DFT)^i	84
Ir(4′,6′-dF-2,3′-bpy)3	0.0675	404 (−87)	SM4	403	0.778	61	14	−0.3807	0.0105	588
Ir(4′,6′-dNH2-2,3′-bpy)3	0.1134	415 (−76)	SM4	415	0.982	56	17	−0.3430	0.0493	592
Ir(4′,6′-dOH-2,3′-bpy)3	0.0535	395 (−96)	SM4	395	0.821	65	12	−0.3599	0.0357	566
Ir(5′-CN-2,3′-bpy)3	0.0658	446 (−45)	SM4	445	0.738	46	22	−0.3879	−0.0064	637
Ir(5′-NO2-2,3′-bpy)3	0.0665	418 (−73)	SM4	416	0.728	41	24	−0.3967	−0.0110	622
Ir(4′,6′-dF-5′-CN-2,3′-bpy)3	0.0737	374 (−117)	SM4	373	0.728	54	17	−0.4154	−0.0176	584
Ir(4′,6′-dF-5′-NO2-2,3′-bpy)3	0.0568	412 (−79)	SM4	412	0.234	10	49	−0.4326	−0.0143	^j
Ir(4′,6′-dNH2-5′-CN-2,3′-bpy)3	0.1195	390 (−101)	SM4	389	0.926	56	17	−0.3776	0.0248	576
Ir(4′,6′-dOH-5′-CN-2,3′-bpy)3	0.0506	371 (−120)	SM4	370	0.746	64	12	−0.3951	0.0080	557

---

Introduction of a nitrogen atom into the ppy ligands

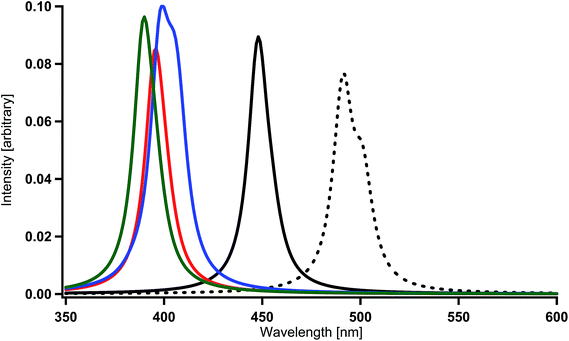
When one of the methine groups in the pyridine ring of each ppy ligand (3, 4, 5, or 6 site shown in the top part of Fig. 1(a)) is replaced by a nitrogen atom [Ir(1,3-pdz)₃, Ir(1,4-pdz)₃, Ir(1,5-pdz)₃, and Ir(1,6-pdz)₃ in Table 2 and S1†], the spectral shifts that occur in these four geometrical isomers are discussed in this section. This replacement is equivalent to that of the three ppy ligands by pdz ligands. The most stable isomer among the four isomers is Ir(1,5-pdz)₃, while Ir(1,6-pdz)₃ is considerably unstable because of N–N bonds in the diazine rings (Table 3). As shown in Table 2 and Fig. 4(a), the spectral peaks λ of phosphorescence in these complexes are shifted to the red region by 3–73 nm. These spectral shifts can be explained by the fact that the replacement results in the energetic lowering of the ligands' orbitals because of the introduction of an electronegative atom “nitrogen” into each ligand. Accordingly, since the LUMO mainly possessing the ligands' π* components is energetically lowered by the replacement and the HOMO mainly possessing the iridium's d components is almost unchanged energetically by the replacement (Fig. 2),⁵⁹ the energy difference between the HOMO and LUMO becomes smaller and, as a result, the spectral peaks are shifted to the red region as shown in Table 2.

Table 3 Relative energies (kcal mol⁻¹) among geometrical isomers

Complex^a	DFT	MCSCF	+SOCI^b	+SOC^c
a The facial isomers were used.b The MCSCF calculation followed by the SOCI calculation.c The MCSCF calculation followed by the SOCI and SOC calculations.
Ir(1,3-pdz)3	10.9	9.3	9.0	9.3
Ir(1,4-pdz)3	26.6	28.1	32.8	32.5
Ir(1,5-pdz)3	8.0	4.9	4.4	4.9
Ir(1,6-pdz)3	74.7	82.4	87.5	88.1
Ir(2,3′-bpy)3	18.6	21.0	20.9	21.7
Ir(2,4′-bpy)3	14.6	15.4	16.8	16.9
Ir(2,5′-bpy)3	6.7	3.3	4.2	4.4
Ir(2,6′-bpy)3	0.0	0.0	0.0	0.0

---

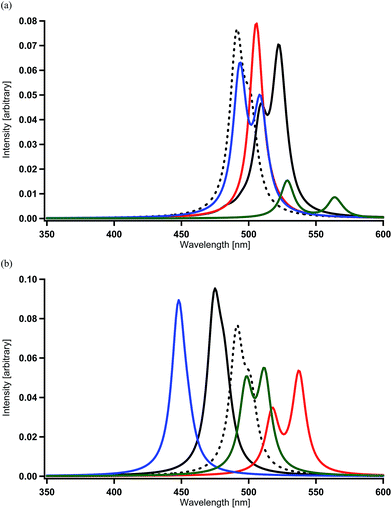Fig. 4 Spectra calculated for Ir complexes at the MCSCF+SOCI+SOC/SBKJC+p level of theory (see Table 2 and S1†). (a) Spectral shifts by the replacement of a methine group of each pyridine ring by a nitrogen atom in Ir(ppy)₃. Black (broken) = Ir(ppy)₃, black = Ir(1,3-pdz)₃, red = Ir(1,4-pdz)₃, blue = Ir(1,5-pdz)₃, and green = Ir(1,6-pdz)₃. (b) Spectral shifts by the replacement of a methine group of each benzene ring by a nitrogen atom in Ir(ppy)₃. Black (broken) = Ir(ppy)₃, black = Ir(2,3′-bpy)₃, red = Ir(2,4′-bpy)₃, blue = Ir(2,5′-bpy)₃, and green = Ir(2,6′-bpy)₃.

On the other hand, when a methine group in the benzene ring of each ppy ligand is replaced by a nitrogen atom or when the ppy ligands are replaced by bpy ligands, a red shift is not always induced as shown in Table 2 and Fig. 4(b) [Ir(2,3′-bpy)₃, Ir(2,4′-bpy)₃, Ir(2,5′-bpy)₃, and Ir(2,6′-bpy)₃; also see Table 3]. An explicit blue shift of a spectral peak is induced in Ir(2,3′-bpy)₃ (X = H, Y = H in Fig. 1(b)) and Ir(2,5′-bpy)₃ (X = H in Fig. 1(c)), Ir(2,3′-bpy)₃ being the most stable (Table 3). These results are consistent with the DFT calculations and experimental evidences reported previously.⁸⁴ These suggest that other factors are more effective than energetic lowering of the ligands' orbitals.

For the purpose of analyzing these results, DFT geometrical optimizations were performed for the four geometrical isomers of bi-pyridine (a hydrogen-terminated ligand; bpy-H), the geometries of which were assumed to be planar. These isomers correspond to four kinds of replacements of a methine group at the 3′, 4′, 5′, and 6′ sites of a benzene ring in phenyl-pyridine (a hydrogen- terminated ligand; ppy-H), respectively (See the sites shown in the bottom part of Fig. 1(a)). In Fig. 5, it is assumed that the top pyridine ring corresponds to that of the ppy ligand and the bottom ring is provided by the replacement of a methine group in a benzene ring of the ppy ligand by a nitrogen atom. The HOMO in ppy-H is also shown in this figure for comparison. In Ir(2,3′-bpy)₃, Ir(2,4′-bpy)₃, Ir(2,5′-bpy)₃, and Ir(2,6′-bpy)₃, since a covalent bond is formed between the iridium atom and the 2′ site of the bottom pyridine ring (a benzene ring in Ir(ppy)₃), the electron densities at the 2′ site must provide stronger effects when a complex is formed. As shown in Fig. 5, it is natural that the π density distribution is almost the same in the top pyridine rings of the four isomers as that in ppy-H, but a different distribution was obtained in the bottom rings of the four isomers, since a different methine group is replaced by a nitrogen atom. In the following discussion, the atom numbering for the ppy ligand is maintained after the replacement of a methane group by a nitrogen atom for simplicity. Then, it is easily found that the density at the 2′ site in 2,5′-bipyridine is less than half of those in the others and even smaller than that in ppy-H. This result indicates that when a complex is formed, the π-electron donation from ligands to the iridium atom in Ir(2,5′-bpy)₃ should be explicitly weaker than that in the other isomers and even weaker than that in the parent complex Ir(ppy)₃. As a result, the iridium's d orbitals are rarely pushed up energetically by ligands' π orbitals in Ir(2,5′-bpy)₃, and the HOMO of Ir(2,5′-bpy)₃ shown in Fig. 6(b) is thus lower in energy than those in the others shown in Fig. 6(c) and even lower than that in ppy-H shown in Fig. 6(a). This must be the reason why an energetically higher (d−π*) triplet state is obtained and a relatively large spectral shift of phosphorescence to the blue region is obtained in Ir(2,5′-bpy)₃ in comparison with that in the parent complex Ir(ppy)₃.

Fig. 5 Structures and HOMO of phenyl-pyridine (ppy-H) and four isomers of bipyridine (bpy-H) calculated by the B3LYP/SBKJC+p level of theory. All structures are assumed to be planar, and the value of equi-surfaces is 0.05 [e bohr⁻³]. Note that the atom numbering for the ppy ligands is maintained after the replacement of a methane group by a nitrogen atom for simplicity.

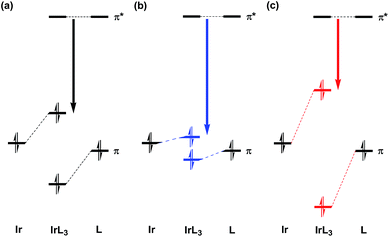Fig. 6 Schematic diagram of the orbital interaction between an iridium atom and the four isomers of bipyridine shown in Fig. 5. (a) Forming a covalent bond between the iridium atom and the 2′ carbon atom of the ligand in fac-Ir(ppy)3. (b) Forming a bond weaker than (a). (c) Forming a bond stronger than (a).

As shown in Fig. 5, although the π electron density of the HOMO is relatively large at the 2′ site in 2,3′-bipyridine, a spectral shift to the blue region was also obtained in Ir(2,3′-bpy)₃ as shown in Table 2 and Fig. 4(b). This result can be explained by the fact that a stronger electronegative atom “nitrogen” is introduced to the next site of the C–Ir covalent bond. In other words, the ligands' π electrons are withdrawn by not only the iridium atom but also the neighboring nitrogen atom. As a result, it can be said that the same effects appear in Ir(2,3′-bpy)₃ as described in the previous paragraph and shown in Fig. 6(b).

In order to confirm the above discussion, the components of the low-lying excited states in Ir(2,3′-bpy)₃, Ir(2,4′-bpy)₃, Ir(2,5′-bpy)₃, and Ir(2,6′-bpy)₃ were calculated and analyzed, and the results are shown in the columns “T₁” and “singlets” in Table 2, where the values in the column “T₁” are the percent weights of the lowest triplet state “T₁” in the third or fourth excited spin-mixed state, denoted by SM3 or SM4, obtained after inclusion of the SOC effects, and the values in the column “singlets” are the percent weights of all singlet states in the SM3 or SM4 state. The largest contribution to the emission in these complexes is the transition from the SM3 or SM4 state to the SM0 state. The largest component in the SM3 and SM4 states is always T₁, and the main electron configuration of T₁ is given by the single excitation from the HOMO to LUMO, which must be the reason why the discussion based on one-electron approximation is reasonable as stated above. However, the weight of T₁ is not always explicitly large as shown in the column “T₁” of Table 2. This is caused by strong SOC mixing among the low-lying triplet states and excited singlet states in these complexes. Even though one-electron approximation is applicable to such considerations, these results suggest that the discussion based on one-electron approximation sometimes needs to be examined by using some advanced theoretical methods.

Substituent effects in Ir(2,3′-bpy)₃ and Ir(2,5′-bpy)₃

In our recent investigations,^55–60 the difference between calculated and observed peaks of phosphorescence was found to be 24–29 nm [14 nm in Ir(ppy)₃]. When the available experimental data for Ir(ppy)₃,⁹ Ir(4′,6′-dF-ppy)₃,⁹ and Ir(5′-CN-4′,6′-dF-ppy)₃ ¹³ (see Table S1†) are compared with our calculated results, a more reliable estimated value λ_est (nm) for such kinds of iridium complexes can be proposed for the spectral peaks by using the following equation:

λ_est = 0.785 × λ + 120, (1)

where λ (nm) in the right-hand side is the calculated spectral peak shown in Table 2. When this equation is applied to the calculated results, Ir(2,5′-bpy)₃ (X = H in Fig. 1(c)) is estimated to have a phosphorescent peak at the wavelength of 472 nm and its phosphorescence is not deep blue. In fact, the spectral peak at the wavelength of 496 nm was observed when Ir(2,5′-bpy)₃ was doped into the emissive layer of OLEDs.⁸⁴ Therefore, it is necessary to combine the effects caused by the replacement of a methine group by a nitrogen atom with the substituent effects in order to design materials for deep blue phosphorescence. Since these induce spectral shifts to the blue region in comparison with the parent complex Ir(ppy)₃ as discussed above, the discussion in this section is focused on the substituent effects in Ir(2,3′-bpy)₃ (X = H and Y = H in Fig. 1(b)) and Ir(2,5′-bpy)₃ (X = H in Fig. 1(c)).

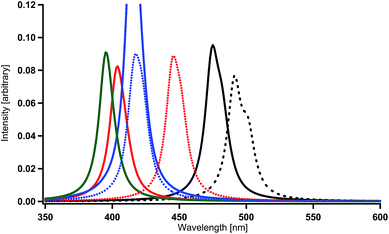
The LUMO in Ir(2,5′-bpy)₃ is very similar to that in the parent complex Ir(ppy)₃ (Fig. 2). Namely, the coefficients at the 4′ and 6′ sites are relatively large, so that the introduction of fluorine, amino, or hydroxy substituents to these sites is expected to induce a large shift of the phosphorescent peak to the blue region, on the basis of the discussion in our previous investigations.⁵⁹ In fact, the present calculations provide spectral shifts of 92–101 nm to the blue region in Ir(4′,6′-dF-2,5′-bpy)₃ (X = F in Fig. 1(c)), Ir(4′,6′-dNH₂-2,5′-bpy)₃ (X = NH₂ in Fig. 1(c)), and Ir(4′,6′-dOH-2,5′-bpy)₃ (X = OH in Fig. 1(c)) as shown in Table 2 and Fig. 7. By using eqn. (1), the phosphorescent peaks are estimated to appear at the wavelengths of 431 nm in Ir(4′,6′-dF-2,5′-bpy)₃, 433 nm in Ir(4′,6′-dNH₂-2,5′-bpy)₃, and 426 nm in Ir(4′,6′-dOH-2,5′-bpy)₃. These results are supported by the experimental observations that the emission maximum of Ir(4′,6′-dF-2,5′-bpy)₃ appears at the wavelength of 438 nm (room temperature),¹⁶ 430 nm (77 K),⁸⁴ and 437 nm (room temperature).⁸⁴

Fig. 7 Spectral shifts by the introduction of electron-donating substituents into each benzene ring in Ir(2,5′-bpy)₃. Black (broken) = Ir(ppy)₃, black = Ir(2,5′-bpy)₃, red = Ir(4′,6′-dF-2,5′-bpy)₃, blue = Ir(4′,6′-dNH₂-2,5′-bpy)₃, and green = Ir(4′,6′-dOH-2,5′-bpy)₃.

Now, it is experimentally suggested that the amino and hydroxy substituents are inappropriate in functional materials because of easy donation or acceptance of a hydrogen atom or ion.⁸⁵ In the present investigation, the differences between the effects of the amino and dimethyl-amino substituents and between hydroxy and methoxy substituents were investigated first (Table 4). The spectral shift to the blue region by the introduction of a dimethyl-amino substituent to the 4′ or 6′ site of Ir(ppy)₃ (Fig. 1(a)) is calculated to be only 2-nm or 10-nm smaller than that by the introduction of an amino substituent. Similarly, the spectral shift to the blue region by the introduction of a methoxy substituent to the 4′ or 6′ site of Ir(ppy)₃ (Fig. 1(a)) is calculated to be only 4-nm or 3-nm smaller than that by the introduction of a hydroxy substituent. Since the largest change (10 nm) can be caused by the steric effect at the crowded 6′ site, it can be understood that almost no difference appears between the complexes possessing amino and hydroxy substituents and those possessing dimethylamino and methoxy substituents. If a broad interpretation is applied to the present discussion, it can be said that a dialkyl-amino (NR₂) or alchoxy (OR) substituent (R = alkyl group) can be used for obtaining spectral shifts to the blue region, even though the magnitude of spectral shifts might become slightly smaller. Therefore, the complexes of X = F, NR₂, and OR in Fig. 1(c) should be good candidates for blue phosphorescent materials.

Table 4 Spectral shifts caused by the terminal methyl groups^a

Complex	ΔQS0−T1^a (Å)	λ (nm)	Principal contribution	Wavelength (nm)	TDM (e bohr)
a See the footnote in Table 2.b The terminal methyl groups of dimethyl amino groups are rotated by the steric effect at the crowded 6′ site (see the text).
Ir(4′-NH2-ppy)3	0.0318	442	SM4	442	0.934
Ir(4′-NMe2-ppy)3	0.0517	444 (+2)	SM4	444	0.979
Ir(6′-NH2-ppy)3	0.0618	482	SM4	482	0.974
			SM2	497	0.120
Ir(6′-NMe2-ppy)3	0.2445^b	492 (+10)	SM4	492	0.951
			SM2	506	0.168
Ir(4′-OH-ppy)3	0.0289	438	SM4	438	0.899
			SM3	444	0.171
Ir(4′-OMe-ppy)3	0.0425	443 (+5)	SM4	442	0.902
			SM3	449	0.220
Ir(6′-OH-ppy)3	0.0687	469	SM4	469	0.900
			SM3	477	0.247
Ir(6′-OMe-ppy)3	0.0711	472 (+3)	SM4	472	0.903
			SM3	480	0.251

---

Likewise, the LUMO in Ir(2,3′-bpy)₃ (X = H and Y = H in Fig. 1(b)) is very similar to that in the parent complex Ir(ppy)₃ (Fig. 2). Namely, a large spectral shift to the blue region can be obtained when X = F, NH₂, or OH and Y = H in Fig. 1(b). The wavelengths of the spectral peaks calculated for Ir(4′,6′-dF-2,3′-bpy)₃ (X = F and Y = H), Ir(4′,6′-dNH₂-2,3′-bpy)₃ (X = NH₂ and Y = H), and Ir(4′,6′-dOH-2,3′-bpy)₃ (X = OH and Y = H) are shown in Table 2 and Fig. 8, and they need to be corrected to 437 nm in Ir(4′,6′-dF-2,3′-bpy)₃, 446 nm in Ir(4′,6′-dNH₂-2,3′-bpy)₃, and 430 nm in Ir(4′,6′-dOH-2,3′-bpy)₃ by using eqn. (1). As described in the previous paragraph, since negligible changes are expected to be obtained by using dialkyl-amino or alchoxy substituents instead of amino or hydroxy substituents, it can be said that the complexes of X = F, NR₂, and OR, together with Y = H, in Fig. 1(b) are also good candidates for blue phosphorescent materials.

Fig. 8 Spectral shifts by the introduction of electron-donating and withdrawing substituents into each benzene ring in Ir(2,3′-bpy)₃. Black (broken) = Ir(ppy)₃, black = Ir(2,3′-bpy)₃, red = Ir(4′,6′-dF-2,3′-bpy)₃, blue = Ir(4′,6′-dNH₂-2,3′-bpy)₃, green = Ir(4′,6′-dOH-2,3′-bpy)₃, red (dotted) = Ir(5′-CN-2,3′-bpy)₃, and blue (dotted) = Ir(5′-NO₂-2,3′-bpy)₃.

A substituent cannot be introduced to the 5′ sites in Ir(2,5′-bpy)₃ (Fig. 1(c)), but it can be introduced to the 5′ sites in Ir(2,3′-bpy)₃ (Fig. 1(b)). Even though the magnitude of spectral shift in Ir(2,3′-bpy)₃ is smaller than that in Ir(2,5′-bpy)₃ in comparison with Ir(ppy)₃, remarkable shifts to the blue region are expected when appropriate substituents are introduced into appropriate sites of the ligands. According to the discussion in our previous paper,⁵⁹ spectral shifts to the blue region can be obtained by the introduction of an electron-donating substituent, such as a cyano or nitro substituent, into the 5′ site in each bpy ligand (Fig. 1(b)). The calculated results shown in Table 2 and Fig. 8 are consistent with our discussion. By using eqn. (1), the peaks are estimated to appear at the wavelengths of 470 nm in Ir(5′-CN-2,3′-bpy)₃ (X = H and Y = CN) and 448 nm in Ir(5′-NO₂-2,3′-bpy)₃ (X = H and Y = NO₂). As discussed in our previous paper,⁵⁹ the reason why such results are obtained is that the low-lying π* orbitals of the substituents effectively interact with the iridium's d orbitals and make the HOMO lower in energy in the complexes. Although the magnitudes of these spectral shifts are not so large as those of Ir(2,5′-bpy)₃, the present discussion and consideration are proved to be reasonable.

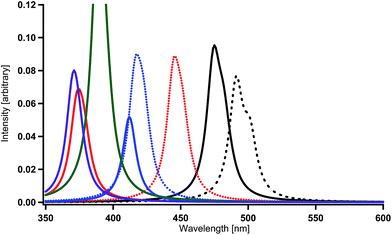
Finally, as performed in our previous study, the combination effects of the substituents in Ir(2,3′-bpy)₃ were examined in order to obtain deep blue-color phosphorescence. The present calculations for Ir(4′,6′-dF-5′-CN-2,3′-bpy)₃ (X = F and Y = CN) and Ir(4′,6′-dF-5′-NO₂-2,3′-bpy)₃ (X = F and Y = NO₂) provide spectral shifts of 117 nm and 79 nm to the blue region when the spectral peaks are compared with that in Ir(ppy)₃ (Table 2 and Fig. 9). The sum of the magnitudes of spectral shifts to the blue region induced by the introductions of fluorine substituents (87 nm for Ir(4′,6′-dF-2,3′-bpy)₃) and a cyano substituent (45 nm for Ir(5′-CN-2,3′-bpy)₃) is comparable with that for obtained for Ir(4′,6′-dF-5′-CN-2,3′-bpy)₃ (see Table 2). This seems to be simply caused by the linear structure of the cyano substituent and by the weak interaction among the substituents. Similarly, large spectral shifts of 101 nm and 120 nm to the blue region obtained for Ir(4′,6′-dNH₂-5′-CN-2,3′-bpy)₃ (X = NH₂ and Y = CN) and Ir(4′,6′-dOH-5′-CN-2,3′-bpy)₃ (X = OH and Y = CN) as shown in Table 2 and Fig. 9 are comparable with the sums of the magnitudes of spectral shifts obtained for Ir(4′,6′-dNH₂-2,3′-bpy)₃ and Ir(5′-CN-2,3′-bpy)₃ (76 + 45 = 121 nm) and for Ir(4′,6′-dOH-2,3′-bpy)₃ and Ir(5′-CN-2,3′-bpy)₃ (96 + 45 = 141 nm). Accordingly, it can be concluded that the complexes of X = F, NR₂, or OR, together with Y = CN, are good candidates for blue phosphorescent materials.

Fig. 9 Spectral shifts by the combination effects of substituents in each benzene ring in Ir(2,3′-bpy)₃. Black (broken) = Ir(ppy)₃, black = Ir(2,3′-bpy)₃, red (dotted) = Ir(5′-CN-2,3′-bpy)₃, blue (dotted) = Ir(5′-NO₂-2,3′-bpy)₃, red = Ir(4′,6′-dF-5′-CN-2,3′-bpy)₃, blue = Ir(4′,6′-dF-5′-NO₂-2,3′-bpy)₃, green = Ir(4′,6′-dNH₂-5′-CN-2,3′-bpy)₃, and purple = Ir(4′,6′-dOH-5′-CN-2,3′-bpy)₃.

The spectral shifts (79 nm) obtained for Ir(4′,6′-dF-5′-NO₂-2,3′-bpy)₃ is remarkably smaller than the sum of the magnitudes of spectral shifts obtained for Ir(4′,6′-dF-2,3′-bpy)₃ and Ir(5′-NO₂-2,3′-bpy)₃ (87 + 83 = 160 nm). This is consistent with the results reported in our previous investigation;⁵⁹ the combination of the nitro substituent with electron-donating substituents makes the spectral shifts smaller because of strong electrostatic and steric interactions among neighboring substituents. Such strong interaction sometimes derives strange geometrical structures for the lowest triplet states. In fact, when the combination of X = NH₂ or OH and Y = NO₂ was used, the geometry optimizations for the lowest triplet states derive a new bond between a terminal oxygen atom of the nitro substituents and the closest hydrogen atom of the amino or hydroxy substituents. These results suggest that such complexes could be broken when they are promoted to the lowest triplet state by the electric field and should not be used as functional materials. As described above, if X = NR₂ or X = OR instead of X = NH₂ or X = OH, such new bonds may not be created in the lowest triplet states and effective spectral shifts to the blue region could be obtained even though the magnitudes of spectral shifts may be small. Since the nitro substituent could get hydrogen atoms or ions from host molecules in the emissive layers of OLEDs, the OLEDs created by such materials may have very short lifetime.

Summary

In the present investigation, MCSCF+SOCI+SOC/SBKJC+p calculations were performed in order to examine the effects of replacement of a methine group in each ppy ligand of fac-Ir(ppy)₃ by a nitrogen atom for the purpose of obtaining deep blue phosphorescence. Only the replacements of methine groups at the 3′ and 5′ sites of each ppy ligand by nitrogen atoms were calculated to induce a spectral shift to the blue region. These results can be explained by the strong electronegativity of nitrogen atoms and by the magnitude of the electron density at the 2′ carbon atom of the ppy or bpy ligands. Subsequently, the substituent effects in fac-Ir(bpy)₃ were investigated and found to be similar to those in fac-Ir(ppy)₃ reported in our previous paper.⁵⁹ Based on systematic calculations and theoretical consideration, the most effective modification for deep blue phosphorescence should be the introduction of a nitrogen atom into the 3′ or/and 5′ site of benzene rings of the ppy ligands in fac-Ir(ppy)₃ together with the combination of the substituents X = F, NR₂, or OR (R = alkyl group) and Y = CN or NO₂ (see Fig. 1). The same investigations when an ancillary ligand such as a picolinate (pic) or acetylacetonate (acac) ligand is introduced into fac-Ir(ppy)₃ are in progress.

References

1. C. W. Tang, S. W. Van Slyke and C. H. Chen, J. Appl. Phys., 1989, 65, 3610–3616.
2. M. A. Baldo, S. Lamansky, P. E. Burrows, M. E. Thompson and S. R. Forrest, Appl. Phys. Lett., 1999, 75, 4–6.
3. C. Adachi, M. A. Baldo and S. R. Forrest, Appl. Phys. Lett., 2000, 77, 904–906.
4. K. Pierloot, A. Ceulemans, M. Merchán and L. Serrano-Andrés, J. Phys. Chem. A, 2000, 104, 4374–4382.
5. J. Brooks, Y. Babayan, S. Lamansky, P. I. Djurovich, I. Tsybam, R. Bau and M. E. Thompson, Inorg. Chem., 2002, 41, 3055–3066.
6. A. B. Tamayo, B. D. Alleyne, P. I. Djurovich, S. Lamansky, I. Tsyba, N. N. Ho, R. Bau and M. E. Thompson, J. Am. Chem. Soc., 2003, 125, 7377–7387.
7. A. Beeby, S. Bettington, I. D. Samuel and Z. Wang, J. Mater. Chem., 2003, 13, 80–83.
8. Y. Kawamura, K. Goushi, J. Brooks, J. J. Brown, H. Sasabe and C. Adachi, Appl. Phys. Lett., 2005, 86, 071104.
9. K. Dedeian, J. Shi, N. Shepherd, E. Forsythe and D. C. Morton, Inorg. Chem., 2005, 44, 4445–4447.
10. R. Ragni, E. A. Plummer, K. Brunner, J. W. Hofstraat, F. Babudri, G. M. Farinola, F. Naso and L. de Cola, J. Mater. Chem., 2006, 16, 1161–1170.
11. X. Y. Cai, A. B. Padmaperuma, L. S. Sapochak, P. A. Vecchi and P. E. Burrows, Appl. Phys. Lett., 2008, 92, 083308.
12. X. Gu, T. Fei, H. Zhang, H. Xu, B. Yang, Y. Ma and X. Liu, J. Phys. Chem., 2008, 112, 8387–8393.
13. S. H. Kim, J. Jang, S. J. Lee and J. Y. Lee, Thin Solid Films, 2008, 517, 722–726.
14. S. Reineke, F. Lindner, G. Schwartz, N. Seidler, K. Walzer, B. Lüssem and K. Leo, Nature, 2009, 459, 234–238.
15. H. Wang, Q. Liao, H. Fu, Y. Zeng, Z. Jiang, J. Ma and J. Yao, J. Mater. Chem., 2009, 19, 89–96.
16. S. J. Lee, K.-M. Park, K. Yang and Y. Kang, Inorg. Chem., 2009, 48, 1030–1037.
17. X. Li, Z. Wu, X. Li, H. Zhang and X. Liu, J. Comput. Chem., 2011, 32, 1033–1042.
18. J. Wang, B. Xia, F. Bai, L. Sun and H. Zhang, Int. J. Quantum Chem., 2011, 111, 4080–4090.
19. A. Kadari, A. Moncomble, I. Ciofini, M. Brahimi and C. Adamo, J. Phys. Chem. A, 2011, 115, 11861–11865.
20. Y. Hisamatsu and S. Aoki, Eur. J. Inorg. Chem., 2011, 5360–5369.
21. E. Baranoff, B. F. E. Curchod, J. Frey, R. Scopelliti, F. Kessler, I. Tavernelli, U. Rothlisberger, M. Grätzel and M. K. Nazeeruddin, Inorg. Chem., 2012, 51, 215–224.
22. Y. Su and L. Kang, Int. J. Quantum Chem., 2012, 112, 2422–2428.
23. J. Su, X. Sun, G. Gahungu, X. Qu, Y. Liu and Z. Wu, Synth. Met., 2012, 162, 1392–1399.
24. Q. Cao, J. Wang, Z. Tian, Z. Wie and F. Bai, J. Comput. Chem., 2012, 33, 1038–1046.
25. H. Li, P. Winget, C. Risko, J. S. Sears and J. Bredas, Phys. Chem. Chem. Phys., 2013, 15, 6293–6302.
26. D. Han, G. Zhang, H. Cai, X. Zhang and L. Zhao, J. Lumin., 2013, 138, 223–228.
27. X. Shang, D. Han, D. Li and Z. Wu, Chem. Phys. Lett., 2013, 565, 12–17.
28. X. Shang, Y. Liu, X. Qui and Z. Wu, J. Lumin., 2013, 143, 402–408.
29. X. Shang, D. Han, D. Li, S. Guan and Z. Wu, Chem. Phys. Lett., 2013, 588, 68–75.
30. Y. Si, Y. Liu, X. Qu, Y. Wang and Z. Wu, Dalton Trans., 2013, 42, 14149–14157.
31. J. M. Younker and K. D. Dobbs, J. Phys. Chem. C, 2013, 117, 25714–25723.
32. R. Srivastava, Y. Kada and B. Kotamarthi, Comput. Theor. Chem., 2013, 1009, 35–42.
33. X. Qu, Y. Liu, G. Godefroid, Y. Si, X. Shang, X. Wu and Z. Wu, Eur. J. Inorg. Chem., 2013, 3370–3383.
34. M. Song, Z. Hao, Z. Wu, S. Song, I. Zhou, R. Deng and H. Zhang, J. Phys. Org. Chem., 2013, 26, 840–848.
35. X. Shang, Y. Liu, J. Su, G. Gahungu, X. Qu and Z. Wu, Int. J. Quantum Chem., 2014, 114, 183–191.
36. Y. Si, X. Sun, Y. Liu, X. Qu, Y. Wang and Z. Wu, Dalton Trans., 2014, 43, 714–721.
37. X. Qu, Y. Liu, Y. Si, X. Wu and Z. Wu, Dalton Trans., 2014, 43, 1246–1260.
38. Y. Li, L.-Y. Zou, A.-M. Ren, M.-S. Ma and J.-X. Fan, Chem.– Eur. J., 2014, 20, 4671–4680.
39. D. Han, C. Li, L. Zhao, X. Sun and G. Zhang, Chem. Phys. Lett., 2014, 595–596, 260–265.
40. K. Mori, T. P. M. Goumans, E. Lenthe and F. Wang, Phys. Chem. Chem. Phys., 2014, 16, 14523–14530.
41. L. Wang, Y. Wu, G. Shan, Y. Geng, J. Zhang, D. Wang, G. Yang and Z. Su, J. Mater. Chem. C, 2014, 2, 2859–2868.
42. J. Frey, B. F. E. Curchod, R. Scopelliti, I. Tavernelli, U. Rothlisberger, M. K. Nazeeruddin and E. Baranoff, Dalton Trans., 2014, 43, 5667–5679.
43. B. F. Minaev, S. Knuts, H. Agren and O. Vahtras, Chem. Phys., 1993, 175, 245–254.
44. H. Agren, O. Vahtras and B. F. Minaev, Adv. Quantum Chem., 1996, 27, 71–162.
45. B. F. Minaev, Opt. Spectrosc., 2005, 98(3), 336–340.
46. B. F. Minaev, E. Jansson, H. Ågrena and S. Schrader, J. Chem. Phys., 2006, 125, 234704.
47. E. Jansson, B. Minaev, S. Schrader and H. Ågren, Chem. Phys., 2007, 333, 157–167.
48. B. Minaev, V. Minaeva and H. Ågren, J. Phys. Chem. A, 2009, 113, 726–735.
49. B. Minaev, H. Ågren and F. de Angelis, Chem. Phys., 2009, 358, 245–257.
50. X. Li, B. Minaev, H. Ågren and H. Tian, J. Phys. Chem. C, 2011, 115, 20724–20731.
51. X. Li, B. Minaev, H. Ågren and H. Tian, Eur. J. Inorg. Chem., 2011, 2517–2524.
52. D. Volyniuk, V. Cherpak, P. Stakhira, B. F. Minaev, G. V. Baryshnikov, M. Chapran, A. Tomkeviciene, J. Keruckas and J. V. Grazulevicius, J. Phys. Chem. C, 2013, 117, 22538–22544.
53. B. F. Minaev, G. Baryshnikov and H. Agren, Phys. Chem. Chem. Phys., 2013, 16, 1719–1758.
54. V. Cherpak, P. Stakhira, B. Minaev, G. Baryshnikov, E. Stromylo, I. Helzhynskyy, M. Chapran, D. Volyniuk, D. Tomkuté-Lukšiené, T. Malinauskas, V. Getautis, A. Tomkeviciene, J. Simokaitiene and J. V. Grazulevicius, J. Phys. Chem. C, 2014, 118, 11271–11278.
55. T. Matsushita, T. Asada and S. Koseki, J. Phys. Chem. A, 2006, 110, 13295–13302.
56. S. Koseki, Y. Kagita, S. Matsumoto, T. Asada, S. Yagi, H. Nakazumi and T. Matsushita, J. Phys. Chem. C, 2014, 118, 15412–15421.
57. T. Matsushita, T. Asada and S. Koseki, J. Phys. Chem. C, 2007, 111, 6897–6903.
58. S. Koseki, N. Kamata, T. Asada, S. Yagi, H. Nakazumi and T. Matsushita, J. Phys. Chem. C, 2013, 117, 5314–5327.
59. S. Koseki, H. Yoshinaga, T. Asada and T. Matsushita, RSC Adv., 2015, 5, 35760–35772.
60. S. Ikawa, S. Yagi, T. Maeda, H. Nakazumi, H. Fujiwara, S. Koseki and Y. Sakurai, Inorg. Chem. Commun., 2013, 38, 14–19.
61. S. Koseki, M. S. Gordon, M. W. Schmidt and N. Matsunaga, J. Phys. Chem., 1995, 99, 12764–12772.
62. S. Koseki, M. W. Schmidt and M. S. Gordon, J. Phys. Chem. A, 1998, 102, 10430–10435.
63. S. Koseki, D. G. Fedorov, M. W. Schmidt and M. S. Gordon, J. Phys. Chem. A, 2001, 105, 8262–8268.
64. S. Koseki, M. W. Schmidt and M. S. Gordon, J. Phys. Chem., 1992, 96, 10768–10772.
65. N. Matsunaga, S. Koseki and M. S. Gordon, J. Chem. Phys., 1996, 104, 7988–7996.
66. S. Koseki, Y. Ishihara, U. Umeda, D. G. Fedorov and M. S. Gordon, J. Phys. Chem. A, 2002, 106, 785–794.
67. S. Koseki, Y. Ishihara, H. Umeda, D. G. Fedorov, M. W. Schmidt and M. S. Gordon, J. Phys. Chem. A, 2004, 108, 4707–4719.
68. S. Koseki, T. Matsushita and M. S. Gordon, J. Phys. Chem. A, 2006, 110, 2560–2570.
69. S. Koseki, Computational Methods in Sciences and Engineering, Theory and Computation: Old Problems and New Challenges, ed. G. Maroulis and T. Simos, AIP, New York, 2008, CP963, Vol. 1, pp. 257–267.
70. S. Koseki, N. Shimakura, Y. Fujimura, T. Asada and H. Kono, J. Chem. Phys., 2009, 131, 044122.
71. T. Hisashima, T. Matsushita, T. Asada and S. Koseki, Theor. Chem. Acc., 2008, 120, 85–94.
72. S. Koseki, T. Hisashima, T. Asada, A. Toyota and N. Matsunaga, J. Chem. Phys., 2010, 133, 174112.
73. D. G. Fedorov, S. Koseki, M. W. Schmidt and M. S. Gordon, Int. Rev. Phys. Chem., 2003, 22, 551–592.
74. D. G. Fedorov, M. W. Schmidt, S. Koseki, and M. S. Gordon, Recent Advances in Relativistic Molecular Theory, World Scientific, Singapore, 2004, Vol. 5, pp. 107–136.
75. R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules, Oxford, 1989, pp. 1–333 and references therein.
76. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
77. M. W. Schmidt and M. S. Gordon, Annu. Rev. Phys. Chem., 1998, 49, 233–266.
78. W. J. Stevens, H. Basch, M. Krauss and P. Jasien, Can. J. Chem., 1992, 70, 612–630.
79. T. R. Cundari and W. J. Stevens, J. Chem. Phys., 1993, 98, 5555–5565.
80. Exponents of 0.938 are used for f functions on Ir. The d exponents are 0.800 (C and N). The p exponents are 1.100 (H). This basis set is referred to as SBKJC+p.
81. B. H. Lengsfield III, J. A. Jafri, D. H. Phillips and C. W. Bauschlicher Jr, J. Chem. Phys., 1981, 74, 6849–6856.
82. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363.
83. M. S. Gordon and M. W. Schmidt, Advances in electronic structure theory: Gamess a decade later in Theory and Applications of Computational Chemistry: The First Forty Years, ed. C. E. Dykstra, G. Frenking, K. S. Kim and G. E. Scuseria, Elsevier, Amsterdam, 2005.
84. J.-Y. Tsai, G. Kottas, W. Yeager, Z. Elshenawy, C. Xia, G. Szigethy and J. Brooks. Organic electroluminescent materials and devices. U. S. Patent 0 194 612 A1, Jul. 9, 2015.
85. For example, R. R. Morrison and R. N. Boyd, Organic Chemistry, Prentice-Hall Inc, 6th edn, 1992.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra07778a

---