Effect of electric field on creep and stress-relaxation behavior of carbon nanotube forests
Piyush Jagtap,
Amit Kumar and
Praveen Kumar*
Department of Materials Engineering, Indian Institute of Science, Bangalore-560012, India. E-mail: praveenk@materials.iisc.ernet.in; Tel: +91-80-2293-3369
First published on 11th July 2016
Abstract
Carbon nanotube forests (CNTFs) are porous ensembles of vertically aligned carbon nanotubes, exhibiting excellent reversible compressibility and electric field tunable stress–strain response. Here, we report the effects of electric field on the time dependent mechanical behavior, namely creep and stress-relaxation, of CNTFs. Creep and stress-relaxation experiments were conducted under constant compressive stress and constant compressive strain, respectively, wherein variation of the strain and the stress, respectively, as functions of time were measured. Creep strain–time data of CNTFs showed a primary creep regime followed by a steady-state creep regime. The creep rate was substantially retarded upon application of electric field. The steady-state strain rate showed a power-law dependence on the stress; however, the stress exponent reduced when an electric field was applied. On other hand, electric field enhanced stress-relaxation in CNTFs, leading to a lower value of stress at a given time. However, the effect of electric field on the stress-relaxation reduced with compressive strain. Based on the Garofalo model of creep, a unified model for explaining the overall time dependent mechanical behavior of CNTFs and the observed experimental results was developed.
1. Introduction
Vertically aligned carbon nanotube forests (CNTFs) grown with or without substrates have recently attracted significant scientific interest due to their ease of production on a large scale with low cost and an extraordinary mix of mechanical, electrical and optical properties.1–8 Such multi-functionality of these carbon nanotube (CNT) based engineering materials allows their active usage in a myriad of applications, such as shock absorbers, gas sensors, photo-actuators, micro-/nano-electro-mechanical systems (MEMS/NEMS), etc. Fig. 1 shows a few representative scanning electron micrographs of a CNTF at various magnifications. As shown in Fig. 1, a CNTF consists of numerous vertically aligned CNTs, which crisscross each other forming nodes at points of intersection. Because of van der Waal's interactions, these nodes resist both sliding and debonding, and hence impart strength to the CNTF.1,9–14 Under quasistatic compression loading conditions, segments of CNT strands between adjacent nodes can bend to accommodate the macro-strain. Upon release of the load, the bent CNT strand can completely recover its original shape, thus giving rise to the very large reversible compressibility of CNTF.9,15,16 In the process of bending of CNT strands, they often slide over each other, and sometimes, CNT strands may also slide at nodes, resulting in a net dissipation of strain energy due to the friction involved in the aforementioned motions.9,17 This causes formation of distinct stress–strain hysteresis during a loading–unloading cycle, giving rise to very large energy dissipation or absorption per unit mass by CNTF.9,18 This facilitates application of CNTF as shock absorbers and dampers, especially in miniaturized systems that are prone to fall, but has severe space restriction, such as mobile phones, laptops, mobile MEMS/NEMS based medical diagnostic systems, etc.Furthermore, careful inspection of Fig. 1 also reveals that much of the volume of a CNTF is unoccupied (>70%). In addition, the unoccupied volume in CNTFs is often interconnected. Thus, the microstructure of the CNTF, which may thus be qualified as foam, can be easily tailored by impregnating it with liquids, nanoparticles, etc.19–22 This allows further tuning of the mechanical behavior of CNTF for a particular application. Furthermore, the mechanical response of CNTF can also be manipulated by application of an electric field as well as a magnetic field.18,23–25 Particularly, application of electric field or current across the height of the CNTF has been shown to significantly enhance its mechanical strength as well as its total energy absorption capacity.18,23 Since electric field (and, in some case, magnetic field also) is readily available in several active devices, such as MEMS/NEMS based systems, this additional tunability of CNTF makes it technologically quite attractive. Thus, it can be concluded that CNTF and its derived structures have excellent mechanical behavior, which can be further improved for a particular application through various means. Hence, as mentioned previously, CNTF is an important engineering material based on CNT, which can potentially be used for several structural applications, especially at small length scales ranging from a few tens of micrometers to a few millimeters.
Mechanical behavior of CNTF under quasistatic and dynamic loading conditions has been widely studied.9,13–16 However, the literature on the time dependent mechanical response of CNTF, which is crucial for predicting long-term structural integrity and load bearing capacity of structures comprising CNTF, is scantier. Nevertheless, it is now well established that CNTF shows standard time dependent responses of creep and stress-relaxation even at room temperature.26–33 Summarily, the creep behavior of CNTF is marked with continuous accumulation of strain at a constant load,27,28,31 whereas its stress-relaxation behavior is manifested in a continuous decrease in the stress required to maintain a fixed macro-strain.27–29,31,34 Although the mechanistic origin of time dependent behavior of CNTF is not fully understood, it is generally attributed to the following set of events:28,29,33–36 (i) sliding of CNT nodes, (ii) irreversible re-orientation of CNT, and (iii) sliding of CNT over each other.
There are broadly two types of quantitative models that have been proposed for explaining the time dependent behavior of CNTF, namely exponential and power-law type. The exponential behavior, primarily based on “spring-dashpot element” type of viscoelastic models, has been shown to capture viscoelasticity-induced stress-relaxation in CNTF, both in the presence and the absence of an electric field.33–35 However, no attempt has been made to develop a similar “exponential” model for the creep. On other hand, power-law behavior has been shown to quantitatively capture both the stress-relaxation and the creep behavior of CNTF.28,31 However, a power-law model does not clearly distinguishes between the primary and secondary creep stages, which, as will be shown later in this study, usually occurs in CNTF. In addition, although the “spring-dashpot element” based models have elegance of being physically more appealing as compared to the power-law models, they do not perform well in quantitatively capturing the strain–time and the stress–time data under the creep and the stress-relaxation conditions, respectively. This is attributed to the fact that, as it will be shown latter, both types of the time dependent behaviors of CNTFs often show a very rapid change in the beginning, followed by a gradual change over long periods of time. Interestingly, the creep and stress-relaxation in CNTFs may originate from the same viscoelastic processes, involving sliding and reconfiguration of CNT strands and nodes. Hence, it is imperative to develop a mechanistic model, which not only quantitatively captures the experimental data, but also seamlessly unifies both creep and stress-relaxation; this is one of the goals of this study.
Since, as mentioned previously, the mechanical response of CNTF depends on the electric field,18,23,24,37 it is also imperative to study the effects of electric field on the time dependent mechanical response, namely creep and stress-relaxation, of CNTF. This is particularly important as both the stress bearing and the energy absorption capacities of CNTFs under quasistatic compressive loading are shown to dramatically enhance upon application of an electric field.18,23 In this regard, although a study was conducted discussing the effects of electric field on the stress-relaxation of CNTF,33 the effect of electric field on creep has never been reported. In addition, the effect of electric field on the unification of the creep and the stress-relaxation phenomena in the CNTF is also not understood. Accordingly, this study first experimentally highlights the effects of electric field on the creep and the stress-relaxation of CNTF, and then presents a novel unified paradigm for quantitatively describing the aforementioned two time dependent phenomena, both in the absence and the presence of electric field.
2. Experimental procedure
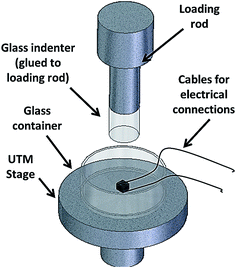
A 1 mm thick mat of CNTF was grown using thermal chemical vapor deposition (CVD). Details of the CVD processing are available in ref. 15 and it is summarized here for continuity. Toluene, ferrocene and argon were used as the carbon source, the iron source (i.e., the catalyst), and the carrier gas, respectively. The solution of ferrocene and toluene was brought over SiO2–Si substrate kept at 827 °C for reaction enabling growth of CNT on the substrate to take place. Through this process, nominally vertical CNT grew on the substrate. A representative microstructure of the as-grown CNT sample is shown in Fig. 1. Hence, the grown sample in this study qualified as the CNTF. Subsequently, test specimens of 5 × 5 × 1 mm3 size were cut from an extended mat of CNTF using a sharp surgical blade. The length of a CNT strand was nominally along the height or thickness of the CNTF sample (see Fig. 1).Both creep and stress-relaxation experiments were performed using a universal testing machine (UTM) (Instron 5967), equipped with a 5 kN load cell. Fig. 2 shows a schematic of the test set-up used in this study. Creep experiments were conducted by applying a constant compressive load onto the CNTF sample and simultaneously, recording the deformation as function of time. Thus, true stress during creep decreased with the compressive strain. The nominal stress applied on the sample during creep experiment was 0.5, 1.0, 3 or 7 MPa, and the set load was applied onto the sample by increasing the force at a constant loading rate of 0.5 N s−1. On the other hand, the stress-relaxation experiments were performed at constant nominal strain, i.e., strain relative to the height of the as-grown CNTF sample, of 5, 10, 15 or 20%, and the nominal stress as function of time was recorded. During stress relaxation experiments, the samples were pre-strained to the desired value at constant nominal strain rate of 0.01 s−1. It should be noted that both types of experiments were conducted under the ambient conditions.
Both types of experiments were conducted in the presence as well as in the absence of electric field applied along the height of the CNTF sample, i.e., along length of a CNT strand or in the direction of mechanical loading. For applying electric field, thin sheets of Cu were placed in between the sample and the loading rods at both the top and the bottom of the sample. The Cu sheets were then soldered to thin Cu wires connected to a source meter unit (Keithley 2602A). The compressive load applied on the sample ensured good electrical contact between Cu electrodes and the CNTF sample. In the case of experiments under electric field, the field was applied at least 5 minutes before the initiation of the test so that the sample is stabilized under the electric field. A fixed potential difference of 1 V, corresponding to an electric field of 1 kV m−1, was applied in the experiments performed in the presence of electric field. Our previous works18,23,24,33 have shown that the effects of electric field a mechanical behavior of CNTF, such as strength, energy absorption, viscoelastic relaxation, etc., are monotonous, i.e., an increase in the value of electric field will further magnify the fundamental effects of electric field on the respective mechanical behavior. Ref. 23 shows representative stress–strain curves for CNTF under compression and it also documents of the effect of electric field on the stress–strain behavior of CNTF samples. Therefore, it is speculated that the dependence of various parameters defining the generic time-dependent phenomenon of the creep and the stress relaxation on electric field will also be monotonous.
It should be noted that since the all experiments in this study were conducted under a fixed electric potential of 1 V, a decrease in the sample height will increase the value of true electric field applied across the sample. Thus, in creep experiments, there will be difference in the electric field applied across samples compressed to different instantaneous strains prior the start of a creep experiment. However, the maximum instantaneous strain during creep experiments in this study was ≤16.8%, which will cause an increase in the true electric field by only ≤20%, which may be neglected within the scatter of experimental data reported in this study. Now, the maximum compressive strain imposed on the sample for performing stress relaxation experiments was 20%, which will result in a maximum increase in electric field by 25%. However, as it will be shown later, the effect of such a small difference in the electric field should be insignificant as compared to other effects (such as effect of strain). Moreover, this study attempts to qualitatively highlight the fundamental effect of electric field on the generic time-dependent mechanical behavior of CNTF, the effects of small differences in the values of nominal and true electric fields have been neglected.
3. Results
Fig. 3 shows representative creep curves showing creep strain as function of time, in both the absence (W/O) and the presence (W/E) of electric field. The time independent or instantaneous strain, measured as the strain at the end of the load-ramp segment (i.e., before reaching the desired load), was subtracted from the total strain to calculate the time dependent or creep deformation. Irrespective of the electric field and the applied stress, the CNTF sample showed standard power-law type of creep behavior in compression: the creep curve comprised of a primary stage, where the creep strain increased rapidly with time, and a secondary stage where the creep curve appeared linear, suggesting attainment of a constant strain rate. The aforementioned creep responses are generally demonstrated by crystalline materials, e.g. metals, ceramics, etc.,38 as well as polymers.39 In general, the primary stage is considered as the stage where the microstructure of a sample evolves to the steady-state microstructure. It is evident that the microstructure of the CNTF tested in this study hardened during the primary stage, as reflected by the continuously decreasing slope of the creep curve, suggesting occurrence of primary creep often observed in crystalline materials. In addition, Fig. 3 also shows that the total creep strain as well as the apparent strain rate in the steady-state increased with the applied stress.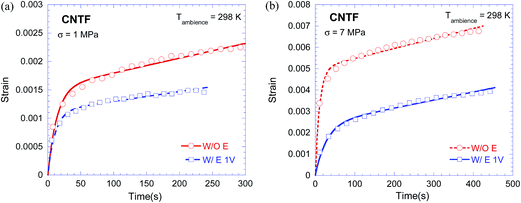 | ||
| Fig. 3 Representative creep strain versus time graphs for CNTF samples in the absence (W/O E) and in the presence (W/E 1 V) of electric field under a constant nominal stress of (a) 1 and (b) 7 MPa. The shown symbols are 20 representative datum points for each experimental condition, whereas the curves show the best-fit curves using eqn (1). The values of parameters a, b and c of eqn (1) as well as the curve fitting parameter, R, are shown in Table 1. A value of R close to 1 indicates curve fitting with high confidence. | ||
Fig. 3 clearly shows that, irrespective of the applied stress, application of an electric field decreased the total creep strain. It should be noted that the temperature of CNTF samples upon passing of electric current increased by <20 °C. As mentioned earlier, the mechanical behavior of CNTF samples has been shown to be less sensitive to temperature26,28 and given only a small increase in the temperature of CNTF samples in this study upon passage of electric current through them, it is reasonable to assume that the observed effects of electric field on creep (and later on stress relaxation) are insignificantly affected by the Joule heating induced temperature rise. Furthermore, a careful observation of Fig. 3 also reveals a slight decrease in the steady-state strain rate at a fixed stress upon application of electric field. These observations suggest that CNTF strengthened or became creep resistant upon application of electric field. This is consistent with a previous study showing an increase in the compressive stress required to be applied for maintaining a strain upon application of electric field.23 Such strengthening of CNTF due to electric field has been attributed to the electric field induced unidirectional polarization of CNT and the resulting electrostriction induced actuation.23,37
Garofalo equation of creep is a phenomenological model, which captures both the primary and the secondary creep, is given as follows:40,41
| ε = a[1 − exp(−bt)] + ct | (1) |
Fig. 3 also shows the curve fitting exercise performed using eqn (1) and the Table 1 shows various values of creep parameters (i.e., a, b and c) extracted from the curve fit using eqn (1). As shown by Fig. 3 and also supported by the high value of curve fitting parameter, R, of ≥0.98 (see Table 1), eqn (1) aptly captures the creep behavior of CNTF in both the absence and the presence of the electric field. It should be noted that plotting the creep data using ln(ε) versus ln(t) graph does not result in a curve with constant slope (as it will be required by power-law), as also predicted by eqn (1). This clearly suggests that creep of CNTF cannot be aptly captured by power-law only.
| σ = 1 MPa | σ = 7 MPa | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| a | b (s−1) | c (s−1) | ε0 | R | a | b (s−1) | c (s−1) | ε0 | R | |
| W/O E | 1.5 10−3 | 7.3 × 10−2 | 2.6 × 10−6 | 0.101 | 0.99 | 5.0 × 10−3 | 9.1 × 10−2 | 4.7 × 10−6 | 0.168 | 0.99 |
| W/E | 1.1 × 10−3 | 9.0 × 10−2 | 1.7 × 10−6 | 0.060 | 0.98 | 2.4 × 10−3 | 3.5 × 10−2 | 3.8 × 10−6 | 0.159 | 0.99 |
Fig. 4 shows the variation of parameters a, b and c as function of the applied stress. However, except for the variation of c, i.e., the steady-state strain rate, the variation of all other creep parameters, i.e., a and b, do not show a monotonous or well-defined dependence on the stress. Qualitatively, Fig. 4a and b suggest that the primary creep and the exhaustion rate increase and decrease with the stress, respectively. These trends are mutually consistent, as an enhanced rate of exhaustion of primary stage will lead to a smaller primary creep. Fig. 4a and b also suggest that the total primary creep was systematically smaller if the CNTF was tested under an electric field, whereas exhaustion rate, b, might be independent of the applied electric field (of 1 kV m−1). Therefore, the transformation to the steady state structure in presence of electric current occurred at lower strain, which may suggest a smaller difference in the initial and the steady state microstructure in the presence of electric field.
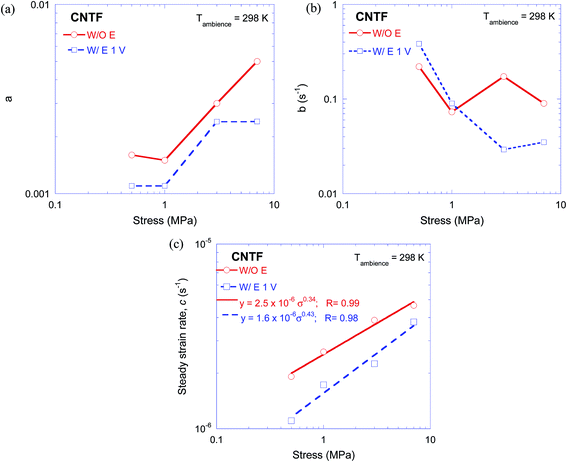 | ||
| Fig. 4 Variation of creep parameters: (a) a, (b) b and (c) c as function of the applied stress. In (c), the data was fitted with a power-law (eqn (4)), and both the equation and the corresponding curve fitting parameter, R, are shown in the legend. The lines in (a) and (b) represent linear interpolation between consecutive points. | ||
Fig. 4c clearly reveals a power-law type of variation of the steady-state strain rate, i.e., c or ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ss, with the stress:
ss, with the stress:
c = ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ss = Aσn ss = Aσn
| (2) |
Fig. 5 shows a few representative graphs revealing the stress-relaxation in CNTF samples in the absence and in the presence of an electric field. The ordinate axis of Fig. 5 shows the normalized stress, defined as ratio of the instantaneous stress, σ(t), and the initial stress, σ0 (i.e., σ at time, t = 0). Such a scheme allows direct comparison of stress-relaxation behavior irrespective of the initial values of the stress at the fixed strain. It should be noted that the initial stress, σ0, is a function of both the applied strain and the electric field. As shown in Fig. 5, irrespective of the applied electric field and the compressive strain, CNTF showed considerable stress-relaxation, wherein the stress dropped rapidly in the beginning, followed by a gradual, albeit linear, drop at longer time. Fig. 5 also reveals that application of electric field enhanced the initial drop in the normalized stress, leading to an overall enhanced stress-relaxation. However, effect of the electric field on the stress-relaxation reduced with an increase in the compressive strain. These observations are consistent with a previous report on viscoelasticity-induced stress-relaxation of CNTF.33 It should be noted that an increase in the compressive strain from 10% to 20% while applying a fixed electric potential of 1 V will increase the true electric field across the sample by ∼15%. However, as shown in Fig. 5 and noting that effect of electric field on a mechanical response of CNTF is often monotonous,18,23,24,33 it can be concluded that effect of small changes in the electric field due to the difference in compressive strains imposed on the samples in this study on the overall stress relaxation behavior of CNTF was insignificant as compared to that of the strain.
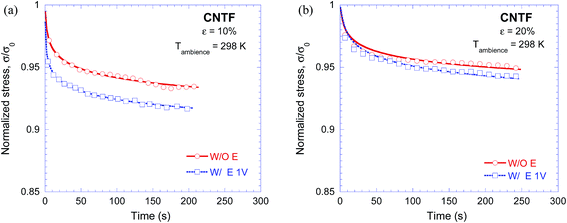 | ||
| Fig. 5 Effect of electric field on stress-relaxation of CNTF with an initial compressive strain of (a) 10% and (b) 20%. The symbols are 20 representative datum points for each experimental condition, whereas the curves show the best-fit curves using eqn (7). | ||
4. Discussion
4.1 Transition from primary stage to secondary stage of creep: a qualitative picture
The standard creep curve of CNTF tested under compression showed a distinct region of primary creep, where the material became harder to deform with accumulation of strain, followed by a secondary or steady-state region, where the creep rate became constant with strain. In crystalline materials, this behavior is often attributed to the formation of dislocation sub-structures during primary stage, and their steadiness in the secondary stage.38 However, CNTF does not have dislocations, and hence a different mechanism must be responsible for the above observation. In order to investigate the structure–property relationship in the CNTF samples, performing in situ experiments inside an SEM or transmission electron microscope will be ideal, as then one can visualize the movement of CNT strands during creep and stress relaxation processes. Nevertheless, some valuable insights regarding the mechanism of deformation can also be gained from the creep and stress-relaxation curves, as obtained from the ex situ tests performed in this study. Below, we propose a mechanism which may explain the experimentally observed existence of primary and secondary stages of creep in CNTF.It is now generally accepted that the strength of CNTF in compression primarily originate from the van der Waals forces between adjacent CNT strands. In addition, it is also shown that the creep of CNTF does not evolve significantly due to temperature change between −150 and 600 °C.26,28 This firstly, is consistent with the fact that van der Waals forces are not very sensitive to temperature, especially in the low temperature regime42,43 and secondly, suggests that creep of CNTF at low temperatures is not governed by thermally activated process. Hence, the evolution of van der Waals forces in the compression creep of CNTF may hold the key of understanding the existence of different stages of creep. As the CNTF is compressed under creep loading, the CNTF becomes denser, the nodes formed at intersection of two or more CNTF strands may start to slide downwards and the CNT strands in between two nodes start to bend. During this process, several CNT strands come closer to each other, resulting in overall increase in the attractive van der Waals forces. This process may also cause formation of new nodes, resulting in further strengthening of CNTF. Therefore, through this process, continued compression will make the CNTF stiffer. However, as the compressive strain increases, the resultant force on the nodes by the severely bent CNT strands being held at the node will also increase, resulting in enhanced probability of local sliding or breaking of the nodes. In addition, the overlap area between CNT strands will decrease with their bending, which will decrease overall van der Waals forces. These two processes, which will soften CNTF, will readily occur when CNT strands are highly bent, whose probability will increase with compressive strain. Given a random configuration of CNTs in CNTF in the beginning of the creep deformation, the above stiffening and softening process will occur simultaneously right from the onset of the creep. However, the difference between the stiffening and softening processes will reduce with strain, giving rise to a primary stage where strain rate decreases with the strain and finally, attainment of steady-state when the hardening and the softening processes become equal. It should be noted that on local scale, some regions of CNTF might show unbalanced “stiffening–softening” as the deformation in CNTFs is often inhomogeneous;9 however, these two processes will overall balance each other in the steady-state or secondary creep.
In presence of electric field, the CNT strands are polarized37 and therefore the columbic interaction between adjacent CNT strands does not allow them to bend easily. This, therefore, increases the creep resistance of CNTF under an electric field (see Fig. 3 and 4). However, at higher stresses the effect of columbic interaction will become less significant as compared to the applied load. Thus, columbic interaction can be represented as a threshold stress, σth, which then gives the effective stress, σeff, equal to the difference between the applied stress, σ, and σth. Therefore, eqn (2) can be rewritten as:
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ss = A(σ − σth)n ss = A(σ − σth)n
| (3) |
Eqn (3) predicts a diminishing effect of σth (or columbic interaction) at higher σ, as shown in Fig. 4c. Use of eqn (2) for curve fitting instead of eqn (3) will result in a higher n. σth of ∼0.3 MPa due to the columbic interaction in the CNTF samples will result in a stress exponent of 0.34 in the presence of electric field, which is same as that in absence of electric field.
Interestingly, during stress relaxation tests, where the CNT strands are already compressed to a certain strain, the electric field induced polarization of CNT strands and ensuing columbic repulsion between them reduce the overall van der Waals attractive interaction between CNT strands. This, therefore, leads to a rapid increase in the stress relaxation, as shown in Fig. 5. It should be noted that finite element analysis have shown that electro-magnetic interaction between adjacent CNT strands does not play important role in the deformation of CNTF.18
4.2 Creep equation for CNTF
Putting eqn (2) in eqn (1) gives the following form of the Garofalo creep model for CNTF:| ε = a[1 − exp(−bt)] + Aσnt | (4) |
The above form of creep equation linearly superimposes the strain due to an exponentially decaying function of time (i.e., first term in eqn (1)) with the strain due to a linearly increasing function of time (i.e., second term in eqn (1)) for determining total creep strain. According to eqn (4), the exponential term dominates the behavior at beginning of creep whereas the linear term dominates at longer times. This prediction is consistent with creep behavior shown in Fig. 3.
Taking derivative of eqn (4) with respect to time for creep condition where the applied stress is constant gives the following expression for strain rate:†
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = ab = ab![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−bt) + Aσn exp(−bt) + Aσn
| (5) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 1.2 × 10−5t−0.7 s−1. This results in an infinite strain rate at t = 0, which is physically not possible. Furthermore, eqn (5) also suggests that the initial strain rate will be 1 + ab/c times larger than the steady-state strain rate, providing further physical meaning to creep parameters a and b, and correlating the primary creep strain, exhaustion rate of primary creep and the steady-state creep. Thus, eqn (5) has the elegance of physical interpretation of individual parameters, along with the ability of quantitatively capturing the creep data of CNTF sample with high confidence.
= 1.2 × 10−5t−0.7 s−1. This results in an infinite strain rate at t = 0, which is physically not possible. Furthermore, eqn (5) also suggests that the initial strain rate will be 1 + ab/c times larger than the steady-state strain rate, providing further physical meaning to creep parameters a and b, and correlating the primary creep strain, exhaustion rate of primary creep and the steady-state creep. Thus, eqn (5) has the elegance of physical interpretation of individual parameters, along with the ability of quantitatively capturing the creep data of CNTF sample with high confidence.
4.3 Stress relaxation model for CNTF
As shown in Fig. 3 and 5, both time dependent phenomena (i.e., creep and stress-relaxation) of CNTF show a rapid change in the beginning, followed by a gradual change over long period of time. Hence, mathematical expressions developed for capturing these two should also reflect this similarity. Hence, it is expected that creep model should yield a model suitable for predicting the stress-relaxation behavior also. Below, we transform eqn (4) for stress relaxation condition, i.e., when the applied strain is fixed and the stress evolves with time.Taking derivative of eqn (4) with respect to time for the condition where the applied strain is fixed (i.e., ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 0), but the applied stress evolves with time, we get the following expression:
= 0), but the applied stress evolves with time, we get the following expression:
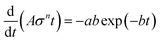 | (6) |
It should be noted that the left hand side of eqn (6) represents the rate of change of steady-state strain. Accordingly, eqn (6) shows that, at any instant, the total strain rate due to the steady-state process is equal in magnitude and opposite in sign to the strain rate due to the primary stage process, thus resulting in a net strain rate of zero. For mathematical simplicity, we can assume the parameters a and b to be independent of the applied stress and hence time. This is a good first order assumption, as these parameters did not show monotonous dependencies on stress (see Fig. 4). Integrating eqn (6) with respect to time between the limits of 0 and current time, t, and then, imposing the initial condition of σnt = 0 when t = 0, and finally, applying L'Hospital's rule for calculating the value of σ as t tends to zero (i.e., σ0), we get the following relationship for stress, σ, as function of σ0 and t:
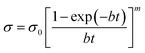 | (7) |
Fig. 5 shows the best-fit curve analysis of the stress-relaxation data for various CNTF samples tested at different compressive strains using eqn (7) and the values of parameters b and m of eqn (7) as well as the curve fitting parameter, R, are shown in Table 2. Fig. 5 clearly shows that, irrespective of values of the applied strain and the electric field, eqn (7) aptly captures the stress-relaxation behavior of CNTF samples tested in this study. However, the values of m (or 1/n) and b as observed from the stress relaxation tests are quite different than those observed in the creep tests. This can be attributed to the significant difference in the strains obtained during creep tests, which were <0.1%, and the stress relaxation tests, which were >10%. Nevertheless, qualitative validation of eqn (7), which has the origin in the creep model, suggests that, as expected, the underlying mechanism for creep and stress-relaxation of CNTF may be the same. Therefore, study of one of these two phenomena can be used to highlight the response in another condition also.
| ε = 10% | ε = 20% | |||||||
|---|---|---|---|---|---|---|---|---|
| b (s−1) | m | σ0 (MPa) | R | b (s−1) | m | σ0 (MPa) | R | |
| W/O E | 2.4 | 0.01 | 2.28 | 0.99 | 1.1 | 0.095 | 5.25 | 0.91 |
| W/E | 19.0 | 0.01 | 1.95 | 1 | 0.68 | 0.012 | 4.83 | 0.95 |
5. Conclusions
CNTF samples show standard power-law creep behavior consisting of a primary stage followed by a steady-state creep regime. Total creep as well as steady-state strain rate increases with stress. The dependence of the steady-state strain rate on the applied stress can be described using standard power-law. CNTF samples also show stress-relaxation, marked by a rapid decrease in the stress at the beginning, followed by a gradual decrease over long period of time. Application of electric field reduces the overall creep strain and the steady-state strain rate, while it increases the stress-relaxation. Stress relaxation decreases with increase in the strain and also the effect of electric field reduces with increase in the compressive strain.Garofalo model for creep, comprising an exponentially decaying term and a linearly increasing term, aptly captures the primary-cum-steady-state creep behavior of CNTF, both in the presence and the absence of electric field. Model for creep can be transformed for stress-relaxation test condition also. This results in an amalgamation of an exponentially decaying term and a power-law term with negative power for predicting variation of stress with time during stress relaxation. Above similitude suggests that the time-dependent phenomena of creep and stress-relaxation in CNTFs can be interpreted using same model.
Acknowledgements
Authors would like to thank Council of Scientific and Industrial Research (CSIR) for financial support (# CSIR 0366).References
- B. Chen, M. Gao, J. M. Zuo, S. Qu, B. Liu and Y. Hunag, Appl. Phys. Lett., 2003, 83, 3570 CrossRef CAS.
- F. A. Hill, T. F. Havel and C. Livermore, Nanotechnology, 2009, 20, 255704 CrossRef CAS PubMed.
- M. F. L. De Volder, S. H. Tawfick, R. H. Baughman and A. J. Hart, Science, 2013, 339, 535 CrossRef CAS PubMed.
- G. Lalwani, A. T. Kwaczala, S. Kanakia, S. C. Patel, S. Judex and B. Sitharaman, Carbon, 2013, 53, 90 CrossRef CAS PubMed.
- K. Fu, O. Yildiz, H. Bhanushali, Y. Wang, K. Stano, L. Xue, X. Zhang and F. D. Bradford, Adv. Mater., 2013, 25, 5109 CrossRef CAS PubMed.
- F. A. Hill, T. F. Havel, D. Lashmore, M. Schauer and C. Livermore, Energy, 2014, 76, 318 CrossRef CAS.
- B. N. Shivananju, S. Asokan and A. Misra, J. Phys. D: Appl. Phys., 2015, 48, 275502 CrossRef.
- P. Gowda, S. Mukherjee, S. K. Reddy, R. Ghosh and A. Misra, RSC Adv., 2015, 5, 26157 RSC.
- A. Cao, P. L. Dickrell, W. G. Sawyer, M. N. Ghasemi-Nejhad and P. M. Ajayan, Science, 2005, 310, 1307 CrossRef CAS PubMed.
- K. M. Liew, C. H. Wong and M. J. Tan, Appl. Phys. Lett., 2005, 87, 041901 CrossRef.
- V. R. Coluci, A. F. Fonseca, D. S. Gavlvao and C. Daraio, Phys. Rev. Lett., 2008, 100, 086807 CrossRef CAS PubMed.
- Y. Li and M. Kroger, Carbon, 2012, 50, 1793 CrossRef CAS.
- J. R. Raney, F. Fraternalli, A. Amendola and C. Daraio, Comput. Struct., 2011, 93, 3013 CrossRef.
- Z. Zeng, X. Gui, Q. Gan, Z. Lin, Y. Zhu, W. Zhang, R. Xiang, A. Cao and Z. Tang, Nanoscale, 2014, 6, 1748 RSC.
- A. Misra, J. R. Greer and C. Daraio, Adv. Mater., 2008, 20, 1 CrossRef.
- S. Pathak, E. J. Lim, P. P. S. S. Abadi, S. Graham, B. A. Cola and J. R. Greer, ACS Nano, 2012, 6, 2189 CrossRef CAS PubMed.
- P. P. S. S. Abadi, M. R. Maschmann, S. M. Mortuza, S. Banerjee, J. W. Baur, S. Graham and B. A. Cola, Carbon, 2014, 69, 178 CrossRef.
- P. Jagtap, S. K. Reddy, D. Sharma and P. Kumar, Carbon, 2015, 95, 126 CrossRef CAS.
- P. M. F. J. Costa, K. S. Coleman and M. L. H. Green, Nanotechnology, 2005, 16, 512 CrossRef CAS.
- S. K. Reddy, A. Suri and A. Misra, Appl. Phys. Lett., 2013, 102, 241919 CrossRef.
- A. Misra, P. Kumar, J. R. Raney, A. Singhal, L. Lattanji and C. Daraio, Appl. Phys. Lett., 2014, 104, 221910 CrossRef.
- S. Reddy, A. Mukherjee and A. Misra, Appl. Phys. Lett., 2014, 104, 261906 CrossRef.
- P. Jagtap, P. Gowda, B. Das and P. Kumar, Carbon, 2013, 60, 169 CrossRef CAS.
- P. Jagtap and P. Kumar, Rev. Sci. Instrum., 2014, 85, 113903 CrossRef PubMed.
- S. Reddy and A. Misra, J. Phys. D: Appl. Phys., 2015, 48, 265301 CrossRef.
- M. Xu, D. N. Futaba, T. Yamada, M. Yumura and K. Hata, Science, 2010, 330(6009), 1364 CrossRef CAS PubMed.
- Q. Zhang, Y. C. Lu, F. Du, L. Dai, J. Baur and D. C. Foster, J. Phys. D: Appl. Phys., 2010, 43, 315401 CrossRef.
- M. Xu, D. N. Futaba, M. Yumura and K. Hata, Adv. Mater., 2011, 23, 3686 CrossRef CAS PubMed.
- A. Qiu, S. P. Fowler, J. Jiao, D. Kiener and D. F. Bahr, Nanotechnology, 2011, 22, 295702 CrossRef CAS PubMed.
- M. Xu, D. N. Futaba, M. Yumura and K. Hata, Nano Lett., 2011, 11, 3279 CrossRef CAS PubMed.
- L. Lattanzi, J. R. Raney, L. De Nardo, A. Misra and C. Daraio, J. Appl. Phys., 2012, 111, 074314 CrossRef.
- K. Eom, K. Nam, H. Jung, P. Kim, M. S. Strano, J. H. Han and T. Kwon, Carbon, 2013, 65, 305 CrossRef CAS.
- A. Misra and P. Kumar, Nanoscale, 2014, 6, 13668 RSC.
- H. Radhakrishnan, S. D. Mesarovic, A. Qiu and D. F. Bahr, Int. J. Solids Struct., 2013, 50, 2224 CrossRef CAS.
- S. D. Mesarovic, C. M. McCarter, D. F. Bahr, H. Radhakrishnan, R. F. Richards, C. D. Richards, D. McClain and J. Jao, Scr. Mater., 2007, 56, 157 CrossRef CAS.
- A. Misra, J. R. Raney, A. E. Craig and C. Daraio, Nanotechnology, 2011, 22, 425705 CrossRef CAS PubMed.
- W. Guo and Y. Guo, Phys. Rev. Lett., 2003, 91, 115501 CrossRef PubMed.
- M. E. Kassner, Fundamentals of Creep in Metals and Alloys, Elsevier Science, 2nd edn, 2009 Search PubMed.
- I. M. Ward and J. Sweeney, An Introduction the Mechanical Properties of Solid Polymers, John Wiley & Sons, Ltd, 2nd edn, 2004 Search PubMed.
- F. Garofalo, C. Richmond, W. F. Domis and F. Gemmingen, in Proc. Joint Int. Conf. Creep, Inst. Mech. Eng., London, 1963, vol. 178, p. 31 Search PubMed.
- R. W. Evans and B. Wilshire, Creep of Metals and Alloys, The Institute Metals, London, UK, 1985 Search PubMed.
- H. Margenau, Rev. Mod. Phys., 1939, 11, 1 CrossRef CAS.
- I. E. Dzyaloshinskii, E. M. Lifshitz and L. P. Pitaevskii, Usp. Fiz. Nauk, 1961, 73, 381 CrossRef CAS.
Footnote |
| † It should be noted that at small strains, as incurred during the creep experiments in this study, the values of true strain and nominal (or engineering) strain as well as true stress and nominal stress can be assumed to be equal. Therefore, form of eqn (5) will be the same for both true stress–strain and nominal stress–strain cases. |
| This journal is © The Royal Society of Chemistry 2016 |