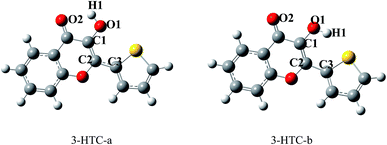Ab initio study of the excited-state proton transfer mechanisms for 3-hydroxy-2-(thiophen-2-yl)chromen-4-one

Abstract

The optical absorption properties and fluorescence properties of 3-hydroxy-2-(thiophen-2-yl)chromen-4-one (3-HTC) were simulated by the time-dependent density functional theory (TDDFT) method. The experimental absorption spectrum and fluorescence spectrum were reproduced well by the calculated vertical excitation energies of 3-HTC-a, which corresponds to the intramolecular hydrogen bond O2⋯H1–O1. The excited state intramolecular proton transfer (ESIPT) mechanism of 3-HTC has been systematically investigated. The constructed potential energy curves (PECs) of 3-HTC-a in the S₀ and S₁ states indicate that, after photo-excitation, the intramolecular proton transfer reaction with the H1 atom moving from O1 to O2 occurs more readily in both the dynamics and thermodynamics aspects. In sharp contrast, the weak S⋯H1–O1 bond in 3-HTC-b was weakened in the S₁ state compared with that in the S₀ state, suggesting that the ESIPT process is forbidden. For the first time, it is found that the strong hydrogen bond is further strengthened and the weak hydrogen bond is further weakened in the excited state of 3-HTC. Moreover, the vibrational frequencies of the C=O and O–H groups involved in the hydrogen bonds were also studied, and a more clear-cut signature of the hydrogen-bonding dynamics of 3-HTC is provided in this work.

---

Introduction

The hydrogen bond, one of the most significant weak interactions, is ubiquitous in the natural world and plays an important role in many branches of the natural science and engineering fields. It is operative in the crystallization of material, the formation of specific properties of associated liquids, and the determination of the three-dimensional structures adopted by biomolecules such as proteins and nucleic bases.^1–5 A double effect of hydrogen bonds has been found in biological systems. As a collectively strong directional interaction, the hydrogen bond can lead to relatively stable supramolecular structures; however, it can also serve as an active site for initiating a plethora of chemical reactions due to the dynamic features of the proton.⁵ Therefore, intensive study of hydrogen bond interactions is vital to elucidate many phenomena occurring not only in crystal packing, but also in solution and biological processes.

Actually, many different mechanisms of photochemical reactions and photophysical processes can be greatly clarified via hydrogen bond interactions, such as intramolecular charge transfer (ICT), photo-induced electron transfer (PET), fluorescence quenching, and excited state proton transfer (ESTP). In particular, excited state intramolecular proton transfer (ESITP) has received enormous attention during the past half century; interest in ESITP has been revitalized recently due to its potential applications in optoelectronics, bio-imaging and sensing. ESIPT molecules possess an intramolecular hydrogen bond between the proton donor and proton acceptor from which proton transfer takes place upon photoexcitation, resulting in an isomer that is dubbed a proton-transfer tautomer or phototautomer. Due to the drastic structural alteration, the phototautomer possesses different photophysical properties than the original (normal) species, offering great versatility in a variety of applications, such as lasing materials, UV photostabilizers, optical filters, radiation scintillators, and molecular recognition.⁶

As a class of typical molecules that undergo ESIPT, 3-hydroxychromone and its derivatives (3-HCs) are a unique kind of flavonoid composed of fused phenyl and pyranyl rings. 3-HCs are mainly found in a wide variety of natural sources and are known to affect various biological processes, including the development of cancer, platelet aggregation, detoxification, and inflammatory and immune responses.⁷ 3-HCs have attracted considerable interest in recent years due to their photochemistry and potential applications, especially as molecular probes, based on their spectrally separated dual fluorescence.^8–13 Luthman et al. synthesized and characterized a series of 3-hydroxychromone derivatives with strong fluorescence for live-cell imaging.¹⁰ Diller et al. studied the ESIPT and photodissociation of 3-hydroxychromone in solution, and static and femtosecond time-resolved spectroscopy were used to identify and characterize the elementary processes and intermediate states in the photocycle of 3-HC.¹¹ Tomin and Ushakou investigated the effect of salt ions on the ESIPT rate of 3-hydroxyflavone. The results clearly showed that the salt ions can modulate intramolecular proton transfer in the excited state and then lead to increases in the short wavelength, band intensity and fluorescence quantum yield of 3-hydroxyflavone.¹² Recently, another important intermediate, 3-hydroxy-2-(thiophen-2-yl)chromen-4-one (3-HTC), was designed and reported by Chou et al.;¹³ the absorption and emission spectra were studied in acetonitrile and in the relatively low polarity solvents CH₂Cl₂ and benzene. However, spectroscopic techniques, such as time resolved fluorescence spectroscopy, provide only indirect information about the photo-physical properties and geometries of compounds. As such, it is difficult to extract information from experiments alone; much effort has been made to complement experiment by theory to better understand the mechanisms and fundamental aspects of hydrogen bond formation in different electronic states. Therefore, it is very urgent to study the nature of 3-HTC in detail. In order to give a clear and detailed picture of this proton transfer mechanism, in this work, we were motivated to theoretically study the ground state and excited states of the molecule 3-HTC that are relevant to the hydrogen transfer mechanism using density functional theory (DFT) and time-dependent density functional theory (TDDFT) methods, respectively. Geometric optimizations of 3-HTC with two types of intramolecular hydrogen bonds (O2⋯H1–O1 and S⋯H1–O1) were performed. We further calculated and analyzed the electronic spectra, Frontier molecular orbitals, and homologous ground-state (S₀) and first excited state (S₁) potential energy curves (PECs) of 3-HTC to provide direct information on the ESIPT process. Additionally, the infrared spectra at both the C=O and O–H stretching vibrational regions of the 3-HTC molecule were investigated.

Computational methods

In the present work, all electronic structure calculations were carried out with the Gaussian 09 program suite.¹⁴ Geometry optimizations of the S₀ state and the S₁ state of 3-HTC were implemented using the DFT method and TDDFT methods, respectively. Previous studies have proven that the TDDFT method is a useful tool to describe hydrogen bonding in the excited states of possible hydrogen bond systems;^15,16 the Becke's three-parameter hybrid exchange functional with Lee–Yang–Parr gradient-corrected correlation (B3LYP functional)¹⁷ and triple-zeta valence quality with one set of polarization functions (TZVP)¹⁸ is the appropriate functional and basis set for most organic compounds.^19–22 Recently, Guerra and co-workers computationally investigated the structure and stability of DNA base pairs, and their results indicated that the dispersion-corrected DFT method performed well to study the hydrogen bonding and solvation effects in DNA.^23–25 In order to validate the accuracy of the theoretical method, a test with a series of functionals and basis sets (B3LYP/TZVP, B3LYP-D3BJ/TZVP and CAM-B3LYP/def2-qzvpd) was performed for 3-HTC-a and 3-HTC-b. For the ground state, the geometry structures optimized using B3LYP-D3BJ/TZVP are very similar to those obtained with the B3LYP/TZVP (see Tables 1 and S1†); also, the UV-Vis spectra established that these structures are nearly the same, as shown in Fig. 2a and S1 in the ESI,† which suggests that the dispersion effect has no obvious influence on the calculation results. Moreover, by using 3-HTC-a and 3-HTC-b as a reference set, the performances of B3LYP/TZVP and CAM-B3LYP/def2-qzvpd were compared; the B3LYP/TZVP results are in better agreement with the experimental reference data of Tseng et al. (see Fig. 2b and S2b in the ESI†). Therefore, we selected B3LYP/TZVP for both the DFT and TDDFT calculations. The self-consistent field (SCF) convergence thresholds of the energy for both the ground state and excited state optimization used the default setting (10⁻⁶). Harmonic vibrational frequencies in both the ground state and excited state were determined by diagonalization of the Hessian. The excited state Hessian was obtained by numerical differentiation of analytical gradients using central differences and default displacements of 0.02 Bohr. The infrared intensities were determined from the gradients of the dipole moment.²⁶ The geometry optimizations were performed without constraints on bond lengths, angles, or dihedral angles except when constructing the PECs. The S₀ and S₁ PECs of 3-HTC were scanned by constrained optimizations to obtain the thermodynamic corrections in the corresponding electronic state, and the O–H distance was maintained at a fixed series of values. All the local minima were confirmed by the absence of an imaginary mode in vibrational analysis calculations. To evaluate the solvent effects, CH₂Cl₂ was selected as the solvent in the calculations using the conductor-like screening model (COSMO) method²⁷ in the Gaussian 09 program.

Table 1 Calculated bond lengths (Å), angles and dihedral angles of the 3-HTC-a and 3-HTC-b structures of the S₀ states in vacuum and in CH₂Cl₂, as well as the S₁ states in vacuum, at the B3LYP/TZVP level

Molecule	O1–H1		O2–H1		S–H1		O1–H1–O2/S		C1–C2–C3–S
	S0	S1	S0	S1	S0	S1	S0	S1	S0	S1
3-HTC-a	0.978	1.003	2.046	1.831	3.832	3.935	117.5	124.4	0.0	0.0
3-HTC-b	0.967	0.967	3.627	3.516	2.424	2.535	126.6	108.5	28.6	12.9
3-HTC-a (CH2Cl2)	0.977	—	2.064	—	3.831	—	116.8	—	0.0	—
3-HTC-b (CH2Cl2)	0.968	—	3.622	—	2.455	—	125.0	—	30.5	—

---

Results and discussion

1 Geometric structures

From the molecular structures of 3-HTC, we speculated that two types of intramolecular hydrogen bond might exist: that is, the normal hydrogen bond O2⋯H1–O1 and the weak hydrogen bond S⋯H1–O1. These two structures were optimized using the DFT and TDDFT methods in the ground state and excited state, respectively. As shown in Fig. 1, 3-HTC-a represents the first type of intramolecular hydrogen bond, while 3-HTC-b represents the second type of intramolecular hydrogen bond. We numerically labeled the atoms connected to the hydrogen bonds to describe them more clearly. For the ground state S₀, the calculated bond length, bond angle and dihedral angle are listed in Table 1. The optimized results of 3-HTC-a showed that the O1–H1 bond length was 0.978 Å and that of O2⋯H1 was 2.046 Å, which indicated the formation of a typical intramolecular hydrogen bond (O2⋯H1–O1). The inter-ring torsion angle (dihedral angle C1–C2–C3–S) of 3-HTC-a was below the measurement accuracy (<0.1°), which suggests that the whole molecule is quasi-planar. For the 3-HTC-b molecule, we can see that the bond length of O1–H1 is 0.967 Å, slightly shorter than that in 3-HTC-a, which indicates a relatively weak interaction between H atom and S atom due to the lower electronegativity of S atom compared to O atom. The S⋯H distance is about 2.424 Å, which is much longer than the O2⋯H1 bond length but significantly shorter than the sum of the van der Waals radii of the S and H atoms (2.90 Å). Therefore, an intramolecular hydrogen bond or analogous intramolecular hydrogen bond can be formed between the S and H atoms, although this hydrogen bond is much weaker than the O2⋯H1 bond. Additionally, the inter-ring dihedral angle of 3-HTC-b is greater than 10°, suggesting that the planarity of the whole molecule is significantly disrupted; this may induce high molecular energy and poor stability compared with 3-HTC-a. The energy calculations of the 3-HTC-a and 3-HTC-b molecules using the B3LYP/TZVP sets show that the energy of 3-HTC-b is about 10.63 kcal mol⁻¹ higher than that of 3-HTC-a under vacuum conditions, which is consistent with our structural analysis. It is noteworthy that the energy difference between the 3-HTC-a and 3-HTC-b molecules could be effectively reduced by solvent effects, as discussed below.

Fig. 1 Optimized structures of 3-HTC-a and 3-HTC-b.

In order to investigate the solvent effects on the intramolecular hydrogen bonds and conveniently compare our findings with available experimental results,¹³ dichloromethane was used in the conductor-like screening model of solvation. The related structure parameters of the stable structures are also collected in Table 1. It can be seen that the O2–H1 length of 3-HTC-a in CH₂Cl₂ changed to 2.064 Å, slightly longer than the bond length in vacuum. As for 3-HTC-b, the length of S–H1 increased from 2.424 Å in vacuum to 2.455 Å in CH₂Cl₂. In comparison, the solvent effect of CH₂Cl₂ has little influence on the bond angle and the inter-ring dihedral angles of 3-HTC-a and 3-HTC-b. As shown in Table 1, the variations in the bond angles and dihedral angles were less than 2°. The geometry variations in the 3-HTC-a and 3-HTC-b molecules indicate that the intramolecular hydrogen bond was weakened due to the effects of CH₂Cl₂. This may be related to stabilization of the lone pairs involved in these bonds.²³ Furthermore, the energies of 3-HTC-a and 3-HTC-b in CH₂Cl₂ were calculated. It was found that the energies of 3-HTC-a and 3-HTC-b decreased by 4.87 kcal mol⁻¹ and 7.82 kcal mol⁻¹, respectively, compared with the energies in vacuum. This indicates that the solvent effect apparently lowered the molecular energies, especially for the 3-HTC-b molecule. Thus, we believe that two hydrogen bonding mechanisms may coexist under some extreme conditions.

The excited-state structures of 3-HTC-a and 3-HTC-b were also optimized, and the related structure parameters are shown in Table 1. Comparison of the geometry structures in the exited state and in the ground state shows that the geometry of 3-HTC-a retains its planar structure in the transition from S₀ to S₁. However, the bond length of O1–H1 increases and the bond length of O2⋯H1 decreases. In addition, the bond angle (∠O1–H⋯O2) of 3-HTC-a changes from 117.54° in the S₀ state to 124.38° in the S₁ state. Hence, the bond angle in the S₁ state is closer to 180° than that in the S₀ state. All these structural variations suggest that the intramolecular hydrogen bond O2⋯H1–O1 in the S₁ state is stronger than that in the ground state, which is consistent with the ESIPT process observed experimentally by Chou et al.¹³ Interestingly, the intramolecular hydrogen bond (S⋯H1–O1) of 3-HTC-b is weakened during the photo-excited process, which is quite different from the case of O2⋯H1–O1. As shown in Table 1, the bond length of S⋯H1 in 3-HTC-b changed from 2.424 Å to 2.535 Å, and the angle decreased from 126.56° to 108.54°. From the above analysis, we can conclude that the ESIPT process may be forbidden in the weak hydrogen bond S⋯H1–O1.

2 Electronic spectra and Frontier molecular orbitals

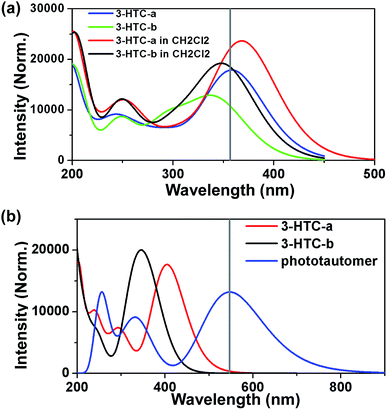
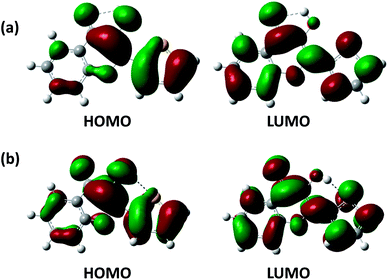
Herein, we firstly calculated the UV-Vis absorption spectra of 3-HTC-a and 3-HTC-b in vacuum and in CH₂Cl₂ solution according to the above optimized geometries. In order to validate our theoretical method, we compared the calculated absorption spectra in CH₂Cl₂ with the experimental data. As shown in Fig. 2a, the calculated maximum absorption bands of 3-HTC-a and 3-HTC-b in CH₂Cl₂ are located at 369 nm and 352 nm, respectively. Considering the fact that the energy of 3-HTC-a is about 7.69 kcal mol⁻¹ lower than that of 3-HTC-b, we could conclude that 3-HTC-a is the main conformation and contributes predominately to the formation of the experimental absorption spectra; thus, the calculated absorption peaks of 3-HTC-a can be used for comparison with the corresponding experimental absorption peaks. Chou et al. reported that the maximum absorption band is observed in the near-UV region and is represented by the peak at 357 nm for 3-HTC in CH₂Cl₂, which is in agreement with our calculation results for 3-HTC-a. Moreover, the fluorescence spectra of 3-HTC-a and 3-HTC-b were also simulated, and the results are shown in Fig. 2b. The excited state fluorescence maximum of 3-HTC-a is located at 405 nm, which agrees well with the weak band (∼410 nm) observed experimentally. The red-shift of 46 nm should be ascribed to the normal Stokes shift. At the same time, another large Stokes-shifted fluorescence with a peak at 547 nm, which originates from the proton transfer phototautomer emission, was also found; its position is consistent with the phototautomer emission band (539 nm) determined experimentally. The much greater strength of the emission peak located at 539 nm compared to the one located at 410 nm in experimental spectra suggests that fast ESIPT takes place during the photoexcitation process. For 3-HTC-b, the dual fluorescence bands do not appear in the time-resolved fluorescence spectra due to the forbidden ESIPT. The emission maximum of 3-HTC-b is located at 347 nm, which is attributed to the normal emission, and only a very small red-shift relative to the absorption peak is observed.

Fig. 2 (a) Calculated UV-Vis absorption spectra of 3-HTC-a and 3-HTC-b in vacuum (blue and green lines) and in CH₂Cl₂ (red and black lines); (b) the fluorescence spectra of 3-HTC-a (red line), the phototautomer of 3-HTC-a (blue line), and 3-HTC-b (black line) based on the B3LYP/TZVP level. The cross vertical line shows the experimental data in CH₂Cl₂.

To deeply understand the spectral character, the exited states and the Frontier molecular orbitals (FMOs) of the two molecular structures were analyzed in detail; these can provide information about the nature of the excited state conformations and qualitative discussion of the charge distribution and charge transfer. As shown in Table 2, our theoretical calculations show that an intense S₀ → S₁ transition of 3-HTC-a exists at 369.24 nm with an oscillator strength of 0.4345. The first singlet excited (S₁) state of 3-HTC-a is dominantly formed by the transitions from the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO). The HOMO and LUMO of 3-HTC-a are shown in Fig. 3a. It is evident that the HOMO distribution localized on the hydrogen bond O2⋯H1–O1 is quite different from the LUMO distribution. This difference indicates that the S₁ state corresponding to the HOMO–LUMO transition should have intramolecular charge-transfer (ICT) character. Further analysis of these FMOs, shown in Fig. 3a, shows that the O1–H1 bond contributes to the HOMO in a bonding fashion, while the LUMO localized on the O1–H1 bond has a strong nonbonding character. This variation of charge distribution inevitably induces changes in bond order and alters bond lengths. Considering the relationship between the local bonding character and bond order,²⁸ it is easy to understand the increase of the O1–H1 bond length in the exited state. Also, the charge distribution localized on C=O changes slightly during the photo-excitation process. As shown in Fig. 3a, the percentage of antibonding character is obviously larger in the LUMO than in the HOMO, which contributes to the longer C=O bond length in the S₁ state than in the S₀ state. In addition, it should be noted that the H1 atom was completely naked in the S₁ state, which effectively improves its electron-accepting ability; thus, the interaction between the H1 and O2 atoms is enhanced after photoexcitation to the S1 state. Our analysis of the shapes of the FMOs greatly rationalizes the hydrogen bond enhancement in the exited state.

Table 2 Electronic excitation energies (nm), oscillator strengths, and corresponding compositions for 3-HTC-a and 3-HTC-b in vacuum and in CH₂Cl₂ and for the phototautomer of 3-HTC-a in vacuum

	Transition	λ (nm)	f	Composition	CI
3-HTC-a	S0 → S1	359.4	0.4345	H → L	96.9%
Phototautomer of 3-HTC-a	S0 → S1	547.2	0.3258	H → L	100%
	S0 → S3	348.7	0.1388	H−2 → L	81.5%
3-HTC-b	S0 → S2	342.8	0.2630	H → L	83.7%
	S0 → S3	295.9	0.1993	H−1 → L	47.5%
				H−2 → L	48.2%
	S0 → S8	251.6	0.1104	H → L+2	81.8%
3-HTC-a (CH2Cl2)	S0 → S1	369.2	0.5750	H → L	97.9%
	S0 → S2	308.7	0.1274	H−1 → L	95.4%
3-HTC-b (CH2Cl2)	S0 → S1	352.0	0.4407	H → L	97.1%
	S0 → S3	303.1	0.1833	H−1 → L	93.8%

---

Fig. 3 HOMO and LOMO features of 3-HTC-a (a) and 3-HTC-b (b) obtained from DFT/B3LYP/TZVP calculations, respectively.

Meanwhile, the molecular orbitals of 3-HTC-b have also been calculated, and the shapes of the FMOs are shown in Fig. 3b. It can be seen that an intense S₀ → S₁ transition for 3-HTC-b is predicted at about 352 nm with a large oscillator strength of 0.4407; specific information can be found in Table 2. Similar to 3-HTC-a, the S₀ → S₁ transition can be described as a predominantly ππ*-type transition from the HOMO to the LUMO. From Fig. 3b, we can also see that the HOMO localized on the C2–C3 bond shows a strong antibonding character, while the LUMO shows an obvious bonding character, which suggests that C2 and C3 are inclined to form a single bond in the ground state and to form a double bond in the exited state. This provides a good explanation for the larger dihedral angles (C1–C2–C3–S) in the ground state (28.57°) than in the exited state (12.90°). Moreover, it should be noted that there is a vertical node at right angles in the LUMO localized on S⋯H1–O1, which increases the distances between S and O1; thus, the hydrogen bond S⋯H1–O1 is weakened to some extent.

3 Potential energy curves

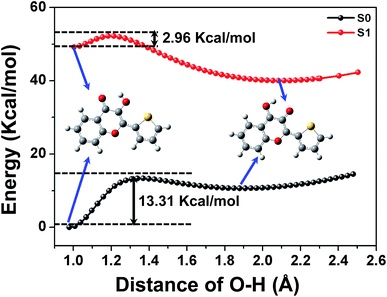
The construction of potential curves is an effective method for investigating molecular properties and hydrogen transfer reactions; PECs can provide more intuitive information about the ESIPT process. Herein, the calculations of PECs were performed using the constrained optimizations in the S₀ state and S₁ state geometrical structures along with the fixed O1–H1 bond length at the (TD) DFT/B3LYP/TZVP level. The constructed PECs in the S₀ and S₁ states as functions of the O1–H1 length were fixed at values in the range from 0.96 Å to 2.5 Å (see Fig. 4). Previous work has indicated that the TDDFT/B3LYP method is reliable for the determination of qualitative energetic pathways for intramolecular proton-transfer processes, although this method may not be expected to be sufficiently accurate in yielding the correct ordering of the closely spaced excited states.^{15,16,19–22}

Fig. 4 Potential energy curves of the S₀ and S₁ states of 3-HTC-a as a function of O–H bond length.

As shown in Fig. 4, we can see clearly that the energy of the S₀ state increases as the O1–H1 bond lengthens from its stable structure, producing a potential barrier of 13.31 kcal mol⁻¹. This indicates that the ground state intramolecular proton transfer (GSIPT) process is difficult due to the high potential barrier in the process of the transfer of proton H1 from O1 to O2. In terms of thermodynamics, GSIPT of 3-HTC-a is an endothermic reaction and ΔH = 10.63 kcal mol⁻¹, which indicates that the energy of the molecular system is improved by 10.63 kcal mol⁻¹ after the process of the transfer of proton H1 from O1 to O2 in the S₀ state. Therefore, the GSIPT process is unfavorable from the dynamics and thermodynamics points of view. In comparison, a barrier of only 2.96 kcal mol⁻¹ is exhibited between the excited state equilibrium geometry of 3-HTC-a and its stable proton transfer phototautomer. Therefore, we can conclude that the intramolecular proton transfer process of 3-HTC is more likely to occur in the S₁ state from the point of view of dynamics. Also, the ESIPT process is an exothermic reaction, and the energy of the molecular systems decreased by 9.20 kcal mol⁻¹ after the process of the transfer of proton H1 from O1 to O2. Therefore, the intramolecular proton transfer can easily occur in the excited state.

4 Infrared spectra

It is well known that the vibrational frequencies of the stretching vibrations of C=O and O–H groups involved in hydrogen bonds can provide a clear-cut signature of the hydrogen-bonding dynamics. Herein, the infrared spectra (IR) spectra of 3-HTC in the ground state (S₀) and in the single excited state (S₁) were calculated using the (TD) DFT method. The vibrational spectra of 3-HTC in the conjunct vibrational regions of the O–H and C=O stretching modes can be seen in Fig. 5. The calculated O1–H1 stretching vibrational frequency of the molecule 3-HTC-a in the S₀ state is located at 3583 cm⁻¹, and it moves to 3176 cm⁻¹ in the S₁ state. A strong red-shift of 407 cm⁻¹ for the O1–H1 stretching band can be driven by changes in the local charge distribution because the electronic state hopping from the S₀ state to the S₁ state is followed by the intramolecular charge redistribution in the S₁ state of 3-HTC-a, as discussed in the Electronic spectra and Frontier molecular orbitals section.

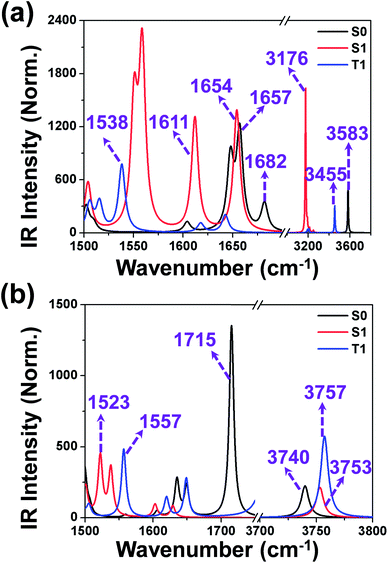Fig. 5 The calculated IR spectra of 3-HTC-a (a) and 3-HTC-b (b) for the ground state (S₀) and single excited state (S₁) in the spectral region of the O–H and C=O strengthening bands.

For the 3-HTC-b molecule, the vibration mode of the intramolecular hydrogen bond O1–H1 is blue shifted from 3753 cm⁻¹ in the S₁ state to 3740 cm⁻¹ in the S₀ state, which is opposite to the previous changes of the O1–H1 stretching band in 3-HTC-a. According to the effective rule for verifying the changes in hydrogen bonds in the excited state proposed by Han,^4,29,30 we can conclude that the intramolecular hydrogen bond O1–H1⋯O2 is strengthened in the excited state through an electronic spectral redshift, and the intramolecular hydrogen bond O1–H1⋯S is weakened in the excited state through an electronic spectral blueshift. This conclusion is consistent with our frontal structural analysis.

For the convenience of our discussion about the influence of hydrogen bonds on the vibrational mode of C=O bonds, the infrared spectra of the C=O bonds in the 3-HTC-a and 3-HTC-b molecules were investigated for comparison. As shown in Fig. 5, it can be clearly seen that the calculated C=O stretching vibrational frequency in the S₀ state is located at 1715 cm⁻¹ in the 3-HTC-b molecule, and it changes to 1682 cm⁻¹ and 1657 cm⁻¹ in 3-HTC-a due to the formation of the intramolecular hydrogen bond (O1–H1⋯O2). This indicates that the hydrogen bond could effectively weaken the bond order of C=O due to the strong interaction between H1⋯O2, as can also be seen from the slightly longer C=O bond length in 3-HTC-a (1.24 Å) than that in 3-HTC-b (1.22 Å). According to Hooke's rule 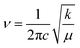(c denotes the velocity of light, k denotes the force constant, and μ denotes the reduced mass), it is easy to understand the observation that the vibration frequency red shifts with the decrease of the force constant of the carbonyl. Furthermore, we also analyzed the influence of different electronic states on the vibrational mode of the C=O bond. As shown in Fig. 5, the calculated C=O stretching vibrational frequencies in the S₁ state are located at 1611 cm⁻¹ and 1654 cm⁻¹, separately, corresponding to the symmetric and antisymmetric stretching vibrations in 3-HTC-a; these frequencies are strongly upshifted by 46 cm⁻¹ and 28 cm⁻¹, respectively, compared with that in the S₀ state. That is to say, the C=O stretching mode undergoes a large redshift which is induced by the strengthening of the intramolecular hydrogen bond in the excited state. This is consistent with previous analysis results showing that the hydrogen bond is strengthened in the exited state.

Conclusion

In summary, the optical absorption properties and fluorescence properties of 3-HTC were systematically investigated by the time-dependent density functional theory method. The experimental absorption spectrum was well reproduced by the calculated vertical excitation energies of 3-HTC-a, which correspond to the intramolecular hydrogen bond O2⋯H1–O1. Also, we predicted the dual fluorescence behavior of the fluorescence spectrum of 3-HTC, which is in good agreement with experimental results. One of the fluorescence maxima at 405 nm (∼410 nm) is attributed to normal emission; the other fluorescence maximum at 547 nm (539 nm) originates from the proton transfer phototautomer emission. The excited state intramolecular proton transfer (ESIPT) mechanism of 3-HTC has been investigated in detail. Upon excitation, the intramolecular hydrogen bond O2⋯H1–O1 was significantly strengthened in the S₁ state, which provides a driving force to effectively facilitate the proton transfer process. The constructed potential energy curves (PECs) of 3-HTC-a in the S₀ and S₁ states further confirm that, after photo-excitation, the IPT reaction occurs more readily, with the H1 atom moving from O1 to O2, in both the dynamics and thermodynamics aspects. In sharp contrast, the weak hydrogen bond S⋯H1–O1 in 3-HTC-b was weakened in the S₁ state compared with that in the S₀ state, suggesting that the ESIPT process is forbidden. For the first time, it was found that the strong hydrogen-bond is further strengthened and the weak hydrogen-bond is further weakened in the excited state of 3-HTC. Based on the FMOs analysis, the local bonding character correlated with the local structural adjustment were discussed, which rationalizes the changes in hydrogen bonds and geometric structures of 3-HTC. Moreover, the vibrational frequencies of C=O and O–H groups involved in hydrogen bonds were also studied, and a more clear-cut signature of the hydrogen-bonding dynamics of 3-HTC were provided in this work.

Acknowledgements

This work was supported by the National Science Foundation of China (Grant No. 21503034, 81601825), Fundamental Research Funds for the Central Universities (Grant No. DC15013705), Program for Science and Technology Project of Liaoning Province (Grant No. 201601237), Educational Committee Foundation of Liaoning Province (Grant No. L2015150), and the Initial Funds for Imported Talents' Research Projects, Dalian Nationalities University (Grant No. 20136131).

References

1. A. G. Slater, L. M. A. Perdigao, P. H. Beton and N. R. Champness, Acc. Chem. Res., 2014, 47, 3417–3427.
2. Y. Takezawa and M. Shionoya, Acc. Chem. Res., 2012, 45, 2066–2076.
3. M. Egli, Acc. Chem. Res., 2012, 45, 1237–1246.
4. G.-J. Zhao and K.-L. Han, Acc. Chem. Res., 2012, 45, 404–413.
5. L. Sobczyk, S. J. Grabowski and T. M. Krygowski, Chem. Rev., 2005, 105, 3513–3560.
6. V. S. Padalkar and S. Seki, Chem. Soc. Rev., 2016, 45, 169–202.
7. S. Gunduz, A. C. Goren and T. Ozturk, Org. Lett., 2012, 14, 1576–1579.
8. S. Basu, S. Mondal and D. Mandal, J. Chem. Phys., 2010, 132, 034701.
9. A. P. Demchenko, K.-C. Tang and P.-T. Chou, Chem. Soc. Rev., 2013, 42, 1379–1408.
10. C. Dyrager, A. Friberg, K. Dahlen, M. Friden-Saxin, K. Borjesson, L. M. Wilhelmsson, M. Smedh, M. Grotli and K. Luthman, Chem.–Eur. J., 2009, 15, 9417–9423.
11. K. Chevalier, A. Gruen, A. Stamm, Y. Schmitt, M. Gerhards and R. Diller, J. Phys. Chem. A, 2013, 117, 11233–11245.
12. V. I. Tomin and D. V. Ushakou, J. Appl. Spectrosc., 2015, 82, 193–199.
13. H.-W. Tseng, J.-Y. Shen, T.-Y. Kuo, T.-S. Tu, Y.-A. Chen, A. P. Demchenko and P.-T. Chou, Chem. Sci., 2016, 7, 655–665.
14. G. W. T. M. J. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford CT, 2009.
15. G.-Y. Li and T. Chu, Phys. Chem. Chem. Phys., 2011, 13, 20766–20771.
16. G.-Y. Li, G.-J. Zhao, Y.-H. Liu, K.-L. Han and G.-Z. He, J. Comput. Chem., 2010, 31, 1759–1765.
17. C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
18. O. Treutler and R. Ahlrichs, J. Chem. Phys., 1995, 102, 346–354.
19. J. Zhao, J. Chen, Y. Cui, J. Wang, L. Xia, Y. Dai, P. Song and F. Ma, Phys. Chem. Chem. Phys., 2015, 17, 1142–1150.
20. J. Zhao, J. Chen, J. Liu and M. R. Hoffmann, Phys. Chem. Chem. Phys., 2015, 17, 11990–11999.
21. J. Zhao and P. Li, RSC Adv., 2015, 5, 73619–73625.
22. J. Zhao, H. Yao, J. Liu and M. R. Hoffmann, J. Phys. Chem. A, 2015, 119, 681–688.
23. J. Poater, M. Swart, C. F. Guerra and F. M. Bickelhaupt, Comput. Theor. Chem., 2012, 998, 57–63.
24. J. Poater, M. Swart, F. M. Bickelhaupt and C. F. Guerra, Org. Biomol. Chem., 2014, 12, 4691–4700.
25. J. Poater, M. Swart, C. F. Guerra and F. M. Bickelhaupt, Chem. Commun., 2011, 47, 7326–7328.
26. F. Furche and R. Ahlrichs, J. Chem. Phys., 2002, 117, 7433–7447.
27. A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805.
28. Y. C. Chang and I. Chao, J. Phys. Chem. Lett., 2010, 1, 116–121.
29. G.-J. Zhao and K.-L. Han, J. Phys. Chem. A, 2007, 111, 2469–2474.
30. G.-J. Zhao and K.-L. Han, Biophys. J., 2008, 94, 38–46.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra16907d

---