Computational insights into CH₃MX (M = Cu, Ag and Au; X = H, F, Cl, Br and I)

Abstract

The C–X bond activation products, CH₃MX (M = Cu, Ag and Au; X = H, F, Cl, Br and I) formed by the insertion of coinage metal atoms into C–X bonds of methane and halomethanes, were investigated by density functional theory (DFT). Equilibrium geometries, harmonic vibrational frequencies, and energies were calculated. Bader's atoms-in-molecule (AIM), natural population charge (NPA) and fuzzy bond orders (FBO) calculations were performed to investigate the bonding interactions in CH₃MX. As X varies from F to I, the thermodynamic stability of CH₃MX with respect to CH₃X + M increases, and the order of the thermodynamic stability for different coinage metals is CH₃CuX > CH₃AuX > CH₃AgX. Although the CH₃MX (M = Cu, Ag and Au; X = Cl, Br and I) were predicted to be more stable thermodynamically than the others (e.g. CH₃MH and CH₃MF) observed in matrix isolation experiments, they have not been identified experimentally yet, and one of the probably key reasons is that their vibrational fingerprints (ν_C–M and ν_M–X) are so low that they are beyond the detection limit of an infrared spectrometer. AIM analyses show that both C–M and M–X bonds in CH₃MX exhibit mainly closed-shell interaction character, and partial covalent character contributes to them. The BCP of M–H bond just locates at the boundary between the charge concentration region and the charge depletion region, which lead to the covalent character of M–H bond being overestimated by the AIM topological parameters.

---

1. Introduction

Selective metal-mediated activation of C–H and C–X (X = F, Cl, Br and I) bonds is an active research field in organometallic chemistry. In recent years, various kinds of small transition-metal complexes were produced by the reactions of laser-ablated transition metals with small alkanes and halomethanes.^1–26 These simple metal complexes usually have unique structures and often show interesting photochemical properties.

Group 11 metals, the so-called coinage metals, are at the borderline between the main group elements and transition metals, and have high electronegativity and catalytic activity due to their d¹⁰ electronic configuration and single valence electron (s¹).^8,9 Unlike other transition metals, the coinage metals often behave as Lewis acids because of their relatively high electron affinities. CH₃MH (M = Cu, Ag and Au) and its negative ion form have been identified in low-temperature matrix isolation experiments by the insertion of coinage metals into C–H bond of methane,⁶ moreover, the electron affinities of the insertion complexes are higher than the coinage metals, which is believed to be the driving force to form the rare anionic insertion complex.

The investigations of the reactions of transition metal with halomethanes CH₃X (X = F, Cl, Br and I) can provide us an insight into C–X bond activation. On one hand, CH₃X are interesting substrates for reactions with metals (and their cations) because they constitute a simple gas-phase model that can provide an opportunity for analyzing the competition between C–H and C–X bond activation. On the other hand, the stabilities and reactivities of the products usually have considerable variations by halogen substitution, which mainly due to the general preference for the M–X bond over the M–H bond.^1,15,25,27 CH₃CuF was first prepared by the reaction of laser-vaporized Cu atoms with methyl fluoride in the matrix ESR spectra,^7,28 CH₃MF (M = Ag and Au) have been identified in the matrix IR spectra,⁸ and reactions of Au with CH₃Cl and CH₃Br yield CH₃AuX (X = Cl and Br) as well.⁹ In addition, M⁺CH₃F complexes for coinage metal cations have been observed using mass spectroscopy.²⁹ In addition, some anionic adducts, [CH₃AuI]⁻ (ref. 10) and [CH₃MH]⁻ (M = Cu, Ag and Au),⁶ have been characterized experimentally. To our best knowledge, CH₃MI (M = Cu, Ag and Au) and other CH₃MX (M = Cu and Ag; X = Cl and Br) have not been prepared and identified experimentally yet. Of what interest is the causes for the failure of the preparation of these species. Are the failures caused by technological reason? Or are these species not stable enough to be detected? Or is it something else? In the light of these questions, a systematic theoretical research on CH₃MX (M = Cu, Ag and Au; X = H, F, Cl, Br and I) was performed in this paper. Our aims are to understand the nature of CH₃MX and explore the reason for the failure of the preparation of some CH₃MX species by studying the thermodynamically stability, IR character and bonding interactions of CH₃MX. This article is organized as follows. The next section (Section 2) provides an overview of the theoretical methods used in the calculations. In Section 3, the reliable geometries and the relative energies of CH₃MX were calculated, then the bonding interactions in CH₃MX were analyzed. A short summary is given in Section 4.

2. Theoretical calculations

For H, C, F and Cl atoms, the augmented Dunning's correlation consistent valence triple-zeta (aug-cc-pVTZ) basis sets^30,31 were used. To consider relativistic effect of heavy elements, the aug-cc-pVTZ-PP small-core relativistic effective core potential (RECP) together with their corresponding basis sets^32,33 were used for all other atoms, and the RECP retains 25 and 19 explicit electrons for halogen atoms (Br and I) and coinage-metal atoms (Cu, Ag and Au), respectively. The Becke's three-parameter hybrid exchange functional³⁴ with Lee–Yang–Parr correlation functional (B3LYP)³⁵ were used to optimize the structures of the molecules under investigation. The equilibrium structures of CH₃MX (M = Cu, Ag and Au; X = H, F, Cl, Br and I) were optimized by synchronous transit-guided quasi-Newton (STQN) method. Harmonic vibrational frequencies calculation using analytic second derivatives at the same level for all species were performed in order to confirm that the structures were minima and evaluate zero-point vibrational energies (ZPVE). Base on the optimized geometries, the single-point CCSD(T)^36–38 energies have been carried out to obtain more accurate energies using the same RECP and basis sets.

Bader's atoms-in-molecule (AIM),^39,40 natural population charge (NPA) and fuzzy bond orders (FBO)^41,42 calculations were performed to understand the nature of the bonding interactions in CH₃MX (M = Cu, Ag and Au; X = H, F, Cl, Br and I). To avoid the negative effects of diffuse functions, the cc-pVTZ/cc-pVTZ-PP basis sets removing diffuse functions were used to NPA calculations. In order to obtain reasonable results in chemical sense, all-electron basis sets (WTBS basis set^43,44 for both I and Xe, and cc-pVTZ for other atoms) rather than ECP basis sets mentioned above were used to generate wave functions for AIM analysis, moreover, the same basis sets were also used for the FBO calculations since FBO with diffuse function augmentation of basis sets may be unreliable.⁴⁵ The DFT and NPA calculations were carried out using the Gaussian09 program.⁴⁶ FBO and AIM calculations were performed by the software Multiwfn.⁴⁷

3. Results and discussions

3.1 Structures

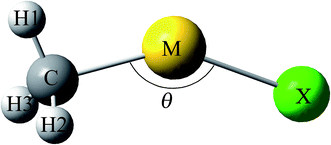
The model of CH₃MX (M = Cu, Ag and Au; X = H, F, Cl, Br and I) molecules was illustrated in Fig. 1, and the selected structural parameters were listed in Table 1. Some CH₃MX molecules have been synthesized in solid noble-gas matrices. For example, CH₃MH and CH₃MF (M = Cu, Ag and Au) has been observed in reactions of coinage-metal with methane in solid matrices,^6–8 and reactions of Au with CH₃Cl and CH₃Br yield CH₃AuX (X = Cl and Br) as well.⁹ This is the first report on all other CH₃MX molecules (including CH₃MI, CH₃CuCl, CH₃AgCl, CH₃CuBr and CH₃AgBr) since no concerning experimental or theoretical result is found.

Fig. 1 The model of CH₃MX (M = Cu, Ag and Au; X = H, F, Cl, Br and I) molecules.

Table 1 The molecular electronic state, symmetry and structural parameters (bond length: Å; bond angle: degree) of CH₃MX (M = Cu, Ag and Au; X = H, F, Cl, Br and I) calculated at the B3LYP/aug-cc-pvtz-pp/aug-cc-pvtz level of theory^a,b

	CH3MH	CH3MF^c	CH3MCl	CH3MBr	CH3MI
a Atomic covalent radii:^48 C: 0.750; H: 0.320; F: 0.640; Cl: 0.990; Br: 1.140; I: 1.330; Cu: 1.120; Ag: 1.280; Au: 1.240.b Bond lengths R in Å, bond angle θ in degree.c CH3AgF is only one with a highly symmetry of C3v, and its electronic state is ^2A1 rather than ^2A′.
Electronic state	^2A′	^2A′	^2A′	^2A′	^2A′
Symmetry	Cs	Cs	Cs	Cs	Cs
M = Cu
RC–Cu (ΔRC–Cu)	1.938 (0.068)	1.903 (0.033)	1.909 (0.039)	1.912 (0.042)	1.917 (0.047)
RCu–X (ΔRCu–X)	1.508 (0.068)	1.751 (−0.009)	2.102 (−0.008)	2.235 (−0.025)	2.423 (−0.027)
θC–Cu–X	129.0	140.0	142.4	141.9	141.5
M = Ag
RC–Ag (ΔRC–Ag)	2.182 (0.152)	2.098 (0.068)	2.150 (0.120)	2.154 (0.124)	2.159 (0.129)
RAg–X (ΔRAg–X)	1.649 (0.049)	1.985 (0.065)	2.318 (0.048)	2.442 (0.022)	2.611 (0.001)
θC–Ag–X	130.4	180.0	146.6	143.1	141.7
M = Au
RC–Au (ΔRC–Au)	2.120 (0.130)	2.036 (0.046)	2.059 (0.069)	2.063 (0.073)	2.071 (0.081)
RAu–X (ΔRAu–X)	1.605 (0.045)	1.965 (0.085)	2.291 (0.061)	2.420 (0.040)	2.593 (0.023)
θC–Au–X	138.3	146.2	146.1	145.7	146.0

---

As illustrated in Table 1, all CH₃MX molecules except CH₃AgF are non-planar with C_s symmetry and belong to ²A′ electronic state. The ground-state ²A₁ CH₃AgF is only one with a highly symmetry of C_3v, and the F, Ag and C atoms are collinear. Generally, the M–X bond is constituted by the sp/sd hybrid orbitals of M atoms and the sp hybrid orbitals (mainly p orbital) of X atoms. However, the Ag–F bond is constituted by the sd hybrid orbital (mainly s orbital) of Ag atoms and the sp hybrid orbitals (mainly p orbital) of F, which is mainly responsible for the C_3v structure of CH₃AgF. As shown in Table 1, θ_C–Cu–X of CH₃CuH is 129.0° and is smaller than those of CH₃CuX (X = F, Cl, Br and I), which fall in the range of 140–142.5°. Similar things happen in CH₃AgX and CH₃AuX (X = H, F, Cl, Br and I) since θ_C–M–H of CH₃MH (M = Ag and Au) is the smallest, which attribute to that the p orbitals of halogen atoms are involved the M–X bonds. For CH₃MX (X = F, Cl, Br and I) with the same coinage metal, the C–M bond is weakened as X varies from F to I due to its elongation, so the smallest R_C–M is found in CH₃MF, which indicates that the C–M bond in CH₃MF is the strongest. Moreover, the C–M bond in CH₃MH is the weakest C–M bond since its C–M bond length is the longest. It is noteworthy that information concerning the strength of C–M bond with different coinage metals cannot be given directly by their lengths. Likewise, although the M–H bond in CH₃MH is the shortest among M–X bonds in CH₃MX (X = H, F, Cl, Br and I) with the same coinage metal, we cannot infer that the M–H bond in CH₃MH is the strongest due to the different atomic radius of different X atoms. In this situation, the M–X bond length is also inappropriate to be used to evaluate the strength of M–X bond directly. Therefore, in order to compare M–X (or C–M) bonds involving different M (or X) atoms, we define one structural parameter ΔR which allow us to unify interactions to estimate their strengths even if different pairs of atoms:^49,50

ΔR_A–B = R_A–B − R_A − R_B (1)

where R_A–B is the bond length of A–B bond, R_A and R_B are the covalent radii of A and B atoms,⁴⁸ respectively. The smaller ΔR_A–B is, the stronger the interaction is, and vice versa. The calculated ΔR_C–M (or ΔR_M–X) for C–M (or M–X) bond in CH₃MX (M = Cu, Ag and Au; X = H, F, Cl, Br and I) were also listed in Table 1. As shown in Table 1, the negative ΔR_Cu–X in CH₃CuX (X = F, Cl, Br and I) indicates that the Cu–X bond should stronger than the typical Cu–X bond, whereas other M–X (M = Ag and Au; X = H, F, Cl, Br and I) and all C–M bonds have positive ΔR, so the strengths of these bonds seems to be weaker than the concerning typical M–X or C–M bonds, respectively. For CH₃MX (X = H, F, Cl, Br and I) with the same coinage metal, the smallest ΔR_C–M of CH₃MF indicates that the C–M bond in CH₃MF is the strongest, which is consistent with discussion above. Meanwhile, the C–M bond in CH₃MH is the weakest since it has the largest ΔR_C–M, and the C–M bond is weakened as X varies from F to I. Moreover, the order of the strengths of C–M bond in CH₃MX is CH₃CuX > CH₃AuX > CH₃AgX. Note that such statement on the is order of the strengths of C–M bond just a roughly assess, and more analyses will be performed and discussed later. Unlike C–M bond, the M–X bond is strengthened as X varies from F to I due to the decreasing of ΔR_M–X, and the order of the strengths of M–X bond in CH₃MX is CH₃CuX > CH₃AgX > CH₃AuX. To sum it up, CH₃CuX (X = F, Cl, Br and I) seems to be more stable than corresponding CH₃AuX and CH₃AgX since it has stronger C–Cu and Cu–X bonds. To be clear, the covalence radii used here might not be very appropriate for the description of C–M and M–X bond strengths because they demonstrates ionic bond character which will be discussed later, therefore, although the preliminary information on the strengths of bonds can be obtained by ΔR, it is not the unique criterion for the evaluation of these bonds.

3.2 Fragmentation energies of CH₃MX

To test the stability of CH₃MX (M = Cu, Ag and Au; X = H, F, Cl, Br and I) molecules, the energies associated with different formation pathways were calculated using the CCSD(T) method with the same RECP and basis sets to B3LYP, in which ZPVE correction was not considered since it is very time-consuming at the CCSD(T) level. Three possible formation paths that might reasonably occur

CH₃X + M → CH₃MX (1)

ΔE₁ = E(CH₃MX) − E(CH₃X) − E(M)

CH₃ + MX → CH₃MX (2)

ΔE₂ = E(CH₃MX) − E(CH₃) − E(MX)

CH₃M + X → CH₃MX (3)

ΔE₃ = E(CH₃MX) − E(CH₃M) − E(X)

The formation energies of CH₃MX were given in Table 2. The formations of CH₃MX (M = Cu, Ag and Au; X = Cl, Br and I) and CH₃CuF along path (1) were expected to be exothermic, while the formations of CH₃MH (M = Cu, Ag and Au) and CH₃MF (M = Ag and Au) along path (1) were expected to be endothermic, so the preparations of CH₃MH (M = Cu, Ag and Au) and CH₃MF (M = Ag and Au) via CH₃X react with coinage metals are unfavorable thermodynamically. However, previously studies showed that the excitation of coinage-metal atoms in laser ablation process and subsequent UV irradiation can provide the required energy for C–X insertion by excited M*. For example, the lowest-lying excited Cu (²D), Ag (²P) and Au (²D) are 134.0, 353.4 and 109.6 kJ mol⁻¹ higher than their ground state (²S),^51–53 respectively. Therefore, it is favorable thermodynamically for the C–X insertion of CH₃X by excited coinage metals. As shown in Table 2, as X varies from H to I, the decreasing of ΔE₁ indicates the thermodynamically stability of CH₃MX increases with respect to CH₃X + M, and CH₃MI is the most thermodynamically stable although it has not been identified experimentally so far. For different coinage metals, the order of the thermodynamically stability is CH₃CuX > CH₃AuX > CH₃AgX (X = F, Cl, Br and I). Indeed, only CH₃AgF has been identified experimentally,⁸ while other CH₃AgX (X = H, Cl, Br and I) have not been characterized experimentally yet. Of course, one plausible reason is that it is difficult to excite Ag atom since it requires 3 times more energy than the excitation of Au atom.

Table 2 Fragmentation energies (in kcal mol⁻¹) of CH₃MX (M = Cu, Ag and Au; X = H, F, Cl, Br and I) along different pathways without ZPE corrections at the CCSD(T)/aug-cc-pvtz-pp/aug-cc-pvtz level of theory

CH3MX	CH3X + M			CH3 + MX			CH3M + X
	Cu	Ag	Au	Cu	Ag	Au	Cu	Ag	Au
H	100.2	186.8	59.4	−95.7	−51.9	−96.5	−126.1	−95.9	−137.8
F	−78.5	58.0	7.6	−145.5	−82.1	−180.8	−311.0	−230.9	−195.8
Cl	−121.4	−8.6	−74.1	−120.3	−64.2	−155.8	−237.7	−181.3	−161.4
Br	−125.1	−23.3	−93.9	−115.4	−62.4	−151.8	−204.2	−158.9	−144.0
I	−122.9	−37.3	−115.7	−106.7	−60.6	−144.3	−160.5	−131.5	−124.3

---

Previous matrix isolation experimental researches showed that CH₃X can be decomposed to X atom and CH₃ radical in solid matrices by laser ablation, and subsequent CH₃M and MX are formed conveniently by coinage metals reacting with CH₃ radical as well as X atom, respectively.⁶ Therefore, it is possible that CH₃MX is formed along path (2) or path (3) although the amount of CH₃M and MX are very small. However, we think that path (1) should be the main pathway of the formation of CH₃MX because the amount of CH₃X is significantly larger than those of MX or CH₃M in solid matrices. The formations of CH₃MX along paths (2) and (3) were expected to be exothermic, which indicates that CH₃MX is thermodynamically stable with respect to CH₃ + MX or CH₃M + X, respectively. Moreover, because both CH₃ + MX and CH₃M + X are less thermodynamically stable than CH₃X + M, CH₃MX shows more thermodynamically stabilities with respect to CH₃ + MX (or CH₃M + X) than that with respect to CH₃X + M.

3.3 Frequencies

IR spectroscopy is generally viewed as a powerful tool to characterize active species in matrix isolation experiments because the vibrational fingerprints can provide important information for molecular identification and structural analysis. The selected harmonic vibrational frequencies of CH₃MX (M = Cu, Ag and Au; X = H, Cl, Br and I) calculated at the B3LYP level of theory were listed in Table 3, and the selected harmonic vibrational frequencies of CH₃X (X = H, Cl, Br and I) and CH₃M (M = Cu, Ag and Au) calculated at the same level were listed in Table S1 (see ESI†). For most of CH₃MX molecules, the most intense peak is the CH₃ deform mode, however, one thing to be careful of is that both CH₃M and CH₃X have similar peaks. The calculated the CH₃ deform frequencies (τ_CH3) of CH₃MF (M = Cu, Ag and Au) and CH₃AuX (X = Cl and Br) are in line with previous works.^8,9 The CH₃ deform mode in CH₃MX (X = H, F, Cl, Br and I) illustrates larger red shift with respect to that of CH₃X, meanwhile it also shows smaller red-shift behavior compared with that of CH₃M. Such different shift behaviors combined with isotopic shift can be used to identify these CH₃MX molecules in matrix isolation experiments, especially when other vibrational fingerprints (such as the C–M and M–X stretching vibrational modes) are beyond the detection limit of infrared spectrometer.

Table 3 The selected frequencies of the CH₃MX (M = Cu, Ag and Au; X = H, F, Cl, Br and I) calculated at the B3LYP level of theory^a

	CH3MH	CH3MF	CH3MCl	CH3MBr	CH3MI
a Frequencies are in cm^−1 and intensities (in parentheses) are in km mol^−1.b Mixes heavily with CH3 rocking vibrational mode.c Mixes with CH3 rocking vibrational mode.d Mixes with Ag–F stretching vibrational mode.e Mixes heavily with C–Ag rocking vibrational mode.f The C–Au stretching mixes with the Au–X stretching vibrational mode.
M = Cu
νC–Cu, stretch	491.3 (0)	522.4 (1)^b	537.9 (17)	530.0 (10)	523.4 (8)
νCu–X, stretch	1774.3 (46)	638.2 (107)^c	376.9 (23)	276.1 (13)	230.2 (7)
τCH3, deform	1079.3 (48)	1138.8 (33)	1106.0 (96)	1099.2 (121)	1090.4 (166)
νCH2, sys stretch	3017.9 (6)	3010.7 (3)	3010.0 (3)	3012.9 (4)	3015.0 (4)
νCH2, asys stretch	3117.6 (7), 3148.4 (4)	3110.3 (8), 3147.9 (2)	3113.3 (7), 3150.4 (2)	3115.2 (7), 3150.1 (2)	3116.4 (7), 3149.8 (2)
M = Ag
νC–Ag, stretch	356.1 (2)	395.5 (45)^d	368.5 (8)	367.9 (19)	367.9 (23)
νAg–X, stretch	1641.3 (20)	532.6 (92)	308.8 (35)^e	221.0 (10)	176.5 (4)
τCH3, deform	989.6 (101)	1002.5 (128)	986.6 (170)	987.9 (234)	987.1 (353)
νCH2, sys stretch	3054.8 (2)	3039.6 (0)	3051.4 (0)	3053.1 (0)	3055.0 (0)
νCH2, asys stretch	3176.2 (2), 3205.6 (1)	3167.0 (1)	3181.0 (1), 3211.1 (0)	3180.9 (1), 3209.9 (0)	3180.5 (1), 3207.3 (0)
M = Au
νC–Au, stretch	424.5 (2)	530.4 (16)^f	502.7 (0)	497.6 (0)	492.0 (0)
νAu–X, stretch	1927.5 (11)	511.7 (45)^f	324.6 (18)	216.8 (6)	172.0 (2)
τCH3, deform	1093.7 (42)	1165.2 (51)	1146.5 (113)	1146.2 (144)	1142.7 (206)
νCH2, sys stretch	3033.1 (2)	2992.2 (2)	3011.4 (1)	3018.6 (1)	3025.6 (1)
νCH2, asys stretch	3146.3 (3), 3183.1 (1)	3121.9 (7), 3170.2 (0)	3128.8 (8), 3171.9 (1)	3129.8 (10), 3169.2 (1)	3130.7 (11), 3165.5 (1)

---

Because the C–M and M–X stretching vibrational modes (ν_C–M and ν_M–X) cannot be observed in CH₃M and CH₃X, they are regarded as the vibrational fingerprints of CH₃MX although they are usually weaker than the CH₃ deform mode. As shown in Table 3, the ν_M–H of CH₃MH and the ν_M–F of CH₃MF are within the ranges of 1640–1930 cm⁻¹ and 510–640 cm⁻¹, respectively, which have been used to identify these molecules in matrix isolation experiments.^6,8 It is noticeable that both the Cu–F and Au–F stretching frequencies are considerably underestimated by the DFT calculation, which is due to the mixture of these vibrational modes with the CH₃ deformation mode. The ν_M–X of other CH₃MX (M = Cu, Ag and Au; X = Br and I) are lower than 400 cm⁻¹, which are beyond the detection limit of infrared spectrometer. Perhaps this is one of the reasons why some CH₃MX molecules with enough thermodynamically stabilities have not been identified by IR spectroscopy in matrix isolation experiments yet, so other techniques besides IR spectroscopy are required to identify such molecules, and ESR might be an appropriate alternative since it has been used to characterized CH₃CuF molecules in noble-gas matrix.²⁸ Similarly, although the calculated harmonic ν_C–M of CH₃MX (M = Cu, Ag and Au; X = Br and I) are higher than 490 cm⁻¹, it can hardly play an active role in the characterization of these CH₃MX molecules due to the weak intensity. Nevertheless, some useful information on the bonding of CH₃MX can probably be learned from these vibrational modes. As shown in Table 3, the decreasing ν_C–M of CH₃MX (X = F, Cl, Br and I) with the same coinage metal indicates that the C–M bond is weakened as X varies from F to I, which is agree with the above-mentioned structural results. Moreover, the ν_C–M of CH₃MH is the smallest than those in CH₃MX (X = F, Cl, Br and I), so the C–M bond in CH₃MH should be the weakest one. Similar things also happened in M–X stretching vibrational mode since its frequency decreases as X varies from F to I as well, and the ν_M–H is the largest, which is different from the case of C–M stretching vibrational mode. However, this cannot be the adequate basis for the evaluation on the order of the strength of M–X bond because that different X atoms are involved in M–X stretching vibrational modes, and the decreasing of the ν_M–X is partly attributed to the increasing of the reduced mass concerning to the M–X stretching modes as X varies from F to I. Likewise, as M varies from Cu to Au, the decreasing of the ν_M–X in CH₃MX (M = Cu, Ag and Au) does not provide the adequate evidence for the evaluation on the order of the strengths of M–X bonds with the same halogen atom as well. However, unlike M–X stretching vibrational mode, the ν_C–M in CH₃AuX with the same halogen atom is the larger than that of CH₃AgX, especially the ν_C–M in CH₃AuF is the largest one among those of CH₃MF (M = Cu, Ag and Au), so it is reasonable to assume that the C–Au bond seems to stronger than C–Ag bonds even the effects of reduced mass is taken into account.

3.4 Bond analyses

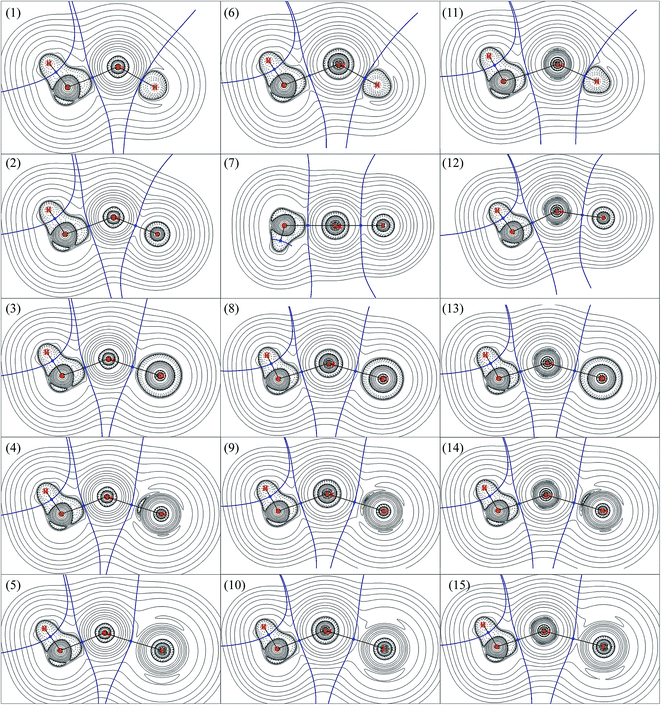
AIM is a useful tools to explore the nature of the bonding interactions and has been used widely. According to AIM, the first descriptor of bond is the existence of the bond critical point (BCP), and the various characters at BCP are used to analyze the nature of interactions, such as the electron density (ρ_b) as well as its Laplacian (∇²ρ_b), potential energy density (V_b), kinetics energy density (G_b), total energy density (H_b), ratio of |V_b|/G_b,⁵⁴ and eta index (η_b). It has been proved that both H_b and ∇²ρ_b at the BCP can be used to discriminate interaction types:^54–57 H_b < 0 and ∇²ρ_b < 0 means an accumulation of charge density at BCP and therefore a covalent interaction between the interacting atoms; H_b > 0 and ∇²ρ_b > 0 means a depletion of charge density at BCP and therefore a closed-shell interaction between the interacting atoms; H_b < 0 but ∇²ρ_b > 0 means partially covalent interactions. The |V_b|/G_b ratio allow the interaction to be characterized: |V_b|/G_b < 1 indicates pure closed-shell interaction; |V_b|/G_b > 2 indicates pure covalent (open-shell) interaction; while 1 < |V_b|/G_b < 2 indicates intermediate interaction.⁵⁴

AIM analyses have also been carried out to explore the nature of bonds in CH₃MX (M = Cu, Ag and Au; X = H, F, Cl, Br and I), and the results were presented in Table 4. The contour line diagrams of Laplacian of electron density (∇²ρ_b) for CH₃MX were presented in Fig. 2. As shown in Fig. 2, the presence of dashed isosurfaces around C–H suggest that valence-shell electrons are strongly concentrated on these regions, it is typical pattern of covalent bonding. No shell structure can be found for the hydrogen atom since it just has 1s valence shell. The C atom has a region of charge concentration towards the metal atom, while the metal atom has a region of charge depletion region along the M–C bond line direction. Similar things also happened in the M–X bond in all studied molecules. Therefore, both the M–X and M–C bonds illustrate closed-shell interaction characters, and there is charge transfer (CT) from the metal atom to the X atom and CH₃ group. It is noteworthy that the BCP of M–H bond just locates at the boundary between the charge concentration region and the charge depletion region, which must be taken into account for the study of the nature of M–H bond, otherwise, a unreliable information might be obtained just by the topological parameters (e.g. ∇²ρ_b, H_b and |V_b|/G_b ratio), which will be discussed later.

Table 4 The AIM results of CH₃MX (M = Cu, Ag and Au; X = H, F, Cl, Br and I) calculated at the B3LYP level with all-electron basis sets

	M–C					M–X
	ρb	∇^2ρb	|Vb|/Gb	Hb	ηb	ρb	∇^2ρb	|Vb|/Gb	Hb	ηb
CH3CuH	0.116	0.149	1.561	−0.048	0.348	0.127	0.055	1.844	−0.075	0.457
CH3CuF	0.128	0.134	1.630	−0.057	0.373	0.138	0.817	1.197	−0.050	0.198
CH3CuCl	0.126	0.131	1.628	−0.055	0.370	0.103	0.297	1.329	−0.036	0.235
CH3CuBr	0.124	0.132	1.622	−0.054	0.367	0.089	0.202	1.368	−0.029	0.248
CH3CuI	0.122	0.132	1.615	−0.053	0.363	0.071	0.103	1.480	−0.024	0.269
CH3AgH	0.079	0.184	1.333	−0.023	0.247	0.111	0.118	1.677	−0.062	0.382
CH3AgF	0.099	0.175	1.454	−0.036	0.293	0.100	0.656	1.087	−0.016	0.150
CH3AgCl	0.085	0.180	1.375	−0.027	0.261	0.078	0.307	1.183	−0.017	0.170
CH3AgBr	0.084	0.180	1.368	−0.026	0.259	0.069	0.228	1.206	−0.015	0.177
CH3AgI	0.083	0.184	1.355	−0.025	0.253	0.053	0.159	1.190	−0.009	0.162
CH3AuH	0.103	0.201	1.426	−0.037	0.280	0.140	0.056	1.870	−0.094	0.457
CH3AuF	0.126	0.188	1.545	−0.057	0.318	0.117	0.786	1.109	−0.024	0.157
CH3AuCl	0.119	0.191	1.514	−0.050	0.308	0.093	0.340	1.226	−0.025	0.185
CH3AuBr	0.118	0.192	1.507	−0.049	0.306	0.081	0.246	1.252	−0.021	0.192
CH3AuI	0.115	0.195	1.489	−0.047	0.299	0.059	0.174	1.208	−0.011	0.169

---

Fig. 2 Contour line diagrams of ∇²ρ_b for CH₃MX (M = Cu, Ag and Au; X = H, F, Cl, Br and I), obtained by B3LYP method with all-electron basis sets. (1) CH₃CuH; (2) CH₃CuF; (3) CH₃CuCl; (4) CH₃CuBr; (5) CH₃CuI; (6) CH₃AgH; (7) CH₃AgF; (8) CH₃AgCl; (9) CH₃AgBr; (10) CH₃AgI; (11) CH₃AuH; (12) CH₃AuF; (13) CH₃AuCl; (14) CH₃AuBr; (15) CH₃AuI. Dashed lines indicate areas of charge concentration (∇²ρ_b < 0), while solid lines show areas of charge depletion (∇²ρ_b > 0). The bold brown solid lines connecting the atomic nuclei are the bond paths and the solid blue lines separating the atomic nuclei indicate the zero-flux surfaces in the molecular plane. The crossing points of the bond paths and zero-flux surfaces are the bond critical points (BCP).

As shown in Table 4, the ∇²ρ_b at the BCPs of both M–C and M–X in all studied molecules are positive, and their total energy density (H_b) are negative, which reveals that both M–C and M–X bonds are partially covalent interactions. The point was confirmed by the |V_b|/G_b ratios since all |V_b|/G_b ratios are within the range of 1–2. The BCP of M–C in CH₃MH (M = Cu, Ag and Au) has larger H_b > 0 and ∇²ρ_b than other that of M–C in CH₃MX (M = Cu, Ag and Au; X = F, Cl, Br and I), which indicates that the M–C bond in CH₃MH is weaker than the one in CH₃MX. Of particular note is that the |V_b|/G_b ratio at the BCP of M–H bond, especially Cu–H and Au–H bonds, is obviously larger than those of M–X bonds, so the M–H bond seems to be stronger and exhibits more covalent than the M–X bonds, which is supported by the more negative H_b and smaller ∇²ρ_b. However, such conclude is inconsistent with the discussions mentioned above, and the covalent character of M–H bond is overestimated because the BCP of M–H bond just locates at the boundary between the charge concentration region and the charge depletion region. Therefore, it is not advisable to study the nature of bonds by AIM descriptors without considering the particular circumstances of each case.

The |V_b|/G_b ratio of M–C BCP in CH₃MX decrease as X varies from F to I, which indicates that the M–C bond is weakened simultaneously with the decreasing of the electronegativity of X atom, and such trend can also be learned from the decreasing ∇²ρ_b and the increasing H_b. The M–X bond shows a reverse trend with respect to the M–C bond, and is strengthened due to the increasing |V_b|/G_b ratio and H_b as well as the decreasing ∇²ρ_b as X varies from F to I. Compare the descriptors including ∇²ρ_b, H_b as well as |V_b|/G_b ratios of BCPs of either M–X bonds in CH₃MX (M = Cu, Ag, Au) containing the same halogen atom, it is not hard to find that the Cu–X bond is stronger than both Ag–X and Au–X, and the Ag–X bond is the weakest bond. Similarly, the order of the strengths of M–C bond is Cu–C > Au–C > Ag–C. Therefore, CH₃CuX is expected to be more stable than CH₃AuX and CH₃AgX which attribute to the stronger Cu–C and Cu–X bonds, whereas CH₃AgX should have the less stability due to the weakest M–C and M–X bonds.

To understand the bonding interactions in CH₃MX (M = Cu, Ag and Au; X = Cl, Br and I), the fuzzy bond order (FBO) were calculated using B3LYP method, and cc-pVTZ basis sets removing the diffusion basis functions were used to obtain reliable results. The calculated fuzzy bond orders (FBO) of CH₃MX were listed in Table 5. As shown in Table 5, the order of FBOs of C–M bond in CH₃MX (M = Cu, Ag and Au) with the same halogen is C–Cu > C–Au > C–Ag, so the C–Cu bond is stronger than the other two, while the C–Ag bond is the weakest one, which is consistent with the discussion above. The FBO of the M–X bond demonstrates a similar order of Cu–X > Au–X > Ag–X. As X varies from F to I, the FBO of C–M in CH₃MX decreases, which means that the C–M bond is weakened. However, the M–X illustrates one reverse trend and is strengthened as X varies from F to I due to the increasing FBO.

Table 5 Fuzzy Bond Order (FBO) of CH₃MX (M = Cu, Ag and Au; X = H, F, Cl, Br and I) calculated using the B3LYP method with all-electron basis sets

	C–M			M–X
	Cu	Ag	Au	Cu	Ag	Au
CH3MH	1.188	0.954	1.063	0.992	0.949	1.029
CH3MF	1.232	1.017	1.128	1.634	1.307	1.384
CH3MCl	1.195	0.915	1.075	1.719	1.524	1.588
CH3MBr	1.184	0.912	1.065	1.751	1.578	1.642
CH3MI	1.164	0.898	1.039	1.697	1.515	1.565

---

The calculated NPA charges of CH₃MX (M = Cu, Ag and Au; X = Cl, Br and I) were presented in Table 6. As shown in Table 6, the charge of M is positive, which indicates that there is electron transfer occured from metal atom to CH₃ group and the halogen atom. The extent of CT decreases as X varies from F to I due to the decreasing charge of M, which is attributed mainly to the influence of halogen atoms. Moreover, the first ionization potential of Au is the highest among coinage-metal atoms, which is in line with that the extent of CT in CH₃AuX is the largest. However, although the first ionization potential of Cu is larger than that of Ag, our results show that the extent of CT is CH₃CuX > CH₃AgX. The charge of halogen atom is more negative than that of methyl group, which reveals that the halogen atom is the main electron acceptor rather than the methyl group. Due to the smaller electronegativity of the H atom, the charge of the H atom in CH₃MH is obviously larger than that of the halogen atom in CH₃MX, which lead to the smallest CT effect happened in CH₃MH.

Table 6 The NPA charges of CH₃MX (M = Cu, Ag and Au; X = H, F, Cl, Br and I) calculated using the B3LYP method with the cc-pVTZ/cc-pVTZ-PP basis sets removing diffuse functions

	CH3CuX			CH3AgX			CH3AuX
	CH3	Cu	X	CH3	Ag	X	CH3	Au	X
CH3MH	−0.315	0.585	−0.270	−0.171	0.400	−0.229	−0.165	0.272	−0.107
CH3MF	−0.347	0.984	−0.637	−0.114	0.861	−0.747	−0.148	0.694	−0.546
CH3MCl	−0.288	0.781	−0.493	−0.078	0.619	−0.541	−0.137	0.501	−0.364
CH3MBr	−0.284	0.705	−0.421	−0.095	0.554	−0.459	−0.144	0.427	−0.283
CH3MI	−0.281	0.603	−0.322	−0.116	0.468	−0.352	−0.159	0.328	−0.170

---

4. Conclusions

CH₃MX (M = Cu, Ag and Au; X = H, F, Cl, Br and I) have been investigated by DFT calculation. Equilibrium geometry, harmonic vibrational frequencies, energies were calculated, and AIM calculations were also performed to understanding the bonding interactions in the studied molecules.

(1) The ground states of all molecules are doublet, and all molecules except for CH₃AgF are planar structures with C_s symmetry, while CH₃AgF has C_3v symmetry with a linear H–Ag–C bond angle.

(2) As X varies from F to I, the thermodynamically stability of CH₃MX with respect to CH₃X + M increases, and the order of the thermodynamically stability for different coinage metals is CH₃CuX > CH₃AuX > CH₃AgX. Such conclusion is supported by the AIM and FBO calculations.

(3) Although CH₃MH (M = Cu, Ag and Au) and CH₃MF (M = Ag and Au) were predicted to be unstable with respect to CH₃X + M, most of them have been prepared and identified in low-temperature matrix isolation experiments. Besides the involvement of the excited coinage-metal atoms in laser ablation process and UV irradiation, the strong M–H (or M–F) stretching vibrational modes make a crucial contribution to the identification of these species.

(4) The most intense peak in CH₃MX is the CH₃ deform mode, which illustrates larger red shift with respect to that of CH₃X, and smaller red shift with respect to that of CH₃M. Such different shift behaviors combined with isotopic shift can be used to identify these CH₃MX molecules in matrix isolation experiments. Of note is that some CH₃MX molecules with enough thermodynamically stabilities have not been identified by IR spectroscopy in matrix isolation experiments yet, and one of probably reasons is that their vibrational fingerprints (C–M and M–X stretching vibrational modes) are weak or too low to be detected by infrared spectrometer.

(5) AIM analyses show that both C–M and M–X bonds exhibit mainly closed-shell interaction character, and partial covalent character contributes to them. The BCP of M–H bond just locates at the boundary between the charge concentration region and the charge depletion region, which lead to that the covalent character of M–H bond is overestimated by the AIM topological parameters.

In brief, although the CH₃MX molecules with more stabilities should be more chances to be observed experimentally, one of the challenges is that both ν_C–M and ν_M–X are weak and are beyond the detection limit of infrared spectrometer, so how to overcome such challenge should be the next research direction, and this paper might provide useful information for the next research.

Acknowledgements

This work is supported by the Natural Science Foundation of Tianjin (No. 12JCYBJC13400) and the Program for Innovative Research Team in University of Tianjin (TD12-5038).

References

1. L. Andrews and H. G. Cho, Organometallics, 2006, 25, 4040–4053.
2. H.-G. Cho and L. Andrews, Organometallics, 2007, 26, 4098–4101.
3. H.-G. Cho and L. Andrews, Organometallics, 2007, 26, 633–643.
4. J. T. Lyon, H.-G. Cho and L. Andrews, Organometallics, 2007, 26, 6373–6387.
5. H. G. Cho, J. T. Lyon and L. Andrews, Organometallics, 2008, 27, 5241–5251.
6. H. G. Cho and L. Andrews, Dalton Trans., 2011, 40, 11115–11124.
7. L. B. Knight, J. T. Petty Jr, S. T. Cobranchi, D. Feller and E. R. Davidson, J. Chem. Phys., 1988, 88, 3441–3450.
8. H.-G. Cho and L. Andrews, Inorg. Chem., 2011, 50, 10319–10327.
9. H.-G. Cho and L. Andrews, Organometallics, 2013, 32, 2753–2759.
10. S. Muramatsu, K. Koyasu and T. Tsukuda, J. Phys. Chem. A, 2016, 120, 957–963.
11. L. Andrews and H. G. Cho, J. Phys. Chem. A, 2005, 109, 6796–6798.
12. H.-G. Cho and L. Andrews, J. Phys. Chem. A, 2007, 111, 2480–2491.
13. J. T. Lyon and L. Andrews, Organometallics, 2007, 26, 2519–2527.
14. H.-G. Cho and L. Andrews, J. Phys. Chem. A, 2008, 112, 12293–12295.
15. H.-G. Cho and L. Andrews, J. Am. Chem. Soc., 2008, 130, 15836–15841.
16. H.-G. Cho and L. Andrews, Eur. J. Inorg. Chem., 2008, 2537–2549.
17. H.-G. Cho and L. Andrews, Organometallics, 2008, 27, 1786–1796.
18. H.-G. Cho and L. Andrews, Inorg. Chem., 2008, 47, 1653–1662.
19. H.-G. Cho, J. T. Lyon and L. Andrews, J. Phys. Chem. A, 2008, 112, 6902–6907.
20. J. T. Lyon and L. Andrews, Eur. J. Inorg. Chem., 2008, 1047–1058.
21. H.-G. Cho and L. Andrews, Organometallics, 2009, 28, 1358–1368.
22. H.-G. Cho, L. Andrews, B. Vlaisavljevich and L. Gagliardi, Organometallics, 2009, 28, 6871–6879.
23. H.-G. Cho, L. Andrews, B. Vlaisavljevich and L. Gagliardi, Organometallics, 2009, 28, 5623–5632.
24. H.-G. Cho and L. Andrews, J. Phys. Chem. A, 2010, 114, 8056–8068.
25. H.-G. Cho and L. Andrews, Dalton Trans., 2010, 39, 5478–5489.
26. H.-G. Cho and L. Andrews, Organometallics, 2010, 29, 2211–2222.
27. H. G. Cho and L. Andrews, Organometallics, 2009, 28, 1358–1368.
28. L. G. Knight Jr, S. T. Cobranchi, B. W. Gregory and G. C. Jones Jr, J. Chem. Phys., 1988, 88, 524–532.
29. X. Zhao, G. K. Koyanagi and D. K. Bohme, J. Phys. Chem. A, 2006, 110, 10607–10618.
30. R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
31. T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023.
32. K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113–11123.
33. K. A. Peterson, B. C. Shepler, D. Figgen and H. Stoll, J. Phys. Chem. A, 2006, 110, 13877–13883.
34. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
35. L. Chengteh, Y. Weitao and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
36. M. Sprik and M. L. Klein, J. Chem. Phys., 1987, 87, 5987–5999.
37. G. E. Scuseria, C. L. Janssen and H. F. Schaefer, J. Chem. Phys., 1988, 89, 7382–7387.
38. G. E. Scuseria and H. F. Schaefer, J. Chem. Phys., 1989, 90, 3700–3703.
39. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, U.K., 1990.
40. C. F. Matta and R. J. Boyd, The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design, WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim, 2007.
41. L. George, A. Kalume, B. J. Esselman, J. Wagner, R. J. McMahon and S. A. Reid, J. Chem. Phys., 2011, 135, 124503.
42. I. Mayer and P. Salvador, Chem. Phys. Lett., 2004, 383, 368–375.
43. S. Huzinaga and M. Klobukowski, Chem. Phys. Lett., 1993, 212, 260–264.
44. S. Huzinaga and B. Miguel, Chem. Phys. Lett., 1990, 175, 289–291.
45. L. Goodman and R. R. Sauers, J. Comput. Chem., 2007, 28, 269–275.
46. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian09, E.01, 2009.
47. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
48. P. Pyykko and M. Atsumi, Chem.–Eur. J., 2009, 15, 186–197.
49. H. K. Wang, Z. G. Huang, T. T. Shen and L. F. Guo, Struct. Chem., 2012, 23, 1163–1172.
50. Q. Wang, B. Zhang and Z. Huang, Chem. Phys. Lett., 2014, 614, 5–9.
51. J. Sugar and A. Musgrove, J. Phys. Chem. Ref. Data, 1990, 19, 527–616.
52. T. Badr, M. D. Plimmer, P. Juncar, M. E. Himbert, J. D. Silver and G. D. Rovera, Eur. Phys. J. D, 2004, 31, 3–10.
53. J. C. Ehrhardt and S. P. Davis, J. Opt. Soc. Am., 1971, 61, 1342–1349.
54. E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529–5542.
55. W. D. Arnold and E. Oldfield, J. Am. Chem. Soc., 2000, 122, 12835–12841.
56. S. Jenkins and I. Morrison, Chem. Phys. Lett., 2000, 317, 97–102.
57. S. J. Grabowski, W. A. Sokalski and J. Leszczynski, J. Phys. Chem. A, 2006, 110, 4772–4779.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra18033g

---