Open Access Article
Open Access ArticleSolvatochromism of dye-labeled dendronized polymers of generation numbers 1–4: comparison to dendrimers†
Chiara
Gstrein
a,
Baozhong
Zhang
 *b,
Mona Ahmed
Abdel-Rahman
c,
Oscar
Bertran
d,
Carlos
Alemán
def,
Gerhard
Wegner
g and
A. Dieter
Schlüter
*a
*b,
Mona Ahmed
Abdel-Rahman
c,
Oscar
Bertran
d,
Carlos
Alemán
def,
Gerhard
Wegner
g and
A. Dieter
Schlüter
*a
aLaboratory of Polymer Chemistry, Department of Materials, ETH Zurich, Vladimir-Prelog-Weg 5, 8093 Zürich, Switzerland. E-mail: ads@mat.ethz.ch
bCentre of Analysis and Synthesis, Lund University, P.O. Box 124, SE-22100 Lund, Sweden. E-mail: baozhong.zhang@chem.lu.se
cChemistry Department, Faculty of Science, Assiut University, 71516, Assiut, Egypt
dDepartament de Física Aplicada, EEI, Universitat Politècnica de Catalunya, Av. Pla de la Massa, 8, 08700 Igualada, Spain
eDepartament d'Enginyeria Quimica, E. T. S. d'Enginyeria Industrial de Barcelona, Universitat Politechnica de Catalunya, Diagonal 647, Barcelona, E-08028, Spain
fCenter for Research in Nano-Engineering, Universitat Politècnica de Catalunya, Campus Sud, Edifici C', C/Pasqual i Vila s/n, Barcelona E-08028, Spain
gMax-Planck-Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany
First published on 15th April 2016
Abstract
Two series of dendronized polymers (DPs) of generations g = 1–4 with different levels of dendritic substitution (low and high) and a solvatochromic probe at g = 1 level are used to study their swelling behavior in a collection of solvents largely differing in polarity as indicated by the Kamlet–Taft parameters. This is done by measuring the UV-Vis spectra of all samples in all solvents and determining the longest wavelength absorptions (λmax). The λmax values fall into a range defined by the extreme situations, when the solvatochromic probe is either fully surrounded by solvent or completely shielded against it. The former situation is achieved in a model compound and the latter situation is believed to be reached when in a poor solvent the dendritic shell around the backbone is fully collapsed. We observe that solvent penetration into the interior of the DPs decreases with increasing g and does so faster for the more highly dendritically substituted series than for the less highly substituted one. Interestingly, the swelling of the more highly substituted DP series already at the g = 4 level has decreased to approximately 20% of that at the g = 1 level which supports an earlier proposal that high g DPs can be viewed as nano-sized molecular objects. Furthermore, when comparing these two DP series with a g = 1–6 series of dendrimers investigated by Fréchet et al. it becomes evident that even the less substituted series of DPs is much less responsive to solvent changes as assessed by the solvatochromic probe than the dendrimers, suggesting the branches around the (polymeric) core in DPs to be more densely packed compared to those in dendrimers, thus, establishing a key difference between these two dendritic macromolecules.
Introduction
The structure of the interior of dendrimers, that is the local arrangement and packing of the segments of the dendrons, has fascinated researchers from the early days of these regularly branched macromolecules.1 Questions raised include whether (i) there exists a radial density gradient and how much it is counteracted by backfolding of the dendron branches,2 (ii) there is a synthetically accessible maximum generation,3 (iii) guest molecules can be up-loaded and retained like in a box,4 and whether (iv) directional photoenergy transfer within dendrimers can be achieved.5 Already in 1993 Hawker, Wooley and Fréchet investigated a set of dendrons with generations (g) ranging from g = 0–6 for their solvent accessibility6 in dependence of g.7 For that purpose the focal points of the members of this series were equipped with a p-nitroaniline moiety, and the solvatochromism of this probe studied for seven solvents considerably differing in polarity. For increasing g the λmax values were observed to slowly converge to a range lying between λ = 383–404 nm. The authors concluded that the probe was increasingly wrapped by its own dendron segments, thus, decreasing the probability of interaction with the solvent. Furthermore the authors suggested that the polarity of the interior of their dendrons is similar to DMF despite the differences in molecular structure between DMF and the dendrons. Even now, some 20 years and quite a few more related investigations later, this initial study is still amongst the most comprehensive ones, however, its main conclusions were disputed in the meantime.8 In particular it was shown that the impact of dendritic branches on the solvatochromic probe is smaller than proposed because of substantial swelling. Dendronized polymers (DPs) differ from dendrimers by the nature of the core.9 While in DPs the core is a linear polymer with a dendron attached to each repeat unit, dendrimers arrange their dendrons around a small core entity which typically connects three or four dendrons. This structural difference has substantial consequences which over the years have been delineated in quite some detail.10 In the present context it shall be stressed that for one and the same dendron type the branch density around the core of DPs is much larger than in dendrimers. This can be rationalized by considering the space available to each dendron in both kinds of macromolecules. While for DPs this is a cylindrical slice the thickness of which corresponds to the length of a repeat unit of its core polymer, in dendrimers it is a third or a fourth of an entire sphere (depending on core multiplicity). This greater branch density has led to the view of DPs of sufficient g as being molecular objects11 and this will have significant bearing on solvent penetration. It is expected that already a lower generation g than in dendrimers will suffice to cause the effect of solvents on internally installed solvatochromic probes to vanish. This is due to the increased volume occupation by the branches reducing the available space for solvent molecules. In context with solvent penetration it is noted that we see the branches surrounding the backbone similar to a fluid except that all elements of this fluid are tightly connected to one another and can form hydrogen bonds as well as π–π stacking. In other words, the uptake of solvent molecules into the interior of the DP molecular objects is seen as a process related to mixing of two solvents. The driving force for solvation is the osmotic pressure of the solvent in contact with the DP. All segments of the object can in principle be affected by the uptake once thermodynamic equilibrium is reached. Finally, there is an interesting report on DPs with solvatochromic probes by Zhang et al., however, it is limited to g = 1 and g = 2 representatives and thus to be considered a starting point only.12 Also, it refers to water-soluble DPs and is being conducted in aqueous medium which poses a key difference to the present study.In this report we describe the synthesis of two sets of DPs each with g = 1–4 both of which carry p-nitroaniline solvatochromic probes covalently connected to g = 1. These sets, which we call hs-PGg and ls-PGg (Fig. 1), differ in openness of the dendritic structure as well as in frequency of probe attachment along the backbone. While the representatives of the high substitution (hs) series are homopolymers with the probe at every repeat unit, those of the low substitution (ls) series are copolymers where only 2% of the repeat units carry the probe. The terms high and low substitution refer to the amount of branch substitution with solvatochromic probe which in the hs-series is high because one of the two available branches on the g = 1 level is substituted by the solvatochromic probe on every repeat unit, while in the ls-series practically all repeat units (98%) still carry fully developed dendrons.
Both series were analyzed by UV-Vis spectroscopy in ten solvents, which were selected according to the Kamlet–Taft polarity scale13 and span the broadest possible polarity range (DMSO to toluene). The λmax values were plotted in dependence of generation g for each solvent to observe the expected shielding effects and, in particular, to see whether these effects differ from those reported for dendrimers. It was of obvious further interest to see whether the two series show the expected differences in their shielding capabilities, with the hs-PGg series to shield less than ls-PGg. The choice of solvents also comprised toluene which, given the knowledge of a closely related other series,10e was expected to be a thermodynamically poor solvent for both hs-PGg and ls-PGg, and anticipated to cause interesting effects induced by possible dendron collapse phenomena. The poor solubilizing capability of toluene was additionally supported for DPs without solvatochromic probes using MD simulations. Based on the collected λmax values we also estimate the extent of swelling for the different solvents and generations. Finally, the solvent and g dependence of the two series studied here was compared with the data by Hawker, Wooley and Fréchet on dendrons with different chemical structure, with the aim to find out whether the differences in packing and density of the branches of DPs and dendrimers can actually be recognized.
Methods
UV-Vis spectroscopy
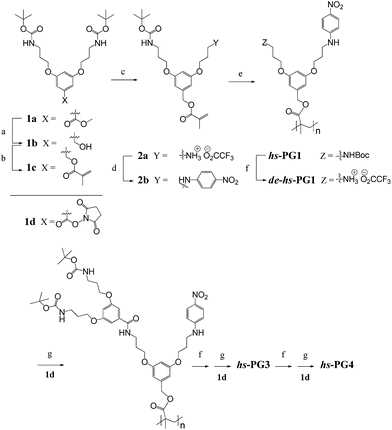
All measurements were performed in a thermostat ensuring 25 °C throughout the measurement unless otherwise noted. A number of control experiments were performed for at least one representative of each of the two series, hs-PGg and ls-PGg, of dendronized polymers used. At first it was investigated whether there is a concentration and time dependence of the UV-Vis spectra. The applied concentrations for the series hs-PGg and ls-PGg were different due to the rather different ratio of solvatochromic probe to the rest of the polymer, which required using more of ls-PGg to obtain reasonable signal intensities. Typical concentration ranges were hs-PG1: 3–30 μM in DMF and ls-PG2: 0.14–1.4 mM in MeOH. Fig. 2a shows representative spectra for hs-PG1 in DMF and for ls-PG2 in methanol which indicate negligible concentration dependence (within ±0.5 nm). The time dependence was explored to determine whether equilibrium conditions were reached and whether eventual adsorption phenomena of dendronized polymers to glass surfaces would occur. In general, the time elapsing between sample preparation and measurement was 1 h. Fig. 2b shows two extreme cases. One in which the waiting time was on the order of 1 d and the other on the order of 4 months. Because there was no detectable change compared to the spectra recorded after 1 h, equilibrium conditions were reached already then. Changes in absorbance during the 4 months were due to evaporation. Also, adsorption to glass surfaces was not observed. Thus there are no dependences on the above factors that would have to be considered in data analysis. Next, the temperature dependence of the UV-Vis spectra was explored in the range of 25–85 °C using the examples: hs-PG1, dioxane; hs-PG3, dioxane; hs-PG3, DMSO; ls-PG3, dioxane. Fig. 2c shows the development of λmax values for the two cases hs-PG3 and ls-PG3 in DMSO and dioxane, respectively. As can be seen, there is in fact some temperature dependence but in no case it exceeds 7 nm. The trend in this development is always the same. With increasing temperature, λmax values gradually (and reversibly) decrease (Fig. 2d) by virtually the same amount.Toluene was treated as a special case because of its generally poor solubilizing capability which furthermore differed for the two series investigated. While for the g = 3–4 members of the hs-PGg series, toluene is a particularly poor solvent in the entire temperature range from 25–85 °C, for the ls-PGg series, the same solvent is poor for all temperatures below the theta temperature (which varies with g and lies in the temperature range investigated), and a good solvent above. Corresponding UV-Vis spectra are shown for the latter case where one sees the impact poor solubility has on spectral appearance (Fig. 2e). With decreasing temperature an increasing offset from the baseline is observed which originates from superimposed scattering effects. Depending on the wavelength dependence of the scattering intensity such effects could result in a shift of λmax values. Literature evidence points towards a hypsochromic direction of this shift.14 In a first approximation we consider the λmax values of the hs-PGg series in toluene a lower threshold. Finally, Fig. 2f shows the UV-Vis spectra of the hs-PG1–4 series in chloroform as they were used for determination of λmax. For comparison purposes the spectrum of the corresponding monomer 2b (hs-MG1) is added. The appearance of this series in all other solvents (except toluene) and of the other series in all solvents (except toluene) is identical. All other UV-Vis spectra are compiled in Fig. S1–S10 in the ESI.† The UV-Vis spectra of ls-PG3 in methanol and ls-PG4 in several solvents showed scattering effects which were corrected for by a routine procedure delineated in the ESI.†
In a first attempt to rationalize the data, we make the simplified approximation that λmax values in different media are additive as indicated by eqn (1).
| λ = xsλs + xDPλDP | (1) |
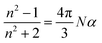 | (2) |
This equation shows the refractive index, which is proportional to the dielectric constant (εr ∝ n2), to be dependent on density. The dielectric constant in turn is related to the magnitude of the solvatochromism (λmax). As the present study aims at unraveling the differences in λmax values of series of DPs with different generations g rather than at an interpretation of absolute values, neither volume changes were considered nor possible non-linear effects in the relation between the composition (xi) and Δλ.
Results and discussion
The hs-PGg series was synthesized by a homopolymerization/post-polymerization dendronization protocol while the ls-PGg series was obtained from a copolymerization/post-polymerization dendronization protocol. In all post-polymerization dendronizations the targeted final g was realized in a g by g fashion. The monomer for the hs-PGg series was methacrylate 2b and the monomers for ls-PGg series were 1c and 2b (all shown in Scheme 1). The synthesis of monomer 1c starting from the known compounds 1a and 1b has already been reported.16 Monomer 2a was obtained from 1c by deprotection with trifluoroacetic acid (TFA) which resulted in a statistical mixture of two deprotection products (2a and the completely deprotected analog) and unreacted starting material. Column chromatographic work-up afforded multigram quantities of the desired product 2a. Reaction of 2a with p-fluoronitrobenzene gave macromonomer 2b. Polymer hs-PG1 was obtained from macromonomer 2b by free-radical polymerization using azobisisobutyronitrile (AIBN) as initiator. Since nitroaromatic compounds are known to retard radical polymerization,17 3.3 mol% of initiator were applied. hs-PG1 was obtained on the 500 mg scale as an amorphous powder. Polymer ls-PG1 was synthesized in analogy to hs-PG1 starting from a mixture of both monomers 1c and 2b in the ratio 1c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2b = 98
2b = 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (Scheme 2). Copolymer composition was confirmed by quantitative UV-Vis spectroscopy to be the same as the monomer feed. While it has not been verified, it is assumed that this copolymer is random. The molar masses of both polymers were determined by GPC using standard polystyrene calibration. Typical chain lengths were Pn = 150 (PDI = 2) for hs-PG1 and Pn = 700 for ls-PG1 (PDI = 3). While these chain lengths were considered long enough to not have to consider main chain end effects, this of course needed to be shown. TM-AFM analysis confirmed the chains of both polymers to be linear. Next both polymers were subjected to sequential dendronizations (Schemes 1 and 2) using the commercially available g = 1 dendronization reagent 1d (Scheme 1). The procedures were identical to those reported for the homopolymers of 1c.16 The structural perfection (conversion per postpolymerization dendronization) of the dendronized polymers from our laboratory are commonly determined by labeling of eventually present non-dendronized peripheral amine groups with the Sanger reagent.18 As in the present two series the installed solvatochromic probe absorbs very similarly to polymers modified by the Sanger reagent, this method could not be reasonably applied anymore. We therefore departed to dansyl labeling which had also proved successful in related quantification studies.19 Both polymers carrying the solvatochromic probe showed negligible fluorescence themselves. Typical perfections were >98% for all g. These very high values were independently confirmed by thermogravimetric analysis, with which the content of Boc-protecting groups can be determined (±3%).20 The spectroscopic work was started by doing several control experiments in order to assess and possibly exclude eventual concentration and temperature effects and to ensure that the measurements were done under equilibrium conditions. Furthermore it was of interest to see whether measurements in the poor solvent toluene could reasonably be performed. As Fig. 2 in the Methods section shows, all measurements were unproblematic and furnished interpretable results. The solvents used are listed in Fig. 3b.
2 (Scheme 2). Copolymer composition was confirmed by quantitative UV-Vis spectroscopy to be the same as the monomer feed. While it has not been verified, it is assumed that this copolymer is random. The molar masses of both polymers were determined by GPC using standard polystyrene calibration. Typical chain lengths were Pn = 150 (PDI = 2) for hs-PG1 and Pn = 700 for ls-PG1 (PDI = 3). While these chain lengths were considered long enough to not have to consider main chain end effects, this of course needed to be shown. TM-AFM analysis confirmed the chains of both polymers to be linear. Next both polymers were subjected to sequential dendronizations (Schemes 1 and 2) using the commercially available g = 1 dendronization reagent 1d (Scheme 1). The procedures were identical to those reported for the homopolymers of 1c.16 The structural perfection (conversion per postpolymerization dendronization) of the dendronized polymers from our laboratory are commonly determined by labeling of eventually present non-dendronized peripheral amine groups with the Sanger reagent.18 As in the present two series the installed solvatochromic probe absorbs very similarly to polymers modified by the Sanger reagent, this method could not be reasonably applied anymore. We therefore departed to dansyl labeling which had also proved successful in related quantification studies.19 Both polymers carrying the solvatochromic probe showed negligible fluorescence themselves. Typical perfections were >98% for all g. These very high values were independently confirmed by thermogravimetric analysis, with which the content of Boc-protecting groups can be determined (±3%).20 The spectroscopic work was started by doing several control experiments in order to assess and possibly exclude eventual concentration and temperature effects and to ensure that the measurements were done under equilibrium conditions. Furthermore it was of interest to see whether measurements in the poor solvent toluene could reasonably be performed. As Fig. 2 in the Methods section shows, all measurements were unproblematic and furnished interpretable results. The solvents used are listed in Fig. 3b.
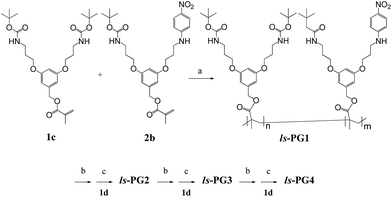 | ||
| Scheme 2 Synthesis of copolymer series ls-PG1 to ls-PG4. Reagents, conditions and yields: (a) AIBN, DMF, 65 °C, 15 h, 92%. (b) TFA, 15 h, ∼100%. (c) 1d, Et3N, DMAP, DMF, 6–20 d, ∼70%. | ||
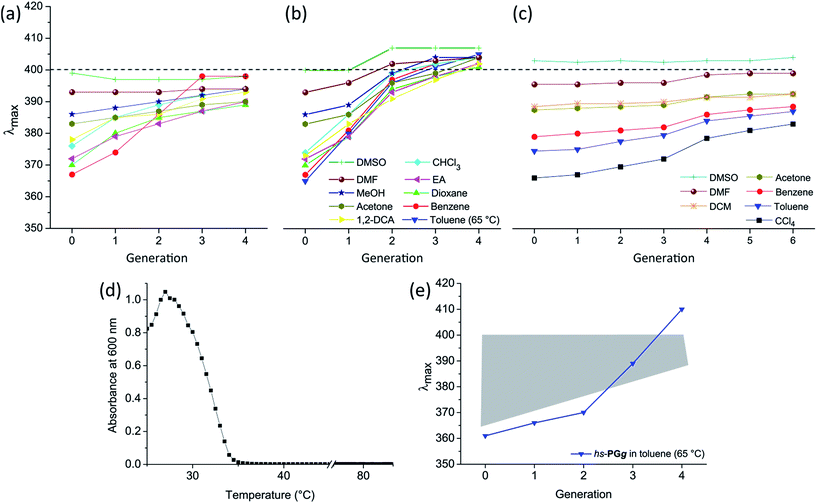 | ||
| Fig. 3 UV-Vis spectroscopic results. Comparison of dependence of λmax on solvent and on g for the hs-PGg series (without toluene) (a), the ls-PGg series (b) and Fréchet-type g = 1–6 dendrons of different chemical structures (c). The right hand graph was generated using the λmax values of ref. 7. The dashed line serves as an aid to the eye. (d) ls-PG3 in toluene studied in the temperature range 25–85 °C. Plot created with data from Fig. 2e. Blue curve: λmaxversus temperature. Black curve: Absorbance at 600 nm versus temperature (applied for determination of Tθ). (e) Dependence of λmax on g for the hs-PGg series in toluene at 65 °C contrasted to a grey area covering all other solvents (at 25 °C) as shown in (a). | ||
Fig. 3a–c compares the solvent and g-dependence of the hs-PGg series, the ls-PGg series and Fréchet-type dendrons from a previous study by different authors.7 All series start from a “g = 0” representative which for the hs-PGg series refers to monomer 2b and for the ls-PGg series to the monomer mixture 1c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2b = 98
2b = 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. For the three g = 0 cases the λmax range is similarly broad and covers a range of 32–37 nm for all solvents (a list of λmax and
2. For the three g = 0 cases the λmax range is similarly broad and covers a range of 32–37 nm for all solvents (a list of λmax and ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) max values can be found in the ESI†). This shows the validity of comparing the discussed DPs with the previous work on dendrons by Hawker, Wooley and Fréchet who utilized a closely related solvatochromic probe in a variety of solvents. In all series there is a tendency for the more polar solvents to exhibit larger λmax values than the less polar solvents. Also there is a trend towards larger λmax values with increasing g. A more detailed look in the arrays of curves discloses significant differences though. For example, when going from g = 1 to g = 4 the hs-PGg series narrows down to a λmax range of 11 nm centered around 395 nm. The ls-PGg series instead narrows down more strongly to a range of approximately 7 nm and centers at an even higher λmax (400 nm). It seems that for a given g the solvatochromic probes in the ls-series are more effectively shielded from solvent interactions than the hs-series. In other words, the narrowness of the λmax range observed for g = 4 in ls-PGg suggests the different solvents to only have a minor impact on the probe anymore. While the osmotic pressure forces the solvents to still penetrate the DP, the probe increasingly “feels” the branches only and thus the λmax observed should be near the value intrinsic to the branches. Extending this argumentation to the ls-PGg series with g > 4 (for ls-PG5 see ESI;† since scattering was so pronounced, we had to refrain from further usage of this data) makes us propose λmax at the hypothetical maximum generation gmax to be somewhat above 400 nm. Although there are structural differences between the ls- and hs-series, given the identical nature of their dendrons, it is likely that higher g representatives of the hs-series would also exhibit λmax > 400 nm when reaching gmax.
max values can be found in the ESI†). This shows the validity of comparing the discussed DPs with the previous work on dendrons by Hawker, Wooley and Fréchet who utilized a closely related solvatochromic probe in a variety of solvents. In all series there is a tendency for the more polar solvents to exhibit larger λmax values than the less polar solvents. Also there is a trend towards larger λmax values with increasing g. A more detailed look in the arrays of curves discloses significant differences though. For example, when going from g = 1 to g = 4 the hs-PGg series narrows down to a λmax range of 11 nm centered around 395 nm. The ls-PGg series instead narrows down more strongly to a range of approximately 7 nm and centers at an even higher λmax (400 nm). It seems that for a given g the solvatochromic probes in the ls-series are more effectively shielded from solvent interactions than the hs-series. In other words, the narrowness of the λmax range observed for g = 4 in ls-PGg suggests the different solvents to only have a minor impact on the probe anymore. While the osmotic pressure forces the solvents to still penetrate the DP, the probe increasingly “feels” the branches only and thus the λmax observed should be near the value intrinsic to the branches. Extending this argumentation to the ls-PGg series with g > 4 (for ls-PG5 see ESI;† since scattering was so pronounced, we had to refrain from further usage of this data) makes us propose λmax at the hypothetical maximum generation gmax to be somewhat above 400 nm. Although there are structural differences between the ls- and hs-series, given the identical nature of their dendrons, it is likely that higher g representatives of the hs-series would also exhibit λmax > 400 nm when reaching gmax.
We note that the value for gmax of λmax > 400 nm might, misleadingly, suggest the interior of the DPs to have a ‘polarity’ comparable to the solvent DMSO despite the differences in structure that would not suggest this similarity. The fact that λmax values of chromophores dissolved in bulk polymeric matrices are higher than in low molecular weight solvents has been reported earlier21 and can be rationalized by the above mentioned Lorentz–Lorenz eqn (2). This equation links the refractive index, which is proportional to λmax, to the density of the solution (molecules per unit volume). Thus, λmax values appear higher because of the increased density within the dendritic structure suggesting that polarity comparisons of this nature may not be valid. Following the observations and data of Fuoss et al. on the dependence of the dielectric constant of organic fluids on pressure,22 one is tempted to explain this effect as a consequence of the high internal pressure of DPs which counteracts the osmotic pressure of the solvent.
When comparing both series of DPs with the dendron series (Fig. 3c), the differences between these two substance classes immediately become evident. While both DP series converge fast, the dendrons even at g = 6 have by far not converged to the same degree. Their structures are more open and better solvent penetrable and even higher g representatives (than g = 6) would be required to have similar effects as observed for DPs already at g ≤ 4. It can be argued that the studied types of DPs and dendrimers differ in their chemical structure of the branch units and that this could cause the differences in the UV-Vis results. While chemical structure will certainly play a role, the distance between the branch points in the dendrimer are shorter than in the DPs. Thus, the branches in the dendrimer are tighter, suggesting that if all dendrons would be of the same kind, the observed effect would even be more pronounced. Looking at the analysis from a different vantage point one recognizes that this difference in openness may have impact on reactions within a dendritic branch work. While for a given g the choice of solvent will have little effect for DPs, for dendrimers different solvent polarities will still show to a larger degree, and can be taken advantage of.
So far we excluded toluene from the discussion as far as the hs-PGg series was concerned and also did not draw the attention to the fact that for the ls-PGg series the measurements in toluene were performed at elevated temperature. We would now like to turn our attention to this solvent. A g = 4 DP whose chemical structure resembles very much the ls-PGg series, has been studied in toluene by means of light scattering.10e The only structural difference of this particular g = 4 DP, which is here referred to as PG4, to the polymers used in this study is that it does not contain any solvatochromic probe (m = 0 in ls-PGg, Fig. 1). PG4 was found to have a theta-temperature (Tθ) at 28 °C which means that below this temperature the branched side chains are collapsed meaning that they are de-solvated and above, the branches are solvated to equilibrium. A consequence of the side chain collapse is aggregation of the entire macromolecules causing the previously transparent solutions to turn opaque. Given the fact that the ls-PGg series of interest in the present work differs from this polymer only by the 2% of the repeat units that carry the solvatochromic probe it was expected that ls-PG4 and possibly also the lower generations of this series show similar effects. And in fact, when measuring temperature dependent UV-Vis spectra of toluene solutions of ls-PG2–4 (not ls-PG1 though) Tθ were observed which differed from g to g and for ls-PG3 was at Tθ = 34 °C. This was concluded from the absorbance at 600 nm versus temperature plot, where extrapolation of the slope gave Tθ (Fig. 3d). The absorbance at λ = 600 nm was chosen because it is mainly caused by scattering of the aggregates rather than intrinsic polymer absorption. With this series, all measurements were therefore performed at 65 °C, and the resultant curve of the λmax dependency on solvent and g fits well within the normal range (Fig. 3b). Please note that a slight λmax dependence of temperature was observed in the control experiments for several solvents (Methods section) and that therefore the λmax values given for toluene when extrapolated to room temperature will be a few nm higher.
The structural differences between the hs- and the ls-PGg series are more pronounced than between the latter series and PG4. It was thus expected that toluene may exhibit even stronger effects for hs-PGg, which in fact proved to be the case. Polymers hs-PG3–4 did not fully dissolve even at the highest applicable temperature of 85 °C. Nevertheless, all members of this series showed at least a minimum solubility which enabled to record UV-Vis spectra. Although this limited solubility led to superposition of absorption and scattering effects, the λmax values were still considered reliable (see Methods section). Fig. 3e shows the λmax values obtained for the different g contrasting them by means of a grey area to the entire range of λmax values for all other solvents, as is detailed in Fig. 3a. This comparison makes clear that the polymers hs-PGg in toluene behave rather uniquely. Not only is the slope of the λmaxversus g dependence much steeper, but also the λmax value of 410 nm observed for g = 4 is beyond what was observed before. At this point we remind of a study mentioned above according to which PG4 collapses in toluene below Tθ. Although the chemical structures of PG4 and hs-PG4 are different, it is likely that such collapse also takes place here. If this was the case the λmax value of 410 nm would reflect the effect of the intrinsic polarity of the branch work on the solvatochromic probe.
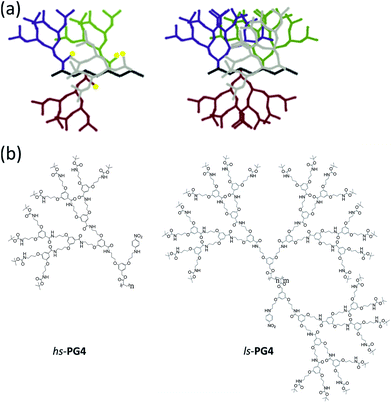
In an attempt to shed more light on this aspect, MD simulations were performed on PGg (without solvatochromic probes) for the solvents chloroform and toluene. Fig. 4a shows the dependence of the volume fraction for the two solvents on the radius for the generations g = 2–4 and Fig. 4b and c show a cross-sectional view of the incorporated solvent molecules for a slice of PG4 consisting of 90 repeat units. Both kinds of representations indicate that chloroform is the better solvent than toluene. The cross-sectional views nicely exhibit chloroform to penetrate deeper into the DPs interior than toluene which supports the above proposal that toluene can lead to collapse of branches.
Having collected all these results we next used them to estimate a degree of swelling Q for the DPs in dependence of solvent and g. Typically Q is defined as the relative increase of volume of a sample or object (here: DP) swollen with solvent compared to the same object in bulk. Here we use an approach that is based on analysis of the various λmax values obtained and assume that the mixing rule formulated by eqn (1) holds true. We define two extreme points, λs and λDP, and conclude where in the range spanned by these values the λmax values of the various sample are and the relative degree of swelling the samples therefore encounter. The first point refers to monomer 2b for which it is reasonable to assume that its chromophore is fully solvated irrespective of the nature of the solvent. Its λmax values are thus comparable to those of a fully swollen DP and are therefore referred to as λs (where s stands for solvent). The other point refers to chromophores which are not solvated but rather fully surrounded by branches. Based on the above argumentation, hs-PG4 collapsed in toluene is likely to represent that situation. The corresponding λmax value is thus referred to as λDP because it reflects the situation of the chromophore within a solvent-free DP independent of g. All λmax values of Fig. 5 were then normalized by the reference point λs using eqn (3), resulting in λnorm values independent of solvent-specific effects. These values define each sample's position in the range of λmax values between the two reference points λs and λDP and thus provide a measure for the swelling for each sample.
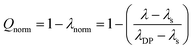 | (3) |
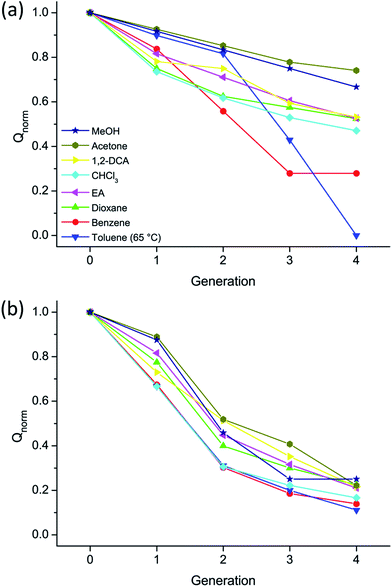 | ||
| Fig. 5 Comparison of degree of swelling Qnormversus g for hs-PGg (a) and ls-PGg (b) in various solvents at room temperature (except for toluene). | ||
Fig. 5 displays the dependence of λnorm on g for the ls-PGg and the hs-PGg series. It does not consider the samples measured in DMSO and DMF because for these solvents the g dependence was particularly weak. As can be seen, there are significant differences between the two series. In general, Qnorm decreases more gently for the hs-PGg series than for the ls-PGg series as long as one does not consider the solvents benzene and toluene. In the former series these two solvents result in the most drastic decrease in swelling while in the latter series they behave similarly to the other solvents. The molecular scale reason for this difference still needs to be worked out. It is noted that for the ls-PGg series the degree of swelling already for g = 4 drops to 0.2 of the maximally possible value for some of the solvents.
Conclusions
The combined synthetic and UV-Vis spectroscopic study using two series of dendronized polymers (DP; g = 1–4), hs-PGg and ls-PGg, with different levels of substitution shows that these structural differences have a substantial effect on the solvation of the branches and thus on solvatochromic probes covalently attached at the innermost generation g = 1. In general, a higher substitution with chromophores, which is equivalent to a lower substitution with dendrons (hs-PGg series), allows for a better solvation of the solvatochromic probe. While this may be considered intuitive, there are substantial differences between the two series studied and also between these DPs and a series of dendrimers (g = 1–6) reported earlier by Fréchet et al. using a very similar probe. Despite the considerable differences in the level of substitution with dendrons, the two DP series converge much faster with g than the dendrimers. Already at g = 4, the solvent polarity impacts λmax of the solvatochromic probe by a few nm only, while for the dendrons investigated the λmax values for g = 4 still span a range of some 20 nm, which even for g = 6 does only decrease to 15 nm. This nicely reflects the differences in these two types of dendritic structures with the DPs having much less space available for their dendrons than the Fréchet-dendrimers (precisely: dendrons). In this context we emphasize that both DP series converge that strongly despite the fact that the hs-PGg series carries only about half of the dendrons of the ls-PGg, corresponding to a mass loss of 45% (for g = 4). Nevertheless, even this so heavily truncated series, hs-PGg, still behaves like a typical DP rather than a dendrimer in regard to its swelling behavior. End group effects therefore do not seem to play a role, as was already assumed. We conclude that for a given g, the interior of DPs is much less solvent penetrable, rendering it effectively independent of the medium used for dissolution. This is further support for our perception that high g DPs (g ≥ 5) are best viewed as molecular objects or nano-sized molecular colloids for which internal density fluctuation can exist and that, in contrast to porous solids, are able to swell (below gmax). In accordance with this perception, the degree of swelling as obtained from normalized λmax values decreases rapidly with g, in particular for the ls-PGg series.Another question of interest concerned information about the λmax value characteristic for pure probe-branch interactions. While for the described dendrimers such information could only be expected for even higher g representatives than the ones studied and is thus not available, two relevant observations were made for the DPs. Firstly, the ls-PGg series seems to converge at λmax = 405 nm and, secondly, the hs-PGg series, which in the studied solvents converges at somewhat lower values, in toluene shows λmax = 410 nm for g = 4. As discussed, in toluene even at 85 °C hs-PG4 is below the θ-point and thus in a collapsed state. Since this is supposedly the closest situation to a state where all solvent molecules are squeezed out, we propose λmax = 410 nm to reflect the probes to be surrounded by branches only. This is the first time that such an estimate can be given for a dendritic structure. Uncertainties however remain in regard to the impact of g-dependent densities on λmax values which may amount to a few nm. While not directly applicable because of slight structural differences, MD simulations support toluene to be in fact a poor solvent for hs-PG3 and hs-PG4 as can be seen from the finding that toluene cannot penetrate deep into the interior of the DPs studied while chloroform can.
Finally we note that the value of λmax = 410 nm might, misleadingly, suggest the interior of the DPs to have a polarity comparable to the solvent DMSO. Such comparison does not consider density differences of a chromophore dissolved in a solvent and embedded into a highly branched dendritic structure and should therefore be considered with care.
Acknowledgements
We acknowledge a long-lasting exchange with Prof. A. Halperin on the ‘nature’ of DPs. D. Messmer is thanked for his help with AFM measurements. Simulations have been supported by MINECO-FEDER funds (MAT2012-34498) and CESCA. C. G. thanks the Swiss National Science Foundation for financial support.Notes and references
- (a) D. A. Tomalia, A. M. Naylor and W. A. Goddard III, Angew. Chem., Int. Ed. Engl., 1990, 29, 138–175 CrossRef; (b) G. R. Newkome, C. N. Moorefield and F. Vögtle, Dendrimers and Dendrons: Concepts, Syntheses, Applications, Wiley-VCH, Weinheim, 2001 CrossRef; (c) J. M. J. Fréchet and D. A. Tomalia, Dendrimers and other Dendritic Polymers, John Wiley & Sons, New York, 2001 Search PubMed; (d) D. A. Tomalia, J. B. Christensen and U. Boas, Dendrimers, Dendrons and Dendritic Polymers: Discovery, Applications and the Future, Cambridge University Press, Cambridge, 2012 Search PubMed.
- (a) D. Boris and M. J. Rubinstein, Macromolecules, 1996, 29, 7251–7260 CrossRef CAS; (b) M. Ballauff and C. N. Likos, Angew. Chem., Int. Ed., 2004, 43, 2998–3020 CrossRef CAS PubMed.
- (a) P. G. DeGennes and H. J. Hervet, J. Phys., Lett., 1983, 44, 351–360 CrossRef CAS; (b) D. A. Tomalia, New J. Chem., 2012, 36, 264–281 RSC; (c) A. D. Tomalia, Adv. Polym. Sci., 2013, 261, 321–390 CrossRef; (d) M. Kröger, A. D. Schlüter and A. Halperin, Macromolecules, 2013, 46, 7550–7564 CrossRef.
- J. F. G. A. Jansen, E. M. M. de Brabander-van den Berg and E. W. Meijer, Science, 1994, 266, 1226–1229 CAS.
- P. Ceroni and G. Bergamini, Antenna Effects in Dendrimers in Encylopedia of Polymeric Nanomaterials, Springer-Verlag, Berlin-Heidelberg 2013, pp. 1–7 Search PubMed.
- We consider the term accessibility not ideal in this context as it commonly is used in relation with porous hard matter.
- C. J. Hawker, K. L. Wooley and J. M. J. Fréchet, J. Am. Chem. Soc., 1993, 115, 4375–4376 CrossRef CAS.
- (a) C. M. Cardona, J. Alvarez, A. E. Kaifer, T. D. McCarley, S. Pandey, G. A. Baker, N. J. Bonzagni and F. V. Bright, J. Am. Chem. Soc., 2000, 122, 6139–6144 CrossRef CAS; (b) S. Koenig, L. Müller and D. K. Smith, Chem.–Eur. J., 2001, 7, 979–986 CrossRef CAS PubMed; (c) S. C. Zimmerman, Y. Wang, P. Bharathi and J. S. Moore, J. Am. Chem. Soc., 1998, 120, 2172–2173 CrossRef CAS; (d) C.-H. Wong, H.-F. Chow, S.-K. Hui and K.-H. Sze, Org. Lett., 2006, 8, 1811–1814 CrossRef CAS PubMed; (e) Y. Tomoyose, D.-L. Jiang, R.-H. Jin, T. Aida, T. Yamashita, K. Horie, E. Yashima and Y. Okamoto, Macromolecules, 1996, 29, 5236–5238 CrossRef CAS.
- (a) R. Freudenberger, W. Claussen, A. D. Schlüter and H. Wallmeier, Polymer, 1994, 35, 4496–4501 CrossRef CAS; (b) A. D. Schlüter and J. Rabe, Angew. Chem., Int. Ed., 2000, 39, 864–883 CrossRef; (c) H. Frauenrath, Prog. Polym. Sci., 2005, 30, 325–384 CrossRef CAS; (d) A. Zhang, Prog. Chem., 2005, 17, 157–171 CAS; (e) A. D. Schlüter, Top. Curr. Chem., 2005, 245, 151–191 Search PubMed; (f) B. M. Rosen, C. J. Wilson, D. A. Wilson, M. Peterca, M. R. Imam and V. Percec, Chem. Rev., 2009, 109, 6275–6540 CrossRef CAS PubMed; (g) Y. Chen and X. Xiong, Chem. Commun., 2010, 46, 5049–5060 RSC; (h) J. I. Paez, M. Martinelli, V. Brunetti and M. C. Strumia, Polymers, 2012, 4, 355–395 CrossRef.
- (a) B. Zhang, R. Wepf, K. Fischer, M. Schmidt, S. Besse, P. Lindner, B. T. King, R. Sigel, P. Schurtenberger, Y. Talmon, Y. Ding, M. Kröger, A. Halperin and A. D. Schlüter, Angew. Chem., Int. Ed., 2011, 50, 737–740 CrossRef CAS PubMed; (b) B. Zhang, R. Wepf, M. Kröger, A. Halperin and A. D. Schlüter, Macromolecules, 2011, 44, 6785–6792 CrossRef CAS; (c) R. Pasquino, B. Zhang, R. Sigel, H. Yu, M. Ottiger, O. Bertran, C. Alemán, A. D. Schlüter and D. Vlassopoulos, Macromolecules, 2012, 45, 8813–8823 CrossRef CAS; (d) O. Bertran, B. Zhang, A. D. Schlüter, A. Halperin, M. Kröger and C. Alemán, RSC Adv., 2013, 3, 126–140 RSC; (e) A. Kroeger, B. Zhang, C. Rosenauer, A. D. Schlüter and G. Wegner, Colloid Polym. Sci., 2013, 291, 2879–2892 CrossRef CAS PubMed; (f) O. Bertran, B. Zhang, A. D. Schlüter, M. Kröger and C. Alemán, J. Phys. Chem. B, 2013, 117, 6007–6017 CrossRef CAS PubMed.
- A. D. Schlüter, A. Halperin, M. Kröger, D. Vlassopoulos, G. Wegner and B. Zhang, ACS Macro Lett., 2014, 3, 991–998 CrossRef.
- L. Liu, W. Li, J. Yan and A. Zhang, J. Polym. Sci., Part A: Polym. Chem., 2014, 52, 1706–1713 CrossRef CAS.
- M. J. Kamlet, J.-L. M. Abboud, M. H. Abraham and R. W. Taft, J. Org. Chem., 1983, 48, 2877–2887 CrossRef CAS.
- M. A. R. B. Castanho, N. C. Santos and L. M. S. Loura, Eur. Biophys. J., 1997, 26, 253–259 CrossRef CAS.
- (a) W. Heller, J. Phys. Chem., 1965, 69, 1123–1129 CrossRef CAS; (b) J. G. Dawber, J. Ward and R. A. Williams, J. Chem. Soc., Faraday Trans. 1, 1988, 84, 713–727 RSC.
- Y. Guo, J. D. van Beek, B. Zhang, M. Colussi, P. Walde, A. Zhang, M. Kröger, A. Halperin and A. D. Schlüter, J. Am. Chem. Soc., 2009, 131, 11841–11854 CrossRef CAS PubMed.
- P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, Ithaca, 9th print, 1975, p. 167 Search PubMed.
- B. Zhang, H. Yu, A. D. Schlüter, A. Halperin and M. Kröger, Nat. Commun., 2013, 4, 1993–2002 Search PubMed.
- R. Al-Hellani, J. Barner, J. P. Rabe and A. D. Schlüter, Chem.–Eur. J., 2006, 12, 6542–6551 CrossRef PubMed.
- Y. Hao, A. D. Schlüter and B. Zhang, Macromolecules, 2014, 47, 4127–4135 CrossRef.
- M. S. Paley, R. A. McGill, S. C. Howard, S. E. Wallace and J. M. Harris, Macromolecules, 1990, 23, 4557–4564 CrossRef CAS.
- J. F. Skinner, E. L. Cussler and R. M. Fuoss, J. Phys. Chem., 1968, 72, 1057–1064 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental procedures, characterization data, UV-Vis data and spectra, and data on MD simulations. See DOI: 10.1039/c5sc04609b |
| This journal is © The Royal Society of Chemistry 2016 |