2D 7Li Ultrafast CT-COSY: a new tool for the rapid measurement of tiny homonuclear lithium scalar couplings†
G.
Hamdoun
a,
B.
Gouilleux
b,
M.
Sebban
a,
G.
Barozzino-Consiglio
a,
A.
Harrison-Marchand
a,
P.
Giraudeau
bc,
J.
Maddaluno
a and
H.
Oulyadi
*a
aNormandie Univ, UNIROUEN, INSA Rouen, CNRS, COBRA (UMR 6014 & FR 3038), 76000 Rouen, France
bCEISAM, Université de Nantes, UMR CNRS 6230, 2 rue de la Houssinière, 44322 Nantes, France
cInstitut Universitaire de France, 1 rue Descartes, 75005, Paris, France
First published on 28th November 2016
Abstract
The measurement of small homonuclear 2J7Li–7Li scalar couplings relying on constant time (CT) COSY NMR suffers from strong time limitations. We describe the first Ultrafast CT COSY experiment on lithium 7, which provides a considerable acceleration in the study of the aggregation state and dynamics of n-BuLi/MeLi complexes.
Because they behave as both versatile bases and potent nucleophiles, organolithium derivatives are regarded as routine reagents in organic synthesis. However, these highly polar species tend to oligomerize in solution to form flexible aggregates of which reactivity can vary significantly and interfere with the envisaged applications. Practically, chemists seldom check the aggregation state of their reagents before handling because accessing this information is perceived as complex and tedious. Thus, organolithium reagents are employed, in most cases, empirically and their behaviour is seen as a black box requiring multiple experiments, fine-tuning of the reaction conditions and, often, unexplained addition of metallic salts of various kinds.
High-resolution NMR spectroscopy is the technique most frequently used to characterize the structures of organolithium derivatives directly in solution.1–8 This analysis gives a straight access to primary data such as the spin–spin6,7 Li–X (X: 13C, 15N) coupling constant and the multiplicity of the X nucleus,9–15 affording valuable clues about the structure of the aggregates adopted by the R–Li systems in solution. However, when lithium derivatives such as 15N unlabelled lithium amides, lithium alkoxides or lithium enolates are at stake, the multiplicity of nucleus X and the Li–X coupling constant are generally not observed, and the information provided by all conventional NMR experiments remains insufficient to conclude about the structure and aggregation of these compounds. In this context, that is not uncommon, a simple access to homonuclear Li–Li couplings becomes of fundamental importance.4
In practice, the identification of the 6Li homonuclear scalar coupling has been resolved in a conventional 1D 6Li NMR spectrum in only one case,16 this measurement being prevented by the signal line-widths in most cases.
Among the various homonuclear 2D NMR experiments used to detect and measure scalar spin–spin coupling, one can mention the CT-COSY,17 DQF-COSY18 and INADEQUATE16,19 experiments. With regards to lithium 6 nuclei, the INADEQUATE experiment is certainly the most commonly employed for ease of use and appreciable time saving in its 1D version.4,19,20 However, measuring 2J6Li–6Li scalar coupling remains difficult because of line broadening due to dynamic exchanges and may result in a poor estimate of the real value of the coupling constant. Moreover, the relatively long duration of the mixing period (1/4J) (≈1.25 s) in this experiment also causes a strong attenuation leading to an extremely poor signal-to-noise ratio.
Experiments with 6Li generally profit from the smaller linewidth of 6Li as compared to 7Li signals, but the larger 7Li homonuclear couplings (factor 2.64 due to the ratio γ(7Li)/γ(6Li)) are an attractive feature of 7Li experiments. Information about small 7Li homonuclear scalar coupling constants can be obtained by manipulating the time evolution of scalar couplings. Typically, we recently published a study based on the CT–COSY NMR experiment, from which 2J7Li–7Li coupling constants were obtained using different scalar J-coupling evolution times and by fitting the signal intensity ratio as a function of this J-evolution time.17 But the major limitation of this methodology is the long experiment time (several hours) required to record the associated arrayed 2D spectra. A long time is indeed necessary to acquire each 2D FID s(t1, t2), due to the repetition of numerous transients with incremented delays. Moreover, this limitation is amplified by the need to record series of 2D spectra with an incremented constant-time period. The most evident consequence is the timetable constraint, but a more fundamental limitation is the sensitivity to temporal instabilities leading to noise ridges along the F1 dimension. Moreover, the long experiment duration makes 2D NMR experiments unsuitable for unstable lithiated samples that evolve during the acquisition and also require keeping the NMR probe at low temperature for extensive periods of time.
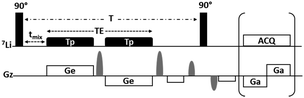
For a fast and easy measuring of 2J7Li–7Li coupling constants, Ultrafast (UF) NMR spectroscopy is an appealing alternative to reduce by several orders of magnitude the time required to carry out the 2D CT-COSY experiment.21,22 In this method, the incrementation of the evolution period t1 is replaced by a spatial encoding which is decoded during the detection period by an echo planar spectroscopic imaging (EPSI)23 detection scheme (Fig. 1) allowing the acquisition of a 2D spectrum in a sub-second duration.
Over the last ten years, the performance of UF experiments has been greatly enhanced by numerous methodological developments, which have made UF NMR applicable to a wide range of analytical situations such as quantitative metabolomics24 or real-time reaction monitoring.25 UF NMR is characterized by specific peculiarities and limitations which have been widely described,26 but when the sample concentration allows single-scan acquisitions, it is the fastest among the family of accelerated 2D NMR experiments.27 The first detection of quadrupolar nuclei by UF 2D NMR has been reported very recently on the example of deuterium (I = 1),28 but UF 2D NMR has never been exploited for nuclei with larger quadrupolar moments such as Lithium 7 (I = 3/2).
In this paper, we report on the first examples of 2D 7Li UF CT-COSY spectra from lithiated samples and on the usefulness of 2D UF CT-COSY NMR experiments for the characterization and quantitative estimation of the lithium coupling constants on various complexes of n-BuLi/MeLi as a model mixture.
The study begins with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 n-BuLi/MeLi solution in THF-d8 at 185 K,29 which corresponds to typical experimental conditions for these reagents. The 7Li NMR spectrum of 1
1 n-BuLi/MeLi solution in THF-d8 at 185 K,29 which corresponds to typical experimental conditions for these reagents. The 7Li NMR spectrum of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 n-BuLi/MeLi solution in THF-d8 at 185 K reveals the presence of eight separate signals corresponding to a statistical distribution of mixed tetramers with the following formula: (n-BuLi)4−n(MeLi)n (with n between 0 and 4).
1 n-BuLi/MeLi solution in THF-d8 at 185 K reveals the presence of eight separate signals corresponding to a statistical distribution of mixed tetramers with the following formula: (n-BuLi)4−n(MeLi)n (with n between 0 and 4).
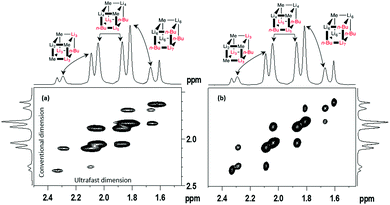
The assignment of the 7Li signals refers to the work by F. Paté et al.,30 and shows that each mixed aggregate is characterized by two signals in the 7Li NMR spectrum (Fig. 2).
The 7Li UF CT-COSY spectra are recorded thanks to the pulse sequence described in Fig. 1. This experiment includes a spatial encoding step achieved by a pair of linear frequency-swept pulses with a duration Tp applied together with a bipolar excitation gradient Ge, whose value is fixed to provide a dispersion in Hz equivalent to the frequency sweep of the pulses. The resulting signal is then decoded by an EPSI block consisting in a train of bipolar gradients Ga. Both power and duration of Ga are set according to the required spectral widths. Further details on acquisition and processing parameters are available in ESI.†
The resulting 2D 7Li UF CT-COSY NMR spectrum (Fig. 2a) shows the same correlation peaks as those observed on the conventional one at the following (F2; F1) positions: 2.29 ppm and 2.09 ppm, 2.04 ppm and 1.86 ppm, 1.81 ppm and 1.67 ppm. These values are typical of a homonuclear weak scalar coupling between the lithium signals belonging to the same mixed aggregates Li2/Li3 (n-BuLi)3(MeLi)1, Li4/Li5 (n-BuLi)2(MeLi)2 and Li6/Li7 (n-BuLi)1(MeLi)3, respectively.
The resolution of the UF spectrum is lower in F2 owing to intrinsic characteristics of spatial encoding, but is similar in F1. The asymmetric appearance of peak intensities for correlated signals of (n-BuLi)3(MeLi)1 and (n-BuLi)1(MeLi)3 complexes on each side of the diagonal should be noted; this effect is expected because such signals undergo different J-modulation effects in A3X spin systems as recently described by B. Gouilleux et al. (see below).31 These effects also explain the missing diagonal peak in the UF spectrum.
This comparison sheds light on the great potential of this UF approach as it provides similar information while considerably reducing the experiment duration (0.34 s versus 1 h 35 min). This time saving is particularly relevant in this study, which requires the time-consuming acquisition of a series of 2D NMR experiments with different J-coupling evolution times. Still, specific features of the UF approach should be taken into account such as the compromise between sensitivity, spectral width and resolution. These aspects have been widely described for 1H UF NMR,32–34 and similar effects should be expected here. However, some usual limitations of UF NMR become less critical in the case of 7Li. First, the impact of translational diffusion35,36 is much reduced since the spectra are recorded at low temperature (T = 185 K). Second, the small spectral width of 7Li makes the compromise between resolution and spectral width much less critical than for 1H.
A significant source of sensitivity losses that the UF experiment shares with its conventional counterpart is the J-modulation arising from the constant-time nature of the spatial encoding step.31 A theoretical description of this effect applied to a system of two coupled spins was already proposed by Wu et al.,37 who established an expression for the density matrix at the beginning of detection, which showed a J-modulation that was different for the diagonal peaks (cosine modulation: cos((2 × I)·π·J·T)) and cross-peaks (sine modulation: sin((2 × I)·π·J·T)). This modulation – depending on the scalar coupling constant J, on the total time spent in the transverse plane T and on the nature of the spins-system – can lead to sensitivity losses and even to missing spectral peaks for samples including different spins-systems. But as described by B. Gouilleux et al.,31 this J-modulation can also be controlled by adding a delay (tmix) prior to the spatial encoding step to tune this total time T = (TE + tmix) spent in the transverse plane. Due to the trigonometric nature of this J-modulation, there is an optimal T value, which maximizes the sensitivity for a given spin-system.
Here, this effect was optimized by recording a series of 2D 7Li UF CT-COSY spectra on the mixture of (n-BuLi)4−n(MeLi)n with different tmix values ranging from 0 to 0.16 s (Fig. S1, ESI†). From these spectra, an optimum delay tmix of 0.05 s can be chosen in order to optimize the overall sensitivity and avoid missing peaks.
Recently, we showed that the 2D CT-COSY technique in 7Li observation was an excellent method to accurately measure scalar 2J7Li–7Li couplings, regardless of the complexity and resolution of the 7Li NMR spectrum. The remarkable efficiency of this method for extracting small 2J7Li–7Li was demonstrated, for the first time, on a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 n-BuLi/MeLi model solution in THF-d8 with a total experimental time of ≈24 h.17 Here, our aim is to test the ability of the UF CT-COSY experiment, as a constant time approach, to predict homonuclear 7Li–7Li scalar coupling constant in a much shorter time.
1 n-BuLi/MeLi model solution in THF-d8 with a total experimental time of ≈24 h.17 Here, our aim is to test the ability of the UF CT-COSY experiment, as a constant time approach, to predict homonuclear 7Li–7Li scalar coupling constant in a much shorter time.
By performing a series of 2D 7Li UF CT-COSY experiments with different T values and then by graphically plotting the ratio of the cross peak volumes Icversus the diagonal peak volumes Id as a function of T, it is possible to determine 2J7Li–7Li from the simulation of the experimental graph as a tangent function of eqn (1). The discontinuity in the plot of the tangent function at T = 1/(6JLi–Li) contributes to the precision in the measurement of 2J7Li–7Li.38
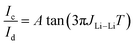 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 n-BuLi/MeLi complexes, 7Li–7Li scalar couplings measured from the conventional 2D CT-COSY experiments were very small and discontinuities in the graph showing Ic/Idversus T were attained for about 300–400 ms. Unfortunately, such constant time delays lead to large sensitivity losses in the 2D 7Li UF CT-COSY spectrum and no peaks could be detected for these values. These SNR losses were attributed to the transverse relaxation effect of the lithium nuclei. This observation is consistent with experimental measurements of T2, which show that the average lifetime of the 7Li signals in the transverse plane would be around 220 ms (Table S1, ESI†).
1 n-BuLi/MeLi complexes, 7Li–7Li scalar couplings measured from the conventional 2D CT-COSY experiments were very small and discontinuities in the graph showing Ic/Idversus T were attained for about 300–400 ms. Unfortunately, such constant time delays lead to large sensitivity losses in the 2D 7Li UF CT-COSY spectrum and no peaks could be detected for these values. These SNR losses were attributed to the transverse relaxation effect of the lithium nuclei. This observation is consistent with experimental measurements of T2, which show that the average lifetime of the 7Li signals in the transverse plane would be around 220 ms (Table S1, ESI†).
An approach that could avoid this complication involves the incrementation of the time duration of the adiabatic pulse Tp instead of the free evolution period tmix. This idea is based on recent theoretical investigations of relaxation effects in the rotating frame during adiabatic pulses.39,40 These works revealed that the relaxation rates R1ρ and R2ρ can be significantly decreased when increasing Tp while the time-bandwidth product of the pulse remains constant.
Fig. S2 (ESI†) shows several 2D 7Li UF CT-COSY spectra obtained from a solution of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 n-BuLi/MeLi in THF-d8 at 185 K with a spatial encoding delay “Tp” ranging from 50 ms to 215 ms.
1 n-BuLi/MeLi in THF-d8 at 185 K with a spatial encoding delay “Tp” ranging from 50 ms to 215 ms.
While for the 2D 7Li UF CT-COSY experiments with an incremented tmix delay, an almost total loss of signal occurs at a time T = (TE + tmix) around 250 ms (Fig. S1, ESI†), incrementing the length of the adiabatic pulse Tp results in a significantly enhanced lifetime in the transverse plane − greater than 440 ms (Table 1). The significant long life lithium signals due to an adiabatic pulse makes the 2D 7Li UF CT-COSY experiment well suited for the measurement of very weak homonuclear Li–Li scalar coupling. Still, 64 scans were necessary to obtain a sufficient SNR for peak integration, resulting in an experiment time of about 12 min, which remains much shorter than the duration required to record the conventional spectrum (1 h 35 min).
| TE (s) | 0.11 | 0.17 | 0.21 | 0.25 | 0.26 | 0.33 | 0.37 | 0.40 | 0.44 |
|---|---|---|---|---|---|---|---|---|---|
| I c/Id | 0.17 | 0.40 | 0.63 | 1.11 | 2.72 | 2.26 | 0.85 | 0.54 | 0.12 |
| SNR | 2934 | 1484 | 619 | 400 | 360 | 226 | 184 | 120 | 110 |
The 2D 7Li UF CT-COSY sequence was run for 15 spatial encoding adiabatic pulse delays “Tp” ranging from 50 ms to 200 ms on a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 n-BuLi/MeLi solution in THF-d8 at 185 K. 64 scans were recorded for each experiment for a total experimental time of ≈3 h (versus ≈24 h if a conventional experiment was used). All the 2D 7Li UF CT-COSY spectra were processed with the same parameters as described previously and the resulting data (ratio of the integrals as a function of “TE”) were then processed with GraphPad® software in order to obtain a graph representing the variation of the intensity ratio of the correlation peaks and diagonal peaks for the (n-BuLi)3(MeLi)1 and (n-BuLi)1(MeLi)3 tetrameric structures as a function of TE (Fig. 3). The resulting graph can be fitted to extract the active coupling for each cross-peak.
1 n-BuLi/MeLi solution in THF-d8 at 185 K. 64 scans were recorded for each experiment for a total experimental time of ≈3 h (versus ≈24 h if a conventional experiment was used). All the 2D 7Li UF CT-COSY spectra were processed with the same parameters as described previously and the resulting data (ratio of the integrals as a function of “TE”) were then processed with GraphPad® software in order to obtain a graph representing the variation of the intensity ratio of the correlation peaks and diagonal peaks for the (n-BuLi)3(MeLi)1 and (n-BuLi)1(MeLi)3 tetrameric structures as a function of TE (Fig. 3). The resulting graph can be fitted to extract the active coupling for each cross-peak.
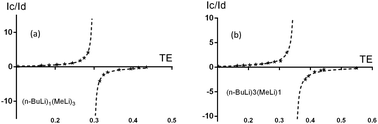 | ||
| Fig. 3 Variations of integration ratios Ic/Id as a function of TE for (a) (n-BuLi)1(MeLi)3, (b) (n-BuLi)3(MeLi)1 aggregates. | ||
Fig. 3 shows the correlation peak to diagonal peak intensity ratio plotted against TE for the Li6–Li7, Li2–Li3 pairs. The curve is adjusted using the function A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) tan(3πJLi–LiTE) where A is a scaling factor to account for misrepresentation of intensities in integrals.
tan(3πJLi–LiTE) where A is a scaling factor to account for misrepresentation of intensities in integrals.
The derived J splittings for (n-BuLi)3(MeLi)1 and (n-BuLi)1(MeLi)3 tetramers lithium signals were 0.558 ± 0.005 Hz and 0.475 ± 0.005 Hz, respectively. These values, in perfect agreement with those obtained by the standard 2D CT-COSY method,17 highlight the effectiveness of the 2D 7Li UF CT-COSY approach, if the delay of the encoding adiabatic pulse is incremented, in the measurement of very weak 7Li–7Li scalar coupling, with a total experiment time divided by eight.
In the present work, we have demonstrated the usefulness of the UF CT-COSY experiments for the case of quadrupolar nuclei such as 7Li. Moreover, it is the first time that UF experiments are performed at low temperature. Therefore, this technique can certainly be regarded as a tool worthy of being added to existing NMR toolbox for the determination of mixed-aggregates arrangements in the field of organolithium chemistry.
We have also presented a robust and fast method for the assignment and determination of homonuclear splitting in cases where scalar couplings cannot be extracted because of the signal linewidths, due to the large quadrupole moments of the 7Li nucleus. Our strategy was to increment the length of the adiabatic pulse instead of the tmix delay to describe modulation of signal intensities by the spin–spin J-coupling. This led to a greater lifetime of lithium signals in the transverse plane, allowing easier measurements of weak 2J7Li–7Li homonuclear couplings, as illustrated in the case of a mixed tetramers (n-BuLi)4−n(MeLi)n. This approach may still show limitations in cases where the species at hand are structurally and dynamically inhomogeneous. In this case, different cluster sizes could coexist or interconvert and some signals of interest may decrease faster than others under transverse relaxation.
Still, we believe that the 2D 7Li UF CT-COSY experiment can be extended to other systems in which lithium cations are in close interaction. Work towards this goal is in progress.
This work has been partially supported by Rouen University, CNRS, INSA Rouen, ERDF and the Labex SynOrg (ANR-11-LABX-0029). We thank the Région Normandie for its support to this research through the CRUNCh network.
Notes and references
- L. M. Seitz and T. L. Brown, J. Am. Chem. Soc., 1967, 89, 1602 CrossRef CAS.
- H. L. Lewis and T. L. Brown, J. Am. Chem. Soc., 1970, 92, 4664 CrossRef CAS.
- F. W. Wehrli, J. Magn. Reson., 1978, 30, 193 CAS.
- H. Günther, J. Braz. Chem. Soc., 1999, 10, 241 CrossRef.
- A. C. Jones, A. W. Sanders, M. J. Bevan and H. J. Reich, J. Am. Chem. Soc., 2007, 129, 3492 CrossRef CAS PubMed.
- D. Li, I. Keresztes, R. Hopson and P. G. Williard, Acc. Chem. Res., 2009, 42, 270 CrossRef CAS PubMed.
- H. J. Reich, Chem. Rev., 2013, 113, 7130 CrossRef CAS PubMed.
- A. Harrison-Marchand and F. Mongin, Chem. Rev., 2013, 113, 7470 CrossRef CAS PubMed.
- P. I. Arvidsson and Ö. Davidsson, Angew. Chem., Int. Ed., 2000, 39, 1467 CrossRef CAS.
- T. Koizumi and O. Kikuchi, Organometallics, 1995, 14, 987 CrossRef CAS.
- R. D. Thomas, R. M. Jensen and T. C. Young, Organometallics, 1987, 6, 565 CrossRef CAS.
- J. Granander, R. Sott and G. Hilmersson, Chem. – Eur. J., 2006, 12, 4191 CrossRef CAS PubMed.
- R. Sott, J. Granander and G. Hilmersson, J. Am. Chem. Soc., 2004, 126, 6798 CrossRef CAS PubMed.
- W. Bauer, W. R. Winchester and P. V. R. Schleyer, Organometallics, 1987, 6, 2371 CrossRef CAS.
- A. Corruble, D. Davoust, S. Desjardins, C. Fressigné, C. Giessner-Prettre, A. Harrison-Marchand, H. Houte, M.-C. Lasne, J. Maddaluno, H. Oulyadi and J.-Y. Valnot, J. Am. Chem. Soc., 2002, 124, 15267 CrossRef CAS PubMed.
- O. Eppers, H. Günther, K.-D. Klein and A. Maercker, Magn. Reson. Chem., 1991, 29, 1065 CrossRef CAS.
- G. Hamdoun, M. Sebban, V. Tognetti, A. Harrison-Marchand, L. Joubert, J. Maddaluno and H. Oulyadi, Organometallics, 2015, 34, 1932 CrossRef CAS.
- D. Moskau, W. Frankmölle, O. Eppers, H.-E. Mons and H. Günther, Proc. – Indian Acad. Sci., Chem. Sci., 1994, 106, 1471 CAS.
- O. Eppers, T. Fox and H. Günther, Helv. Chim. Acta, 1992, 75, 883 CrossRef CAS.
- H. Oulyadi, C. Fressigné, Y. Yuan, J. Maddaluno and A. Harrison-Marchand, Organometallics, 2012, 31, 4801 CrossRef CAS.
- B. Gouilleux, L. Rouger and P. Giraudeau, eMagRes, 2016, 5, 913 Search PubMed.
- L. Frydman, T. Scherf and A. Lupulescu, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 15858 CrossRef CAS PubMed.
- P. Mansfield, Magn. Reson. Med., 1984, 1, 370 CrossRef CAS PubMed.
- T. Jézéquel, C. Deborde, M. Maucourt, V. Zhendre, A. Moing and P. Giraudeau, Metabolomics, 2015, 11, 1231 CrossRef.
- A. Herrera, E. Fernández-Valle, R. Martínez-Álvarez, D. Molero-Vílchez, Z. D. Pardo-Botero and E. Sáez-Barajas, Magn. Reson. Chem., 2015, 53, 952 CrossRef CAS PubMed.
- P. Giraudeau and L. Frydman, Annu. Rev. Anal. Chem., 2014, 7, 129 CrossRef CAS PubMed.
- L. Rouger, B. Gouilleux and P. Giraudeau, in Encyclopedia of Spectroscopy and Spectrometry, ed. G. E. Tranter and D. W. Koppenaal, Academic Press, Oxford, 3rd edn, 2017, p. 588 DOI:10.1016/B978-0-12-409547-2.12107-9.
- P. Lesot, P. Berdague and P. Giraudeau, Chem. Commun., 2016, 52, 2122 RSC.
- A temperature less than 200 K is required to reach a sufficient level of resolution for lithium 7 spectrum of n-BuLi/MeLi (1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), but we chose to work at 185 K, that is, in conditions which the lithium nuclei undergo a slow intra-aggregate exchange.
1), but we chose to work at 185 K, that is, in conditions which the lithium nuclei undergo a slow intra-aggregate exchange. - F. Paté, H. Oulyadi, A. Harrison-Marchand and J. Maddaluno, Organometallics, 2008, 27, 3564 CrossRef.
- B. Gouilleux, L. Rouger, B. Charrier, I. Kuprov, S. Akoka, J.-N. Dumez and P. Giraudeau, ChemPhysChem, 2015, 16, 3093 CrossRef CAS PubMed.
- Y. Shrot and L. Frydman, J. Chem. Phys., 2009, 131, 224516 CrossRef PubMed.
- P. Pelupessy, L. Duma and G. Bodenhausen, J. Magn. Reson., 2008, 194, 169 CrossRef CAS PubMed.
- Z. Wei, L. Lin, Q. Ye, J. Li, S. Cai and Z. Chen, J. Chem. Phys., 2015, 143, 024201 CrossRef PubMed.
- Y. Shrot and L. Frydman, J. Chem. Phys., 2008, 128, 164513 CrossRef PubMed.
- P. Giraudeau and S. Akoka, J. Magn. Reson., 2008, 192, 151 CrossRef CAS PubMed.
- C. Wu, M. Zhao, S. Cai, Y. Lin and Z. Chen, J. Magn. Reson., 2010, 204, 82 CrossRef CAS PubMed.
- F. Tian, P. J. Bolon and J. H. Prestegard, J. Am. Chem. Soc., 1999, 121, 7712 CrossRef CAS.
- M. Shalom, J. S. Dennis and G. Michael, Curr. Anal. Chem., 2008, 4, 8 CrossRef.
- S. Mangia, T. Liimatainen, M. Garwood and S. Michaeli, J. Magn. Reson. Imaging, 2009, 27, 1074 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cc08744b |
| This journal is © The Royal Society of Chemistry 2017 |