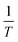Open Access Article
Open Access ArticleHighly effective adsorption of xanthene dyes (rhodamine B and erythrosine B) from aqueous solutions onto lemon citrus peel active carbon: characterization, resolving analysis, optimization and mechanistic studies†
Gholamhasan Sharifzade,
Alireza Asghari * and
Maryam Rajabi
* and
Maryam Rajabi
Department of Chemistry, Semnan University, Semnan 35195-363, Iran. E-mail: aasghari@semnan.ac.ir; Fax: +982333654110
First published on 17th January 2017
Abstract
The aim of this work is to study the adsorption of xanthene dyes, erythrosine B (EB) and rhodamine B (RB), in aqueous binary dye solution. A novel adsorbent powder was prepared by heating lemon citrus peels impregnated with phosphoric acid at 500 °C; the adsorbent was characterized by scanning electron microscopy (SEM), FT-IR spectroscopy, and surface potential studies. A speciation method was developed for two dyes that have overlapping spectral peaks using ratio derivative UV-visible spectrophotometry. The experiments were designed and optimized by experimental design and response surface methodology (RSM). The optimized adsorption conditions in the batch system were pH 4, an adsorbent dose of 0.3 g L−1, and an extraction time of 21 min. The isotherm adsorption capacities for EB and RB were 296 and 254 mg g−1, respectively. The adsorption rate studies showed that the removal of the dyes obeyed pseudo-second order kinetics. Thermodynamic studies showed that removal of the dyes from the binary solution was endothermic and spontaneous.
1. Introduction
Many countries face serious challenges regarding the preparation of safe drinking and sanitary water for human use because their natural sources of water are continuously contaminated by human activities.1The main factors involved in water contamination are industry, agriculture, and municipal waste effluents. These contaminated effluents comprise compounds such as nutrients, pesticides, heavy metals, petroleum derivatives, dyes, and other synthetic compounds.2–4 Some dyes are introduced into water from textile and dye-producing industries; other industries also play roles in water contamination.5 Dyes absorb sunlight, causing a decrease in the penetration of light into water; this is detrimental to the ecological cycle of water. In addition, dyes contain toxic compounds, such as benzene, xanthene, and aromatic amines, which are potentially hazardous to living organisms.6–8
Erythrosine B (EB) (Fig. 1) is a water-soluble anionic xanthene dye. It is used in cosmetics, pharmaceuticals, and foodstuffs, as well as for the analysis of vitamins, proteins, and diagnostic medicines. From these sources, EB is introduced into water and thus has undesirable effects on human health.9–11 It has previously been removed from aqueous solutions by adsorption.9,12–16 EB in dye mixtures has been analyzed by electrophoresis and derivative spectrophotometry.17–19
Rhodamine B (RB) (Fig. 1) is a cationic xanthene dye. It is used in the printing, textile, and photography industries. RB is toxic to human beings. Its use in foodstuffs is prohibited in many countries; however, it is still used illegally.20,21 RB has previously been removed from aqueous solution by adsorption,1,20,22,23 photo-catalytic degradation,24–27 coagulation, and flocculation.6,28 RB has also been traced by methods such as electrochemistry, HPLC,30 derivative spectrophotometry,21 chemoluminescence, fluorimetry, and UV-visible spectrophotometry.29
Adsorption is defined as the aggregation of liquid or gaseous molecules on the surface of a solid.8 Adsorption processes have many applications in industry, such as purification, preparation,31 gas storage, preconcentration,32 solar energy,33 and wastewater treatment.32 The physical forces involved in adsorption include interactions such as van der Waals forces, dipole–dipole forces, π–π interactions, and hydrogen bonding.8 Due to these relatively weak interactions, adsorption and desorption processes do not have high energy demands.34 The other processes used in dye removal are photochemical degradation, chemical reactions, biological degradation, and separation processes such as filtration and coagulation. Adsorption has some advantages over these processes, such as low initial cost, simple equipment, and facile removal without reminder particles.8
Derivative spectrophotometry is more selective than conventional spectrophotometry and allows for multi-component analysis.35,36
In multi-component mixtures in which the spectral peaks of two or more components overlap or a weak spectrum is obscured by a stronger peak or by impurities, derivative spectrophotometry can increase spectral signals and reveal peaks; thus, it can be used to produce background spectra and alter the structures of analytic spectra.37,38
Response surface methodology (RSM) is an optimization method that uses mathematical modeling to extract an empirical equation. In the involved equation, the dependent variable (response) is directly related to the independent variable:
| y = f(Bi,xi) + ε | (1) |
In eqn (1), y is the dependent variable (response), xi is the independent variable, Bi is the empirical coefficient, and ε is the residual error.
Compared with classical optimization methods, RSM gives more precise relationships between the parameters involved and requires fewer experiments. It also presents an equation (a model) to consider the interaction factor.39,40
In the present study, the adsorptions of xanthene dyes onto a novel adsorbent were investigated. Erythrosin B was used as a model anionic xanthene dye and rhodamine B was used as a model cationic xanthene dye. These dyes are similar in color and exist in wastewater effluent; therefore, their removal and determination are important. The adsorbent used was a novel low-cost active carbon which was prepared using lemon citrus waste peels. RSM and central composite design (CCD) were used in order to design and optimize the adsorption factors involved. The amount of adsorbent (g), extraction time (min), and pH were the three factors that were optimized using RSM. Ratio-derivative spectrophotometry was developed for speciation of these two dyes in their binary aqueous solution. The adsorption capacities of the adsorbent in single and binary dye solutions were determined by isotherm studies. It was determined that the adsorption capacity of this adsorbent is higher than that found in previous work. Also, the kinetics and thermodynamic parameters involved in the adsorption process were determined for single and binary dye solutions. A method is also presented in this work for the desorption of the dyes from the adsorbent. The adsorptions and desorptions were carried out in batch systems. To the best of our knowledge, there are no similar studies on the removal and determination of these dyes in their aqueous binary solution.
2. Experimental
2.1. Apparatus
Lemon citrus peel was carbonized in a simple electric furnace (Badi, Iran) without a blanket gas. SEM images of the adsorbent were acquired with a scanning electron microscope (CAM scan MV2300, Canada). FT-IR spectra were obtained on a Shimadzu FT-IR 8400 (Shimadzu, Japan). Dissolution and digestion of the dye stocks were carried out using an ultrasonic bath (Elma Sonic E 30H, Germany). The pH measurements were carried out using a pH 211 microprocessor pH meter and an HI 1131 electrode (HANA Instruments, Italy). The dye solutions and the adsorbent mixtures were stirred with a magnetic stirrer (IKA Labor Technik, Germany). Settlement and separation of the adsorbent from the dye solution were performed using a laboratory centrifuge (Pars Azma Co., Iran). The dye concentrations were measured with a Shimadzu UV-1650 PC UV-visible spectrophotometer equipped with UV-probe 2.42 software (Shimadzu, Japan).2.2. Materials
The EB and RB dyes were purchased from Sigma-Aldrich Company (USA) and were used without further purification. Hydrochloric acid, sodium hydroxide, phosphoric acid, and potassium nitrate solutions were all analytical grade and were purchased from Merck Company (Darmoshtat, Germany).2.3. Methodology
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 weight ratio with phosphoric acid solution (38%). This mixture was then left undisturbed for 24 h to allow acid penetration into the powder particles;23 the mixture was then transferred to an electric furnace; the temperature was increased by 5 °C min−1 up to 500 °C and was then fixed at this temperature for 3 h. The mixture was then cooled and subsequently transferred to a hot water container. The produced charcoal was washed with deionized water to pH 7 and until the conductivity of the rinse water decreased below 50 μs cm−1. The resulting active carbon was then dried at 80 °C, milled, and passed through an 80-mesh sieve.
3 weight ratio with phosphoric acid solution (38%). This mixture was then left undisturbed for 24 h to allow acid penetration into the powder particles;23 the mixture was then transferred to an electric furnace; the temperature was increased by 5 °C min−1 up to 500 °C and was then fixed at this temperature for 3 h. The mixture was then cooled and subsequently transferred to a hot water container. The produced charcoal was washed with deionized water to pH 7 and until the conductivity of the rinse water decreased below 50 μs cm−1. The resulting active carbon was then dried at 80 °C, milled, and passed through an 80-mesh sieve.The temperature was varied only during the thermodynamic studies. The adsorbent was weighed with an analytical balance and added to the dye solution. After the dye removal process, the adsorbent was separated by centrifugation at 3000 rpm. The solution pH was adjusted by the addition of hydrochloric acid solution or sodium hydroxide solution and was measured with a pH meter and a pH electrode. The adsorption capacity was calculated using eqn (2):
| q = [(C0 − C)/m] × V | (2) |
In eqn (2), q is the adsorption capacity (mg g−1), C0 and C are the initial and final concentrations (mg L−1) of the dye solution, V is the volume of the dye solution (L), and m is the adsorbent mass (g). The dye removal was calculated using eqn (3):
| Removal = [(C0 − C)/C0] × 100 | (3) |
A calibration curve was plotted based on the amplitudes of the peaks of the ratio derivative spectra at 532 nm for ER and at 552 nm for RB.
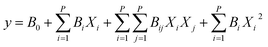 | (4) |
On the left side of eqn (4), y is the response phrase. On the right side, the 1st to 4th phrases relate to the constant effects, linear effects, interaction effects, and second-order effects, respectively. CCD comprises 2P + 2P + nc experiments, where P is the number of factors, 2P is the number of orthogonal (factorial) points, 2P is the number of axial (star) points, and nc is the number of central points.41 For 3 factors, 20 experiments were suggested (Fig. S1†).
3. Results and discussion
3.1. Physical and chemical characteristics of the adsorbent
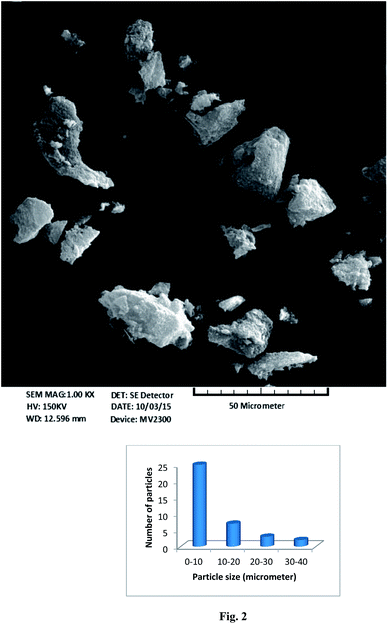
SEM images provide information about the morphologies of adsorbent particles.42 The size range of the adsorbent particles was approximately 2 to 40 μm (Fig. 2). The particles were not uniform, and two kinds of particles were observed: one was constructed from sheets attached to each other, and the other possessed a rough surface with a fine structure (Fig. S2†). The structures of these rough surfaces and parallel sheets may be responsible for the high adsorption capacity of the adsorbent.The chemical structure of an adsorbent affects the adsorption properties of the adsorbed matter. FT-IR spectroscopy can be used to determine the functional groups present in the adsorbed matter. In this study, dry KBr powder was mixed with the prepared adsorbent in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
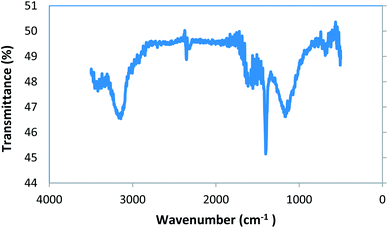
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 ratio, and a sample pellet was made. The resulting sample pellet was exposed to IR radiation. Important adsorption peaks were seen in the regions of 3000 to 3500 cm−1, 1400 to 1700 cm−1, and 1000 to 1300 cm−1 (Fig. 3).
100 ratio, and a sample pellet was made. The resulting sample pellet was exposed to IR radiation. Important adsorption peaks were seen in the regions of 3000 to 3500 cm−1, 1400 to 1700 cm−1, and 1000 to 1300 cm−1 (Fig. 3).
The intense broad peak in the area of 3000 to 3500 cm−1 may be assigned to the O–H bond stretching vibrations. This may be due to the presence of carboxylic acid and phenol groups in the adsorbent structure, together with the presence of a very small amount of water in the sample. The absorption peaks present from 1400 to 1700 cm−1 were assigned to the stretching vibrations of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and C–O bonds. The presence of these groups may also correspond to carboxylic acids or phenols. The absorption peaks from 1000 to 1300 cm−1 were assigned to two independent vibration stretches, C–O–C and P–O–P bonds. The presence of these groups may be related to the aromatic ethers, phosphate esters or polyphosphate chains present in the structure of the adsorbent.23,43–45
O and C–O bonds. The presence of these groups may also correspond to carboxylic acids or phenols. The absorption peaks from 1000 to 1300 cm−1 were assigned to two independent vibration stretches, C–O–C and P–O–P bonds. The presence of these groups may be related to the aromatic ethers, phosphate esters or polyphosphate chains present in the structure of the adsorbent.23,43–45
The surface charge of an adsorbent influences the adsorption of ionic dyes. Because ER and RB are, under varying conditions, anionic or cationic species in solution, the surface charge of the adsorbent was studied.
When the dissolution of an adsorbent in water decreases the pH of the solution, the surface charge of the adsorbent is negative. On the other hand, when dissolution of the adsorbent in water increases the pH of the solution, the surface charge of the adsorbent is positive.46,47 Also, when the dissolution of the adsorbent in water does not affect the solution pH, the adsorbent is neutral and has a zero potential surface.
In order to determine the surface charge of the adsorbent used, the pH value for 50 mL of KNO3 solution (0.1 M) was adjusted in the range of 1 to 8; then, 0.015 g of the adsorbent was added to the solution. This solution was then stirred with a magnetic stirrer for 24 h.
The new pH of the solution was subsequently determined and recorded. The difference between the final and initial pH values (pHf − pHi) was plotted against the initial pH value (pHi) (Fig. S3†). As can be seen in Fig. S3,† at a pH value between 3 and 4, the surface potential was almost zero. However, at other pH values, the surface potential was negative. The same results have been reported by others23,48 for natural active carbon adsorbents.
3.2. Determination of binary solution dyes
Because the UV-visible signals for the dyes overlap in their binary solution, it is difficult to determine the concentration of each dye. In Fig. 4, the UV-visible spectra for ER and RB in their pure and binary solutions can be observed. To resolve the overlapping peaks, ratio derivative spectrophotometry was used.35According to the Salinas method,35 eqn (5) was derived for the calculation of the concentration of erythrosine B in the binary dye solution.
| d/dλ(At/AR) = d/dλ(εE/εR × CR)CE | (5) |
Therefore, the plot of d/dλ(At/AR) vs. CE is a straight line with the inclination d/dλ(εE/εR × CR); this must remain constant at each wavelength. εR and εE are the molar absorption coefficients, and CR is the divider concentration. In this study, CR was empirically determined (5 mg L−1).
The same equation can be used to determine the concentration of RB in the binary solution.
In Fig. S4,† the ratio-derivative spectra of EB and RB are shown in the dye concentration range of 1 to 8 mg L−1 in the presence of 5 mg L−1 of the other dye. By plotting the amplitudes of the peaks at 532 nm for erythrosine B (EB) and at 552 nm for rhodamine B (RB) against the dye concentration, calibration equations were produced (Table 1).
3.3. Model development and evaluation
In this study, the effects of pH, adsorbent dose, and extraction time on the dye removal percentages were studied; the temperature and dye concentration were fixed at 25 °C and 20 mg L−1, respectively. The primary approximation range for each factor was found using the one-at-a-time approach. Five levels were defined for each factor using central composite design (CCD, Table 2).| Value | ||||||
|---|---|---|---|---|---|---|
| Factors | x1 (pH) | 2 | 2.81 | 4 | 5.19 | 6 |
| x2 (adsorbent) g | 0.005 | 0.0091 | 0.015 | 0.021 | 0.025 | |
| x3 (time) min | 5 | 9.1 | 15 | 21 | 25 | |
| Coded | X | 1.68 (−α) | −1 | 0 | +1 | +1.68 (+α) |
Table 3 shows the factors involved and the results obtained for 20 experiments (runs). The level of each factor and the order of each experiment were both designed according to special software based on the experimental design.
| No. of experiment | pH | Adsorbent (g) | Time (min) | EB Removal | RB Removal | ||
|---|---|---|---|---|---|---|---|
| Experimental | Predicted | Experimental | Predicted | ||||
| 1 | 6.00 | 0.0150 | 15.0 | 74 | 75.1 | 96.8 | 97.1 |
| 2 | 5.19 | 0.0091 | 9.1 | 63.6 | 64.0 | 95.0 | 94.9 |
| 3 | 4.00 | 0.0050 | 15 | 80.0 | 81.0 | 93.0 | 93.8 |
| 4 | 2.00 | 0.0150 | 15 | 99.8 | 100.0 | 97.0 | 97.2 |
| 5 | 4.00 | 0.0150 | 15 | 95.0 | 94.7 | 95.0 | 96.1 |
| 6 | 5.19 | 0.0210 | 9.1 | 95.4 | 92.8 | 95.9 | 95.6 |
| 7 | 4.00 | 0.0150 | 15 | 93.7 | 94.7 | 95.9 | 96.1 |
| 8 | 2.81 | 0.0091 | 21.0 | 99.6 | 100.9 | 97.6 | 97.5 |
| 9 | 4.00 | 0.0150 | 25 | 96.5 | 96.6 | 94.9 | 95.2 |
| 10 | 2.81 | 0.0210 | 9.1 | 99.7 | 100.3 | 90.0 | 90.3 |
| 11 | 4.00 | 0.0150 | 15 | 96.0 | 94.7 | 96.6 | 96.1 |
| 12 | 4.00 | 0.0150 | 5.0 | 89.0 | 90.8 | 90.0 | 90.2 |
| 13 | 4.00 | 0.0150 | 15 | 94.2 | 94.7 | 96.4 | 96.1 |
| 14 | 2.81 | 0.0210 | 21 | 95.0 | 93.2 | 99.3 | 99.0 |
| 15 | 4.00 | 0.0150 | 15 | 93.4 | 94.7 | 96.0 | 96.1 |
| 16 | 5.19 | 0.0210 | 21.0 | 94.4 | 95.6 | 96.3 | 96.6 |
| 17 | 4.00 | 0.0150 | 15.0 | 96.2 | 94.7 | 96.7 | 96.1 |
| 18 | 5.19 | 0.0091 | 21 | 80.0 | 78.0 | 92.8 | 92.0 |
| 19 | 4.00 | 0.0250 | 15 | 97.9 | 98.8 | 96.0 | 95.9 |
| 20 | 2.81 | 0.0091 | 9.1 | 99.3 | 96.8 | 93.2 | 92.6 |
Calculation of the equation coefficients and evaluation of the model were accomplished using analysis of variance (ANOVA, Table S1†).
3.4. Optimization of dye removal
The coded equation for the removal of EB from the binary dye solution is given by eqn (6):| R1 = 94.7 − 7.59X1 + 5.27X2 + 1.73X3 + 6.31X1X2 + 2.47X1X3 − 2.8X2X3 − 2.42X12 − 1.7X22 | (6) |
Removal of RB from the binary dye solution is given as eqn (7):
| R2 = 96.11 + 0.59X2 + 1.46X3 + 0.75X1X2 − 1.93X1X3 + 0.95X2X3 − 0.46X22 − 1.20X32 | (7) |
Eqn (8) can be used to convert the real value for each factor to the coded value, and vice versa:41
| Xi = (xi − x0i)/Δx | (8) |
Using eqn (6)–(8) and the values for all factors, it is possible to calculate the removal percentages in all areas where the model was established. The effectiveness of the dye removal shows the amount of desirability. For EB, the minimum dye removal was 63.6%, corresponding to a desirability of zero, and the maximum dye removal was 99.84%, corresponding to a desirability of 1. By considering the desirabilities for other dyes, the total desirability can be calculated by 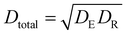 .41 Optimum conditions were selected to maximize the desirability (Table 4).
.41 Optimum conditions were selected to maximize the desirability (Table 4).
| Time (min) | pH | Adsorbent dose (g L−1) | Dye concentration (mg L−1) |
|---|---|---|---|
| 21 | 4.0 | 0.30 | 20 |
3.5. Surface response studies
Both the pH and the amount of adsorbent affect the removal of ER from a binary dye solution. The effects of these factors and their interactions are shown in Fig. 5a. | ||
| Fig. 5 Response surface diagrams for the removal percentages of EB (a–c) and RB (d–f) by the adsorbent. Initial dye concentration: 20 mg L−1; temperature: 25 °C; volume of dye solution: 50 mL. | ||
When drawing the diagrams of the surface responses, time was assumed to be the mean value (15 min). Increasing the amount of adsorbent enhanced the dye removal percentage. This is a common effect that has been observed in other studies.12 This effect is due to the increase in the number of active sites that react with the dye molecules. An increase in pH led to a decrease in the removal percentage of ER from the binary dye solution. This effect can also be seen in other studies of anionic dye removal by active carbon adsorbents.12–14,47–49 The reaction of a dye and an adsorbent is due to van der Waals forces, Π–Π polar interactions, and ionic interactions.8 It appears that attractive and repulsive ionic forces vary with changing pH, while other forces are constant.
EB (an acidic dye) has pKa = 5.3. Thus, when the pH is below 5.3, molecular EB is dominant. However, if the pH is higher than 5.3, anionic EB is dominant. Due to the negative charge on the adsorbent surface, EB is adsorbed at low pH, where there is no repulsive interaction.
Time has also been suggested to affect the adsorption of EB (Fig. 5b). The amount of adsorbent was assumed to be 0.015 g. With increasing time, the surface areas having high removal percentages will expand. This effect is due to mass transfer and diffusion in solution as well as to the surface of the adsorbent particles. With increasing time, adsorption increases.14
Time and the adsorbent dose have synergic effects on dye removal (Fig. 5c). When both factors are at a minimum, the removal amount will also be low.
The effects of pH, the adsorbent dose, and their interactions on the removal of RB from the binary dye solution are shown in Fig. 5d. In this surface response diagram, time was assumed to be the mean amount (15 min). An intermediate area with low dye removal is seen in this graph; the removal increases on either side of this area.
The pH value affects the ionization of acidic and basic dyes. It also changes the potential charge of the adsorbent surface. The potential charge of the adsorbent surface was negative in the pH range of 2 to 8; the negative charge increased at pH > 4 and pH < 3. Three forms have been reported for RB in aqueous solution: positively charged RB at low pH values (pH < 7), a zwitterion at high pH values (pH > 7), and a neutral molecule (lactonic) in non-polar or aprotic solvents.1,6
RB is positively charged in the entire pH region of the study; also, the dye adsorption depends on the surface charge of the adsorbent, which was minimal at pH 3 and 4 and high at the high and low ends of the region.
The effects of pH, extraction time, and their interactions on the removal of RB are shown in Fig. 5e. In this diagram, the assumed amount of the adsorbent was 0.015 g. By increasing the extraction time, the RB removal can be increased; this is due to mass transfer and the dependence of the diffusion on time.
The extraction time and the adsorbent dose had synergic effects on the removal of the dye (Fig. 5f). In this case, the pH was assumed to be 4.0. Maximum dye removal took place in the area with the maximum extraction time and adsorbent dose. Others have also mentioned this effect.22
3.6. Desorption
Desorption of the dyes from the adsorbent was carried out using NaOH solution (0.1 M). Approximately 0.5 g adsorbent was added to 50 mL of the solution in each experiment. The adsorbent was regenerated by soaking it for 24 h and stirring it for 1 h. Then, the adsorbent was rinsed away using deionized water until no dye remained in the effluent, the conductivity was 10 μs cm−1 and the pH was 7. As mentioned in Section 3.5, EB dye was not adsorbed at high pH. Regarding RB dye, at pH values greater than 7, RB converts from the cationic form to a zwitterion. It appears that at high pH, the RB zwitterion and EB anion were desorbed from the anionic surface and rinsed with OH− ions. The regenerated adsorbent was separated, dried at 80 °C, and reused. No change was distinguished in the removal capacity when the adsorbent was used three times.3.7. Adsorption isotherm
An isotherm is an equation that relates the adsorbate concentration in solution, Ce (mg L−1), to the amount of adsorbate on the adsorbent surface, qe (mg g−1). There are various types of isotherms. An isotherm curve gives information about the surface characteristics of an adsorbent and its affinity to the adsorbate. An isotherm was also used to determine the maximum amount of adsorbate (qmax) to be adsorbed.1The Langmuir isotherm is suitable for studying adsorption phenomena in which the adsorbent surface is homogenous and can adsorb a limited number of adsorbate molecules with constant energy during the entire adsorption process.
| Ce/qe = Ce/qm + 1/qmb | (9) |
The Freundlich isotherm is appropriate for heterogeneous surfaces in which multilayer adsorption can be explained by isotherm eqn (10).
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe = 1/n qe = 1/n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce + ln Ce + ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kf kf
| (10) |
In eqn (10), kf is the Freundlich constant (L mg−1) and 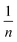 is the uniformity constant, for which n > 1 is favorable.20,49,50
is the uniformity constant, for which n > 1 is favorable.20,49,50
The Temkin isotherm assumes a linear decrease of the thermal energy of adsorption as it progresses. It is appropriate for heterogeneous surfaces. In contrast to the previous isotherms, it considers adsorbate–adsorbent interactions.
q = B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KT + B KT + B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce Ce
| (11) |
In eqn (11), KT is a constant related to the binding energy of adsorption (L mg−1) and B is a constant relating to the thermal energy of adsorption.1,20,49
The Dubinin–Radushkevich isotherm is appropriate for surfaces with unequal adsorption energies and porous adsorbents. It considers a heterogeneous surface with varying energy during the process.
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe = ln qe = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qD − BD[RT qD − BD[RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1 + 1/Ce)]2 ln(1 + 1/Ce)]2
| (12) |
The adsorption data for the ER and RB dyes in single solutions are compatible with the Langmuir, Freundlich, Temkin, and Dubinin–Radushkevich isotherms. The Langmuir isotherm is the most compatible with the experimental data. The R2 values of the equations for ER and RB are 0.994 and 0.998, respectively (Table 5); this means that the adsorbent surface is homogenous for a dye in a single solution.
| Isotherm | Parameter | Single solution | Binary solution | ||
|---|---|---|---|---|---|
| EB | RB | EB | RB | ||
| Langmuir | |||||
| Ce/qe = Ce/qm + 1/qmb. A plot of Ce/qe versus Ce should indicate a straight line with a slope of 1/qm and an intercept of 1/qmb | Qmax (mg g−1) | 296 | 254 | — | 129 |
| b (L mg−1) | 0.241 | 0.656 | — | 1.23 | |
| R2 | 0.994 | 0.998 | — | 0.990 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Freundlich | |||||
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe =1/n qe =1/n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce + ln Ce + ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kf. A linear plot of ln kf. A linear plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe versus ln qe versus ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce gives values of kf and 1/n Ce gives values of kf and 1/n |
n | 2.93 | 4.67 | 0.8562 | 5.1 |
| kf (L mg−1) | 86.64 | 124 | 2.57 | 73 | |
| R2 | 0.962 | 0.964 | 0.865 | 0.945 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Temkin | |||||
qe = B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KT + B KT + B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce. A plot of qe versus ln Ce. A plot of qe versus ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce gives the values of B and KT Ce gives the values of B and KT |
B | 58.23 | 34.99 | 64.14 | 16.57 |
| KT (L mg−1) | 3.12 | 37.9 | 0.186 | 104.58 | |
| b = RT/B | 42.55 | 70.80 | 38.63 | 149.52 | |
| R2 | 0.986 | 0.974 | 0.952 | 0.964 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Dubinin–Radushkevich | |||||
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe = ln qe = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qD − BD[RT qD − BD[RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1 + 1/Ce)]2 the values of qD and BD were calculated from the plot of ln ln(1 + 1/Ce)]2 the values of qD and BD were calculated from the plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe versus [RT qe versus [RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1 + 1/Ce)]2 ln(1 + 1/Ce)]2 |
qD (mg g−1) | 222 | 210 | 119.1 | 109 |
| BD (mol2 kJ−2) | 6.8 × 10−7 | 8.21 × 10−8 | 2.11 × 10−5 | 4.85 × 10−8 | |
| R2 | 0.832 | 0.830 | 0.979 | 0.877 | |
For the adsorption of RB in the binary dye solution, the data for RB is compatible with the Langmuir, Freundlich, Temkin, and Dubinin–Radushkevich isotherms, although the Langmuir isotherm is the most compatible, with R2 = 0.990 (Fig. S5† and Table 5).
The adsorption data for the adsorption of ER in the binary dye solution is compatible with the Freundlich, Temkin, and Dubinine–Radushkevich isotherms; however, the Dubinin–Radushkevich isotherm is the most compatible, with R2 = 0.979 (Fig. S5† and Table 5). This may be due to adsorbent–adsorbate interactions. In the binary dye solution, RB adsorption causes the homogenous surface of the adsorbent to convert to a heterogeneous surface for EB. Thus, RB adsorption obeyed the homogenous surface law, while EB adsorption obeyed the heterogeneous surface law. Other studies have found similar results.20 Comparing the adsorption of dyes in single solutions showed that the adsorption capacity of the adsorbent for EB is greater than that for RB. This is due to higher molecular weight of EB relative to RB and corresponds to van der Waals forces between the adsorbent and the adsorbate. However, the adsorption capacity of the adsorbent for EB in the binary solution was lower than that for the RB dye solution (Table 5). This is due to the positive charge of the RB dye molecules and the negative surface potential of the adsorbent, which facilitates the competitive adsorption of RB compared to EB. A comparison of the results of this work with other results shows that the adsorption capacities are higher relative to previous work; also, the adsorption times are better or comparable, and the pH values are comparable. This is obvious for both EB and RB dyes (Table 6).
| Dye | Adsorbent | Time of adsorption (min) | pH | Capacity of adsorbent (mg g−1) | Reference |
|---|---|---|---|---|---|
| EB | Commercial active carbon | — | 7.0 | 89.3 | 9 |
| Nanoparticle-loaded active carbon | 3.8 | 3.6 | 31.0 | 12 | |
| Nanoparticle-loaded active carbon | 4.5 | 4.0 | 37.5 | 13 | |
| De-oiled mustard active carbon | 60 | 3.5 | 3.52 | 15 | |
| Lemon waste active carbon | 21 | 4.0 | 296 | This study | |
| RB | Modified NiO nanoparticles | 30 | 7.0 | 111.1 | 1 |
| Modified montmorillonite | 120 | 4.0 | 188.6 | 20 | |
| Magnetic nanocomposites | 60 | 2.0 | 46.9 | 22 | |
| Lemon waste active carbon | 21 | 4.0 | 256 | This study |
3.8. Kinetics of adsorption
A sorption process consists of several steps that take place simultaneously or successively. It includes mass transfer in solution, diffusion in the vicinity of particles, adsorption reactions, and inter-particle diffusion. Thus, it is very difficult to simulate sorption with an equation. The pseudo-first order (eqn (13)) and pseudo-second order (eqn (14)) equations can be used to assess and model a sorption process. In the following equations, qt is the adsorption capacity, and t is the extraction time.51
ln(qe − qt) = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe − K1t qe − K1t
| (13) |
| t/qt = 1/k2qe2 + t/qe | (14) |
By fitting the experimental data to eqn (13) and (14), useful parameters such as K1, K2, and qe can be determined. K1 (min−1) and K2 (g mg−1 min−1) are the rate constants of the pseudo-first order and pseudo-second order kinetics, respectively, and qe (mg g−1) is the equilibrium amount of the adsorption capacity. These parameters are important in adsorption processes.
Fitting the experimental data to pseudo-first order kinetics shows that the R2 values for dye removal in single and binary dye solutions are low. Additionally, the calculated qe differs greatly from the experimental qe. Thus, it seems that pseudo-first order kinetics is not appropriate for simulating these adsorption data (Table S2†). However, fitting the experimental data to the pseudo-second order kinetics equation results in an R2 value near 1 and a calculated qe that is close to the experimental qe; this shows the suitability of the pseudo-second order kinetics equation (Table S2 and Fig. S6†).
3.9. Thermodynamics of adsorption
The equilibrium constant, K, is a temperature-dependent parameter. Because K has relationships to many thermodynamic parameters, it is possible to determine the thermodynamic parameters involved by changing the temperature during the experiments.52
ΔG0 = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K
| (15) |
| ΔG0 = ΔH0 − TΔS0 | (16) |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = −ΔH0/R × 1/T + ΔS0/R K = −ΔH0/R × 1/T + ΔS0/R
| (17) |
In eqn (15)–(17), ΔG0 (kJ mol−1) is the variation in the Gibbs free energy, ΔH0 (kJ mol−1) is the thermal energy of the reaction, and ΔS0 (J mol−1 K−1) is the variation in the randomized energy.
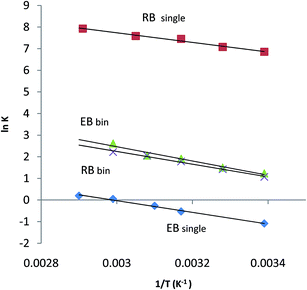
By carrying out the adsorption experiments at various temperatures and by plotting ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(ln
K(ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe/ce) vs.
qe/ce) vs. 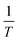 , the thermodynamic parameters were obtained; they are shown in Table 7.20,53
, the thermodynamic parameters were obtained; they are shown in Table 7.20,53
The ΔH0 values for the adsorption of a dye from single and binary dye solutions in this work are positive; however, they are low (18.66 to 27.43 kJ mol−1). This means that these processes are endothermic and physical sorption processes. In physical sorption, the equilibrium is rapidly attained and easily reversible because the energy demand is low.54,55 The randomized energy variations of adsorption (ΔS0) for single and binary dye solution experiments are also positive; this indicates an increase in entropy in all cases. The Gibbs energy variation, ΔG0, indicates the degree of feasibility of biosorption; it can be positive or negative.54,55 In binary and single biosorption of dyes, ΔG0 decreases with increasing temperature, indicating increasing feasibility of the reaction. Adsorption of RB in the binary dye solution on the surface of an adsorbent gives an opposite charge to its surface and aids the adsorption of ER in the binary dye solution (Fig. 6).
4. Conclusion
Erythrosine B (EB) and rhodamine B (RB) dyes were selected as models of xanthene dyes for dye adsorption from aqueous solution; both were removed effectively. Ratio derivative UV-visible spectrophotometry was used as an analysis and speciation method for the binary aqueous solution dye.A biomass-based active carbon was prepared and characterized. It was found that the lemon citrus active carbon was a suitable adsorbent for these dyes in single and binary dye solutions. Specific adsorbents have been previously used for the removal of acidic and basic dyes; however, in this study, one adsorbent was used for the adsorption of both acidic and basic dyes. The optimized conditions were distinguished by the response surface methodology. Using the Dubinin–Radushkevich and Langmuir isotherms, we calculated the adsorption capacities for EB and RB in dye solutions. It was also found that the rate of dye removal followed pseudo-second order kinetics. The desorption reactions for the dyes in the binary dye solution were endothermic and spontaneous. The Gibbs free energy variation (ΔG) for EB and RB adsorption in their binary dye solution were −3.194 and −2.967 kJ mol−1, respectively. The adsorbent used was regenerated in 0.1 M NaOH solution.
Acknowledgements
Some parts of this study were performed in the laboratories of Khayam Power Generation Management Company. The authors are grateful for this cooperation.References
- F. Motahari, M. R. Mozdian fard and M. Salavati-Niasar, Process Saf. Environ. Prot., 2015, 93, 282–292 CrossRef CAS.
- K. Chon, J. Cho, S. J. Kim and A. Janng, Chemosphere, 2014, 117, 20–26 CrossRef CAS PubMed.
- G. Mosavi and M. Mahmodi, J. Hazard. Mater., 2009, 168, 806–812 CrossRef PubMed.
- M. E. Rueda, L. A. Sarabia, A. Herrero and M. C. Ortiz, Anal. Chim. Acta, 2001, 446, 269–279 CrossRef CAS.
- L. A. Ramirez-Montaya, V. Hernandez-Montaya and M. A. Montes Mora, J. Anal. Appl. Pyrolysis, 2014, 109, 9–20 CrossRef.
- K. Shakir, A. Faouzy Elkafrawy, H. F. Ghoneimy, S. G. Elrab Beheir and M. Refaat, Water Res., 2010, 44, 1449–1461 CrossRef CAS PubMed.
- Z. XU, L. Zheng, Y. Yin, J. Wang, P. Wang, L. Ren, S. A. Ermin, X. He, M. Meng and R. Xi, Food Control, 2015, 47, 472–477 CrossRef CAS.
- M. T. Yagub, T. Kantisen, S. Afroze and H. M. Any, Adv. Colloid Interface Sci., 2014, 209, 172–184 CrossRef CAS PubMed.
- Y. S. Al-Degs, R. Abu-El-Halawa and S. S. Abu-Alrub, Chem. Eng. J., 2012, 191, 185–194 CrossRef CAS.
- L. Jin, T. Wang, C. Cui, H. Wu, H. Ron and M. Wei, Dyes Pigm., 2014, 111, 39–44 CrossRef CAS.
- A. S. Jennings, S. L. Schwartz, N. J. Balter, D. Gardner and P. J. Witorsch, Toxicol. Appl. Pharmacol., 1990, 103, 549–556 CrossRef CAS PubMed.
- M. Roosta, M. Ghaedi, A. Daneshfar, S. Darafarin, R. Sahraei and M. K. Purkait, Ultrason. Sonochem., 2014, 21, 1441–1450 CrossRef CAS PubMed.
- M. Roosta, M. Ghaedi, A. Daneshfar, R. Sahraei and A. Asghari, J. Ind. Eng. Chem., 2015, 21, 459–469 CrossRef CAS.
- M. Ghaedi, Z. Rozkhoosh, A. Asfaram, B. Mirtamiz doust, Z. Mahmoodi and A. A. Bazarafshan, Spectrochim. Acta, Part A, 2015, 138, 176–186 CrossRef CAS PubMed.
- R. Jain and S. Sikarwar, J. Hazard. Mater., 2009, 164, 627–633 CrossRef CAS PubMed.
- A. Tabara, C. Yamane, M. Abe and M. Seguchi, Cellulose, 2011, 18, 45–55 CrossRef CAS.
- T. Perez Ruiz, C. Martinez-Lozano, A. Sanaz and E. Bravo, Chromatographia, 1998, 48(3/4), 263–267 CAS.
- M. Ryvolova, P. Taborsky, P. Vrabel, P. Krasensky and J. Preisler, J. Chromatogr. A, 2007, 1141, 206–211 CrossRef CAS PubMed.
- J. J. Berzas Nevada, J. Rodrigue Flores and M. J. Villasenor Lierena, Fresenius. J. Anal. Chem., 1994, 350, 610–613 CrossRef.
- K. G. Bhatta Charyya, S. Sen Gupta and G. Kumar Sarma, Appl. Clay Sci., 2014, 99, 7–17 CrossRef CAS.
- N. Xia, J. Deng, K. Huang, S. Juu, C. Hu and J. Liang, Spectrochim. Acta, Part A, 2014, 128, 312–318 CrossRef PubMed.
- K. P. Singh, S. Gupta, A. K. Singh and S. Sinha, Chem. Eng. J., 2010, 165, 151–160 CrossRef CAS.
- M. E. Fernandez, G. V. Nunell, P. R. Bonelli and A. L. Cukierman, Ind. Crops Prod., 2014, 62, 437–445 CrossRef CAS.
- M. M. Jafar Sadiq and A. Samson Nesaraj, J. Nanostruct. Chem., 2015, 5, 45–54 CrossRef.
- R. Ojani, J. B. Raoof and E. Zarei, J. Solid State Electrochem., 2012, 16, 2143–2149 CrossRef CAS.
- X. M. Mao and C. M. Fan, Int. J. Miner., Metall. Mater., 2013, 20, 1089 CrossRef CAS.
- L. Li, J. Xu, C. Guo and Y. Zhang, Front. Environ. Sci. Eng., 2013, 7(3), 382–387 CrossRef CAS.
- P. V. Nidheesh and R. Gandhimathi, Environ. Sci. Pollut. Res., 2014, 21, 8585–8594 CrossRef CAS PubMed.
- L. Yu, Y. Mao and L. Qu, Food Analytical Methods, 2013, 6, 1665–1670 CrossRef.
- L. Gagliardi, D. D. Orsi, G. Cavazzutti, G. Multari and D. Tonelli, Chromatographia, 1996, 43(1/2), 76–78 CAS.
- L. Y. Yao, Y. Xiang Zhu, C. A. Lu, R. H. Jiao, Y. H. Lu and R. X. Tan, J. Chromatogr. B: Anal. Technol. Biomed. Life Sci., 2015, 989, 122–128 CrossRef CAS PubMed.
- J. G. Yu, L. Y. Yu, H. Yang, A. Liu, X. H. Chen, X. Y. Jiang, X. Q. Chen and F. P. Jiao, Sci. Total Environ., 2015, 502, 70–79 CrossRef CAS PubMed.
- A. N. Shmroukh, A. H. Ali and S. Oo Kawara, Renewable Sustainable Energy Rev., 2015, 50, 445–456 CrossRef CAS.
- C. Z. Liang, S. P. Sun, F. Y. Li, Y. K. Ong and T. S. Chung, J. Membr. Sci., 2014, 469, 306–315 CrossRef CAS.
- F. Salinaz, J. J. Berzas Nevado and A. Espinosa Mansilla, Talanta, 1990, 37(3), 347–351 CrossRef.
- M. Blanco, J. Gene, H. Iturriaga, S. Maspochand and J. Riba, Talanta, 1987, 34(12), 987–993 CrossRef CAS PubMed.
- T. C. O. Haver and G. L. Green, Anal. Chem., 1976, 48(2), 312–318 CrossRef.
- C. Bosch Ojeda and F. Sanchez Rojas, Microchem. J., 2013, 106, 1–16 CrossRef CAS.
- R. Subramaniam and S. K. Ponnusamy, Water Resources and Industry, 2015, 11, 64–70 CrossRef.
- M. Novic and N. Fjodorova, Anal. Chim. Acta, 2015, 891, 90–100 CrossRef PubMed.
- L. A. Sarabia and M. C. Ortiz, Reference module in chemistry, 2009, 1, 345–390 Search PubMed , current as of 23 April 2014.
- N. M. Mahmoodi, R. Salehi and M. Arami, Desalination, 2011, 272, 187–195 CrossRef CAS.
- S. Tazibat, Y. Boucheffa, P. Lodewyckx, L. F. Vlasco and Y. Boutillara, Microporous Mesoporous Mater., 2016, 221, 67–75 CrossRef.
- D. Cuhadaroglu and O. Aydemir uygun, Afr. J. Biotechnol., 2000, 7(20), 3703–3710 Search PubMed.
- T. Monearuny, Y. Liew, Y. Dai, S. Kawi, C. Chang and C. Hwa Wang, Bioresour. Technol., 2016, 200, 350–359 CrossRef PubMed.
- S. Rngabhashiyam, N. Anu and N. Selvaraju, J. Environ. Chem. Eng., 2013, 1(4), 629–641 CrossRef.
- P. K. Malik, Dyes Pigm., 2003, 56, 239–240 CrossRef CAS.
- N. Ozbay and A. S. Yargic, J. Cleaner Prod., 2015, 100, 333–343 CrossRef CAS.
- F. Nekouei, S. Nekouei, I. Tyagi and V. K. Gupta, J. Mol. Liq., 2015, 201, 124–133 CrossRef CAS.
- P. Wang, Y. Ye, D. Liang, H. Sun, J. Liu, Z. Tian and C. Liang, RSC Adv., 2016, 6, 26977–26983 RSC.
- T. Wang, X. Xu, Z. Ren, B. Gao and H. Wang, RSC Adv., 2016, 6, 5089–5099 RSC.
- S. Banerjee, R. K. Gautam, A. Jaiswal, M. C. Chttopdhyaya and Y. C. Shama, RSC Adv., 2015, 5, 14425 RSC.
- B. Liao, W. Sun, N. Guo, S. Ding and S. Jun su, Colloids Surf., A, 2016, 501, 32–41 CrossRef CAS.
- M. El-Haddad, A. Regti, M. R. Laamari, R. Slimai, R. Mamouni, S. El Antari and S. Lazar, J. Taiwan Inst. Chem. Eng., 2014, 45(2), 533–540 CrossRef CAS.
- L. Lv, J. Zhang, S. Yuan, L. Huang, S. Tang, B. Liang and S. O. Pehkonon, RSC Adv., 2016, 6, 78136–78150 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra23157h |
| This journal is © The Royal Society of Chemistry 2017 |