Mechanisms and stereoselectivities of the DABCO-catalyzed Rauhut–Currier reaction of α,β-unsaturated ketones and aryl acrylates: a computational investigation

Abstract

It has been experimentally reported that a great acceleration of the Rauhut–Currier reaction of aryl acrylates with α,β-unsaturated ketones is achieved in the presence of phenol (PhOH) [W. Liu, G. Zhao, Org. Biomol. Chem., 12 (2014) 832–835]. A theoretical investigation on the mechanisms as well as stereoselectivities of the 1,4-diazabicyclo[2.2.2]octane (DABCO)-catalyzed RC reaction of phenyl acrylate R₁ with (E)-2-benzoyl-3-phenyl-acrylonitrile R₂ in the absence and in the presence of PhOH has been performed using density functional theory (DFT). Multiple possible reaction pathways (associated with RRS, RSR, SRS and SSR configurations) have been explored. The whole reaction process can be characterized by four steps: (1) the conjugate addition of DABCO to R₁, (2) the nucleophilic attack at R₂, (3) the 1,3-H-shift process (direct H-shift in the absence of PhOH and stepwise H-shift in the presence of PhOH) and (4) the catalyst release affording the final product. The calculated results show a relatively high energy barrier (42.2–46.0 kcal mol⁻¹, corresponds to the direct 1,3-H-shift step) for the reaction in the absence of PhOH. For the reaction in the presence of PhOH, the pathway leading to the (SSR)-product is the most favorable pathway. The first step of the hydrogen-shift process is found to be the rate-determining step, whereas the second step is the stereoselectivity determining step. The role of PhOH on the title reaction is discussed.

---

1. Introduction

It is well known that the Rauhut–Currier (RC) reaction (also known as the vinylogous Morita–Baylis–Hillman (MBH) reaction), addition of the α-position of one activated alkene to the β-position of a second alkene in the presence of a nucleophilic catalyst, is one of the effective methods in creating carbon–carbon bonds.^1–6 Due to its high atom- and step-economy, the RC reaction has become an increasingly active area, since it was first discovered by Rauhut and Currier in 1963.¹ Up to now, a large number of experimental studies have been reported on the RC dimerization of acrylonitrile,^7–9 vinyl ketones,¹⁰ acrylates,¹¹ and nitroalkenes.¹² The cross coupling versions of the RC reaction have also been reported.^13–20 Furthermore, the enantioselective RC reactions have been studied and significant progress has been achieved.^21–27 Moreover, the RC reaction has been developed for the synthesis of many natural products and pharmaceuticals.^28–33

However, compared to the rich knowledge of experimental studies, much less theoretical studies have been reported on the RC reaction. In 2011, Gu, Xiao and co-workers explored the enantioselective crossed RC reaction between nitroolefins and α,β-unsaturated esters by using a combined experimental and theoretical approach, and their calculation results support the experimental findings (reaction mechanism and enantioselectivity).³⁴ Subsequently, Houk and co-workers investigated the enantioselective cysteine-catalyzed RC reaction using the density functional theory method. Their computational study demonstrated that the water and counterions (K⁺/Na⁺) play an important role in determining the stereochemistry of the reaction.³⁵

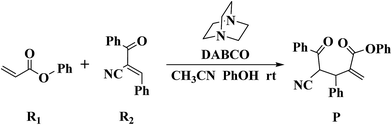
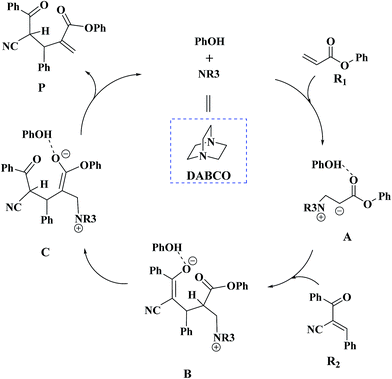
Recently, Zhao and co-workers investigated 1,4-diazabicyclo[2.2.2]octane (DABCO)-catalyzed cross RC reaction of aryl acrylates with α,β-unsaturated ketone, which serve as a key step for the synthesis of pyran-2-ones (Scheme 1).³⁶ Pyran-2-ones as structural motifs are often found in many natural products, bioactive molecules, and organic intermediates.^37–41 Preliminary experimental results led Zhao et al. to propose the possible catalytic cycle. As depicted in Scheme 2, the originally proposed mechanism consists of four steps: the nucleophilic addition of DABCO to aryl acrylate to form a zwitterionic intermediate A, addition of the zwitterion A to α,β-unsaturated ketone to form B, 1,3-hydrogen shift affording C and catalyst regeneration. On the experimental observations, Zhao and coworkers demonstrated that phenol (PhOH) could be used as a Brønsted acid additive to accelerate the reaction. Zhao and co-workers also suggested that addition of the zwitterion A to α,β-unsaturated ketone is the rate-determining step (RDS). Although the mechanism for the DABCO-catalyzed RC reaction between aryl acrylates and α,β-unsaturated ketone has been proposed, the details are still unclear. Particularly unclear issues concern the following questions: how does each of the catalytic steps take place? What is the role of PhOH? How the PhOH promote the reaction? To the best of our knowledge, no theoretical investigation on the mechanism of the current RC reaction has been reported up to now.

Scheme 1 DABCO-catalyzed Rauhut–Currier (RC) reaction.

Scheme 2 The proposed mechanism for the DABCO-catalyzed RC reaction in experiment.

In this work, we investigated the mechanism of the DABCO-catalyzed RC reaction between phenyl acrylate and (E)-2-benzoyl-3-phenyl-acrylonitrile with the aid of density functional theory (DFT) calculations and try answer the questions raised above. For this purpose, the reaction pathways both in the absence and presence of PhOH have been studied.

The remainder of this paper is organized as follows: we first describe the Computational methods in Section 2. Then we present the Results and discussion in Section 3, followed by the Comparison with experiments in Section 4. Finally, we finish with some concluding remarks in Section 5.

2. Computational method

The geometry optimizations of the critical points (reactants, products, intermediates and transition states) were carried out using the M06-2X⁴² method in conjunction with 6-31G(d) basis set.⁴³ It has been shown that M06-2X provide a better description of kinetics and thermodynamics.^44–49 Frequency calculations were performed at the same level of theory, to check whether the obtained species was a minimum (with all real frequencies) or a transition state (with only one imaginary frequency), as well as to obtain zero point energy (ZPE) and thermodynamic corrections at 298.15 K and 1 atm. Intrinsic reaction coordinate (IRC) calculations were performed to ensure that the transition state is connected with its designated isomers.⁵⁰ Single point energy calculations were performed at the M06-2X/6-311++G(d,p) level of theory. The solvation effects of acetonitrile (CH₃CN) were considered during geometry optimization, frequency calculation and single point energy calculation by using the Cramer–Truhlar continuum solvation model SMD.⁵¹ The Gibbs free energies were used to discuss the reaction mechanisms. The natural bond orbital (NBO) analysis was applied to calculate the charge distributions.^52–54 The Gaussian 09 program package was used for all DFT calculations described herein.⁵⁵

3. Results and discussion

As noted in the introduction, Zhao et al.'s experimental studies indicated that phenol (PhOH) can promote the RC reaction.³⁶ To examine the role of PhOH, the DABCO-catalyzed RC reaction of phenyl acrylate R₁ with (E)-2-benzoyl-3-phenyl-acrylonitrile R₂ in both the absence and the presence of PhOH have been investigated with the aid of DFT calculations.

3.1 Reaction mechanism in the absence of PhOH

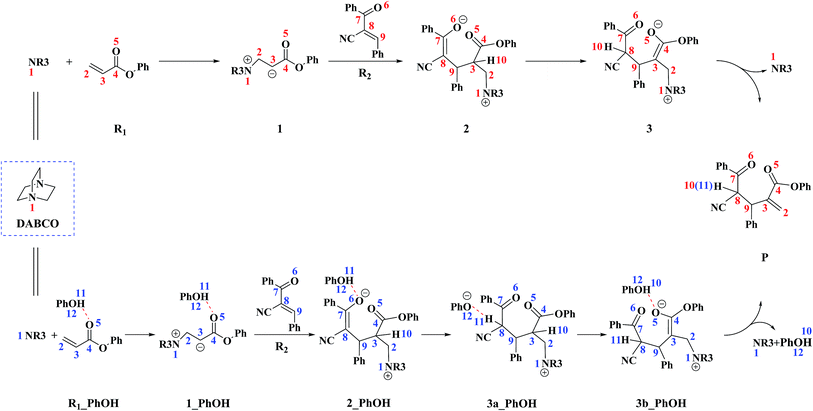
On the basis of previous experimental studies³⁶ and our calculation results, the reaction mechanism of the RC reaction between R₁ and R₂ is depicted in Scheme 3. The corresponding potential energy profile is shown in Fig. 1. In the following part of this section, we will detail the reaction mechanism step by step.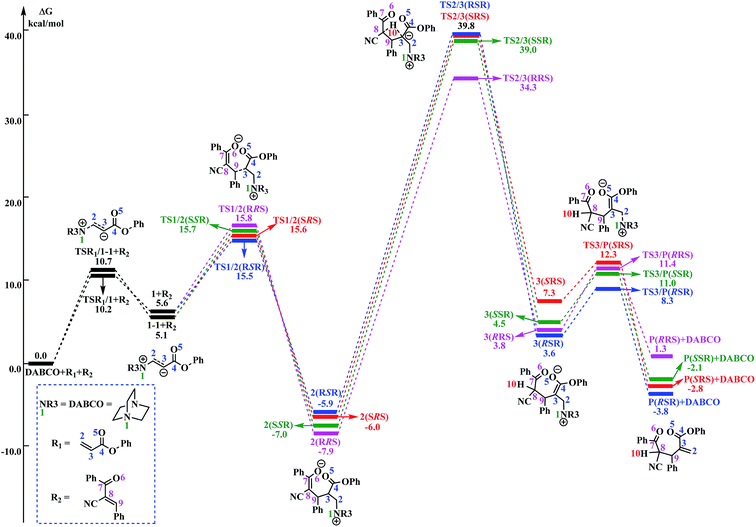

Scheme 3 The reaction mechanism in the absence and in the presence of PhOH.

Fig. 1 Free energy profile of the reaction mechanism in the absence of PhOH. The solvation-corrected relative free energies at SMD(CH₃CN)/M06-2X/6-311++G(d,p) level are given in kcal mol⁻¹.

First step. The first step of the current RC reaction is a nucleophilic attack process, i.e. the N1 atom of DABCO attacks on the C2 atom of R₁ to generate the zwitterionic intermediates 1 and 1-1, which depending on the orientations of DABCO to R₁. The corresponding transition states are TSR₁/1 and TSR₁/1-1, respectively. The N1–C2 bond distance is shortened from 2.085 Å in TSR₁/1, and 2.072 Å in TSR₁/1-1, to 1.566 Å in 1, and 1.565 Å in 1-1. The above results imply that N1–C2 bond is formed via the nucleophilic attack of DABCO to R₁. As shown in Fig. 1, the activation energy barrier associated with the first step (addition of DABCO to R₁) is calculated to be 10.2 kcal mol⁻¹ for TSR₁/1, and 10.7 kcal mol⁻¹ for TSR₁/1-1. This step is endergonic by 5.6/5.1 kcal mol⁻¹, which implies that this step is not thermodynamically favorable.

Second step. The second step is the addition of the C3 atom in zwitterionic intermediate 1/1-1 to the C9 atom in R₂ to form the intermediate 2(RRS&RSR&SRS&SSR) via the corresponding transition states TS1/2(RRS&RSR&SRS&SSR). It should be pointed out that after the formation of C3–C9 bond, the C3 and C9 atoms become chiral centers. In addition, the prochiral atom C8 can finally become chiral. The three letters in bracket present the chirality of C3, C8 and C9 atoms, respectively. Moreover, the chiral atom C3 can finally become achiral. For the sake of clarity, when the atom is prochirality or the atom becomes achiral, the italic R/S was used. This label does not change in the present paper. The distance of C3–C9 bond is shortened from 2.517/2.523/2.555/2.491 Å in TS1/2(RRS&RSR&SRS&SSR), to 1.573/1.561/1.561/1.579 Å in 2(RRS&RSR&SRS&SSR), indicating the C3–C9 bond is formed in 2. The activation energy barrier for this step is calculated to be 10.2/9.9/10.5/10.6 kcal mol⁻¹ for TS1/2(RRS&RSR&SRS&SSR). It is noteworthy that this step is an exergonic process because the energy of 2(RRS&RSR) are 13.5/11.5 kcal mol⁻¹ lower than the energy of 1 + R₂, and the energy of 2(SRS&SSR) is 11.1/12.1 kcal mol⁻¹ lower than the energy of 1-1 + R₂.

Third step. The third step of this reaction is the direct 1,3-H-shift process via the four-center (C3–H10–C8–C9) transition state. In this step, the H10 atom in 2(RRS&RSR&SRS&SSR) transferred from C3 to C8, the activation energy is calculated to be 42.2/45.7/45.8/46.0 kcal mol⁻¹ for TS2/3(RRS&RSR&SRS&SSR). Thus, direct H-shift is a kinetically inaccessible process, which means that the current RC reaction occurs via direct H-shift mechanism can be excluded.

Fourth step. The last step is the DABCO elimination process. Catalyst DABCO releases from 3(RRS&RSR&SRS&SSR) complete the catalytic cycle and affords the final products P(RRS&RSR&SRS&SSR). As depicted in Fig. 1, the free energy barrier is calculated to be 7.6/4.7/5.0/6.5 kcal mol⁻¹ for TS3/P(RRS&RSR&SRS&SSR).

As shown in Fig. 1, the free energy barrier for the third step (2 → 3) is much higher than those of the other steps (R₁ + DABCO → 1, 1 → 2, and 3 → P). Therefore, the third step is the rate-determining step. On the basis of our calculations, the energy barrier for the third step is inaccessibly high. Considering that the experiments were conducted under room temperature, we can easily deduce that the current RC reaction cannot take place via the direct H-shift mechanism.

3.2 Reaction mechanism in the presence of PhOH

The reaction mechanism in the presence of PhOH is also depicted in Scheme 3. The free energy profile for the complete process is presented in Fig. 2. It should be pointed out that, in order to have unbiased free energies, a molecule of PhOH is included in the reaction system throughout. As shown in Fig. 2, reactants N-phenylmaleimide and 2-benzoyl acrylate were complexed to a molecule of PhOH, which were labeled as R₁_PhOH and R₂_PhOH, respectively. Then the free energy of R₁_PhOH + R₂_PhOH + DABCO is set to 0.0 kcal mol⁻¹ as reference in the potential energy profile.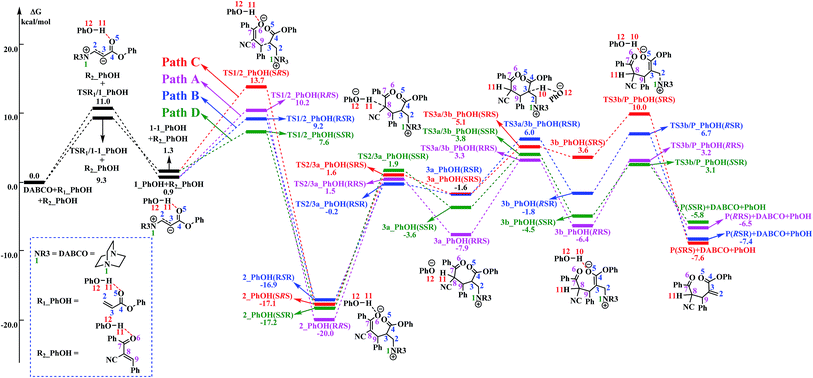

Fig. 2 Free energy profile of the reaction mechanism in the presence of PhOH. The solvation-corrected relative free energies at SMD(CH₃CN)/M06-2X/6-311++G(d,p) level are given in kcal mol⁻¹.

First step. The first step of the reaction in the presence of PhOH is the same as that in the absence of PhOH, that is, the N1 atom of DABCO nucleophilically attack the C2 atom of R₁ to form the zwitterionic intermediate 1_PhOH (or 1-1_PhOH). It should be noted that a PhOH molecule was included in all calculations. Moreover, different coordination modes of the PhOH have been studied and only the lowest energy conformers for each structures were shown. The suffix “_PhOH” represents the PhOH-assisted reaction mechanism. The distance between the N1 atom in DABCO and the C2 atom in R₁ is 2.199/2.169 Å in TSR₁/1_PhOH/TSR₁/1-1_PhOH, which is shortened to 1.551/1.555 Å in 1_PhOH/1-1_PhOH. The energy barrier for the first step is 11.0/9.3 kcal mol⁻¹ via transition state TSR₁/1_PhOH/TSR₁/1-1_PhOH, and this step is endergonic by 0.9/1.3 kcal mol⁻¹ (see Fig. 2). These results indicate that the activation energy of the first step (coupling of DABCO with R₁) is not significantly influenced by the involvement of a molecule of PhOH in the reaction system. However, the stability of 1/1-1 is enhanced by the complexation of PhOH.

Second step. The second step is the addition of 1_PhOH(1-1_PhOH) to R₂. The gradually shortened distance of C3–C9 bond (2.663/2.535/2.497/2.662 Å in TS1/2_PhOH(RRS&RSR&SRS&SSR), and 1.570/1.560/1.562/1.576 Å in 2_PhOH(RRS&RSR&SRS&SSR)) indicates that the C3–C9 bond is formed in 2_PhOH. The energy barrier for this step is calculated to be 9.3/8.3/12.4/6.3 kcal mol⁻¹ for TS1/2_PhOH(RRS&RSR&SRS&SSR), and this step is exergonic by 20.9/17.8/18.4/18.5 kcal mol⁻¹ (associated with RRS, RSR, SRS and SSR configurations, respectively). In view of the fact that in a multi-step process, the selectivity is determined as soon as an irreversible step occurred after the selectivity has been fixed, we can deduce that this step should be the stereochemistry-determining step (see Fig. 2). When compared with the second step in Fig. 1 (in the absence of PhOH), we found that in the presence of PhOH, the energy barrier is slightly decreased (except for TS1/2_PhOH(SRS)) and the stability of 2_PhOH(RRS&RSR&SRS&SSR) is enhanced significantly. These results indicate that PhOH does favor the addition of 1/1-1 and R₂. Moreover, NBO charge analyses indicate that the negative charge values on C8 increased from −0.284e in R₂, to −0.349/−0.367/−0.378/−0.343e in TS1/2_PhOH(RRS&RSR&SRS&SSR), then to −0.412/−0.425/−0.425/−0.433e in 2_PhOH(RRS&RSR&SRS&SSR), demonstrating the coupling of 1/1-1 with R₂ increases the charge on C8, and thus facilitate the subsequent H shift process (from O12 to C8).

Third step. Although Zhao et al. have suggested PhOH can accelerate the H-transfer process,³⁶ it was unclear how the H-transfer occurs in the presence of PhOH. Herein, we proposed a PhOH-assisted H-shift mechanism. On the basis of our calculations, the PhOH-assisted H-shift process is stepwise (see Scheme 3). Firstly, the H11 atom transferred from O12 to C8. The distance of O12–H11 is elongated from 1.341/1.331/1.274/1.281 Å in TS2/3a_PhOH(RRS&RSR&SRS&SSR), then to 2.025/1.960/1.961/2.113 Å in 3a_PhOH(RRS&RSR&SRS&SSR), while the distance of H11–C8 is shortened from 1.310/1.306/1.361/1.340 Å in TS2/3a_PhOH(RRS&RSR&SRS&SSR), to 1.102/1.104/1.104/1.102 Å in 3a_PhOH(RRS&RSR&SRS&SSR). NBO charge analyses indicate that the negative charge values on O12 increased from −0.749/−0.760/−0.754/−0.759e in 2_PhOH(RRS&RSR&SRS&SSR), to −0.831/−0.840/−0.831/−0.826e in TS2/3a_PhOH(RRS&RSR&SRS&SSR), then to −0.883/−0.884/−0.884/−0.880e in 3a_PhOH(RRS&RSR&SRS&SSR), which can facilitate the subsequent H-transfer from C3 to O12. Then, 3a transforms to 3b through the second hydrogen-shift process, which is accomplished via TS3a/3b_PhOH(RRS&RSR&SRS&SSR) (shown in Fig. 2). The energy barriers calculated for the successive H-shift processes are 21.5/16.7/18.7/19.1 kcal mol⁻¹ (associated with TS2/3a_PhOH(RRS&RSR&SRS&SSR)) and 11.2/7.6/6.7/7.4 kcal mol⁻¹ (associated with TS3a/3b_PhOH(RRS&RSR&SRS&SSR)), which are much lower than those for the direct H-shift mechanism (42.2/45.7/45.8/46.0 kcal mol⁻¹ for TS2/3(RRS&RSR&SRS&SSR)). Moreover, the intermediates 3a and 3b are stabilized by the presence of a molecule of PhOH. In summary, the protic additive PhOH not only stabilizes the intermediates/transition states, but also mediates the H-shift process. These two effects could explain the acceleration of RC reaction in the presence of PhOH.

Fourth step. The last step is the catalyst DABCO elimination process to give the final products P(RRS&RSR&SRS&SSR). The energy barrier calculated for this step is 9.6/8.5/6.4/7.6 kcal mol⁻¹ for TS3b/P_PhOH(RRS&RSR&SRS&SSR). The distance between N1 and C2 is 1.550/1.557/1.553/1.557 Å in 3b_PhOH(RRS&RSR&SRS&SSR), which is elongated to 2.287/2.143/2.124/2.183 Å in TS3b/P_PhOH(RRS&RSR&SRS&SSR). At the same time, the distance between C2 and C3 is shortened from 1.481/1.494/1.485/1.481 Å in 3b_PhOH(RRS&RSR&SRS&SSR), to 1.361/1.376/1.376/1.367 Å in TS3b/P_PhOH(RRS&RSR&SRS&SSR), then to 1.335/1.334/1.334/1.335 Å in P(RRS&RSR&SRS&SSR). These results demonstrate that with the elimination of DABCO, the C2–C3 bond becomes a double bond.

By the above, four pathways (paths A, B, C and D, see Fig. 2) for the DABCO-catalyzed RC reaction of phenyl acrylates with α,β-unsaturated ketone in the presence of PhOH have been discussed in detail. The four pathways start from the same reactants, go through different pathways leading to four isomers of product. As shown in Fig. 2, the overall energy barrier for paths A, B, C and D should be the energy difference of 2(RRS) with TS3a/3b(RRS), 2(RSR) with TS3b/P(RSR), 2(SRS) with TS3b/P(SRS), and 2(SSR) with TS3a/3b(SSR), which are calculated to be 23.3, 23.6, 27.1 and 21.0 kcal mol⁻¹, respectively. Consequently, the energy barrier order of the four pathways increases as follows: path D → path A → path B → path C. Since the energy barrier determines the reaction rate of a given pathway, we can easily deduce that path D is the most energy favorable.

4. Comparison with experiments

It would be of interest to compare our calculation results with previous experimental findings. In the experimental report,³⁶ the current RC reaction is initiated by conjugate addition of DABCO to aryl acrylate to form the zwitterionic intermediate A, which subsequently attacks the α,β-unsaturated ketone to give B, followed by the 1,3-hydrogen shift leads to C. Finally, catalyst DABCO releases from C affording the final product P. On the basis of our calculation results, the most energetically favorable pathway is path D (as depicted in Fig. 2). The intermediates A, B, C, and P correspond to 1-1_PhOH, 2_PhOH(SSR), 3b_PhOH(SSR) and P_PhOH(SSR), respectively in our result. Furthermore, Zhao and co-workers suggested that phenol PhOH can stabilize A, and accelerate the reaction between A and R₂. Our calculation results indicate that complexation of 1-1 by one molecule of PhOH induces a decrease of reaction energy of 3.8 kcal mol⁻¹ (see Fig. 1 and 2). Moreover, the energy barrier for 1-1 + R₂ → 2 in the presence of PhOH is lower than that in the absence of PhOH (6.3 vs. 10.6 kcal mol⁻¹, associated with SSR-configuration), and 2_PhOH is much more stable than 2 (−17.2 vs. −7.0 kcal mol⁻¹, associated with SSR configuration). Therefore, based on both kinetical and thermodynamical considerations, the reaction of 1 + R₂ in the presence of PhOH is much more favorable than the corresponding reaction in the absence of PhOH. As for these aspects, our calculation results are in good agreement with the experimental results reported by Zhao and co-workers.³⁶ However, there exist discrepancies. Zhao and co-workers suggested that the addition of A (corresponds to 1-1_PhOH in our result) to R₂ is the rate-determining step. According to our calculations, the overall energy barrier for the hydrogen-shift process is 21.0 kcal mol⁻¹ (corresponds to the energy difference between 2_PhOH and TS3a/3b_PhOH, see path D in Fig. 2), which is much higher than that for the addition of 1-1_PhOH to R₂ (6.3 kcal mol⁻¹ relative to 1-1_PhOH and 7.6 kcal mol⁻¹ with respect to reactants). In other words, we predicted the first step of hydrogen-shift process is the rate-determining step. In view of this discrepancy, future reinvestigation of the current RC reaction is strongly desired.

5. Conclusions

The mechanisms and stereoselectivities of DABCO-catalyzed RC reaction of phenyl acrylate R₁ with (E)-2-benzoyl-3-phenyl-acrylonitrile R₂ both in the absence and presence of phenol (PhOH) have been investigated at the M06-2X/6-311++G(d,p)//M06-2X/6-31G(d) level in CH₃CN solvent using the SMD solvation model. Our calculation results can be summarized as follows:

In the absence of PhOH, the reaction proceeds via four steps, which includes activation of R₁ by DABCO, addition to R₂, direct 1,3-hydrogen shift, catalyst DABCO liberation. The calculated results show that the 1,3-hydrogen shift is rate-limiting and the activation energy barrier for this step is inaccessibly high (42.2–46.0 kcal mol⁻¹), indicating this reaction process is kinetically unfavorable.

In the presence of PhOH, four reaction pathways (paths A, B, C and D) associated with RRS, RSR, SRS and SSR configuration products have been investigated and compared. The most favorable pathway (path D) include four stages: the reaction is initiated with the conjugate addition of DABCO to R₁ to form the zwitterionic intermediate 1-1_PhOH (stage I), which subsequently attacks R₂ to produce 2_PhOH(SSR) (stage II). 1,3-H-shift of 2_PhOH(SSR) is demonstrated to proceed via a stepwise mechanism: the C8 atom of 2_PhOH(SSR) abstracts H11 from O12 to form intermediate 3a_PhOH(SSR), and then the C3 can donate H10 to O12 to complete the H shift process (from C8 to C3) and produce intermediate 3b_PhOH(SSR) (stage III). Finally, the catalyst DABCO releases from 3b_PhOH(SSR) to generate the final product P(SSR) (stage IV). The calculated results show that the first step of H-shift process (2 → 3a) is the rate-determining step. The addition of 1-1_PhOH to R₂ is calculated to be the stereoselectivity-determining step.

The calculated results reveal that the presence of PhOH does stabilize the intermediates and transition states. Moreover, the overall energy barrier for the 1,3-H shift step in the absence and presence of PhOH is calculated to be 46.0 and 21.0 kcal mol⁻¹ (associated with SSR configuration), respectively, which is consistent with previous experimental findings (rate acceleration in the presence of PhOH). The present paper may provide a useful guide for understanding other analogous reactions.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (No. 21403024).

Notes and references

1. M. M. Rauhut and H. Currier, U.S. Pat., 3074999, American Cyanamide, 1963Chem. Abstr., 1963, 58, 11224a.
2. J. L. Methot and W. R. Roush, Adv. Synth. Catal., 2004, 346, 1035.
3. C. E. Aroyan, A. Dermenci and S. J. Miller, Tetrahedron, 2009, 65, 4069.
4. P. Z. Xie and Y. Huang, Eur. J. Org. Chem., 2013, 6213.
5. J. Peng, X. S. Takizawa, T. M.-N. Nguyen, A. Grossmann, D. Enders and H. Sasai, Angew. Chem., Int. Ed., 2012, 51, 5423 (Angew. Chem., 2012, 124, 5519).
6. F. Zheng and Y. C. Chen, Org. Lett., 2013, 15, 5534.
7. M. M. Baizer and J. D. Anderson, J. Org. Chem., 1965, 30, 1357.
8. J. D. McClure, J. Org. Chem., 1970, 35, 3045.
9. L. Yu, J. Wang, X. Zhang, H. E. Cao, G. L. Wang, K. H. Ding, Q. Xu and M. Lautens, RSC Adv., 2014, 4, 19122.
10. D. Basavaiah, V. V. L. Gowriswari and T. K. Bharathi, Tetrahedron Lett., 1987, 28, 4591.
11. H. Amri, M. Rambsud and J. Villieras, Tetrahedron Lett., 1989, 30, 7381.
12. P. Shanbhag, P. R. Nareddy, M. Dadwal, S. M. Mobin and I. N. N. Namboothiri, Org. Biomol. Chem., 2010, 8, 4867.
13. X. L. Dong, L. Liang, E. Q. Li and Y. Huang, Angew. Chem., Int. Ed., 2015, 54, 1621.
14. W. J. Yao, Y. H. Wu, G. Wang, Y. P. Zhang and C. Ma, Angew. Chem., 2009, 121, 9893.
15. P. Shanbhag, P. R. Nareddy, M. Dadwal, S. M. Mobin and I. N. N. Namboothiri, Org. Biomol. Chem., 2010, 8, 4867.
16. P. Z. Xie, Y. Huang, W. Q. Lai, X. T. Meng and R. Y. Chen, Org. Biomol. Chem., 2011, 9, 6707.
17. R. Kumar, T. Kumar, S. M. Mobin and I. N. N. Namboothiri, J. Org. Chem., 2013, 78, 5073.
18. W. Liu and G. Zhao, Org. Biomol. Chem., 2014, 12, 832.
19. W. Zhou, X. Su, M. N. Tao, C. E. Zhu, Q. J. Zhao and J. L. Zhang, Angew. Chem., 2015, 127, 15066.
20. Q. Zhao, C. Pei, X. Guan and M. Shi, Adv. Synth. Catal., 2011, 353, 1973.
21. S. Takizawa, T. M. N. Nguyen, A. Grossmann, D. Enders and H. Sasai, Tetrahedron, 2013, 69, 1202.
22. X. Dong, L. Liang, E. Li and Y. Huang, Angew. Chem., Int. Ed., 2015, 54, 1621.
23. J. H. Robert, O. G. Scanes, G. André and R. S. David, Org. Lett., 2015, 17, 2462.
24. X. Zhao, J. J. Gong, K. Yuan, F. Sha and X. Y. Wu, Tetrahedron Lett., 2015, 56, 2526.
25. W. Zhou, X. Su, M. Tao, C. Zhu, Q. Zhao and J. Zhang, Angew. Chem., Int. Ed., 2015, 54, 14853.
26. X. Su, W. Zhou, Y. Li and J. Zhang, Angew. Chem. Int. Ed., 2015, 54, 6874 (Angew. Chem., 2015, 127, 6978).
27. W. Zhou, P. Chen, M. Tao, X. Su, Q. Zhao and J. Zhang, Chem. Commun., 2016, 52, 7612.
28. A. Dermenci, P. S. Selig, R. A. Domaoal, K. A. Spasov, K. S. Anderson and S. J. Miller, Chem. Sci., 2011, 2, 1568.
29. Y. Y. Zhang, R. Gurubrahamam and K. Chen, Adv. Synth. Catal., 2015, 357, 2457.
30. V. Mane, T. Kumar, S. Pradhan, S. Katiyar and I. N. N. Namboothiri, RSC Adv, 2015, 5, 69990.
31. G. Wang, R. Rexiti, F. Sha and X.-Y. Wu, Tetrahedron, 2015, 71, 4255.
32. A. Albrecht, A. Skrzynska, A. Przydacz and L. Albrecht, Synlett, 2015, 26, 2679.
33. A. Bhunia, S. R. Yetra, R. G. Gonnadec and A. T. Biju, Org. Biomol. Chem., 2016, 14, 5612.
34. X. F. Wang, L. Peng, J. An, C. Li, Q. Q. Yang, L. Q. Lu, F. L. Gu and W. J. Xiao, Chem.–Eur. J., 2011, 17, 6484.
35. S. Osuna, A. Dermenci, S. J. Miller and K. N. Houk, Chem.–Eur. J., 2013, 19, 14245.
36. W. Liu and G. Zhao, Org. Biomol. Chem., 2014, 12, 832.
37. J. Staunton, in Comprehensive Organic Chemistry, ed. P. G. Sammes, Pergamon Press, Oxford, England, 1979, vol. 4, p. 629.
38. T. Tombray, A. Blanc, J.-M. Weibel and P. Pale, Org. Lett., 2010, 12, 5362.
39. D. Liu, X.-M. Li, L. Meng, C.-S. Li, S.-S. Gao, Z. Shang, P. Proksch, C.-G. Huang and B.-G. Wang, J. Nat. Prod., 2011, 7, 7487.
40. G. A. Suárez-Ortiz, C. M. Cerda-García-Rojas, A. Hernández-Rojas and R. Pereda-Miranda, J. Nat. Prod., 2013, 76, 72.
41. C. D. Donner, Tetrahedron, 2013, 69, 377.
42. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
43. W. L. Hehre, L. Radom, P. R. Schleyer and J. A. Pople, Ab initio molecular orbital theory, Wiley, New York, 1986, p. 332.
44. E. H. Krenske, E. C. Davison, I. T. Forbes, J. A. Warner, A. L. Smith, A. B. Holmes and K. N. Houk, J. Am. Chem. Soc., 2012, 134, 2434.
45. H. Yang and M. W. Wong, J. Am. Chem. Soc., 2013, 135, 5808.
46. H. Yang and M. W. Wong, J. Org. Chem., 2011, 76, 7399.
47. M. W. Wong and A. M. E. Ng, Aust. J. Chem., 2014, 67, 1100.
48. Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157.
49. H. Xue, D. Jiang, H. Jiang, C. W. Kee, H. Hirao, T. Nishimura, M. W. Wong and C. H. Tan, J. Org. Chem., 2015, 80, 5745.
50. C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523.
51. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378.
52. E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO Version 3.1, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 1996.
53. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899.
54. J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1980, 102, 7211.
55. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, R. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, J. Cossi, N. Rega, J. M. Millam, M. Klene, M. Knox, J. B. Cross, V. Bakken, V. Adamo, J. Jaramillo, J. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, R. L. Morokuma, V. G. Zakrzewski, G. A. Voth, G. A. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (revision B. 01), Gaussian, Inc., Wallingford, CT, 2009.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra25311c

---