Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Wetting characteristics of underwater micro-patterned surfaces†
Surjyasish Mitra,
Naga Siva Kumar Gunda and
Sushanta K. Mitra *
*
Micro & Nano-scale Transport Laboratory, Department of Mechanical Engineering, Lassonde School of Engineering, York University, Toronto, Ontario M3J 1P3, Canada. E-mail: sushanta.mitra@lassonde.yorku.ca; Tel: +1 416 736 5924
First published on 30th January 2017
Abstract
Wetting phenomena of underwater systems are important for marine and other aquatic environment applications. Here, we study the underwater wetting characteristics of textured surfaces, where these surfaces are microfabricated on silicon substrates having pillar configurations. Using relevant experimental data, we have found that the equilibrium configuration of oil drops on such underwater substrates cannot be adequately characterized by the conventional wetting theories of Wenzel and Cassie–Baxter, which have been successful in validating similar wetting phenomena on pillared structures kept in ambient air. Further, we conducted contact angle hysteresis measurements for these underwater substrates and found that, except for large pillar pitch (i.e., 100 μm), the obtained results deviate significantly from the conventional theories. We argue that the energy barrier in terms of the critical pressure associated with displacing an outer dense liquid medium (i.e., water in this case) while filling up the space between the pillars and the dynamics of liquid–liquid displacement (i.e., oil–water system in this case) are equally important for the underwater configuration of liquid drops on such textured surfaces.
1 Introduction
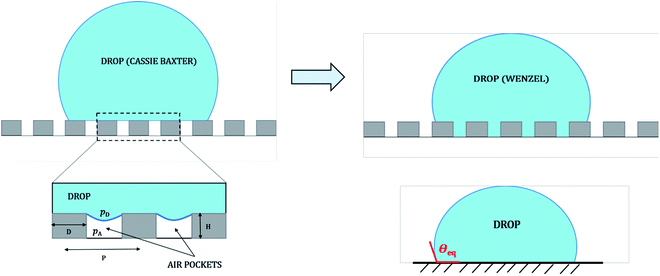
Micro and nano-textured hierarchical structures have found applications in self cleaning windows,1 systems where protection from marine bio-fouling is required,2 biomimetics3–7 as well as surfaces producing low drag in fluid flow.8,9 The theoretical basis of such behavior is attributed to the super-hydrophobic or super-oleophobic nature of such textured surfaces, governed by the well-known Wenzel10 and Cassie–Baxter11 configurations. When a liquid drop is deposited on a rough (or textured) substrate kept in ambient air medium, a Wenzel state corresponds to the drop penetrating the gap between the micro structures resulting in complete wetting, while a Cassie–Baxter state corresponds to the drop hanging on top of the micro structures with a layer of air trapped beneath (see Fig. 1). The validity of these two wetting theories is often debated and a cautious approach to use them is proposed in many recent studies.12–23 The differences mostly stem from the fact that these wetting theories have proved to be insufficient in characterizing contact angle hysteresis (i.e., the range of contact angles exhibited by a liquid drop on a given rough substrate), which is crucial towards understanding of hydrophobicity (or superhydrophobicity).Studies by Extrand et al.,17,21 Gao et al.12,22,23 and others have stressed that the interfacial contact areas are less significant for the wetting configuration of a drop on a rough (heterogeneous or textured) substrate.24–30 Rather, interaction of the three-phases in the vicinity of the three-phase contact line (i.e., the drop–substrate–air contact line) mostly dictates wetting configuration. Alternate models have been proposed in recent times to explain wetting behavior on such surfaces, especially to explain the discrepancies between experimentally observed apparent advancing and receding contact angles (i.e., contact angle hysteresis31)17,19,26–29,32–36 with those predicted by Wenzel and Cassie–Baxter theories. Still, for the majority of the reported studies involving wetting on rough (or textured) surfaces, the conventional form of Wenzel and Cassie–Baxter theories have proved to be successful in describing experimental data.1,2,8,14–16,18,37–42 In a recent work involving the wettability of chemically textured copper slabs having multi-tier roughness, Frankiewicz and Attinger suggested that there could be a possibility of meta-stable Cassie–Baxter configuration and even observed reversible wetting transitions between Wenzel and Cassie–Baxter wetting states.43
Another prominent issue regarding the applicability of these wetting theories is that they are solely based on interfacial area fractions and do not provide adequate clarity related to the transition from a Cassie state to a Wenzel state. Even though a Wenzel state corresponds to a lower energy state for the drop, during the wetting process, often the drop remains in a Cassie state due to a large energy barrier associated with making a transition between the two states.40 In such cases, some external work needs to be done to make the transition.40,44,45 Possibility of multiple equilibrium states40,46 on the same substrate often makes it difficult to decide which of the two wetting theories is to be used for the effective design of superhydrophobic surfaces. Efforts have been made to reconcile this debatable issue of wetting transition and provide a better understanding of the energy barrier associated with such transitions.45,47–54 Such an energy barrier is often expressed in terms of a critical pressure48,49 that exists across the drop–air interface in the gap between any two adjacent pillars, which ensures whether the Cassie–Baxter to Wenzel transition is favorable or not (see Fig. 1). Mathematically the transition condition in terms of liquid pressure can be expressed approximately as48,49
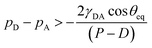 | (1) |
Even though wetting characteristics of textured surfaces kept in ambient air medium have been extensively studied, there is a significant lacuna towards understanding of wetting characteristics of such textured surfaces kept underwater (or under-liquid).55–59 We can look towards nature where fish scales and shark skins have hierarchical structures enabling them to repel oil drops and other contaminants from their surfaces. Hence, a study involving behavior of oil drops on an underwater substrate mimicking such phenomenon observed in nature finds applications in designing surfaces like submerged ship parts, marine pipelines, etc., which can effectively repel oil drops in case of an oil spill.60–62 The question remains is that whether Cassie–Baxter or Wenzel formulation is adequate to characterize wetting for under-liquid micro-structured surfaces? Most hydrophilic surfaces in air exhibit oleophobicity when placed underwater, i.e., the oil drop in its equilibrium configuration shows an underwater contact angle greater than 90°.55 It is the oil–water–solid contact angle which is the focus here, pertinent to a micro-patterned surface. In other words, we aim to check whether the Wenzel and Cassie–Baxter theories hold true for such underwater micro-patterned surfaces. If not, is there a need to have alternate considerations like the analysis of free energy barrier while studying the wetting of such under-liquid surfaces? Also, of interest here is to study the hysteresis of oil drops on such surfaces. Hence, to provide meaningful answers to these new questions related to under-liquid wettability, we have fabricated silicon based micro pillared substrates with a regular square array of cylindrical pillars having constant pillar height and diameter but varying pillar spacing. The substrates were placed underwater and wetting characteristics of millimeter sized oil droplets were studied in terms of their static (or equilibrium), advancing and receding contact angles.
2 Experimental section
2.1 Sample preparation
In this work, we have chosen the simplest and widely used micro-fabricated structure, which is the pillar geometry. The cost of fabrication of such pillared chip is around CAD 10 (based on academic pricing at University of Toronto micro/nano-fabrication facilities). Any other shape would incur huge expense and also additional microfabrication steps. Hence, we have limited our study to this base case with pillar geometry. A 100 mm diameter silicon (Si) substrate (Wafer World Inc., West Palm Beach, FL, USA) was cleaned in a standard piranha solution (H2SO4 and H2O2 in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio), then rinsed with deionised (DI) water, and dried with nitrogen gas. A positive photoresist (PPR) S1818 (MicroChem Corp, Westborough, MA, USA) was spin coated at 3000 rpm for 30 seconds and the coated substrate was soft baked at 115 °C for 60 seconds. The pillars were patterned on PPR with standard photolithography by exposing the substrate at 100 mJ cm−2 and then developing the substrate in MF-319 developer (Rohm and Haas Electronic Materials LLC, Marlborough, MA, USA). Further, the silicon substrate is etched anisotropically using deep reactive ion etching (DRIE) method for about 15 μm. After etching, the photoresist was removed by placing the substrate in PRS-100 stripper (HTA Enterprises, Microchrome Technology Products, San Jose, CA, USA). The substrates were then cut into 6 × 6 mm2 pieces. Using this process, substrates with constant pillar diameter 50 μm and height 15 μm but varying pitch (60 μm, 75 μm and 100 μm, respectively) were fabricated (see Fig. 2). The complete fabrication process flow for this type of pillar structures on a silicon substrate can be found elsewhere.63–65 We have also used one additional 100 mm-diameter silicon wafer and performed all the chemical treatments, outlined earlier, except the patterning process. Such wafer was also diced into 6 × 6 mm2 pieces, which were then used as standard reference substrates for contact angle measurements.
1 ratio), then rinsed with deionised (DI) water, and dried with nitrogen gas. A positive photoresist (PPR) S1818 (MicroChem Corp, Westborough, MA, USA) was spin coated at 3000 rpm for 30 seconds and the coated substrate was soft baked at 115 °C for 60 seconds. The pillars were patterned on PPR with standard photolithography by exposing the substrate at 100 mJ cm−2 and then developing the substrate in MF-319 developer (Rohm and Haas Electronic Materials LLC, Marlborough, MA, USA). Further, the silicon substrate is etched anisotropically using deep reactive ion etching (DRIE) method for about 15 μm. After etching, the photoresist was removed by placing the substrate in PRS-100 stripper (HTA Enterprises, Microchrome Technology Products, San Jose, CA, USA). The substrates were then cut into 6 × 6 mm2 pieces. Using this process, substrates with constant pillar diameter 50 μm and height 15 μm but varying pitch (60 μm, 75 μm and 100 μm, respectively) were fabricated (see Fig. 2). The complete fabrication process flow for this type of pillar structures on a silicon substrate can be found elsewhere.63–65 We have also used one additional 100 mm-diameter silicon wafer and performed all the chemical treatments, outlined earlier, except the patterning process. Such wafer was also diced into 6 × 6 mm2 pieces, which were then used as standard reference substrates for contact angle measurements.
 | ||
| Fig. 2 SEM micrographs of the Si micro-patterned substrates with the different pillar configurations. | ||
2.2 Instrumentation
For the experimental setup, a custom made contact angle measurement system was used. The working liquids used were deionized water (density ρW = 1000 kg m−3, surface tension in air γWA = 72.1 mN m−1) and laser oil (Cargille Laboratories Inc., Cedar Grove, NJ, USA; density ρO = 1100 kg m−3, surface tension in air γOA = 24.5 mN m−1). The oil–water interfacial tension, γOW is 33.33 mN.66 For static contact angle measurements, the substrates were kept at the bottom of a distortion free glass cuvette (Krüss Germany, SC-01) filled with DI water and millimeter sized oil drops were deposited. Care was taken to ensure that no entrapped air was present in between the pillars when the substrates were submerged in water. This was evident from the absence of any bubble within the bulk water phase during the course of experiment. For each set of experiment, the substrates were submerged for 5 min, thereby preventing any diffusion of entrapped air (if any) into the water phase.The images were captured using a CCD camera and analyzed using an in-house developed Drop Shape Analysis software. A tangent method67 was used to extract the contact angle information from the observed slope of the three phase contact line associated with each image of the sessile drop (see Fig. 3). For hysteresis measurements, the needle tip used for drop deposition was inserted into an already deposited sessile drop and the syringe pump associated with the needle-drop assembly of the contact angle measurement system was operated at a flow rate of 10 μL min−1 to increase (or decrease) the drop volume.67 It is to be noted that in the original experiments of Wenzel,10 a quasi-equilibrium condition was maintained by gently moving the plate. In this current set-up, as reported in our earlier work,67 we ensure the quasi-equilibrium process for the oil–water–solid system by controlling the flow rate (injection and retraction) of the needle-drop assembly during the hysteresis measurements. As the drop volume was increased, the contact angle reached a maximum value close to 180° and on further increase, the three phase contact line jumped on to the next pillar. This maximum contact angle, i.e., the advancing contact angle, θA was calculated from the recorded images. In a similar manner, when liquid was withdrawn from the drop by the needle, the receding contact angle, θR was measured. For every micro-pillar configuration, each set of contact angle measurements (advancing, receding and equilibrium) was repeated 5 times to ensure consistency. The contact angle values provided here are the average values of 5 measurements and are reproducible within an experimental error of ±2°. Contact angle measurements were also conducted on the standard reference flat Si substrates, described earlier, for comparison purpose.
 | ||
| Fig. 3 Extraction of contact angle from obtained images of oil/water drop on the given substrate (micro-patterned or flat) kept underwater or in air using the tangent method. | ||
3 Results
3.1 Static contact angles
Fig. 4A and B show the static contact angles of oil in air, water in air and oil in underwater systems for the micro-patterned and flat silicon substrates, respectively. For an oil drop on a flat solid surface placed underwater, the equilibrium contact angle, θOW can be evaluated by applying the Young's equation for water (drop)–air, oil (drop)–air, and oil (drop)–water systems, respectively as,55
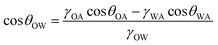 | (2) |
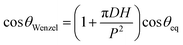 | (3) |
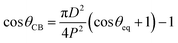 | (4) |
Table 1 compares the equilibrium contact angles measured from experiment with the theoretical Wenzel values for cases where the measurements were conducted in air. It can be concluded that for wetting in air, the water drop exhibited a Wenzel configuration for all cases, while oil exhibited complete wetting with very low contact angles (see the first column from the left in Fig. 4A). But in case of wetting of oil drops in underwater configuration, neither the Wenzel nor the Cassie–Baxter theory was in accordance with the observed static contact angle values (see Table 2).
| Pitch (μm) | Observed equilibrium CA of water in air | Theoretical equilibrium CA of water in air |
|---|---|---|
| 0 (flat) | 80° (θWA) ± 1° | — |
| 60 | 74° ± 1° | 73° |
| 75 | 75° ± 1° | 75° |
| 100 | 80° ± 1° | 77° |
| Pitch (μm) | Observed CA of oil in water | Wenzel CA of oil in water | Cassie–Baxter CA of oil in water |
|---|---|---|---|
| 0 (flat) | 86° (θOW) ± 1° | — | — |
| 60 | 156° ± 1° | 86.6° | 115° |
| 75 | 132° ± 1° | 87° | 129° |
| 100 | 117° ± 1° | 87.5° | 142° |
It can thus be concluded that as far as static configurations are concerned, the Wenzel (or Cassie–Baxter) theory does not accurately capture the wetting dynamics for underwater systems. Jung et al.,55 in their recent study of wetting on underwater micro-patterned substrates, which consists of pillars of constant height and diameter of 30 μm and 14 μm, respectively, with the pillar pitch varied from 21 μm to 210 μm, found that Wenzel and Cassie–Baxter theories match well with their experimental data. In their experiments, they have used hexadecane as the liquid drop (R = 1 mm) and water as surrounding liquid medium and found that the equilibrium contact angles for under-liquid micro-patterned silicon substrates varied from 146° for the 21 μm pitch substrate (Cassie–Baxter) to 104° for the 210 μm pitch substrate (Wenzel). However, no contact angle hysteresis analysis was performed by Jung et al. This mismatch in the equilibrium contact angle value for a drop on an under-liquid substrate between our present study and those provided by Jung et al.,55 has propelled us to perform a hysteresis study to gather more insight into this wetting problem.
3.2 Contact angle hysteresis
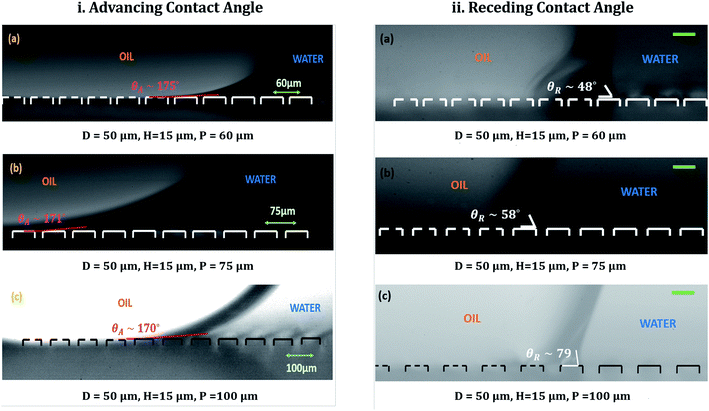
Fig. 5(i) shows the advancing contact angles for different micro-patterned surfaces used. It should be noted here that capturing of images with drop on micro-patterned substrate kept in underwater is a challenge. The pillars are not completely visible from the obtained images (see (a) and (b) of Fig. 5(i)). Only after significant image analysis, which includes changing the image contrast, the pillars become gradually visible (see (c) of Fig. 5(i)) and the three-phase contact line (TPCL) is correctly identified. For all the micro-patterned substrates, the advancing contact angle is close to 180°. The difference in obtained contact angle values can be attributed to the difference in image clarity and hence a slight deviation in the obtained fitting while computing the contact angle using the tangent method. To keep things in perspective, one can compare these values with the more well-studied system of contact angle hysteresis in an ambient air medium.14,17,19,20,41,68 For cases where the substrate is kept in air (i.e., inviscid) medium, the advancing contact angle is always close to 180°, which is obvious since the three-phase contact line needs to reach such an angle to touch the next set of pillars. On the other hand, the receding contact angle values varied significantly with pillar pitch, as shown in Fig. 5(ii). The increase in receding contact angles with increasing pillar pitch is also commonly found in hysteresis studies in air medium.14,20,68 However, the wide spread in hysteresis for under-liquid substrates obtained here is something new and warrants further study.It is also important to understand the motion of the three-phase contact line during advancing and receding motions of the oil drop over the pillars of varying pitch. When liquid was withdrawn from the drop during the course of receding, it was found that for the smallest pillar pitch (i.e., 60 μm), the three-phase contact line receded a number of pillars at once (see ESI video S1†). However, as shown in Fig. 6, for the larger pillar pitches (i.e., 75 μm and 100 μm) the contact line was observed to jump individual pillars while receding (see Fig. 6(a) and (b)). Still, it was not clear whether the drop was in a Wenzel or Cassie–Baxter state. For underwater systems, the problem lies in conventional imaging of drop–substrate system since it usually provides a clear visualization of the three phase contact line (TPCL) only in two axes (x and z, in our case). It does not provides a clear picture of the neighboring TPCLs or the drop–water interface between two adjacent TPCLs. Hence, to ascertain whether the drop was in a Wenzel or Cassie–Baxter state, it was necessary to image the receding mechanism with a clear visualization of the receding TPCL and the neighboring drop–water interface behavior. Such visualization is normally performed under a microscope for static drop configurations. However for dynamic configurations, i.e., a receding drop, observing the process with camera-lens system is more suitable.
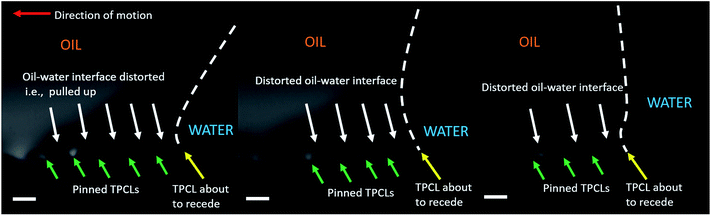
To achieve a visualization of the drop receding motion where all the three axes are visible, images were captured by positioning the camera at an angle of about 10 from the reference plane used earlier. Interestingly, it was found that while receding, for patterned substrate with pitch 75 μm, locally the drop–water interface is pulled up while the TPCL remained pinned on the adjacent pillar tops (see Fig. 7). Then, a single TPCL receded at a time while the neighboring TPCLs remained pinned. Similar phenomenon was also observed for the substrate with pillar pitch 60 μm, but due to the contact line jumping over a number of pillars at once, such motion could not be effectively captured. The pulling up of the drop–water interface while receding, strongly indicates that the wetting for those two substrates is not a Wenzel configuration. Rather it is either a metastable Cassie–Baxter or a mixed wetting state with partial filling of the space between the pillars.69
4 Discussions
4.1 Static configuration
Table 3 reports the comparison of the experimentally observed advancing and receding contact angles for the different underwater micro-patterned substrates with those predicted by Wenzel and Cassie–Baxter equations, i.e., by substituting θeq with θOW,A and θOW,R in eqn (3) and (4), where θOW,A and θOW,R are the experimentally observed advancing and receding contact angles on the corresponding underwater flat reference substrate. This approach is also a major part of this entire debate revolving around the applicability of using these theories to predict hysteresis behavior.14,17,19–21,41,42 Nevertheless, we use this approach to compare our experimentally observed values. It can be seen from Table 3, except for the receding contact angle for the micro-patterned substrate with pitch 100 μm, none of the advancing and receding angles comply with those predicted by either Wenzel or Cassie–Baxter theory. This indicates that a Wenzel configuration observed in air medium does not always necessarily translate to Wenzel configuration for underwater systems. In the present case, since the substrate is underwater, the surrounding pressure is not atmospheric but with the added contribution of the hydrostatic head, pH (∼ρWgh) posed by the height h of water column present in the cuvette. Therefore eqn (1), applicable for substrates kept in air, needs to be modified to take into account this hydrostatic head. Hence, the condition for the critical transition pressure for an under-liquid substrate can be written as:
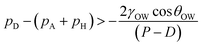 | (5) |
| Pitch (μm) | Observed advancing and receding CAs θA/θR | Theoretical advancing and receding CAs (Wenzel) θA/θR | Theoretical advancing and receding CAs (CB) θA/θR |
|---|---|---|---|
| 0 (flat) | 103° (θOW,A) ± 2°/80° (θOW,R) ± 2° | — | — |
| 60 | 175° ± 2°/48° ± 2° | 112°/73° | 125°/111° |
| 75 | 171° ± 2°/58° ± 2° | 108°/76° | 136°/126° |
| 100 | 170° ± 2°/79° ± 2° | 106°/78° | 147°/140° |
We argue that since the pressure difference across the drop–water interface below the suspended drop between two adjacent pillars, pD − (pA + pH) is significantly lower than the corresponding scenario in air, i.e., pD − pA, for the substrates with relatively smaller pitches (i.e., 60 μm and 75 μm), the critical transition pressure is never reached resulting in a Cassie–Baxter or an intermediate configuration. It is to be noted that existence of such critical pressure for superrepellancy in air for wetting liquids on re-entrant structures has been discussed by Liu and Kim.6 For the substrate with the relatively larger pitch, i.e., 100 μm, it appears that the critical transition pressure was achieved and a Wenzel configuration was realized, evident from its receding contact angle value. It should be noted here that the height of the water column (∼15–18 mm for the present study) cannot be varied as an experimental parameter in terms of order of magnitude. This is due to challenges in our current contact angle measurement system as well as in other commercially available systems, in terms of the vertical needle movement and the drop size requirement, restricting such a variation. A more comprehensive computational study of the critical pressure transition criterion would have been helpful in throwing more light into this complex phenomenon of energy barrier mediated wetting configuration. However, such a study is beyond the scope of the present work and can be treated as a topic for future investigation.
4.2 Receding contact angle values
From the observation of receding motion, even though a metastable Cassie–Baxter state (or even a mixed wetting state) can be inferred for the drop on the underwater substrates with pitches 60 μm and 75 μm, the receding contact angle values exhibited on these substrates appears to be puzzling. A wide hysteresis is indicative of a Wenzel behavior. But our visualization of the receding phenomenon (see Fig. 7) clearly shows a receding mechanism unlikely of a Wenzel-like configuration. Often, the edge effect70,71 on such pillar structures provides results which deviates from the conventional Wenzel and Cassie–Baxter states. However, no such edge effects were noticed in our visualization of either the equilibrium shape and the three phase contact line movement during advancing and receding motion of the drop. For the low contact angles observed, it can be due to the fact that a thin layer of water may have been left behind when the three phase contact line receded, as pointed out by Patankar et al.13 in a similar study carried out for substrates in air medium. Another possibility can be a precursor film formation,72,73 which better explains such curvature close to the three-phase contact line while receding. This is presently not well understood and needs to be investigated further in terms of the dynamics of liquid–liquid displacement. In our recent study related to under-liquid drop coalescence,74 we have delineated the role of the surrounding denser and viscous medium (i.e., water). Commonly observed wetting phenomena like spreading73,75,76 and coalescence of sessile drops74 are very different for under-liquid substrates than substrates in ambient air where parameters like the surrounding liquid density and viscosity play key roles in dictating the dynamics of how one dense liquid displaces another. Hence, new studies are required with significant modification to the governing theories that hold true for air medium by taking into account the role of the surrounding viscous medium, rather than a mere extrapolation of these theories. Also, recent advancement in experimental techniques like laser scanning confocal microscopy77 would be of great help to understand such under-liquid wetting behavior.5 Conclusion
The present study reports a first of its kind detailed investigation of wetting characteristics of oil drops on underwater micro-patterned substrates. For this purpose, we have performed wetting studies of three different micro-pillared substrates, where each substrate has same pillar height and diameter but varying pillar pitch of 60 μm, 75 μm, and 100 μm. It was found that for such cases, the wetting characteristics (in terms of static, advancing and receding contact angles) cannot be formulated using the conventional framework of Wenzel10 and Cassie–Baxter11 theories. It is clear that the conventional theories as well as trends seen for wetting on micro-patterned substrates kept in air medium1,2,8,14–16,18,37–42 do not necessarily translate to similar behavior on under-liquid systems. The static drop configuration for such an underwater substrate was found to conform to a metastable Cassie–Baxter or a mixed wetting state evident from the study of the receding mechanism of the oil drop in underwater system. The energy barrier associated with displacing a surrounding dense medium and filling up the space between the pillars should be accounted for to predict which configuration (Wenzel, Cassie–Baxter, metastable Cassie–Baxter or a mixed wetting state) is thermodynamically favorable. Also, since an outer liquid medium possess significant viscous effects, the dynamics of liquid–liquid displacement needs to be considered to understand the behavior of the three-phase contact line in such systems which is crucial for appropriate characterization of the contact angle, particularly the receding contact angle. With growing number of underwater applications as well as a need to mitigate environmental effects of major oil spills, which has become a growing concern in the wake of the DeepWater Horizon oil spill event by BP,78 this basic study on understanding wettability of underwater micro-patterned substrates garners relevance in designing appropriate oil repellant and corrosion resistant surfaces. The results presented here points to our lack of comprehensive theoretical understanding of the mechanisms that dictate wetting of under-liquid micro-patterned substrates and begs the need to have a new theoretical framework for such systems.Acknowledgements
The authors would like to thank Natural Sciences and Engineering Research Council of Canada for their financial support through Grant # RGPIN-2014-05236 and RTI-2015-472734.References
- M. Nosonovsky and B. Bhushan, Multiscale dissipative mechanisms and hierarchical surfaces: friction, superhydrophobicity, and biomimetics, Springer-Verlag, Heidelberg, Germany, 2008 Search PubMed
.
- J. Genzer and K. Efimenko, Biofouling, 2006, 22, 339–360 CrossRef CAS PubMed
.
- Y. Zheng, X. Gao and L. Jiang, Soft Matter, 2007, 3, 178–182 RSC
.
- M. Nosonovsky and B. Bhushan, Curr. Opin. Colloid Interface Sci., 2009, 14, 270–280 CrossRef CAS
.
- Y. Liu and G. Li, J. Colloid Interface Sci., 2012, 388, 235–242 CrossRef CAS PubMed
.
- T. Liu and C. Kim, Science, 2014, 346, 6213 Search PubMed
.
- P. R. Waghmare, S. Mitra, N. S. K. Gunda and S. K. Mitra, RSC Adv., 2015, 5, 82374–82380 RSC
.
- B. Bhushan, Y. C. Jung and K. Koch, Philos. Trans. R. Soc., A, 2009, 367, 1631–1672 CrossRef CAS PubMed
.
- S. Martin and B. Bhushan, J. Colloid Interface Sci., 2016, 474, 206–215 CrossRef CAS PubMed
.
- R. N. Wenzel, Ind. Eng. Chem., 1936, 28, 988–994 CrossRef CAS
.
- A. Cassie and S. Baxter, Trans. Faraday Soc., 1944, 40, 546–551 RSC
.
- L. Gao and T. J. McCarthy, Langmuir, 2007, 23, 3762–3765 CrossRef CAS PubMed
.
- N. A. Patankar, Langmuir, 2003, 19, 1249–1253 CrossRef CAS
.
- C. Dorrer and J. Rühe, Langmuir, 2006, 22, 7652–7657 CrossRef CAS PubMed
.
- G. McHale, Langmuir, 2007, 23, 8200–8205 CrossRef PubMed
.
- M. Nosonovsky, Langmuir, 2007, 23, 9919–9920 CrossRef PubMed
.
- C. Extrand, Langmuir, 2002, 18, 7991–7999 CrossRef CAS
.
- A. Marmur, Langmuir, 2003, 19, 8343–8348 CrossRef CAS
.
- C. Priest, T. W. Albrecht, R. Sedev and J. Ralston, Langmuir, 2009, 25, 5655–5660 CrossRef CAS PubMed
.
- D. Öner and T. J. McCarthy, Langmuir, 2000, 16, 7777–7782 CrossRef
.
- C. Extrand, Langmuir, 2003, 19, 3793–3796 CrossRef CAS
.
- L. Gao and T. J. McCarthy, Langmuir, 2007, 23, 13243 CrossRef CAS
.
- L. Gao and T. J. McCarthy, Langmuir, 2009, 25, 14105–14115 CrossRef CAS PubMed
.
- F. Bartell and J. Shepard, J. Phys. Chem., 1953, 57, 455–458 CrossRef CAS
.
- J. Joanny and P.-G. De Gennes, J. Chem. Phys., 1984, 81, 552–562 CrossRef CAS
.
- W. Choi, A. Tuteja, J. M. Mabry, R. E. Cohen and G. H. McKinley, J. Colloid Interface Sci., 2009, 339, 208–216 CrossRef CAS PubMed
.
- N. Anantharaju, M. V. Panchagnula, S. Vedantam, S. Neti and S. Tatic-Lucic, Langmuir, 2007, 23, 11673–11676 CrossRef CAS PubMed
.
- R. Raj, R. Enright, Y. Zhu, S. Adera and E. N. Wang, Langmuir, 2012, 28, 15777–15788 CrossRef CAS PubMed
.
- S. T. Larsen and R. Taboryski, Langmuir, 2009, 25, 1282–1284 CrossRef CAS PubMed
.
- A. Gauthier, M. Rivetti, J. Teisseire and E. Barthel, Phys. Rev. Lett., 2013, 110, 046101 CrossRef PubMed
.
- W. Li and A. Amirfazli, J. Colloid Interface Sci., 2005, 292, 195–201 CrossRef CAS PubMed
.
- T. L. Liu, Z. Chen and C.-J. Kim, Soft Matter, 2015, 11, 1589–1596 RSC
.
- A. Shastry, S. Abbasi, A. Epilepsia and K. F. Bohringer, in International Solid-State Sensors, Actuators and Microsystems Conference (Transducers'07), 2007, pp. 599–602 Search PubMed
.
- R. Dufour, M. Harnois, V. Thomy, R. Boukherroub and V. Senez, Soft Matter, 2011, 7, 9380–9387 RSC
.
- T. Wu and Y. Suzuki, Sens. Actuators, B, 2011, 156, 401–409 CrossRef CAS
.
- E. Bormashenko, J. Colloid Interface Sci., 2011, 360, 317–319 CrossRef CAS PubMed
.
- J. Bico, C. Tordeux and D. Quéré, Europhys. Lett., 2001, 55, 214 CrossRef CAS
.
- N. A. Patankar, Langmuir, 2004, 20, 8209–8213 CrossRef CAS PubMed
.
- B. Bhushan and Y. C. Jung, Ultramicroscopy, 2007, 107, 1033–1041 CrossRef CAS PubMed
.
- B. He, N. A. Patankar and J. Lee, Langmuir, 2003, 19, 4999–5003 CrossRef CAS
.
- K.-Y. Yeh, L.-J. Chen and J.-Y. Chang, Langmuir, 2008, 24, 245–251 CrossRef CAS PubMed
.
- Y. Kwon, S. Choi, N. Anantharaju, J. Lee, M. Panchagnula and N. Patankar, Langmuir, 2010, 26, 17528–17531 CrossRef CAS PubMed
.
- C. Frankiewicz and D. Attinger, Nanoscale, 2016, 8, 3982–3990 RSC
.
- J. Bico, C. Marzolin and D. Quéré, Europhys. Lett., 1999, 47, 220 CrossRef CAS
.
- Z. Yoshimitsu, A. Nakajima, T. Watanabe and K. Hashimoto, Langmuir, 2002, 18, 5818–5822 CrossRef CAS
.
- R. E. Johnson Jr and R. H. Dettre, J. Phys. Chem., 1964, 68, 1744–1750 CrossRef
.
- P. Forsberg, F. Nikolajeff and M. Karlsson, Soft Matter, 2011, 7, 104–109 RSC
.
- N. A. Patankar, Langmuir, 2010, 26, 8941–8945 CrossRef CAS PubMed
.
- A. Giacomello, M. Chinappi, S. Meloni and C. M. Casciola, Phys. Rev. Lett., 2012, 109, 226102 CrossRef PubMed
.
- Q.-S. Zheng, Y. Yu and Z.-H. Zhao, Langmuir, 2005, 21, 12207–12212 CrossRef CAS PubMed
.
- H. Kusumaatmaja, M. Blow, A. Dupuis and J. Yeomans, Europhys. Lett., 2008, 81, 36003 CrossRef
.
- E. Bormashenko, Philos. Trans. R. Soc., A, 2010, 368, 4695–4711 CrossRef CAS PubMed
.
- B. Liu and F. F. Lange, J. Colloid Interface Sci., 2006, 298, 899–909 CrossRef CAS PubMed
.
- E. Bormashenko, Adv. Colloid Interface Sci., 2015, 222, 92–103 CrossRef CAS PubMed
.
- Y. C. Jung and B. Bhushan, Langmuir, 2009, 25, 14165–14173 CrossRef CAS PubMed
.
- V. Hejazi and M. Nosonovsky, Langmuir, 2011, 28, 2173–2180 CrossRef PubMed
.
- I. Palamà, S. D'Amone, V. Arcadio, D. Caschera, R. Toro, G. Gigli and B. Cortese, J. Mater. Chem. A, 2015, 3, 3854–3861 Search PubMed
.
- M. Jin, S. Li, J. Wang, Z. Xue, M. Liao and S. Wang, Chem. Commun., 2012, 48, 11745–11747 RSC
.
- Q. Cheng, M. Li, Y. Zheng, B. Su, S. Wang and L. Jiang, Soft Matter, 2011, 7, 5948–5951 RSC
.
- M. Nosonovsky and B. Bhushan, Philos. Trans. R. Soc., A, 2009, 367, 1511–1539 CrossRef CAS PubMed
.
- B. Bhushan, Beilstein J. Nanotechnol., 2011, 2, 66–84 CrossRef CAS PubMed
.
- V. Hejazi, A. E. Nyong, P. K. Rohatgi and M. Nosonovsky, Adv. Mater., 2012, 24, 5963–5966 CrossRef CAS PubMed
.
- N. S. K. Gunda, M. Singh, Y. Purwar, S. L. Shah, K. Kaur and S. K. Mitra, Biomed. Microdevices, 2013, 15, 959–971 CrossRef CAS PubMed
.
- N. S. K. Gunda, J. Joseph, A. Tamayol, M. Akbari and S. K. Mitra, Microfluid. Nanofluid., 2013, 14, 711–721 CrossRef CAS
.
- N. S. K. Gunda, B. Bera, N. K. Karadimitriou, S. K. Mitra and S. M. Hassanizadeh, Lab Chip, 2011, 11, 3785–3792 RSC
.
- P. R. Waghmare, S. Das and S. K. Mitra, Soft Matter, 2013, 9, 7437–7447 RSC
.
- P. R. Waghmare and S. K. Mitra, Langmuir, 2010, 26, 17082–17089 CrossRef CAS PubMed
.
- H. Kusumaatmaja and J. Yeomans, Langmuir, 2007, 23, 6019–6032 CrossRef CAS PubMed
.
- S. Farsinezhad, P. R. Waghmare, B. D. Wiltshire, H. Sharma, S. Amiri, S. K. Mitra and K. Shankar, RSC Adv., 2014, 4, 33587–33598 RSC
.
- F.-M. Chang, S.-J. Hong, Y.-J. Sheng and H.-K. Tsao, J. Phys. Chem. C, 2010, 114, 1615–1621 CAS
.
- F.-M. Chang, Y.-J. Sheng and H.-K. Tsao, Appl. Phys. Lett., 2009, 95, 204107 CrossRef
.
- P.-G. De Gennes, Rev. Mod. Phys., 1985, 57, 827 CrossRef CAS
.
- D. Bonn, J. Eggers, J. Indekeu, J. Meunier and E. Rolley, Rev. Mod. Phys., 2009, 81, 739 CrossRef CAS
.
- S. Mitra and S. K. Mitra, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 033013 CrossRef PubMed
.
- K. Chaudhury and S. Chakraborty, Langmuir, 2015, 31, 4169–4175 CrossRef CAS PubMed
.
- S. Mitra and S. K. Mitra, Langmuir, 2016, 32, 8843–8848 CrossRef CAS PubMed
.
- F. Schellenberger, N. Encinas, D. Vollmer and H.-J. Butt, Phys. Rev. Lett., 2016, 116, 096101 CrossRef PubMed
.
- A. C. Ortmann, J. Anders, N. Shelton, L. Gong, A. G. Moss and R. H. Condon, PLoS One, 2012, 7, e42548 CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra25888c |
| This journal is © The Royal Society of Chemistry 2017 |