Open Access Article
Open Access ArticleRapid determination of complex oil well cement properties using mathematical models
Ghada Bassioni *a,
Mohammed Mohammed Alib,
Ali Almansoorib,
Gabriele Raudaschl-Sieberc and
Fritz E. Kühn
*a,
Mohammed Mohammed Alib,
Ali Almansoorib,
Gabriele Raudaschl-Sieberc and
Fritz E. Kühn c
c
aChemistry Department, Faculty of Engineering, Ain Shams University, P. O. Box 11517, Cairo, Egypt. E-mail: ghada_bassioni@eng.asu.edu.eg; Fax: +20 22630470; Tel: +20 1001832728
bChemical Engineering Program, The Petroleum Institute, P. O. Box 2533, Abu Dhabi, UAE
cMolecular Catalysis, Department of Chemistry, Catalysis Research Center, Technische Universität München (TUM), Lichtenbergstr. 4, D-85747 Garching bei München, Germany
First published on 17th January 2017
Abstract
The chemistry of oil-well cement is very complex. As a result of incompatibility of some simultaneously added chemical combinations to obtain better cement workability, undesirable interactions reflect on the properties of the cement slurry. Experimental investigation of these properties is lengthy and depends on accuracy. In this work, the compatibility between lignosulfonate as a retarder R and NSF polycondensates as dispersants D is studied. Furthermore, optimum dosages are proposed based on the zeta potential technique at ambient conditions. The results show that the optimum dosage for (R2 + D1) is 0.2% by weight of cement. Moreover, the obtained results are supported by adsorption isotherms. The competitive adsorption is attributed to the differences in anionic charge densities between the additives and is postulated to take place on C3A hydrates. The effect of the proposed additive dosages is studied on cement hydration. The obtained dosages show a good setting time (21 h) at a water-to-cement ratio of 0.4 and under ambient conditions. Furthermore, due to complex interactions with cement hydrates, mathematical models are proposed that are able to validate experimental results of surface properties and hydration processes.
1. Introduction
In the oil and gas industry, different operations are applied during drilling and completion of an oil well. Despite the importance of all well cementing functions, zonal isolation is surely the most important and critical objective. To fulfill this aim, all drilling cuttings and drilling fluids must be replaced by the cement slurry. Then the cement slurry is allowed for a certain time to set under physico-chemical reactions, called “hydration”, preventing any flow of formation fluids.1 Gas migration (up or down) between formations through the cement matrix is undesirable and may cause many problems for the well. It forms flow channels (microannuli) at pipe/cement or cement/formations interfaces.As cement is being pumped into the well, the slurry is exposed to aggressive conditions such as high temperature, high pressure and salinity making the process quite challenging and rather complex. Therefore, certain additives are combined and employed in cement formulation in order to enhance its properties and achieve the optimum performance. Retarders and dispersants combination are commonly utilized due to their ability to control the cement early hydration and flow-ability under extreme well conditions. Retarders are defined as the chemical additives that delay cement setting times and prevent premature hardening. Typically, the perfect retarder for oil-well cement is the one which extends the cement setting for adequate time and then suddenly allow the cement hydration to proceed at a rapid rate.2 There are different kinds of oil-well cement retarders such as calcium and sodium lignosulfonates.3 As summarized recently the proposed retardation mechanisms fall into four categories: (1) calcium complexation by chelating the free calcium ions preventing C–S–H formation and/or portlandite precipitation, (2) formation of a semipermeable layer, later broken down by osmotic pressure gradients, (3) direct surface adsorption on cement anhydrous particles, (4) nucleation and growth poisoning of cement hydrates.4 A fifth mechanism (“dissolution–precipitation”) has been proposed and considered a special case of surface adsorption.5 Dispersants are used to improve the rheological behavior of cement slurries. In deep oil well – because of the increased temperature – the viscosity of cement slurry is low leading to undesirable flow characteristics of the cement slurry.6 This behavior affects the cementing job negatively and thus zonal isolation does not get complete since the low viscosity jeopardizes the success of cement placement. Dispersants have the ability to overcome the van der Waals attractive inter-particle forces by imparting a stronger repulsive force at the surface–liquid interface, freeing the entrapped water.4 This process is described to occur as follows: (1) the mixing actions break down the cement agglomerates and distribute the dispersant agents, fully miscible in the high ionic strength pore water, through the cement slurry; (2) an attractive force between the dispersant additives, which usually bears a negative charge at the relatively high pH of the pore water, and the positively charged cement surfaces, causes fairly rapid adsorption of the dispersants onto the cement particles; and (3) the adsorbed compounds, forming a layer of a certain thickness and conformation, produce some combination of electrostatic and steric repulsive forces (steric hindrance) that prevent re-agglomeration of cement particles and liberate water that has been trapped within the flocculated structure. The types of dispersant include polymelamine sulfonate (PMS), polynaphthalene sulfonate (PNS or NSFC), polystyrene sulfonate and other types of hydroxycarboxylic acids such as citric acid.6
The use of different additive formulations in cement systems make the cement chemistry very complex and may cause undesired interaction. As a result, well cementing operation is compromised due to the loss in cement/additives system performance. This loss can be referred to the low flow-ability of cement slurry, over retardation, low early strength development and high cement fluid loss. Incompatibilities in the cement system are mainly attributed to the competitive adsorption of the additives on limited adsorption sites on cement and hydration products surfaces and it is depended mainly on the chemical nature of additives.
The main goal of this work is to find a way to simplify data access, usually resulting from complex experimental measurements. First, a systematic study is conducted that produces highly economic cement recipes with maximum efficient workability and experimental results are validated with simple mathematical models. This objective can be achieved by linking the chemical and mechanical properties. This work is focusing on two important additives, retarders and dispersants. The study starts with analyzing chemical characteristics of two commercially available additives: sodium lignosulfonate (retarder R) and sodium naphthalene sulfonic acid–formaldehyde condensate (dispersant D). Moreover, the study proposes the optimum dosages for those additives based on zeta potentials, adsorption isotherms and studying the interaction between additive systems as well as the compatibility between different additive dosages on the adsorptions sites. Furthermore, the effect of the proposed dosages on the cement hydration is shown. Also, mathematical models validating the zeta potential measurements and hydration processes are suggested.
2. Experimental
2.1 Sample preparation
The experiments are conducted at the Center for Applied and Environmental Chemistry at the Petroleum Institute (PI) in Abu Dhabi, UAE, and at the Technische Universität München (TUM), Department of Chemistry, Munich, Germany. Commercially available sodium lignosulfonate (retarders R1 and R2) and sodium naphthalene sulfonic acid formaldehyde condensate (dispersant D1 and D2) are obtained from international service companies without further purification. The water to cement ratio (w/c) is set at 0.4 for all experiments.2.2 Chemical characterization
XRD and FT-IR measurements for oil well cement class G under investigation have been previously reported.7,8 Different qualitative and quantitative chemical analyses are performed on the utilized additives in order to evaluate their properties.1H NMR spectroscopy on the retarders is carried out using a 400 MHz spectrometer (Bruker AMX 400, BRUKER, Germany) at a resonance frequency of 400.13 MHz for 1H with D2O as a solvent.
29Si MAS-NMR and 27Al MAS-NMR measurements are conducted for hydrated cement with 0.5% by weight of cement (bwoc) of both retarders (R1 and R2) and compared to the blank one by a 300 MHz spectrometer (Bruker Avance 300, BRUKER, Germany) using Bruker TopSpin 2.1 software. 29Si MAS-NMR measurements (resonance frequency of 59.62 MHz) are performed in 7 mm ZrO2 rotors at a spinning speed of 5 kHz with 1050–1200 scans. 27Al MAS-NMR measurements (resonance frequency of 78.21 MHz) are performed in 4 mm ZrO2 rotors at a spinning speed of 15 kHz with 3000 scans.
Elemental analysis (C, H, N, S) of the utilized retarders and dispersant is determined with a CHNS-O elemental analyzer (EA 3000, Euro Vector SPA, Italy).9 In order to determine the amounts of calcium, sodium and potassium in the cement's additives atomic absorption spectroscopy technique is used. Standards solutions of Ca, Na and K are prepared at different concentrations (1 ppm to 6 ppm). The samples are dissolved in 1% of sulfuric acid (H2SO4) and 1% (HNO3) and heated until the color of the solution become light. After that the sample is diluted in distilled water. Solutions of the acids and the distilled water are prepared as background. The AAS measurements are conducted using (AAS, Varian AA280 FS, Australia) coupled with SpectrAA software.
Ion chromatography technique is utilized to evaluate the sulfate ions concentration (degree of sulfonation) presented in the studied additives. Solutions of 200 mg L−1 of the chemical additives (R1, R2 and D1) are prepared and measured using (DIONEX, ICS3000, USA). External anions standards with sulfate (SO42−) concentration 0, 5, 10, 15 ppm are obtained from (DIONEX, USA) and 4 points calibration curve are generated in order to measure the sulfate anions' concentration in the samples.
The molecular weights for the used additives (R1, R2 & D1) are determined by using (Agilent HPLC 1200, Agilent Technologies, USA) using PL aquagel-OH MIXED-H 8 μm, inner diameter (I.D) 7.5 × 300 mm column obtained from (Agilent Technologies, USA) and it's equipped with a refractive index (RI) detector. The additives are dissolved in 0.2 mol L−1 NaNO3 aqueous solutions to a concentration of 0.2 wt% and the samples are filtered through 0.2 μm syringe filter (Supor membrane, Pall life sciences, USA). A 0.2 mol L−1 of NaNO3 aqueous solution is used as an eluent (adjusted to pH = 8 by adding 10 drops of 0.01 mol L−1 NaOH) at a flow rate of 1 mL min−1 and the sample is injected with volume of 50 μL. The column is calibrated using polyethylene oxide/polyethylene glycol (PEO/PEG) standards and the separation range is 100 to 1000k Da (dalton). The molecular weight calculations are carried out using GPC software and a 6th order polynomial fit is used.
2.3 Surface charge measurements
The anionic charge densities of the studied additives are measured using a particle charge detector (MütekTM PCD-04 Travel, BTG Mütek GmbH, Germany).8,10 Chemical additives solutions are prepared with concentration of 100 ppm. 10 mL of the solution sample are poured into the measuring cell and titrated with 0.001 N polydadmac solution. The cationic polymer is added continuously from a burette by an automatic feeder system until the isoelectric point is reached. The consumed volume (mL) of polydadmac to reach this point is recorded and the anionic charge densities are calculated.The zeta potential approach is used in order to determine the surface charge on the cement particles and the electrostatic stabilization of the cement/additive system. The electro-acoustic instrument (DT 1200, Dispersion Technology, USA) is used. The instrument is opted due to its ability of measuring zeta potential for high volume fraction solid/liquid system such as cement slurry.11 Prior to zeta potential titration measurements for cement slurry, 6.4 mL of distilled water is poured into the centrifuge tube using a micropipette. Then, 16 gram of oil well cement class G is added to the distilled water. The sample tubes are mixed for 1 minute homogeneously by a test tube shaker (Vortex-Genie 2, Scientific Industries, USA) at 2550 rpm. The sample tubes are centrifuged by (Eppendorf Centrifuge 5804 R, Eppendorf, Germany) for 20 min at 4000 rpm and 25 °C. Then the extracted pore solution is transferred to zeta probe container in order to determine the ionic vibration current (IVI). The ionic vibration current is sat to be subtracted from the measured zeta potential values during additives titration experiment.11 Then, additives solutions of 2% bwoc are prepared as follows: (1) R2, (2) D1, (3) D2, (4) R2 + D1 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). The preparation of cement slurry is performed at room temperature 25 °C and at constant water to cement ratio (w/c = 0.4) according to ASTM C-305.12 A 550 g of oil-well cement class G and 220 g of distilled water are weighted using an electronic balance. The cement slurries are prepared and mixed using cement blender (ToniMIX, Toni Technik Baustoffprüfsysteme GmbH, Germany). The water is subsequently poured into the mixing bowl. The cement is added gently to the water and is allowed to settle for almost 30 s. The cement is mixed at low speed (145 ± 5 rpm) for 30 s. The mixer is stopped for 15 s. During this time the cement on the side of the bowl is scraped down into the batch. The cement is mixed again at medium speed (285 ± 10 rpm) for 1 min. Then cement slurry is poured immediately into the special glass cell as with motorized stirrer speed of 475 rpm.12 The additives 2% bwoc (50 mg mL−1) solution is then added with an increment of 1 mL with a rate of 1 mL min−1 until a plateau is reached.
1). The preparation of cement slurry is performed at room temperature 25 °C and at constant water to cement ratio (w/c = 0.4) according to ASTM C-305.12 A 550 g of oil-well cement class G and 220 g of distilled water are weighted using an electronic balance. The cement slurries are prepared and mixed using cement blender (ToniMIX, Toni Technik Baustoffprüfsysteme GmbH, Germany). The water is subsequently poured into the mixing bowl. The cement is added gently to the water and is allowed to settle for almost 30 s. The cement is mixed at low speed (145 ± 5 rpm) for 30 s. The mixer is stopped for 15 s. During this time the cement on the side of the bowl is scraped down into the batch. The cement is mixed again at medium speed (285 ± 10 rpm) for 1 min. Then cement slurry is poured immediately into the special glass cell as with motorized stirrer speed of 475 rpm.12 The additives 2% bwoc (50 mg mL−1) solution is then added with an increment of 1 mL with a rate of 1 mL min−1 until a plateau is reached.
2.4 Thermal analysis
The thermal analytical measurements of the cement/additives mixtures are conducted by isothermal calorimetry (TAM air, TA, U.S.A) at ambient temperature.18 In the beginning, the eight channels are balanced using the General Performance Test (GPT). The system is calibrated using the Gain Calibration Criteria for almost one hour. The system is stabilized for 24 h. The results are normalized to the mass of cement (4 g). The resulting data are exported to spreadsheets for further analysis. The heat evolved during the hydration process is measured in [mW g−1]. The time elapsed for the cement to hydrate is measured in [h].2.5 Adsorption isotherm
In order to measure the free chemical additives concentration in the pore solution, the organic carbon content is determined using a total organic carbon (TOC) analyzer (Elementar, Vario TOC cube, Germany). For each system 9 different additive dosages (0.1–2% bwoc) are prepared and measured. The following procedure is used: a 1.6 mL of additive solution is poured into the centrifuge tube using a micropipette. Then, a 4 gram of oil well cement class G is added to the additive solution. The sample tubes are mixed for 1.5 min homogeneously by a test tube shaker (Vortex-Genie 2, Scientific Industries, USA) at 2550 rpm. The sample tubes are centrifuged by (Eppendorf Centrifuge 5804 R, Eppendorf, Germany) for 20 min at 4000 rpm and 25 °C. The pore solutions are extracted and filtrated through 0.2 μm syringe filter (Supor membrane, Pall life sciences, USA) and transferred to the TOC analyzer glass ampoule. The exact obtained amount of pore solution is measured and recorded. The pore solution is diluted with 0.1 M HCl (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100) to prevent carbonization from the atmosphere. The sample is analyzed at 850 °C and 1000 mbar with 0.2 μL injection volume. The amount of chemical additives adsorbed is calculated from the difference in the concentration of chemical additives in the liquid phase before and after contact with cement (depletion method).13
100) to prevent carbonization from the atmosphere. The sample is analyzed at 850 °C and 1000 mbar with 0.2 μL injection volume. The amount of chemical additives adsorbed is calculated from the difference in the concentration of chemical additives in the liquid phase before and after contact with cement (depletion method).13
2.6 Mathematical models
In order to predict properties of polymeric cement slurries, the support vector regression (SVR) mathematical method is used and compared to the model tree (MT) method, M5 model rules. The comparison parameters are the correlation coefficient (R2), Mean Absolute Error (MAE) and the Root Mean Squared Error (RMSE).
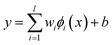 | (1) |
The coefficients {wi}li=1 and b are calculated by minimizing the regularized risk function in eqn (2).14
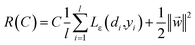 | (2) |
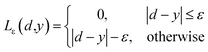 | (3) |
Data are normalized into the interval [0, 1] by using eqn (4).
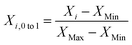 | (4) |
The comparison parameters are the correlation coefficient (R2), Mean Absolute Error (MAE), Root Mean Squared Error (RMSE). These parameters can be written as show in eqn (5)–(7).
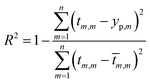 | (5) |
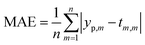 | (6) |
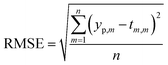 | (7) |
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) m,m is the mean value of all measure data points.
m,m is the mean value of all measure data points.
3. Results and discussion
3.1 Chemical characterization
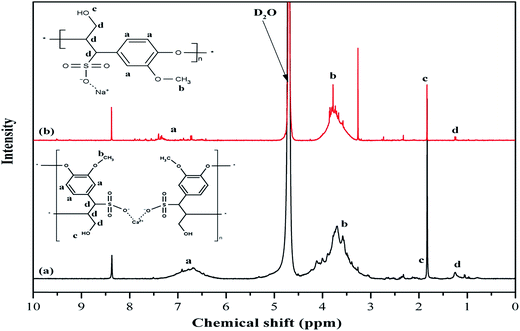
Spectroscopic analysis is conducted for the utilized additives using 1H NMR measurements in order to detect any chemical structural differences and to confirm FT-IR findings.7 The 1H NMR spectra for R1 and R2 are displayed in Fig. 1. The broad peak (point a) between 6 and 8 ppm for both retarders is associated with protons in the aromatic ring. While the peaks between 3.05 to 4.01 ppm for R1 and 3.20 to 4 ppm for R2 (point b) can be assigned to protons in the methoxyl group (–OCH3). It has to be noted that the peaks in the 3 to 4 ppm range vary between the two retarders. This can be attributed to the different ratios of guaiacyl and syringyl units in the molecule.16 It also explains the differences between the aromatic range peaks for both retarders. Similar peaks are observed at 1.83 and 1.84 ppm (point c) for R1 and R2, respectively corresponding to aliphatic hydrogen in the hydroxyl group, while the peaks at 1.25 to 1.26 ppm (point d) are assigned to the aliphatic hydrogen in the molecule. Other similar peaks are observed at 8.37–8.38 ppm and attributed to the presence of aldehyde and/or carboxyl group and this could be confirmed with the FT-IR for this system.8,17,18 The peak around 4.12 ppm in R1 corresponds to the proton in the ether structure.19Although FT-IR and 1H NMR results indicate a similar structure for R1 and R2, differences in the mechanical behavior of the retarders necessitated the conduction of additional tests.7 Therefore, further chemical analyses have been conducted to evaluate the differences between both retarders and the results are shown in Table 1.
| Additive | Mw (Da) | Mn (Da) | % C | % H | % N | % S | % Na | % Ca | SO42− | ACD (μeq. g−1) |
|---|---|---|---|---|---|---|---|---|---|---|
| R1 | 2164.5 | 801.14 | 39.16 | 4.94 | 0.17 | 5.05 | 0.8 | 8.4 | 0.90 | 1521 |
| R2 | 1237.3 | 534.34 | 43.86 | 4.6 | 0.14 | 3.28 | 7.6 | 0.1 | 2.48 | 2353 |
| D1 | 1063.6 | 390.41 | 42.14 | 3.86 | <0.1 | 12.16 | 10.5 | 0.5 | 7.63 | 3050 |
Molecular weight distribution of different cement additives is considered as one of the factors that affect the adsorption behavior. As can be seen, R1 has a higher average molecular weight (Mw = 2164.50 g mol−1) compared to R2 (Mw = 1237.30 g mol−1). Moreover, the anionic charge density (ACD) is considered a key factor that controls the interaction with cement components. According to Table 1, the sulfate content is higher for R2 but the sulfur amount in R1 is higher than in R2. This variation between the two analytical methods indicates the presence of other sulfur components in R1, which is attributed to the existence of some impurities. This has a significant impact on compatibility with other additives like dispersants. The results show that sodium is the counter-ion in retarder R2 while calcium is the counter ion of R1. Interestingly, the findings show remarkable differences between R1 and R2.
The findings on the effect of molecular weight on the adsorption performance show a high consistency with previously presented studies.20 The fraction with higher molecular weight is found to have more sulfonic groups in each molecule and it is more likely to twist.14 Based on previous studies it is expected that the adsorption amounts (retardation effectiveness) of R1 would be higher than R2. However, the thermal analysis results show a different behavior.18 Moreover, the slump loss value of cement/additives paste with higher molecular weight additive is more effective among the lowest molecular weight additives. This behavior is attributed to the movement variation in pore solution between different molecular sizes of the additive towards the cement active sites; the bigger molecules take a longer time to reach there and hence, the smaller ones are consumed first. As a result, no free additive in solution is left for the cement to maintain its high fluidity (no slump loss).
Although R1 possesses a higher average molecular weight (Mw) than R2, the results show that ACD of R2 is higher than R1 by approximately 35%. These differences in ACD between the retarders are assigned to the variation in the degree of sulfonation. Lignosulfonate contains different polar groups such as sulfonic, phenylic, hydroxyl and alcoholic hydroxyl groups so that these values for the charge densities of both retarders represent the sum of the charges of all those groups.21 In other words, the actual charges of the sulfonate groups for both retarders are lower than the values represented in Table 1. Quyang et al. modified lignosulfonate by increasing the degree of sulfonation (sulfonic groups) and compared its performance on zeta potential to the non-modified ones.21b It is reported that the modified component possesses a higher charge density compared to the original ones, and thus a higher zeta potential is achieved.
Presumably, the differences between R1 and R2 or lignosulfonates in general are related to the different types of wood from which they are isolated, the pulping process, method of sulfonation and other variables.22 D1 and D2 dispersants share similarities in their chemical composition. Some minor differences exist in the sulfate contents and anionic charge densities, while microstructure analysis reveals a major difference between them.
Particular focus will be further made on the mixture R2/D1 due to the above described indications regarding performance, especially that dispersant (D1) has a higher anionic charge density (ACD) compared to the retarder (R2) by almost 22%. Heat flow calorimetric results obtained are in favor of that combination, too.7
3.2 Solid state NMR
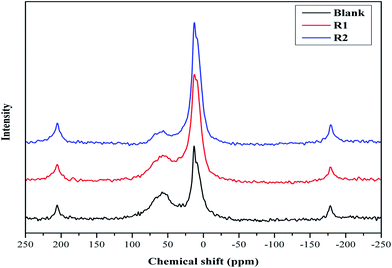
MAS NMR spectroscopy of hydrated cement samples is conducted in order to study the effect of both retarders on the cement hydration processes and their interaction with hydration products as illustrated in Fig. 2 and 3. In general, 29Si MAS NMR is used to characterize the polymerization state of silicates (tetrahedral SiO44−) in cement pastes.23 Furthermore, the individual tetrahedrons (called monomer, Q0) represent mono-silicates and mainly are attributed to anhydrous silicate phases of the cement (C2S and C3S).21,24 As stated before, during the cement hydration those components are transformed to C–S–H phases through silicate polymerization and additional Q1 and Q2 are formed.25 While a silicate polymerization process is taking place, the tetrahedrons connect through their oxygen atoms giving rise to polymeric states, known as dimers (Q1) and polymeric chains (Q2).25 Moreover, Q1 represents di-silicates and chain end groups within the silicate network, while Q2 indicates a middle group in chains due to SiO4 bridging.25,26 Each of these states reflects the degree of polymerization of the silicate in the paste as well as they are related to the formation of Si–O–Si network.8,25 In addition, states like Q3 can appear in 29Si MAS NMR spectra of cement, which are referred to chain branching sites and Q4 representing a three dimensional cross-linked framework.25 As seen in Fig. 2, the spectra show a peak at −71.2 ppm, which is assigned to Q0 and is related to anhydrous silicate phases for all cement systems. For the blank system, the spectrum shows three peaks, one at −78.9 ppm (attributed to Q1), and others at −84.8 ppm (assigned to Q2) and at −93.0 ppm with a small intensity (referred to Q3). For both retarders system, it can be seen that the assigned Q1 peak is shifted and the peak intensity is lowered while the Q3 peak is missing. Also, it is noticed that the retarders affect the Q2 peak in comparison to the blank sample. In more details, in presence of R1, the Q2 peak is shifted to −85.3 ppm while for R2 two peaks are found at −84.2 and −84.7 ppm. Moreover, it can be concluded that both retarders are incorporated with C–S–H hydrates, which affect their nucleation growth. However, the Q2 peak in R2 is more broadened than in R1, which may be attributed to their difference in the retardation effectiveness.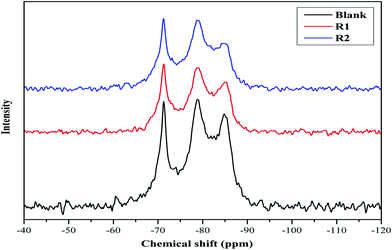 | ||
| Fig. 2 29Si MAS NMR spectra of hydrated blank cement, hydrated cement + 0.5% bwoc R1 and hydrated cement + 0.5% bwoc R2. | ||
 | ||
| Fig. 3 27Al MAS NMR spectra of hydrated blank cement, hydrated cement + 0.5% bwoc R1 and hydrated cement + 0.5% bwoc R2. | ||
The 27Al MAS NMR analysis of cement/additives is executed and compared to the blank sample as illustrated in Fig. 3. For the blank sample the expected two main signals are found, one at 13.0 ppm (assigned to ettringite) and one at 9.2 ppm (attributed to monosulfate). It is reported that anhydrous cement exhibits tetrahedral and octahedral coordination at chemical shifts of 80–90 ppm and 0–20 ppm, respectively.23 As can be seen, the peak maximum of tetrahedral coordinated aluminum is shifted to 58.0 ppm due to the hydration process because Si is substituted by Al in the C–S–H phase as reported in the literature.27 For the additive system it can be seen that the ettringite formation is affected due to the addition of retarders and the peak is found at 12.6 ppm while, for the R2 system, the ettringite peak intensity does not change. In addition, the monosulfate peak is found at 8.8 ppm for both retarders. Therefore, it can be concluded that R1 is more effective on ettringite hydration than R2.
3.3 Zeta potential and adsorption isotherms
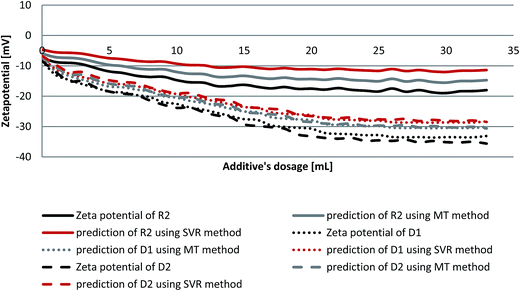
When cement is dispersed in water, the cement grains develop a heterogeneous surface structure formed by different hydrate phases. As a result the surface of hydrating cement particles shows domains where a certain mineral phase prevails8,28 and exhibit heterogeneous charge distributions on the surface of hydrating cement grains. Moreover, the zeta potentials of different pure cements without additives depend on their aluminate phase (C3A) content as well as the sulfate content due to higher amounts of ettringite formation during hydration.29 Generally, charge, spatial arrangement and conformation play an important role in the adsorption behavior of the involved anions.30 Solvent, temperature and ionic strength can influence both structure and properties of the adsorbate and this can be detected by evaluating the zeta potential of the particles.30 Therefore, the zeta potentials of different cement/additive systems are investigated in order to study the adsorption behavior as well as to determine the optimum dosages for each system. As shown in Fig. 4, the zeta potential is studied with increasing additive dosages for three different systems. The zeta potential of the oil-well cement without additives (starting point) is negative indicating poor C3A content and rich silicate phases. This finding is consistent with the XRD analysis reported earlier.8 The zeta potential value decreases with increasing the additives volume (% bwoc of the additive) until it reaches a constant value (plateau). The zeta potential of R2 decreases from the starting point until it reaches a value of −17.32 mV at 0.2% bwoc (22 mL). While, for D1 the zeta potential significantly drops until it reaches −32.39 mV at 0.2% bwoc and beyond that, no remarkable changes in zeta potential are observed. This variation in electrostatic repulsion (zeta potential) behavior between retarder and dispersant is due to the anionic charge density differences (Table 1). D1, which possess the highest anionic charge density, has the lowest zeta potential values in comparison to R2. Therefore, it is concluded that the charge density is the dominant factor that controls the electrostatic repulsion behavior of cement/additives systems.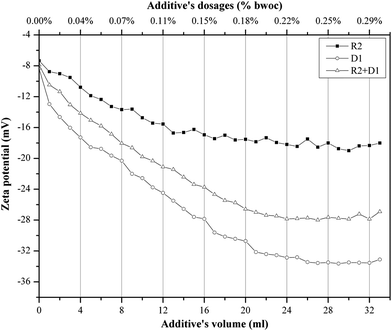 | ||
Fig. 4 Zeta potential of oil well cement class G treated with 0–33 mL of 50 mg mL−1 of R2, D1 and R2 + D1 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) with a 1 mL min−1 addition rate. 1) with a 1 mL min−1 addition rate. | ||
The combination of both retarders and dispersants are studied in order to evaluate the compatibility between both of them. From Fig. 4 it can be seen that the zeta potential values for the mixture of (R2 + D1) are increased (towards positive value), relatively, when compared to D1. This behavior is referred to a competitive adsorption between the highest anionic charge density (D1) and the lowest (R2) onto cement active sites. The zeta potential of the mixture reaches a plateau approximately at 0.2% bwoc. Therefore, depending on the obtained zeta potential results, the optimum dosage for the studied cement/additive systems appears to be 0.2% bwoc.
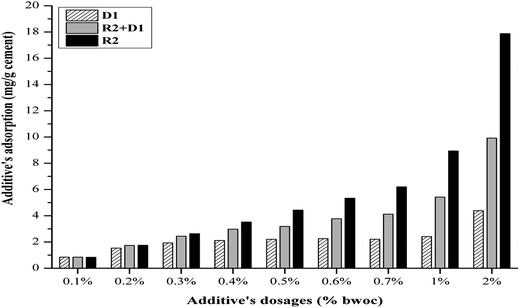
The zeta potential measurement of the cement/additives systems is recognized as a method to study the additives' adsorption on the hydrated cement surface (Fig. 5). In general, it can be assumed that the lower the zeta potential, the higher the adsorption of additives on the cement particles. This statement may hold only when the dispersion mechanism of the additive on cement suspension is induced by their electrostatic repulsion. It is stated that if the zeta potential only changes slightly during continuous addition of superplasticizer, the cement particles will be dispersed by the steric hindrance mechanism.30,31
Although, both R1 and R2 have the same structure, their retardation potential is different. This can be attributed to a number of reasons. It is proposed that the lignosulfonate retardation mechanism is appearing by a combination of calcium complexation and precipitations onto anhydrate clinker phases. The origin of calcium ions is due to the rapid dissolution of anhydrous cement clinker phases especially, C3S once it gets contacted with water. Furthermore, the experimental work proofed that lignosulfonate concentration decreases with increasing calcium ion concentration in the solution. Furthermore, the microscopy analysis showed a layer of polymer (LS–Ca complexes) precipitate on anhydrous cement clinker phases providing a barrier preventing the water to penetrate into the cement hydration shell to produce more hydration products. Assuming this hypothesis is valid although it is stated that the complexation mechanism is unlikely because chelators can be moderate retarders while strong retarders can be moderate chelators the counter-ion effect should not be discounted.4 From the elemental analysis results it can be seen that calcium is present in R1 by about 8.4 wt% while, IC result shows the calcium ions in water present by about 17.8 mg L−1 in 200 mg L−1 sample. That means that by adding R1 to the cement slurry, the calcium concentration will increase and thus, the lignosulfonate concentration in the suspension will decrease because it is consumed by additional calcium ions if our assumption still holds. Consequently, the amount of lignosulfonate available for hydration retardation is not enough and provides better effectiveness. R1 contains higher amounts of inorganic carbon in form of CO32− ions. As a result those ions compete with lignosulfonate particles for the positive active sites on hydration products mainly on early C3A hydrates and therefore reduces the effectiveness of R1. The anionic charge density differs from R2 and is almost by 35% less. That means that at the same dosage the amount available is not effective enough to retard the cement hydration for a certain time. Moreover, the R1 amount is adsorbed or even chemisorbed. The effective functional group (sulfonate and hydroxyl) amounts are not sufficient to retard the cement hydration in comparison to the performance of R2 (Table 2).
| Blank | 0.1% bwoc | 0.2% bwoc | 0.3% bwoc | 0.4% bwoc | 0.5% bwoc | 0.6% bwoc | 0.7% bwoc | |
|---|---|---|---|---|---|---|---|---|
| Time elapsed to reach peak maximum for R1 | 10.7 h | 16.9 h | 31 h | 1.76 days | 2.3 days | 4.46 days | 6.87 days | 15.8 days |
| Time ratio between two concentrations for R1 | 0.1/0.0% bwoc | 0.2/0.1% bwoc | 0.3/0.2% bwoc | 0.4/0.3% bwoc | 0.5/0.4% bwoc | 0.6/0.5% bwoc | 0.7/0.6% bwoc | |
| 1.58 | 1.84 | 1.36 | 1.33 | 1.91 | 1.54 | 2.30 | ||
| Time elapsed to reach peak maximum for R2 | 10.7 h | 16.1 h | 37 h | 4.23 days | 8 days | 15 days | 18.4 days | 24.76 days |
| Time ratio between two concentrations for R2 | 0.1/0.0% bwoc | 0.2/0.1% bwoc | 0.3/0.2% bwoc | 0.4/0.3% bwoc | 0.5/0.4% bwoc | 0.6/0.5% bwoc | 0.7/0.6% bwoc | |
| 1.51 | 2.30 | 2.74 | 1.88 | 1.88 | 1.22 | 1.35 | ||
| R2/R1 ratio at the same concentration | 0.95 | 1.19 | 2.41 | 3.43 | 3.37 | 2.67 | 1.57 |
3.4 Thermal analysis
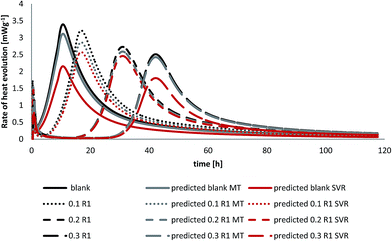
Upon addition of water to cement powder heat evolves due to the exothermic reaction accompanying this process. Therefore, isothermal calorimetry is a useful technique to monitor that heat release. The effect of different additives on cement hydration compared to the plain ones are observed using heat flow calorimetry as well. The hydration peaks are the sum of simultaneous ongoing hydration processes of different clinker phases in presence of different additives.32 Fig. 7 represents the effect of R1 on the hydration process. It is shown that R1 prolongs the dormant period (stage 2) by decreasing the peak maximum of heat released during the hydration process. In other words the hydration peak is shifted by increasing R1 concentration compared to the blank cement at constant water to cement ratio. As can be seen in Fig. 7 the peak maximum for the blank cement sample is found at 10.7 (h) while at 0.3% bwoc of R1 the hydration peak maximum starts to rise after 42 h, which is considered as an overdose of R1. This suggests that lignosulfonate molecules (sulfonate and hydroxyl groups) are adsorbed on anhydrous cement compounds and thus, create a barrier that slows down the cement hydration.33 The inhibition of crystal growth (nucleation theory) suggests that adsorption occurs on the hydration products and not the anhydrous ones.323.5 Mathematical prediction
Results using the support vector regression method for different dosages of R1 are listed in Table 3 and compared to the model tree method. It can be seen from the results, that the model indicates the surface behavior of the slurry in the presence of different additives and it would be able to predict any possible combinations of these additives on the cement slurry. Fig. 6 shows that there is some deviation to the actual experimental result, but the model can be surely used as a trend for dosage optimization.
| Polymer | Performance measures | |||||
|---|---|---|---|---|---|---|
| R2 | MAE | RMSE | ||||
| MT | SVR | MT | SVR | MT | SVR | |
| R2 | 0.8177 | 0.6325 | 0.1128 | 0.1096 | 0.1558 | 0.1586 |
| D1 | 0.9084 | 0.8548 | 0.0892 | 0.1092 | 0.1163 | 0.1484 |
| D2 | 0.8595 | 0.8001 | 0.1105 | 0.0952 | 0.1447 | 0.1543 |
Comparison of the predicted to the experimental heat evolution values during the cement hydration process with and without polymer R1 is shown in Fig. 7. The data are obtained by the Support Vector Regression method (SVR) and the Model Tree (MT) method, the M5 model rules (see Table 4).
| Polymer | Performance measures | |||||
|---|---|---|---|---|---|---|
| R2 | MAE | RMSE | ||||
| MT | SVR | MT | SVR | MT | SVR | |
| Blank | 0.9177 | 0.6349 | 0.0354 | 0.2509 | 0.3809 | 0.7413 |
| 0.1 R1 | 0.8914 | 0.8015 | 0.0441 | 0.1652 | 0.4118 | 0.5431 |
| 0.2 R1 | 0.9491 | 0.9012 | 0.0305 | 0.2461 | 0.296 | 0.4036 |
| 0.3 R1 | 0.9662 | 0.7192 | 0.0268 | 0.3108 | 0.2111 | 0.5521 |
As can be seen in Fig. 7, the model tree method applied on the investigated cement mixtures revealed that calculated values are in good agreement with experimental data and are in better accord than the equivalent calculations using support vector regression. Despite a slight deviation from the actual heat evolution compared to the experimental data the results of the mathematical models can be used to identify the setting time of the cement pastes. The good correlation obtained with these mathematical models in comparison to experimental results encourages the complete reliance on them rather than using expensive and lengthy experiments to assess the performance of additives on oil well cements in the oilfield.
4. Conclusions
This study enables a better understanding of the compatibility of additives (a dispersant D1 and a retarder R2) on oil well cement mechanical performance. The chemical characterization shows that both additives differ somewhat in molecular weights, in sulfonation degree and in anionic charge density. The zeta potential measurements show that both additives (R2 and D1) contribute to the electrostatic repulsion due to their adsorption; the dispersant has a larger contribution due to its higher anionic charge density. The adsorption isotherms confirm the zeta potential findings. It is noticed that the adsorbed amount of R2 is higher than of D1 due to the differences in the chemical nature and selectivity of the adsorption sites. The proposed optimum dosages are 0.2% bwoc for all individual systems and 0.1% each for the mixed systems (R2 + D1). The NSF is found to be incompatible with the cement used due to the low content of C3A and/or its hydrates because it is considered a favorable active site for NSF. Competitive adsorption is observed in solution mixtures and a big contribution is found at higher concentrations, especially for R2 + D1 systems. Mathematical models using support vector regression and model trees approaches validate the experimental results obtained from zeta potential and heat flow calorimetric measurements to an extent considered to be satisfying.Acknowledgements
The authors would like to thank Prof. N. Ghali and A. Taha of Al-Azhar University for the initial help with the mathematical models, Mrs Nicy Kallely of the Center for Applied and Environmental Chemistry of the PI for performing the measurement on the particle charge detector and the gel permeation chromatograph and Mrs Ulrike Ammari and Mrs Petra Ankenbauer of the Microanalytical laboratory of the TUM for their help with elemental analysis and atomic absorption measurements.References
- C. V. Umeokafor and O. F. Joel, Modeling of Cement Thickening Time at High Temperatures With Different Retarder Concentrations, paper presented in Nigeria Annual International Conference and Exhibition, Tinapa – Calabar, Nigeria, Jul 31–Aug 7 2010 Search PubMed
.
- M. Bishop and A. R. Barron, Cement Hydration Inhibition with Sucrose, Tartaric Acid, and Lignosulfonate: Analytical and Spectroscopic Study, Ind. Eng. Chem. Res., 2006, 45, 7042–7049 CrossRef CAS
.
- E. B. Nelson, Well cementing, Schlumberger Educational Services, Sugar land, 1st edn, 1990 Search PubMed
.
- J. Cheung, A. Jeknavorian, L. Roberts and D. Silva, Impact of admixtures on the hydration kinetics of Portland cement, Cem. Concr. Res., 2011, 41, 1289–1309 CrossRef CAS
.
- M. Bishop, S. G. Bott and A. R. Barron, A New Mechanism for Cement Hydration Inhibition: Solid-State Chemistry of Calcium Nitrilotris(methylene)triphosphonate, Chem. Mater., 2003, 15, 3074–3088 CrossRef CAS
.
- J. K. Fink, Oil field chemicals, Gulf Professional Publishing, Amsterdam, 1st edn, 2003 Search PubMed
.
- Y. Al-Wahedi, J. Awayes and G. Bassioni, Influence of classical and modern superplasticisers on the chemical and rheological behaviour of oil well cement: a comparative study, Adv. Cem. Res., 2011, 23, 175–184 CrossRef CAS
.
- G. Bassioni and M. M. Ali, The effect of counterion in lignosulfonates as oil-well cement retarders, Adv. Cem. Res., 2013a, 25(5), 245–253 Search PubMed
.
- F. Rouessac and A. Rouessac, Chemical Analysis: Modern Instrumentation Methods and Techniques, John Wiley & Sons, Chichester, 2nd edn, 2007 Search PubMed
.
- J. Plank and B. Sachsenhauser, Experimental Determination of the Effective Anionic Charge Density of Polycarboxylate Superplasticizers in Cement Pore Solution, Cem. Concr. Res., 2009, 39, 1–5 CrossRef CAS
.
- J. Plank and B. Sachsenhauser, Effectiveness of Polycarboxylate Superplasticizers in Ultra-High Strength Concrete: The Importance of PCE Compatibility with Silica Fume, J. Adv. Concr. Technol., 2006, 4, 233–239 CrossRef CAS
.
- ASTM, Journal, 1999, ASTM C 305–99.
- L. Ferrari, J. Kaufmann, F. Winnefeld and J. Plank, Multi-method approach to study influence of superplasticizers on cement suspensions, Cem. Concr. Res., 2011, 41, 1058–1066 CrossRef CAS
.
- S. K. Shevade, S. S. Keerthi, C. Bhattacharyya and K. R. K. Murthy, Improvements to the SMO Algorithm for SVM Regression, in IEEE Transactions on Neural Networks, 2000 Search PubMed
.
- V. Ceperic, G. Gielen and A. Baric, Recurrent sparse support vector regression machines trained by active learning in the time-domain, Expert Syst. Appl., 2012, 39, 10933–10942 CrossRef
.
- M. Hall, G. Holmes and E. Frank, Generating rule sets from model trees, Proceedings of the Twelfth Australian Joint Conference on Artificial Intelligence, Springer-Verlag, Sydney, Australia, 1999, pp. 1–12 Search PubMed
.
- A. Awal and M. Sain, Spectroscopic studies and evaluation of thermorheological properties of softwood and hardwood lignin, J. Appl. Polym. Sci., 2011, 122, 956–963 CrossRef CAS
.
- X. Zhao and D. Liu, Chemical and thermal characteristics of lignins isolated from Siam weed stem by acetic acid and formic acid delignification, Ind. Crops Prod., 2010, 32, 284–291 CrossRef CAS
.
- G. Bassioni and M. M. Ali, Studying the physico-chemical properties of commercially available oil-well cement additives using calorimetry, J. Therm. Anal. Calorim., 2013, 111(1), 295–303 CrossRef CAS
.
- A. Toledano, L. Serrano, A. Garcia, I. Mondragon and J. Labidi, Comparative study of lignin fractionation by ultrafiltration and selective precipitation, Chem. Eng. J., 2010, 157, 93–99 CrossRef CAS
.
-
(a) H. Lou, K. Ji, H. Lin, Y. Pang, Y. Deng, X. Qiu, H. Zhang and Z. Xie, Effect of molecular weight of sulphonated acetone-formaldehyde condensate on its adsorption and dispersion properties in cementitious system, Cem. Concr. Res., 2012, 42, 1043–1048 CrossRef CAS
; (b) X. Ouyang, X. Qiu and P. Chen, Physicochemical characterization of calcium lignosulfonate – A potentially useful water reducer, Colloids Surf., A, 2006, 282–283, 489–497 CrossRef
.
- J. Zhor, Molecular structure and performance of lignosulfonates in cement-water systems, Ph.D. thesis, Civil Engineering, University of New Brunswick, Canada, 2005 Search PubMed
.
- J. Roncero, S. Valls and R. Gettu, Study of the influence of superplasticizers on the hydration of cement paste using nuclear magnetic resonance and X-ray diffraction techniques, Cem. Concr. Res., 2002, 32(1), 103–108 CrossRef CAS
.
- A. M. Olaru, O. Weichold and A. Adams, The hydration of reactive cement-in-polymer dispersions studied by nuclear magnetic resonance, Cem. Concr. Res., 2011, 41(11), 1123–1129 CrossRef CAS
.
- J. Rottstegge, M. Wilhelm and H. W. Spiess, Solid state NMR investigations on the role of organic admixtures on the hydration of cement pastes, Cem. Concr. Compos., 2006, 28(5), 417–426 CrossRef CAS
.
- F. Puertas, H. Santos, M. Palacios and S. Martínez-Ramírez, Polycarboxylate superplasticiser admixtures: effect on hydration, microstructure and rheological behaviour in cement pastes, Adv. Cem. Res., 2005, 17, 77–89 CrossRef CAS
.
- G. Le Saout, E. Lécolier, A. Rivereau and H. Zanni, Chemical structure of cement aged at normal and elevated temperatures and pressures: Part I. Class G oilwell cement, Cem. Concr. Res., 2006, 36(1), 71–78 CrossRef CAS
.
- G. Bassioni, A study towards “greener” construction, Appl. Energy, 2012, 93, 132–137 CrossRef CAS
.
- G. Bassioni, The Influence of Cement Composition on Superplasticizers Efficiency, Int. J. Eng., 2010, 3, 577–587 Search PubMed
.
- G. Bassioni, Mechanistic aspects on the influence of inorganic anion adsorption on oilfield scale inhibition by citrate, J. Pet. Sci. Eng., 2010, 70, 298–301 CrossRef CAS
.
- J. Plank and B. Sachsenhauser, Impact of Molecular Structure on Zeta Potential and Adsorbed Conformation of α-allyl-ω-methoxypolyethylene Glycol – Maleic Anhydride Superplasticizers, J. Adv. Concr. Technol., 2006, 4, 233–239 CrossRef CAS
.
- O. Burgos-Montes, M. Palacios, P. Rivilla and F. Puertas, Compatibility between superplasticizer admixtures and cements with mineral additions, Construct. Build. Mater., 2012, 31, 300–309 CrossRef
.
- A. Zingg, F. Winnefeld, L. Holzer, J. Pakusch, S. Becker and R. Figi, et al., Interaction of polycarboxylate-based superplasticizers with cements containing different C3A amounts, Cem. Concr. Compos., 2009, 31(3), 153–162, DOI:10.1016/j.cemconcomp.2009.01.005
.
| This journal is © The Royal Society of Chemistry 2017 |