Spontaneous onion shape vesicle formation and fusion of comb-like block copolymers studied by dissipative particle dynamics

Abstract

A dissipative particle dynamics (DPD) simulation is performed to investigate the spontaneous onion shape vesicle formation and fusion of A₆(B₂)₃ type comb-like block copolymers with a semiflexible hydrophobic backbone. Our results show that comb-like block copolymers of A₆(B₂)₃ type may be a good candidate for onion shape vesicle formation. The spontaneous fusion dynamics between the onion shape vesicles is studied, and the fusion process can be characterized as having two parts: outer and inner membrane fusion. However, both parts have similar fusion dynamics which coincide with that observed in vesicles formed of linear diblock copolymers. In addition, the mixed systems containing amphipathic linear and comb-like block copolymers are investigated in dilute solution. By systemically varying the amount of linear block copolymers and the bond angle potential of the hydrophobic blocks, we construct a diagram to indicate the thermodynamically stable region, in which irregular vesicles, tubular vesicles, spherical vesicles, rod-like and toroidal micelles are observed. Nevertheless, no difference in the vesicle fusion dynamics is found. The main reason may be attributed to the molecular structures which possess the same hydrophobic but different hydrophilic block.

---

I. Introduction

Vesicles are important three-dimensional assemblies. Nowadays, the vesicle phase has attracted more and more attention owing to its great potential applications in biomedical sciences and industry, such as promoting cell recognition, the communication and adhesion process, microcapsules, microreactors, drug delivery and so on.^1–7 Therefore, it is very significant to seek out an appropriate approach to assemble vesicles of a desired morphology and dimension.

In the past few years, people have successfully obtained vesicular structures by self-assembly of block copolymers. For example, the diblock,⁴ coil–rod–coil triblock copolymers,⁸ toothbrush-like block copolymer,⁹ miktoarm star terpolymers,¹⁰ supramolecular amphiphiles¹¹ and the comb-like block copolymers,¹² which are designed to form stable vesicles with specific shapes, such as oblate shaped vesicles, prolate shaped vesicles, tubular vesicle, spherical vesicle and so forth. Nonetheless, it is rare for onion shape vesicle both in theoretical simulation and experiments. Onion shape vesicle, as a new drug delivery vehicle, is advantageous to control drug release, enhance the activity of anti-tumor drugs and improve the long term stability,¹³ will become the ideal alternative to resist some rigorous environment in some ways, such as high pressure, heat, strong alkali, strong sour and so on. However, the morphology of self-assembled structures can be controlled by many factors, such as molecular interactions,^14,15 molecular architecture and composition,^9,16 temperature,¹⁷ pH,¹⁸ foreign substance,^14,19,20 polymer chain stiffness²¹ and volume of the confinement.^22,23 Other than the above-mentioned factors, interaction parameter between particles is a critical factor to control the structure of the vesicles. Ma et al. used the dissipative particle dynamics (DPD) approach to research the self-assembly of amphiphiles consisting of a hydrophilic head and one or more hydrophobic tails, they found that the shape can transform from vesicles to worm-like cylinders and further to spheres due to the increase of interaction parameter.²⁴ Therefore, it is difficult to obtain target structures from the self-assembly of block copolymers. In our DPD simulations, the backbones of comb-like block copolymers are semiflexible, controlled by adopting a bond angel potential between the backbone beads. We find the repulsive strength between backbone and side chains has a major impact on vesicle shape. We observe onion shape vesicles formation process by deliberately varying the repulsive strength between backbone and side chains. We then exclusively focus on the spontaneous fusion between the onion shape vesicles formed by comb-like block copolymers with a semiflexible hydrophobic backbone.

We notice that the fusion mechanism of vesicles play an important role in exerting their specific functions, many fusion mechanisms have been found by scientists. For example, Knecht and Marrink performed coarse-grained MD simulation to investigate the fusion mechanism of the vesicle on the atomistic level.²⁵ They found two typical fusion pathways, one of them is that, first, a stalk forms quickly in between the vesicles. Then, a hemifusion diaphragm (HD) appears and keeps stable for a while. At last, a pore is induced by the defect and the pore expands quickly until the fusion is finished. The different of another fusion pathway is that a hole appears near the HD for facilitating the exchange of lipid molecules. However, Noguchi and Takasu employed Brownian dynamics (BD) simulations to study the fusion between to vesicles, and a different fusion pathway was found at high temperature.²⁶ Firstly, a thin stalk is formed. Secondly, two holes appear in both vesicles near the feet of the stalk, respectively. Finally, the stalk bends to encircle two holes until the fusion is completed. In previous study, we have studied the fusion dynamics of vesicles with monolayer structures by using the DPD method. We found our fusion dynamic is fairly similar to Takasu's. In addition, the adhesion of the membranes can be mediated by one or two types of receptor–ligand complexes. Weikl et al. employed simulations^27–29 to study the adhesion of membranes with anchored receptor and ligand molecules, and they did a good job of explaining that how the membranes affect binding kinetics. Meanwhile, they found a cooperative binding from receptor–ligand smoothen out the membranes and facilitated the formation of additional bonds, which accelerated the adhesion. All of fusion mechanisms mentioned above is based on single layer vesicles, while multilayer vesicle fusion mechanism has been barely mentioned in the past. In the present DPD simulation study, we focus on spontaneous fusion between the onion shape vesicles, which are favor to investigate the dynamic evolution of the fusion processes.

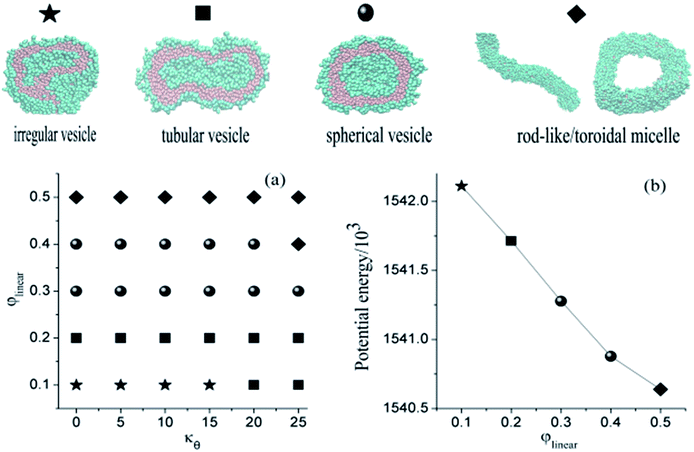
In recent years, cooperative self-assembly of different polymer mixtures has been proved to be a practical method to acquire aggregates with controllable morphologies and structures.^14,16,20,30 For example, Ouarti et al. examined the effect of polystyrene homopolymer on the morphology of micelles self-assembled from polystyrene-b-polyisoprene (PS-b-PI) in a selective solvent for the PI block (heptane). They found the morphological structure of micelles will transit from spherical to linear cylindrical and to toroidal with the increase of PS homopolymer.²⁰ In another work, Xin et al. studied the formation of multicompartment micelles in the mixture systems of star and linear triblock copolymers by applying dissipative particle dynamics (DPD) simulations. It revealed that both mixing ratio and copolymer chain composition played an important role in the micelle structures.³⁰ In order to better understand the formation and fusion of vesicles formed by comb-like block copolymers, we investigate the self-assembly behavior of mixture systems consisting of the comb-like and the linear block copolymers. We discover that binary mixtures are able to self-assemble into kinds of aggregates, such as single layer vesicles (irregular vesicle, tubular vesicle, spherical vesicle), rod-like micelle including linear rod-like micelle and toroidal micelle. The morphologies of the aggregates can be controlled by the relative concentration of the linear block copolymer, and the bond angle potential strength k_θ. The corresponding results are summarized in a phase diagram.

II. Models and simulation method

The DPD method is a mesoscopic simulation technique introduced by Hoogerbrugge and Koelman.^31,32 A DPD bead represents a group of atoms or a volume of fluid.^33,34 The force acting on a particle contains three parts, a conservative force, a dissipative force, and a random force, each of which is pairwise additive and whose maximum interaction radius is r_c = 1.

The time evolution of interacting particles is governed by Newton's equations of motion.³⁴ A modified version of the velocity-Verlet algorithm³⁵ is used here to integrate the equations of motion. The time step is Δt = 4.0 × 10⁻²τ for the temperature control at k_BT = 1. All simulations are performed using the GALAMOST³⁶ package on Nvidia GTX780 GPU cards.

A special property of comb-like block copolymers is that they can bend spontaneously because of the uneven distribution of side chains in bad solvents. Given this property, we have obtained tube like vesicles by using comb-like block copolymers.³⁷ It is naturally expected the self-assembled flat vesicles of comb-like block copolymers, if possible, may possess spontaneous curvatures. Therefore, we mainly consider the comb-like block copolymer A₆(B₂)₃ as show in Fig. 1(a) and symmetric linear block copolymer A₆B₆ as shown in Fig. 1(b). The red A represents hydrophobic backbone particles and the blue B hydrophilic side chain particles, the solvents S are denoted by single DPD beads. The adjacent particles of copolymers are connected by an extra harmonic spring force F_s = −kr_ij, where parameter k is the spring constant, in our model system, the k is 4. The main chain rigidity of the backbone of the comb-like block copolymer and linear block copolymer are controlled by a three-body potential,³⁸ U_θ = k_θ(1 − cos(θ − θ₀)) where k_θ is the bond angle potential strength, θ is the bond angle between the two bonds connecting particles (i − 1, i) and (i, i + 1), and θ₀ = 0 the equilibrium bond angle. After several tests, we choose an optimal cubic box with a side length equal to 48 at density is 3, so the particle number is 331 776, periodic boundary conditions are applied in all three simulated finite size effect,³⁹ we also checked out the thermodynamic consistency of our structures by monitoring the local temperature and pressure. The repulsive strength between the same type of particle is α_AA = α_BB = α_SS = 25. Groot and Warren had shown that the DPD interaction parameters between unlike species can be proportionally mapped onto Flory–Huggins-parameters χ parameters,³⁵ and therefore the amphiphilicity of the block copolymer can be reflected from DPD interaction parameters between unlike species. It is possible to build up a DPD model by systematically coarse-graining from experimental data, which is in accordance with a specific block copolymer system.⁴⁰ However, in present work, we have not coarse-grained model from a specific polymer system because we are trying to find out the general behavior of onion shape vesicle in dilute solution.

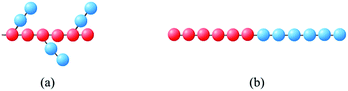Fig. 1 Schematic representation of (a) comb-like block copolymer, (b) linear block copolymer. Hydrophobic backbone, red beads; hydrophilic side chains, blue beads.

III. Results and discussion

A. The onion shape vesicle formation

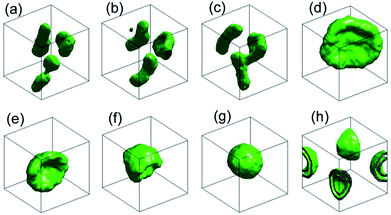
In order to reduce the parameter space of this system, we fix the repulsive strength α_BS = 27, similar to that of the same particles, and α_AS = 100. By deliberately varying the repulsive strength between backbone and side chains, we observe a series of morphology changes of vesicles, especially, as we expect the onion shape vesicles arise under proper condition.

It should be noted that there is no artificial manipulation on the onion shape vesicle formation. We always start our simulations from random distributed block copolymers in dilute solution and trace the evolution of these polymers by a snapshot of the simulation box. The choice of polymer concentration is an important part that we should be focusing on. The larger polymer concentration always lead to connected structures and the smaller one always result in micelles.³⁷ Therefore, we conduct the simulations with different block copolymer concentration (here, we select 0.036, 0.05 and 0.1 to ensure obtain stable vesicles and avert connected structures) and comb-like block copolymers with various wights (A_2n(B₂)_n with n = 2–5), we always observe the only spontaneous formation mechanism of onion shape vesicles. A typical onion shape vesicle formation process for A₆(B₂)₃ in dilute solution is illustrated in Fig. 2, in which the iso-density surfaces between components A and B at different time steps are plotted. In this simulation, the dimension of box is 48r_c × 48r_c × 48r_c, the concentration is 0.10. In order to describe the shape of the vesicles, we calculate the ratio of length to width and asphericity parameter of the vesicles. We can obtain three eigenvalues via Jacobian transformation of the matrix of the radius of gyration tensor,^41,42 and the ratio of length to width is defined as the largest values of the three eigenvalues divided by the smallest one. The asphericity parameter can well describe the shape of vesicles, when the value is close to 0, the shape is closed to a sphere, whereas it denotes a tube when the value is close to 1. At the beginning of the simulation, these block polymers start to self-assemble into small micelles and then to small vesicles under the impetus of the hydrophobic interaction force (see the iso-density surface in Fig. 2(a), at t = 6000). When two small vesicles contact each other closely, they fuse and become larger tubular vesicle with the value of the ratio of length to width is about 3.625 (see the iso-density surface in Fig. 2(b) and (c), at t = 6500 and t = 8000 separately) and the potential energy reduces by 670k_BT during the process in Fig. 2(a)–(c). After a 10 000 time steps simulation, these vesicles fuse to an oblate shape vesicle (see the iso-density surface in Fig. 2(d), at t = 18 000) and the potential energy reduces by 151k_BT in this process. As time goes by, when the undulation of the oblate shape vesicle is strong enough, the structure starts to bend quickly and finally forms a stable onion shape vesicle with diameter about 28 DPD units (see the iso-density surface in Fig. 2(e)–(g), at t = 20 000, t = 21 000 and t = 25 000 separately), and the potential energy reduces by 230k_BT. The asphericity parameter of the onion shape vesicle we calculate is 0.044, which denotes the vesicle possesses spherical shape. From Fig. 2(h), we can observe the typical double molecular layers structure of the onion shape vesicle clearly. In conclusion, the onion shape vesicle formation process can be roughly divided into four stages: first, the random distributed comb-like block copolymers self-assemble into small vesicles in a short time; second, these small vesicles fuse to a oblate shape vesicle; third, the oblate shape vesicle starts to bend and finally close to form a stable onion shape vesicle. There are two mechanism for vesicle formation,⁴³ one is due to the solvents diffuse into the center of micelles, and the other is the membrane bending and closing to form a vesicle. However, our simulation results are similar to the second vesicle formation mechanism, the difference is the membrane is replaced by oblate shape vesicle which is obtained by spontaneous fusion between small vesicles. There is no the first mechanism appears in our simulations, the reason is the solvents diffuse into the bilayer–micelle need to overcome very big free energy barrier, it is nearly impossible for dynamic simulations. In addition, the value of α_AB and α_AS are key factors in onion shape vesicle formation. After a series of simulations, we note that large α_AB will lead to form stable tube like vesicles, because it increases the surface tension of the membrane. The α_AS should be selected large enough in order to overcome the surface tension of oblate shape vesicle. We find that, while α_AB = 50, the α_AS = 90–120 is needed to ensure the onion shape vesicle formation. Other factors influencing the vesicle shape will be discussed in section B.

Fig. 2 Time evolution of the formation of onion shape vesicle, formed by comb-like block copolymer A₆(B₂)₃ with repulsive strength α_AB = 50 and polymer concentration φ = 0.1. The snapshots are taken at (a) 6000; (b) 6500; (c) 8000; (d) 18 000; (e) 20 000; (f) 21 000; (g) 25 000, and (h) shows the internal structure of (g). In the figure, we show the iso-density surface between components A and B, the side chain structures and the solvent beads are not shown for clarity.

B. The fusion process of onion shape vesicle

Understanding vesicle fusion process is essential for discovering its application value. In our previous study, we have studied the fusion of vesicle with single molecular layer formed of comb-like block copolymers.³⁷ Here, we focus on the spontaneous onion shape vesicle fusion.

All the parameters are unchanged except α_AS = 120 for accelerating simulation. It should be noted that the initial states are always setup by the self-assemble of randomly distribute comb-like block copolymers in dilute solution. We ensure obtain two onion shape vesicles by introducing a repulsive strength which like a paddle divides the comb-like block copolymers in half, and it will vanish when the stable onion shape vesicle is observed. Similar results of onion shape vesicle fusion are obtained for comb-like block copolymers A_2n(B₂)_n with n varying from 2 to 5 with 1 as step. Therefore, we will take comb-like block copolymer A₆(B₂)₃ as an example to expand the fusion dynamics.

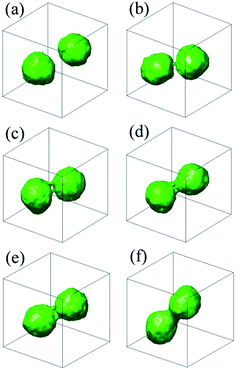
Five independent simulations are conducted for better statistics, the spontaneous fusion mechanism of which is highly reproducible. In a typical simulation, after about 5.0 × 10⁴ DPD time steps, we can observe two well-formed onion shape vesicles from the comb-like block copolymer A₆(B₂)₃, the diameter of which are about 20 DPD units and the asphericity parameter we calculate is 0.023 (see the iso-density surface at Fig. 3(a), here, we take as the initial state). The spontaneous fusion process of outer membrane can be depicted as follows: firstly, the two onion shape vesicles close to each other and a thin stalk is formed between them (see the iso-density surface at Fig. 3(b)); secondly, the second thin stalk is formed and a hole appears near the foot of one onion shape vesicle (see Fig. 3(c)). Then, the two thin stalks gradually expand together, and another hole merges in the other onion shape vesicle quickly, meanwhile, the third stalk appears (see the iso-density surface at Fig. 3(d)). Finally, the two onion shape vesicles complete their outer membrane fusion by stalks circling the two holes (see the iso-density surface at Fig. 3(e)), and a peanut-like hemifusion shape is formed (see the iso-density surface at Fig. 3(e) or profile at Fig. 4(a)). The potential energy reduces by 51k_BT during the fusion process of outer membrane. Further evolution of the outer membrane triggers the spontaneous fusion between the two vesicles in the peanut-like structure. It should be noted that Fig. 4(a) shows the internal structure of Fig. 3(f). With the deepening fusion of the outer membrane, the two inner vesicles close to each other and a stalk forms slowly, meanwhile, two holes appear near the root of the stalk respectively (see the iso-density surface at Fig. 4(b)). We can observe a brief contact of the outer and inner membranes from this process (see the iso-density surface at Fig. 4(b) and (c)). This may be conducive to reordering chain structures of comb-like block copolymer. Then, the inner membranes fuse together by stalk bending and circling the two vesicles. Finally, the stalk closes and a tubular vesicle with bilayer shape appears. The ratio of length to width of the tubular vesicle is about 2.16. The potential energy reduces by 47k_BT. Regardless, this fusion mechanism is favor to membrane fusion dynamics found by using Brownian dynamics,²⁶ dynamic SCFT,⁴⁴ and Monte Carlo,⁴⁵ roughly, in which the linear diblock copolymer were considered.

Fig. 3 Spontaneous fusion process for comb-like block polymer A₆(B₂)₃, in (a)–(f). The snapshots are selected at (b) 6500; (c) 7000; (d) 7250; (e) 7500; (f) 12 500; and (a) is the initiate state. The two onion shape vesicles in (a) are spontaneous formed by comb-like block copolymer A₆(B₂)₃, respectively. The iso-density surfaces between components A and B are shown here, the chain structures and solvents are omitted for clarity.

Fig. 4 The inner membrane fusion process of comb-like block polymer A₆(B₂)₃, the iso-density surfaces between components A and B of profile are shown here. This figure is the continuation of Fig. 3, and part (a) (Fig. 3(f)), (b), (c), and (d) correspond to t = 22 000, 22 500, and 23 000 DPD time steps, respectively.

We then investigate the self-assembly progress of mixture systems containing amphipathic linear and comb-like block copolymers in dilute solution. The initiate states are always set by randomly distributed copolymers. The concentration of the block copolymers φ = 0.036, and φ_linear is the relative concentration of linear block copolymer which is defined as the percentage of linear block copolymers occupy all mixed block copolymers. At least five independent simulations are conducted for better statistics. All the repulsive strengths and simulation details are coincide with the values we select in onion shape vesicle formation.

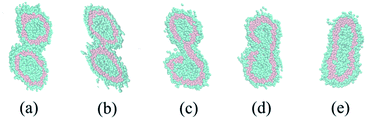
We construct a phase diagram by varying φ_linear and the bond angle potential to indicate the thermodynamically stable structures. As shown in Fig. 5(a), φ_linear changes from 0.1 to 0.5 with 0.1 as the step, and the bond angle potential k_θ ranges from 0 to 25 with 5 as the step. In order to obtain stable structures, all the snapshots are captured at 80 000 DPD time steps. We observe the morphological transitions of aggregate from irregular vesicle to tubular vesicle further to spherical vesicle final to rod-like or toroidal micelle with the increase of linear block copolymer, and the larger k_θ will accelerate the morphological transition. Among all of the structure, toroidal micelle is surprising discovery which is similar to Ouarti's study.²⁰ The morphologies may have relations with potential energy and molecular structures. The potential energy of aggregates tends to decrease when more linear block polymers are added (see Fig. 5(b)), and long hydrophilic chains of linear block copolymer will affect the self-assembling process. There is no onion shape vesicle appears in our simulations, the reason may be attributed to the introduction of long hydrophilic chains of linear block copolymer. This change may prevent the formation of oblate shape vesicle which is a vital part of onion shape vesicle formation. Therefore, we can control the structures by adjusting the ratio of amphipathic linear and comb-like block copolymers. We also check the fusion dynamics of two vesicles formed of a mixture of comb-like A₆(B₂)₃ and linear block copolymer A₆B₆, but no different fusion mechanisms is found. An example is shown in Fig. 6. The main reason may be attributed to the molecular structures which possess the same hydrophobic but different hydrophilic block, especially, the rigidity of the hydrophobic chains may yield higher membrane tension which is a key factor to determine the vesicle fusion dynamic. We conclude that the adding of linear block copolymers will lead to the morphological transition and not lead to the change of fusion dynamics. Toward the goal of obtaining vesicles, it is necessary to introduce asymmetry which causes the membrane bending in dilute solution. In most simulations, block copolymer with asymmetry two components is always considered. However, in our simulations, we use a comb-like block copolymer with two equal components, asymmetry is introduced by the uneven distribution of side chains. This specific molecular structure may open a new way for the design of vesicles for specific usages.

Fig. 5 (a) Morphological phase diagram of aggregates formed by the comb-like block copolymers and linear block copolymer as a function of the different relative concentration of the linear block copolymer and the bond angle potential strength k_θ. Characteristic morphological snapshots illustrate for various structures, such as irregular vesicle, tubular vesicle, spherical vesicle, micelle including rod-like micelle and toroidal micelle. (b) The potential energy change with the different relative concentration of the linear block copolymer.

Fig. 6 Spontaneous vesicles fusion process with φ_linear = 0.2. Hydrophobic chains, red beads; hydrophilic chains, blue beads. Water beads are not shown for clarity. The parts (a), (b), (c), (d) and (e) correspond to t = 22 800, 23 400, 23 600, 23 800 and 28 000 (DPD time steps), respectively.

IV. Conclusions

DPD simulation is carried out to investigate the onion shape vesicle formation and fusion dynamics. We show that comb-like block copolymers with A₆(B₂)₃ type may be a good candidate for onion shape vesicle formation. The spontaneous fusion dynamics between the onion shape vesicles is studied, whose mechanism is similar to that observed in vesicles formed of linear diblock copolymers. The mixture systems containing amphipathic linear and comb-like block copolymers are investigated in dilute solution. We found that the adding of linear block copolymers lead to the structure transition but has no effect on fusion dynamics. The asymmetry of the molecules is a key factor for vesicle formation. Therefore, how the asymmetry affects the organization of the molecules will be the focus of our continuative study. Further studies are ongoing.

Acknowledgements

This work is supported by the Natural Science Foundation of China (Grant No. 21364009).

References

1. S. A. Jenekhe and C. X. Linda, Science, 1998, 279, 1903–1907.
2. B. M. Discher, Y. Y. Won, D. Ege, J. Lee, F. Bates, D. Discher and H. A. Daniel, Science, 1999, 284, 1143–1146.
3. R. Savic, L. Luo, A. Eisenberg and D. Maysinger, Science, 2003, 300, 615–618.
4. L. F. Zhang and A. Eisenberg, J. Am. Chem. Soc., 1996, 118, 3168–3181.
5. J. Zhu, Y. Jiang, H. Liang and W. Jiang, J. Phys. Chem. B, 2005, 109, 8619–8625.
6. D. Paprocki, D. Koszelewski, P. Walde and R. Ostaszewski, RSC Adv., 2015, 5, 102828–102835.
7. D. Paprocki, D. Koszelewski, A. Zadlo, P. Walde and R. J. Ostaszewski, RSC Adv., 2016, 6, 68231–68237.
8. Z. L. Chen, X. H. Wang, L. X. Zhang and L. L. He, Polymer, 2014, 55, 2921–2927.
9. A. P. Martinez, Z. Cui, C. Hire, T. A. P. Seery and D. H. Adamson, Macromolecules, 2015, 48, 4250–4255.
10. Y. Guo, Z. Ma, Z. Ding and R. K. Li, Langmuir, 2013, 29, 12811–12817.
11. P. Xing, T. Sun and A. Hao, RSC Adv., 2013, 3, 24776–24793.
12. H. F. Qi and C. L. Zhong, J. Phys. Chem. B, 2008, 112, 10841–10847.
13. H. J. Qian, Z. Y. Lu, L. J. Chen, Z. S. Li and C. C. Sun, Macromolecules, 2005, 38, 1395–1401.
14. Y. Zhao, G. Milano, Y. Cong, N. Yu, Y. He, Y. Cong, Q. Yuan and B. Dong, J. Phys. Chem. C, 2015, 119, 25009–25022.
15. X. Yu, S. Zhong, X. Li, Y. Tu, S. Yang, R. M. Van Horn, C. Ni, D. Pochan, R. Quirk, C. Wesdemiotis, W. B. Zhang and S. Z. Cheng, J. Am. Chem. Soc., 2010, 132, 16741–16744.
16. L. Chen, T. Jiang and J. Lin, Langmuir, 2013, 29, 8417–8426.
17. C. Sanson, J. F. L. Meins, C. Schatz, A. Soum and S. Lecommandoux, Soft Matter, 2010, 6, 1722–1730.
18. E. Betthausen, C. Hanske, M. Müller, A. Fery, H. F. Schacher, H. E. A. Müller and J. D. Pochan, Macromolecules, 2014, 47, 1672–1683.
19. A. Rørviglund, A. Bahadori, S. Semsey, P. M. Bendix and L. B. Oddershede, Nano Lett., 2015, 15, 4183–4188.
20. N. Ouarti, P. Viville, R. Lazzaroni, E. Minatti, M. Schappacher, A. Deffieux and R. Borsali, Langmuir, 2005, 21, 1180–1186.
21. F. Aydin, G. Uppaladadium and M. Dutt, Colloids Surf., B, 2015, 128, 268–275.
22. F. Aydin, G. Uppaladadium and M. Dutt, J. Phys. Chem. B, 2015, 119, 10207–10215.
23. A. C. Shi and B. Li, Soft Matter, 2013, 9, 1398–1413.
24. S. Y. Ma, Y. Hu and R. Wang, Macromolecules, 2015, 48, 3112–3120.
25. V. Knecht and S. J. Marrink, Biophys. J., 2007, 92, 4254–4261.
26. H. Noguchi and M. Takasu, J. Chem. Phys., 2001, 115, 9547–9551.
27. T. R. Weikl, M. Asfaw, H. Krobath, B. Rózycki and R. Lipowsky, Soft Matter, 2009, 5, 3213–3224.
28. G. K. Xu, J. Hu, R. Lipowsky and T. R. Weikl, J. Chem. Phys., 2015, 143, 243136.
29. J. Hu, G. K. Xu, R. Lipowsky and T. R. Weikl, J. Chem. Phys., 2015, 143, 243137.
30. J. Xin, D. H. Liu and C. L. Zhong, J. Phys. Chem. B, 2007, 111, 13675–13682.
31. P. J. Hoogerbrugge and J. M. V. A. Koelman, Europhys. Lett., 1992, 19, 155–160.
32. P. J. Hoogerbrugge and J. M. V. A. Koelman, Europhys. Lett., 1993, 21, 363–368.
33. Y. Kong, C. W. Manke, W. G. Madden and A. G. Schlijper, Int. J. Thermophys., 1994, 15, 1093–1101.
34. A. G. Schlijper, P. J. Hoogerbrugge and C. W. Manke, J. Rheol., 1995, 39, 567–579.
35. R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435.
36. Y. L. Zhu, H. Liu, Z. W. Li, H. J. Qian, G. Milano and Z. Y. Lu, J. Comput. Chem., 2013, 34, 2197–2211.
37. Y. T. Liu, Y. Zhao, H. Liu, Y. H. Liu and Z. Y. Lu, J. Phys. Chem. B, 2009, 113, 15256–15262.
38. J. C. Shillcock and R. Lipowsky, J. Chem. Phys., 2002, 117, 5048–5061.
39. L. He, Z. Chen, R. Zhang, L. Zhang and Z. Jiang, J. Chem. Phys., 2013, 138, 94907.
40. V. Ortiz, S. O. Nielsen, D. E. Discher, M. L. Klein, R. Lipowsky and J. Shillcock, J. Phys. Chem. B, 2005, 109, 17708–17714.
41. B. Li, Y. L. Zhu, H. Liu and Z. Y. Lu, Phys. Chem. Chem. Phys., 2012, 14, 4964–4970.
42. C. M. Lin, Y. Z. Chen, Y. J. Sheng and H. K. Tsao, React. Funct. Polym., 2009, 69, 539–545.
43. Y. Han, H. Yu, H. Du and W. Jiang, J. Am. Chem. Soc., 2010, 132, 1144–1150.
44. G. J. A. Sevink and A. V. Zvelindovsky, Macromolecules, 2005, 38, 7502–7513.
45. M. Müller, K. Katsov and M. Schick, Biophys. J., 2003, 85, 1611–1623.

---