Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Wettability of vertically-oriented graphenes with different intersheet distances†
Xiaorui Shuai,
Zheng Bo *,
Jing Kong,
Jianhua Yan and
Kefa Cen
*,
Jing Kong,
Jianhua Yan and
Kefa Cen
State Key Laboratory of Clean Energy Utilization, Institute for Thermal Power Engineering, College of Energy Engineering, Zhejiang University, Hangzhou, Zhejiang Province 310027, China. E-mail: bozh@zju.edu.cn; Fax: +86 571 87951616; Tel: +86 571 87951369
First published on 12th January 2017
Abstract
Vertically-oriented graphenes (VGs), i.e., graphene nanosheets arranged perpendicularly to the substrate surface, possess great promise as electrode materials for supercapacitors, mainly due to the vertical orientation on the substrate, open intersheet space, and exposed sharp edges. In this work, the dependence of VGs' wettability on their surface morphologies is investigated with experiments and numerical simulations. VGs with different intersheet distances are fabricated with plasma-enabled methods employing different plasma sources. The results show that the contact angle of VGs changes from 111° to 34.5° with a decreasing intersheet distance from ∼306.2 to ∼14.5 nm, indicating that the graphene intersheet distance plays an critical role on the wettability of VGs. Lattice Boltzmann (LB) simulation is further conducted to explore the mechanism on the flow and transport of electrolytes within VG channels. The behavior of electrolyte flow and its permeation into VG interiors is found to be strongly dominated by the capillary force across the air–liquid interface, while the gravity of the bulk electrolyte and the viscous force produced by the graphene surface could be ignored. A 3-fold improvement in the accessible surface area of VGs is achieved with reducing intersheet distance. Electrochemical results indicate that the hydrophilic VG electrode with a small intersheet distance of 14.5 nm exhibits a high specific capacitance (up to 147 F g−1) at a high cyclic voltammetry scan rate of 500 mV s−1, due to the effective wetting and utilization of VG surfaces. The results of the current work could provide instructive information in the morphology optimization of VGs for high performance energy storage applications.
Introduction
Vertically-oriented graphenes (VGs) are a class of network of few-layer graphenes perpendicularly standing on a substrate.1,2 Compared with the conventional graphene stacks obtained with a modified Hummer's method,3,4 VGs own a number of unique features, such as vertical orientation, non-agglomerated morphology, large surface-to-volume ratio, open inter-sheet channels, and exposed ultra-thin graphene edges.5,6 These advantages make VGs quite promising for a variety of applications.6–9Typically, VGs have emerged as a promising electrode material for supercapacitors.10–13 Different from conventional graphene stacks, VGs feature a free-standing, self-supported rigid structure without obvious agglomeration of the graphene sheets, which could significantly enlarge the specific surface area and further the ability of energy storage.6,14 For example, Zhao et al. reported that the area capacitance of VG electrode could reach 76 mF cm−2 with a high specific surface area of 1100 m2 g−1.15 Zhang et al. reported the area capacitance of VG electrode reached 8.4 mF cm−2, owing to the increased surface area which was as large as 800 times of planar graphene.16 Hung et al. fabricated a 3-D VG electrode with a high specific surface area of 1580 m2 g−1, resulting in a gravimetric capacitance of 198 F g−1.17 Ostrikov's group reported that VG-based supercapacitors presented a high gravimetric capacitance of 230 F g−1, taking advantages of the massive graphene edge planes.18
On the other hand, although the non-agglomerated morphology of VGs with a high surface-to-volume ratio and open channels could benefit the utilization of graphene surface for the effective adsorption of ions, the extent of wetting of the VG interior surface determines the fraction of the total surface area, i.e., the energy storage effective surface area.6,19
It has been extensively demonstrated that VGs obtained from plasma-enabled processes are hydrophobic with water contact angle (CA) of 102–153°.19–21 Various methods, such as plasma treatment, wet-chemical reactions and deposition conditions control, have been employed to the surface chemical modification of VGs. For instance, Watanabe et al. used the Ar plasma treatment to decrease the CA of VGs from 137° to 6.2° with the O/C ratios increasing from 0.01 to 0.2.22 They further reported a CA of 147° with CF4 plasma treatment.23 Stancu et al. found that the CA of VGs transitioned from 122° to 4–11° with NH3 and N2 plasma functionalization, which was ascribed to the increasing of N and O concentrations for 16.3–19.1% and 13.9–17.3%, respectively.24 Zhou et al. turned the CA of VGs between 0° and 140.1° by the adding and elimination of carbonyls and epoxide groups with O2 and H2 plasma modifications.25 On the other hand, it was reported that CA of VGs were modified from 133° to 53.1° with the effect of carboxyl and hydroxyl groups while recovered to 133.7° due to the functionalization of alkane chains.26 Moreover, growth time and gas species were regulated to change the oxygen groups on the VG surface, leading to the formation of CA in the range of 28.5–142°.27
It is well known that the surface energy of a material can be controlled by both the surface chemical composition and the surface morphology.28–30 However, the dependence of the wettability of VGs on their morphologies has been rarely reported. Yang et al. found that roughness could enhance the hydrophobic property of VG surface.21 Feng's group revealed that the wettability of VGs could be controlled from hydrophobic to hydrophilic nature by introducing different densities of defects.19,31 In fact, the resulting apparent wettability of VGs is determined by the interplay between the capillary force arising from the wetting of VG walls and the repulsion from the compressed air. Consequently, an investigation on the dependence of the wettability of VGs and an understanding on the liquid electrolyte permeation inside VG interiors are needed.
In this work, the influence of graphene intersheet distance on the wettability of VGs was investigated through experimental studies and numerical simulations. VGs with different graphene intersheet distances were fabricated via plasma-enhanced chemical vapor deposition (PECVD) methods with different plasma sources. A multi-phase and multi-component lattice Boltzmann (LB) model based on the Shan–Chen scheme was employed to unveil the fundamental wetting mechanism of electrolyte transport in VG channels. Finally, the electrochemical performance of VGs with different graphene intersheet distances and wettability were presented.
Experimental and simulation methods
Fabrication of VGs
VGs with various morphologies were fabricated via PECVD methods employing direct current (DC), inductively coupled (ICP), and microwave (MW) plasma sources. The as-grown VG samples were labeled as DC-VGs, ICP-VGs, and MW-VGs, respectively. The whole preparation processes were presented in detail as follows.DC-VGs were fabricated in an atmospheric pressure DC-PECVD system. Four uniformly distributed conical profile tungsten pins were used as the discharge cathode by connecting to negative direct current high voltage supplies. A grounded quadrat nickel foil was employed as the growth substrate as well as the discharge anode. Prior to the growth, the nickel foil substrate was heated to 650 °C in the mixing flow of H2/Ar. During the growth, 250 sccm CH4 bubbled through a deionized water bath was introduced into the chamber with a mixture of 2500 sccm Ar. DC glow discharge was ignited in −10 kV applying voltage.
ICP-VGs were fabricated in a ICP-PECVD system. Briefly, ICP was created by a 400 W RF power. A nickel foil was positioned in the center of the cylindrical quartz tube. Prior to the fabrication process, the reactor device was pumped to a low pressure of 30 mTorr. The growth substrate was brought to 700 °C under the vacuum condition. Subsequently, 5 sccm CH4 mixed with 5 sccm H2 were used as the precursor gases and fed into the cylindrical quartz tube during the growth process.
MW-VGs were fabricated in a MW-PECVD system. A 2.45 GHz MW source was coupled to the VG growth in a transverse electric mode driven by a rectangular cavity waveguide. A nickel foil was placed on the top surface of stainless steel platform as the growth substrate. The system was heated to 600 °C with 50 sccm H2 under 450 W microwave. During the growth, 10 sccm CH4 was introduced into the reactor. After the VG growth, the nickel foil was cooled down to room temperature.
Materials characterization
The surface morphology of VGs were inspected by a SU-70 scanning electron microscope (SEM, Hitachi S-4800). The crystal structure was investigated by a Tecnai G2 F30 S-Twin transmission electron microscopy (TEM, Philips-FEI). In order to perform TEM and high-resolution (HR-TEM) characterizations, the VG samples were dispersed in ethanol and coated on a 230 mesh holey carbon grid. The Raman spectra was obtained with a DXR 532 Raman spectrometer (Thermo Fischer Scientific) with an excitation wavelength of 532 nm. X-ray photoelectron spectroscopy (XPS) measurement was characterized by a VG Escalab Mark II system with a monochromatic Mg Kα X-ray source (hm = 1253.6 eV, West Sussex). Static CAs of the water droplets on the VG surfaces were tested by a DropMeter™ Professional A-200 digital goniometer (MAIST Vision Inspection & Measurement Co., Ltd). A deionized water droplet (5 μL) was dripped above the surface by using an automatic driven syringe device. For the accurate evaluation of CA, Young–Laplace, circle, and conic methods were introduced by capturing the droplet shape. Dynamic droplet impact experiment was conducted with the high-speed camera (REDLAKE MotionXtra HG-100K). The height of the water droplet was predetermined as 50 mm, providing the impact velocity of 1 m s−1.Electrochemical measurements
VG-Based supercapacitors were assembled into a two-electrode system with nickel foil as the current collector. The current testing system employed a coin cell with a layered structure, in which all the components were sandwiched between two pieces of stainless steel spacers. The active area of the electrode is 1 × 1 cm2 with a loading mass of 0.02 mg. 6 M KOH solution was used as the aqueous electrolyte. Electrochemical performances were characterized by cyclic voltammetry (CV), galvanostatic charge/discharge, and electrochemical impedance spectroscopy (EIS) on an electrochemical workstation (PGSTAT302N, Metrohm Autolab B.V.) at room temperature.LB simulation method
The electrolyte transport in VG channels was investigated by the LB simulation method. Multi-phase and multi-component D2Q9-LBGK model based on the Shan–Chen scheme was implemented to depict the liquid electrolyte permeation inside VG interiors.32 Specifically, rectangular shape was selected as the computational domain size with 162 × 162 lu2 (lu: lattice unit). The densities of liquid droplet and gaseous air were set as 1.0 mu lu−2. In Shan–Chen scheme, the Green's function was chosen as 2.0 through the validation of Laplace's law to ensure the realization of sharp interface between two phases.33 The interaction intensity factors acting on the two phases were fixed as −0.05 and 0.05 to maintain the intrinsic CA of 87° on the single layer graphene via the static droplet test.34,35 In order to ensure the reliability of the simulation results, iterative residual was set as 1 × 10−6 during the simulations. For the comparison between the LB simulations and the experimental results, relationship between the dimensionless lattice unit and realistic length space was established by adjusting the relaxation time through the dimensional analysis. To eliminate the domain scale effects, periodic boundary conditions were adopted for the side planes of the computational domain. No-slip bounce back rule was implemented on the bottom substrate and the top surface.Results and discussion
Morphology and microstructure of VGs
The surface morphology of VGs was observed by SEM. As shown in Fig. 1a–c, all the VG networks produced by different plasma sources showed large amount of exposed graphene edges and exhibited high degree of coagulation. Significant difference of the geometric structures of VGs obtained from different plasma sources was observed. The graphene nanosheets of DC-VGs presented a highly-branched cauliflower morphology while ICP-VGs and MW-VGs had a maze-like morphology. The intersheet distance between two adjacent graphene nanosheets of VGs increased in the order of DC-VGs < ICP-VGs < MW-VGs, indicating the formation of different growth densities on the substrates. The morphology and structure of VGs were also investigated using TEM and HR-TEM techniques. As shown in Fig. 1d–f, the folded and crumpled graphene nanosheets were found in all samples, demonstrating the intrinsic feature of graphene materials.36 Fig. 1g–i exhibit the HR-TEM images of VGs. It could be seen that no obvious defects were detected in the basal planes. The edges are multi-layer graphene with an interlayer spacing of ∼0.354 nm, in accordance with the values in previous literatures.37,38 The mechanisms (e.g., vapor–liquid–solid or vapor–solid–solid) widely used to explain the growth of laminar graphene, vertically aligned carbon nanotubes or graphene nanoribbons can not be directly applied for VG growth as the process requires no catalyst.39–43 Details on the growth mechanisms and parameter control of plasma-enabled growth of VGs can be found in our previous reviews.2,6Raman and XPS analysis
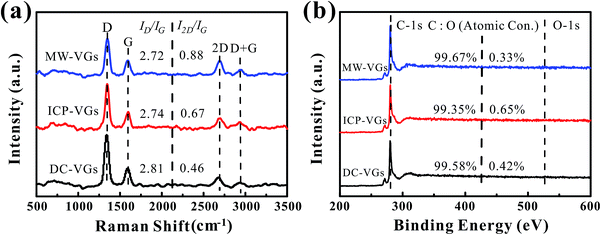
The crystal structure of VGs was characterized by Raman spectroscopy. Fig. 2a shows the Raman spectra of VGs. Each Raman spectra of VGs contained four prominent bands at ∼1340 cm−1, ∼1590 cm−1, ∼2685 cm−1, ∼2935 cm−1, respectively, which were closed to the typical spectra of carbon materials.31,44 The intensity ratios of ID/IG were calculated as 2.81, 2.74, and 2.72 for DC-VGs, ICP-VGs, and MW-VGs, respectively, suggesting similar defects level and disorder in the sp2 graphene structure.13,44 On the other hand, the I2D/IG ratios of DC-VGs, ICP-VGs, and MW-VGs were 0.46, 0.67, and 0.88, respectively, indicating the multi-layer graphenes in VG nanosheets.45,46 Moreover, the overall information of Raman results from Table S1 in ESI† further confirmed a high level of crystalline quality and graphite structure in all samples.Fig. 2b shows the XPS survey spectra of VGs. The contents of carbon and oxygen were obtained by calculating the C-1s and O-1s peak areas. A high carbon content above 99% was detected for each sample, showing a similar chemical composition of VGs. Besides, the fractions of C atom in C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C/C–C, C–OH, C
C/C–C, C–OH, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, and O
O, and O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–OH (Table S2 in ESI†) were calculated from the Gaussian line fitted C-1s XPS spectrum of VGs (Fig. S1 in ESI†).47 No significant difference was observed among the C-1s peaks of VGs.
C–OH (Table S2 in ESI†) were calculated from the Gaussian line fitted C-1s XPS spectrum of VGs (Fig. S1 in ESI†).47 No significant difference was observed among the C-1s peaks of VGs.
Surface wettability of VGs
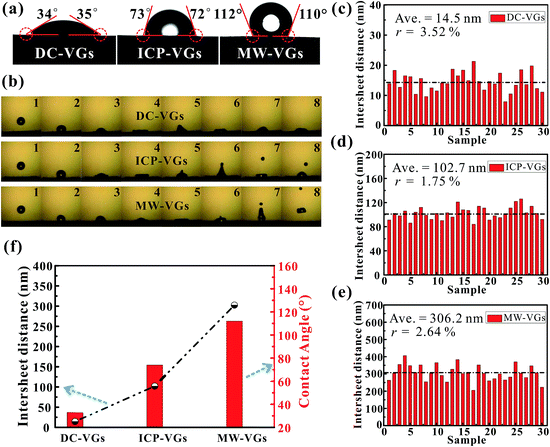
Static CA measurement was conducted to investigate the wettability of VGs. As shown in Fig. 3a, the CA on the VG surface increased in the order of DC-VGs (34.5°) < ICP-VGs (72.5°) < MW-VGs (111°) with wetting transition from hydrophilic to hydrophobic state. Fig. 3b shows the successive images of the droplet free falling on the VG surface for the first impact. For the impact on the DC-VGs, the whole droplet anchored on the top surface and no jetting of any part of the droplet was observed. High dissipation of kinetic energy converted into the surface energy associated with the increased free-surface area during the spread stage.48,49 For ICP-VGs and MW-VGs, an obvious droplet was jetted at the top during the deformation process. During the impact, the droplet stored its kinetic energy in surface deformation and less energy was consumed by viscous dissipation of the droplet on the surfaces.50,51 The bounce of the main water droplet was captured on the MW-VGs owing to its strong hydrophobicity.As a consequence, the surface energy of VG samples decreased in the order of DC-VGs > ICP-VGs > MW-VGs, suggesting different interaction intensity between the liquid and different VG surface.52
Generally, the wetting behavior of a solid surface is closely related to the surface morphology and the chemical composition.28–30 Given the previous analysis of surface morphology, crystal structure and elemental detection, it is reasonable that the varying wettability of VGs should be attributed to the diverse surface morphologies rather than the chemical composition, disorder and defects. Consequently, the distance between two adjacent graphene nanosheets is the key factor in determining the wettability of VGs. Based on the SEM images of VGs, corresponding statistics on the graphene intersheet distance distribution of VGs were obtained by measuring 30 samples of randomly selected gaps. The average graphene intersheet distance and its precision error rate were calculated using the Student t-distribution with a confidence level of 95%.53 Fig. 3c–e shows that the graphene intersheet distance was distributed in different orders of magnitude with an average value of ∼14.5, ∼102.7, and ∼306.2 nm for DC-VGs, ICP-VGs, and MW-VGs, respectively. Meanwhile, the error rate was calculated in the same level, suggesting a similar size uniformity of VGs.
Fig. 3f reveals that a positive correlation was formed between CA and average graphene intersheet distance of VGs, indicating that a smaller graphene intersheet distance contributed to a smaller contact angle and vice versa. The above observation confirms that graphene intersheet distance is able to significantly modify the wettability of VGs.
Electrolyte transport mechanism
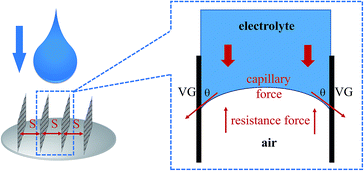
To study the mechanism of electrolyte transport in VGs, a single VG channel was specifically selected to figure out the force analysis. Fig. 4 presents the schematic of interface between the liquid phase (electrolyte) and gas phase (air). In principle, the electrolyte flow behavior is determined by several forces along the liquid permeation direction, mainly including the gravity of the bulk electrolyte, the capillary force across the air–liquid interface, the resistance force from the existing gaseous air in the VG channel, and the viscous force produced by the VG surface. The underlying electrolyte flow is governed by the representative values of several non-dimensional numbers,32 which are defined as follows.Reynolds number reflecting the ratio of the inertia force to the viscous force:33
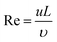 | (1) |
Capillary number which is the ratio of the viscous force to the capillary force:35
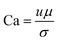 | (2) |
Bond number denoting the ratio of the gravitational force to the capillary force:54
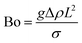 | (3) |
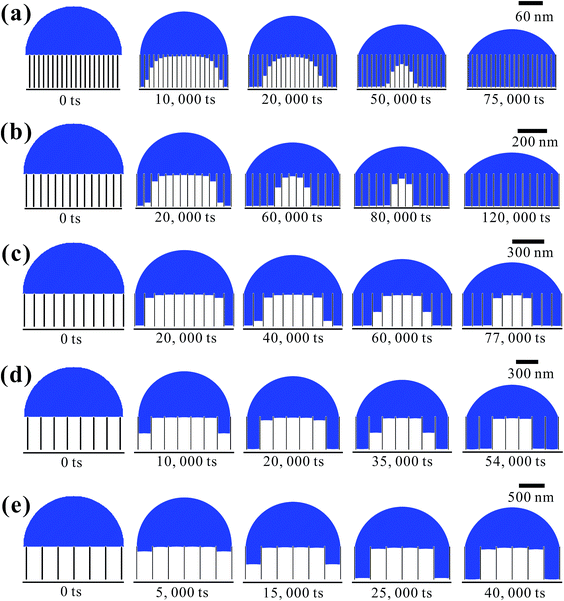
Based on the above analysis, five groups of VGs with various graphene intersheet distances (S) of 12–322 nm were chosen to simulate the electrolyte transport process. The whole dynamic displacement is shown in Fig. 5. At the initial state, the liquid droplet was on the top surface of VGs. No additional external force was added to the bulk electrolyte. The displacement was finished until the two-phase equilibrium and the final wetting state depended on the relative magnitude of capillary force and resistance force in VG channels. To evaluate the extent of wetting of the VG interior surface, a coefficient Se was introduced, defined as
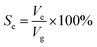 | (4) |
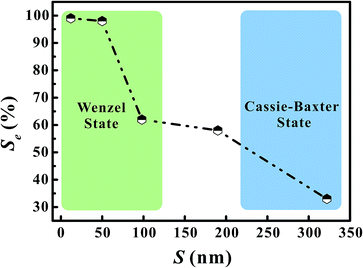
Fig. 6 shows the as-calculated Se in VG channels with different S after the convergence of simulations. Obviously, Se increased with the decrease of S, confirming the liquid electrolyte permeation inside VG interiors depend strongly on the graphene intersheet distance. According to the Laplace equation, the capillary pressure across the air–liquid interface induced by the capillary force was inversely proportional to the intersheet distance.33,35 For S = 322 nm, the capillary pressure was not enough to overcome the resistance from the air phase, resulting in the electrolyte flow blockage in VG channels. The majority of the bulk electrolyte still remained on the top surface of VGs. No significant displacement between two phases was achieved, leading to an ultra-low Se of 33%. In this case, liquid electrolyte contacted with VG interior surface and trapped air simultaneously, forming the Cassie–Baxter state.57,58 Although Se increased for 24–29% after S decreased to 190 and 98 nm, a portion of air was still trapped in the middle VG channels, which was caused by the limited increase in capillary pressure. When S further decreased to 50 and 12 nm, nearly all the VG interior surfaces were wetted sufficiently by the electrolyte owing to the one magnitude higher capillary pressure compared to that in the VG channels with much larger S. After the complete displacement, the original Cassie–Baxter state transitioned to Wenzel state in which liquid electrolyte only contacted with the VG interior surfaces.57,59
Electrochemical performances
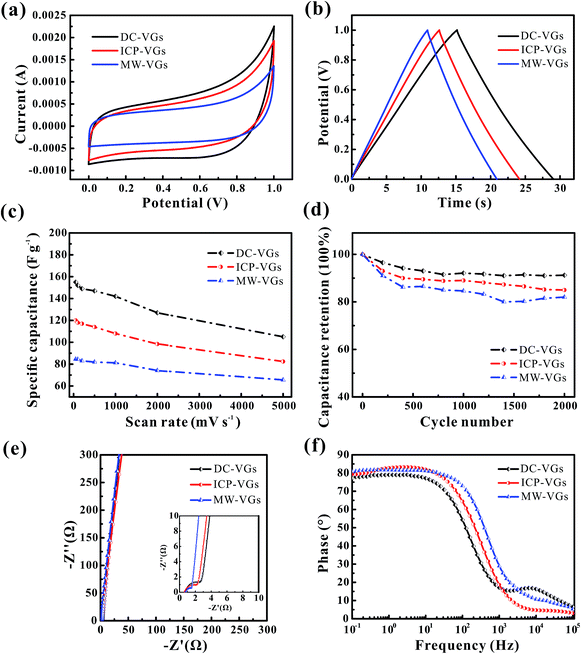
The electrochemical performances of VG-based supercapacitors were measured using CV and galvanostatic charge/discharge tests in a 6 M KOH aqueous solution. Fig. 7a illustrates the CV curves at a scan rate of 500 mV s−1. It is found that the CV curves of all the VG electrodes presented an unaltered and quasi-rectangular shape, consistent with a typical predominant electric double layer capacitive behavior.16 Based on the calculation of areas of CV profiles, the resulting specific capacitances were in the order of MW-VGs (82 F g−1) < ICP-VGs (114 F g−1) < DC-VGs (147 F g−1), suggesting that the specific capacitance of VG electrode increase with the enhanced surface wettability. Therefore, the decrease in graphene intersheet distance of VGs could increase the utilization of surface area and facilitate the ion capture ability during the charge storage.Fig. 7b depicts the galvanostatic charge/discharge plots of VG electrodes at a current density of 5 A g−1. As it could be observed, the potential–time curves were nearly linear and symmetric for all the electrodes. No obvious potential drop was found, indicating a low internal resistance in all the VG electrodes.12 The specific capacitances were calculated as 149, 115, and 91 F g−1 for DC-VGs, ICP-VGs, and MW-VGs, respectively, also confirming that small graphene intersheet distance is in favor of increasing accessible surface area by improving the wettability.
For a better understanding of effects of wettability on capacitive performance, CV tests were further conducted on VG electrodes at scan rates varying from 50 to 5000 mV s−1. All the detailed curves are presented in Fig. S2 in ESI.† Fig. 7c shows the specific capacitances versus scan rates of different VG electrodes. With an increasing scan rate, all the VG electrodes exhibited a good rate performance with an excellent capacitance retention ratio higher than 90% for a scan rate up to 1000 mV s−1. Notably, DC-VGs still retained a high specific capacitance of 105 F g−1 at an ultrahigh scan rate of 5000 mV s−1, significantly superior to that of ICP-VGs (82 F g−1) and MW-VGs (66 F g−1). This phenomenon indicates that the surface area of DC-VGs could still be accessible to a large extent during the fast ions adsorption process, which is ascribed to the outstanding wettability with a densely porous structure.
Fig. 7d shows the electrochemical cycling stability of VGs conducted at a scan rate of 500 mV s−1. Compared with ICP-VGs and MW-VGs electrodes, DC-VGs electrode presented the best stability with a high capacitance retention of 91.2% after 2000 cycles. This demonstrates that intersheet distance is critical for wetting behavior which can further influence the cycling performance of the electrodes. Additionally, the capacitance of MW-VGs electrode followed an increase of 2% in the last 600 cycles, which could be attributed to the improvement in wettability over soak time.
To further investigate the dielectric and transfer kinetics, EIS was examined on the VG electrodes. Fig. 7e shows the Nyquist plots for VG electrodes. For the current work, a near-vertical curve in low frequency region was observed in each Nyquist plot of VG electrode. In the high frequency region (inset of Fig. 7e), a semicircle related to the charge-transfer resistance was depressed and extremely small, demonstrating effective electronic conductivity in VG nanosheets.14 Moreover, the 45° line intersecting the real axis which corresponded to the Warburg resistance, was nearly negligible, indicating the effective ions diffusion towards the VG electrodes.31 Fig. 7f shows the phase response of the frequency for VG electrodes. The phase angles were found to closely approach to −90° in each plot of VG electrodes, exhibiting a rapid charge/discharge process.1 Meanwhile, the MW-VGs electrode showed a slight higher knee frequency than that of ICP-VGs and DC-VGs electrodes, which could be attributed to the alleviated porous effects with large graphene intersheet distance.5
Conclusions
In summary, the influence of topographical surface structure on the wettability of VGs in supercapacitors was investigated through a combination of experimental research and numerical simulations. VGs with different graphene intersheet distances were obtained via PECVD methods by employing different plasma sources. Material characterizations demonstrated that VGs fabricated by different plasma sources exhibited similar chemical composition and crystal structure but different graphene intersheet distances. The static CA and droplet impact experiments revealed that VG surfaces with different morphologies presented a strikingly different wetting behavior with CAs of 34.5–111°. Furthermore, the LB simulation depicted the liquid electrolyte permeation in VG channels, confirming that the capillary force across the air–liquid interface played a dominant role on the electrolyte transport process. The simulations results indicated that the decrease of the graphene intersheet distance could lead to a significant increase in the capillary force and further a high-efficiency wetting of VG surface area. DC-VGs with rapidly decreased graphene intersheet distance achieved the highest specific capacitance, compared with the ICP-VGs and MW-VGs counterparts, due to the efficient utilization of the wetted surface area.Acknowledgements
Financial support for this work was provided by the National Natural Science Foundation of China (No. 51306159), the Zhejiang Provincial Natural Science Foundation of China (No. LR17E060002), and the Foundation of National Excellent Doctoral Dissertation of China (No. 201238).Notes and references
- J. R. Miller, R. Outlaw and B. Holloway, Science, 2010, 329, 1637–1639 CrossRef CAS PubMed.
- Z. Bo, Y. Yang, J. Chen, K. Yu, J. Yan and K. Cen, Nanoscale, 2013, 5, 5180–5204 RSC.
- S. Stankovich, D. A. Dikin, R. D. Piner, K. A. Kohlhaas, A. Kleinhammes, Y. Jia, Y. Wu, S. T. Nguyen and R. S. Ruoff, Carbon, 2007, 45, 1558–1565 CrossRef CAS.
- P. Song, X. Zhang, M. Sun, X. Cui and Y. Lin, RSC Adv, 2012, 2, 1168–1173 RSC.
- M. Cai, R. A. Outlaw, R. A. Quinlan, D. Premathilake, S. M. Butler and J. R. Miller, ACS Nano, 2014, 8, 5873–5882 CrossRef CAS PubMed.
- Z. Bo, S. Mao, Z. J. Han, K. Cen, J. Chen and K. K. Ostrikov, Chem. Soc. Rev., 2015, 44, 2108–2121 RSC.
- Z. Bo, K. Yu, G. Lu, S. Cui, S. Mao and J. Chen, Energy Environ. Sci., 2011, 4, 2525–2528 CAS.
- H. Kim, Z. Wen, K. Yu, O. Mao and J. Chen, J. Mater. Chem., 2012, 22, 15514–15518 RSC.
- S. Mao, K. Yu, J. Chang, D. A. Steeber, L. E. Ocola and J. Chen, Sci. Rep., 2013, 3, 1696 Search PubMed.
- S. Lee, S. H. Lee, T. H. Kim, M. Cho, J. B. Yoo, T.-i. Kim and Y. Lee, ACS Appl. Mater. Interfaces, 2015, 7, 8070–8075 CAS.
- Y. Ma, M. Wang, N. Kim, J. Suhr and H. Chae, J. Mater. Chem. A, 2015, 3, 21875–21881 CAS.
- J. L. Qi, X. Wang, J. H. Lin, F. Zhang, J. C. Feng and W.-D. Fei, J. Mater. Chem. A, 2015, 3, 12396–12403 CAS.
- B. Ouyang, Y. Zhang, Z. Zhang, H. J. Fan and R. Rawat, RSC Adv., 2016, 6, 23968–23973 RSC.
- L. Liu, Z. Niu and J. Chen, Chem. Soc. Rev., 2016, 45, 4340–4363 RSC.
- X. Zhao, H. Tian, M. Zhu, K. Tian, J. Wang, F. Kang and R. Outlaw, J. Power Sources, 2009, 194, 1208–1212 CrossRef CAS.
- Y. Zhang, Q. Zou, H. S. Hsu, S. Raina, Y. Xu, J. B. Kang, J. Chen, S. Deng, N. Xu and W. P. Kang, ACS Appl. Mater. Interfaces, 2016, 8, 7363–7369 CAS.
- T.-C. Hung, C.-F. Chen and W.-T. Whang, Electrochem. Solid-State Lett., 2009, 12, K41–K44 CrossRef CAS.
- D. H. Seo, Z. J. Han, S. Kumar and K. K. Ostrikov, Adv. Energy Mater., 2013, 3, 1316–1323 CrossRef CAS.
- L. Zhang, Z. Sun, J. Qi, J. Shi, T. Hao and J. Feng, Carbon, 2016, 103, 339–345 CrossRef CAS.
- E. Stancu, M. Ionita, S. Vizireanu, A. Stanciuc, L. Moldovan and G. Dinescu, Mater. Sci. Eng., B, 2010, 169, 119–122 CrossRef CAS.
- C. Yang, H. Bi, D. Wan, F. Huang, X. Xie and M. Jiang, J. Mater. Chem. A, 2013, 1, 770–775 CAS.
- H. Watanabe, H. Kondo, M. Sekine, M. Hiramatsu and M. Hori, Jpn. J. Appl. Phys., 2012, 51, 01AJ07 CrossRef.
- H. Watanabe, H. Kondo, M. Hiramatsu, M. Sekine, S. Kumar, K. Ostrikov and M. Hori, Plasma Processes Polym., 2013, 10, 582–592 CrossRef CAS.
- E. C. Stancu, A.-M. Stanciuc, S. Vizireanu, C. Luculescu, L. Moldovan, A. Achour and G. Dinescu, J. Phys. D: Appl. Phys., 2014, 47, 265203 CrossRef.
- H.-T. Zhou, N. Yu, F. Zou, Z.-H. Yao, G. Gao and C.-M. Shen, Chin. Phys. B, 2016, 25, 096106 CrossRef.
- J. Dong, Z. Yao, T. Yang, L. Jiang and C. Shen, Sci. Rep., 2013, 3, 1733 Search PubMed.
- S. Deheryan, D. J. Cott, P. W. Mertens, M. Heyns and P. M. Vereecken, Electrochim. Acta, 2014, 132, 574–582 CrossRef CAS.
- A. Adamson and A. Gast, Physical chemistry of surfaces, New York, Wiley, 1997 Search PubMed.
- H. Liu, J. Zhai and L. Jiang, Soft Matter, 2006, 2, 811–821 RSC.
- D. Quéré, Annu. Rev. Mater. Res., 2008, 38, 71–99 CrossRef.
- J. L. Qi, X. Wang, J. H. Lin, F. Zhang, J. C. Feng and W.-D. Fei, Nanoscale, 2015, 7, 3675–3682 RSC.
- L. Chen, Q. Kang, Y. Mu, Y.-L. He and W.-Q. Tao, Int. J. Heat Mass Transfer, 2014, 76, 210–236 CrossRef CAS.
- S. G. Lee, D. H. Jeon, B. M. Kim, J. H. Kang and C.-J. Kim, J. Electrochem. Soc., 2013, 160, H258–H265 CrossRef CAS.
- H. Li and X. C. Zeng, ACS Nano, 2012, 6, 2401–2409 CrossRef CAS PubMed.
- K. N. Kim, J. H. Kang, S. G. Lee, J. H. Nam and C.-J. Kim, J. Power Sources, 2015, 278, 703–717 CrossRef CAS.
- Z. Bo, X. Shuai, S. Mao, H. Yang, J. Qian, J. Chen, J. Yan and K. Cen, Sci. Rep., 2014, 4, 4684 Search PubMed.
- N. Soin, S. S. Roy, T. H. Lim and J. A. McLaughlin, Mater. Chem. Phys., 2011, 129, 1051–1057 CrossRef CAS.
- Z. Wang, M. Shoji and H. Ogata, Appl. Surf. Sci., 2011, 257, 9082–9085 CrossRef CAS.
- D. V. Kosynkin, A. L. Higginbotham, A. Sinitskii, J. R. Lomeda, A. Dimiev, B. K. Price and J. M. Tour, Nature, 2009, 458, 872–876 CrossRef CAS PubMed.
- P. Y. Huang, C. S. Ruiz-Vargas, A. M. van der Zande, W. S. Whitney, M. P. Levendorf, J. W. Kevek, S. Garg, J. S. Alden, C. J. Hustedt and Y. Zhu, Nature, 2011, 469, 389–392 CrossRef CAS PubMed.
- H. Zanin, C. Rosa, N. Eliaz, P. May, F. Marciano and A. Lobo, Nanoscale, 2015, 7, 10218–10232 RSC.
- X. Chen, B. Wu and Y. Liu, Chem. Soci. Rev., 2016, 45, 2057–2074 RSC.
- A. Peterlevitz, P. May, R. Harniman, J. Jones, H. Ceragioli and H. Zanin, Thin Solid Films, 2016, 616, 698–702 CrossRef CAS.
- B. Dehghanzad, M. K. R. Aghjeh, O. Rafeie, A. Tavakoli and A. J. Oskooie, RSC Adv., 2016, 6, 3578–3585 RSC.
- A. Ferrari, J. Meyer, V. Scardaci, C. Casiraghi, M. Lazzeri, F. Mauri, S. Piscanec, D. Jiang, K. Novoselov and S. Roth, Phys. Rev. Lett., 2006, 97, 187401 CrossRef CAS PubMed.
- Z. Ni, H. Wang, J. Kasim, H. Fan, T. Yu, Y. Wu, Y. Feng and Z. Shen, Nano Lett., 2007, 7, 2758–2763 CrossRef CAS PubMed.
- X. Feng, W. Chen and L. Yan, Nanoscale, 2015, 7, 3712–3718 RSC.
- T. Mao and D. C. S. Kuhn, AIChE J., 1997, 43, 2169–2179 CrossRef CAS.
- K. K. S. Lau, K. B. K. Teo, M. Chhowalla, G. A. J. Amaratunga, G. H. Mckinley and C. Cambridge, Nano Lett., 2003, 3, 1701–1705 CrossRef CAS.
- R. Rioboo, M. Marengo and C. Tropea, Exp. Fluids, 2002, 33, 112–124 CrossRef.
- A. L. Yarin, Annu. Rev. Fluid Mech., 2005, 38, 159–192 CrossRef.
- A. Tuteja, W. Choi, J. M. Mabry, S. A. Mazzella, G. C. Rutledge, G. H. Mckinley and R. E. Cohen, Science, 2007, 318, 1618 CrossRef CAS PubMed.
- X. Zhang, E. Wu, Z. Bo, W. Q. Zhu, K. Yu, C. Yu, Z. Wang, J. Yan and K. Cen, Phys. Status Solidi B, 2014, 251, 829–837 CrossRef CAS.
- P. P. Mukherjee, C. Wang and Q. Kang, Electrochim. Acta, 2009, 54, 6861–6875 CrossRef CAS.
- B. Han and H. Meng, Int. J. Hydrogen Energy, 2013, 38, 5053–5059 CrossRef CAS.
- S. G. Lee and D. H. Jeon, J. Power Sources, 2014, 265, 363–369 CrossRef CAS.
- J. Zang, S. Ryu, N. Pugno, Q. Wang, Q. Tu, M. J. Buehler and X. Zhao, Nat. Mater., 2013, 12, 321 CrossRef CAS PubMed.
- A. B. D. Cassie and S. Baxter, Trans. Faraday Soc., 1944, 40, 546–551 RSC.
- R. N. Wenzel, J. Phys. Chem., 1949, 53, 1466–1467 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra27428e |
| This journal is © The Royal Society of Chemistry 2017 |