Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The effect of different hydrogen terminations on the structural and electronic properties in the triangular array graphene nanomeshes
G. P. Tang *,
Z. H. Zhang
*,
Z. H. Zhang *,
X. Q. Deng,
Z. Q. Fan,
H. L. Zhang and
L. Sun
*,
X. Q. Deng,
Z. Q. Fan,
H. L. Zhang and
L. Sun
Institute of Nanomaterial and Nanostructure, Changsha University of Science & Technology, Changsha 410114, China. E-mail: guipingtang@163.com; cscuzzh@163.com
First published on 30th January 2017
Abstract
Constructing periodic nanoscale holes on graphene to form graphene nanomeshes (GNMs) is an effective way for opening band gaps. The effect of different hydrogen terminations on the structural and electronic properties in the triangular array graphene nanomeshes is investigated systematically from first-principles. The calculated results from the formation energy, Gibbs free energy, and phonon band structure reveal that the di-hydrogenated sp3 hybridization is the most favorable structure for the hole edges of GNMs except that the other hydrogen terminations may be stable under extremely-poor hydrogen conditions. The electronic properties of GNMs are very sensitive to edge hydrogen terminations, the GNM could be a semimetal, semiconductor, magnetic half-semimetal, or Bipolar Magnetic Semiconductor (BMS) by varying the edge hydrogen terminations, and the GNMs terminated by di-hydrogenation could open a sizable band gap due to the stronger on-site potential between holes, while the gap width could be tuned between semimetallic and semiconducting states by varying the neck width.
1. Introduction
As carbon nanomaterials of the two-dimensional honeycomb lattice, graphene has aroused tremendous research interests in the past decade. Graphene has a fairly simple atomic structure, a rather unique electronic structure, a high in-plane mobility of charge carrier, a long spin relaxation length and lifetime, and acts as an excellent ballistic spin transport channel.1–3 Therefore, it is predicted to be a promising material for next-generation high-performance nano-size electronic and spintronic devices, and the experimental work continues to make progress in applications.4–8 However, for pristine graphene, the semimetal nature (narrow band gap) limits its applications. Accordingly, enormous efforts have been devoted to open its band gap.9–12 For example, the approach of cutting two-dimensional graphene into a one-dimensional graphene nanoribbon (GNR) has been proven efficiently in making a sizable band gap, and substitution of doping guest element into graphene could also open the band gap by breaking the sublattice equivalence, etc. However, these approaches are faced with some critical challenges because the manipulation is very difficult in experiments.Recently, energetic investigations have been implemented on constructing periodic nanoscale holes on graphene,13–17 known as the graphene antidot lattice, that is the graphene nanomesh (GNM). GNM displays promising advantages relative to existing graphene. Some techniques have been developed to fabricate and operate such nanomesh lattices, for example, electron-beam irradiation etching,18 oxygen reactive ion etching,19 atomic force microscopy etching,20 laser shock,21 block copolymer lithography,14,22 nanoimprint lithography,23 and nanosphere lithography.24 These experimental progresses in fabricating GNM shed light on the feasibility of GNM applied in nanodevices. More recently, the GNM-based field-effect transistor with superior on/off ratio was confirmed to support nearly 100 times greater currents than individual GNR device.14 Significant results have also been achieved in the theoretical investigations on GNMs. Theoretical calculations have predicted that lattice modification by perforating would realize a transition of properties of graphene from semimetallic to semiconducting, where the opened band gap could be tuned by the size, shape, density and symmetry of the perforated hole.13,17,25–34 For instance, Pedersen et al. found a simple scaling rule for band gap with respect to the numbers of removed and original total carbon atoms in a unit cell.13 But previous theoretical works have not sufficiently considered the arrays of perforated holes in graphene, especially, another interesting issue about different terminations of the hole edges affecting the structural stability and the electronic properties of GNM has been less addressed. From the view of both fundamental and application studies, it is worthy of detailed studies for these cases.
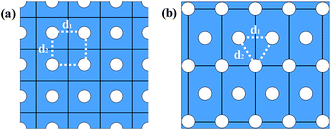
In fact, there are several array methods of holes which can ensure the all holes periodically aligned in the GNM system, the two most conventional arrays among them are the rectangular array and the triangular array as shown in Fig. 1, and the triangular array of holes is the most likely generate form of experimental techniques such as block copolymer lithography, nanoimprint lithography, and nanosphere lithography. The electronic structures of the rectangular array GNMs have investigated in the previous work.13,15,34 In the present work, based on the first principles calculations, we systematically investigate the structural and electronic properties of the triangular array GNM, in particular, the effect on properties due to the various hydrogen terminations of the hole edges. Meanwhile, we analyze in depth the fundamental mechanism for the intriguing properties. We believe that our findings can benefit further theoretical and experimental studies on the graphene-based nanostructures.
2. Models and methods
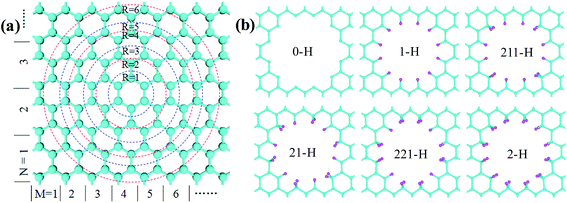
As illustrated in Fig. 1, the GNM system can be characterized by d1, d2 and r, where d1 and d2 represent the distances between neighbor nanoholes (i.e. neck widths) along the length and the other orientations, respectively, r represents the radius of nanohole. The GNM systems contain triangular arrays of hole, which all consist of the repeating rectangular unit cell shown as the area surrounded by one black rectangle in Fig. 1(b). One unit cell contains two holes (one hole plus four quarter of one hole). We only consider quasi-circle shapes of the perforated hole since it is the most conventional and realistic shape hole experimentally. Consequently, the unit cells of these GNMs can be described by the parameters M, N and R as illustrated in Fig. 2(a). Here M and N indicate the periodicities of unit cell for the graphene matrix along the zigzag and armchair edge orientations, respectively. All the above parameters can be expressed with the graphene lattice constant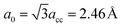 , where acc = 1.42 Å is the bond length between neighboring carbon atoms. Furthermore, there exists a well-defined relationship between the geometrical parameters of GNM and its unit cell parameters as follow:
, where acc = 1.42 Å is the bond length between neighboring carbon atoms. Furthermore, there exists a well-defined relationship between the geometrical parameters of GNM and its unit cell parameters as follow: 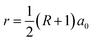 , d1 = (M − 2r)a0 = (M − R − 1)a0, and
, d1 = (M − 2r)a0 = (M − R − 1)a0, and 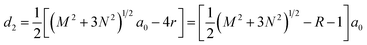 .
.
The periodically perforating holes on graphene matrix, can arise a dangling bond for each carbon atom of the hole edges. It is confirmed that the GNM with unpassivated holes edges can exist in super vacuum,35 but the dangling bonds of carbon atoms of the hole edges are easy to be saturated with various ways once the GNM is exposed to environment. For example, hydrogenation is the simplest way to realize. At an extremely-low hydrogen-concentration, the hole edges are generally terminated with one hydrogen atom per carbon atom to form a sp2-type topology, namely, mono-hydrogenation. In contrast, under a rich hydrogen-concentration, the hole edges are probably terminated with two hydrogen atoms per carbon atom, known as di-hydrogenation inducing sp3 hybridization. And there is a possible to form a mono- and di-hydrogenated composite type for a properly hydrogen-concentration. In order to address conveniently, in term of the hydrogen-concentration from a low value to a high value, we select six hydrogen terminations for the hole edge of the GNM include unpassivation, mono-hydrogenation, three mono- and di-hydrogenated composite types, and di-hydrogenation, which are denoted as 0-H, 1-H, 211-H, 21-H, 221-H, and 2-H, respectively. The corresponding structural schemes are shown in Fig. 2(b).
We consider well-fledged first-principle calculations using the density functional theory (DFT) which can provide the most detailed and accurate description of the electronic structure. According to the theory of KS (Kohn and Sham), the ground state energy is uniquely determined by the ground state electron density, density can be obtained from a single-particle picture of non-interacting electrons. The corresponding Hamiltonian for the single-particle KS orbitals ψi is expressed by the KS equations as
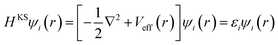 | (1) |
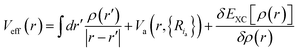 | (2) |
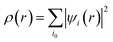 with the sum running over occupied KS orbitals. Here, Va(r,{Ria}) is the external potential due to the atoms at positions Ria. The so-called exchange–correlation term EXC(r) accounts for all many-body effects and is not known exactly, but must be appropriately approximated. Finally, the ground state energy of the interacting problem is
with the sum running over occupied KS orbitals. Here, Va(r,{Ria}) is the external potential due to the atoms at positions Ria. The so-called exchange–correlation term EXC(r) accounts for all many-body effects and is not known exactly, but must be appropriately approximated. Finally, the ground state energy of the interacting problem is
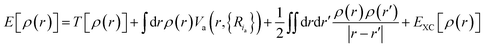 | (3) |
In this work, the geometry optimization and electronic structure are calculated by using DFT as implemented in Atomistix ToolKit (ATK). The generalized gradient approximation (GGA) and the single-zeta polarized basis set (SZP) are full used; the local density approximation (LDA) and the meta generalized gradient approximation (MGGA) are occasionally used for comparing. To examine the accuracy and completeness of the results, we have also performed calculations using spin-polarized DFT (SGGA) for the typical cases. The convergence criteria of force and energy are set to be 0.01 eV Å−1 and 1 × 10−3 eV, respectively, and the electron temperature is fixed at 300 K.
3. Results and discussion
3.1 Structural stability of GNM
We first investigate the structural stability of the GMM with different edge hydrogen terminations; the stability is normally determined by the formation energy. GNM segments in one rectangular unit cell consist of nC carbon atoms and nH hydrogen atoms. The segment formation energy per area is then calculated using:| ES = (Etotal − nCEC − nHEH)/A | (4) |
| R = 1, M = 6, N = 4 | R = 3, M = 9, N = 5 | |||||
|---|---|---|---|---|---|---|
| ρC (Å−2) | ρH (Å−2) | ES (eV Å−2) | ρC (Å−2) | ρH (Å−2) | ES (eV Å−2) | |
| 0-H | 0.3333 | 0.0000 | −3.0911 | 0.2797 | 0.0000 | −2.5459 |
| 1-H | 0.3333 | 0.0476 | −3.3940 | 0.2797 | 0.0508 | −2.8767 |
| 211-H | 0.3333 | 0.0635 | −3.4525 | 0.2797 | 0.0678 | −2.9420 |
| 21-H | 0.3333 | 0.0714 | −3.4760 | 0.2797 | 0.0763 | −2.9741 |
| 221-H | 0.3333 | 0.0794 | −3.5150 | 0.2797 | 0.0848 | −3.0018 |
| 2-H | 0.3333 | 0.0952 | −3.5792 | 0.2797 | 0.1017 | −3.0587 |
We can find the formation energies per area (ES) of both GNM segments become lower as increasing the numbers of H atoms terminated around the hole edges, and the maximum and minimum of ES occur in the case of an unpassivation (0-H) and di-hydrogenation (2-H), respectively. It indicates the unpassivated GNMs are not stable enough, the structural stabilities of GNMs are gradually enhanced with the increase of the number of terminated H atoms, and the structures are the most stable when the hole edges of GNMs are di-hydrogenated. It can be also found the ES of the former (GNM for R = 1, M = 6, N = 4) is lower than that of the latter (GNM for R = 1, M = 6, N = 4) with the same hydrogen termination. It suggests the former structure is more stable than the later, which can be understood from the later one having a smaller ρC due to the bigger perforated hole.
The above calculations are only considered at a zero-temperature ideal condition, but the formation energy per area ES can be used to determine the stability of different structures as a function of the experimental conditions, one reason is that the chemical potential of hydrogen is variable in experiment. In order to consider a molecular hydrogen gas atmosphere around the GNM edge, the relative stability is generally obtained by comparing the Gibbs free energies of systems:36,37
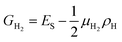 | (5) |
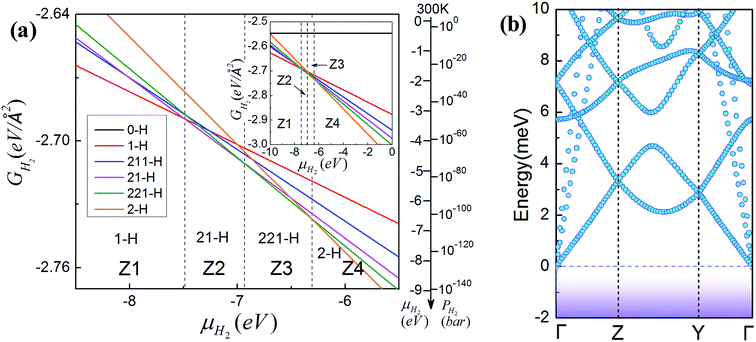 | ||
| Fig. 3 (a) Gibbs free energy GH2 versus chemical potential μH2 for GNM with different edge hydrogen terminations. The right upper inset shows a larger range. The alternative right axis shows the pressure of molecular H2 gas corresponding to the chemical potentials at T = 300 K (data adapted from ref. 36). (b) Phonon band structure of GNM terminated with di-hydrogenation for R = 1, M = 6, N = 4. It can be observed clearly that there are no negative bands. | ||
To examine the structural stability of GNM terminated with di-hydrogenation, we have calculated the phonon band structure of the typical GNM with 2-H termination for R = 1, M = 6, N = 4. The calculated phonon band structure is shown in Fig. 3(b). It can be observed clearly that there are no negative bands under the zero energy level, namely, no phonon imaginary frequencies appear. This just confirms that GNM with 2-H termination is a stable configuration. It is worth noting that there are obvious differences in the structural stability between the two-dimensional GNM and one-dimensional GNR terminated by hydrogen.36,37
3.2 Electronic properties of GNM
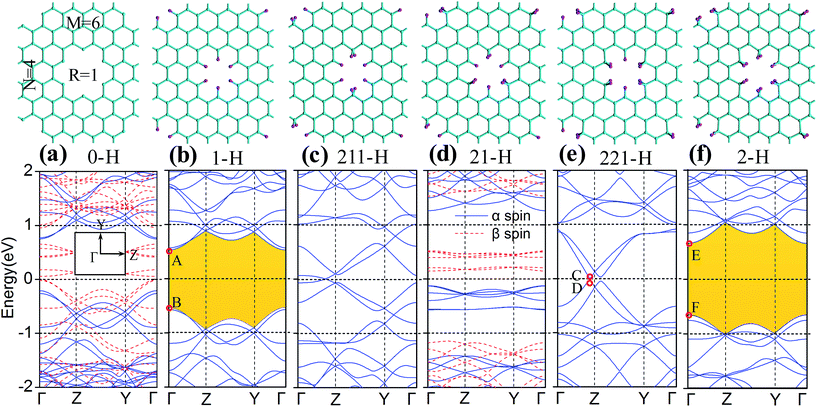
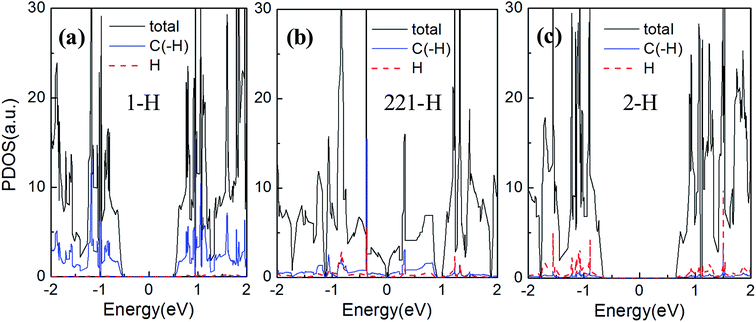
We now turn to explore the electronic properties of GNM with different edge hydrogen terminations. For the consideration of computing cost, we only select the GNM for R = 1, M = 6, and N = 4 as the prototype for detailed studies. A number of GNMs with other parameters such as R = 3, M = 9, and N = 5 have also been adopted to examine our conclusions. The calculated energy band structures are shown in Fig. 4. It is clear that the band structures of GNM are very sensitive to edge hydrogen terminations, as more complex edge terminations should result in dramatic changes of the electronic structure.38To understand the impacts of 1-H, 211-H, and 2-H terminations on electronic structures, we have calculated the Bloch states at six points of CBM and VBM (i.e. A, B, C, D, E, and F shown in Fig. 4) and the corresponding partial density of states (PDOS) as shown in Fig. 6 and 7, respectively.
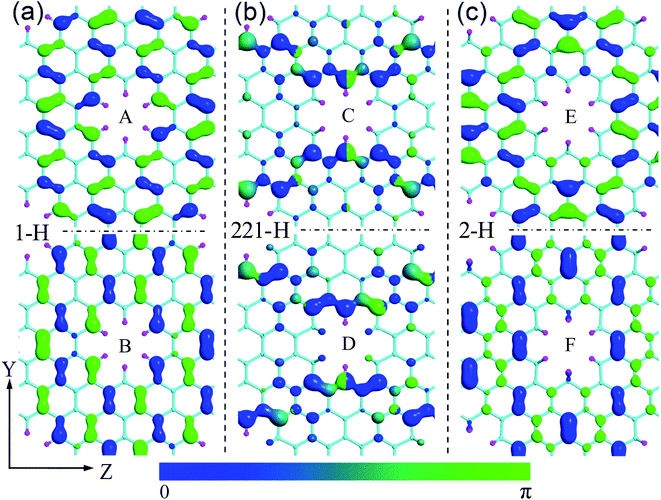 | ||
| Fig. 6 Bloch states at six points of CBM and VBM. (a)–(c) Correspond to the cases for 1-H, 221-H, and 2-H, respectively. A, B, C, D, E, and F just are the six points shown in Fig. 4. The isosurface value is fixed at 0.025 a.u. Y and Z are two coordinate axes along the armchair and zigzag lattice orientations of GNM, respectively. | ||
In Fig. 6(b), the Bloch states at both C and D are delocalized enough to form electron transmission channels along the Z axis orientation while there is no channel due to the localization of Bloch states along the Y axis orientation. As a result, the GNM for 221-H possesses a very narrow band gap along the Γ–Z direction while a wide band gap along the Γ–Y direction (cf. Fig. 4(e)). In Fig. 6(a) and (c), the Bloch states at A, B, E, and F are all localized so as to no electron transmission channel either Z or Y axis orientation, and the localization for 2-H is slightly stronger than that for 1-H, especially, near the hole edge, Bloch wave for 2-H almost disappears compared with 1-H. Consequently, the band gap of GNM with 2-H termination is slightly larger than the case for 1-H (cf. Fig. 4(b) and (f)).
In Fig. 7(a)–(c), the energy gaps, namely, the energy ranges of DOS maintaining at zero around the Fermi level, are well consistent with the band gaps in Fig. 4(b), (e) and (f), respectively. And just the DOS peak does not appears at Fermi level, but rather a narrow energy gap, so the GNM for 221-H is semi metallic rather than metallic. We can also find comparing the Fig. 7(a) and (c), the PDOS of H atoms for 2-H is a little stronger than that for 1-H as the number of H atoms for 2-H is double number for 1-H; but the PDOS of C atoms terminated by hydrogen atoms for 2-H is significantly weaker than that for 1-H. These lead to a larger energy gap for GNM with di-hydrogenation.
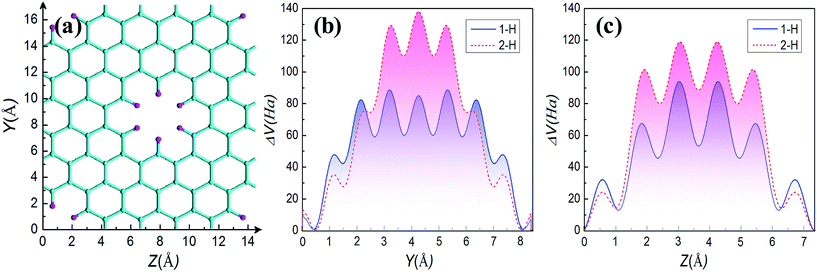
In the following, we further explore the underlying mechanisms for opening energy gap by mono- and di-hydrogenation. The introduction of periodic holes in graphene will certainly bring a perturbative on-site potential,38 causing wave functions to degenerate at the hole edge and to change the energy dispersion. Therefore, one common origin of energy gap for GNMs is the quantum-confinement effect due to the on-site potential. Furthermore, the on-site potential is very sensitive to boundary conditions such as mono- and di-hydrogenated terminations. We have calculated the on-site potential of one unit cell of GNM for R = 1, M = 6, N = 4, and have projected it on Y and Z axes for comparing. The calculated results are shown in Fig. 8. It can be clearly found the on-site potential between neighbor holes is much stronger than that of hole whether for 2-H or for 1-H, and the on-site potential between holes for 2-H is some stronger than the case for 1-H whether on Y or on Z axis, just the on-site potential exhibits gravitational interaction to electrons, which causes the electron wave functions of hole edge states to be degenerate for 1-H and 2-H, and the case for 2-H to be more degenerate than the case for 1-H (cf. Fig. 6(a) and (c)). As a consequence, the energy gap for 2-H is larger than that for 1-H (cf. Fig. 4(b), (f) and 7(a), (c)).
3.3 Energy-gap altering regularities of GNM
We finally investigate the altering regularities of the energy (band) gap of GNM. We only consider the GNM terminated with mono- and di-hydrogenation owing to their structures being stable. As stated above, the unit cell of GNM is described by three parameters: R, M, and N. For the convenience of study, we change one parameter and fix the other two parameters for the value of M, N, and R in sequence. Increasing the value of M is equivalent to increase the distance between neighboring holes along the zigzag lattice direction, and similarly, increasing the value of N is to increase the distance between neighboring holes along the armchair lattice direction. The GNMs for R = 1, 3, and 4 are chosen as examples and the calculated results are plotted in Fig. 9.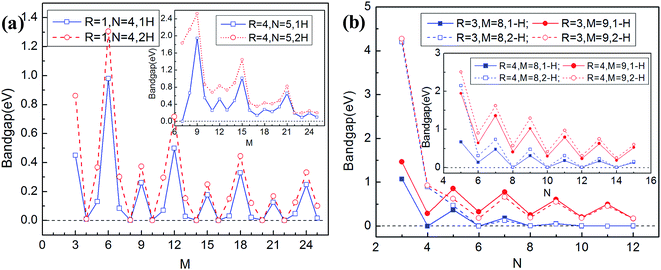 | ||
| Fig. 9 The band gap of GNM terminated with mono- (solid line) and di-hydrogenation (dashed line) as a function of structural parameter M, N and R. | ||
As can be seen from Fig. 9(a) and (b), for the GNMs terminated with mono- or di-hydrogenation, the band gap displays an oscillatory decrease with the increasing parameter M by a periodicity of 6 at the fixed R and N, this is different from the oscillation periodicity of 3 for the rectangular array GNM;34 the necessary condition is not a sufficient condition to generate a maximal band gap is M = 3p (p is a positive integer). It suggests that varying M would lead to a variation between semimetallic and semiconducting behaviors. This case demonstrates that the periodicity along the zigzag edge orientation of GNM also plays crucial role in band gap opening, in addition to the quantum-confinement. And it can be found that if the parameter M and R remain unchanged while only change parameter N, the band gap displays an odd–even oscillatory effect, the band gaps for N = odd are the tops of the oscillation plotlines while the cases for N = even are the bottoms. It can be also noted that the band gap decrease to a steady nonzero value gradually with the increasing parameter N while M = 3p, but it drop to zero rapidly with the increasing parameter N while M ≠ 3p. Furthermore, for a specific perforated hole, the bigger the unit cell size is, the smaller the band gap would be, as the bigger unit cell size corresponds to the wider neck width and the lower hole density correspondingly. In short, the band gap could be opened in the GNM with size M = 3p, and it could be tuned by varying the neck width or edge terminations. This is greatly useful for the experimental investigations. In addition, it is worth noting that the band gap of the triangular array GNM is not proportional to the size of hole similar to the rectangular array GNM.
4. Conclusions
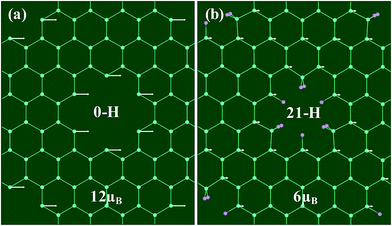
Based on the first-principles method, we systematically investigate the effect of different hydrogen terminations on the structural and electronic properties in the triangular array graphene nanomeshes. We firstly calculated the formation energy ES under zero-temperature ideal condition and the Gibbs free energy GH2 under room-temperature general condition, respectively. The both calculated results reveal that the di-hydrogenated (2-H) sp3 hybridization is the most favorable structure for the hole edges of GNM except that the other hydrogen terminations may be stable under extremely-poor hydrogen conditions. And the GNM with 2-H termination is a stable configuration which is confirmed by the calculated phonon band structure. Then we focus on the effect on electronic properties due to the various hydrogen terminations and the related fundamental mechanism. We find that the electronic structures of GNM are very sensitive to edge hydrogen terminations. The unpassivated GNM is a magnetic half-semimetal, the dangling bonds of hole edge could introduce the magnetic moment which causes the spin degeneracy to be eliminated. By a proper 21-H termination, the GNM is possible to be turned into a Bipolar Magnetic Semiconductor (BMS), which may be of great use in the next generation of information storage, the corresponding energy bands are also split due to the sublattice imbalance. For the other terminations such as mono- and di-hydrogenation, the GNM is non magnetic due to no dangling bonds and the balance of sublattice. We further find that the necessary condition of opening a sizable band gap is structure parameter M = 3p no matter whether the mono- or di-hydrogenation, and di-hydrogenation could brings a larger gap than mono-hydrogenation owing to the stronger on-site potential between holes induced by di-hydrogenation. Furthermore, the gap width could be tuned between semimetallic and semiconducting states by varying the neck width. In short, our present work has solved an outstanding problem on how to properly pattern graphene to induce band gap, our findings could benefit further theoretical and experimental studies on the graphene-based nanostructures.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 61371065 and 11674039), the Hunan Provincial Natural Science Foundation of China (Grant No. 2015JJ2009, 2015JJ2013, and 2015JJ3002), the Scientific Research Fund of Hunan Provincial Education Department (Grant No. 14A013 and 15A004), the Construct Program of the Key Discipline in Hunan Province, and the Aid Program for Science and Technology Innovative Research Team in Higher Educational Institutions of Hunan Province.References
- A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109–154 CrossRef CAS.
- W. Han and R. K. Kawakami, Phys. Rev. Lett., 2011, 107, 047207 CrossRef PubMed.
- T. Nikolaos, J. Csaba, P. Mihaita, T. J. Harry and B. J. V. Wees, Nature, 2007, 448, 571–574 CrossRef PubMed.
- A. K. Geim, Science, 2009, 324, 1530–1534 CrossRef CAS PubMed.
- K. S. Kim, Y. Zhao, H. Jang, S. Y. Lee, J. M. Kim and K. S. Kim, et al., Nature, 2009, 457, 706–710 CrossRef CAS PubMed.
- O. V. Yazyev and S. G. Louie, Nat. Mater., 2010, 9, 806–809 CrossRef CAS PubMed.
- Z. Zheng, C. Zhao, S. Lu, Y. Chen, Y. Li, H. Zhang and S. Wen, Opt. Express, 2012, 20, 23201–23214 CrossRef CAS PubMed.
- H. Zhang, Q. Bao, D. Tang, L. Zhao and K. Loh, Appl. Phys. Lett., 2009, 95, 141103 CrossRef.
- B. Richard, J. Bjarke, N. Louis, A. Mie, R. Emile and B. Marco, et al., Nat. Mater., 2010, 9, 315–319 CrossRef PubMed.
- L. Ci, Z. Xu, L. Wang, W. Gao, F. Ding and K. F. Kelly, et al., Nano Res., 2008, 1, 116–122 CrossRef CAS.
- P. Marco, R. Stefano, M. S. Polina, V. Sergio, E. Markus and P. Daniela, et al., ACS Nano, 2012, 6, 199–204 CrossRef PubMed.
- M. Weinberg, C. Staarmann, C. Ölschläger, J. Simone and K. Sengstock, 2D Mater., 2016, 3, 024005 CrossRef.
- T. G. Pedersen, C. Flindt, J. Pedersen, N. A. Mortensen, A. P. Jauho and K. Pedersen, Phys. Rev. Lett., 2008, 100, 136804 CrossRef PubMed.
- J. Bai, X. Zhong, S. Jiang, Y. Huang and X. Duane, Nat. Nanotechnol., 2010, 5, 190–194 CrossRef CAS PubMed.
- W. Liu, Z. F. Wang, Q. W. Shi, J. Yang and F. Liu, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 233405 CrossRef.
- X. Ji, J. Zhang, Y. Wang, H. Qian and Z. Yu, Nanoscale, 2013, 5, 2527–2531 RSC.
- R. Petersen, T. G. Pedersen and A. P. Jauho, ACS Nano, 2011, 5, 523–529 CrossRef CAS PubMed.
- M. D. Fischbein and M. Drndic, Appl. Phys. Lett., 2008, 93, 113107 CrossRef.
- L. Z. Liu, S. B. Tian, Y. Z. Long, W. X. Li, H. F. Yang and J. J. Li, et al., Vacuum, 2014, 105, 21–25 CrossRef CAS.
- Y. Zhang, Y. Gao, L. Q. Liu, N. Xi, Y. C. Wang and L. P. Ma, et al., Appl. Phys. Lett., 2012, 101, 213101 CrossRef.
- J. Li, R. J. Zhang, H. Q. Jiang and G. J. Cheng, Nanotechnology, 2011, 22, 475303–475309 CrossRef CAS PubMed.
- S. Rasappa, J. M. Caridad, L. Schulte, A. Caglianl, D. Borah and M. A. Momis, et al., RSC Adv., 2015, 5, 66711–66717 RSC.
- X. Liang, Y. S. Jung, S. Wu, A. Ismach, D. L. Olynick and S. Cabrini, et al., Nano Lett., 2010, 10, 2454–2460 CrossRef CAS PubMed.
- L. Liu, Y. L. Zhang, W. L. Wang, C. Z. Gu, X. D. Bai and E. G. Wang, Adv. Mater., 2011, 23, 1246–1251 CrossRef CAS PubMed.
- F. Ouyang, S. Peng, Z. Yang, Y. Chen, H. Zou and X. Xiong, Phys. Chem. Chem. Phys., 2014, 16, 20524–20531 RSC.
- H. Şahin and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 035452 CrossRef.
- S. K. Singh, M. N. Amal and F. M. Peeters, J. Chem. Phys., 2014, 140, 074304 CrossRef PubMed.
- D. M. Chen, P. M. Shenai and Y. Zhao, Phys. Chem. Chem. Phys., 2011, 13, 1515–1520 RSC.
- M. Dvorak, W. Oswald and Z. Wu, Sci. Rep., 2013, 3, 2289 Search PubMed.
- R. Petersen and T. G. Pedersen, J. Phys.: Condens. Matter, 2015, 27, 225502 CrossRef PubMed.
- W. Oswald and Z. Wu, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 115431 CrossRef.
- G. P. Tang, Z. H. Zhang, X. Q. Deng, Z. Q. Fan and H. L. Zhu, Phys. Chem. Chem. Phys., 2015, 17, 638–643 RSC.
- J. Lee, A. K. Roy, J. L. Wohlwend, V. Varshney, J. B. Ferguson and W. C. Mitchel, et al., Appl. Phys. Lett., 2013, 102, 203107 CrossRef.
- G. P. Tang, Z. H. Zhang, X. Q. Deng, Z. Q. Fan, Y. C. Zeng and J. C. Zhou, Carbon, 2014, 76, 348–356 CrossRef CAS.
- K. He, G. D. Lee, A. W. Robertson, E. Yoon and J. H. Warner, Nat. Commun., 2014, 5, 3040 Search PubMed.
- T. Wassmann, A. P. Seitsonen, A. M. Saitta, M. Lazzeri and F. Mauri, Phys. Rev. Lett., 2008, 101, 096402 CrossRef PubMed.
- P. Wagner, V. V. Ivanovskaya, M. Melle-Franco, B. Humbert, J.-J. Adjizian and P. R. Briddon, et al., Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 094106 CrossRef.
- O. V. Yazyev, Acc. Chem. Res., 2013, 46, 2319–2328 CrossRef CAS PubMed.
- E. H. Lieb, Phys. Rev. Lett., 1989, 62, 1201 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2017 |